Effect of Volumetric Flow Rate on Heat Transfer Characteristics of Single-Fractured Rock with Different Surface Morphology and External Temperature
Abstract
1. Introduction
2. Theoretical Background
2.1. Governing Equations
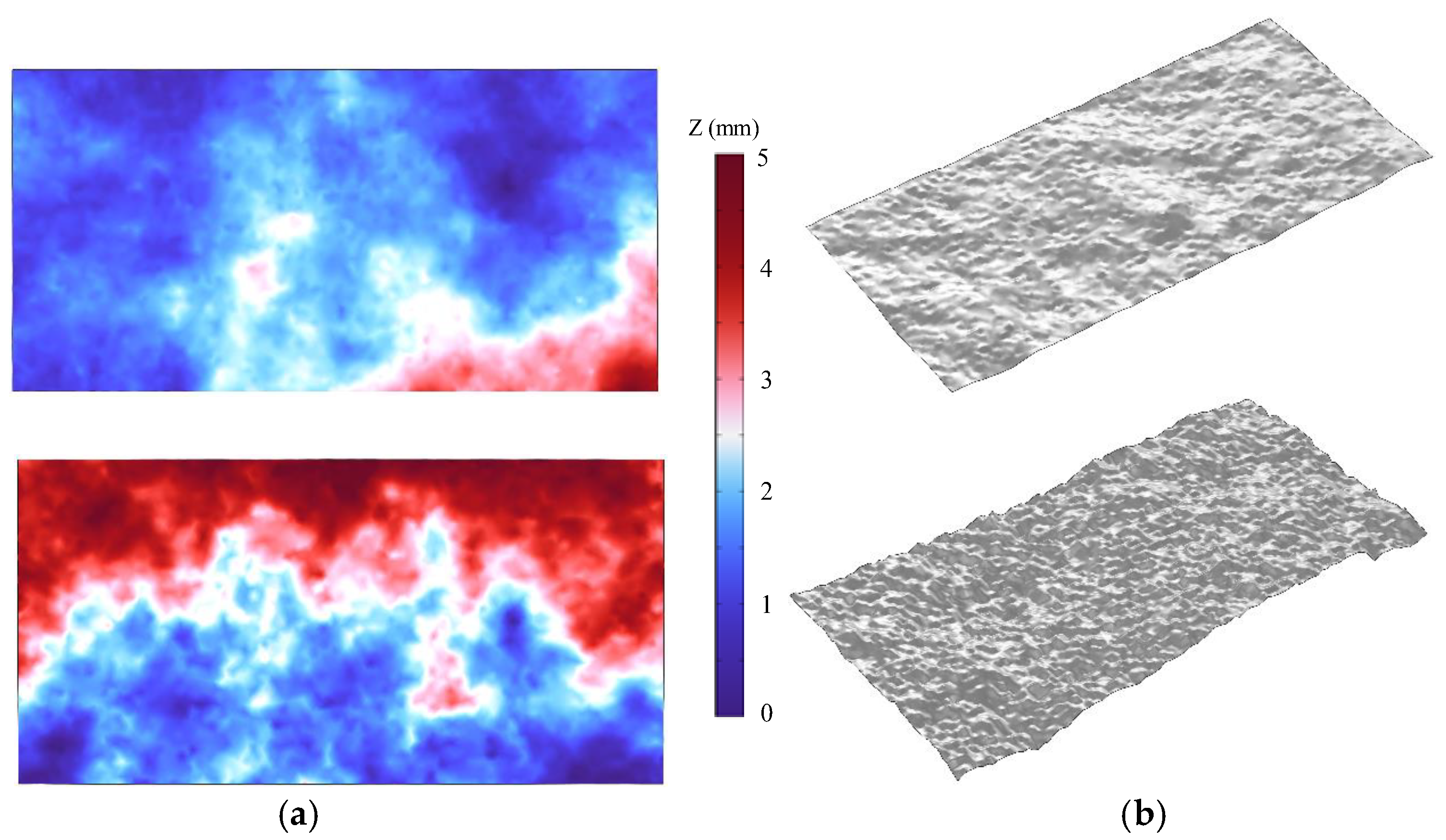
2.2. Generation of Rough Fracture Surface
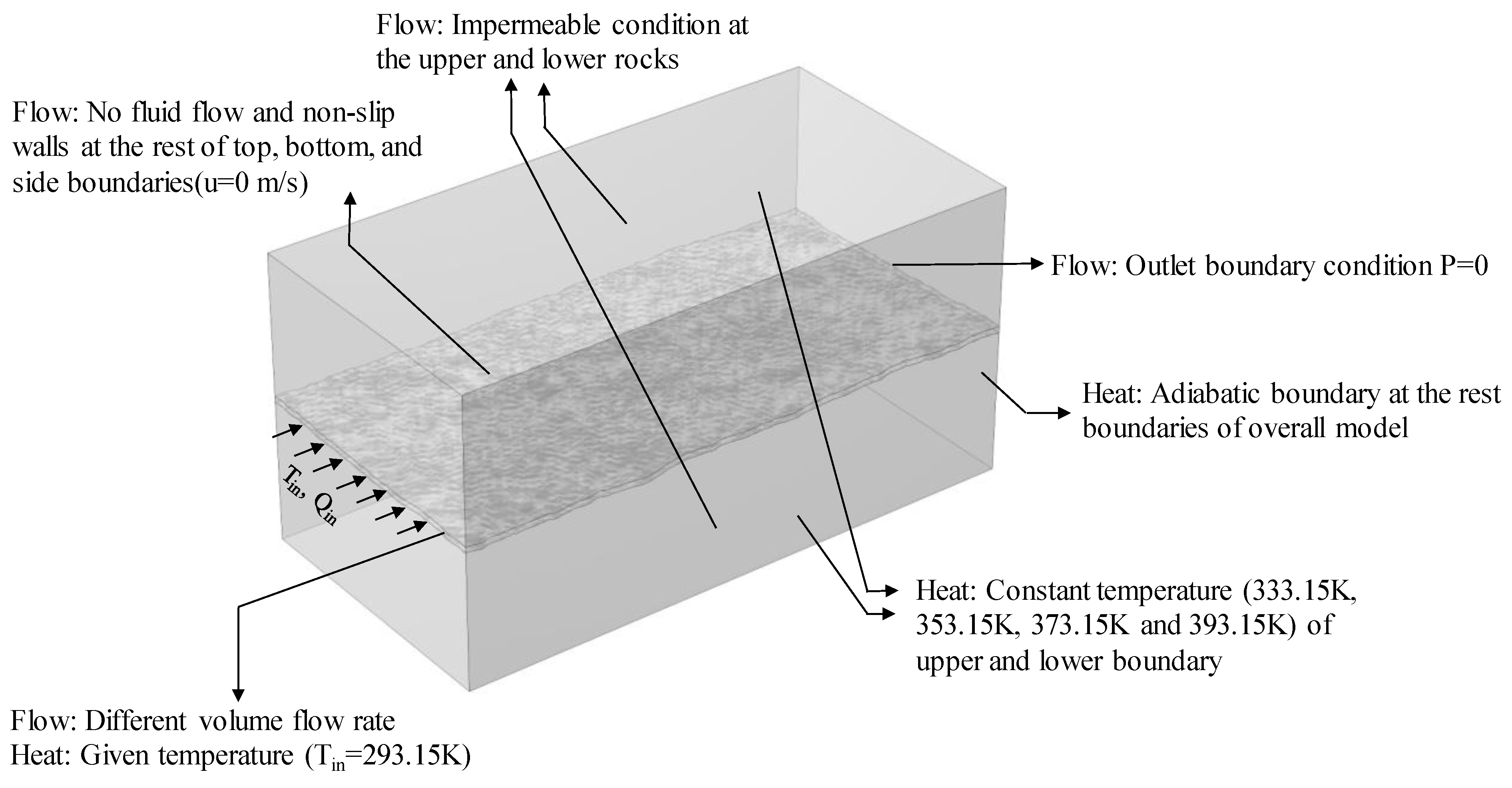
3. Numerical Modeling and Simulation
4. Results
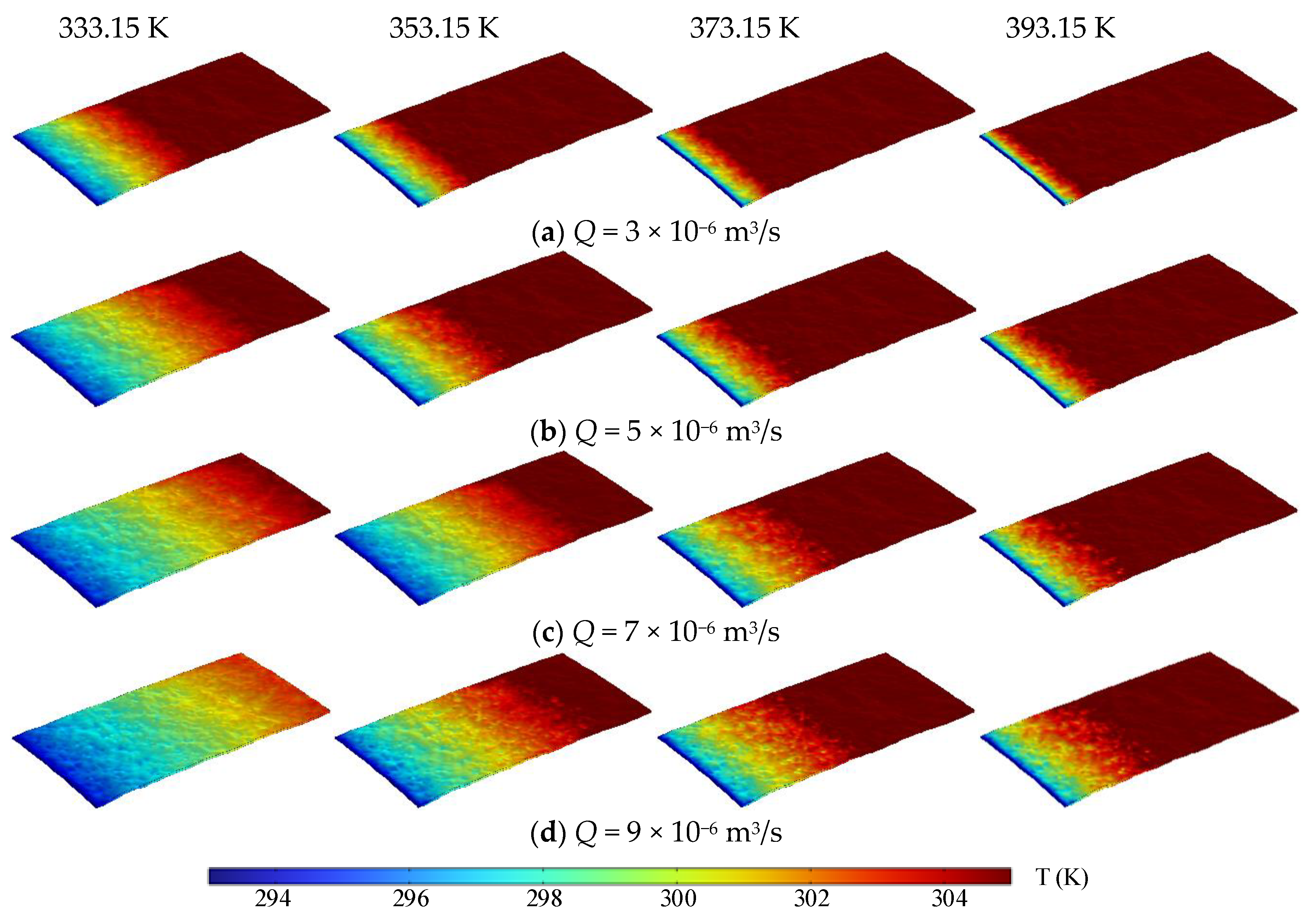
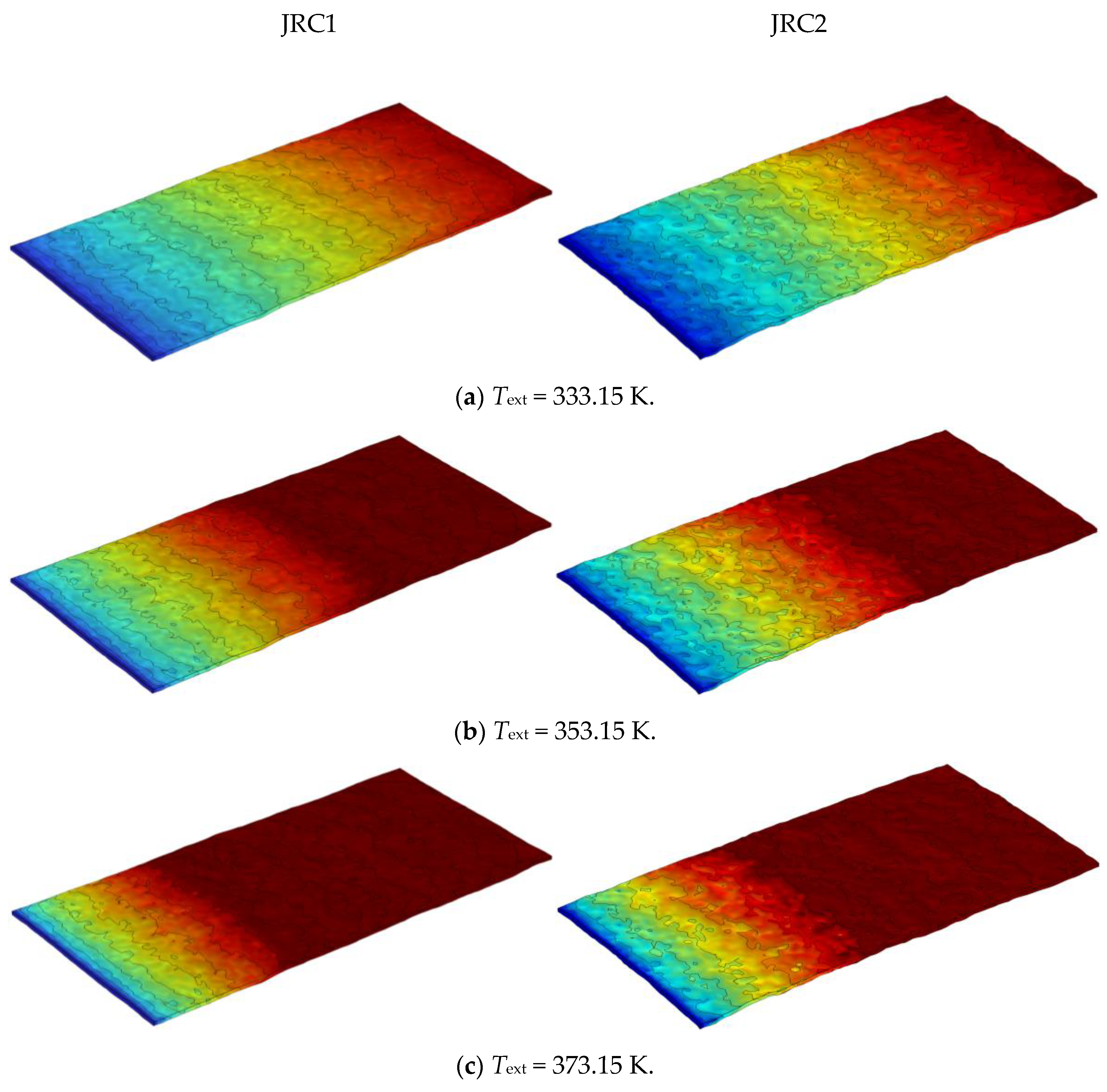
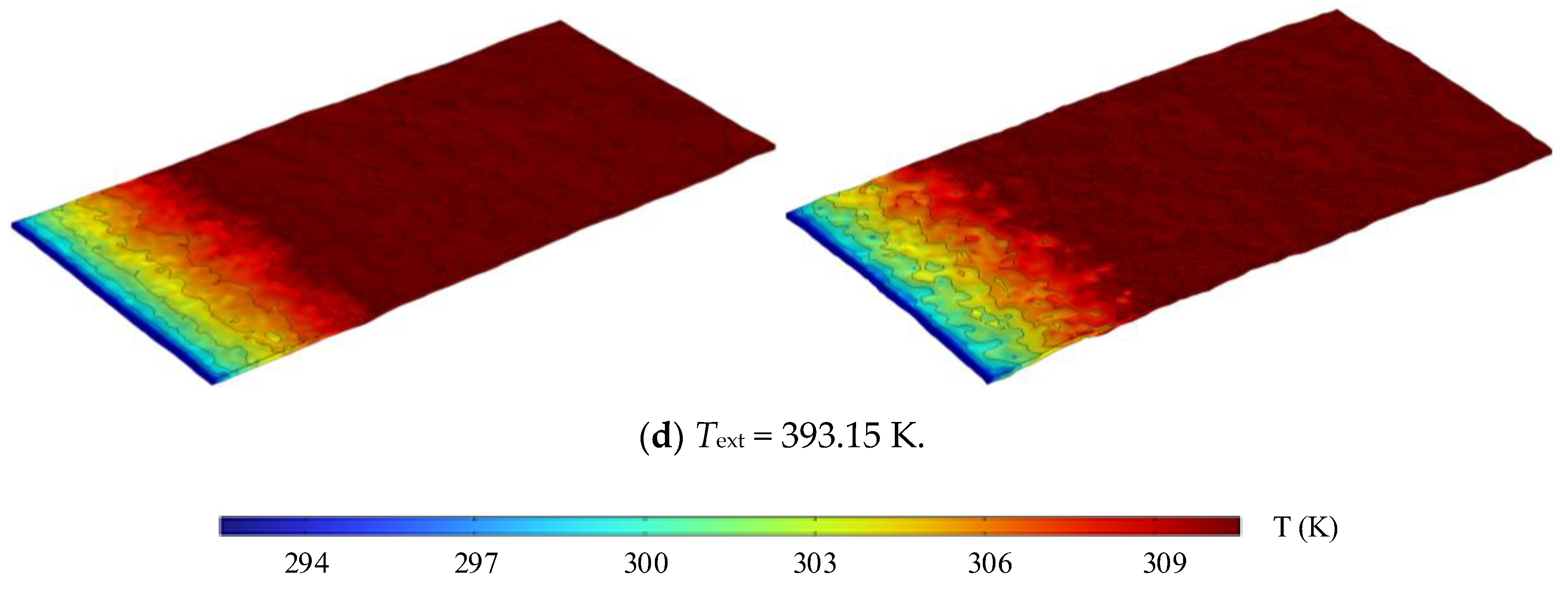
4.1. Comparison of Temperature Field
4.2. Temperature of Outlet Water
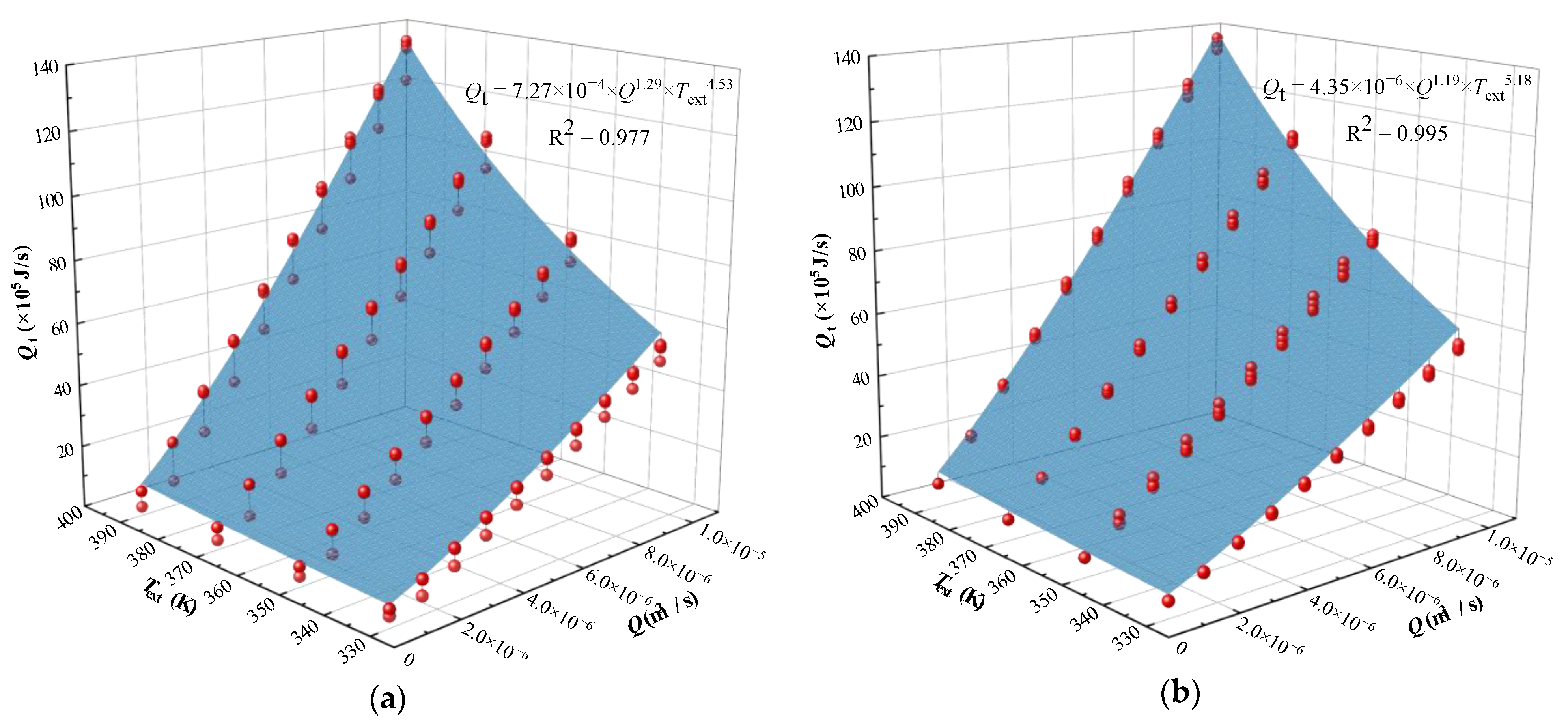
4.3. Energy Extraction Efficiency
4.4. Heat Transfer Coefficient
5. Conclusions
- The results indicate that water flow velocity exerts the most significant influence on heat transfer, followed by fracture surface morphology and rock surface temperature. An increase in flow rate markedly enhances heat transfer and boosts total heat extraction within a certain range. Higher volumetric flow rates exacerbate temperature non-uniformity, resulting in a larger temperature differential that improves heat transfer efficiency. Therefore, in the design of geothermal extraction projects, it is essential to carefully select fluid parameters according to actual conditions to ensure optimal heat extraction efficiency;
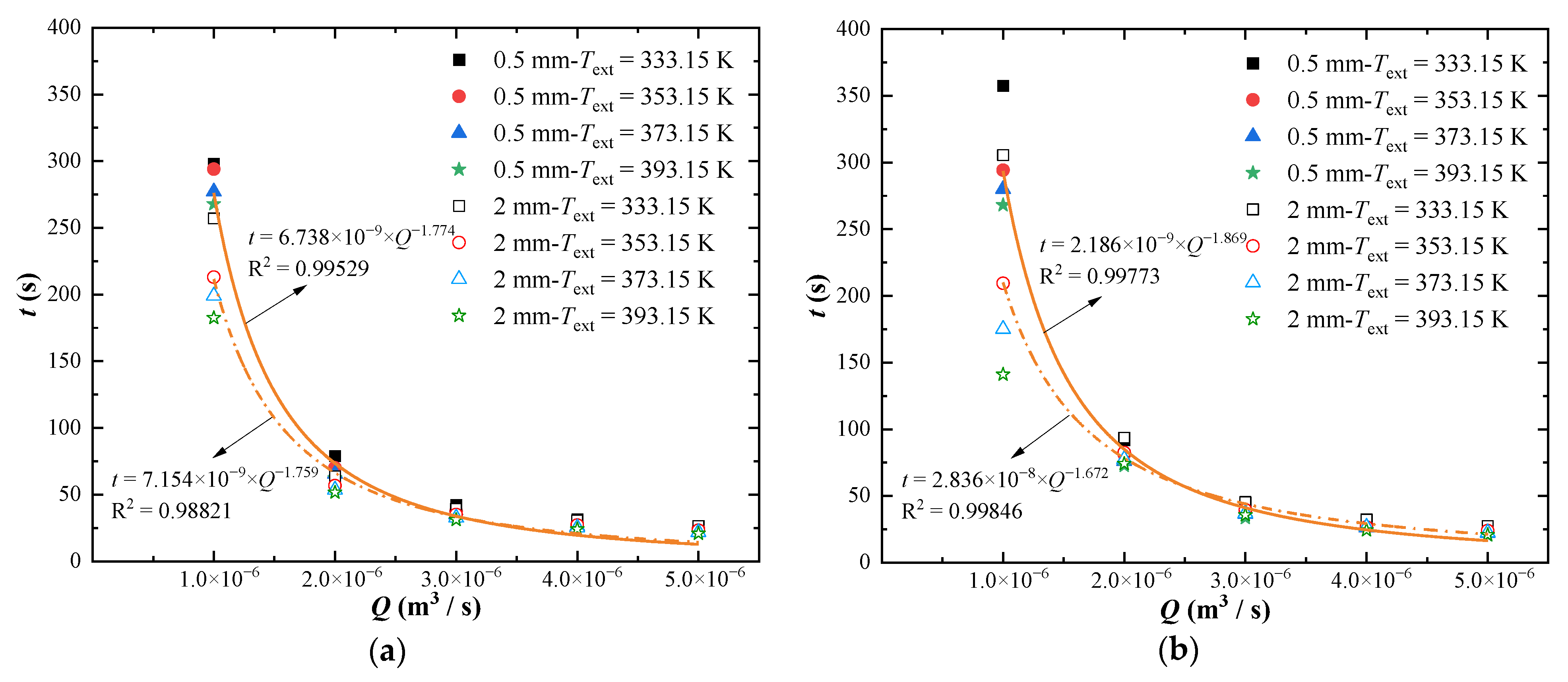
- Surface roughness has a substantial impact on temperature distribution, leading to heterogeneous thermal profiles, especially in narrower fractures where water–rock heat exchange is enhanced. This highlights the critical role of fracture morphology in heat transfer characteristics. Furthermore, the roughness of fracture surfaces facilitates a decrease in temperature, resulting in lower outlet temperatures. This phenomenon is attributed to the longer flow paths and the increased heat transfer area caused by the surface irregularities;
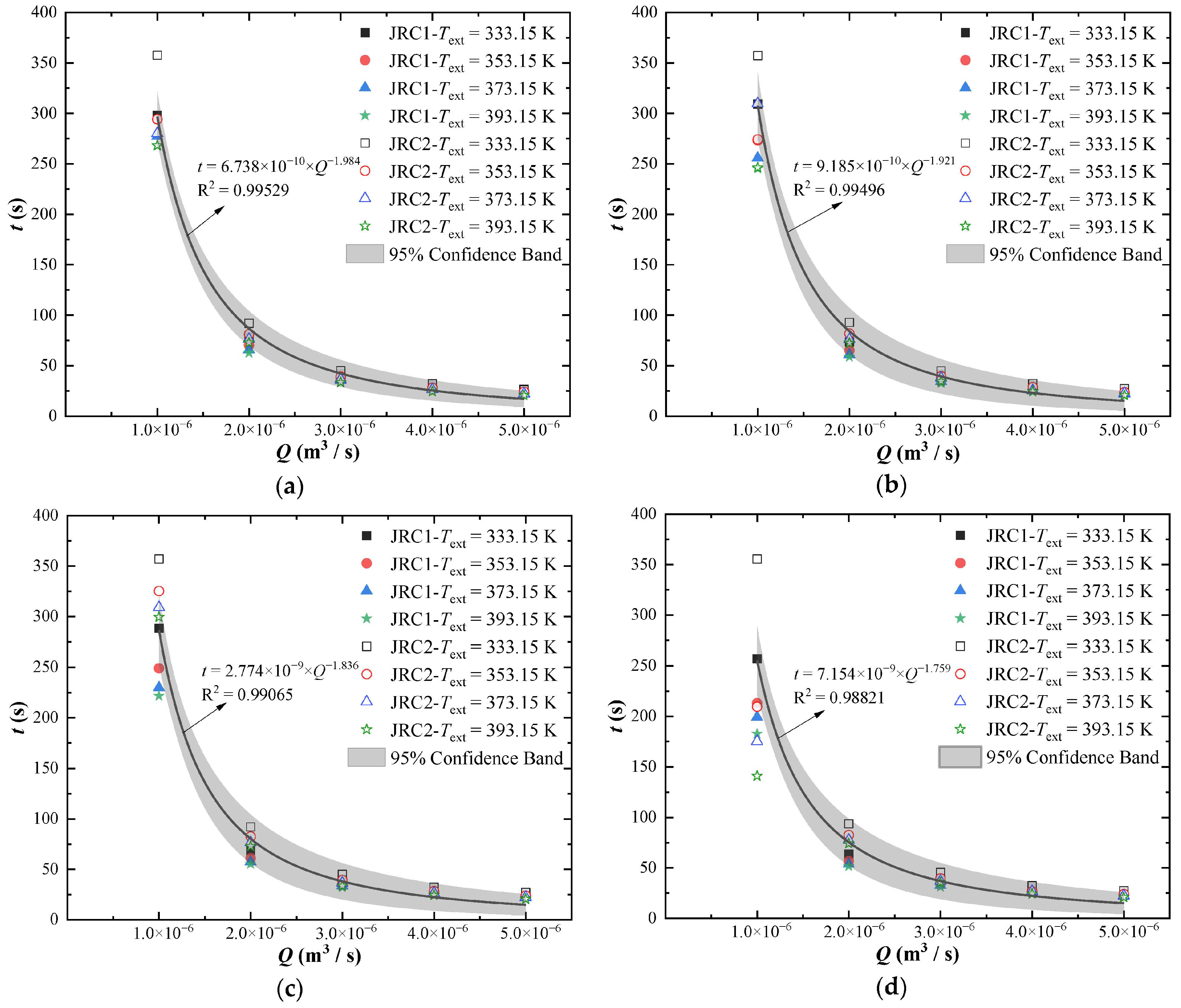
- The timing of thermal breakthrough is significantly influenced by several factors. Higher external temperatures and flow rates result in faster thermal breakthroughs by reducing thermal resistance and enhancing convective heat transfer. By optimizing injection rates, the lifespan of the reservoir can be prolonged by preventing premature thermal breakthroughs. Furthermore, the relationship between surface roughness and thermal breakthrough time is intricate; increased roughness in smaller apertures tends to prolong breakthrough times, whereas in larger apertures, it can yield the opposite effect.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fridleifsson, I.B. Geothermal energy for the benefit of the people. Renew. Sustain. Energy Rev. 2001, 5, 299–312. [Google Scholar] [CrossRef]
- Lund, J.W.; Freeston, D.H. World-wide direct uses of geothermal energy. Geothermics 2001, 30, 29–68. [Google Scholar] [CrossRef]
- Lu, W.; Xiang, Y. Experiments and sensitivity analyses for heat transfer in a meter-scale regularly fractured granite model with water flow. J. Zhejiang Univ. SCIENCE A 2012, 13, 958–968. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, L.; Zhang, F.; Jiang, P. A review on heat transfer and energy conversion in the enhanced geothermal systems with water/CO2 as working fluid. Int. J. Energy Res. 2015, 39, 1722–1741. [Google Scholar] [CrossRef]
- Shaik, A.R.; Rahman, S.S.; Tran, N.H.; Tran, T. Numerical simulation of Fluid-Rock coupling heat transfer in naturally fractured geothermal system. Appl. Therm. Eng. 2011, 31, 1600–1606. [Google Scholar] [CrossRef]
- Abbasi, M.; Mansouri, M.; Daryasafar, A.; Sharifi, M. Analytical model for heat transfer between vertical fractures in fractured geothermal reservoirs during water injection. Renew. Energy 2019, 130, 73–86. [Google Scholar] [CrossRef]
- Zhao, Z. On the heat transfer coefficient between rock fracture walls and flowing fluid. Comput. Geotech. 2014, 59, 105–111. [Google Scholar] [CrossRef]
- Li, Z.W.; Feng, X.T.; Zhang, Y.J.; Zhang, C.; Xu, T.F.; Wang, Y.S. Experimental research on the convection heat transfer characteristics of distilled water in manmade smooth and rough rock fractures. Energy 2017, 133, 206–218. [Google Scholar] [CrossRef]
- Kamali-Asl, A.; Ghazanfari, E.; Perdrial, N.; Bredice, N. Experimental study of fracture response in granite specimens subjected to hydrothermal conditions relevant for enhanced geothermal systems. Geothermics 2018, 72, 205–224. [Google Scholar] [CrossRef]
- Luo, J.; Luo, J.; Zhu, Y.; Guo, Q.; Tan, L.; Zhuang, Y.; Liu, M.; Zhang, C.; Xiang, W.; Rohn, J. Experimental investigation of the hydraulic and heat-transfer properties of artificially fractured granite. Sci. Rep. 2017, 7, 39882. [Google Scholar] [CrossRef]
- Huang, F.; Yao, C.; Zhang, X.; Wu, L.; Shao, Y.; Zhou, C. Effects of fracture parameters and roughness on heat-flow coupling in rock masses with two-dimensional fracture networks. Energy Sci. Eng. 2021, 9, 1216–1231. [Google Scholar] [CrossRef]
- Klepikova, M.; Méheust, Y.; Roques, C.; Linde, N. Heat transport by flow through rough rock fractures: A numerical investigation. Adv. Water Resour. 2021, 156, 104042. [Google Scholar] [CrossRef]
- Luo, S.; Zhao, Z.; Peng, H.; Pu, H. The role of fracture surface roughness in macroscopic fluid flow and heat transfer in fractured rocks. Int. J. Rock Mech. Min. Sci. 2016, 87, 29–38. [Google Scholar] [CrossRef]
- Luo, Y.; Xu, W.; Lei, Y.; Wu, P.; Qin, G.; Ba, R. Experimental study of heat transfer by water flowing through smooth and rough rock fractures. Energy Rep. 2019, 5, 1025–1029. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y.; Hu, Z.; Yu, Z.; Huang, Y.; Zhang, C. Experimental study of the heat transfer by water in rough fractures and the effect of fracture surface roughness on the heat transfer characteristics. Geothermics 2019, 81, 235–242. [Google Scholar] [CrossRef]
- Zhao, J. Experimental study of flow-rock heat transfer in rock fractures. Chin. J. Rock Mech. Eng. 1999, 18, 119–123. [Google Scholar]
- Zhao, J.; Tso, C.P. Heat transfer by water flow in rock fractures and the application to hot dry rock geothermal systems. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 6. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y.; Yu, Z.; Huang, Y.; Zhang, C. Heat transfer by water flowing through rough fractures and distribution of local heat transfer coefficient along the flow direction. Int. J. Heat Mass Transf. 2018, 119, 139–147. [Google Scholar] [CrossRef]
- Bai, B.; He, Y.; Li, X.; Li, J.; Huang, X.; Zhu, J. Experimental and analytical study of the overall heat transfer coefficient of water flowing through a single fracture in a granite core. Appl. Therm. Eng. 2017, 116, 79–90. [Google Scholar] [CrossRef]
- Bai, B.; He, Y.; Li, X.; Hu, S.; Huang, X.; Li, J.; Zhu, J. Local heat transfer characteristics of water flowing through a single fracture within a cylindrical granite specimen. Environ. Earth Sci. 2016, 75, 1460. [Google Scholar] [CrossRef]
- He, Y.; Bai, B.; Hu, S.; Li, X. Effects of surface roughness on the heat transfer characteristics of water flow through a single granite fracture. Comput. Geotech. 2016, 80, 312–321. [Google Scholar] [CrossRef]
- He, Y.; Bai, B.; Li, X. Comparative Investigation on the Heat Transfer Characteristics of Gaseous CO2 and Gaseous Water Flowing Through a Single Granite Fracture. Int. J. Thermophys. 2017, 38, 170. [Google Scholar] [CrossRef]
- Zhang, B.; Qu, Z.; Guo, T.; Wang, J.; Zhang, Y.; Hao, T. Study on heat transfer characteristics and global sensitivity analysis of a rough single fracture. Prog. Geophys. 2022, 37, 1520–1527. [Google Scholar]
- Caulk, R.A.; Ghazanfari, E.; Perdrial, J.N.; Perdrial, N. Experimental investigation of fracture aperture and permeability change within Enhanced Geothermal Systems. Geothermics 2016, 62, 12–21. [Google Scholar] [CrossRef]
- Shu, B.; Zhu, R.; Elsworth, D.; Dick, J.; Liu, S.; Tan, J.; Zhang, S. Effect of temperature and confining pressure on the evolution of hydraulic and heat transfer properties of geothermal fracture in granite. Appl. Energy 2020, 272, 115290. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, P.; Wang, Z.; Xu, R. Convective heat transfer of supercritical CO2 in a rock fracture for enhanced geothermal systems. Appl. Therm. Eng. 2017, 115, 923–936. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, G.; Wang, H. Heat extraction mechanism in a geothermal reservoir with rough-walled fracture networks. Int. J. Heat Mass Transf. 2018, 126, 1083–1093. [Google Scholar] [CrossRef]
- Yao, C.; Shao, Y.; Yang, J.; Huang, F.; He, C.; Jiang, Q.; Zhou, C. Effects of non-darcy flow on heat-flow coupling process in complex fractured rock masses. J. Nat. Gas Sci. Eng. 2020, 83, 103536. [Google Scholar] [CrossRef]
- Mohais, R.; Xu, C.; Dowd, P.A. Fluid Flow Through Branched Channels in a Fracture Plane in an Enhanced Geothermal System. ASME International Mechanical Engineering Congress and Exposition. Am. Soc. Mech. Eng. 2012, 45226, 1687–1691. [Google Scholar]
- Frank, S.; Heinze, T.; Pollak, S.; Wohnlich, S. Transient heat transfer processes in a single rock fracture at high flow rates. Geothermics 2021, 89, 101989. [Google Scholar] [CrossRef]
- Jiang, P.; Zhang, L.; Xu, R. Experimental study of convective heat transfer of carbon dioxide at supercritical pressures in a horizontal rock fracture and its application to enhanced geothermal systems. Appl. Therm. Eng. 2017, 117, 39–49. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, J.; Li, J.; Bai, B.; Zhang, G. Fluid friction and heat transfer through a single rough fracture in granitic rock under confining pressure. Int. Commun. Heat Mass Transf. 2016, 75, 78–85. [Google Scholar] [CrossRef]
- Luo, J.; Qi, Y.; Zhao, Q.; Tan, L.; Xiang, W.; Rohn, J. Investigation of Flow and Heat Transfer Characteristics in Fractured Granite. Energies 2018, 11, 1228. [Google Scholar] [CrossRef]
- Asai, P.; Panja, P.; McLennan, J.; Deo, M. Effect of different flow schemes on heat recovery from Enhanced Geothermal Systems (EGS). Energy 2019, 175, 667–676. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Madadi, M.; Sahimi, M. Lattice Boltzmann simulation of fluid flow in fracture networks with rough, self-affine surfaces. Phys. Rev. E 2003, 67, 026309. [Google Scholar] [CrossRef]
- Voss, R.F. Random Fractal Forgeries. In Fundamental Algorithms for Computer Graphics; Springer: Berlin/Heidelberg, Germany, 1991; pp. 805–835. [Google Scholar]
- Molz, F.J.; Liu, H.H.; Szulga, J. Fractional Brownian motion and fractional Gaussian noise in subsurface hydrology: A review, presentation of fundamental properties, and extensions. Water Resour. Res. 1997, 33, 2273–2286. [Google Scholar] [CrossRef]
- Ye, Z.; Liu, H.-H.; Jiang, Q.; Zhou, C. Two-phase flow properties of a horizontal fracture: The effect of aperture distribution. Adv. Water Resour. 2015, 76, 43–54. [Google Scholar] [CrossRef]
- Family, F.; Vicsek, T. Dynamics of Fractal Surfaces; World Scientific: Singapore, 1991. [Google Scholar]
- Wang, M.; Chen, Y.; Ma, G.; Zhou, J.; Zhou, C. Influence of surface roughness on nonlinear flow behaviors in 3D self-affine rough fractures: Lattice Boltzmann simulations. Adv. Water Resour. 2016, 96, 373–388. [Google Scholar] [CrossRef]
- Liu, H.; Bodvarsson, G.; Lu, S.; Molz, F. A Corrected and Generalized Successive Random Additions Algorithm for Simulating Fractional Levy Motions. Math. Geol. 2004, 36, 361–378. [Google Scholar] [CrossRef]
- Tse, R.; Cruden, D.M. Estimating joint roughness coefficients. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 303–307. [Google Scholar] [CrossRef]
- Ungemach, P.; Antics, M.; Lalos, P.; Borozdina, O.; Foulquier, L.; Papachristou, M. Geomodelling and well architecture, key issues to sustainable reservoir development. In Proceedings of the 36th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 31 January–2 February 2011. [Google Scholar]
- Huang, Y.; Zhang, Y.; Gao, X.; Ma, Y.; Hu, Z. Experimental and numerical investigation of seepage and heat transfer in rough single fracture for thermal reservoir. Geothermics 2021, 95, 102163. [Google Scholar] [CrossRef]
- Shiozawa, S.; McClure, M. EGS designs with horizontal wells, multiple stages, and proppant. In Proceedings of the 39th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 24–26 February 2014. [Google Scholar]
- Griffin, K.P.; Fu, L.; Moin, P. General method for determining the boundary layer thickness in nonequilibrium flows. Phys. Rev. Fluids 2021, 6, 024608. [Google Scholar] [CrossRef]
- Eckert, E.R.; Drake, R.M., Jr. Analysis of Heat and Mass Transfer; Hemisphere Publishing Corporation: Washington, DC, USA, 1987. [Google Scholar]
- Kays, W.M.; Crawford, M.E.; Weigand, B. Convective Heat and Mass Transfer; McGraw-Hill: New York, NY, USA, 1980; Volume 4. [Google Scholar]







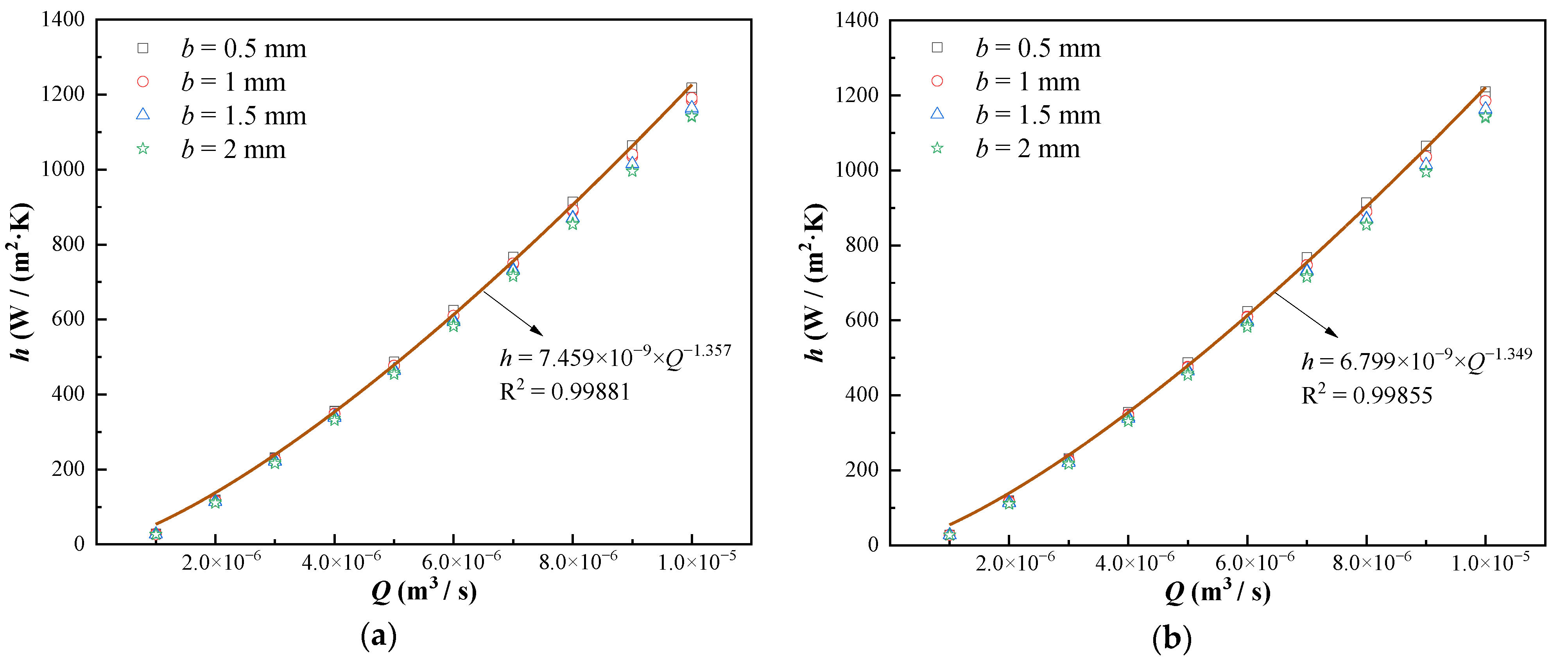

| Parameter | K (W/m·K) | ρ (kg/m3) | Cp (J/kg·K) |
|---|---|---|---|
| rock | 3.5 | 2200 | 880 |
| fluid | 0.662 | 1000 | 4200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, Y.; Huang, N.; Jiang, Y. Effect of Volumetric Flow Rate on Heat Transfer Characteristics of Single-Fractured Rock with Different Surface Morphology and External Temperature. Processes 2024, 12, 2821. https://doi.org/10.3390/pr12122821
Zhuang Y, Huang N, Jiang Y. Effect of Volumetric Flow Rate on Heat Transfer Characteristics of Single-Fractured Rock with Different Surface Morphology and External Temperature. Processes. 2024; 12(12):2821. https://doi.org/10.3390/pr12122821
Chicago/Turabian StyleZhuang, Ying, Na Huang, and Yujing Jiang. 2024. "Effect of Volumetric Flow Rate on Heat Transfer Characteristics of Single-Fractured Rock with Different Surface Morphology and External Temperature" Processes 12, no. 12: 2821. https://doi.org/10.3390/pr12122821
APA StyleZhuang, Y., Huang, N., & Jiang, Y. (2024). Effect of Volumetric Flow Rate on Heat Transfer Characteristics of Single-Fractured Rock with Different Surface Morphology and External Temperature. Processes, 12(12), 2821. https://doi.org/10.3390/pr12122821








