An Investigation into the Creep Characteristics of Nylon Strings Used in Badminton Rackets

Abstract

In order to improve the hitting performance of badminton rackets, the creep characteristics of their nylon string were explored based on the Maxwell and Kelvin models. Special attention was given to the instantaneous elastic deformation coefficient, the delayed elastic deformation coefficient and the retardation time under different conditions. Based on the experimental results, models with high accuracy were developed for nylon, which can describe the changes in the creep rate at different times, relative humidities and stress levels. They all showed that the creep rate increases rapidly with time and then gradually becomes flat. The highest relative humidity led to the lowest instantaneous elastic deformation coefficient and delayed elastic deformation coefficient, but the highest retardation time for nylon. Finally, as the stress level increased, the instantaneous elastic deformation coefficient, delayed elastic deformation coefficient and retardation time all increased. Thus, to improve the hitting performance of badminton rackets, it is necessary to pay attention to the tension and the air humidity in the environment during use.

1. Introduction

With the public’s growing awareness of health, sports have become an indispensable part of people’s cultural lives [1]. Badminton is an indoor sport, which is favored by the public [2] because it not only improves the function of the lungs but also promotes metabolism [3]. According to the statistics of the International Badminton Association, the number of people who take part in badminton is second only to running. In badminton, the impact force acting on a racket ranges from 5 to 50 N. The mechanical performance of badminton strings, especially their creep behavior, is key to determining their hitting effect and stability [4]. Creep is a common mechanical phenomenon in which the strain of a material increases continuously over time while maintaining a constant stress state, meaning that the magnitude and direction of the stress acting on the material remain unchanged for a period of time [5]. At present, the most common badminton string on the market is made of nylon (polyamide, PA), and its structure is divided into a core, an outer layer and coating from the inside to the outside [6]. The mechanical properties of nylon depend on several factors, such as the magnitude of the load, time duration and environmental conditions such as humidity and temperature [7,8].

Recently, the Maxwell [9,10] and Kelvin [11,12] models have been widely used to explore changes in the creep of different materials, which exhibit both elastic and viscous behavior. The Maxwell model consists of a spring and a dashpot (representing viscous behavior) connected in series. This model is used to describe materials that exhibit both instantaneous elastic response and time-dependent viscous flow [13]. The Kelvin model consists of a spring and a dashpot connected in parallel. This model describes materials that deform instantaneously, like a spring under applied stress, but that also exhibit time-dependent viscous behavior [14].

A number of studies have been conducted to explore the creep behavior of nylon-based polymeric materials. Wang et al. conducted a study into the viscoelastic behavior of nylon 66 fibers under a range of creep stress levels. The optimal processing condition was identified at an applied stress of 460 MPa, which yielded the greatest performance of recovery force [15]. Mandlekar et al. investigated the influence of time and temperature on the creep and stress relaxation properties of synthetic fabrics, including nylon 6,6, employing the time–temperature superposition principle [16]. The creep experiment revealed that the initial modulus, glass transition temperature and crystallinity of the fiber had a significant impact on the creep and stress relaxation behavior of the fabrics. This can be elucidated by the Burgers viscoelastic model and the Weibull distribution equation model. Similarly, Mahdavipour et al. examined how the long-term creep response of industrial nylon 6,6 and polyethylene terephthalate (PET) filaments varies in a range of isothermal conditions [17]. The results demonstrated that nylon consistently displays a higher short-term creep strain than PET by about 5–10%. Habeger et al. investigated the influence of humidity cycling parameters on the moisture-accelerated creep of polymeric fibers [18]. They proposed that the observation of fiber-accelerated creep under proper cycling is consistent with the moisture-gradient-driven stress concentration explanation. It is unclear why the degree of accelerated creep in nylon 66 is relatively low. Furthermore, Bell et al. investigated the impact of water on the nanoindentation creep response of nylon 6 [19]. The dimensionless creep parameter exhibited a notable reduction in water. Chevali et al. investigated the flexural creep behavior of nylon 66 and polypropylene-based long-fiber thermoplastic (LFT) compounds in response to ultraviolet illumination and moisture absorption [20]. The creep compliance of nylon 6 LFT exhibited a gradual decline with an increase in UV exposure. The results of the moisture absorption experiments indicated that minimal variations were observed in comparison to the dry/unexposed specimens. As shown by the above literature review, the creep behavior of nylon 6 has been extensively studied. However, there is a lack of systematic research on the combined effects of external environmental humidity and stretching rate, which is one of the primary issues affecting the durability of badminton strings in aggressive service conditions. Previous research has mainly focused on the effect of humidity below 50% on the creep characteristics of nylon. There are few reports investigating the effect of high humidity on creep characteristics, such as the instantaneous elastic deformation coefficient, delayed elastic deformation coefficient and retardation time.

To this end, the creep characteristics of nylon strings used in badminton rackets were investigated at different conditions of relative humidity (30–90%) and stress (20–60%), and special attention was given to the instantaneous elastic deformation coefficient, delayed elastic deformation coefficient and retardation time. This work aims to improve the application of nylon in badminton rackets.

2. Materials and Methods

This work focused on the nylon strings widely used in commercial standard badminton rackets, as shown in Figure 1. The structure of the nylon string consists of three layers, namely, the core, the sheath and the coating. The core is the central part of the badminton string and is composed of multiple nylon filaments. The sheath is a layer of woven material that wraps around the core and is usually made of thicker nylon filaments woven together. The coating is the outermost layer of the string and is the part that directly contacts the shuttlecock. The nylon string in this study was made of polyamide high-molecular-weight polymers. The raw materials were put into an extruder to form threads with a melting temperature of 260 °C, and then the extruded threads were stretched in order to shape them. The tensile creep test was conducted by using an electro-mechanical universal testing machine (UTM4204X, Shanghai Sansi Zongheng Machinery Manufacturing Co., Ltd., Shanghai, China) with the CB/T 1040.2-2006 standard [21]. The tensile strength and maximum strain were measured using the uniaxial tensile test before creep measurement. An acting force of 2 N and a running speed of 1 mm/min were set as entrance conditions, and 20 mm/min was set as the running speed for experimental testing. The processing parameters of relative humidity and stress levels were also investigated. The stress level was measured as the different percentages of tensile strength (618 MPa). The detailed testing parameters are given in

Table 1. Tensile creep test design.

No.	Relative Humidity	Stress Level
1	30%	20%
2	30%	40%
3	30%	60%
4	60%	20%
5	60%	40%
6	60%	60%
7	90%	60%
8	90%	60%
9	90%	60%

. The tensile stress was maintained for 3600 s, and the tensile strain results were obtained at different combinations of processing parameters.

Nylon string is a viscoelastic material; it possesses both viscosity and elasticity. The creep deformation of nylon typically consists of three parts: (1) instantaneous elastic deformation, which occurs instantly and can be modeled using a stiff spring; (2) delayed elastic deformation, which changes over time and can be simulated using a spring and a damper in parallel; (3) viscous flow due to polymer interactions, which results from the mutual sliding of polymer chains and can be modeled using a damper. The total deformation is the sum of these three deformations. Therefore, these three components are connected in series to form a four-element model by combining the Maxwell model and the Kelvin model, known as the Burgers model (Figure 2). This can be used to describe the viscoelasticity under short-term stress of nylon string [22]. Its constitutive equation is listed as Equation (1) [23]:

$$\epsilon =\sigma \left[{\displaystyle \frac{1}{E_{\mathrm{e}}}}+{\displaystyle \frac{1}{E_{\mathrm{d}}}}\left(1-e^{-{\displaystyle \frac{E_{\mathrm{d}}}{{\eta }_2}}t}\right)+{\displaystyle \frac{t}{{\eta }_1}}\right],$$

(1)

where E_e is the instantaneous elastic deformation coefficient of the Maxwell model, E_d represents the delayed elastic deformation coefficient of the Kelvin model in N/mm, η₁ is the viscosity coefficient of the Maxwell model, η₂ stands for the viscosity coefficient of the Kelvin model in N·min/mm, ε is the strain, σ represents the loading stress in Pa, and t is the loading time in min. Then, Equation (2) can be obtained based on Equation (1), which can reflect viscoelastic characteristics [24].

$$Y(\mathrm{t})=A+B\left[1-\exp (-Ct)\right]+Dt,$$

(2)

where Y(t) is the mathematical function of tensile deformation, t is the creep time, and A = σ/E_e, B = σ/E_d, C = E_d/η₂ and D = σ/η₁, which are the undetermined coefficients. A and D reflect elastic deformation and viscous deformation, while B and C reflect viscoelastic deformation. Based on Equation (2), retardation time τ in mm can be obtained as shown in Equation (3).

$$\tau ={\displaystyle \frac{{\eta }_1}{E_{\mathrm{e}}}}$$

(3)

3. Results

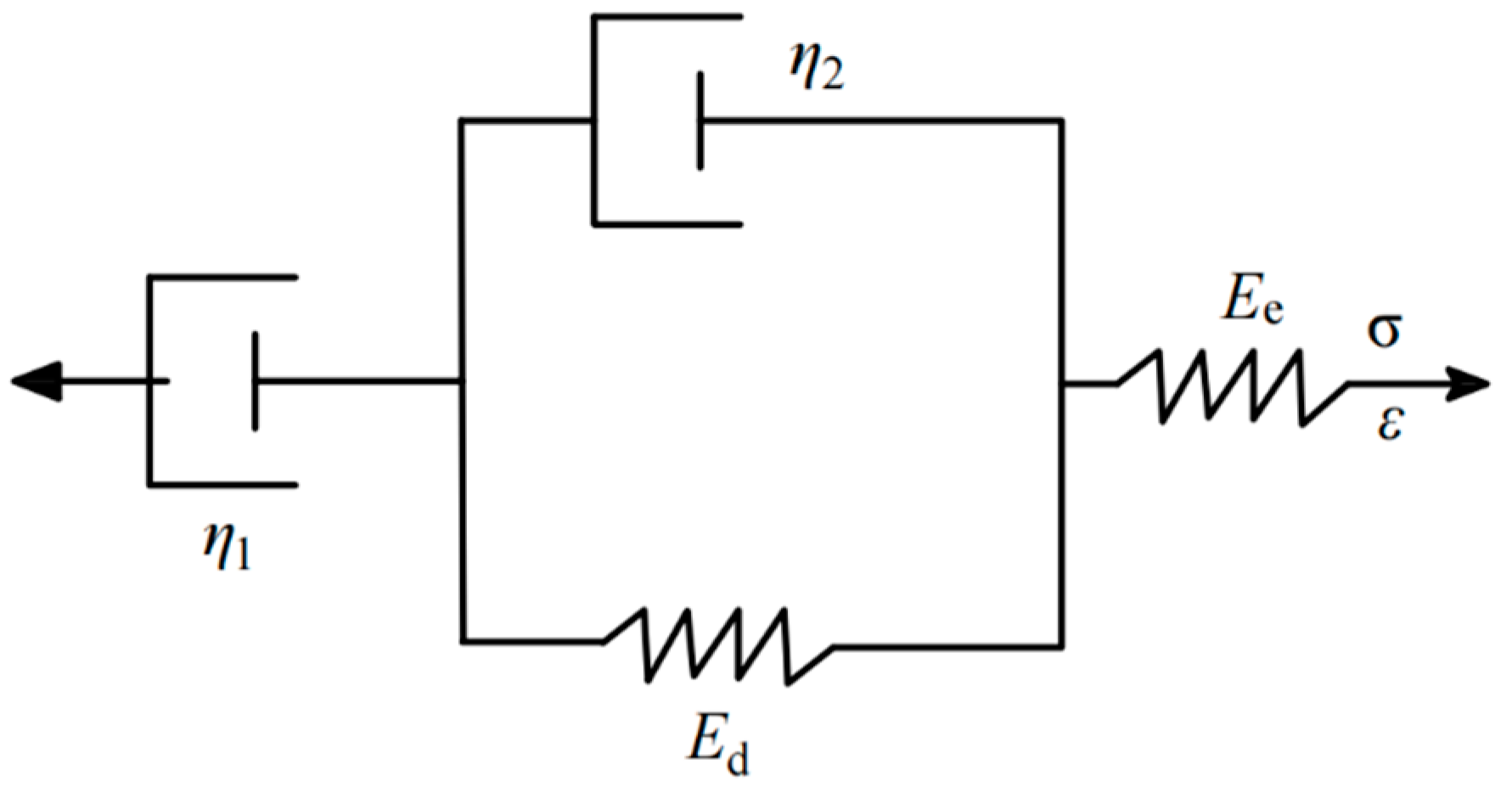
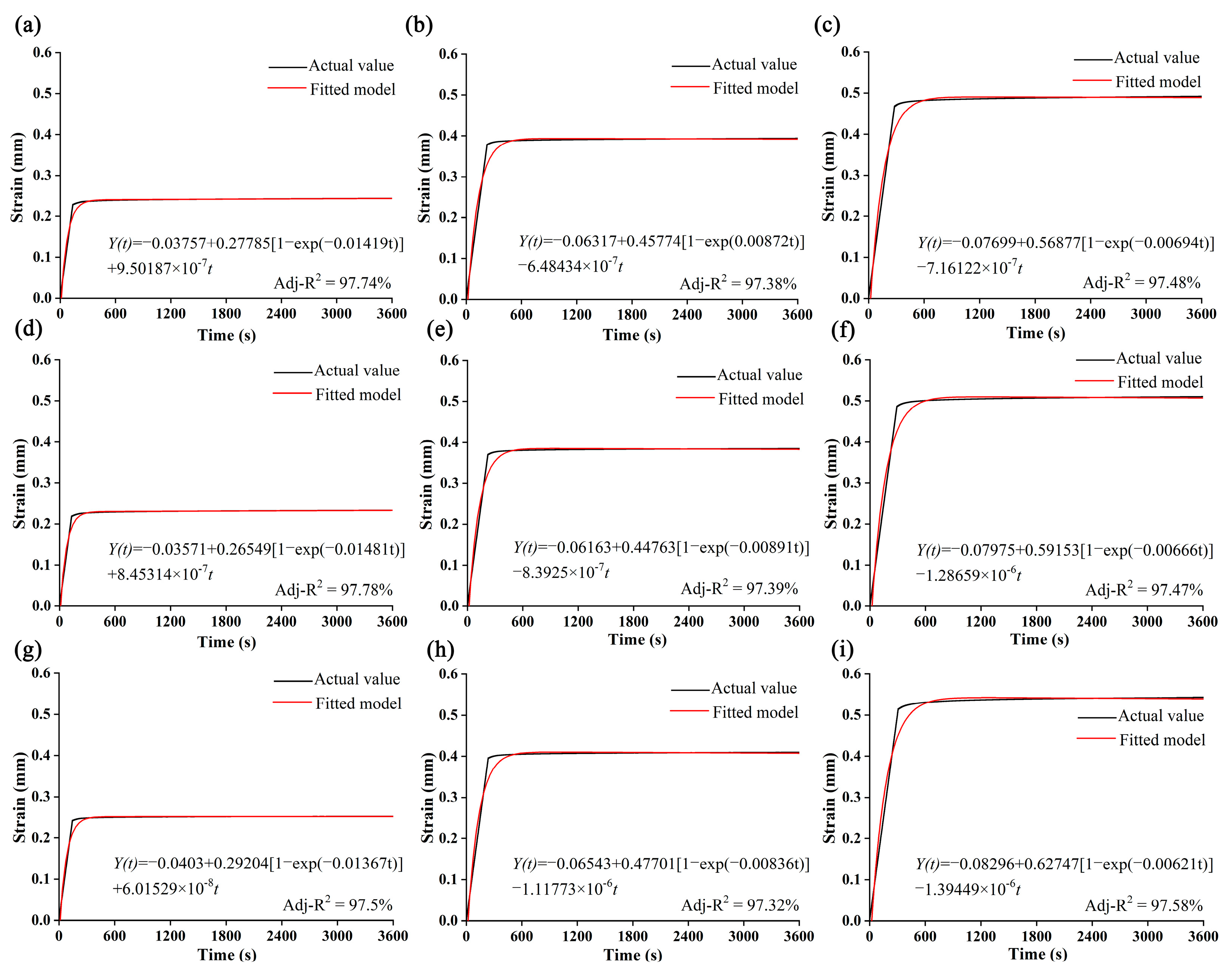
3.1. Creep Model

Figure 3 shows the changes in the creep of nylon strings at different conditions of time, relative humidity and stress. The strain curve reflects the characteristics of the initial creep stage and the constant velocity creep stage; i.e., the strain increased rapidly with time and then gradually became flat. The fitted values were also found to be very close to the actual values. The Adj-R² values of all the developed models are higher than 95%; they have high precision [25], which means that the models can fully simulate the short-term creep behavior of nylon string [26].

3.2. The Effect of Processing Conditions on the Instantaneous Elastic Deformation Coefficient of Nylon Strings

Within the elastic range, E_e reflects the deformation resistance of the nylon thread under tension. Specifically, it reflects the material’s ability to respond elastically to external forces instantly, without any time delay. In other words, when a force is applied to the material, it deforms immediately, and this deformation is fully reversible. As shown in Figure 4, nylon had the highest E_e at a relative humidity of 60%, while a relative humidity of 90% led to the lowest E_e. Humidity is a key factor that influences the instantaneous elastic deformation coefficient of nylon, primarily due to its hygroscopic nature. Nylon, being a polar polymer, can absorb moisture from the environment. When it takes in water, the hydrogen bonds between its molecular chains are partially disrupted by the water molecules, leading to increased chain mobility, which in turn affects the material’s mechanical properties. Specifically, under high humidity, water molecules penetrate nylon’s molecular structure, weakening the intermolecular forces, making the material softer and more prone to deformation. However, a continuous increase in relative humidity resulted in the lowest E_e. Nylon’s hygroscopic nature causes alterations in its molecular structure, weakening the original interactions between its molecular chains. This reduction in intermolecular forces allows the chains to slide more easily under external forces, thereby decreasing the material’s stiffness and its ability to recover elastically. In general, with an increase in relative humidity, E_e first increased and then decreased.

E_e decreased with an increase in stress level at all the different relative humidities. Nylon, as a polymer material, exhibits nonlinear mechanical behavior under high stress conditions. At low stress levels, the material typically remains in the elastic region, where the relationship between elastic deformation and stress is relatively linear, resulting in a higher instantaneous elastic deformation coefficient. However, as the stress increases, the material gradually enters a nonlinear deformation zone, and the elastic modulus decreases, leading to a reduction in the elastic deformation coefficient. Additionally, with rising stress levels, the molecular structure and crystallites within the material may experience increased friction and energy dissipation. This internal friction and hysteresis reduce the material’s ability to resist external forces under high stress as effectively as it does under low stress, weakening its capacity for elastic deformation. Thus, the higher stress level led to a lower E_e value.

3.3. The Effect of Processing Conditions on the Delayed Elastic Deformation Coefficient of Nylon Strings

E_d is the delayed elastic deformation coefficient, also known as the creep deformation coefficient. It describes the amount of elastic deformation a material retains after the external force is removed. This deformation occurs while the force is applied, but the material does not recover immediately, instead gradually returning to its original state over time. The higher the value of E_d, the greater the material’s ability to deform under prolonged stress. As shown in Figure 5, nylon had the highest E_d at a relative humidity of 60%, while a relative humidity of 90% resulted in the lowest E_d. This phenomenon is closely related to the molecular structure of nylon and its ability to absorb water molecules. Nylon, being a polyamide, has a polar molecular structure, which gives it a strong affinity for moisture. When the environmental humidity increases, nylon absorbs water. This occurs because the amide groups (-CONH-) in nylon molecules can form hydrogen bonds with water molecules. Once absorbed, the water molecules infiltrate between the molecular chains of the nylon, partially disrupting the hydrogen bonds and making the chains more mobile. Consequently, in the initial stages of humidity increase, the water molecules enhance the mobility of nylon’s molecular chains, resulting in an increase in the delayed elastic deformation coefficient. However, as humidity continues to rise and the nylon reaches a saturation point, the absorbed water reaches a maximum level. At this stage, the excess water molecules act as “lubricants” between the molecular chains, further weakening the hydrogen bonds. This leads to greater disruption of the internal structure of the molecular chains, reducing the material’s elastic recovery and causing the delayed elastic deformation coefficient to start decreasing.

Meanwhile, E_d showed a decreasing trend with an increase in stress level at three different relative humidities. At low stress levels, the molecular chains in nylon experience weaker interactions, allowing them to move more freely under applied force, which results in a higher capacity for viscoelastic deformation. However, as the stress level increases, the movement of these molecular segments becomes more restricted, and some chains are pulled tighter, reducing their mobility and, consequently, the viscoelastic deformation coefficient. Additionally, under higher stress levels, the molecular chains of nylon tend to align in the direction of the stress. This alignment makes it more difficult for the chains to slide past each other, reducing the material’s fluidity and thus diminishing its viscoelastic deformation under elevated stress.

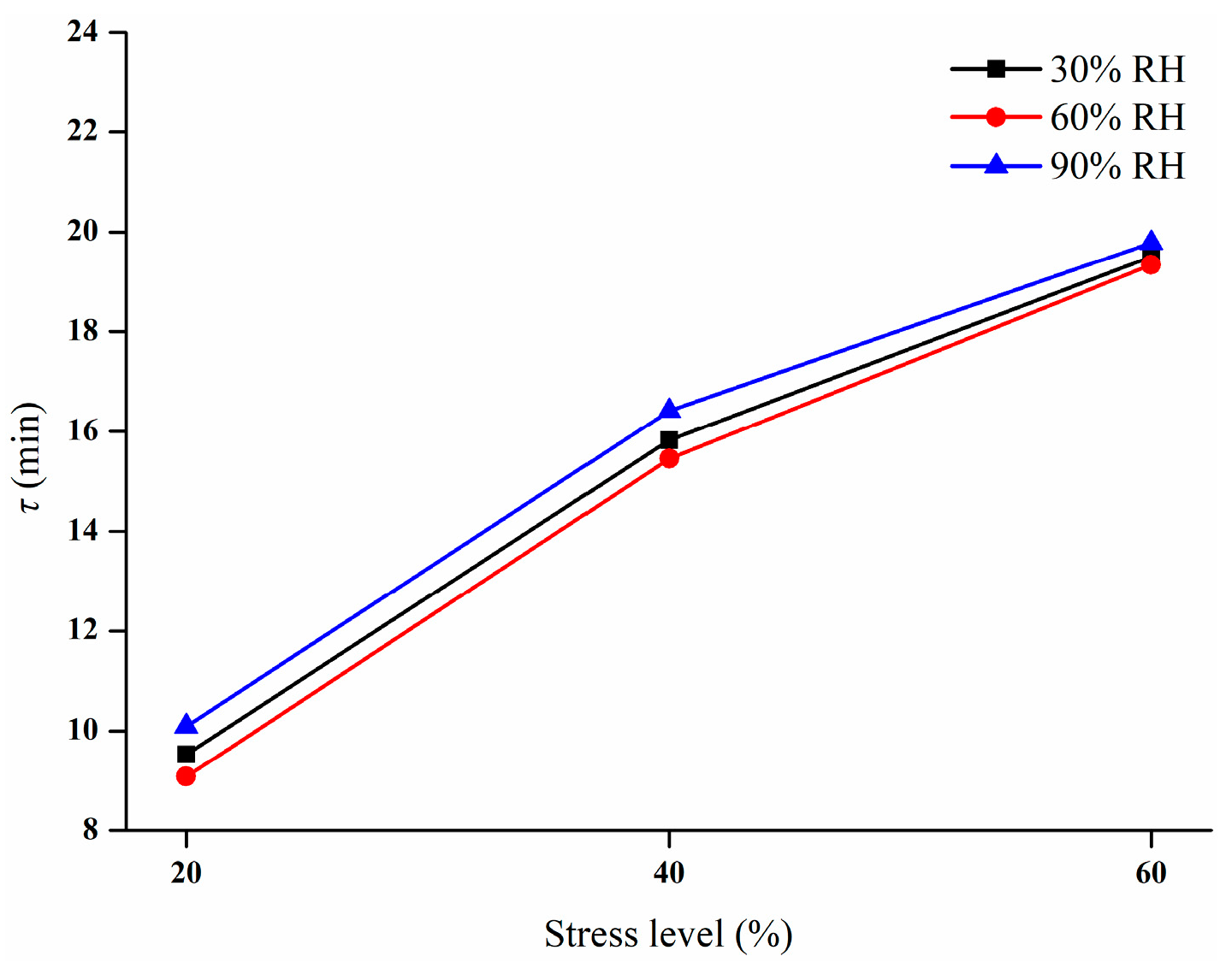
3.4. The Effect of Processing Conditions on the Retardation Time of Nylon Strings

Retardation time τ is a crucial indicator of the creep properties of nylon. A longer retardation time means a stronger resistance to permanent deformation. As shown in Figure 6, the highest τ is obtained at 90% relative humidity, while the lowest is obtained at 60% relative humidity. Nylon is a polar polymer, with molecular chains containing amine and carboxyl groups that can interact with water molecules through hydrogen bonding. When the moisture content is low, water molecules penetrate the spaces between nylon chains and bond with its polar groups, weakening the hydrogen bonds between nylon chains. As the moisture content increases further, an excess of water molecules may lead to the formation of numerous hydrogen bonds and water bridges between the polymer chains, possibly even resulting in small water clusters. This disrupts the nylon’s structure, restricting molecular chain mobility and reducing their flexibility and freedom of movement. Thus, the retardation time of nylon initially decreases and then increases as the relative humidity rises.

From Figure 6, it can be seen that the retardation times, τ, at three different relative humidities all increased with an increase in stress level. At low stress levels, the coiled structure of nylon molecular chains can easily adjust and relax through thermal motion, resulting in a shorter retardation time. However, as the stress increases, the molecular chains become more tightly stretched, and the initially coiled chains begin to straighten. This makes the movement and rearrangement of chain segments more difficult, requiring more time for retardation to occur. Additionally, as the stress rises, the interactions between molecular chains (such as hydrogen bonds and van der Waals forces) are intensified. Higher stress causes these interactions to become stronger, increasing the resistance to chain slippage and movement. As a result, the retardation time τ increases with higher stress levels.

4. Conclusions

In this work, the creep characteristics of nylon string used in badminton rackets were explored using the Maxwell and Kelvin models, with a focus on the instantaneous elastic deformation coefficient, delayed elastic deformation coefficient and retardation time. The main conclusions are as follows:

(1)

Highly accurate creep models were developed for nylon, all of which showed that the creep rate increased rapidly with time and then gradually became flat;

(2)

The instantaneous elastic deformation coefficient, delayed elastic deformation coefficient and retardation time all increased with increasing stress because of molecular chain movement and intermolecular forces;

(3)

With an increase in relative humidity, the instantaneous elastic deformation coefficient and delayed elastic deformation coefficient increased first and then decreased, while the retardation time of nylon decreased initially and then increased as the relative humidity rose;

(4)

In addition to the instantaneous elastic deformation coefficient, delayed elastic deformation coefficient and retardation time, there are other evaluation indicators, such as the delay time, tensile creep rate and viscosity coefficient. These can be further explored to describe the creep characteristics of nylon, especially under different processing conditions.