Design of CO2 Huff-n-Puff Parameters for Fractured Tight Oil Reservoirs Considering Geomechanical Effects
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Parameter Settings
| Component | Molar Fraction | Critical Pressure (Bar) | Critical Temperature (K) | Critical Volume [m3/(kg·mol)] | Molecular Weight | Acentric Factor |
|---|---|---|---|---|---|---|
| CO2 | 0.0096 | 73.886 | 304.700 | 0.0940 | 44.01 | 0.225 |
| N2 | 0.0310 | 33.944 | 126.200 | 0.0900 | 28.01 | 0.040 |
| C1 | 0.4006 | 46.042 | 190.600 | 0.0980 | 16.04 | 0.013 |
| C2–C3 | 0.1297 | 46.257 | 331.841 | 0.1397 | 35.86 | 0.121 |
| C4–C6 | 0.1107 | 34.447 | 455.283 | 0.5466 | 69.49 | 0.234 |
| C7–C12+ | 0.3184 | 20.793 | 663.857 | 0.7997 | 192.17 | 0.704 |
2.2. Simulation of the TPG
2.3. Simulation of the Geomechanical Effects
2.4. CO2-HnP Parameter Settings
2.5. Multi-Factor Analysis Method
3. Results
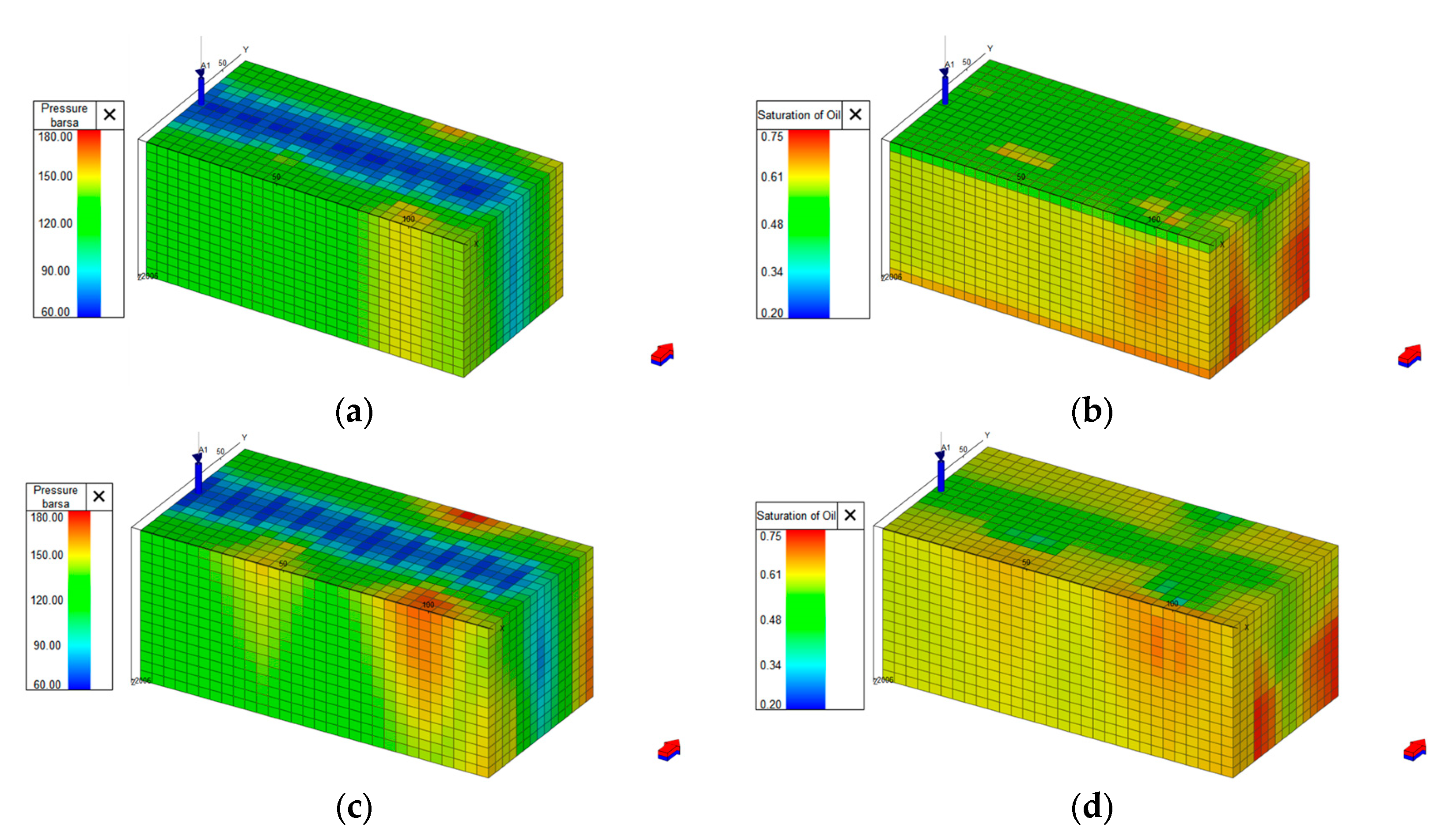
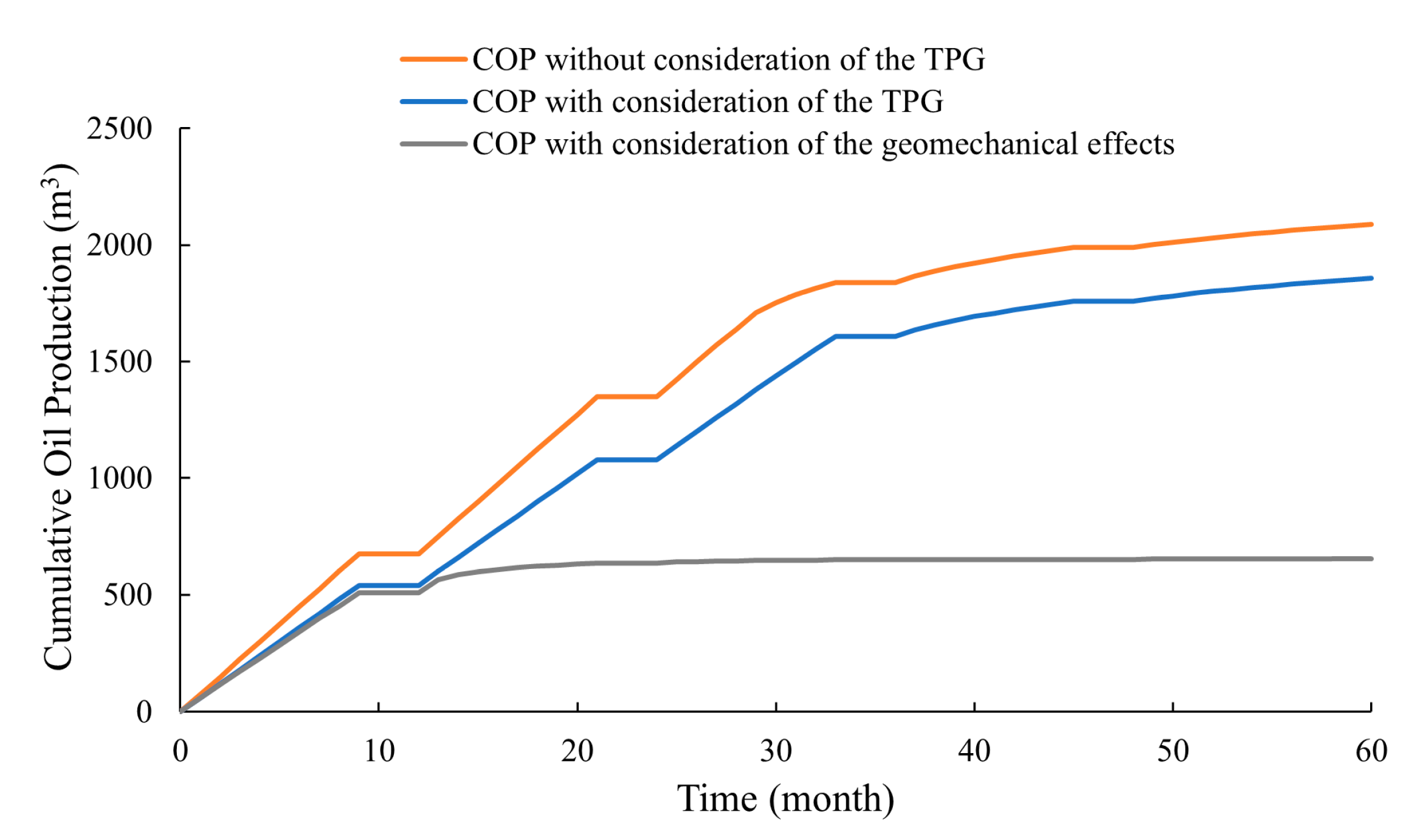
3.1. Impact and Analysis of the TPG
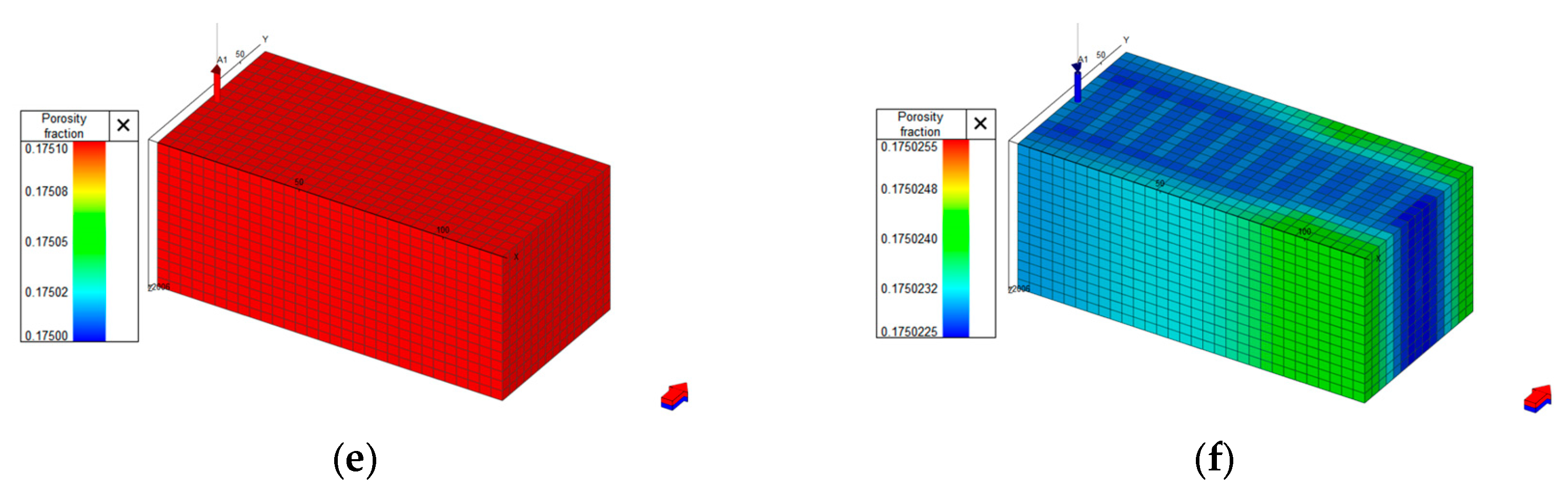
3.2. Impact and Analysis of the Geomechanical Effects
3.3. Impact and Analysis of the CO2-HnP Parameters
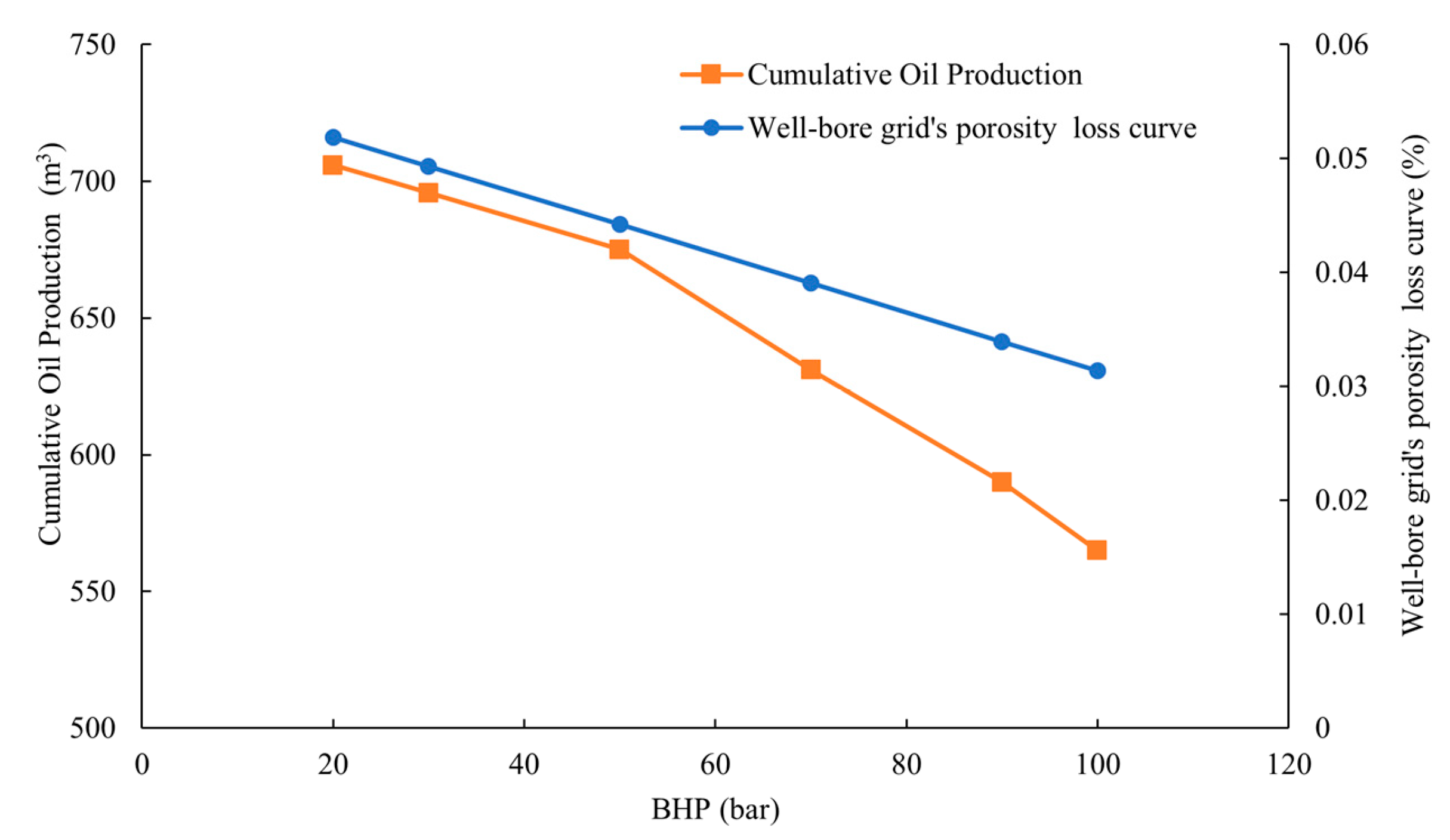
3.3.1. Impact and Analysis of the Bottomhole Pressure
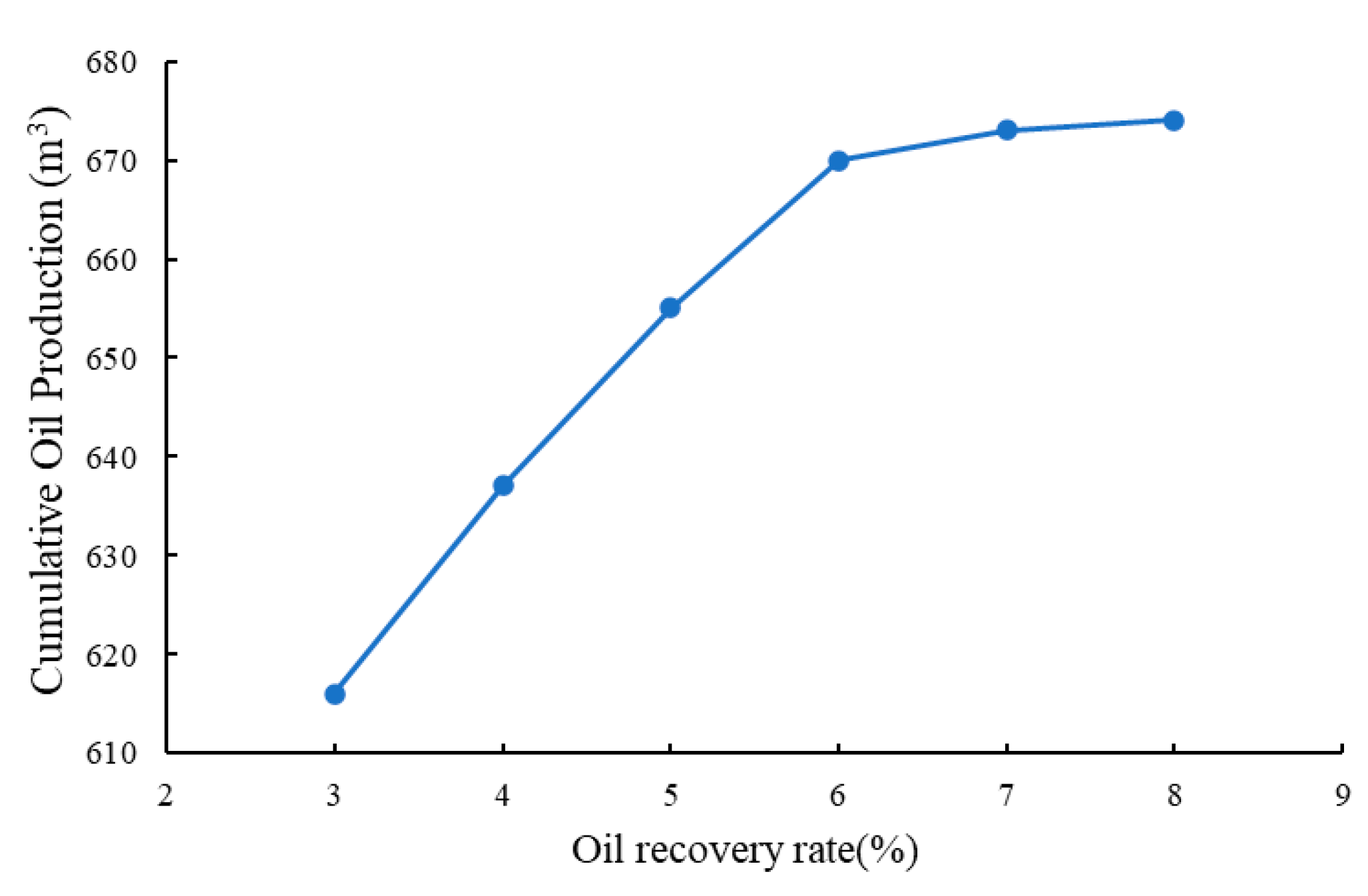
3.3.2. Impact and Analysis of the Oil Recovery Rate
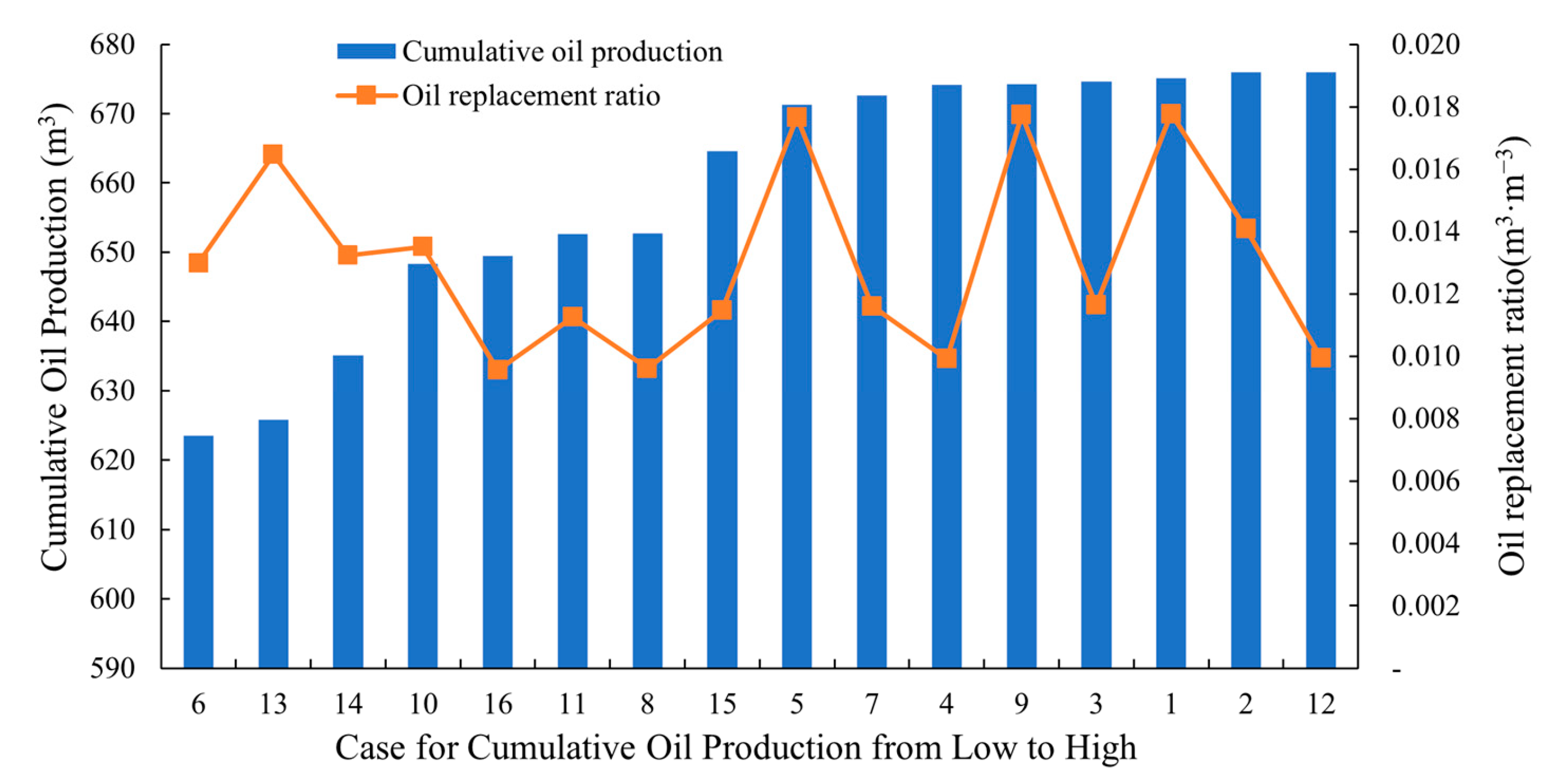
3.3.3. Orthogonal Experimental Results
| Case | Injection Amount (m3) | COP (m3) | Oil Replacement Ratio (m3·m−3) |
|---|---|---|---|
| 6 | 48,000 | 623.53 | 0.0130 |
| 13 | 38,000 | 625.79 | 0.0165 |
| 14 | 48,000 | 635.07 | 0.0132 |
| 10 | 48,000 | 648.31 | 0.0135 |
| 16 | 68,000 | 649.45 | 0.0096 |
| 11 | 58,000 | 652.63 | 0.0113 |
| 8 | 68,000 | 652.70 | 0.0096 |
| 15 | 58,000 | 664.63 | 0.0115 |
| 5 | 38,000 | 671.32 | 0.0177 |
| 7 | 58,000 | 672.66 | 0.0116 |
| 4 | 68,000 | 674.18 | 0.0099 |
| 9 | 38,000 | 674.26 | 0.0177 |
| 3 | 58,000 | 674.69 | 0.0116 |
| 1 | 38,000 | 675.15 | 0.0178 |
| 2 | 48,000 | 675.96 | 0.0141 |
| 12 | 68,000 | 675.99 | 0.0099 |
3.3.4. Multi-Factor Analysis
4. Conclusions
- (1)
- Compared with previous studies, it has been found that the influence of TPG and geomechanical effects cannot be ignored in numerical simulations of fractured tight reservoirs. The porous medium of the reservoir undergoes deformation under the coupling of flow and geomechanical effects, leading to decreases in porosity and permeability. The original development strategy under normal pressure drawdown may cause a sudden and significant change in the BHP gradient due to geomechanical effects; the COP decreased by 64.88% compared to the case where it is not considered, reducing the ultimate recovery rate of the oil field.
- (2)
- In the CO2-HnP simulation, injection time and number of cycles were found to notably affect COP and oil replacement ratio. A positive correlation with COP was found for parameters such as timing of production transfer injection and production time, while negative correlations were found for cycles, soaking time, and injection rate. For oil replacement ratio, soaking time and injection rate were positively correlated, while CO2 injection amount and number of cycles showed negative correlation.
- (3)
- With a constant injection volume, it is crucial to avoid an excessive number of cycles that reduce COP. On the basis of this parameter optimization, the oil replacement ratio can be enhanced by advancing the production transfer injection, shortening the injection time, and extending the soaking time period. These findings can help optimize CO2-HnP strategies to improve oil recovery and economic benefits from the reservoir.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, M.; Li, J.Z.; Wu, X.Z.; Wang, S.; Guo, Q.; Chen, X.; Yu, J. Potential of oil and natural gas resources of main hydrocarbon-bearing basins and key exploration fields in China. Earth Sci.-J. China Univ. Geosci. 2019, 44, 833–847. [Google Scholar]
- Zou, C.N.; Yang, Z.; Dong, D.Z.; Zhao, Q.; Chen, Z.; Feng, Y.; Li, J.; Wang, X. Formation, distribution and prospect of unconventional hydrocarbons in source rock strata in China. Earth Sci. 2022, 47, 1517–1533. [Google Scholar]
- Zhou, J.; Cao, R.; Pu, B.; Wang, J.; Lv, B.; Yi, Q. Study on dynamie in-situ stress and fracture propagation of multi-cycle waterhuff-and-puff in tight oil reservoirs. Chin. J. Rock Mech. Eng. 2024, 1–13. [Google Scholar] [CrossRef]
- Song, Y.L.; Song, Z.J.; Zhang, Y.F.; Xie, Z.H.; Zhang, L.C.; Wang, D.G.; Hui, G. Pore scale performance evaluation and impact factors in nitrogen huff-n-puff EOR for tight oil. Pet. Sci. 2022, 19, 2932–2940. [Google Scholar] [CrossRef]
- Zhao, J.; Peng, M.; Qi, X.; Wen, Q.; Yang, J. Low-carbon and high-efficiency nanosheet-enhanced CO2 huff-n-puff (HnP) for heavy oil recovery. Chem. Eng. J. 2024, 500, 156875. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S.; Li, M.; Husein, M.M. Enhanced oil recovery and carbon sequestration in low-permeability reservoirs: Comparative analysis of CO2 and oil-based CO2 foam. Fuel 2025, 381, 133319. [Google Scholar] [CrossRef]
- Yu, W.; Lashgari, H.R.; Wu, K.; Sepehrnoori, K. CO2 injection for enhanced oil recovery in Bakken tight oil reservoirs. Fuel 2015, 159, 354–363. [Google Scholar] [CrossRef]
- Zhang, K. Experimental and Numerical Investigation of Oil Recovery from Bakken Formation by Miscible CO2 Injection. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 26–28 September 2016; Society of Petroleum Engineers: Calgary, AB, Canada, 2016. [Google Scholar]
- Yang, Z.; Liu, X.; Zhang, Z.; Zhou, T.; Zhao, S. Physical simulation of CO2 injection in fracturing horizontal wells in tight oil reservoirs. Acta Pet. Sin. 2015, 36, 724–729. [Google Scholar]
- Zhang, Y.; Yu, W.; Li, Z.; Sepehrnoori, K. Simulation study of factors affecting CO2 Huff-n-Puff process in tight oil reservoirs. J. Pet. Sci. Eng. 2018, 163, 264–269. [Google Scholar] [CrossRef]
- Sun, R.; Zhang, Y.; Zhang, X. Productivity prediction model and parameter analysis for fractured horizontal wells in double medium tight oil reservoirs. Sci. Technol. Eng. 2019, 19, 89–96. [Google Scholar]
- Zhang, L.H.; Liu, S.; Yong, R.; Li, B.; Zhao, Y.L. EDFM-based numerical simulation of horizontal wells with multi-stage hydraulic fracturing in tight reservoirs. J. Southwest Pet. Univ. Sci. Technol. Ed. 2019, 41, 1–11. [Google Scholar]
- Mahmood, S.; Saraujo, C.; Kamy, S. Using embedded discrete fracture model (EDFM) in numerical simulation of complex hydraulic fracture networks calibrated by microseismic monitoring data. J. Nat. Gas Sci. Eng. 2018, 55, 495–507. [Google Scholar]
- Xiao, Z.; Zhao, Y.; Zhang, L.; Ge, F.; Yang, Z.; Liu, X.; Zhang, D.; Tian, Y. Capacity of Compact Reservoir Based on Dual Medium Embedded Discrete Crack Model. Sci. Technol. Eng. 2023, 23, 10780–10790. [Google Scholar]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R.T. Development of a novel and computationally-efficient discrete-fracture model to study ior processes in naturally fractured reservoirs. In Proceedings of the SPE Improved Oil Recovery Symposium, Tulsa, OK, USA, 14–18 April 2012; Society of Petroleum Engineers: Calgary, AB, Canada, 2012. [Google Scholar]
- Niu, J.; Su, J.; Yan, X.; Wang, Y.; Sun, H. Hydro-mechanical coupling model of fractured shale oil reservoir based on embedded discrete fracture model and extended finite element method. Sci. Technol. Engneering 2020, 20, 2643–2651. [Google Scholar]
- Liu, C.; Gupta, A.; Ates, H.; Yu, W.; Li, N.; Sepehrnoori, K. Automatic calibration of complex 3D discrete fracture networks using EDFM-Al. In Proceedings of the International Petroleum Technology Conference, Riyadh, Saudi Arabia, 21–23 February 2022; SPE: Calgary, AB, Canada, 2022. 185996-MS. [Google Scholar]
- Moinfar, A.; Narr, W.; Hui, M.H.; Mallison, B.; Lee, S.H. Comparison of discrete-fracture and dual-permeability models for multiphase flow in naturally fractured reservoirs. In Proceedings of the SPE Reservoir Simulation Conference, Woodlands, TX, USA, 21–23 February 2011; Society of Petroleum Engineers: Abu Dhabi, United Arab Emirates, 2011. [Google Scholar]
- Zhang, D.; Dai, C.; Chen, S.; Xue, L.; Liu, Y. Intelligent history matching of CO2 huff-n-puff in tight oil reservoirs considering multi-scale fracture characterization. Pet. Geol. Recovery Effic. 2022, 29, 160–167. [Google Scholar]
- Xiang, J.; Wei, T.; Lu, F.; Shen, J.; Liu, H.; Gao, C.C. Adaptability evaluation of DFM and EDFM discrete crack characterization methods. China Offshore Oil Gas 2023, 35, 83–90. [Google Scholar]
- Jiang, R.; Ni, Q.; Zhang, C.; Zhang, F.; Gao, Y.; Lin, J. Research on seepage model and numerical simulation of variable threshold pressure gradient in heavy oil reservoirs based on stress sensitivity. Oil Gas Geol. Recovery 2021, 28, 54–62. [Google Scholar]
- Wang, J.; Liu, H.; Liu, R.; Xu, J. Numerical simulation of low-permeability and ultra-low-permeability reservoirs con- sidering threshold pressure and stress-sensitive effects. Chin. J. Rock Mech. Eng. 2013, 32, 3317–3327. [Google Scholar]
- Zhu, Z.; Jia, Z.; Liu, B.; Liang, W. Numerical simulation of ultra- low permeability reservoirs considering start-up pressure gradient and fracture time-varying. China Offshore Oil Gas 2021, 33, 78–84. [Google Scholar]
- Zhu, M.; Wang, N.; Zhang, H. Influence of start-up pressure gradient and stress sensitivity effect on reservoir productivity. Daqing Pet. Geol. Dev. 2018, 37, 59–63. [Google Scholar]
- Cao, M.; Wu, X.; An, Y.; Zuo, Y.; Wang, R.; Li, P. Numerical simulation and performance evaluation of CO2 huff-n-puff processes in unconventional oil reservoirs. In Proceedings of the Carbon Management Technology Conference, Houston, TX, USA, 17 July 2017. [Google Scholar]
- Li, X.; Zhang, D.; Li, S. A multi-continuum multiple flow mechanism simulator for unconventional oil and gas recovery. J. Nat. Gas Sci. Eng. 2015, 26, 652–669. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, Z.; Wang, B.; Liao, X.; Li, D.; Zhou, B. A Multi-medium and Multi-mechanism model for CO2 injection and storage in fractured shale gas reservoirs. Fuel 2023, 345, 128167. [Google Scholar] [CrossRef]
- Garagash, I.A.; Dubovskaya, A.V.; Korneva, D.A.; Ghasemi, M.F. Coupled Geomechanical and Fluid Flow Simulation of the Oil Field Evolution Induced by Reservoir Production. Presented at the SPE Russian Oil and Gas Exploration & Production Technical Conference and Exhibition. Moscow, Russia, 14–16 October 2014. [Google Scholar] [CrossRef]
- Wang, R.; Duan, Y.; Lü, X.; Guo, D.; Huang, X.; Su, D. Stress sensitivity ex- periment of deep-bed, high-pressure and low-permeability sand- stone reservoirs. Geol. Sci. Technol. Inf. 2014, 33, 90–94. [Google Scholar]
- Zhang, P.; Liu, C. Reservoir stress sensitivity of low permeability reservoirs and its effect on single well production. Inn. Mong. Petrochem. Ind. 2010, 36, 154–156. [Google Scholar]
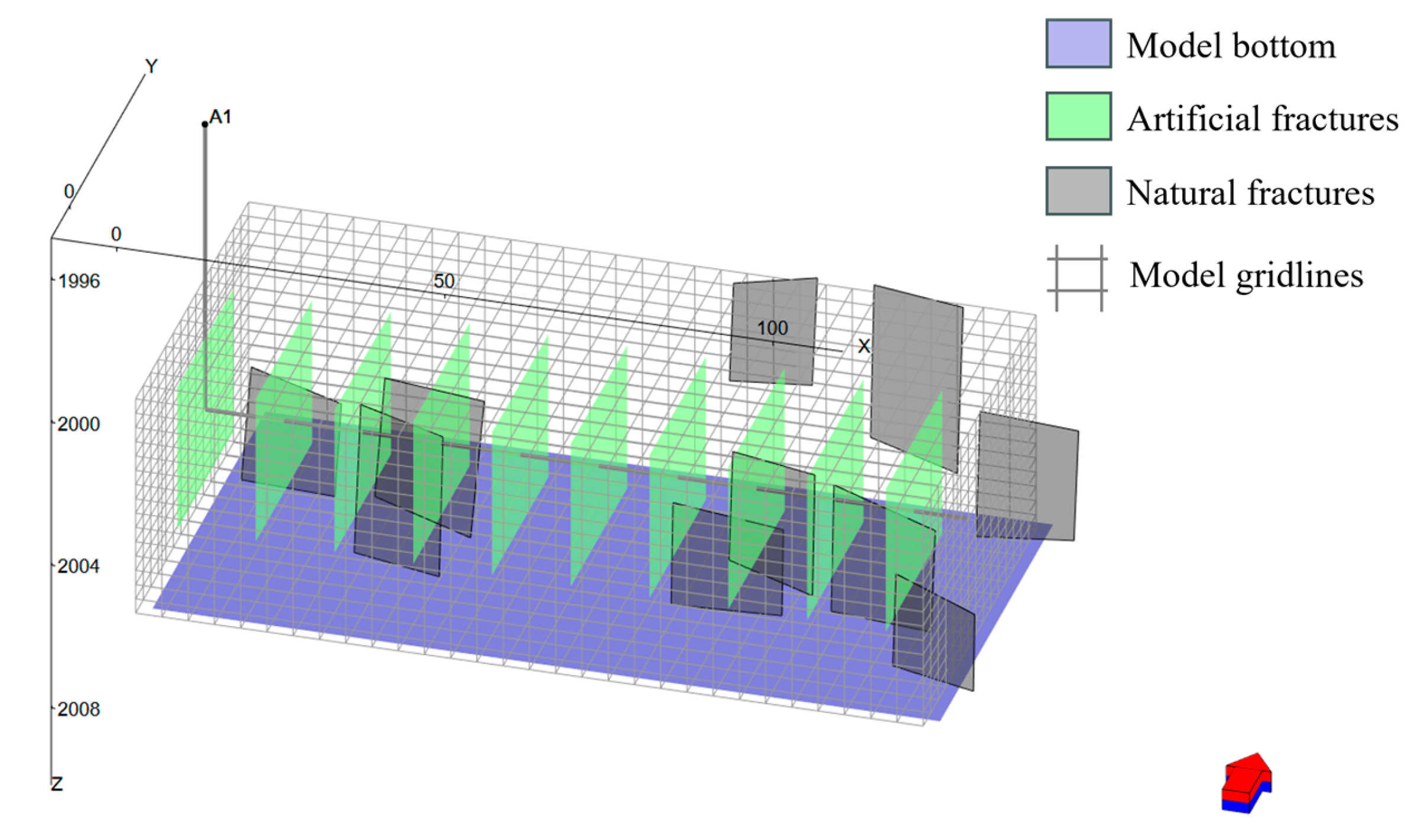






| Parameter | Value | Unit |
|---|---|---|
| Model size (x × y × z) | 120 × 60 × 6 | m |
| Number of grid blocks (x × y × z) | 30 × 15 × 15 | - |
| Reservoir permeability | 0.1 | mD |
| Reservoir porosity | 17.51 | % |
| Rock compressibility | 8.70 × 10−5 | bar−1 |
| Reservoir thickness | 6 | m |
| Horizontal interval length | 116 | m |
| Artificial fracture half-length | 15 | m |
| Artificial fracture height | 4 | m |
| Artificial fracture permeability | 2000 | mD |
| Average length of natural fracture | 15 | m |
| Average height of natural fracture | 3 | m |
| Parameter | Value | Unit |
|---|---|---|
| The rock cohesion value | 2 | bar |
| Poisson’s ratio | 0.2 | - |
| The angle of internal friction | 30 | - |
| Young’s modulus | 200,000 | bar |
| Case | Total Time (Month) | Injection Amount (m3) | Number of HnP Cycles | Timing of Transfer (Month) | Production (Month) | Injection Time (Month) | Injection Rate (m3/d) | Soaking (Months) |
|---|---|---|---|---|---|---|---|---|
| 1 | 60 | 38,000 | 3 | 3 | 11 | 4 | 105.56 | 5 |
| 2 | 60 | 48,000 | 3 | 5 | 11 | 5 | 106.67 | 4 |
| 3 | 60 | 58,000 | 3 | 7 | 11 | 3 | 214.82 | 6 |
| 4 | 60 | 68,000 | 3 | 9 | 11 | 6 | 125.93 | 3 |
| 5 | 60 | 38,000 | 4 | 1 | 9 | 4 | 79.17 | 2 |
| 6 | 60 | 48,000 | 4 | 3 | 9 | 3 | 133.33 | 3 |
| 7 | 60 | 58,000 | 4 | 5 | 9 | 2 | 241.67 | 4 |
| 8 | 60 | 68,000 | 4 | 7 | 9 | 3 | 188.89 | 3 |
| 9 | 60 | 38,000 | 5 | 2 | 7 | 1 | 253.33 | 4 |
| 10 | 60 | 48,000 | 5 | 3 | 7 | 2 | 160.00 | 3 |
| 11 | 60 | 58,000 | 5 | 4 | 7 | 3 | 128.89 | 2 |
| 12 | 60 | 68,000 | 5 | 5 | 7 | 4 | 113.33 | 1 |
| 13 | 60 | 38,000 | 6 | 1 | 5 | 1 | 211.11 | 4 |
| 14 | 60 | 48,000 | 6 | 2 | 5 | 2 | 133.33 | 3 |
| 15 | 60 | 58,000 | 6 | 3 | 5 | 3 | 107.41 | 2 |
| 16 | 60 | 68,000 | 6 | 4 | 5 | 4 | 94.44 | 1 |
| Factor | COP | Oil Replacement Ratio |
|---|---|---|
| Total CO2 injection amount | 0.101 | 0.506 |
| Number of huff-n-puff cycles | 0.130 | 0.013 |
| Timing of production transfer injection | 0.279 | 0.272 |
| Production time | 0.109 | 0.012 |
| Injection time | 0.096 | 0.036 |
| CO2 injection rate | 0.146 | 0.059 |
| Soaking time | 0.138 | 0.101 |
| Factor | COP | Oil Replacement Ratio |
|---|---|---|
| Total CO2 injection amount | 0.155 | −0.971 ** |
| Number of huff-n-puff cycles | −0.537 * | −0.073 |
| Timing of production transfer injection | 0.410 | −0.711 ** |
| Production time | 0.251 | 0.039 |
| Injection time | 0.164 | −0.532 * |
| CO2 injection rate | −0.028 | 0.100 |
| Soaking time | −0.279 | 0.514 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Xin, X.; Yu, G.; Wang, Y.; Lei, Z.; Zhang, L. Design of CO2 Huff-n-Puff Parameters for Fractured Tight Oil Reservoirs Considering Geomechanical Effects. Processes 2024, 12, 2777. https://doi.org/10.3390/pr12122777
Xia Y, Xin X, Yu G, Wang Y, Lei Z, Zhang L. Design of CO2 Huff-n-Puff Parameters for Fractured Tight Oil Reservoirs Considering Geomechanical Effects. Processes. 2024; 12(12):2777. https://doi.org/10.3390/pr12122777
Chicago/Turabian StyleXia, Yicun, Xiankang Xin, Gaoming Yu, Yanxin Wang, Zexuan Lei, and Liyuan Zhang. 2024. "Design of CO2 Huff-n-Puff Parameters for Fractured Tight Oil Reservoirs Considering Geomechanical Effects" Processes 12, no. 12: 2777. https://doi.org/10.3390/pr12122777
APA StyleXia, Y., Xin, X., Yu, G., Wang, Y., Lei, Z., & Zhang, L. (2024). Design of CO2 Huff-n-Puff Parameters for Fractured Tight Oil Reservoirs Considering Geomechanical Effects. Processes, 12(12), 2777. https://doi.org/10.3390/pr12122777






