Finite Element Simulation and Piezoelectric Sensor Array-Driven Two-Stage Impact Location on Composite Structures
Abstract
:1. Introduction
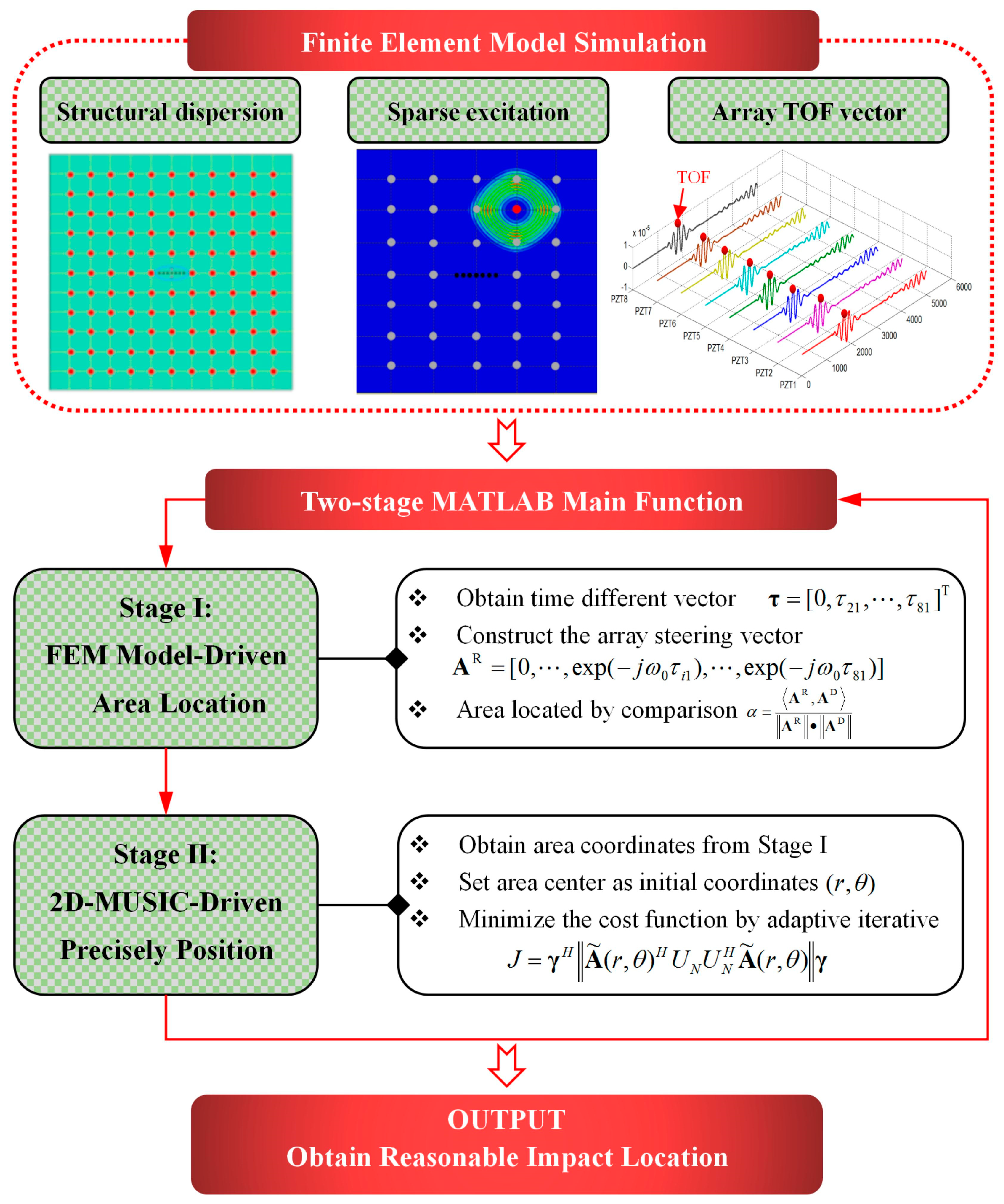
2. Two-Stage Impact Location Method
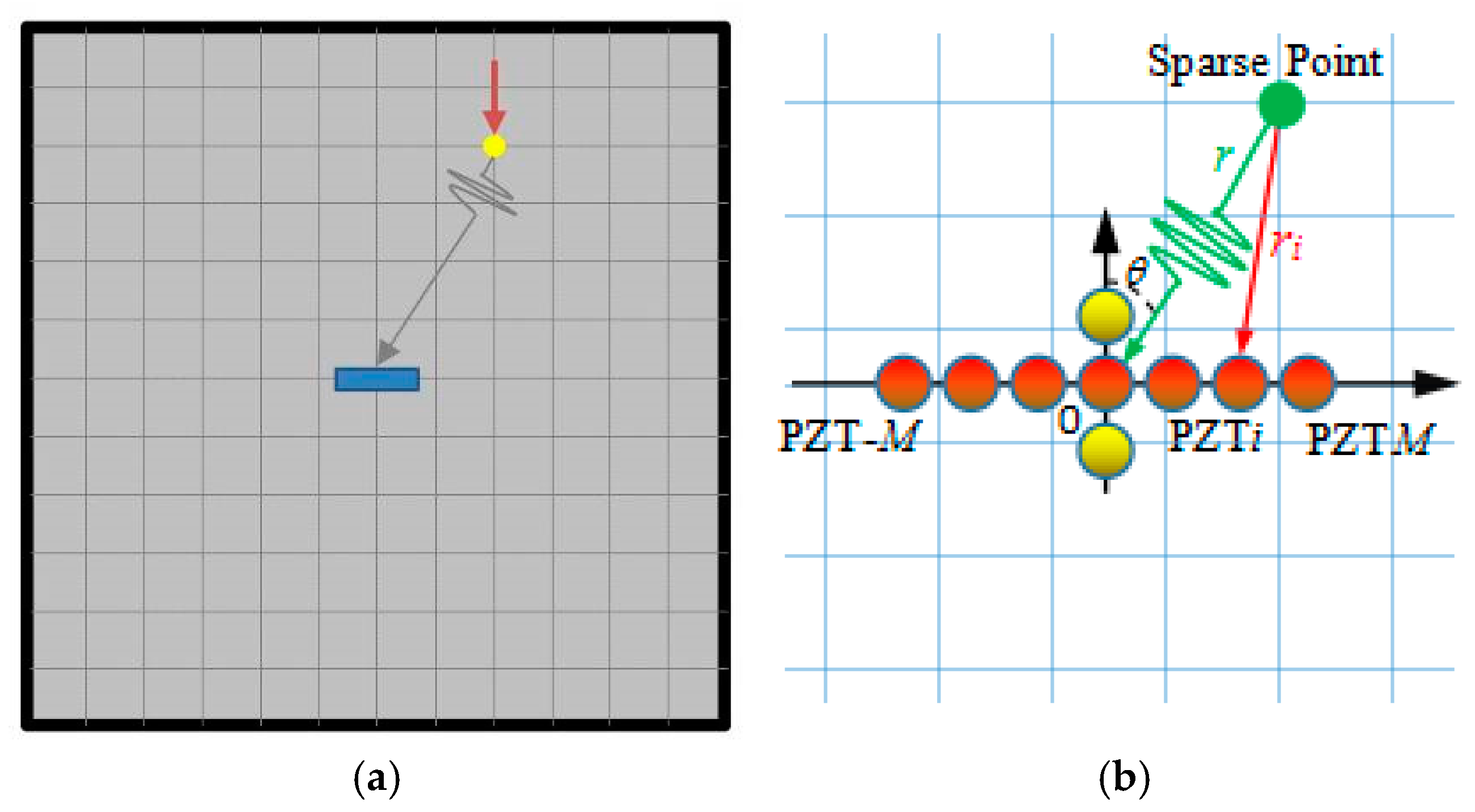
2.1. Array Signal Model
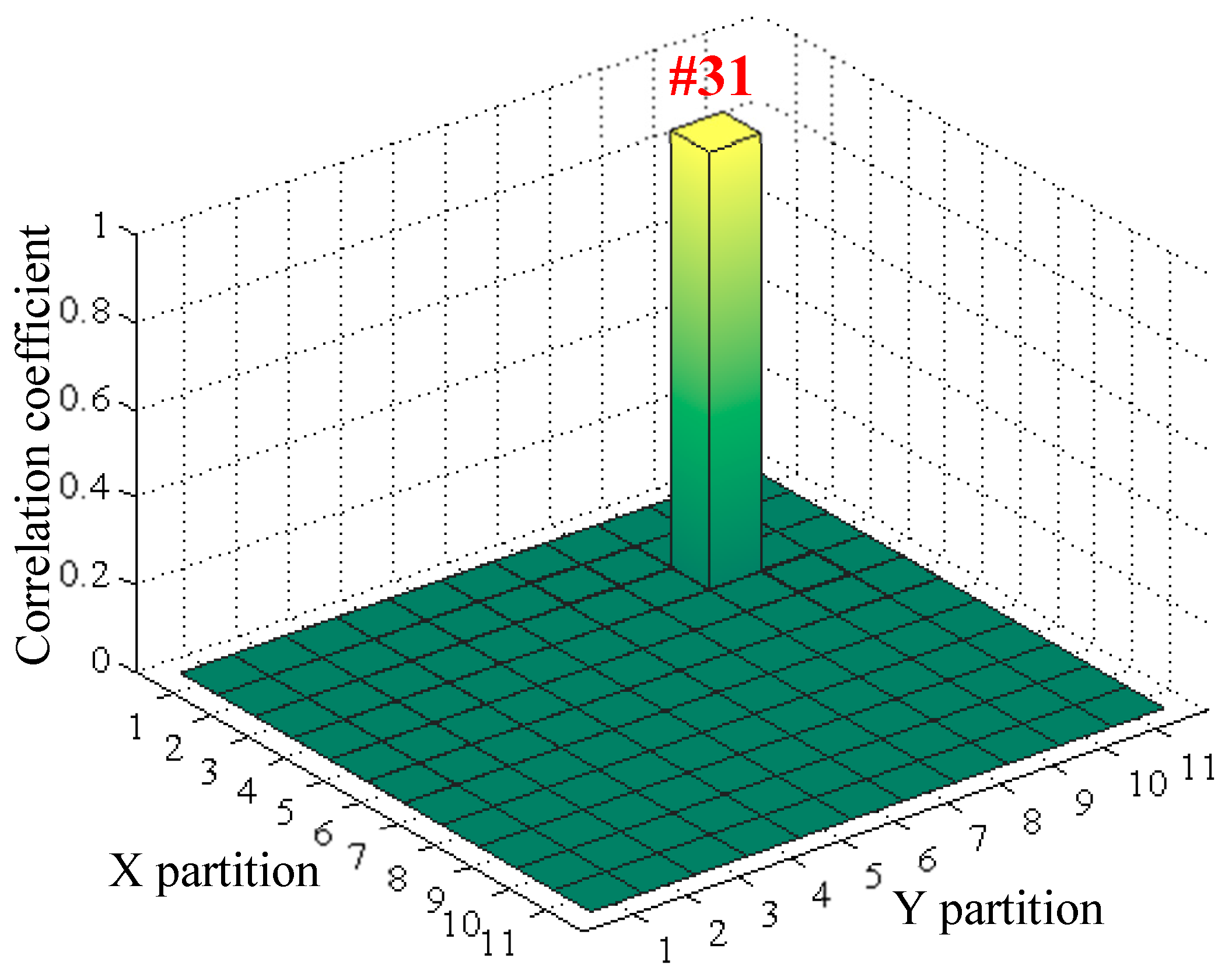
2.2. FEM Model-Driven Area Localization
2.3. Two-Dimensional MUSIC Algorithm-Driven Precise Position
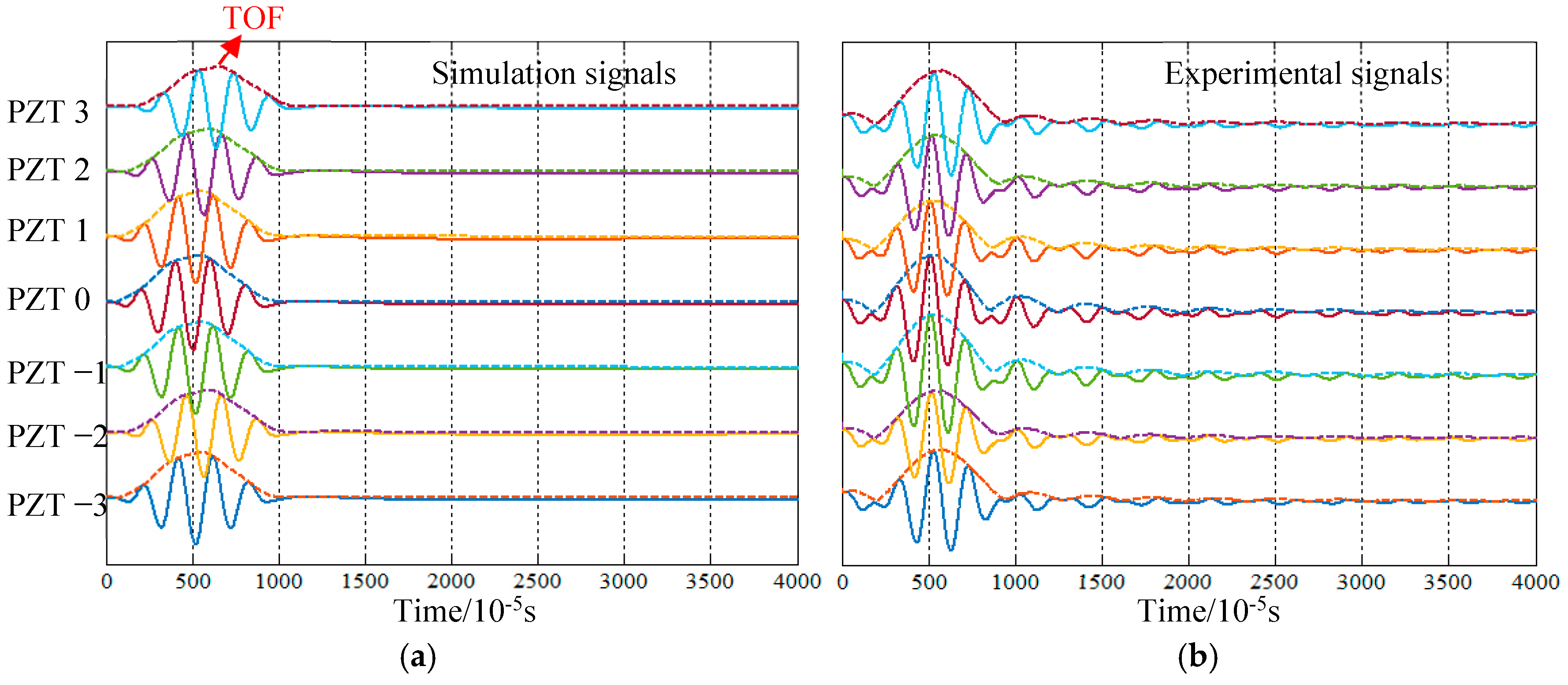
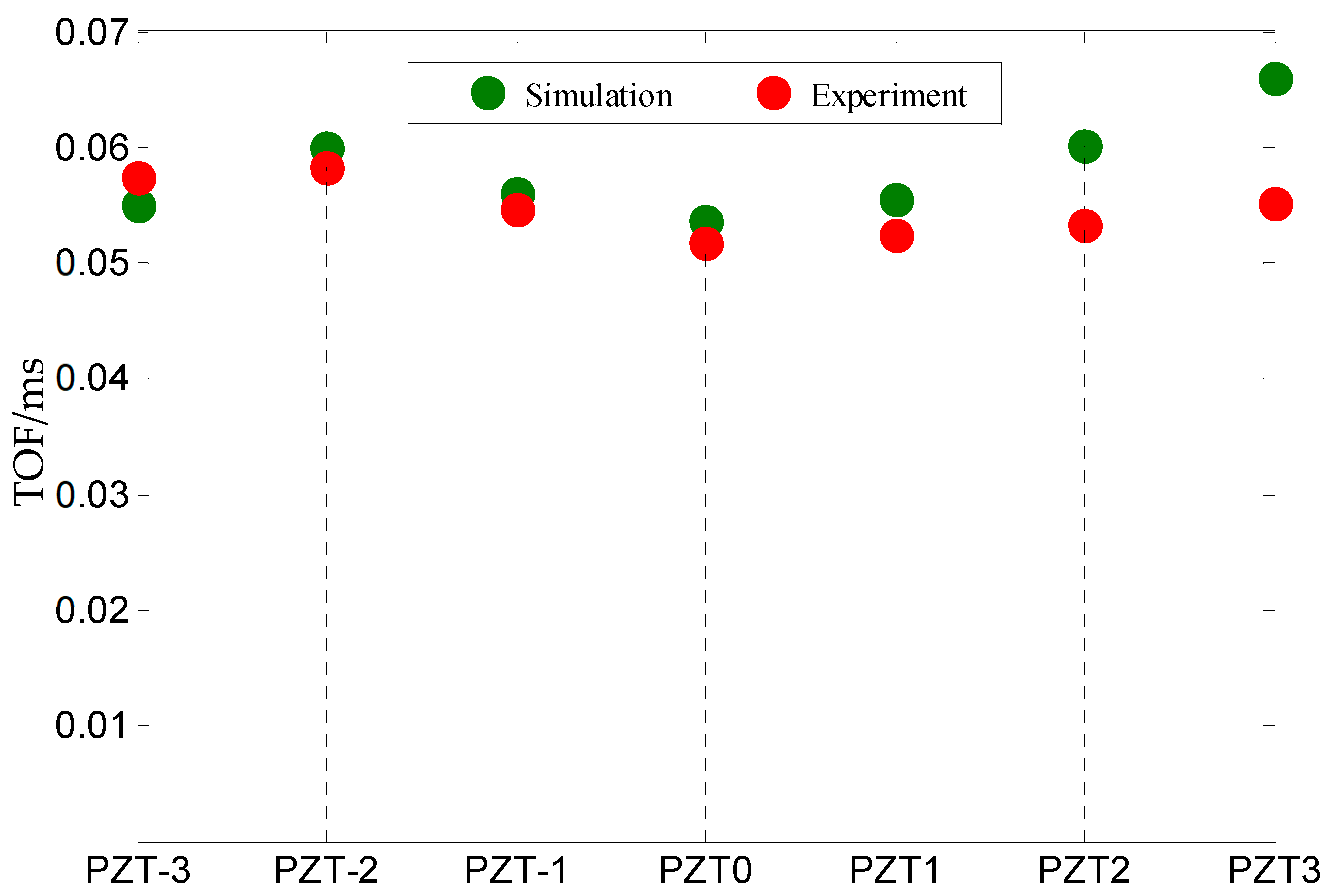
3. Numerical and Experimental Verification
3.1. FEM Model
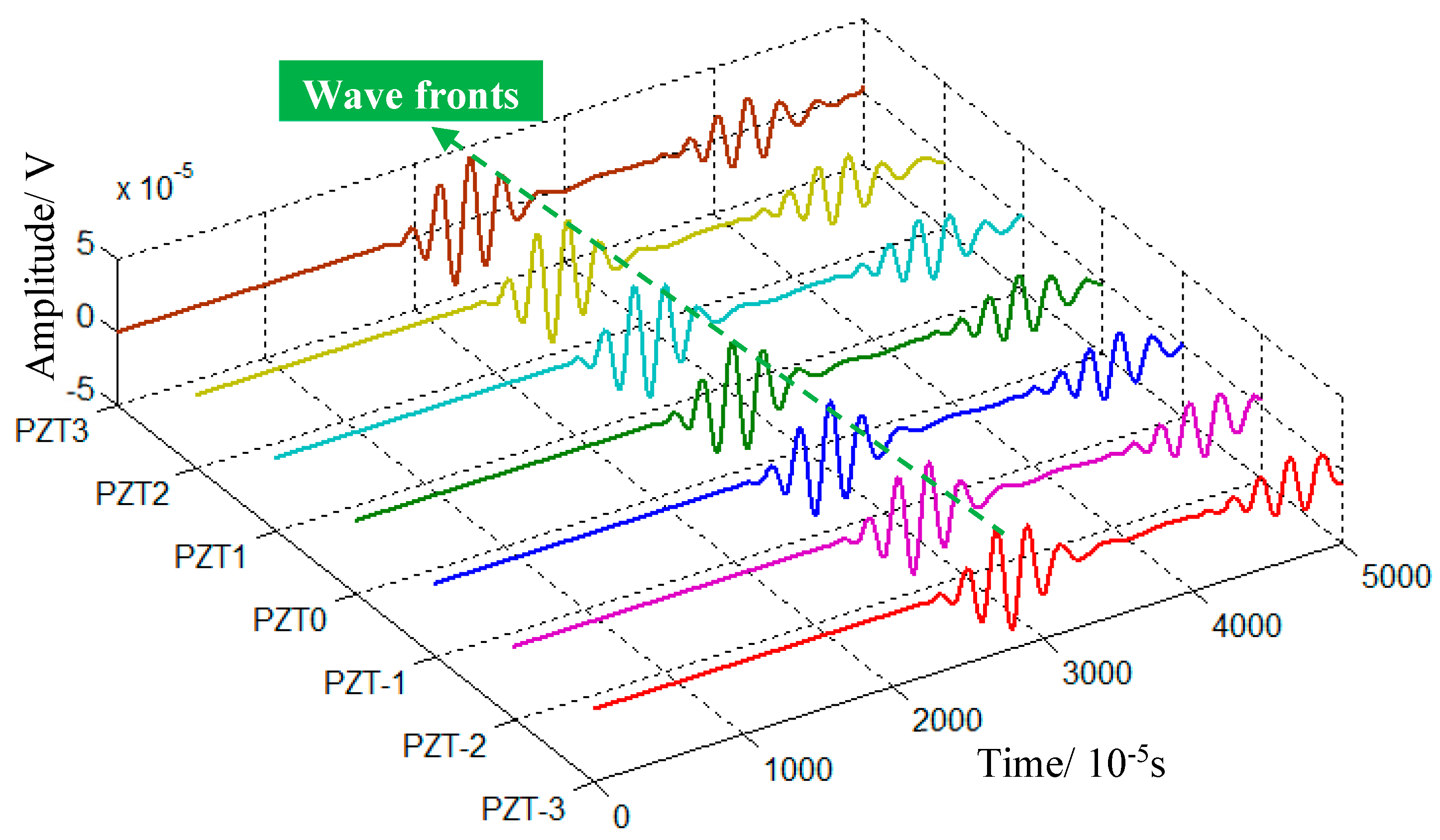
3.2. Numerical Verification
3.3. Experimental Verification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, M.; Guo, S.; He, S.; Li, W.; Yang, D. Structure health monitoring of a composite wing based on flight load and strain data using deep learning method. Compos. Struct. 2022, 286, 115305. [Google Scholar] [CrossRef]
- Zhu, K.; Qing, X.; Liu, B.; He, T. A passive localization method for stiffened composite structures with a parameterized laminate model. J. Sound Vib. 2020, 489, 115683. [Google Scholar] [CrossRef]
- Nucera, C.; White, S.; Chen, Z.M.; Kim, H.; Scalea, D.; Lanza, F. Impact monitoring in stiffened composite aerospace panels by wave propagation. Struct. Health Monit. 2015, 14, 547–557. [Google Scholar] [CrossRef]
- Hu, C.; Yang, B.; Xiao, B.; Xuan, F.Z.; Xiang, Y. Damage Localization In Pressure Vessel Using Guided Wave-Based Techniques: Optimizing The Sensor Array Configuration to Mitigate Nozzle Effects. Appl. Acoust. 2022, 185, 108393. [Google Scholar] [CrossRef]
- Jiang, P.; Liu, X.; Li, W.; Guo, F.; Hong, C.; Liu, Y.; Yang, C. Damage Characterization of Carbon Fiber Composite Pressure Vessels Based On Modal Acoustic Emission. Materials 2022, 15, 4783. [Google Scholar] [CrossRef] [PubMed]
- Memmolo, V.; Maio, L.; Ricci, F. Assessment of Damage in Composite Pressure Vessels Using Guided Waves. Sensors 2022, 22, 5182. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Yang, L.; Wang, H.; Zhao, J.; Li, N.; Chang, L.; Ji, H.; Qiu, J. Laser-Generated Guided Waves For Damage Detection in Metal-Lined Composite-Overwrapped Pressure Vessels. Polymers 2022, 14, 3823. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Chen, C.; Zhou, S.; Zhai, S. A Study on Defect Tomographic Imaging in Pressure Vessel With Liquid Medium. J. Press. Vessel Technol. 2020, 142, 041601. [Google Scholar] [CrossRef]
- Purekar, A.S.; Pines, D.J. Damage Detection in Thin Composite Laminates Using Piezoelectric Phased Sensor Array and Guided Wave Interrogation. J. Intell. Mater. Syst. Struct. 2010, 21, 995–1010. [Google Scholar] [CrossRef]
- Engholm, M.; Stepinski, T. Direction of Arrival Estimation of Lamb Wave Using Circular Arrays. Struct. Health Monit. 2011, 10, 467–480. [Google Scholar] [CrossRef]
- Ren, Y.; Qiu, L.; Yuan, S.; Bao, Q. On-Line Multi-Damage Scanning Spatial-Wavenumber Filter Based Imaging Method for Aircraft Composite Structure. Materials 2017, 10, 519. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Xiang, J. A Two-Dimensional Plum-Blossom Sensor Array-Based Multiple Signal Classification Method for Impact Localization in Composite Structures. Comput.-Aided Civ. Infrastruct. Eng. 2016, 31, 633–643. [Google Scholar] [CrossRef]
- Bao, Q.; Yuan, S.; Wang, Y.; Qiu, L. Anisotropy Compensated Music Algorithm Based Composite Structure Damage Imaging Method. Compos. Struct. 2019, 214, 293–303. [Google Scholar] [CrossRef]
- Zuo, H.; Yang, Z.; Tian, S.; Chen, X. Damage identification for plate-like structures using ultrasonic guided wave based on improved MUSIC method. Compos. Struct. 2018, 203, 164–171. [Google Scholar] [CrossRef]
- Karami, P.; Tabatabaei, S.A.; Zangaraki, R. Experimental and Numerical Analyses of Progressive Damage in Non-Circular Metal/Composite Hybrid Vessels Under Internal Pressure. Int. J. Damage Mech. 2015, 24, 1261–1279. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, Y.; Zhou, J.; Li, C.; Zhong, L. Environmental Effects on Piezoelectric Sensors Array Signals and a Compensated Damage Imaging Method. Materials 2021, 14, 6742. [Google Scholar] [CrossRef] [PubMed]




| E1 | E2 | E3 | G12 | G13 |
|---|---|---|---|---|
| 132 GPa | 8.8 GPa | 8.8 GPa | 4.95 GPa | 4.95 GPa |
| G23 | ρ | |||
| 3.35 GPa | 0.315 | 0.315 | 0.33 | 1540 kg/m3 |
| No. | Simulated Case | Area Localization | Precise Position | ||||||
|---|---|---|---|---|---|---|---|---|---|
| X/mm | Y/mm | r/mm | θ/° | X/mm | Y/mm | Ex/mm | Ey/mm | ||
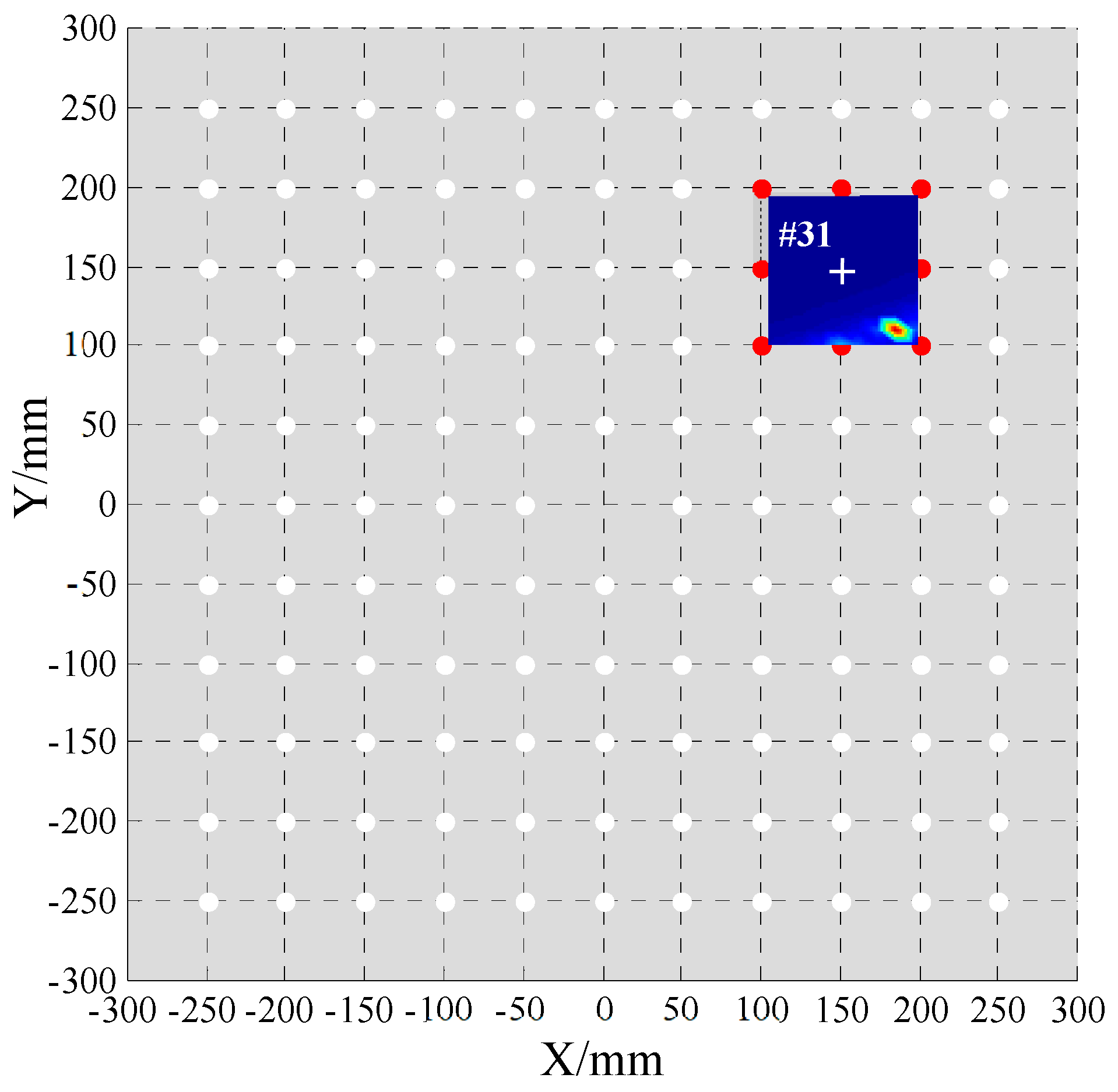
| S1 | 180 | 110 | #31 | 210 | 31 | 180 | 108 | 0 | 2 |
| S2 | −80 | 130 | #27 | 152 | 121 | −78 | 130 | 2 | 0 |
| S3 | 120 | −120 | #85 | 169 | 315 | 119 | −119 | 1 | 1 |
| No. | Simulated Case | Area Localization | Precise Position | ||||||
|---|---|---|---|---|---|---|---|---|---|
| X/mm | Y/mm | r/mm | θ/° | X/mm | Y/mm | Ex/mm | Ey/mm | ||
| E1 | 0 | 50 | #50 | 50 | 90 | 0 | 50 | 0 | 0 |
| E2 | 150 | 120 | #42 | 212 | 41 | 160 | 140 | 10 | 20 |
| E3 | 100 | 150 | #30 | 197 | 59 | 100 | 170 | 0 | 20 |
| E4 | −110 | 70 | #48 | 136 | 144 | −110 | 80 | 0 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhong, Y. Finite Element Simulation and Piezoelectric Sensor Array-Driven Two-Stage Impact Location on Composite Structures. Processes 2024, 12, 2675. https://doi.org/10.3390/pr12122675
Wang Z, Zhong Y. Finite Element Simulation and Piezoelectric Sensor Array-Driven Two-Stage Impact Location on Composite Structures. Processes. 2024; 12(12):2675. https://doi.org/10.3390/pr12122675
Chicago/Turabian StyleWang, Zhiling, and Yongteng Zhong. 2024. "Finite Element Simulation and Piezoelectric Sensor Array-Driven Two-Stage Impact Location on Composite Structures" Processes 12, no. 12: 2675. https://doi.org/10.3390/pr12122675
APA StyleWang, Z., & Zhong, Y. (2024). Finite Element Simulation and Piezoelectric Sensor Array-Driven Two-Stage Impact Location on Composite Structures. Processes, 12(12), 2675. https://doi.org/10.3390/pr12122675








