Enhancing Engine Cylinder Heat Dissipation Capacity Through Direct Optimization (DO) Techniques
Abstract
:1. Introduction
- How do different fin geometries and thicknesses influence the thermal performance of engine cylinder fins in internal combustion engines?
- What is the impact of various materials on the heat dissipation characteristics of optimized fin designs?
- How can direct optimization techniques be effectively applied to enhance the thermal efficiency of engine cylinder fins?
- What are the optimal design parameters (geometry, thickness, and material) that yield the maximum heat dissipation for engine cylinder fins?
2. Materials and Methods
2.1. Development of the 3D Model
2.2. Meshing the Model
2.3. Application of Thermal Boundary Conditions
2.4. Heat Balance and Thermal Management
2.5. Solver Settings
3. Results
3.1. Thermal Distribution Across Engine Cylinder Fins
3.2. Grid Independence and Validation
3.3. Total Heat Flux Distribution in Engine Cylinder
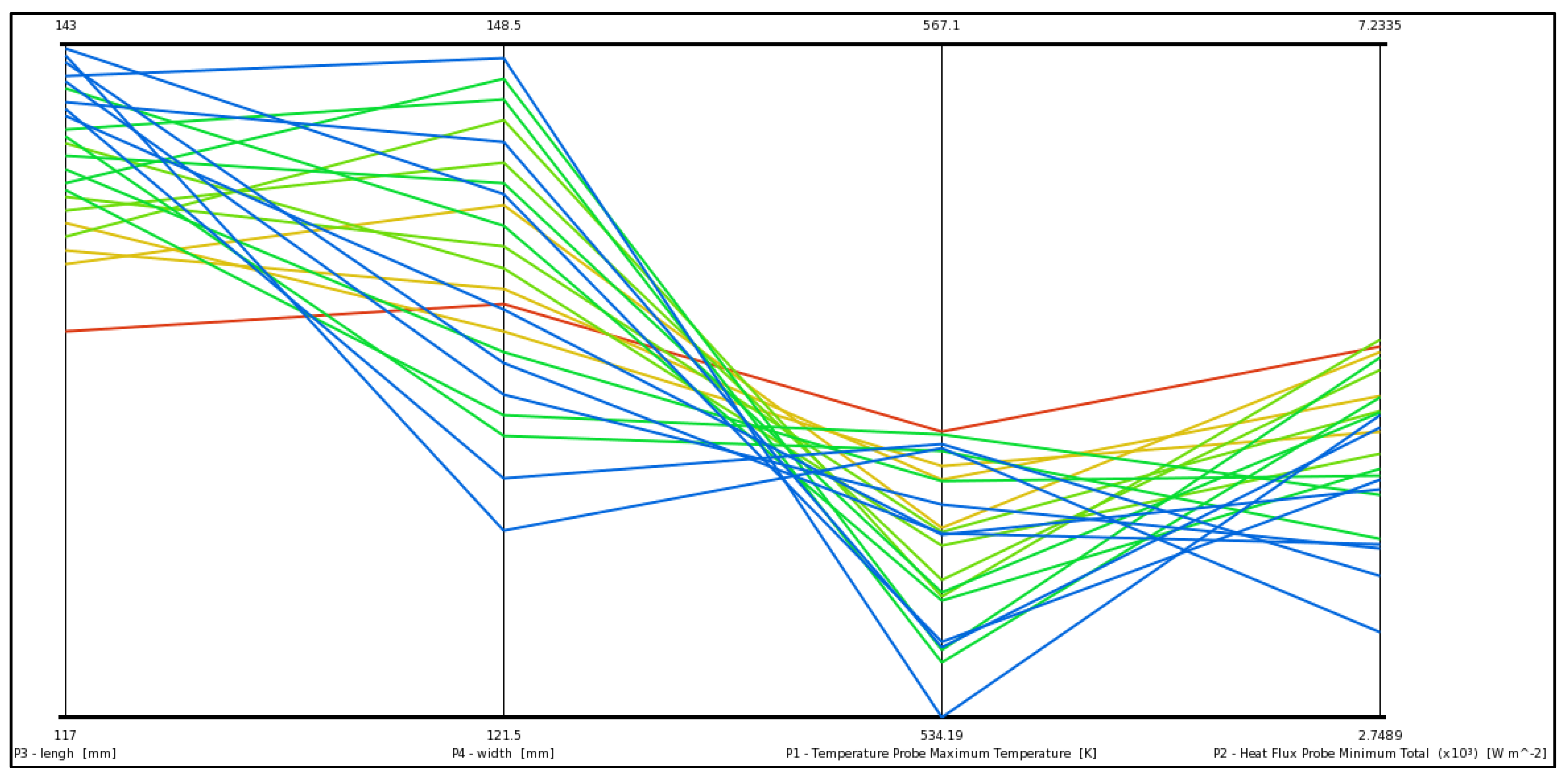
3.4. Optimization Results
3.4.1. Optimal Design Point
3.4.2. Trade-Off Analysis
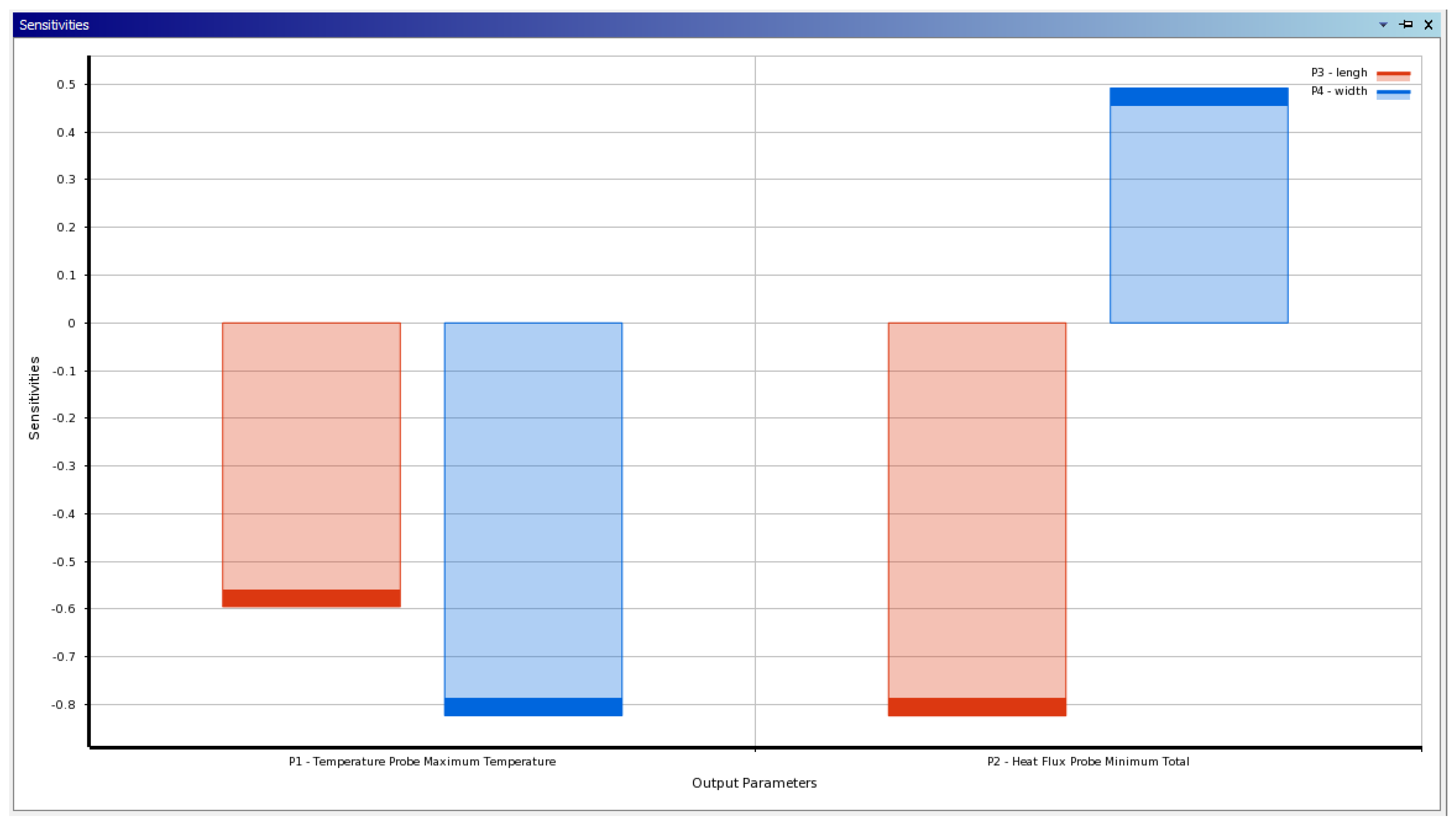
3.4.3. Sensitivity Analysis
3.5. Critical Factors Influencing Performance
3.5.1. Mesh Quality and Element Selection
3.5.2. Material Considerations
3.5.3. Boundary Conditions
3.5.4. Design and Manufacturing Constraints
3.6. Comparative Analysis
4. Discussion
5. Conclusions
- Optimization of fin geometry: The optimization process demonstrated a clear correlation between fin dimensions—specifically length and width—and thermal performance metrics such as maximum temperature and total heat flux. The optimized design measured 118.95 mm in length and 145.26 mm in width and had a capacity for heat dissipation of 7225.31 W/m2, which is 25.87% higher than the capacity of the generic design, 5740.22 W/m2. This enhancement underscores the potential for significant improvements in engine cooling efficiency through targeted geometric modifications.
- Heat transfer characteristics: The analysis indicates that while the fins effectively dissipated heat, the heat flux was notably lower near the fin tips. These findings suggest further refinement of fin geometry or study of alternative materials having better thermal conductivity to realize higher heat flux density overall.
- Importance of material selection: The study used cast iron, which has good thermal properties and the work demonstrated the feasibility of lighter materials or high-conductivity alloys to obtain improved performance. This consideration is particularly relevant to automotive and aerospace applications owing to weight reduction constraints while maintaining thermal efficiency.
- Despite these substantial findings, certain limitations were recognized in the study:
- The reliance on steady-state thermal analysis presents a limitation, as it does not account for the transient heat transfer characteristics inherent in real engine operations under varying loads. This factor may affect fin performance differently depending on changes in engine temperatures during operation, which are not considered in the steady-state model presented here. The potential modeling errors may arise due to assumptions in material properties, boundary conditions, and simplified geometries. Variations in the mesh resolution and external environmental factors may also influence the accuracy of the results.
- The FEA results provide useful information but also indicate the significance of experimental validation. Additional dynamics of fin performance could be found in real-world conditions (such as workflow variations, manufacturing defects, and material behavior under operational stress). In the future, transient heat analysis and experimental studies should be incorporated into research to more fully understand the fin efficiency in engine cooling systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| F | Objective function to be minimized or maximized. |
| Tmax | Maximum temperature at specific points on the fin surface. |
| Tref | Reference temperature. |
| Q | Total heat flux across the surface. |
| qref | Reference heat flux. |
| α and β | Weighting factors used to balance the objectives of temperature reduction and heat dissipation. |
References
- Agarwal, A.; Pitso, I. Modelling & Numerical Exploration of Pulsejet Engine Using Eddy Dissipation Combustion Model. Mater. Today Proc. 2020, 27, 1341–1349. [Google Scholar] [CrossRef]
- Chen, W.; Yang, X.; Zuo, Q.; Wang, H.; Ning, D.; Kou, C.; Zhang, Y.; Zhu, G. Combustion Characteristics and Performance Analysis of a Heavy-Fuel Rotary Engine by Designing Fuel Injection Position. Appl. Therm. Eng. 2024, 247, 123021. [Google Scholar] [CrossRef]
- Förster, F.; Crua, C.; Davy, M.; Ewart, P. Temperature Measurements under Diesel Engine Conditions Using Laser Induced Grating Spectroscopy. Combust. Flame 2019, 199, 249–257. [Google Scholar] [CrossRef]
- Lu, B.; Zhang, Z.; Cai, J.; Wang, W.; Ju, X.; Xu, Y.; Lu, X.; Tian, H.; Shi, L.; Shu, G. Integrating Engine Thermal Management into Waste Heat Recovery under Steady-State Design and Dynamic off-Design Conditions. Energy 2023, 272, 127145. [Google Scholar] [CrossRef]
- Sachar, S.; Parvez, Y.; Khurana, T.; Chaubey, H. Heat Transfer Enhancement of the Air-Cooled Engine Fins through Geometrical and Material Analysis: A Review. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Mert Cuce, P.; Cuce, E. Optimization of Configurations to Enhance Heat Transfer from a Longitudinal Fin Exposed to Natural Convection and Radiation. Int. J. Low-Carbon Technol. 2014, 9, 305–310. [Google Scholar] [CrossRef]
- Subbiah, M.; Balamurugan, S.; Jayakumar, K.; Karthick, R. Analysis of Engine Cylinder Block with Fins by Varying Different Materials. Mater. Today Proc. 2023, 72, 2039–2043. [Google Scholar] [CrossRef]
- Durgam, S.; Kale, A.; Kene, N.; Khedkar, A.; Palve, S.; Gawai, N.M. Thermal Analysis of Fin Materials for Engine Cylinder Heat Transfer Enhancement. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1126, 012071. [Google Scholar] [CrossRef]
- Kadam, S.S.; Umale, S. Effect of Various Fin Geometries on Heat Dissipation of Traction Motors Used in Electric Vehicles. J. Phys. Conf. Ser. 2021, 2007, 012021. [Google Scholar] [CrossRef]
- Jones, D.R.; Martins, J.R.R.A. The DIRECT Algorithm: 25 Years Later. J. Glob. Optim. 2021, 79, 521–566. [Google Scholar] [CrossRef]
- Babu, G. Heat Transfer Analysis and Optimization of Engine Cylinder Fins of Varying Geometry and Material. IOSR J. Mech. Civ. Eng. 2013, 7, 24–29. [Google Scholar] [CrossRef]
- Angamuthu, K.; Krishnan, G.; Gowrishankar, M.; Abraham, J.G. Modeling and Simulation Studies of 100 cc Motor Cycle Engine Cylinder with Groove and Perforated Fin Design Using Different Materials. Mater. Today Proc. 2021, 42, 1447–1455. [Google Scholar] [CrossRef]
- Mahek, M.K.; Al-Aribe, K.M. Heat Transfer Enhancement in Stirling Engines Using Fins with Different Configurations. In Proceedings of the 2022 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 21–24 February 2022; pp. 1–6. [Google Scholar]
- Avinash Kapil, S.; Rameshvamsi, C.O.; Vishal Varma, V. Design and Analysis on Engine Cylinder Fins for Variable Materials. Int. J. Mod. Trends Sci. Technol. 2021, 7, 157–162. [Google Scholar]
- Dobzhanskyi, O.; Narumanchi, S.; Tomerlin, J.; Kekelia, B.; Gouws, R.; Cousineau, E. Modelling a Motor Cooling System with Stator Lamination Fins. In Proceedings of the 2023 IEEE 64th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 9–11 October 2023; pp. 1–5. [Google Scholar]
- Saxena, D.; Chourasia, A.; Dwivedi, S.; Mahore, S. Study and Optimization of Heat Transfer Analysis for Engine Fins Using Ansys. Int. J. Sci. Res. Comput. Sci. Eng. 2019, 7, 22–32. [Google Scholar] [CrossRef]
- Shareef, S.K.M.; Vikas, M.S.; Kumar, A.L.N.A.; Dasore, A.; Chhalotre, S.; Rajak, U.; Nath Verma, T. Design and Thermal Analysis of Engine Cylinder Fin Body Using Various Fin Profiles. Mater. Today Proc. 2021, 47, 5776–5780. [Google Scholar] [CrossRef]
- Agarwal, A.; Letsatsi, M.T. Investigation of the Effect of Engine Cylinder Fin Shape on Heat Transfer Characteristics Under Forced Convection. In Emerging Trends in Mechanical and Industrial Engineering: Select Proceedings of ICETMIE 2022; Springer: Berlin/Heidelberg, Germany, 2023; pp. 113–128. [Google Scholar]
- Khan, S.; Chourasia, B.K. Steady State Thermal Analysis of Cylinder Fins with Varied Materials and Thicknesses. Int. J. Res. Appl. Sci. Eng. Technol. 2023, 11, 915–933. [Google Scholar] [CrossRef]
- Chaitanya, P.S.; Suneela Rani, B.; Kumar, K.V. Thermal Analysis of Engine Cylinder Fin by Varying Its Geometry and Material. IOSR J. Mech. Civ. Eng. 2014, 11, 37–44. [Google Scholar] [CrossRef]
- Gupta, S.; Kumar, D.; Kumar, S. Heat Transfer Analysis of Engine Cylinder Fins by Varying Geometry. Int. J. Res. Publ. Rev. 2022, 3, 969–981. [Google Scholar]
- Kumaravelu, T.; Saadon, S.; Abu Talib, A.R. Heat Transfer Enhancement of a Stirling Engine by Using Fins Attachment in an Energy Recovery System. Energy 2022, 239, 121881. [Google Scholar] [CrossRef]
- Ocłoń, P.; Łopata, S.; Stelmach, T.; Li, M.; Zhang, J.-F.; Mzad, H.; Tao, W.-Q. Design Optimization of a High-Temperature Fin-and-Tube Heat Exchanger Manifold—A Case Study. Energy 2021, 215, 119059. [Google Scholar] [CrossRef]
- Varghese, S.Z.; Paul, B.; Roy, S.M.; John, K. Heuristic Technique for Multi-Objective Optimisation of Engine Cylinder Fins. Mater. Today Proc. 2022, 58, 80–85. [Google Scholar] [CrossRef]
- Godi, N.Y. Thermal Performance Maximisation in a Complex Heat Exchanger with Solid and Hollow Cylindrical Fins. Int. Commun. Heat Mass Transf. 2024, 152, 107286. [Google Scholar] [CrossRef]
- Dahham, R.Y.; Wei, H.; Pan, J. Improving Thermal Efficiency of Internal Combustion Engines: Recent Progress and Remaining Challenges. Energies 2022, 15, 6222. [Google Scholar] [CrossRef]
- Dev, S.; Guo, H.; Liko, B. A Study on the High Load Operation of a Natural Gas-Diesel Dual-Fuel Engine. Front. Mech. Eng. 2020, 6, 545416. [Google Scholar] [CrossRef]
- Zaccardi, J.-M.; Pagot, A.; Vangraefschepe, F.; Dognin, C.; Mokhtari, S. Optimal Design for a Highly Downsized Gasoline Engine. In SAE Technical Paper 2009-01-1794; SAE International: Warrendale, PA, USA, 2009. [Google Scholar]
- Agarwal, A.; Cavicchioli Batista, R.; Gurung, A. Analyzing the Impact of Bumper Height on Pedestrian Injuries Using Explicit Dynamics. In Smart Electric and Hybrid Vehicles; CRC Press: New York, NY, USA, 2024; pp. 57–89. [Google Scholar]
- Sagar, P.; Teotia, P.; Sahlot, A.D.; Thakur, H.C. Heat Transfer Analysis and Optimization of Engine Fins of Varying Surface Roughness. Mater. Today Proc. 2017, 4, 8565–8570. [Google Scholar] [CrossRef]
- Kang, Y.J.; Pandey, S.; Park, S.I.; Kim, Y.S.; Wie, J.H.; Kim, D.H.; Ha, M.Y. Comprehensive Analysis and Design Optimization of Temperature Distribution in Radiant Heaters for Cooking Applications. Case Stud. Therm. Eng. 2023, 52, 103687. [Google Scholar] [CrossRef]
- Boz, Z.; Erdogdu, F.; Tutar, M. Effects of Mesh Refinement, Time Step Size and Numerical Scheme on the Computational Modeling of Temperature Evolution during Natural-Convection Heating. J. Food Eng. 2014, 123, 8–16. [Google Scholar] [CrossRef]
- Huang, G.-J.; Wong, S.-C.; Lin, C.-P. Enhancement of Natural Convection Heat Transfer from Horizontal Rectangular Fin Arrays with Perforations in Fin Base. Int. J. Therm. Sci. 2014, 84, 164–174. [Google Scholar] [CrossRef]
- Armstead, J.R.; Miers, S.A. Review of Waste Heat Recovery Mechanisms for Internal Combustion Engines. J. Therm. Sci. Eng. Appl. 2014, 6, 014001. [Google Scholar] [CrossRef]
- Fakhari, S.M.; Mrad, H. Aerodynamic Shape Optimization of NACA Airfoils Based on a Novel Unconstrained Conjugate Gradient Algorithm. J. Eng. Res. 2024, in press. [Google Scholar] [CrossRef]
- Agarwal, A.; Rimal, A.; Ilunga, M. Non-Linear Contact Analysis and Response Surface Optimization of Railway Wheel Using ANSYS. Math. Model. Eng. Probl. 2024, 11, 2039–2047. [Google Scholar] [CrossRef]
- Jikol, F.; Akop, M.Z.; Arifin, Y.M.; Salim, M.A.; Herawan, S.G. A Study of Steady-State Thermal Distribution on Circular Plate Using ANSYS. Int. J. Nanoelectrics Mater. 2021, 14, 479–488. [Google Scholar]
- Agarwal, A.; Letsatsi, M.T.; Pitso, I. Response Surface Optimization of Heat Sink Used in Electronic Cooling Applications. In Recent Advances in Materials and Modern Manufacturing: Select Proceedings of ICAMMM 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 121–129. [Google Scholar]
- Chavan, V.U.; Guruvasanth, A.S.; Rana, A.; Prabu, S.S. Comparative Study on Thermal Analysis of Disc Brake Using ANSYS Simulation. ECS Trans. 2022, 107, 15693–15700. [Google Scholar] [CrossRef]
- Agarwal, A.; Molwane, O.B.; Letsatsi, M.T. Experimental Investigation & Analysis of Heat Transfer Characteristics in Automotive MMC Disc Brake Under Steady State and Dynamic Conditions. J. Eng. Res. 2021, 9, 1–12. [Google Scholar] [CrossRef]
- Sun, X.; Zhuang, Y.; Liu, L.; Dong, Y.; Zhang, L.; Du, J. Multi-Objective Optimization of Heat Exchange Network and Thermodynamic Cycles Integrated System for Cooling and Power Cogeneration. Appl. Energy 2022, 321, 119366. [Google Scholar] [CrossRef]
- Gupta, D.; Saha, P.; Roy, S. Multi-Objective Optimization of the Perforated Micro Pin-Fin Heat Sink Using Non-Dominated Sorting Genetic Algorithm-II Coupled with Computational Fluid Dynamics Simulation. J. Heat Transfer. 2022, 144, 093301. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, J. Advanced Lightweight Materials for Automobiles: A Review. Mater. Des. 2022, 221, 110994. [Google Scholar] [CrossRef]
- Agarwal, A.; Mthembu, L. Comparative Analysis of Boron-Al Metal Matix Composite and Aluminum Alloy in Enhancing Dynamic Performance of Vertical-Axis Wind Turbine. Processes 2024, 12, 2288. [Google Scholar] [CrossRef]
- Sonawane, C.R.; Rath, P.; Vats, N.; Patekar, S.; Verma, P.; Pandey, A. Numerical Simulation to Evaluate the Thermal Performance of Engine Cylinder Fins: Effect of Fin Geometry and Fin Material. Mater. Today Proc. 2022, 49, 1590–1598. [Google Scholar] [CrossRef]
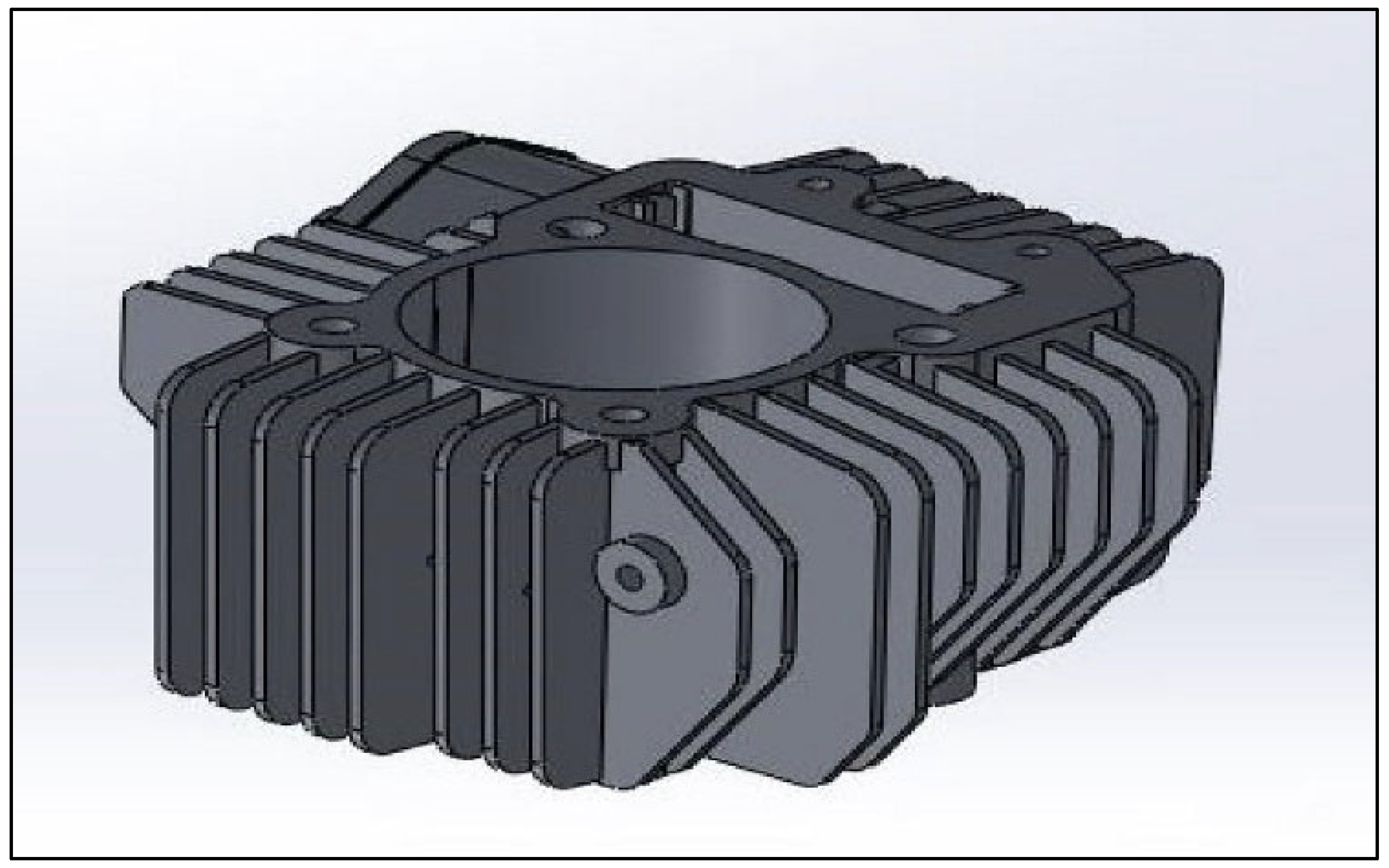










| Parameter | Value |
|---|---|
| Stroke | 49.5 mm |
| Bore | 50 mm |
| No. of fins | 6 |
| Fin pitch (mm) | 7 |
| Fin thickness (mm) | 3 |
| Fin material | Cast iron |
| Number of Elements | Temperature (K) |
|---|---|
| 81,546 | 305.1 |
| 82,145 | 306.4 |
| 83,549 | 306.5 |
| 84,256 | 307.8 |
| 84,569 | 307.8 |
| Optimization Study | |
|---|---|
| Minimize P1; P1 <= 549 k | Goal, minimize P1 (default importance); strict constraint, P1 values less than or equals to 549 K (default importance) |
| Minimize P2; P2 <= 5300 W/m2 | Goal, minimize P2 (default importance); strict constraint, P2 values less than or equals to 5300 W/m2 (default importance) |
| Maximize P3 | Goal, maximize P3 (default importance) |
| Maximize P4 | Goal, maximize P4 (default importance) |
| Design Point | P3-Length (mm) | P4-Width (mm) | P1-Temperature Probe Maximum Temperature (K) | P2-Heat Flux Probe Minimum Total (W/m2) |
|---|---|---|---|---|
| 1 | 117.13 | 121.635 | 567.0899719 | 5740.224301 |
| 2 | 117.39 | 135.135 | 557.2738098 | 6969.619151 |
| 3 | 117.65 | 128.385 | 562.361853 | 6390.156727 |
| 4 | 117.91 | 141.885 | 551.3477539 | 7233.406658 |
| 5 | 118.17 | 125.01 | 564.4932312 | 5962.532627 |
| 6 | 118.43 | 138.51 | 554.1000427 | 7005.728446 |
| 7 | 118.69 | 131.76 | 559.4509338 | 6529.746769 |
| 8 | 118.95 | 145.26 | 547.9578308 | 7225.314662 |
| 9 | 119.21 | 123.3225 | 565.1445068 | 5606.025618 |
| 10 | 119.47 | 136.8225 | 555.1293396 | 6765.61932 |
| 11 | 119.73 | 130.0725 | 560.2942566 | 6224.146702 |
| 12 | 119.99 | 143.5725 | 549.1270508 | 7028.968602 |
| 13 | 120.25 | 126.6975 | 562.4623474 | 5810.567217 |
| 14 | 120.51 | 140.1975 | 551.8947205 | 6819.6902 |
| 15 | 120.77 | 133.4475 | 557.3109802 | 6353.461488 |
| 16 | 121.03 | 146.9475 | 545.6858887 | 7018.54887 |
| 17 | 121.29 | 122.47875 | 564.7088989 | 5182.492672 |
| 18 | 121.55 | 135.97875 | 554.9860596 | 6431.141529 |
| 19 | 121.81 | 129.22875 | 559.9961304 | 5837.584318 |
| 20 | 122.07 | 142.72875 | 549.0932373 | 6736.400213 |
| 21 | 122.33 | 125.85375 | 562.0661377 | 5409.426697 |
| 22 | 122.59 | 139.35375 | 551.7786926 | 6498.572212 |
| 23 | 122.85 | 132.60375 | 557.0473389 | 5990.671368 |
| 24 | 123.11 | 146.10375 | 545.6727966 | 6734.215435 |
| 25 | 123.37 | 124.16625 | 562.6366333 | 5070.445399 |
| 26 | 123.63 | 137.66625 | 552.7248596 | 6242.656236 |
| 27 | 123.89 | 130.91625 | 557.807959 | 5696.35007 |
| 28 | 124.15 | 144.41625 | 546.7604431 | 6541.721514 |
| 29 | 124.41 | 127.54125 | 559.91297 | 5294.350943 |
| 30 | 124.67 | 141.04125 | 549.459967 | 6319.591139 |
| 31 | 124.93 | 134.29125 | 554.7904724 | 5833.608594 |
| 32 | 125.19 | 147.79125 | 543.292395 | 6550.565582 |
| 33 | 125.45 | 122.05687 | 562.8096985 | 4523.352965 |
| 34 | 125.71 | 135.55687 | 553.4365601 | 5824.17605 |
| 35 | 125.97 | 128.80687 | 558.2475952 | 5195.91973 |
| 36 | 126.23 | 142.30687 | 547.678717 | 6188.668439 |
| 37 | 126.49 | 125.43187 | 560.1883606 | 4772.796432 |
| 38 | 126.75 | 138.93187 | 550.2454895 | 5922.780754 |
| 39 | 127.01 | 132.18187 | 555.3192505 | 5362.855782 |
| 40 | 127.27 | 145.68187 | 544.2703308 | 6218.651307 |
| 41 | 127.53 | 123.74437 | 560.6398682 | 4437.160012 |
| 42 | 127.79 | 137.24437 | 551.0786804 | 5666.833954 |
| 43 | 128.05 | 130.49437 | 555.9632935 | 5077.768478 |
| 44 | 128.31 | 143.99437 | 545.2502197 | 6024.683051 |
| 45 | 128.57 | 127.11937 | 557.939978 | 4665.187214 |
| 46 | 128.83 | 140.61937 | 547.8320679 | 5772.503137 |
| 47 | 129.09 | 133.86937 | 552.9684204 | 5246.437272 |
| 48 | 129.35 | 147.36937 | 541.7963623 | 6066.769987 |
| 49 | 129.61 | 122.90062 | 559.8994202 | 4064.157068 |
| 50 | 129.87 | 136.40062 | 550.6368164 | 5351.727535 |
| 51 | 130.13 | 129.65062 | 555.3633179 | 4730.951224 |
| 52 | 130.39 | 143.15062 | 544.9259399 | 5736.147703 |
| 53 | 130.65 | 126.27562 | 557.2427734 | 4312.210891 |
| 54 | 130.91 | 139.77562 | 547.423407 | 5467.564964 |
| 55 | 131.17 | 133.02562 | 552.4074463 | 4906.922827 |
| 56 | 131.43 | 146.52562 | 541.4994873 | 5786.779727 |
| 57 | 131.69 | 124.58812 | 557.6198792 | 4012.067467 |
| 58 | 131.95 | 138.08812 | 548.1778015 | 5222.592291 |
| 59 | 132.21 | 131.33812 | 552.9744934 | 4621.83869 |
| 60 | 132.47 | 144.83812 | 542.4005493 | 5587.637089 |
| 61 | 132.73 | 127.96312 | 554.8890747 | 4242.300543 |
| 62 | 132.99 | 141.46312 | 544.9122375 | 5330.447908 |
| 63 | 133.25 | 134.71312 | 549.9561829 | 4802.859318 |
| 64 | 133.51 | 148.21312 | 538.9321655 | 5642.574958 |
| 65 | 133.77 | 121.8459 | 557.8023438 | 3473.322464 |
| 66 | 134.03 | 135.3459 | 549.0212158 | 4764.084053 |
| 67 | 134.29 | 128.5959 | 553.4863953 | 4120.3156 |
| 68 | 134.55 | 142.0959 | 543.5063843 | 5189.862581 |
| 69 | 134.81 | 125.2209 | 555.2061218 | 3723.137789 |
| 70 | 135.07 | 138.7209 | 545.8576111 | 4896.003902 |
| 71 | 135.33 | 131.9709 | 550.5871948 | 4317.732674 |
| 72 | 135.59 | 145.4709 | 540.1228699 | 5267.76048 |
| 73 | 135.85 | 123.5334 | 555.4531006 | 3439.519901 |
| 74 | 136.11 | 137.0334 | 546.4879822 | 4657.310405 |
| 75 | 136.37 | 130.2834 | 551.026709 | 4053.495899 |
| 76 | 136.63 | 143.7834 | 540.9054932 | 5072.047784 |
| 77 | 136.89 | 126.9084 | 552.7838806 | 3674.591077 |
| 78 | 137.15 | 140.4084 | 543.2735046 | 4793.554788 |
| 79 | 137.41 | 133.6584 | 548.065802 | 4233.895729 |
| 80 | 137.67 | 147.1584 | 537.4812378 | 5150.085797 |
| 81 | 137.93 | 122.6896 | 554.4274658 | 3145.558231 |
| 82 | 138.19 | 136.1896 | 545.7613892 | 4361.00811 |
| 83 | 138.45 | 129.4396 | 550.1418518 | 3757.250785 |
| 84 | 138.71 | 142.9396 | 540.3026489 | 4787.572671 |
| 85 | 138.97 | 126.0646 | 551.8049683 | 3383.136113 |
| 86 | 139.23 | 139.5646 | 542.5856384 | 4512.958036 |
| 87 | 139.49 | 132.8146 | 547.2244934 | 3947.428553 |
| 88 | 139.75 | 146.3146 | 536.9121765 | 4883.55314 |
| 89 | 140.01 | 124.3771 | 551.986853 | 3114.801354 |
| 90 | 140.27 | 137.8771 | 543.1440491 | 4270.544368 |
| 91 | 140.53 | 131.1271 | 547.5952515 | 3698.249939 |
| 92 | 140.79 | 144.6271 | 537.6216187 | 4682.196593 |
| 93 | 141.05 | 127.7521 | 549.2950806 | 3345.591707 |
| 94 | 141.31 | 141.2521 | 539.9206299 | 4407.400711 |
| 95 | 141.57 | 134.5021 | 544.6202454 | 3875.893848 |
| 96 | 141.83 | 148.0021 | 534.1936707 | 4766.812185 |
| 97 | 142.09 | 122.26781 | 551.5043091 | 2748.905208 |
| 98 | 142.35 | 135.76781 | 543.194281 | 3911.140046 |
| 99 | 142.61 | 129.01781 | 547.374762 | 3316.911719 |
| 100 | 142.87 | 142.5178 | 537.8911194 | 4339.659693 |
| Design Genetic | Length (mm) | Width (mm) | Heat Flux (W/m2) |
|---|---|---|---|
| Generic design | 117.13 | 121.635 | 5740.2243 |
| Optimized design (mathematical model) | 118.95 | 145.26 | 7225.31 W/m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agarwal, A.; Dinka, M.O.; Ilunga, M. Enhancing Engine Cylinder Heat Dissipation Capacity Through Direct Optimization (DO) Techniques. Processes 2024, 12, 2659. https://doi.org/10.3390/pr12122659
Agarwal A, Dinka MO, Ilunga M. Enhancing Engine Cylinder Heat Dissipation Capacity Through Direct Optimization (DO) Techniques. Processes. 2024; 12(12):2659. https://doi.org/10.3390/pr12122659
Chicago/Turabian StyleAgarwal, Abhishek, Megersa Olumana Dinka, and Masengo Ilunga. 2024. "Enhancing Engine Cylinder Heat Dissipation Capacity Through Direct Optimization (DO) Techniques" Processes 12, no. 12: 2659. https://doi.org/10.3390/pr12122659
APA StyleAgarwal, A., Dinka, M. O., & Ilunga, M. (2024). Enhancing Engine Cylinder Heat Dissipation Capacity Through Direct Optimization (DO) Techniques. Processes, 12(12), 2659. https://doi.org/10.3390/pr12122659







