Numerical Investigation of Complex Hydraulic Fracture Propagation in Shale Formation
Abstract
1. Introduction
2. Governing Equation
2.1. Stress Equilibrium Equation
2.2. Fracturing Fluid Flow Equation
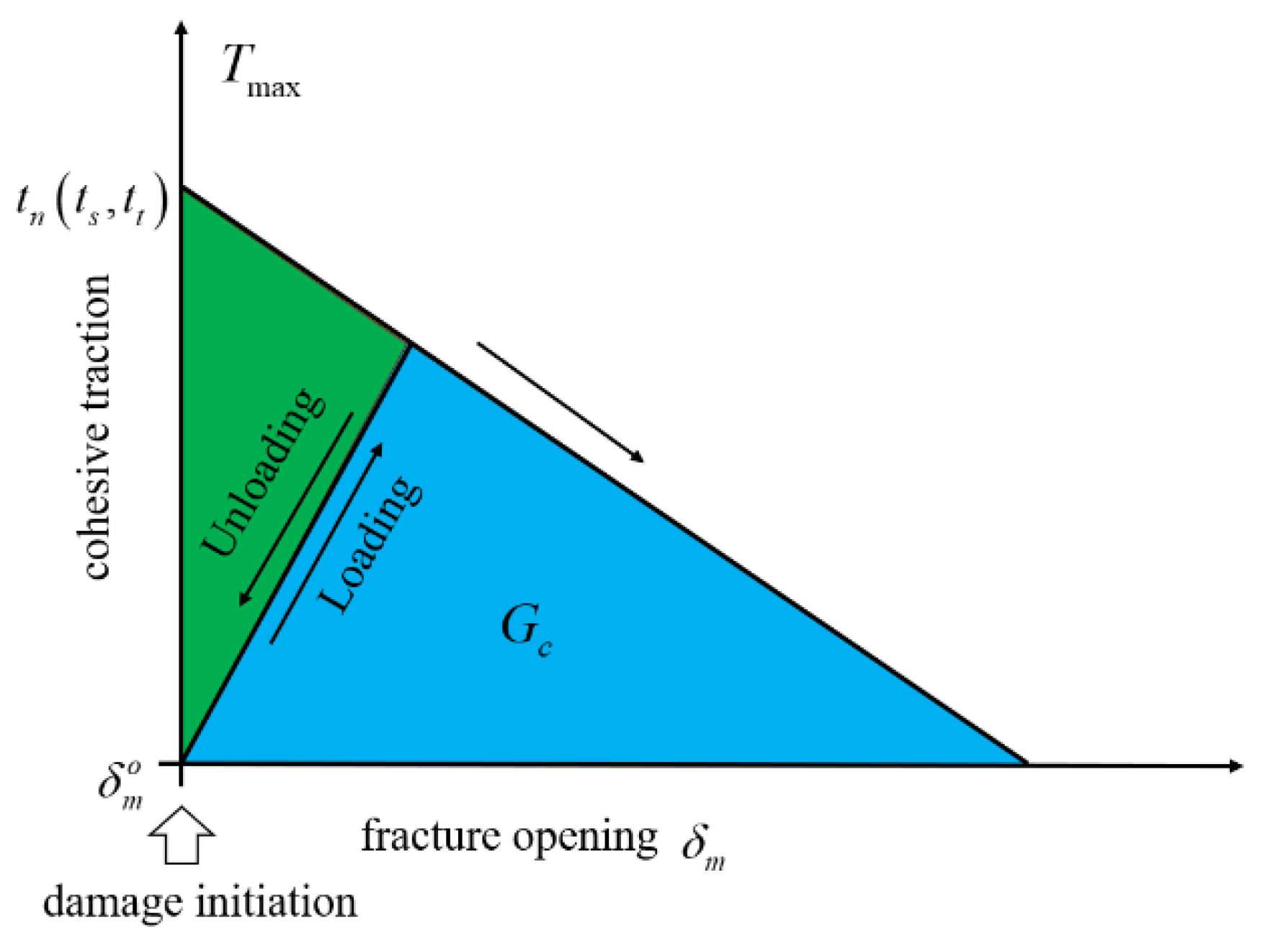
2.3. Fracture Propagation Criterion
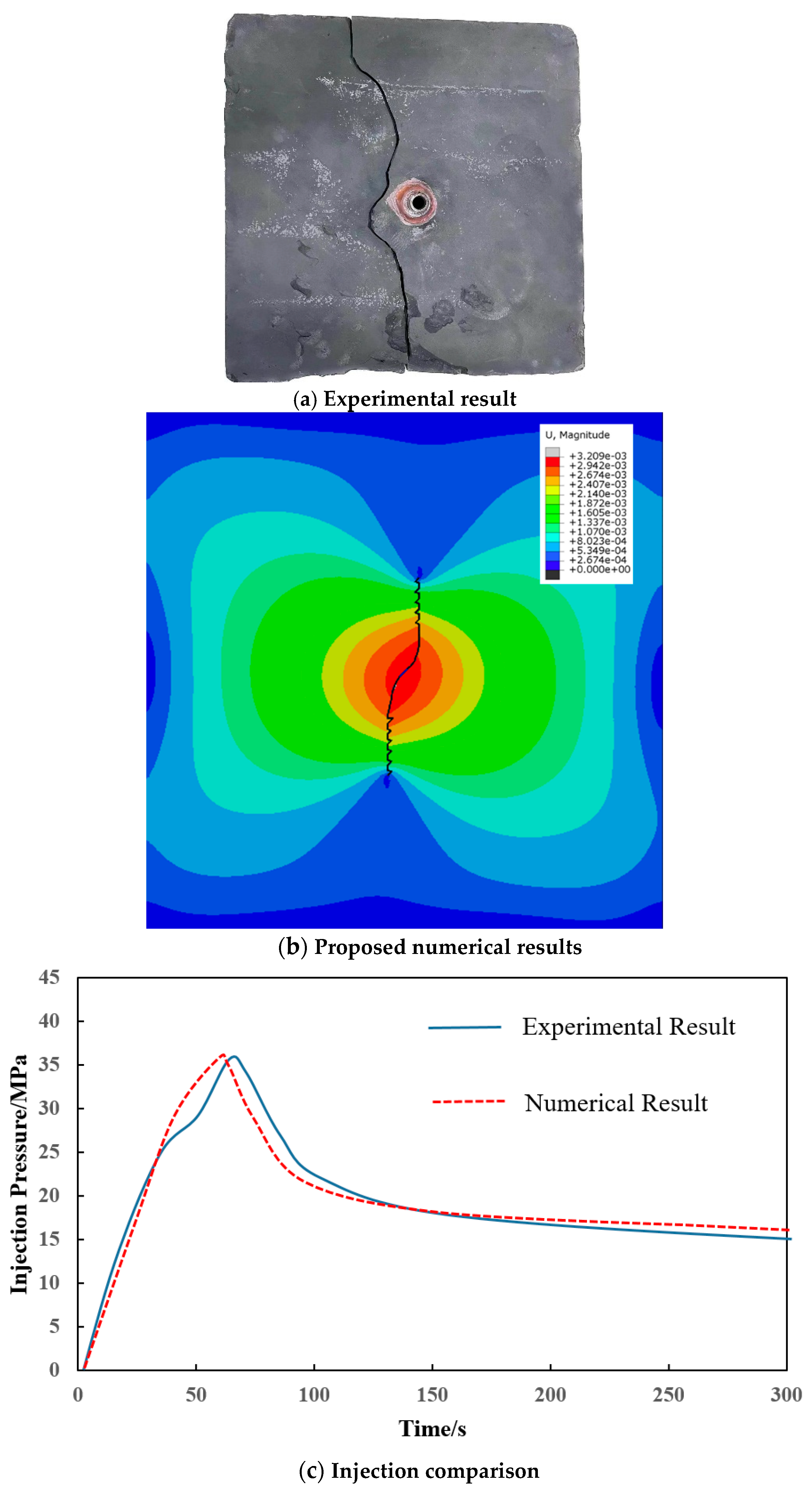
2.4. Verification
3. Simulation and Discussion
3.1. Model Description
3.2. Discussion
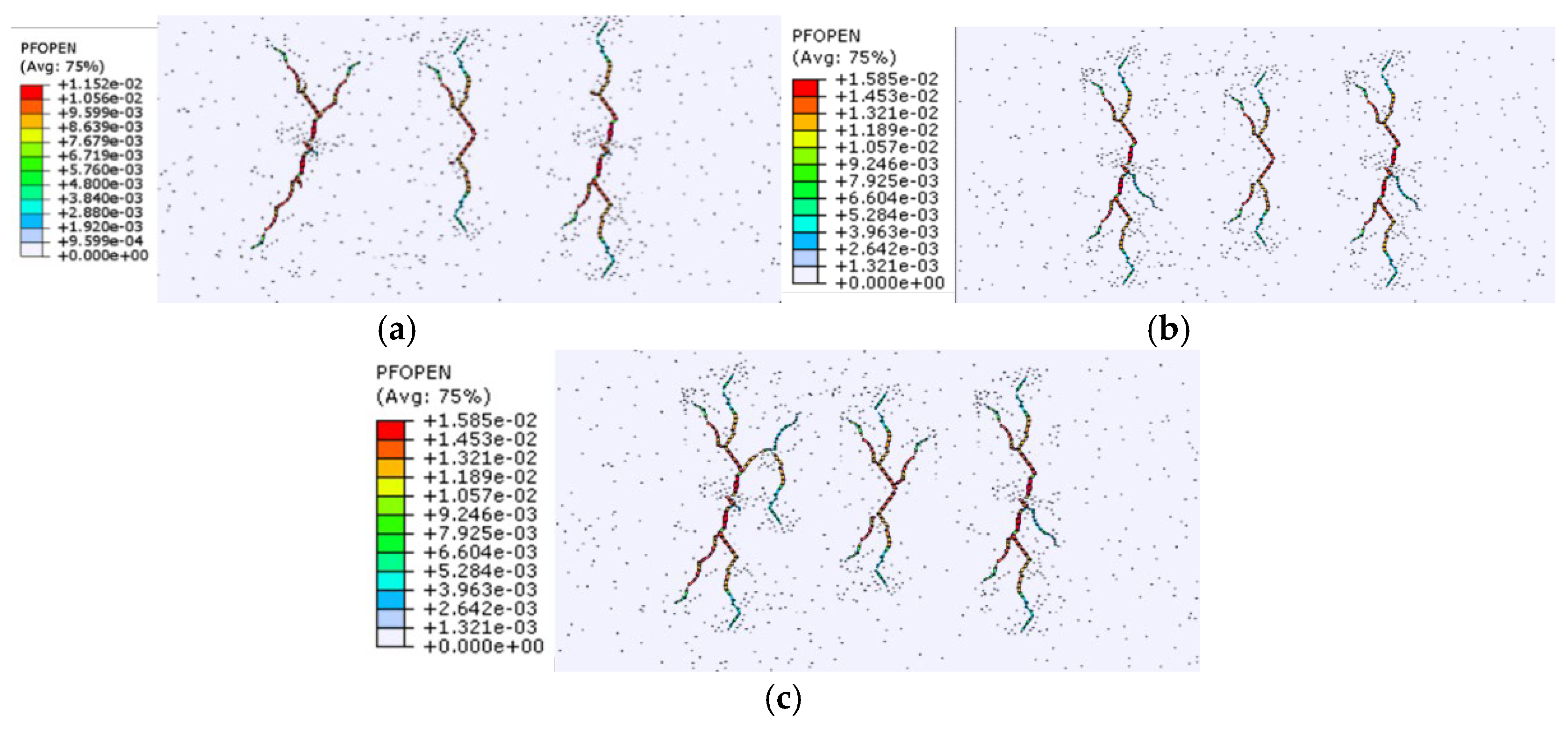
3.2.1. Injection Rate of Fracturing Fluid on Fracture Propagation
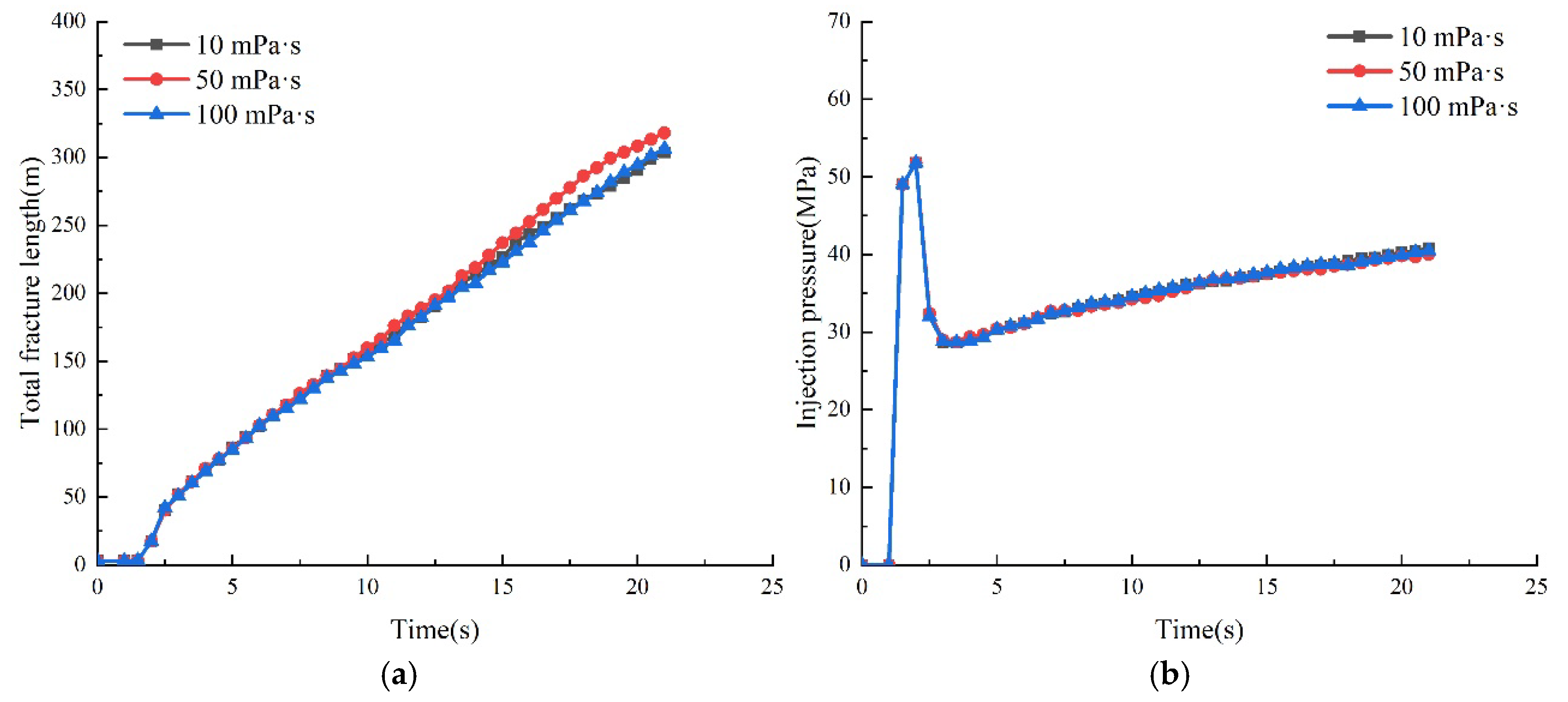
3.2.2. Influence of Viscosity of Fracturing Fluid on Fracture Propagation
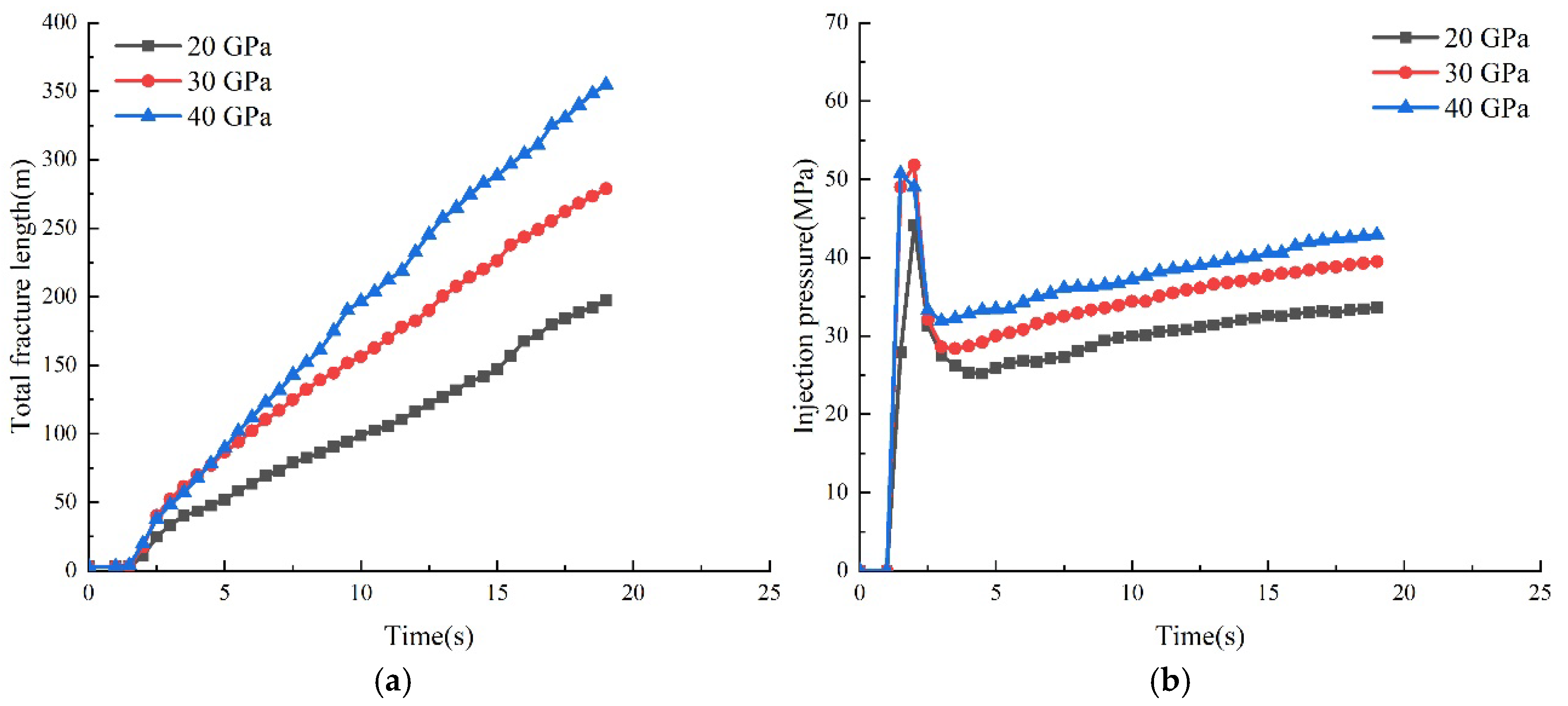
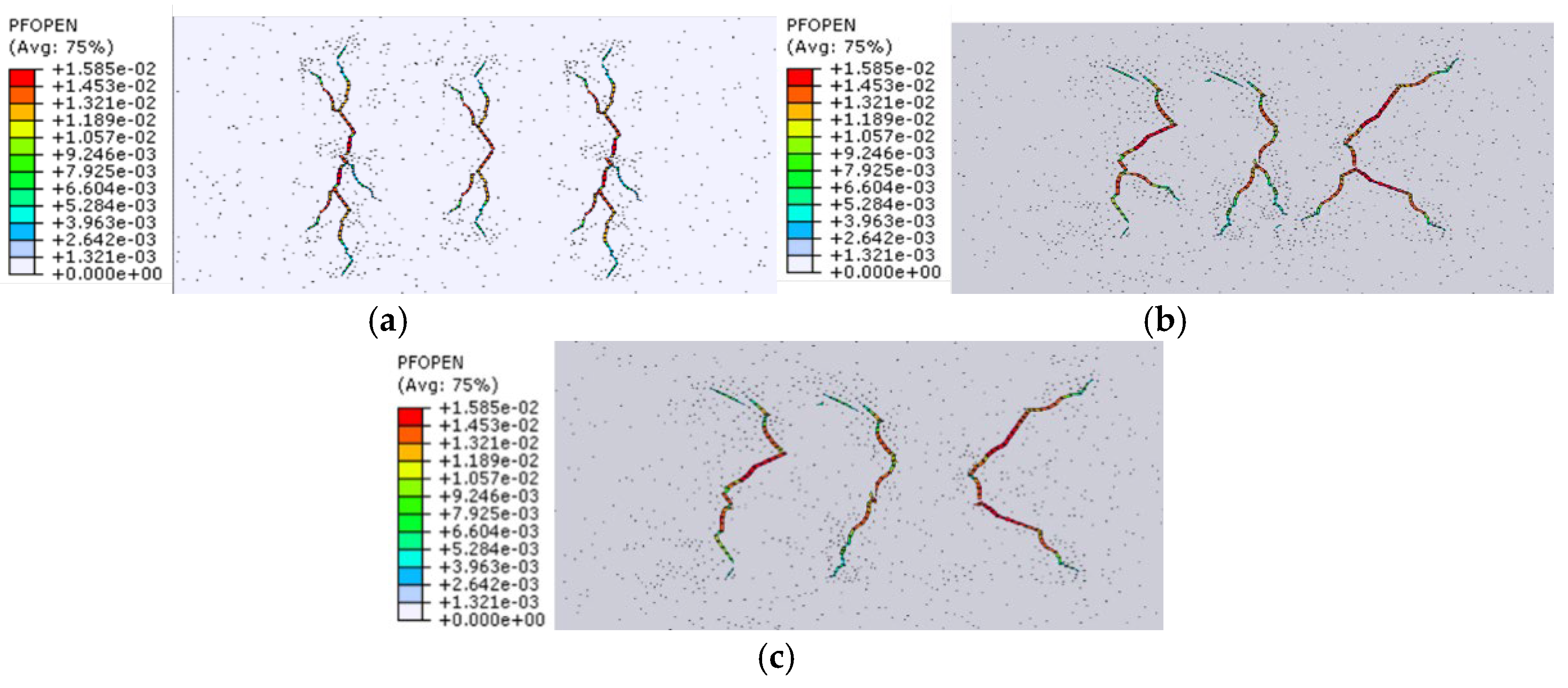
3.2.3. Influence of Elastic Modulus on Fracture Propagation
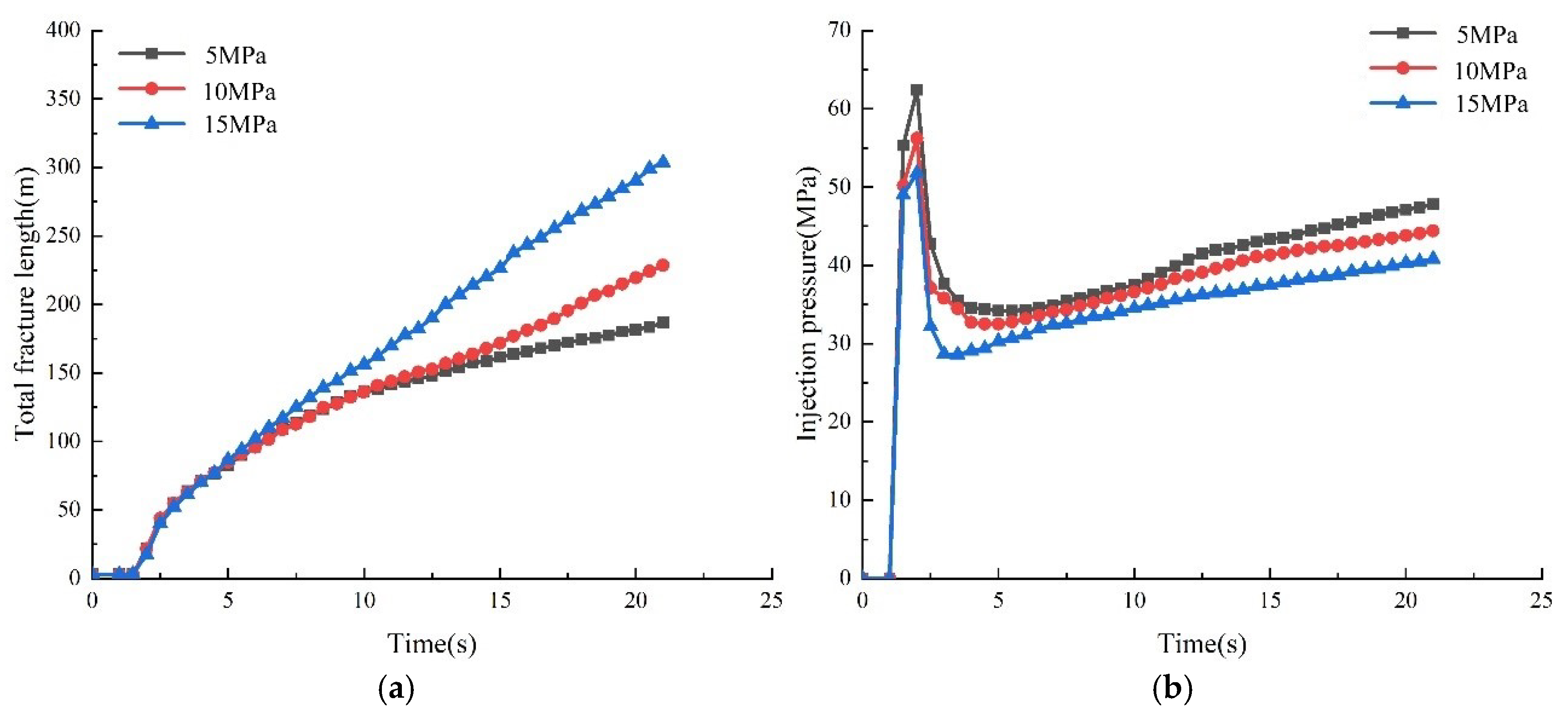
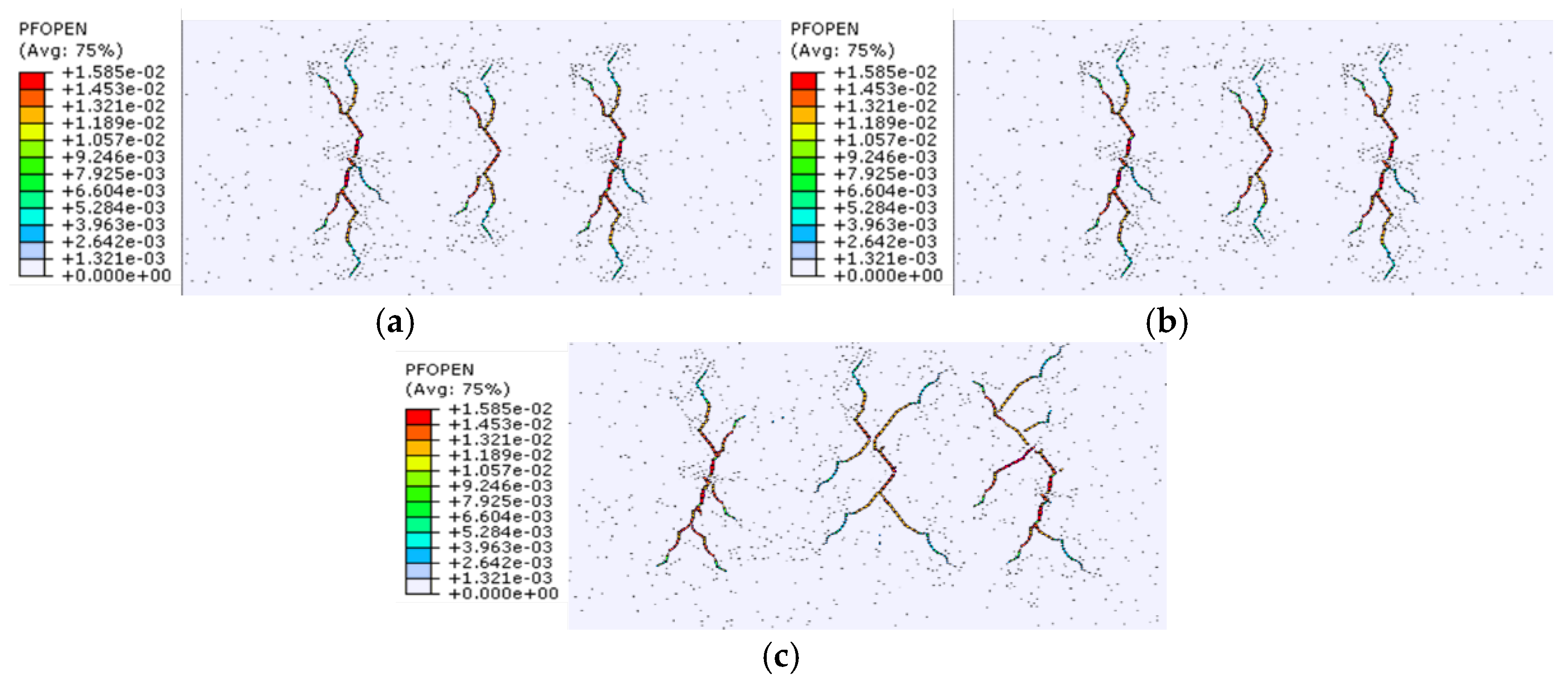
3.2.4. Influence of Horizontal Stress Differences on Fracture Propagation
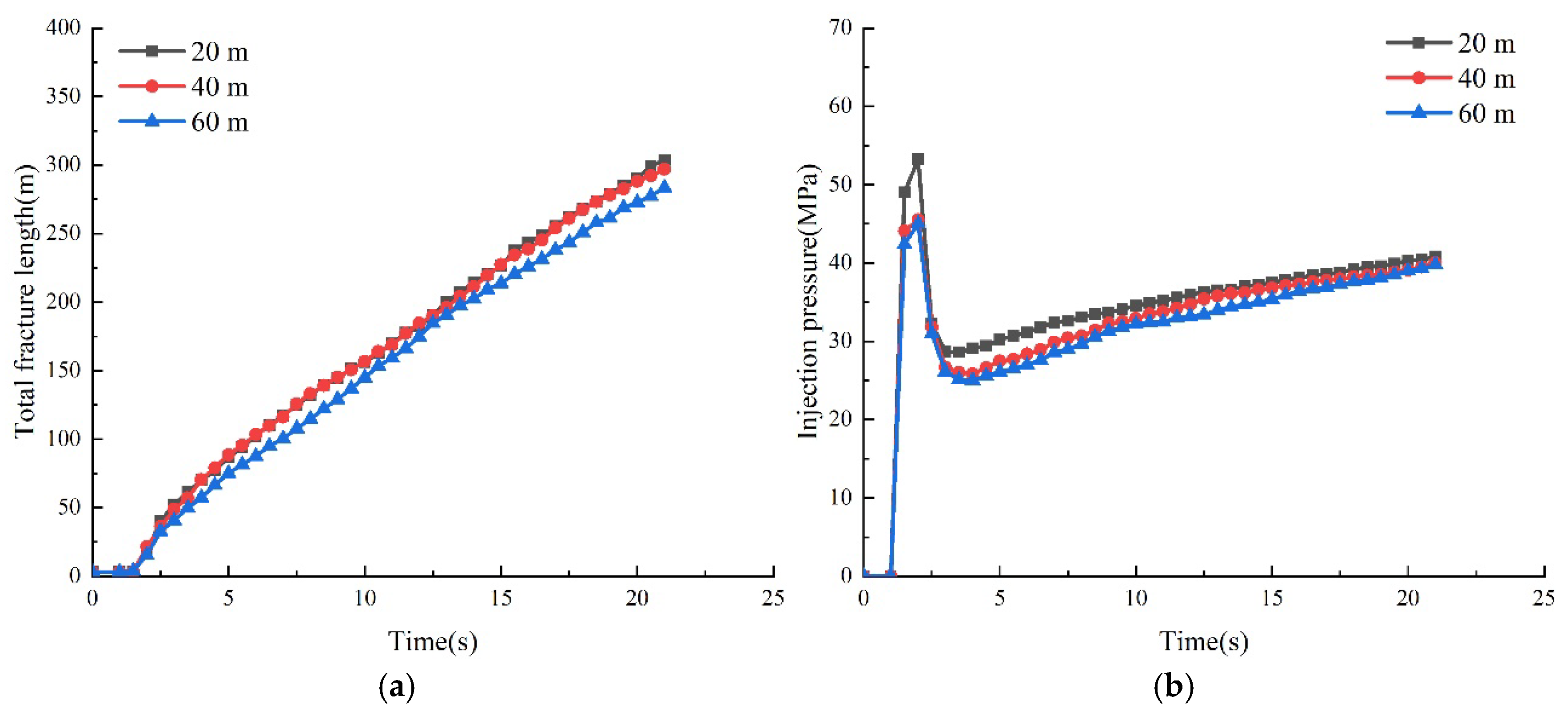
3.2.5. Influence of Cluster Space on Fracture Propagation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, J.; Wang, X.; Guo, J.; Zeng, F.; Zhang, Q. Composite linear flow model for multi-fractured horizonal wells in tight sand reservoirs with the threshold pressure gradient. J. Pet. Sci. Eng. 2018, 165, 890–912. [Google Scholar] [CrossRef]
- Wang, Z.L.; Lou, Y.; Pan, J.P. China’s Oil & gas resources exploration and development and its prospect. Explor. Prod. 2017, 25, 1–6. [Google Scholar]
- Wang, K.; Zhang, H.L.; Zhang, R.H.; Wang, J.P.; Dai, J.S.; Yang, X.J. Characteristics and influencing factors of ultra-deep shale reservoir structural fracture: A case study of Keshen-2 gas field, Tarim Basin. Acta Petrol. Sin. 2016, 37, 714–727. [Google Scholar]
- Yang, T.; Zhang, G.S.; Liang, K.; Zheng, M.; Guo, B.J. The exploration of global shale gas and forecast of the development tendency in China. Strateg. Study CAE 2012, 14, 64–68. [Google Scholar]
- Zeng, L.B.; Ke, S.Z.; Liu, Y. Research Methods of Low Permeability Oil and Gas Reservoir Fractures; Petroleum Industry Press: Beijing, China, 2010; pp. 1–187. [Google Scholar]
- Olson, J.E.; Laubach, S.E.; Eichhubl, P. Estimating natural fracture producibility in tight gas sandstones, coupling diagenesis with geomechanical modeling. Lead. Edge 2010, 29, 1494–1499. [Google Scholar] [CrossRef]
- Zeng, L.; Liu, W.; Li, J.; Zhu, L.; Weng, J.; Yue, F.; Zu, K. Natural fractures and their influence on shale gas enrichment Sichuan Basin, China. J. Pet. Sci. Eng. 2016, 30, 1–9. [Google Scholar] [CrossRef]
- Liu, W.; Zeng, L.; Zhang, B.; Miao, F.; Lyu, P.; Dong, S. Influence of natural fractures on gas accumulation in the Upper Triassic tight gas sandstones in the northwestern Sichuan Basin, China. Mar. Pet. Geol. 2017, 83, 60–72. [Google Scholar] [CrossRef]
- Fisher, M.K.; Wright, C.A.; Davidson, B.M.; Steinsberger, N.P.; Buckler, W.S.; Goodwin, A.; Fielder, E.O. Integrating fracture mapping technologies to optimize stimulations in the Barnett shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. SPE-77411. [Google Scholar]
- Zheng, H.; Liao, R.; Cheng, N.; Shi, S.; Liu, D. Study of mechano-chemical effects on the morphology of hydraulic fractures. J. Pet. Sci. Eng. 2021, 206, 109031. [Google Scholar] [CrossRef]
- Maxwell, S.C.; Urbanci, K.T.; Steinsberger, N.P.; Zinno, R. Microseismic imaging of hydraulci fracture complexity in the barnett shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. SPE-77440. [Google Scholar]
- Perkins, T.K.; Kern, L.R. Width of hydraulic fractures. J. Pet. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Gu, H.; Weng, X. Criterion for fractures crossing frictional interfaces at nonorthogonal angles. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. ARMA-10-198. [Google Scholar]
- Tan, P.; Jin, Y.; Han, K.; Hou, B.; Chen, M.; Guo, X.; Gao, J. Analysis of hydraulic fracture initiation and vertical propagation behavior in laminated shale formation. Fuel 2017, 206, 482–493. [Google Scholar] [CrossRef]
- Zhang, H.; Sheng, J.J. Numerical simulation and optimization study of the complex fracture network in naturally fractured reservoirs. J. Pet. Sci. Eng. 2020, 195, 107726. [Google Scholar] [CrossRef]
- Rui, Z.; Guo, T.; Feng, Q.; Qu, Z.; Qi, N.; Gong, F. Influence of gravel on the propagation pattern of hydraulic fracture in the conglomerate reservoir. J. Pet. Sci. Eng. 2018, 165, 627–639. [Google Scholar] [CrossRef]
- Zhang, G.; Sun, S.; Chao, K.; Niu, R.; Liu, B.; Li, Y.; Wang, F. Investigation of the nucleation, propagation and coalescence of hydraulic fractures in conglomerate reservoirs using a coupled fluid loe-DEM approach. Powder Technol. 2019, 354, 301–313. [Google Scholar] [CrossRef]
- Chen, M.; Sun, Y.; Fu, P.; Carrigan, C.R.; Lu, Z.; Tong, C.H.; Buscheck, T.A. Surrogate-based optimization of hydraulic fracture in pre-existing fracture networks. Comput. Geosci. 2013, 58, 69–79. [Google Scholar] [CrossRef]
- Wang, H.Y. Hydraulic fracture propagation in naturally fractures reservoirs: Complex fracture or fracture networks. J. Nat. Gas Sci. Eng. 2019, 68, 102911. [Google Scholar] [CrossRef]
- Wei, Y.S.; Wang, J.L.; Yu, W.; Qi, Y.D.; Miao, J.J.; Yuan, H.; Liu, C.X. A smart productivity evaluation method for shale gas wells based on 3D fractal fracture network model. Pet. Explor. Dev. 2021, 48, 787–796. [Google Scholar] [CrossRef]
- Wan, X.C.; Rasouli, V.; Damjance, B.; Yu, W.; Xie, H.; Li, N.; Rabiei, M.; Miao, J.; Liu, M. Coupling of fracture model with reservoir to simulate shale gas production with complex fractures and nanopores. J. Pet. Sci. Eng. 2020, 193, 107422. [Google Scholar] [CrossRef]
- Sobhaniaraghn, B.; Mansur, W.J.; Peter, F.C. Three-dimensional investigation of multiple stage hydraulic fracturing in unconventional reservoirs. J. Pet. Sci. Eng. 2016, 146, 1063–1078. [Google Scholar] [CrossRef]
- Khoei, A.R.; Vahab, M.; Ehsani, H.; Rafieerad, M. XFEM modeling of large plasticity deformation; a convergence study on various blending strategies for weak discontinuities. Eur. J. Comput. Mech. 2015, 24, 79–106. [Google Scholar] [CrossRef]
- Hanks, C.L.; Lorenz, J.; Teufel, L.; Krumhardt, A.P. Lithologic and structural controls on natural fracture distribution and behavior within the Lisburne Group, northeastern Brooks Range and North Slope subsurface, Alaska. AAPG Bull. 1997, 81, 1700–1720. [Google Scholar]



| Parameter | Value |
|---|---|
| Injection rate | 8 m3/min |
| Young’s modulus | 35 GPa |
| Poisson’s ratio | 0.35 |
| The minimum horizontal stress | 36 MPa |
| The maximum horizontal stress | 41 MPa |
| Fluid leak-off parameter | 1 × 10−6 m3/Pa·s |
| Fluid viscosity | 10 mPa·s |
| Formation porosity | 0.15 |
| Size of the study area | 400 × 200 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, H.; Li, F.; Wang, D. Numerical Investigation of Complex Hydraulic Fracture Propagation in Shale Formation. Processes 2024, 12, 2630. https://doi.org/10.3390/pr12122630
Zheng H, Li F, Wang D. Numerical Investigation of Complex Hydraulic Fracture Propagation in Shale Formation. Processes. 2024; 12(12):2630. https://doi.org/10.3390/pr12122630
Chicago/Turabian StyleZheng, Heng, Fengxia Li, and Di Wang. 2024. "Numerical Investigation of Complex Hydraulic Fracture Propagation in Shale Formation" Processes 12, no. 12: 2630. https://doi.org/10.3390/pr12122630
APA StyleZheng, H., Li, F., & Wang, D. (2024). Numerical Investigation of Complex Hydraulic Fracture Propagation in Shale Formation. Processes, 12(12), 2630. https://doi.org/10.3390/pr12122630





