Comprehensive Analysis of the Annulus Pressure Buildup in Wells with Sustained Gas Leakage Below the Liquid Level

Abstract

During the process of natural gas development, sustained casing pressure (SCP) frequently occurs within the annulus of the gas wells; we specifically referred to the “A” annular space located between the tubing and the production casing in this paper. SCP in an annulus poses a paramount safety challenge, universally acknowledged as a significant threat to gas field development and production, jeopardizing well integrity, personnel safety, and environmental protection. There are multiple factors that contribute to this issue. Due to the multitude of factors contributing to SCP in an annulus and the unclear mechanisms underlying the pressure buildup in wells, an early assessment of downhole leakage risks remains challenging. Hence, this study focused on a comprehensive analysis of the SCP in the annulus of gas wells. A detailed experimental study on the pressure buildup in an annulus due to tubing leakage below the liquid level was conducted, and the variation patterns of the annulus pressure under various leakage conditions were explored. The findings indicated that the equilibrium attainment time of annulus pressure at the wellhead subsequent to tubing leakage decreases with the increase in the pressure difference between the tubing and the casing, the liquid level height, the leakage orifice diameter, and the quantity, while it increases with the increase in the leakage position and gas temperature. According to the theory of gas fluid dynamics, a predictive model of the annulus pressure buildup with sustained gas leakage below the liquid level was proposed, which was well-validated against experimental results, achieving a model accuracy of over 95%. This study provided a theoretical framework for diagnosing SCP in the annulus of gas wells and developing mitigation strategies, thereby contributing to the advancement of the research field and ensuring the safety of industrial operations.

1. Introduction

Sustained casing pressure (SCP) refers to the phenomenon where abnormal gas pressure accumulates at the wellhead and the annular pressure can be re-generated in a short period of the time after pressure relief [1,2,3]. With the increasing demand for natural gas, the proliferation of gas wells has resulted in a prevalent occurrence of SCP, particularly in high-temperature and high-pressure (HTHP) gas wells [4]. HTHP gas wells are defined as those with reservoir temperatures exceeding 150 °C, bottomhole pressures surpassing 150 MPa, and wellhead pressures above 68.9 MPa, commonly found in regions such as the Junggar Basin, Tarim Basin, South China Sea, Gulf of Mexico, and Norwegian Continental Shelf. According to statistics from the Minerals Management Service (MMS), over 8000 gas wells in the Gulf of Mexico exhibit SCP, with more than 50% having SCP in the annulus between the tube and the production casing [5]. In the Tarim Basin of China, SCP in the annulus has been observed in over 90 wells across just two gas fields. In addition, the injection–production wells of gas storage are prone to micro-leakage in the tubing body and joints due to its alternating load under high-volume “strong extraction and injection”, resulting in SCP during long-term service [6,7]. According to oilfield statistics, the rate of pressure buildup in the annulus of Hutubi gas storage located in northwest China’s Xinjiang Uygur Autonomous Region, has reached 54.8%, and the Xiangguosi gas storage in the Sichuan Basin, China, have reported SCP in 30.7% of their wells, posing significant risks to their well integrity and safety [8]. During service, the tubing is constantly exposed to the impact of high-temperature and high-pressure fluid erosion, corrosion, and sand production from the wellbore [9,10]. This has led to an increasing number of leakage failures in both onshore and offshore natural gas wells. Additionally, the failure of the thread compound in high-temperature environments, the poor quality of the field make-up, or the improper selection of tubing joint thread types can also lead to tubing leakage during service. Once high-pressure gas in the tubing flows into the annulus, it can result in the accumulation of pressure at the wellhead and abnormal gas pressure. In severe cases, it can cause damage and failure of the wellhead equipment, leading to major safety accidents [11,12]. According to the statistical analysis of the field cases mentioned earlier, SCP in a gas well is relatively common and poses relatively significant hazards, as illustrated in Figure 1.

Regarding the issue of SCP in gas wells, numerous scholars have conducted relevant research [13,14,15,16]. Oudeman et al. [17] considered the influence of fluid properties on the annular pressure and derived a theoretical model for calculating annular pressure. Bourgoyne et al. [18] first introduced the concept of SCP and statistically analyzed its occurrence frequency. Xu et al. [19,20,21] summarized five types of pressure buildup in annuluses and analyzed, in detail, the process of gas infiltration through the cement sheath, the annulus protective fluid, and the accumulation at the wellhead based on fluid mechanics theory. Rocha-Valadez et al. [22,23] proposed a dynamic analysis method for annular pressure buildup wells based on wellbore integrity management. Gao et al. [24] conducted a series of theoretical derivations and established a model of the interaction between the casing, cement, and formation, which can be used to predict the annular pressure accumulation caused by the thermal expansion of the fluid from the casing and annulus. Yang et al. [25] analyzed the mechanisms of pressure buildup in technical casing and surface casing in offshore gas wells. The ISO/TS 16530-2 standard released in 2014 provided a method for calculating the maximum allowable pressure in the A/B/C annulus of gas wells, enabling operators to conduct a safety assessment of the SCP [26]. For the detection of leak locations in tubing, Johns et al. [27] developed an ultrasonic logging tool for detecting the location of tubing leakage, capable of detecting a leakage orifice of 1 foot and below. Liu et al. [28] proposed a ground-based diagnostic system for detecting SCP in the “A” annulus based on testing leakage acoustic signals, which can effectively identify the location of leakage orifices above the annular protective fluid, but it is still unable to accurately identify leakage information below the liquid level [29]. Unfortunately, there is a paucity of experimental research on the pressure buildup in wells with sustained gas leakages below the liquid level, and the underlying mechanisms remain unclear.

Therefore, the present work is dedicated to a comprehensive study on the pressure buildup in the annulus. We performed a detailed experimental study on the pressure buildup in an annulus resulting from tubing leakage below the liquid level. We explored the effects of various factors, including the pressure difference between the tubing and casing, the liquid level height, the gas temperature, the leakage position, the leakage orifice diameter, and the quantity, on the pressure buildup. Furthermore, based on the theory of gas fluid dynamics, we proposed a computational model to predict the evolution of the annulus pressure with sustained gas leakage below the liquid level. This model was well-verified through experimental results. This work may provide some useful reference for subsequent security evaluations and solution measures for SCP in the annulus.

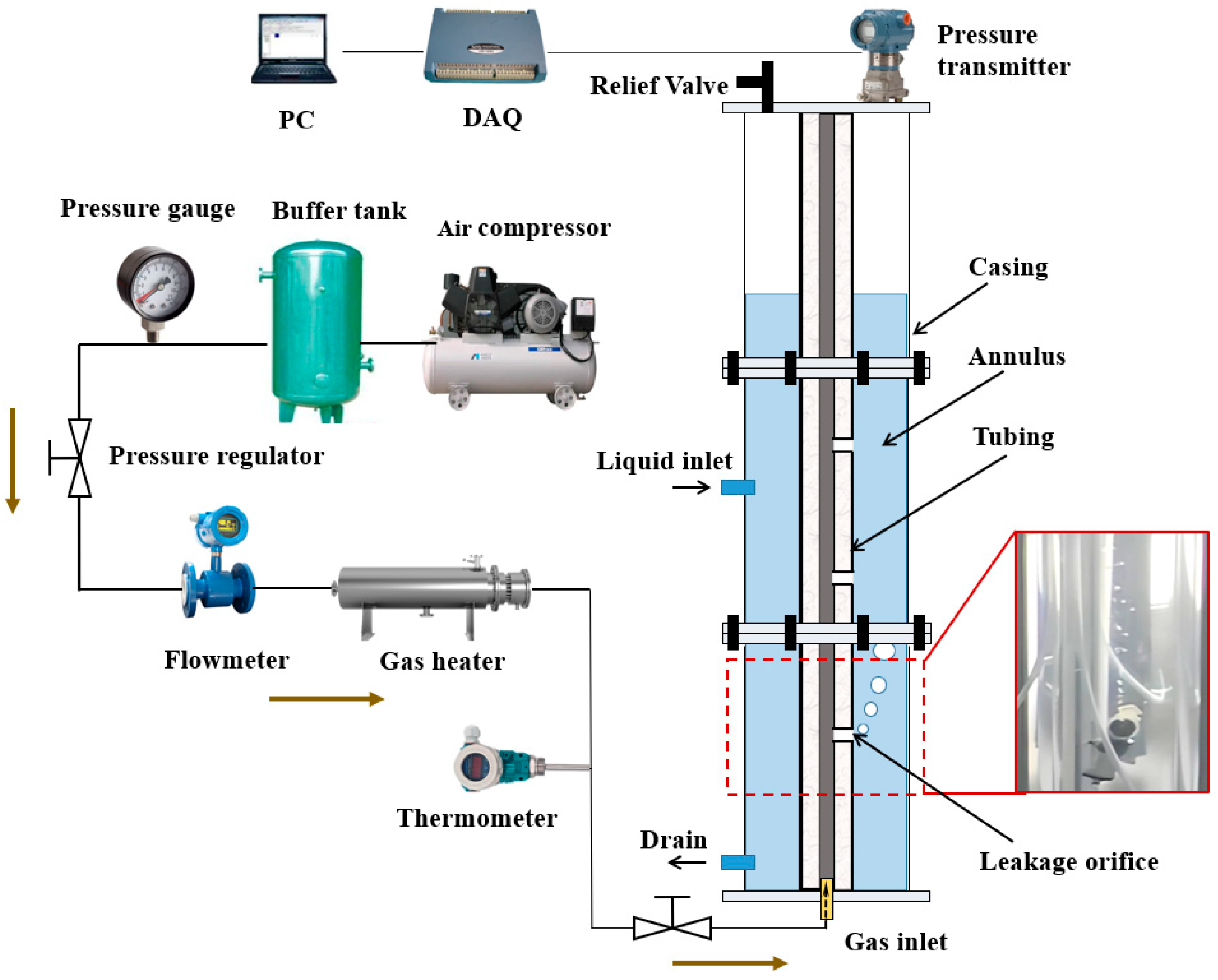
2. Experimental Methodology

2.1. Experimental Setup

In order to analyze the pattern of pressure buildup in the annulus resulting from sustained gas leakage below the liquid level, we have developed a new test apparatus to simulate SCP in the annulus following tubing leakage. The schematic diagram of this apparatus is presented in Figure 2. The test apparatus comprises a gas supply system, a transfer pipeline system, a simulated tubing and casing system, and a pressure monitoring system. The gas supply system consists of an air compressor, a buffer tank, and a pressure regulating valve, which controls the gas volume. The transfer pipeline system incorporates a flow meter, a pressure gauge, a gas temperature control pipe, and an inlet valve, enabling the measurement of the inlet flow rate and pressure through the flowmeter and the pressure gauge. The gas temperature control pipe facilitates rapid heating of the gas within the pipeline. The simulated tubing and casing system features transparent polyvinyl chloride (PVC) tubing (Φ114.3 mm × 7.37 mm) and casing (Φ177.8 mm × 10.36 mm), allowing visualization of the leakage process. Multiple leakage orifices are arranged in the tubing to mimic the leakage characteristics of an oil pipe. Each leakage orifice can be controlled for opening, closing, and adjusting the leakage aperture. Water is used as a substitute for water-based annular protection fluid in the annulus between the tubing and casing. The pressure monitoring system, installed at the top of the annulus, is equipped with a pressure gauge to monitor pressure changes post-tubing leakage and transmit data to a computer in real-time. Furthermore, a needle valve is positioned at the top of the annulus to release pressure, ensuring the complete depressurization of the annulus after each test.

2.2. Experimental Procedure

The factors that affected the pressure buildup in the annulus with sustained gas leakage in our experiments are shown in

Table 1. The parameters and corresponding values involved in the experiments.

Experimental Parameters	Value
Pressure difference between the tubing and casing (KPa)	100, 300, 500, 700
Liquid level height (m)	1, 1.5, 2, 2.5
Gas temperature (°C)	25, 80, 100, 120
Leakage position (m)	0.3, 0.6, 1
Leakage orifice diameter (mm)	0.5, 1, 1.5, 2
Leakage orifice quantity	1, 2, 3

, along with the parameter ranges of each factor. Notably, the leakage location refers to the distance of the leak point from the base of the equipment. The experimental procedure can be described as follows: firstly, the air compressor was started to fill the buffer tank with gas. Then, the pressure regulating valve on the outlet pipeline of the buffer tank was opened to adjust the output pressure. The gas inside the pipeline could be rapidly heated by the gas temperature control pipe. Subsequently, the gas entered the interior of the tubing through an inlet below it, and ultimately flowed into the annulus via the leakage orifice, resulting in an increase in annulus pressure. The change curve of the annulus pressure after the leakage was recorded until the pressure no longer increased and reaches a balanced state, indicating the end of the experiment. Finally, the pressure relief valve was opened to drain the gas pressure in the annulus.

3. Experimental Results and Analysis

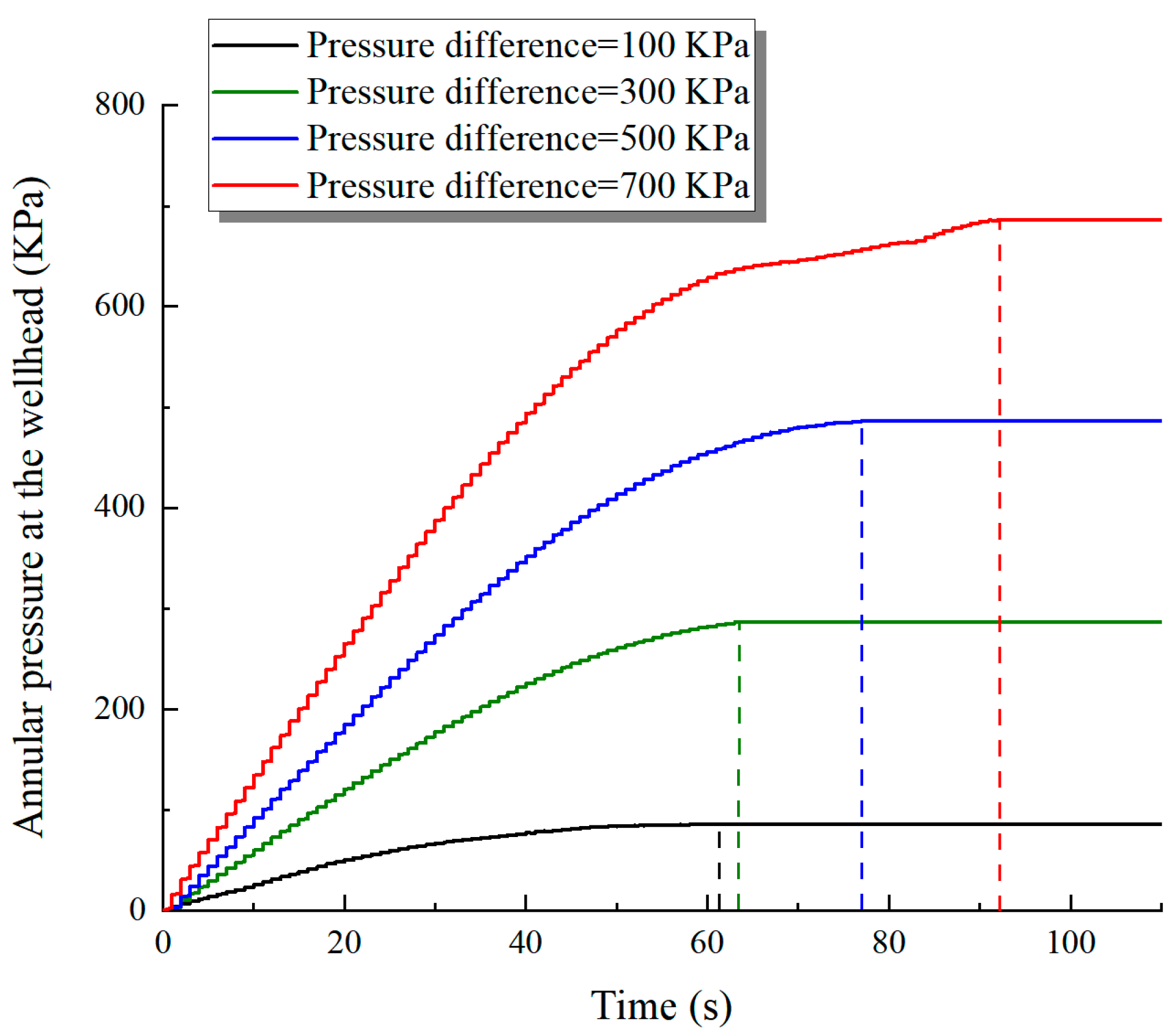
3.1. Effect of Pressure Difference Between the Tubing and Casing

The variations in the annular pressure at the wellhead under various pressure differences between the tubing and casing are shown in Figure 3. The liquid level height was 2 m. The gas temperature was 25 °C. The position of the single leakage orifice was 0.6 m, and its diameter was 1 mm. The pressure differences between the tubing and casing were set to 100 KPa, 300 KPa, 500 KPa, and 700 KPa, respectively. As is evident from the figure, the pressure difference between the tubing and casing had a significant impact on the variation in the annular pressure at the wellhead. Specifically, the larger the pressure difference between the tubing and the casing, the higher the value of the annular pressure at the wellhead after equilibrium. During the initial stage of the leak, due to the large pressure difference, coupled with the relatively low pressure within the annulus, the gas at the leak point was in a critical flow state, leading to a steady increase in the annular pressure at the wellhead. As the annulus pressure gradually increased, the gas flow state transitioned to a subcritical flow state, resulting in a gradual decrease in the gas flow rate at the leakage orifice. Consequently, the rate of increase in the annular pressure at the wellhead gradually slowed down until the annulus–casing pressure differential at the leakage orifice reached zero, at which point the leakage from the tubing ceased.

In accordance with the characteristics of gas flow, the state of gas movement at the leakage orifice could be discernibly classified into two distinct states: critical flow and subcritical flow [30].

For the critical flow

$${\displaystyle \frac{P_2}{P_1}}\le {\left({\displaystyle \frac{2}{k+1}}\right)}^{{\displaystyle \frac{k}{k-1}}}$$

(1)

where P₁ is the pressure on one side of the tubing at the leakage orifice, Kpa; P₂ is the pressure on one side of the annulus at the leakage orifice, Kpa; and k is the adiabatic index of gas.

At the critical flow, Q_c could be expressed as

$$Q_c={\displaystyle \frac{4080P_1{d}_{ch}^2}{\sqrt{{\gamma }_g{T}_1{Z}_1}}}\sqrt{{\displaystyle \frac{k}{k-1}}\left[{\left({\displaystyle \frac{2}{k+1}}\right)}^{{\displaystyle \frac{2}{k-1}}}-{\left({\displaystyle \frac{2}{k+1}}\right)}^{{\displaystyle \frac{k+1}{k-1}}}\right]}$$

(2)

where Q_c is the gas flow rate, m³/d; d_ch is the equivalent diameter of the leakage orifice, mm; γ_g is the relative density of gas; T₁ is the gas temperature in the tubing, K; and Z₁ is the gas deviation factor.

For the subcritical flow

$${\displaystyle \frac{P_2}{P_1}}>{\left({\displaystyle \frac{2}{k+1}}\right)}^{{\displaystyle \frac{k}{k-1}}}$$

(3)

At the subcritical flow, Q_c could be expressed as

$$Q_c={\displaystyle \frac{4080P_1{d}_{ch}^2}{\sqrt{{\gamma }_g{T}_1{Z}_1}}}\sqrt{{\displaystyle \frac{k}{k-1}}\left[{\left({\left({\displaystyle \frac{2}{k+1}}\right)}^{{\displaystyle \frac{k}{k-1}}}\right)}^{{\displaystyle \frac{2}{k}}}-{\left({\left({\displaystyle \frac{2}{k+1}}\right)}^{{\displaystyle \frac{k}{k-1}}}\right)}^{{\displaystyle \frac{k+1}{k}}}\right]}$$

(4)

In addition, P₂ could be solved by the following formula:

$$P_2=P_A+{10}^{-6}{\rho }_{y}g(h_f-h_g)$$

(5)

where P_A is the annular pressure at the wellhead, Kpa; ρ_y is the density of the annulus protection fluid, kg/m³; g is the gravitational acceleration, N/kg; h_f is the liquid level height, m; and h_g is the leakage orifice height, m.

Therefore, it can be inferred that as the tubing pressure at the leakage orifice increases, the gas flow rate at the leakage orifice also increases, resulting in an increase in the rate of annular pressure at the wellhead rise, which can be verified from Figure 3.

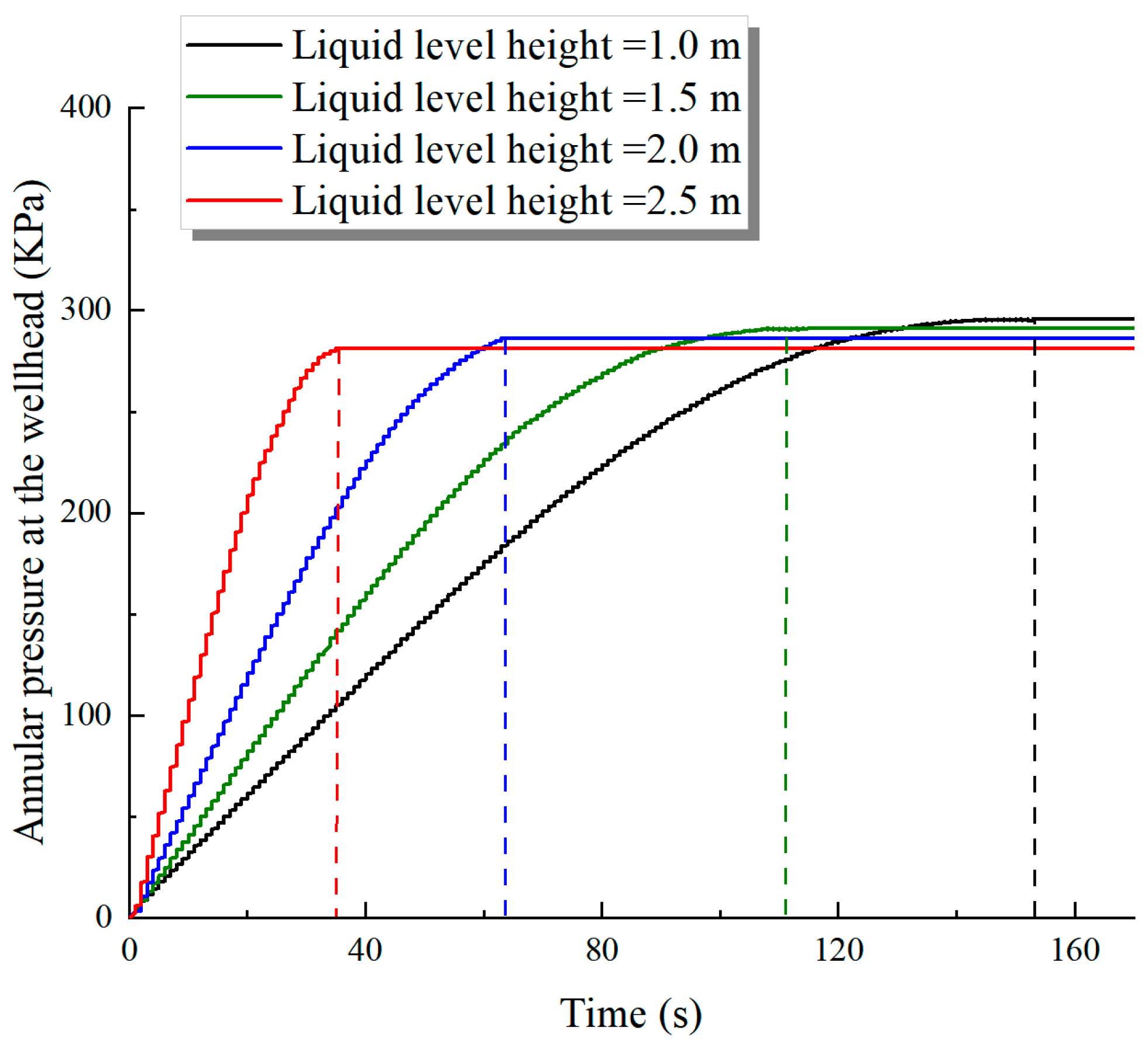
3.2. Effect of Liquid Level Height

Due to variations in the completion design, the liquid level heights of the annular protective fluids in the different gas wells exhibited significant differences. To investigate the effect of the liquid level height on the pressure buildup with sustained gas leakage, we had set the liquid level heights to be 1 m, 1.5 m, 2 m, and 2.5 m, respectively. The pressure difference between the tubing and casing was 300 KPa. The gas temperature was 25 °C. The position of the single leakage orifice was 0.6 m, and its diameter was 1 mm. Figure 4 shows the variation in the annular pressure at the wellhead under various liquid level heights.

As evident from Figure 4, when all the other conditions remained constant, an increase in the level of the annular protection liquid resulted in a corresponding reduction in the air domain above the fluid, leading to a shorter time for the annular pressure at the wellhead to reach equilibrium. Specifically, when the liquid level height was 2.5 m, the time for the annular pressure at the wellhead to reach equilibrium was at its shortest, whereas it was longest at a liquid level of 1 m. Hence, it can be concluded that as the air domain above the fluid decreased, the rate of pressure increased within the annulus after leakage accelerated, resulting in a shorter time to achieve pressure equilibrium. This phenomenon is attributed to the high compressibility of gas, wherein a taller gas cap height necessitates a longer duration for the annular pressure at the wellhead to ascend to its equilibrium value. Furthermore, a higher gas cap height correlates with a greater equilibrium value of the annular pressure at the wellhead, which consequently prolongs the time for the pressure to stabilize. Therefore, in the management of a gas well’s annular pressure, the control of the liquid level height exerts a significant influence on the SCP in an annular.

3.3. Effect of Gas Temperature

Figure 5 shows the variation in annular pressure at the wellhead under various gas temperatures. The gas temperature were 25 °C, 80 °C, 100 °C and 120 °C, respectively. The pressure difference between the tubing and casing was 300 KPa. The liquid level height was 1.5 m. The position of the single leakage orifice was 0.6 m, and its diameter was 1 mm.

It can be seen from Figure 5 that the annular pressure exhibited minimal sensitivity to the temperature variations during the transition to the equilibrium state. As the gas temperature increased, the period during which the annular pressure at the wellhead reached equilibrium slightly elongated. According to Equations (2) and (4), both the critical and subcritical gas flow rates decreased, leading to a slower rise in the annular pressure. This, in turn, resulted in an extended duration for the annular pressure at the wellhead to stabilize at equilibrium. However, due to the cooling effect of the annular protection fluid on the leaked gas, the difference in the pressure buildup caused by the leakage at different gas temperatures was relatively minor.

3.4. Effect of Leakage Position

The identification of a leakage position below the liquid level may pose a significant challenge in diagnosing SCP in an annular. To investigate the effect of the leakage position on the pressure buildup with sustained gas leakage, we had set the leakage positions to be 0.3 m, 0.6 m, and 1 m, respectively. The pressure difference between the tubing and casing was 300 KPa. The gas temperature was 25 °C. The liquid level height was 2 m. The diameter of the single leakage orifice was 1 mm. Figure 6 shows the variation in the annular pressure at the wellhead under various leakage positions.

As depicted in Figure 6, the time required for the annular pressure at the wellhead to reach equilibrium differed across the various leakage locations. This disparity is attributed to the fact that, under the different leakage locations, the pressure at the leakage orifice remained constant. However, as the pressure of the liquid column traversed by the gas post-leakage increased, the gas pressure diminished upon reaching the wellhead, resulting in a shorter duration of pressure buildup. Consequently, when the liquid level height remains unchanged, a lower leakage position below the liquid level leads to a lower pressure at the top of the annulus, subsequently shortening the time required for the pressure to reach equilibrium.

3.5. Effect of Leakage Orifice Diameter

Potential failures in tubing leakage may originate from the corrosion perforation of the pipe body or tiny leakage at the coupling joints, leading to a wide range of leakage orifice diameters. To investigate the effect of the leakage orifice diameter on the pressure buildup during sustained gas leakage, we had set the leakage orifice diameters to be 0.5 mm, 1 mm, 1.5 mm, and 2 mm, respectively. The pressure difference between the tubing and casing was 300 KPa. The gas temperature was maintained at 25 °C. The position of the leakage orifice was at 0.6 m, and the liquid level height was 1.5 m. Figure 7 illustrates the variation in annular pressure at the wellhead under various leakage orifice diameters. As evident from the figure, the leakage orifice diameter significantly influenced the variation in annular pressure at the wellhead after leakage. With the gradual increase in the leakage orifice diameter, the rate of the annulus pressure rise accelerated, and the time required for the pressure to reach equilibrium notably shortened. Specifically, when the leakage orifice diameter was 0.5 mm, the time required for the pressure to reach equilibrium was 184 s, whereas it reduced to merely 15 s for a 2 mm leakage orifice diameter.

The observed pattern of the annular pressure at the wellhead variation with the leakage orifice diameter could also be explained by Equations (2) and (4). As the leakage orifice diameter decreased, the gas flow rate diminished in both the critical and subcritical flow conditions, resulting in a slower rise in the annulus pressure. Consequently, the time required for the annular pressure at the wellhead to reach an equilibrium state increased. Evidently, the magnitude of the leakage orifice diameter in the tubing of the gas wells directly determined the severity of the SCP in the annulus.

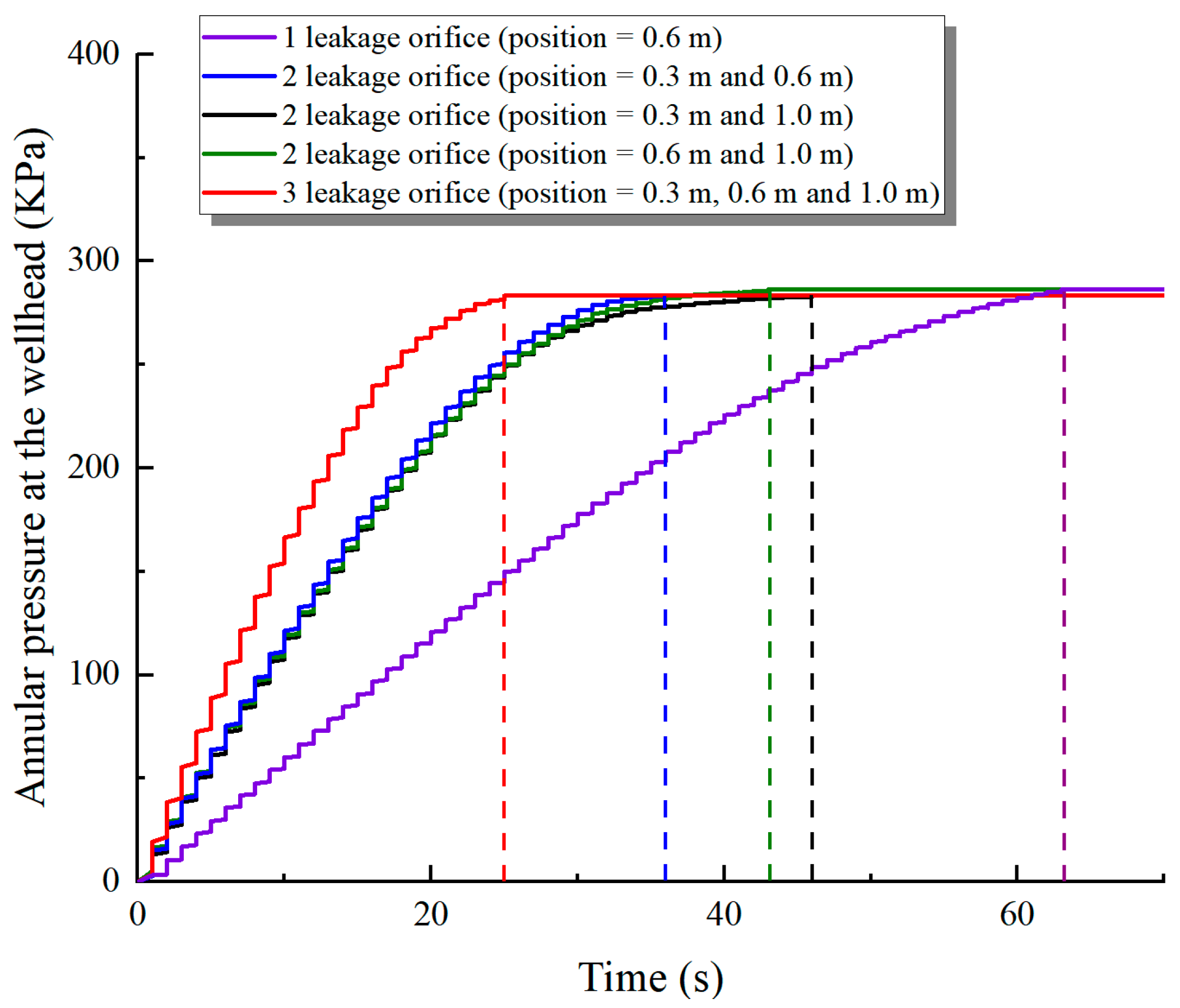
3.6. Effect of Leakage Orifice Quantity

For the gas wells experiencing severe SCP in the annulus, there may be more than one leakage orifice in the tubing. To investigate the effect of the number of leakage orifices on the pressure buildup during sustained gas leakage, we had established five leakage scenarios, involving three different types of leakage orifice quantities. The schematic diagram of these five leakage scenarios is shown in Figure 8. In all the experiments, the liquid level height was 2 m, the gas temperature was 25 °C, and the position of each leakage orifice was 0.6 m with a diameter of 1 mm. The pressure difference between the tubing and casing was set to 300 KPa. Figure 9 illustrates the variation in the annular pressure at the wellhead under various numbers of leakage orifices.

As evident from Figure 9, the rate of annular pressure escalation accelerated with the increasing number of leakage orifices. Notably, when three leakage orifices were present, the time required for the annular pressure at the wellhead to reach equilibrium was the shortest, whereas in the case of a single leakage orifice, this duration was the longest. This trend was attributed to the equivalent enlargement of the effective leakage area as the number of leakage orifices increased, consequently leading to a greater gas leakage flow rate. Furthermore, upon the analysis of the annular pressure values at equilibrium under various operating conditions, it was revealed that the equilibrium annular pressure was determined by the location of the deepest leakage orifice. Irrespective of the varying number of leakage orifices, the final equilibrium annular pressure at the wellhead remained identical, provided that the deepest leakage orifice was positioned at the same depth.

4. Predictive Model of the Pressure Buildup in the Annulus

The transport process of the gas leakage below the liquid surface in the annulus was the upward movement of gas in the form of bubbles in the annulus protection fluid and the gas chamber. Therefore, by analyzing the annulus pressure evolution during the generation of bubbles and the migration towards the top of the annulus, a predictive model of the pressure buildup of the annulus can be established.

4.1. Bubble Generation Below Liquid Surface

When gas from the tubing enters the annulus through a leak hole, it forms bubbles due to the surface tension of the annular fluid. These bubbles undergo a growth process from small to large, during which they are subjected to the combined effects of the gravity force, buoyancy force, and resistance force. If a bubble reaches a certain volume, the upward buoyancy force exceeds the gravity force and resistance force, then the bubble can detach from the leak hole and rise upward. When a bubble is at the critical state of detachment from the leak hole, the force balance equation for the bubble can be given by [31]:

$$F_g-F_l=F_{\sigma }$$

(6)

$$F_g={\displaystyle \frac{1}{6}}\pi d_b^{3}g{\rho }_g$$

(7)

$$F_l={\displaystyle \frac{1}{6}}\pi d_b^{3}g{\rho }_y$$

(8)

$$F_{\sigma }=\pi d_{ch}\sigma cos\theta$$

(9)

where F_g is the gravity of the bubble, N; F_l is the buoyancy of the bubble, N; F_σ is the additional surface force on a bubble, N; d_b is the equivalent diameter of the bubble detachment, m; ρ_g is the gas density at the leakage orifice, kg/m³; ρ_y is the density of the annulus protection fluid, kg/m³, d_ch is the equivalent diameter of the leakage orifice, m; σ is the surface tension of the bubble, N/m; and θ is the angle of the bubble emanating from the leakage orifice.

Thus, it can be inferred that

$${\displaystyle \frac{1}{6}}\pi d_b^{3}g({\rho }_g-{\rho }_y)=\pi d_{ch}\sigma cos\theta$$

(10)

Among these, the surface tension of the bubble and the gas density at the leakage orifice can be expressed by Equations (11) and (12), respectively [21].

$$\sigma =[{\displaystyle \frac{248-1.8T_{1k}}{206}}(76e^{-0.0003625P_2}-52.5+0.00087P_2)+52.5-0.00089P_2]/1000$$

(11)

$${\rho }_g=28.96{\displaystyle \frac{P_2{\gamma }_g}{\mathrm{R}{T}_{1k}}}$$

(12)

where T_1k is the temperature on one side of the annulus at the leakage orifice, K; and R is the gas constant.

Thus, the diameter of the bubble at the instant it detaches from the leak hole can be solved as follows:

$$d_b={\left[{\displaystyle \frac{6\sigma d_{ch}cos\theta }{g({\rho }_y-{\rho }_g)}}\right]}^{{\displaystyle \frac{1}{3}}}$$

(13)

4.2. Bubbles Moving Upwards in the Fluid

After escaping from the leak hole, the bubbles migrate upward through the annular protective fluid. During the migration process, they are mainly affected by two forces: buoyancy force, which propels them upwards, and the viscous resistance of the liquid, which acts as drag. When these two forces achieve a state of equilibrium, the bubbles ascend at a relatively constant velocity. Notably, the ultimate rising velocity of the bubbles is influenced by the initial diameter they possess.

In fact, the leakage aperture on the tubing is minute; it can be postulated that the bubbles are in a small bubble shape during the transportation of the annular protective liquid, and largely remain spherical during the rising process. Therefore, the dynamic characteristics of the bubbles can be analyzed by studying their stress situation. The ascending bubbles are subject to three principal forces: buoyancy force, gravity force, and viscous resistance. The mathematical formulation for the viscous resistance can be shown as follows [31]:

$$F_f={\displaystyle \frac{1}{8}}{C}_D\pi d_b^2{\rho }_y{v}_g^2$$

(14)

where F_f is the viscous drag force on a bubble, N; C_D is the drag coefficient; and v_g is the vertical upward velocity of a bubble, m/s.

The drag coefficient at different Reynolds numbers is [32]

$$C_D=\left\{\begin{array}{ll}{\displaystyle \frac{24}{R_e}}\hfill & R_e<1\hfill \\ {\displaystyle \frac{24(1-0.15R_e^{0.687})}{R_e}}\hfill & 1<R_e<1000\hfill \\ 0.44\hfill & R_e>1000\hfill \end{array}\right.$$

(15)

where R_e is the Reynolds number of moving a bubble, in which

$$R_e={\displaystyle \frac{v_g{d}_b{\rho }_g}{{\mu }_l}}$$

(16)

where μ_l is the dynamic viscosity of liquid, N∙S/m².

Assuming the upward trajectory of a bubble is a straight line, according to Newton’s second law of motion, the dynamic equation of a bubble can be expressed as

$$m_g{a}_b={\displaystyle \frac{1}{6}}\pi d_b^{3}g({\rho }_g-{\rho }_y)-{\displaystyle \frac{1}{8}}{C}_D\pi d_b^2{\rho }_y{v}_g^2$$

(17)

where m_g is the mass of the bubble, kg, a_b is the acceleration of the bubble, m/s², in which

$$m_g={\displaystyle \frac{1}{6}}\pi d_b^3{\rho }_g$$

(18)

Thus, the acceleration of the bubbles moving upwards in the fluid can be expressed as

$$a_b={\displaystyle \frac{g({\rho }_g-{\rho }_y)}{{\rho }_g}}-{\displaystyle \frac{3C_D{\rho }_y{v}_g^2}{4d_b{\rho }_g}}$$

(19)

When the acceleration approaches zero, the velocity of the bubble tends to stabilize, reaching a final velocity:

$$v_g=\sqrt{{\displaystyle \frac{4d_b({\rho }_y-{\rho }_g)g}{3{\rho }_y{C}_D}}}$$

(20)

4.3. Model Establishment

Based on the state of the bubbles emanating from the leakage orifice and their subsequent motion characteristics, we can take the gas column section of the annulus as the research object and discretize it temporally. By applying the gas state equation of the annulus, we can solve for the annular pressure in each discrete unit of time. This allows us to determine the time required for pressure equilibrium in the annulus and to calculate the gas pressure at the wellhead.

To address the challenge of capturing the gas pressure at the wellhead, the entire transport process of the bubbles was discretized in time. Specifically, during the i-th time interval, the leakage flow rates at critical and subcritical flow states could be calculated using Equations (2) and (4), respectively. The detachment diameter of the j-th bubble during the i-th time period could be derived from Equations (10)–(12), with the understanding that the minimum value of j is 1, and when i = 0, j = 1. Once the detachment diameter of the j-th bubble was ascertained, its constant rising velocity could be determined using Equation (20).

Subsequently, upon the bubble exiting the leakage orifice, under the assumption that the amount of substance within each individual bubble remained constant, the amount of substance of the j-th bubble could be expressed as described in [33].

$$N_{bs}^{(j)}={\displaystyle \frac{P_2^{(i)}{V}_{bs}^{(i,j)}}{k{T}_{1k}Z}}$$

(21)

where N_bs is the amount of substance of the bubble, mol, V_bs is the volume of the bubble, m³, j is the index of the bubble after leakage, i is the index of the time interval after leakage, and k is the adiabatic index of gas.

Among them, the volume of the j-th bubble generated during the i-th time period is expressed as

$$V_{bs}^{(i,j)}={\displaystyle \frac{1}{6}}\pi d_b^{{(i,j)}^3}$$

(22)

The duration required for each bubble to expand and subsequently detach from the leakage orifice is defined as the time step, with its computational formulation expressed as

$${\Delta }_t^{(i)}={\displaystyle \frac{V_{bs}^{(i,j)}}{Q_c^{(i)}}}$$

(23)

where Δ_t is the duration of the bubble to expand and detach from the leakage orifice, s.

The entire process of pressure buildup in the annulus can be divided into two stages based on whether the total amount of the substance of gas above the liquid level has changed or not. The first stage is that the bubbles detached from the leakage orifice are still moving upwards in the liquid and have not reached the wellhead. The second stage commences when gas bubbles have migrated and reached above the liquid level.

The displacement distance of a bubble can be utilized to determine whether it is in the first stage or the second stage. Specifically, the displacement of the j-th bubble during the i-th time interval can be denoted as

$$S^{(i,j)}=S^{(i-1,j)}+v_g^{(j)}{\Delta }_t^{(i)}$$

(24)

where S is the displacement of the bubble, m.

In the initial stage, S^(0,1) = 0, which means that the first bubble has no displacement when it first appears.

Before the bubbles migrate to the surface of the liquid, the total amount of gas above the liquid surface remains unchanged. During the process of bubble generation and their upward migration in the liquid column, the liquid level rises, causing the volume of the gas column above the liquid surface to decrease. This, in turn, results in an increase in the annular pressure. In the i-th time period

$$P_A^{(i+1)}{V}_g^{(i+1)}=P_A^{(i)}{V}_g^{(i)}$$

(25)

where P_A is the annular pressure at the wellhead, KPa.

As the number of iteration steps increases, the volume of gas above the liquid surface gradually decreases, for which the decrement can be expressed as

$$V_g^{(i)}-V_g^{(i+1)}=V_b^{(i)}-\Delta V_y^{(i)}$$

(26)

where V_b is the increment in bubble volume within the liquid column, m³; and ΔV_y is the volume of liquid column in the annulus, m³, in which [34]

$$\Delta V_y^{(i)}=c_m\left(P_A^{(i+1)}-P_A^{(i)}\right)V_y^{(i)}$$

(27)

$$V_b^{(i)}={\displaystyle \sum _{k=1}^{j-1}\left(V_{bs}^{(i,k)}-V_{bs}^{(i-1,k)}\right)}+V_{bs}^{(i,j)}$$

(28)

where c_m is the volume compression coefficient of the annular protective fluid.

During the i-th time period, the bubbles that detached from the leakage orifice undergo expansion as they ascend. The primary factors governing the variation in bubble volume are temperature and pressure. According to the mass conservation formula of bubbles and the gas state equation, the pressure and temperature at the position of the k-th bubble (where 0 < k < j) can be determined as follows [35]:

$$P_{bs}^{(i,k)}=P_A^{(i)}+{10}^{-6}{\rho }_{1}g\left(h_f-h_g-S^{(i,k)}\right)$$

(29)

$$T_{bs}^{(i,k)}=T_{1k}-{\displaystyle \frac{S^{(i,k)}}{h_f}}(T_{1k}-T_{wh})$$

(30)

where P_bs is the pressure of the bubble, Kpa; T_bs is the temperature of the bubble, K; and T_wh is the annular temperature at the wellhead, K.

Thus, the volume of the k-th bubble (where 0 < k < j) in the i-th time period can be calculated as

$$V_{bs}^{(i,k)}={\displaystyle \frac{P_{bs}^{(i-1,k)}{T}_{bs}^{(i,k)}}{P_{bs}^{(i,k)}{T}_{bs}^{(i-1,k)}}}{V}_{bs}^{(i-1,j)}$$

(31)

By substituting Equations (26) and (27) into Equation (28), the annular pressure can be expressed as follows:

$$P_A^{(i+1)}={\displaystyle \frac{1}{2}}[-{\displaystyle \frac{V_g^{(i)}-V_b^{(i)}-c_m{V}_y^{(i)}{P}_A^{(i)}}{c_m{V}_y^{(i)}}}+\sqrt{{({\displaystyle \frac{V_g^{(i)}-V_b^{(i)}-c_m{V}_y^{(i)}{P}_A^{(i)}}{c_m{V}_y^{(i)}}})}^2+4{\displaystyle \frac{P_A^{(i)}{V}_g^{(i)}}{c_m{V}_y^{(i)}}}}]$$

(32)

After calculating the annular pressure, it is necessary to update the volumes of the gas column and liquid column to provide numerical values for the subsequent iteration

$$V_g^{(i+1)}=V_g^{(i)}-V_b^{(i)}+c_m\left(P_A^{(i+1)}-P_A^{(i)}\right)V_y^{(i)}$$

(33)

$$V_y^{(i+1)}=V_y^{(i)}-c_m\left(P_A^{(i+1)}-P_A^{(i)}\right)V_y^{(i)}$$

(34)

When bubbles have already migrated above the liquid surface, their integration increases the total amount of the substance and volume of gas, and the volume change in the gas in the annular can be expressed as follows:

$$V_g^{(i+1)}-V_g^{(i)}=V_b^{(i)}-\Delta V_y^{(i)}+V_{bo}^{(i)}$$

(35)

where ΔV_y is the volume compression of the liquid column due to increased annular pressure over a time period, m³.

As mentioned previously, the bubbles can be classified into two distinct groups based on whether their displacement exceeds the length of the liquid column above the leak point: those that are already transported in the gas column above the liquid surface and those that are still in the liquid column. For the bubbles still in the liquid column, the cumulative volume variation can be obtained based on Equation (36). For the bubbles that have already reached the gas column above the liquid surface, their volume can be expressed as follows:

$$V_{bs}^{(i,k)}={\displaystyle \frac{P_{bs}^{(i-1,k)}{T}_{bs}^{(i,k)}}{P_A^{(i)}{T}_{bs}^{(i-1,k)}}}{V}_{bs}^{(i-1,j)}$$

(36)

During the i-th time period, a total of the bubbles ranging from a to b entered the gas column; thus, the cumulative volume of bubbles entering the gas column is

$$V_{bo}^{(i)}={\displaystyle \sum _{k=a}^b\frac{P_{bs}^{(i-1,k)}{T}_{bs}^{(i,k)}}{P_A^{(i)}{T}_{bs}^{(i-1,k)}}}{V}_{bs}^{(i-1,j)}$$

(37)

where V_bo is the total volume of bubbles entering the gas column over a time period, m³.

Subsequently, the total amount of substance in the air column above the liquid surface undergoes a change:

$${\displaystyle \frac{P_A^{(i+1)}{V}_g^{(i+1)}}{N_g^{(i+1)}}}={\displaystyle \frac{P_A^{(i)}{V}_g^{(i)}}{N_g^{(i)}}}$$

(38)

$$N_g^{(i+1)}=N_g^{(i)}+{\displaystyle \sum _{k=a}^b{N}_{bs}^{(k)}}$$

(39)

$$N_g^{(0)}={\displaystyle \frac{P_A^{(0)}{V}_g^{(0)}}{{10}^{-3}R{T}_{wh}Z}}$$

(40)

where N_g is the total amount of substance in the gas column, mol, and a and b are the index of the bubble after leakage.

By substituting Equations (26) and (27) into Equation (28), the annular pressure can be expressed as follows:

$$P_A^{(i+1)}={\displaystyle \frac{1}{2}}\left[-{\displaystyle \frac{V_g^{(i)}+V_{bo}^{(i)}-V_b^{(i)}-c_m{V}_y^{(i)}{P}_A^{(i)}}{c_m{V}_y^{(i)}}}+\sqrt{{\left({\displaystyle \frac{V_g^{(i)}+V_{bo}^{(i)}-V_b^{(i)}-c_m{V}_y^{(i)}{P}_A^{(i)}}{c_m{V}_y^{(i)}}}\right)}^2+4{\displaystyle \frac{N_g^{(i+1)}{P}_A^{(i)}{V}_g^{(i)}}{N_g^{(i)}{c}_m{V}_y^{(i)}}}}\right]$$

(41)

As mentioned earlier, after calculating the annular pressure, it is necessary to update the volumes of the gas column and liquid column. Notably, the volume of the liquid column can be calculated using Equation (34), while the calculation formula for the volume of the gas column is as follows:

$$V_g^{(i+1)}=V_g^{(i)}+V_{bo}^{(i)}-V_b^{(i)}+c_m\left(P_A^{(i+1)}-P_A^{(i)}\right)V_y^{(i)}$$

(42)

As a result, the flow chart of the predictive model of the pressure buildup of the annulus is illustrated in Figure 10. Initially, upon inputting the initial conditions of annulus leakage (including liquid level height, leakage orifice height, the equivalent diameter of the leakage orifice, the annular pressure at the wellhead before leakage, the pressure and temperature in the tubing, the casing and tubing sizes), then the pressure at the leakage orifice within the annulus is calculated. Subsequently, the parameters pertinent to the j-th bubble’s migration process (such as the detachment diameter, the ascending velocity, the volume, the pressure, the temperature, and the amount of substance) are determined. The flow state (critical flow or subcritical flow) at the leak point during the i-th time interval is determined based on the pressure ratio between the inside and outside of the leak point, and the corresponding leakage rate is calculated. Utilizing the parameters of the j-th bubble and the calculated leakage rate, the Δt required for the bubble’s formation at the leak point serves as the computational time interval.

Furthermore, the displacement of the a-th bubble within the i-th time interval is then computed, and its distance from the fluid surface is evaluated to determine whether it has breached the liquid surface and reached the gas cap. If no gas has reached the gas cap, the incremental bubble volume within the liquid column during the current time interval is computed. Alternatively, if the gas cap has been reached, the total volume of bubbles entering the gas cap during the current time interval is calculated. The annulus pressure at wellhead is then estimated separately for the two aforementioned stages. Consequently, the volumes of the gas and liquid columns are updated, and the pressure at the leakage orifice within the annulus is recalculated. This recalculated pressure is then compared with the internal pressure of the tubing at the leakage orifice: if the calculated pressure is lower, it indicates that leakage persists, and the simulation advances to the next time step; if it is equal to or higher, it signifies that leakage has ceased, at which point the computation concludes, and the current time and the annulus pressure at the wellhead are outputted.

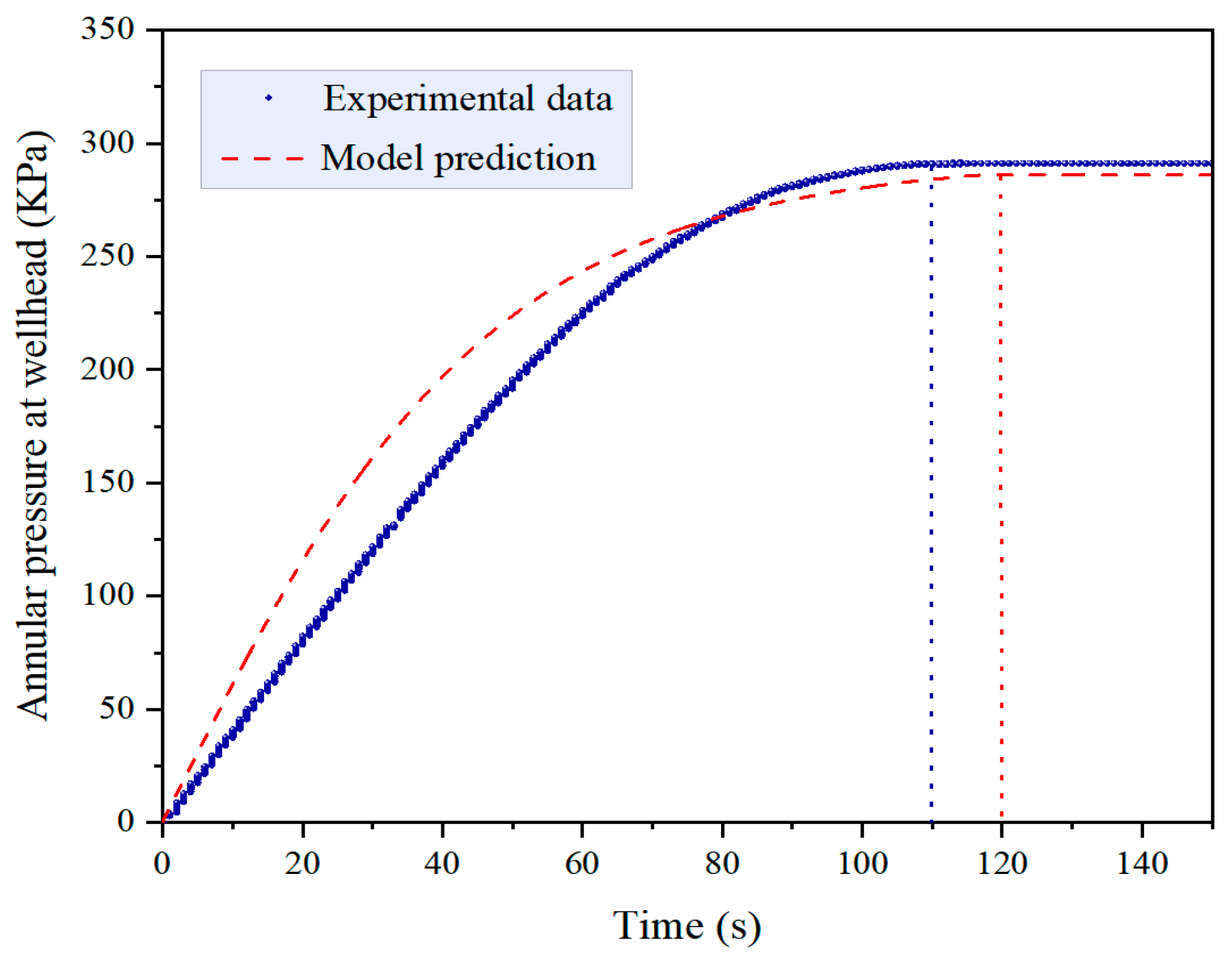
4.4. Model Validation

In this section, the established predictive model of the pressure buildup of the annulus was validated against the experimental results. Figure 11 presents a comparison between the experimental data and model prediction for the annulus pressure buildup with the sustained gas leakage below the liquid level. From the figure, it can be seen that the model prediction has good consistency with the experimental results. Furthermore, we utilized the novel model to comprehensively compare the whole experimental data with the established model, and the results are presented in Figure 12. According to the comparison results, it can be seen that the prediction model can effectively predict the equilibrium attainment time and the equilibrium value of the annular pressure at the wellhead, with R² of 0.951 and 0.996, respectively.

Therefore, by applying this new model, it is anticipated that field operators will be guided in understanding the pressure buildup in the annulus with sustained gas leakage below the liquid level, enabling the early assessment of the downhole leakage risks and facilitating the diagnosis and development of the mitigation strategies for the SCP in the annulus in gas wells.

5. Conclusions

The aim of this study was to conduct a detailed analysis of the mechanism underlying annulus pressure buildup in wells with sustained gas leakage below the liquid level. A detailed experimental study on annulus buildup due to gas leakage below the liquid level, exploring the pressure variation patterns under various leakage conditions, was performed. Then, a predictive model of the pressure buildup of the annulus was proposed and validated with the experimental results. The following conclusions can be drawn:

• Based on the rigorous experimental investigation on the annulus pressure buildup caused by tubing leakage below the liquid, the effects of the pressure difference between the tubing and casing, the liquid level height, the gas temperature, the leakage position, the leakage orifice diameter, and the quantity on the annulus pressure buildup patterns were explored. After tubing leakage, the time required for the annulus pressure at the wellhead to reach equilibrium decreased with an increase in the pressure difference between the tubing and casing, liquid level height, and leakage orifice diameter and quantity. Conversely, this equilibrium time extended with an increase in the leakage position and gas temperature;
• According to the theory of gas fluid dynamics, the evolution mechanism of the annulus pressure during the generation of bubbles and the migration towards the top of the annulus were analyzed, and a predictive model of the pressure buildup of annulus was established. The variation in annular pressure at the wellhead after gas leakage can be predicted through the new model;
• The new model was compared and validated against the experimental results; it could be seen that the prediction model could effectively predict the equilibrium attainment time and the equilibrium value of the annular pressure at the wellhead, with R² of 0.951 and 0.996, respectively. This demonstrates the validity of the prediction model, which can serve as a theoretical reference for advancing the diagnostic technology of SCP in the annulus of gas wells caused by sustained gas leakage below the liquid level.