Simulation and Experiment on Hull Lower Welding Deformation Using Heat Source Shape
Abstract
1. Introduction
2. Experimental Methods and Simulation Conditions
2.1. Welding Experimental Configuration
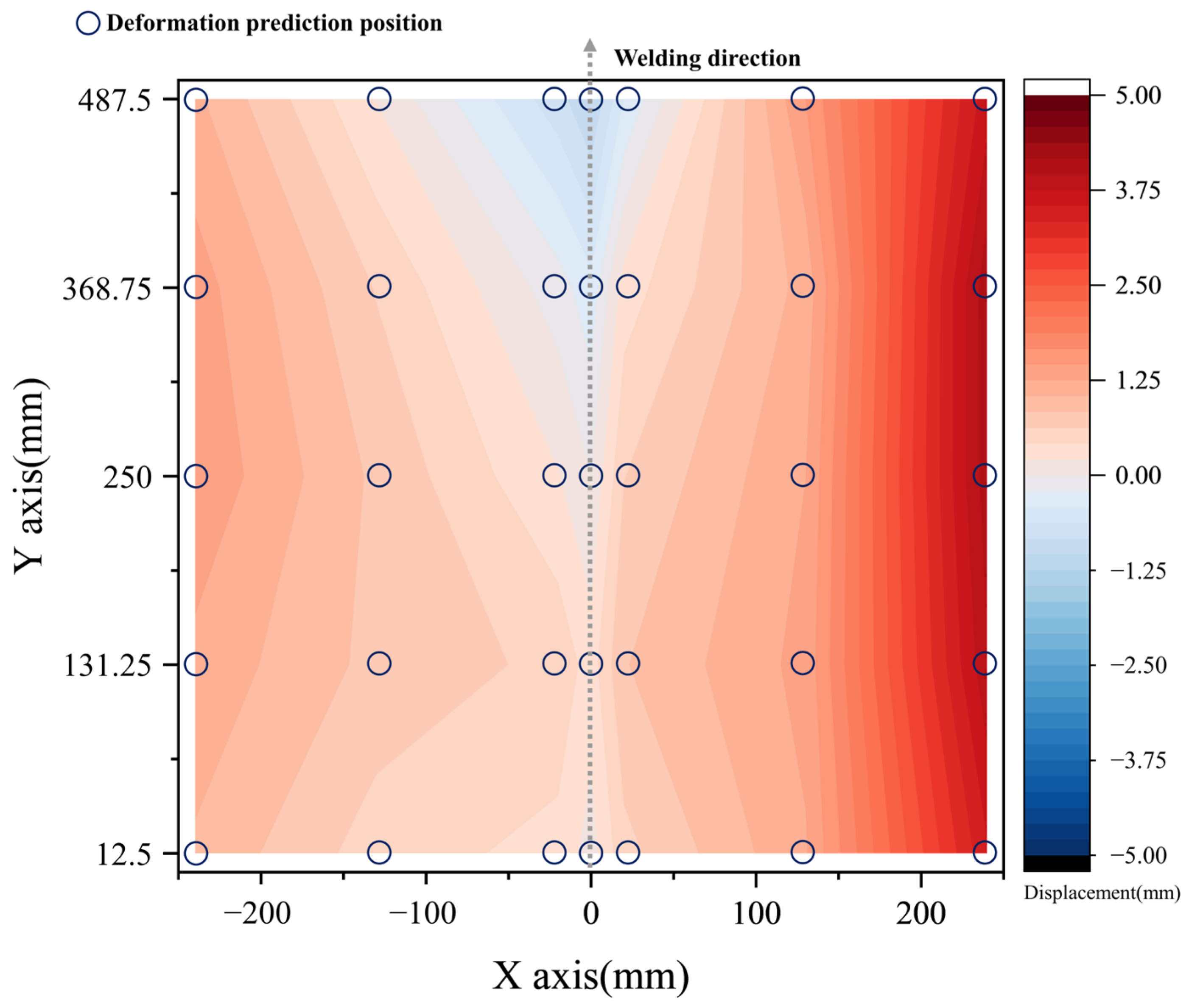
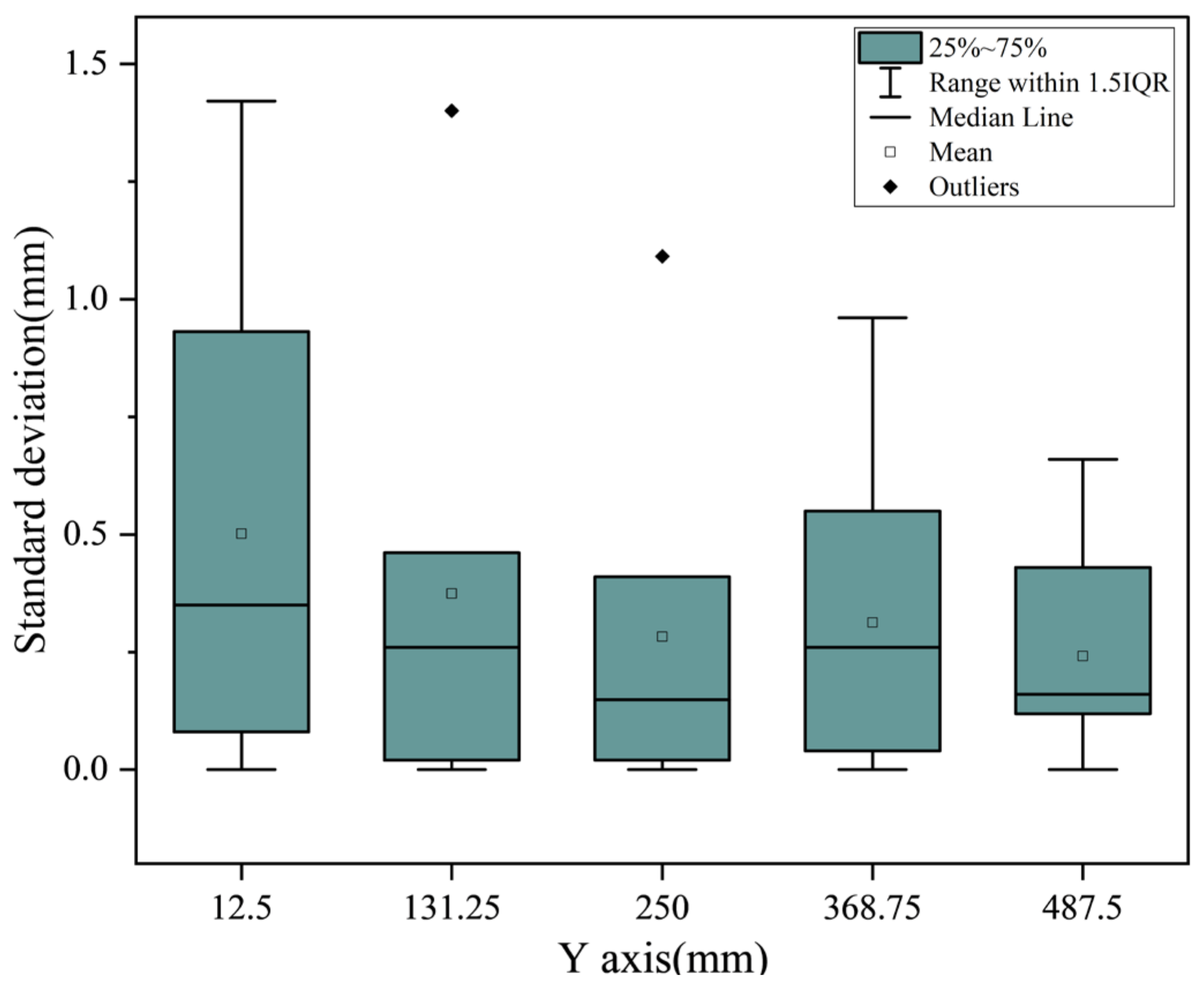
2.2. Deformation Measurement
2.3. Deformation Simulation Conditions
3. FEM Development
3.1. Aluminum Fillet Weld Experimental Results
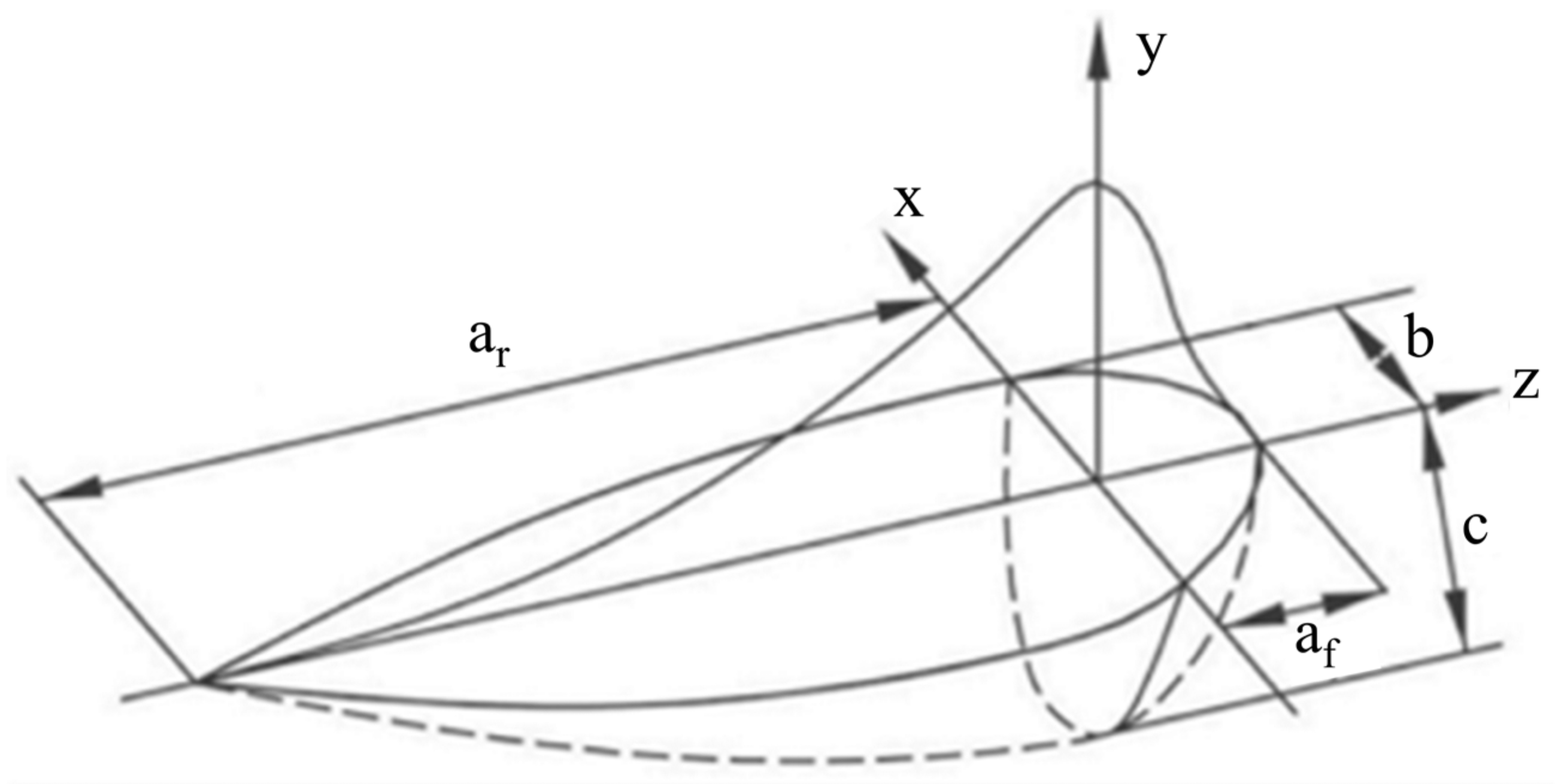
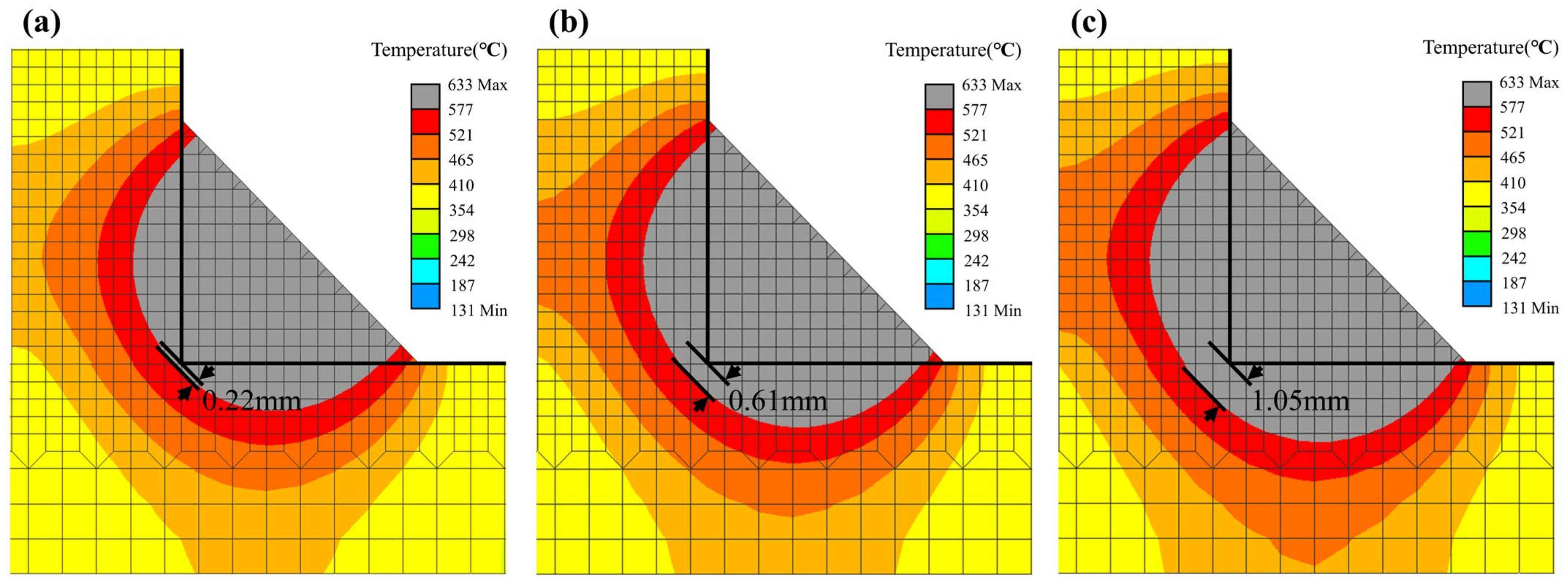
3.2. Heat Source Geometry
3.3. Simulation Model Development
4. Deformation Prediction and Discussion
4.1. Deformation Prediction Results
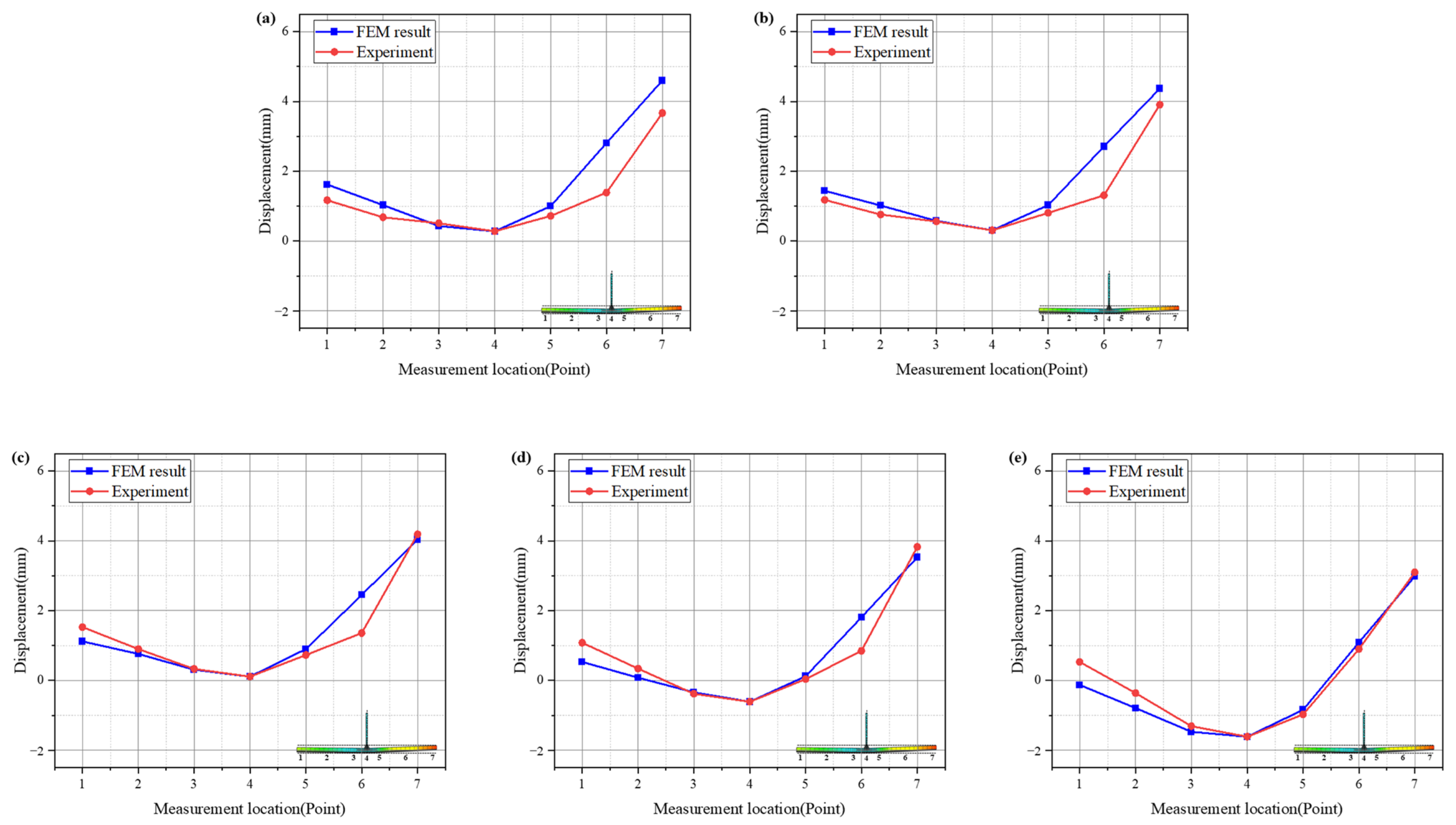
4.2. Comparison of Simulation and Experimental Results
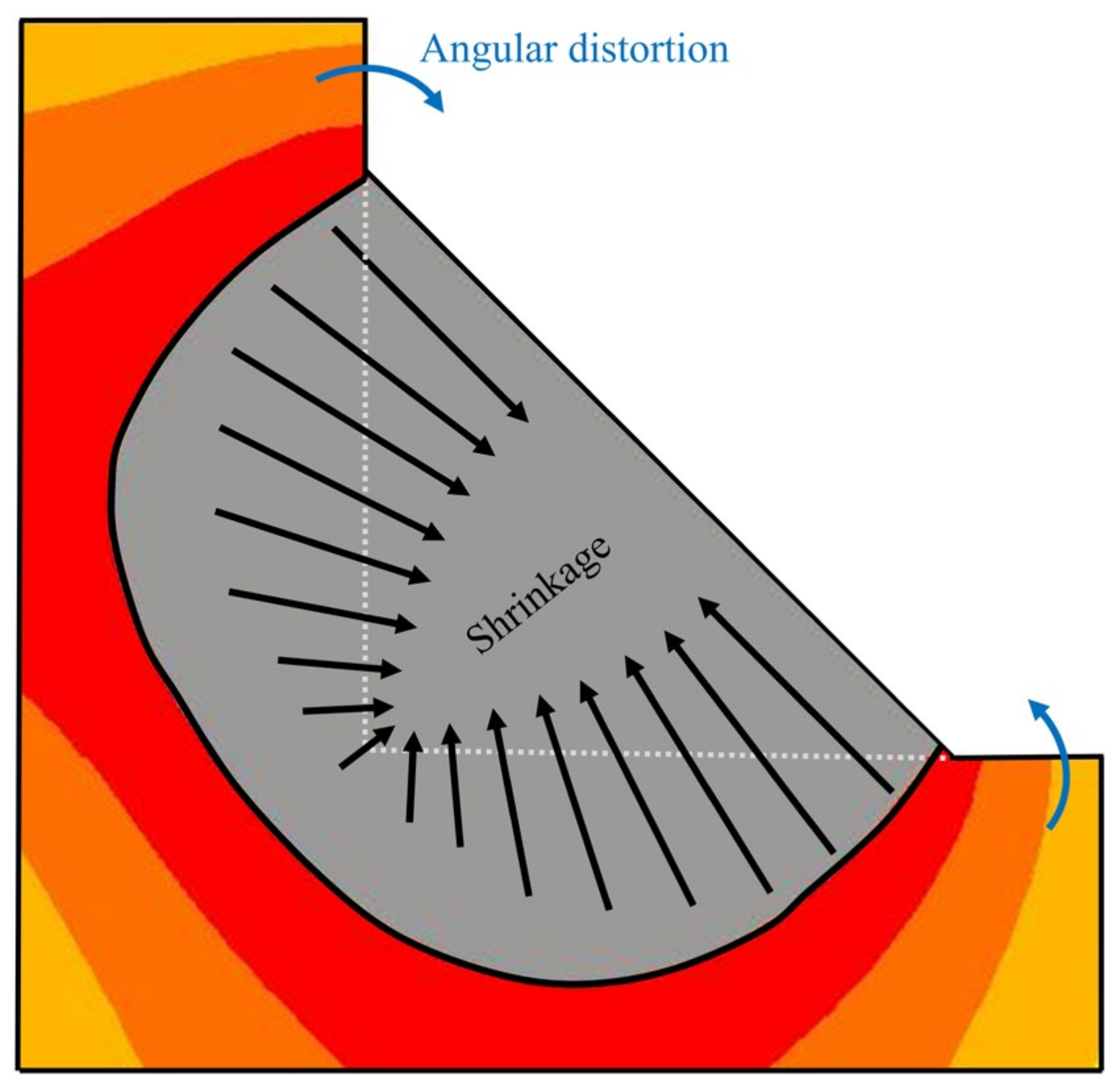
4.3. Consideration and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Farajkhah, V.; Liu, Y. Effect of Fabrication Methods on the Ultimate Strength of Aluminum Hull Girders. Ocean Eng. 2016, 114, 269–279. [Google Scholar] [CrossRef]
- Guo, Z.; Bai, R.; Lei, Z.; Jiang, H.; Zou, J.; Yan, C. Experimental and Numerical Investigation on Ultimate Strength of Laser-Welded Stiffened Plates Considering Welding Deformation and Residual Stresses. Ocean Eng. 2021, 234, 109239. [Google Scholar] [CrossRef]
- Reza Kashyzadeh, K.; Amiri, N.; Maleki, E.; Unal, O. A Critical Review on Improving the Fatigue Life and Corrosion Properties of Magnesium Alloys via the Technique of Adding Different Elements. J. Mar. Sci. Eng. 2023, 11, 527. [Google Scholar] [CrossRef]
- Kishta, E.E.; Darras, B. Experimental Investigation of Underwater Friction-Stir Welding of 5083 Marine-Grade Aluminum Alloy. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 458–465. [Google Scholar] [CrossRef]
- Feng, Z.; Li, J.; Ma, J.; Su, Y.; Zheng, X.; Mao, Y.; Zhao, Z. EBSD Characterization of 7075 Aluminum Alloy and Its Corrosion Behaviors in SRB Marine Environment. J. Mar. Sci. Eng. 2022, 10, 740. [Google Scholar] [CrossRef]
- Kumar Dewangan, S.; Kumar Tripathi, M.; Nandan Banjare, P.; Kumar Manoj, M. Temperature Distribution of Friction Stir Welded Al 7075 alloy using Finite Element Simulation along with Experimental Validation. Mater. Today Proc. 2018, in press. [Google Scholar] [CrossRef]
- Ahmed, S.; Rahman, R.A.u.; Awan, A.; Ahmad, S.; Akram, W.; Amjad, M.; Yahya, M.Y.; Rahimian Koloor, S.S. Optimization of Process Parameters in Friction Stir Welding of Aluminum 5451 in Marine Applications. J. Mar. Sci. Eng. 2022, 10, 1539. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, S. Investigation of Laser-MIG Hybrid Welding of Al-Mg-Si Aluminum Alloy. Metals 2024, 14, 729. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Cheng, L.; Kang, D.; Gao, R.; Qin, Y.; Mei, Z.; Zhang, M.; Yu, M.; Sun, Z. Design and Performance Study of Carbon Fiber-Reinforced Polymer Connection Structures with Surface Treatment on Aluminum Alloy (6061). Coatings 2024, 14, 785. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, J.; Kang, S. A Study on Welding Deformation Prediction for Ship Blocks Using the Equivalent Strain Method Based on Inherent Strain. Appl. Sci. 2019, 9, 4906. [Google Scholar] [CrossRef]
- Li, L.; Luo, C.; Shen, J.; Zhang, Y. Numerical Prediction of Welding Deformation in Ship Block Subassemblies Via the Inhomogeneous Inherent Strain Method. J. Manuf. Process. 2022, 80, 860–873. [Google Scholar] [CrossRef]
- Sun, J.; Nitschke Pagel, T.; Dilger, K. Influence of Strain-Hardening Models and Slopes on the Predicted Residual Stresses in Structural Steel S235 Weldments. J. Mater. Res. Technol. 2022, 19, 4044–4062. [Google Scholar] [CrossRef]
- Jang, H.L.; Ryu, H.; Kang, S. A Study on the Effects of Welding Deformation According to Weld Sequence in Overlay-Welded Structures. Metals 2024, 14, 684. [Google Scholar] [CrossRef]
- Raftar, H.R.; Ahola, A.; Lipiäinen, K.; Björk, T. Simulation and Experiment on Residual Stress and Deflection of Cruciform Welded Joints. J. Constr. Steel Res. 2023, 208, 108023. [Google Scholar] [CrossRef]
- Peng, X.; Yao, D.; Ye, F.; Gong, J.; Zhang, L. Numerical Simulation of Welding Residual Stress in Incoloy 825/L360QS Bimetal Clad Tube. Int. J. Pres. Ves. Pip. 2023, 206, 105080. [Google Scholar] [CrossRef]
- Meléndez-Morales, L.D.; Ruíz-Mondragón, J.J.; Hernández-Hernández, M. In-Service Weld Repair by Direct Deposition: Numerical Simulation and Experimental Validation. Eng. Sci. Technol. Int. J. 2023, 46, 101503. [Google Scholar] [CrossRef]
- Yi, J.; Chen, Z.; Li, D.; Li, J.; Liu, J. Conditional generative adversarial network for welding deformation field prediction of butt-welded plates. J. Constr. Steel Res. 2022, 201, 107755. [Google Scholar] [CrossRef]
- Murakawa, H.; Deng, D.; Ma, N.; Wang, J. Applications of inherent strain and interface element to simulation of welding deformation in thin plate structures. Comput. Mater. Sci. 2012, 51, 43–52. [Google Scholar] [CrossRef]
- Preston, R.V.; Shercliff, H.R.; Withers, P.J.; Smith, S. Physically-based constitutive modelling of residual stress development in welding of aluminium alloy 2024. Acta Mater. 2004, 52, 4973–4983. [Google Scholar] [CrossRef]
- Li, T.; Wang, Y.; Yin, X.; Zhang, Z. Laser welding simulation of large-scale assembly module of stainless steel side-wall. Heliyon 2023, 9, e13835. [Google Scholar] [CrossRef]
- Wu, R.; Huang, Y.; Rong, Y.; Xu, J.; Chen, Q. Solid phase transformation effects on stress and strain in the thick plate EH40 welded butt joint. Opt. Laser. Technol. 2023, 157, 108635. [Google Scholar] [CrossRef]
- Han, Y.H.; Lim, H.B.; Shin, T.S.; Yang, H.I. Prediction of Welding Deformation Using the Thermal Elastic–Plastic Finite Element Method by Considering Welding Interpass Temperature. Materials 2024, 17, 3656. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Zhao, Y.; Chen, J.; Liu, X.; Huang, Y. Experimental and Numerical Investigation on Residual Stress and Deformation of Welded I-Section Curved Steel Beams. Thin Walled Struct. 2024, 199, 111821. [Google Scholar] [CrossRef]
- Sun, J.; Dilger, K. Influence of Welding Sequence and External Restraint on Buckling Distortion in Thin-Plate Arc-Welded Joints. J. Adv. Join. Process. 2023, 8, 100157. [Google Scholar] [CrossRef]
- Sadeghi-Chahardeh, A.; Abdollahi-Mamoudan, F. Temperature-Driven Instabilities in High-Pressure Vessel Flat Plates: A Thermal Buckling Study. Designs 2024, 8, 81. [Google Scholar] [CrossRef]
- Li, C.; Zhai, H.; Liu, Z.; Ma, J.; Ji, H.; Liu, Q. Suppressing Welding Deformation Instability of Vacuum Vessel Considering External Restraint and Welding Sequence. Fusion Eng. Des. 2023, 196, 114007. [Google Scholar] [CrossRef]
- Mcpherson, N.; Galloway, A.; Mcghee, W.; Soares, C.G. Thin plate buckling mitigation and reduction challenges for naval ships. J. Mar. Eng. Technol. 2013, 12, 3–10. [Google Scholar]
- Tan, L.; Zhang, J.; Zhuang, D.; Liu, C. Influences of lumped passes on welding residual stress of a thick-walled nuclear rotor steel pipe by multipass narrow gap welding. Nucl. Eng. Des. 2014, 273, 47–57. [Google Scholar] [CrossRef]
- Su, Y.; Yang, X.; Wu, D.; Meng, T.; Li, W.; Feng, W.; Vairis, A. Optimizing Welding Sequence of TIG Cross-Joint of Invar Steel Using Residual Stresses and Deformations. J. Manuf. Process. 2023, 105, 232–245. [Google Scholar] [CrossRef]
- Woo, D.; Kitamura, M.; Takezawa, A. Method to systemically order welding sequence to efficiently mitigate welding displacement of a general ship grillage structure. Ships Offshore Struct. 2019, 15, 753–768. [Google Scholar] [CrossRef]
- Hashemzadeh, M.; Garbatov, Y.; Guedes Soares, C. Analytically Based Equations for Distortion and Residual Stress Estimations of Thin Butt-Welded Plates. Eng. Struct. 2017, 137, 115–124. [Google Scholar] [CrossRef]
- Ueda, Y.; Yamakawa, T. Analysis of Thermal Elastic-Plastic Stress and Strain During Welding by Finite Element Method. Trans. Jpn. Weld. Soc. 1971, 2, 90–100. [Google Scholar]
- Lee, J.; Chung, H. Modified Equivalent Load Method for Welding Distortion Analysis. J. Mar. Sci. Eng. 2020, 8, 794. [Google Scholar] [CrossRef]
- Burghold, E.M.; Frekers, Y.; Kneer, R. Transient Contact Heat Transfer Mmeasurements Based on High-Speed IR-Thermography. Int. J. Therm. Sci. 2017, 115, 169–175. [Google Scholar] [CrossRef]
- Korean Register. Rules and Guidance for the Classification of Steel Ships: Part 2 Materials and Welding; Korean Register: Busan, Republic of Korea, 2022; pp. 133–140. [Google Scholar]
- Korean Register. Rules and Guidance for the Classification of Steel Ships: Part 3 Hull Structures; Korean Register: Busan, Republic of Korea, 2022; pp. 255–266. [Google Scholar]
- Pyo, C.; Jeong, S.M.; Kim, J.; Park, M.; Shin, J.; Kim, Y.; Son, J.; Kim, J.H.; Kim, M.H. A Study on the Enhanced Process of Elaborate Heat Source Model Parameters for Flux Core Arc Welding of 9% Nickel Steel for Cryogenic Storage Tank. J. Mar. Sci. Eng. 2022, 10, 1810. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. A New Finite Element Model for Welding Heat Sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Lee, C.; Woo, S.; Kim, J. Impact Analysis of Welding Sequence to Reduce Weld Deformation in Aluminum Hulls. J. Mar. Sci. Eng. 2024, 12, 1604. [Google Scholar] [CrossRef]
- Wu, C.; Kim, J.W. Numerical Prediction of Deformation in Thin-Plate Welded Joints Using Equivalent Thermal Strain Method. Thin Walled Struct. 2020, 157, 107033. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, Y.; Wang, J.; Li, R. Research on Simulation and Optimization of Traveling Induction Heating Process for Welding Deformation Rectification in High Strength Steel Sheet. Metals 2023, 13, 425. [Google Scholar] [CrossRef]
- Romanin, L.; Ferro, P.; Berto, F. A Simplified Non-Linear Numerical Method for the Assessment of Welding Induced Deformations. Mar. Struct. 2021, 78, 102982. [Google Scholar] [CrossRef]
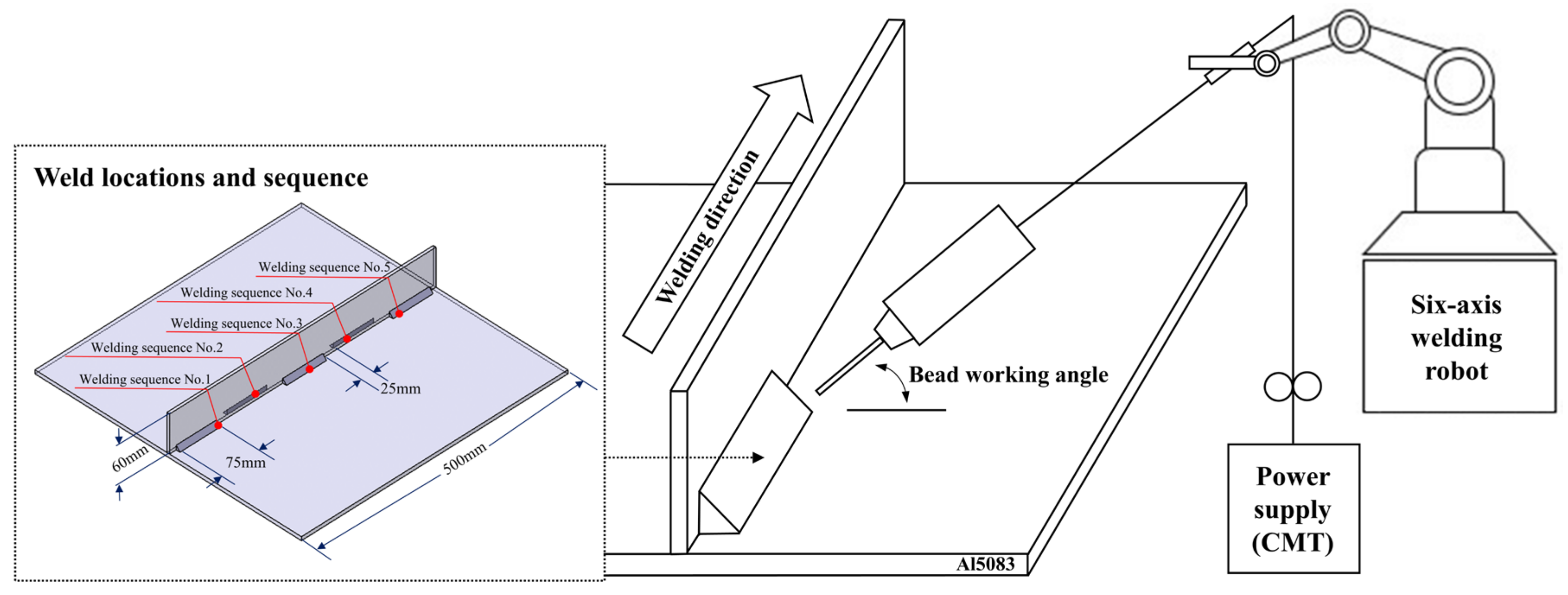
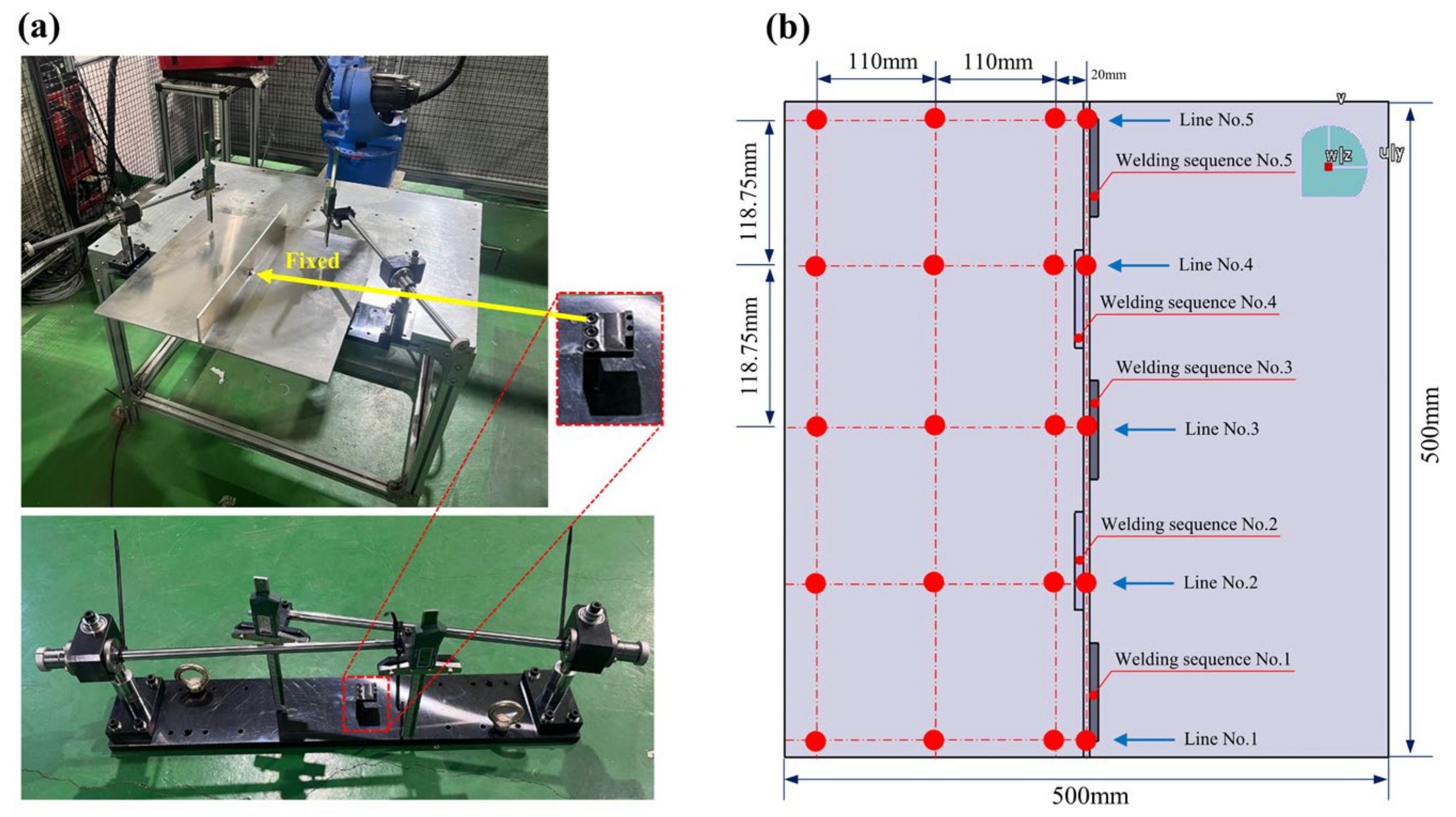
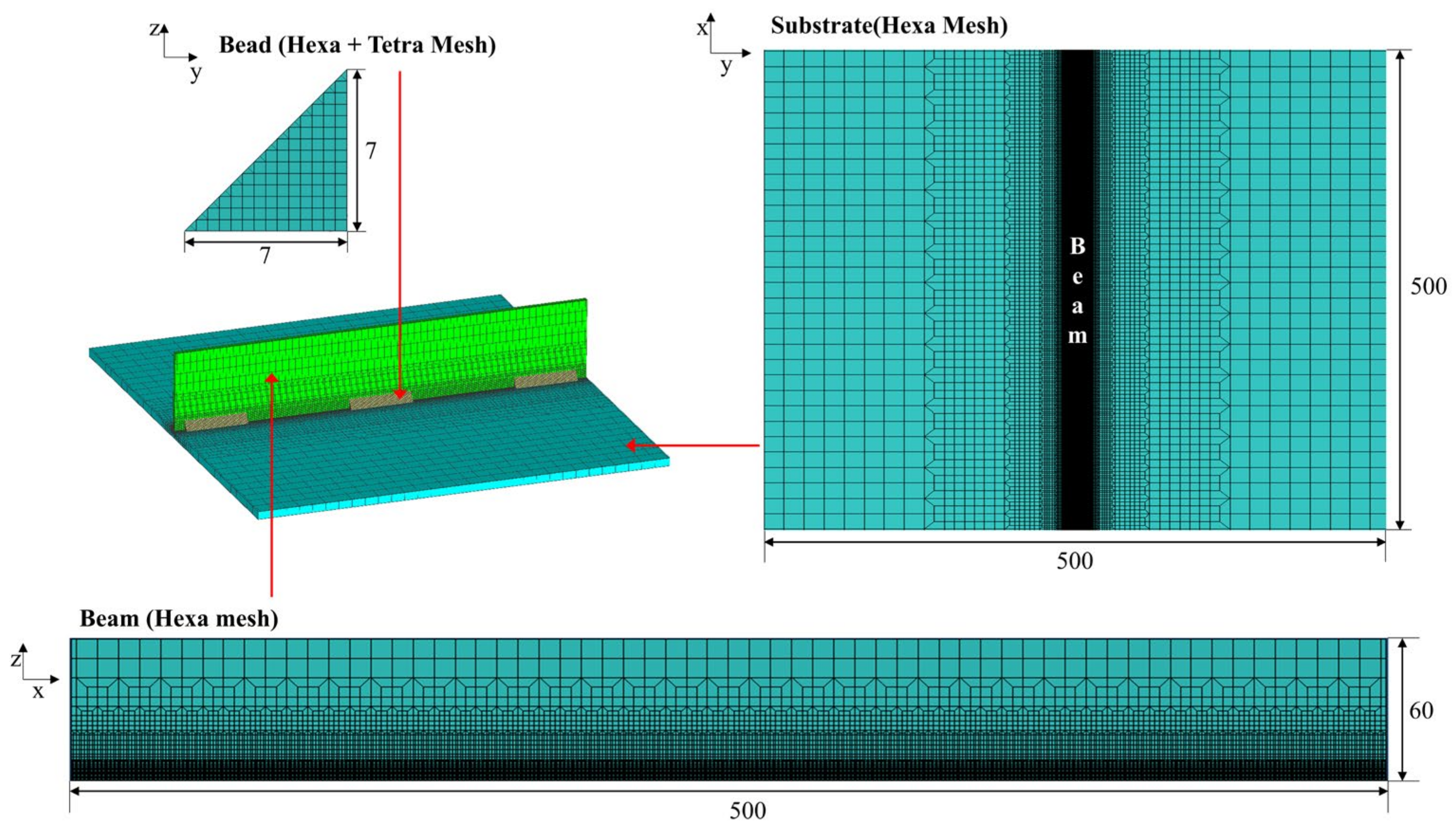


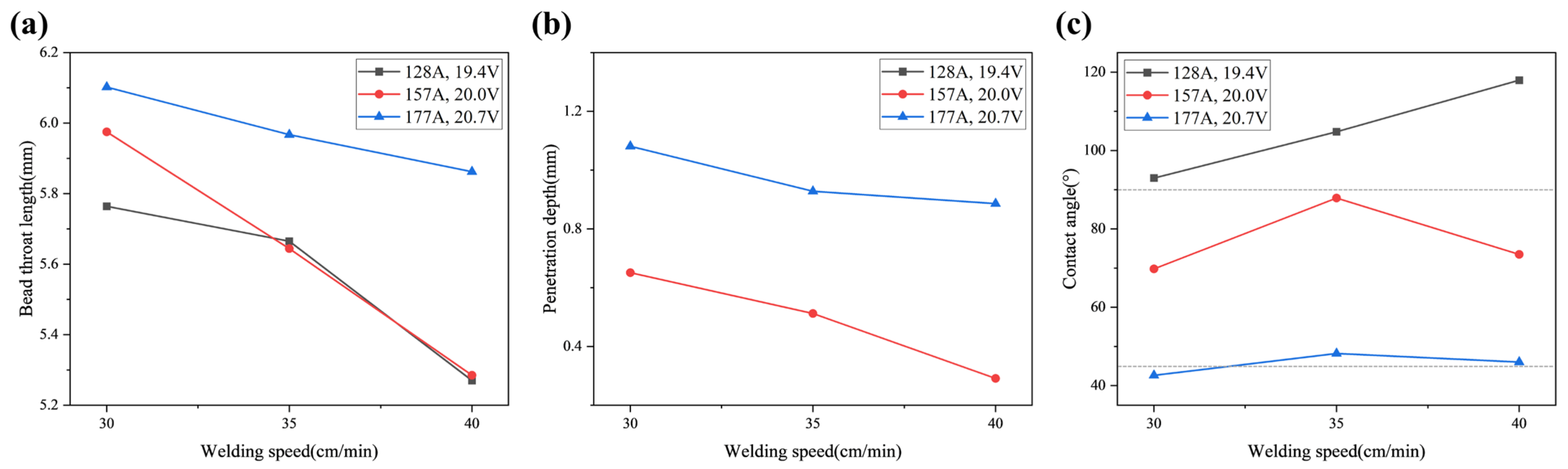


| Fe | Mg | Si | Al |
|---|---|---|---|
| <1 | 4.3~5.2 | <1 | Bal. |
| Fe | Mg | Si | Cu | Mn | Mg | Cr | Zn | Ti |
|---|---|---|---|---|---|---|---|---|
| 0.29 | 4.8 | 0.06 | 0.03 | 0.67 | 4.8 | 0.1 | 0.01 | 0.02 |
| Test No. | Current (A) | Voltage (V) | Welding Speed (cm/min) |
|---|---|---|---|
| 1 | 128 | 19.4 | 30 |
| 2 | 157 | 20.0 | 30 |
| 3 | 177 | 20.7 | 30 |
| 4 | 128 | 19.4 | 35 |
| 5 | 157 | 20.0 | 35 |
| 6 | 177 | 20.7 | 35 |
| 7 | 128 | 19.4 | 40 |
| 8 | 157 | 20.0 | 40 |
| 9 | 177 | 20.7 | 40 |
| Variable | Level |
|---|---|
| Front length (af) | 7.356 mm |
| Rear length (ar) | 12.221 mm |
| Width (b) | 6.102 mm |
| Depth (c) | 7.683 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-W.; Woo, S.; Kim, J. Simulation and Experiment on Hull Lower Welding Deformation Using Heat Source Shape. Processes 2024, 12, 2628. https://doi.org/10.3390/pr12122628
Lee C-W, Woo S, Kim J. Simulation and Experiment on Hull Lower Welding Deformation Using Heat Source Shape. Processes. 2024; 12(12):2628. https://doi.org/10.3390/pr12122628
Chicago/Turabian StyleLee, Chung-Woo, Suseong Woo, and Jisun Kim. 2024. "Simulation and Experiment on Hull Lower Welding Deformation Using Heat Source Shape" Processes 12, no. 12: 2628. https://doi.org/10.3390/pr12122628
APA StyleLee, C.-W., Woo, S., & Kim, J. (2024). Simulation and Experiment on Hull Lower Welding Deformation Using Heat Source Shape. Processes, 12(12), 2628. https://doi.org/10.3390/pr12122628






