Mathematical Modeling and Experimental Validation for a 50 kW Alkaline Water Electrolyzer
Abstract
1. Introduction
2. Mathematical Model for a 50 kW AWE System
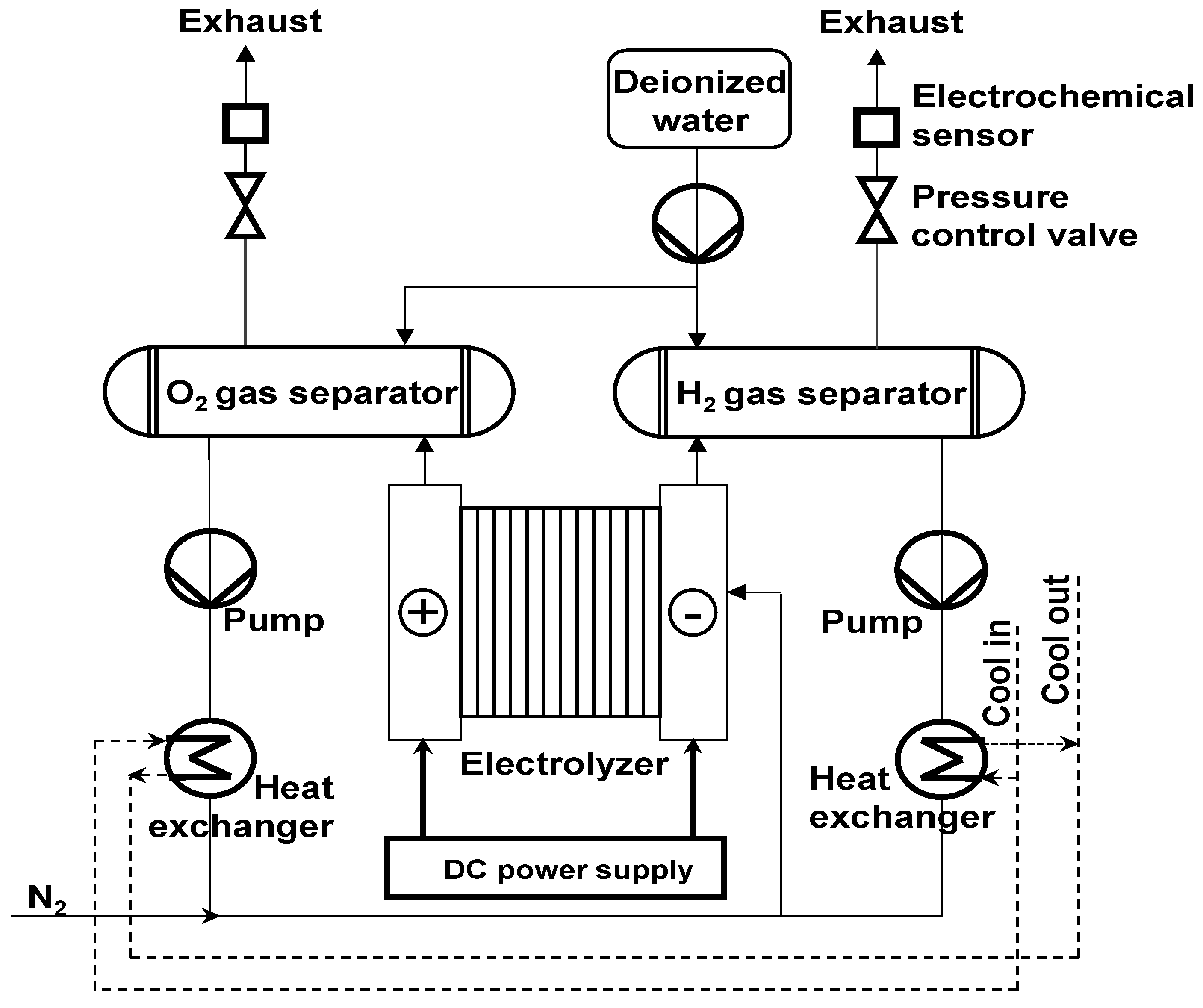
2.1. AWE System Structure
2.2. Electrochemical Model
2.3. Gas Purity Model
3. Experimental Set-Up
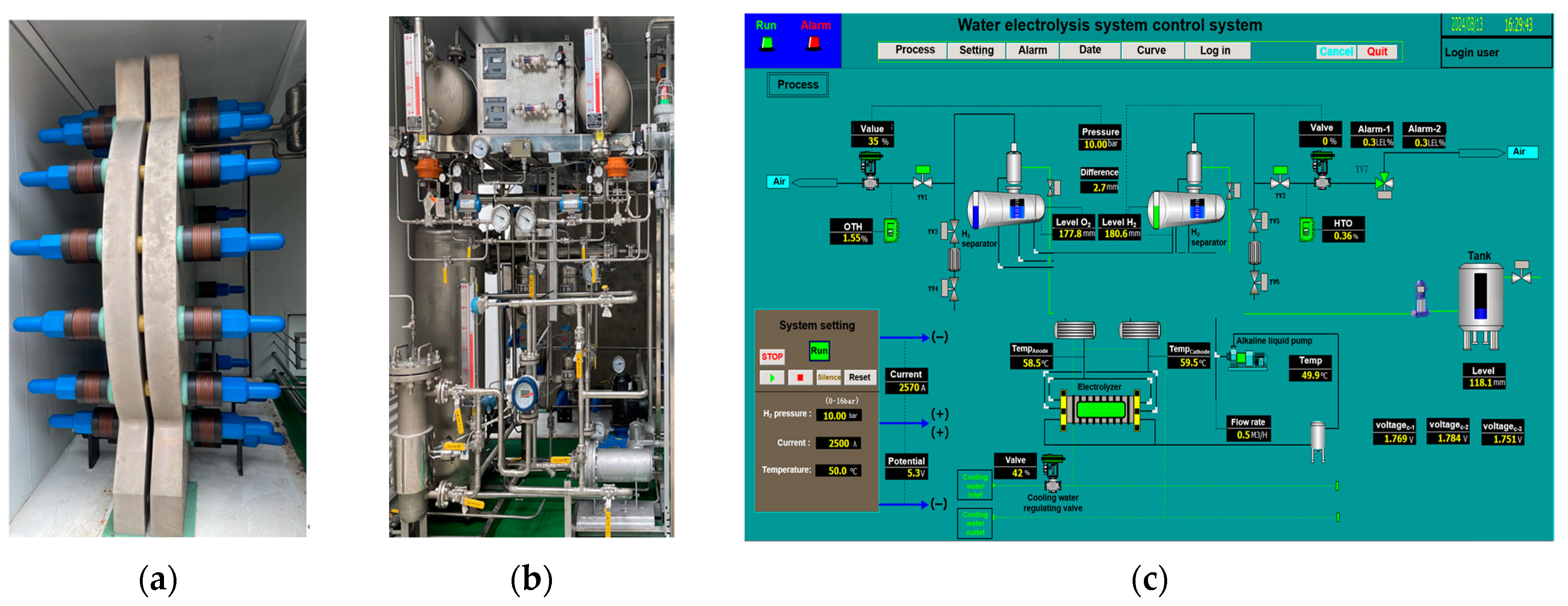
3.1. 50 kW AWE Test Bench
3.2. Test Protocols
4. Results and Discussion
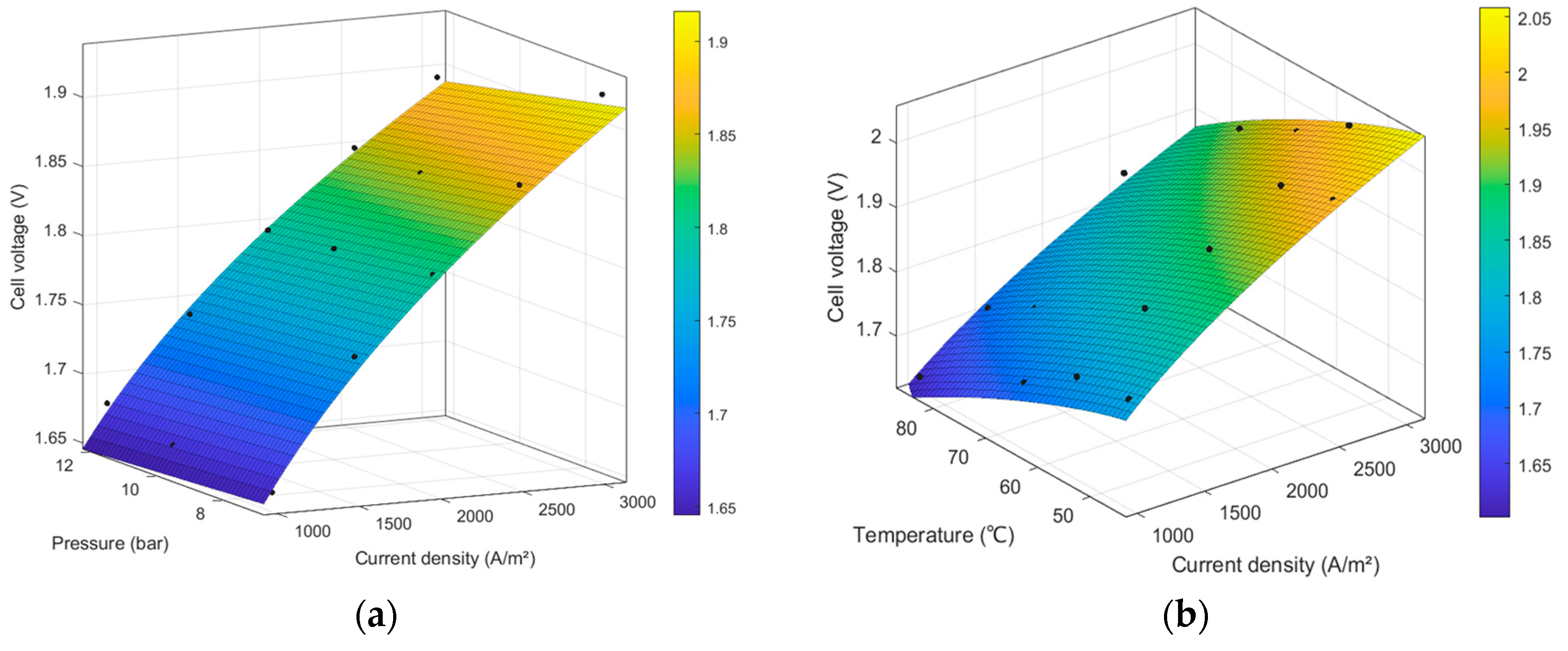
4.1. Results of the Electrochemical Model
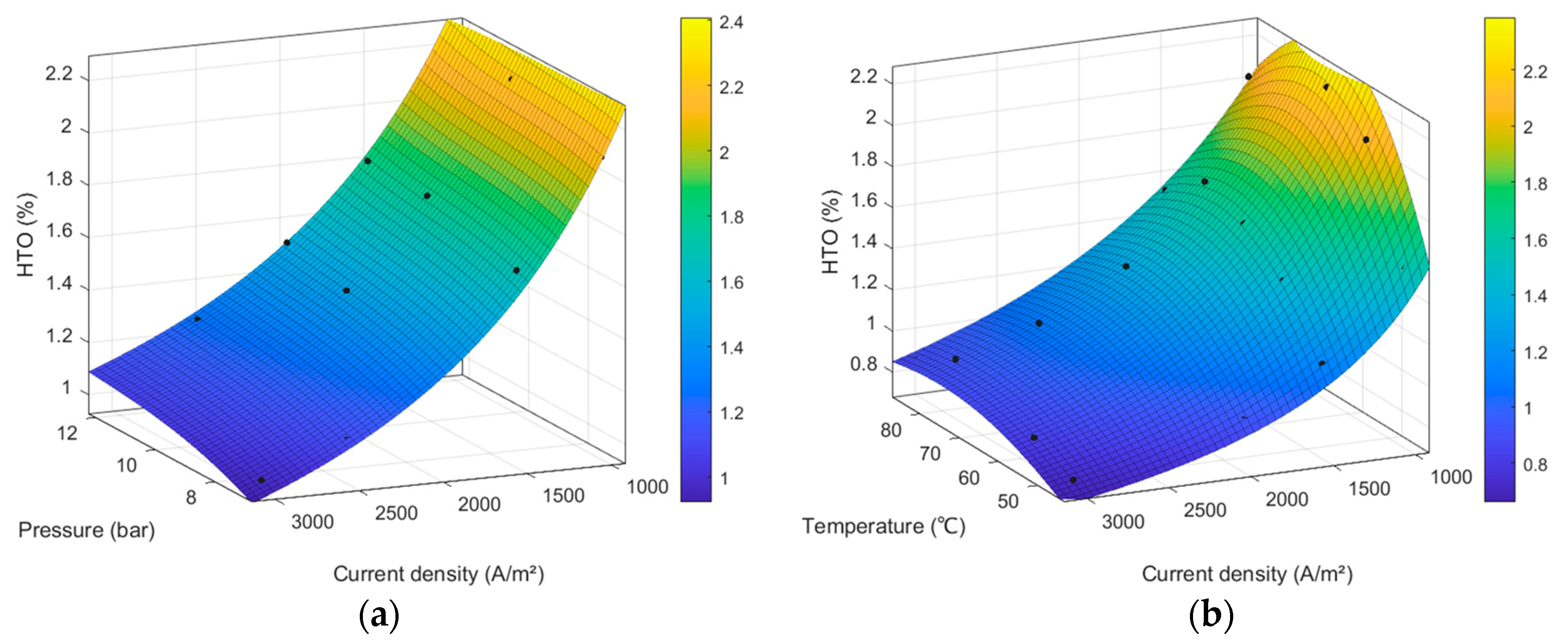
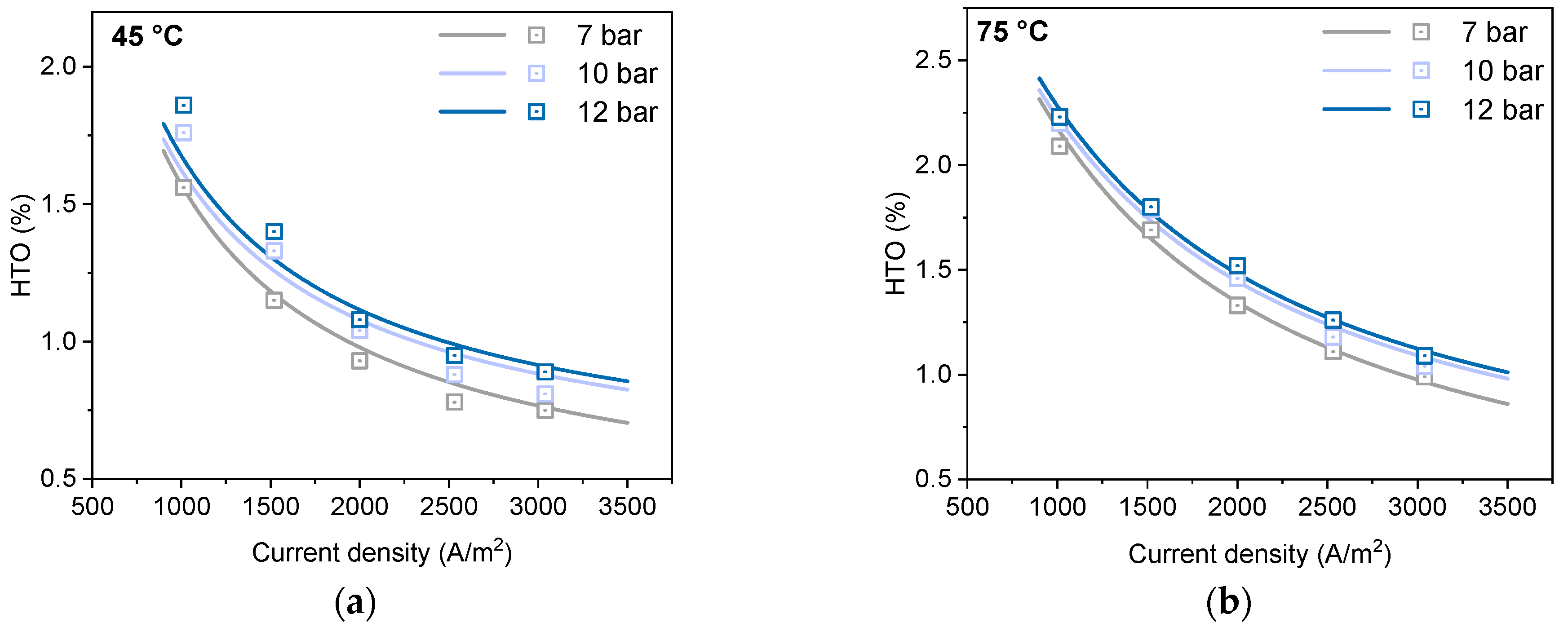
4.2. Results of the Gas Purity Model
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| the standard reversible potential | |
| R | the universal gas constant |
| T | the electrolyzer temperature, °C |
| F | faraday constant |
| P | the electrolyzer pressure, bar |
| the pressure of H2 and O2 gases in the existence of water vapor near the electrode, bar | |
| the pure water’s vapor pressure, bar | |
| the reversible voltage, V | |
| the ohmic overpotential, V | |
| i | the current density, A/m2 |
| r | the electrolyzer ohmic, Ω |
| the reversible voltage for electrolysis, V | |
| the convection flux density of H2, kg/(m2·s) | |
| the diffusion flux density of H2, kg/(m2·s) | |
| the solubility of H2 in the KOH solution, g | |
| the hydraulic permeability, D | |
| the effective diffusion coefficient of H2, m2/s | |
| the thickness of the diaphragm, m | |
| the concentration gradient of dissolved H2 between the cathode and anode, mol/L | |
| Not mentioned symbols | coefficient (noted in Table 3) |
References
- Buttler, A.; Spliethoff, H. Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: A review. Renew. Sustain. Energy Rev. 2018, 82, 2440–2454. [Google Scholar] [CrossRef]
- Glenk, G.; Reichelstein, S. Economics of converting renewable power to hydrogen. Nat. Energy 2019, 4, 216–222. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Y.; Zavabeti, A.; Chen, K.; Guo, Y.; Hu, G.; Fan, X.; Li, G.K. Hydrogen production from the air. Nat. Commun. 2022, 13, 5046. [Google Scholar] [CrossRef] [PubMed]
- Turner, J.A. Sustainable Hydrogen Production. Science 2004, 305, 972–974. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Zhao, Z.; Liu, T.; Wu, Y.; Lan, C.; Jiang, W.; Zhu, L.; Wang, Y.; Yang, D.; Shao, Z. A membrane-based seawater electrolyser for hydrogen generation. Nature 2022, 612, 673–678. [Google Scholar] [CrossRef]
- Haoran, C.; Xia, Y.; Wei, W.; Yongzhi, Z.; Bo, Z.; Leiqi, Z. Safety and efficiency problems of hydrogen production from alkaline water electrolyzers driven by renewable energy sources. Int. J. Hydrogen Energy 2024, 54, 700–712. [Google Scholar] [CrossRef]
- Hu, S.; Guo, B.; Ding, S.; Yang, F.; Dang, J.; Liu, B.; Gu, J.; Ma, J.; Ouyang, M. A comprehensive review of alkaline water electrolysis mathematical modeling. Appl. Energy 2022, 327, 120099. [Google Scholar] [CrossRef]
- Kwon, J.; Choi, S.; Park, C.; Han, H.; Song, T. Critical challenges and opportunities for the commercialization of alkaline electrolysis: High current density, stability, and safety. Mater. Chem. Front. 2024, 8, 41–81. [Google Scholar] [CrossRef]
- Daoudi, C.; Bounahmidi, T. Overview of alkaline water electrolysis modeling. Int. J. Hydrogen Energy 2024, 49, 646–667. [Google Scholar] [CrossRef]
- Sharshir, S.W.; Joseph, A.; Elsayad, M.M.; Tareemi, A.A.; Kandeal, A.W.; Elkadeem, M.R. A review of recent advances in alkaline electrolyzer for green hydrogen production: Performance improvement and applications. Int. J. Hydrogen Energy 2024, 49, 458–488. [Google Scholar] [CrossRef]
- Gomez Vidales, A.; Semai, M. Platinum nanoparticles supported on nickel-molybdenum-oxide for efficient hydrogen production via acidic water electrolysis. J. Mol. Struct. 2023, 1290, 135956. [Google Scholar] [CrossRef]
- Gomez Vidales, A.; Millan, N.C.; Bock, C. Modeling of anion exchange membrane water electrolyzers: The influence of operating parameters. Chem. Eng. Res. Des. 2023, 194, 636–648. [Google Scholar] [CrossRef]
- Burton, N.A.; Padilla, R.V.; Rose, A.; Habibullah, H. Increasing the efficiency of hydrogen production from solar powered water electrolysis. Renew. Sustain. Energy Rev. 2021, 135, 110255. [Google Scholar] [CrossRef]
- Iribarren, A.; Barrios, E.; Ibaiondo, H.; Sanchez-Ruiz, A.; Arza, J.; Sanchis, P.; Ursua, A. Dynamic modeling and simulation of a pressurized alkaline water electrolyzer: A multiphysics approach. IEEE Trans. Ind. Appl. 2023, 59, 3741–3753. [Google Scholar] [CrossRef]
- Janssen, H.; Bringmann, J.C.; Emonts, B.; Schroeder, V. Safety-related studies on hydrogen production in high-pressure electrolysers. Int. J. Hydrogen Energy 2004, 29, 759–770. [Google Scholar] [CrossRef]
- Zhang, T.; Song, L.; Yang, F.; Ouyang, M. Research on oxygen purity based on industrial scale alkaline water electrolysis system with 50 Nm3 H2/h. Appl. Energy 2024, 360, 122852. [Google Scholar] [CrossRef]
- Cheng, H.; Xia, Y.; Hu, Z.; Wei, W. Optimum pulse electrolysis for efficiency enhancement of hydrogen production by alkaline water electrolyzers. Appl. Energy 2024, 358, 122510. [Google Scholar] [CrossRef]
- Speckmann, F.-W.; Bintz, S.; Birke, K.P. Influence of rectifiers on the energy demand and gas quality of alkaline electrolysis systems in dynamic operation. Appl. Energy 2019, 250, 855–863. [Google Scholar] [CrossRef]
- Ursúa, A.; Marroyo, L.; Gubía, E.; Gandía, L.M.; Diéguez, P.M.; Sanchis, P. Influence of the power supply on the energy efficiency of an alkaline water electrolyser. Int. J. Hydrogen Energy 2009, 34, 3221–3233. [Google Scholar] [CrossRef]
- Xia, Y.; Cheng, H.; He, H.; Hu, Z.; Wei, W. Efficiency Enhancement for Alkaline Water Electrolyzers Directly Driven by Fluctuating PV Power. IEEE Trans. Ind. Electron. 2024, 71, 5755–5765. [Google Scholar] [CrossRef]
- Xia, Y.; Cheng, H.; He, H.; Wei, W. Efficiency and consistency enhancement for alkaline electrolyzers driven by renewable energy sources. Commun. Eng. 2023, 2, 22. [Google Scholar] [CrossRef]
- Xiong, J.; Xia, Y.; Peng, Y.; Wei, W. A Multimode Self-Optimization Electrolysis Converting Strategy for Improving Efficiency of Alkaline Water Electrolyzers. IEEE Trans. Ind. Electron. 2024, 39, 3738–3748. [Google Scholar] [CrossRef]
- Milewski, J.; Guandalini, G.; Campanari, S. Modeling an alkaline electrolysis cell through reduced-order and loss-estimate approaches. J. Power Sources 2014, 269, 203–211. [Google Scholar] [CrossRef]
- Olivier, P.; Bourasseau, C.; Bouamama, P.B. Low-temperature electrolysis system modelling: A review. Renew. Sustain. Energy Rev. 2017, 78, 280–300. [Google Scholar] [CrossRef]
- Haug, P.; Kreitz, B.; Koj, M.; Turek, T. Process modelling of an alkaline water electrolyzer. Int. J. Hydrogen Energy 2017, 42, 15689–15707. [Google Scholar] [CrossRef]
- Abdin, Z.; Webb, C.J.; Gray, E.M. Modelling and simulation of an alkaline electrolyser cell. Energy 2017, 138, 316–331. [Google Scholar] [CrossRef]
- Henao, C.; Agbossou, K.; Hammoudi, M.; Dubé, Y.; Cardenas, A. Simulation tool based on a physics model and an electrical analogy for an alkaline electrolyser. J. Power Sources 2014, 250, 58–67. [Google Scholar] [CrossRef]
- Kirati, S.K.; Hammoudi, M.; Mousli, I.M.A. Hybrid energy system for hydrogen production in the Adrar region (Algeria): Production rate and purity level. Int. J. Hydrogen Energy 2018, 43, 3378–3393. [Google Scholar] [CrossRef]
- Hug, W.; Bussmann, H.; Brinner, A. Intermittent operation and operation modeling of an alkaline electrolyzer. Int. J. Hydrogen Energy 1993, 18, 973–977. [Google Scholar] [CrossRef]
- Ulleberg, Ø. Modeling of advanced alkaline electrolyzers: A system. Int. J. Hydrogen Energy 2003, 28, 21–33. [Google Scholar] [CrossRef]
- Sánchez, M.; Amores, E.; Rodríguez, L.; Clemente-Jul, C. Semi-empirical model and experimental validation for the performance evaluation of a 15 kW alkaline water electrolyzer. Int. J. Hydrogen Energy 2018, 43, 20332–20345. [Google Scholar] [CrossRef]
- Ren, Z.; Wang, J.; Yu, Z.; Zhang, C.; Gao, S.; Wang, P. Experimental studies and modeling of a 250-kW alkaline water electrolyzer for hydrogen production. J. Power Sources 2022, 544, 231886. [Google Scholar] [CrossRef]
- Sillen, C.W.M.P.; Barendrecht, E.; Janssen, L.J.J.; van Stralen, S.J.D. Gas bubble behaviour during water electrolysis. Int. J. Hydrogen Energy 1982, 7, 577–587. [Google Scholar] [CrossRef]
- Angulo, A.; van der Linde, P.; Gardeniers, H.; Modestino, M.; Fernández Rivas, D. Influence of Bubbles on the Energy Conversion Efficiency of Electrochemical Reactors. Joule 2020, 4, 555–579. [Google Scholar] [CrossRef]
- Sakas, G.; Ibáñez-Rioja, A.; Pöyhönen, S.; Järvinen, L.; Kosonen, A.; Ruuskanen, V.; Kauranen, P.; Ahola, J. Sensitivity analysis of the process conditions affecting the shunt currents and the SEC in an industrial-scale alkaline water electrolyzer plant. Appl. Energy 2024, 359, 122732. [Google Scholar] [CrossRef]
- Altuntepe, A.; Erkan, S.; Olgar, M.A.; Çelik, S.; Zan, R. Investigating surface area and hydrogen pressure effects on LiH and NaH. J. Solid State Chem. 2024, 330, 124483. [Google Scholar] [CrossRef]
- Kuleshov, N.V.; Kuleshov, V.N.; Dovbysh, S.A.; Grigoriev, S.A.; Kurochkin, S.V.; Millet, P. Development and performances of a 0.5 kW high-pressure alkaline water electrolyser. Int. J. Hydrogen Energy 2019, 44, 29441–29449. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, T.; Deng, X.; Liu, B.; Ma, J.; Yang, F.; Ouyang, M. Active pressure and flow rate control of alkaline water electrolyzer based on wind power prediction and 100% energy utilization in off-grid wind-hydrogen coupling system. Appl. Energy 2022, 328, 120172. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, T.; Ma, J.; Deng, X.; Gu, J.; Yang, F.; Ouyang, M. Study the effect of lye flow rate, temperature, system pressure and different current density on energy consumption in catalyst test and 500W commercial alkaline water electrolysis. Mater. Today Phys. 2022, 22, 100606. [Google Scholar] [CrossRef]
- Schalenbach, M.; Lueke, W.; Stolten, D. Hydrogen Diffusivity and Electrolyte Permeability of the Zirfon PERL Separator for Alkaline Water Electrolysis. J. Electrochem. Soc. 2016, 163, F1480–F1488. [Google Scholar] [CrossRef]


| Main Features | Values | Unit |
|---|---|---|
| Capacity of hydrogen production | 10.00 | Nm3 h−1 |
| Maximum operating pressure | 1.60 | MPa |
| Electrolyte concentration | 30 | wt% KOH |
| Voltage range | 0–6.5 | V |
| Electrical current range | 0–7600 | A |
| Maximum power | 50 | kW |
| No. | Current (A) | Pressure (bar) | Temperature (°C) | Cell Voltage (V) | HTO (%) |
|---|---|---|---|---|---|
| 1 | 2533 | 7 | 45 | 1.79 | 1.56 |
| 2 | 3800 | 7 | 45 | 1.86 | 1.15 |
| 3 | 5000 | 7 | 45 | 1.93 | 0.93 |
| 4 | 6330 | 7 | 45 | 2.00 | 0.78 |
| 5 | 7600 | 7 | 45 | 2.04 | 0.75 |
| 6 | 2533 | 7 | 55 | 1.78 | 2.07 |
| 7 | 3800 | 7 | 55 | 1.85 | 1.44 |
| 8 | 5000 | 7 | 55 | 1.91 | 1.13 |
| 9 | 6330 | 7 | 55 | 1.97 | 0.90 |
| 10 | 7600 | 7 | 55 | 2.03 | 0.84 |
| 11 | 2533 | 7 | 65 | 1.72 | 2.21 |
| 12 | 3800 | 7 | 65 | 1.80 | 1.60 |
| 13 | 5000 | 7 | 65 | 1.85 | 1.25 |
| 14 | 6330 | 7 | 65 | 1.91 | 1.01 |
| 15 | 7600 | 7 | 65 | 1.97 | 0.85 |
| 16 | 2533 | 7 | 75 | 1.66 | 2.09 |
| 17 | 3800 | 7 | 75 | 1.75 | 1.69 |
| 18 | 5000 | 7 | 75 | 1.81 | 1.33 |
| 19 | 6330 | 7 | 75 | 1.87 | 1.11 |
| 20 | 7600 | 7 | 75 | 1.93 | 0.99 |
| 21 | 2533 | 7 | 85 | 1.64 | 2.03 |
| 22 | 3800 | 7 | 85 | 1.71 | 1.53 |
| 23 | 5000 | 7 | 85 | 1.76 | 1.21 |
| 24 | 6330 | 7 | 85 | 1.81 | 1.00 |
| 25 | 7600 | 7 | 85 | 1.87 | 0.87 |
| 26 | 2533 | 10 | 75 | 1.67 | 2.20 |
| 27 | 3800 | 10 | 75 | 1.73 | 1.79 |
| 28 | 5000 | 10 | 75 | 1.80 | 1.46 |
| 29 | 6330 | 10 | 75 | 1.85 | 1.18 |
| 30 | 7600 | 10 | 75 | 1.91 | 1.04 |
| 31 | 2533 | 12 | 75 | 1.68 | 2.23 |
| 32 | 3800 | 12 | 75 | 1.74 | 1.80 |
| 33 | 5000 | 12 | 75 | 1.79 | 1.52 |
| 34 | 6330 | 12 | 75 | 1.85 | 1.26 |
| 35 | 7600 | 12 | 75 | 1.89 | 1.09 |
| Coefficient | Value | Unit |
|---|---|---|
| 5.5137 × 10−5 | Ω·m2 | |
| −1.2270 × 10−7 | Ω·m2·°C | |
| 8.2132 × 10−6 | Ω·m2 | |
| −1.6911 × 10−6 | Ω·m2·bar−1 | |
| s | 0.1467 | V |
| −0.0357 | m2·A−1 | |
| 4.9644 | m2·°C·A−1 | |
| −90.4262 | m2·°C·A−1 | |
| 16.0995 | \ | |
| −0.2259 | °C−1 | |
| 8.4417 × 10−4 | °C−2 | |
| −14.8585 | \ | |
| 0.1948 | °C−1 | |
| −6.5825 × 10−4 | °C−2 | |
| 151.4947 | A·m−2 | |
| 0.0052 | A·m−2·°C−1 | |
| −0.1755 | A·m−2·°C−2 | |
| 0.1172 | \ | |
| −1.2924 | bar−1 | |
| 0.0940 | bar−2 | |
| −0.9123 | \ | |
| 1.4749 | bar−1 | |
| −0.1018 | bar−2 | |
| 1.8452 | A·m−2 | |
| 0.9521 | A·m−2·bar−1 | |
| −0.7132 | A·m−2·bar−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Zheng, X.; Jia, Y.; Shao, G.; Shi, J.; Zeng, S.; Wang, K.; Li, Y.; Gu, C. Mathematical Modeling and Experimental Validation for a 50 kW Alkaline Water Electrolyzer. Processes 2024, 12, 2616. https://doi.org/10.3390/pr12122616
Liu M, Zheng X, Jia Y, Shao G, Shi J, Zeng S, Wang K, Li Y, Gu C. Mathematical Modeling and Experimental Validation for a 50 kW Alkaline Water Electrolyzer. Processes. 2024; 12(12):2616. https://doi.org/10.3390/pr12122616
Chicago/Turabian StyleLiu, Min, Xinyu Zheng, Yansong Jia, Guining Shao, Jianfeng Shi, Sheng Zeng, Kun Wang, Yang Li, and Chaohua Gu. 2024. "Mathematical Modeling and Experimental Validation for a 50 kW Alkaline Water Electrolyzer" Processes 12, no. 12: 2616. https://doi.org/10.3390/pr12122616
APA StyleLiu, M., Zheng, X., Jia, Y., Shao, G., Shi, J., Zeng, S., Wang, K., Li, Y., & Gu, C. (2024). Mathematical Modeling and Experimental Validation for a 50 kW Alkaline Water Electrolyzer. Processes, 12(12), 2616. https://doi.org/10.3390/pr12122616






