Abstract
Improvements in heat exchanger thermal efficiency are crucial for achieving energy use and cost reductions. The use of nanofluids and the rotation of the exchanger inner tube may enhance heat transfer and exchanger efficiency. In this work, after having performed experiments on such a heat exchanger, a three dimensional numerical model was developed to simulate the transitional forced convection flow of a horizontal double-tube heat exchanger, with the aim of obtaining insight into the effects of the inner tube rotation, fluid flow rate and type of nanofluid employed. It was found that an increase in the nanoparticle concentration up to 3% increased the exchanger efficiency. Al2O3, Al2O3-Cu and Cu-water nanofluids were studied, with the Cu-water being the fluid with the best performance (19.33% improvement). Heat transfer was enhanced with inner tube rotation up to 500 rpm (41.2%). Nevertheless, pressure drop and friction values were increased due to both phenomena, leading to higher pumping power values for the operation of the heat exchanger. Hence, a balance between the performance and pumping power increase must be considered when modifications are made on a heat exchanger. The development of the numerical model might help in further optimizing, redesigning and scaling up heat exchangers.
1. Introduction
Improvements in heat exchanger thermal efficiency are crucial for achieving energy use and cost reductions. Several methods to increase the efficiency of heat exchangers may be found in the literature. They may be classified into three groups: active, passive and combined methods. Active methods rely on an external power supply to increase heat transfer, such as a magnetic field, an assistant mechanical system, injection or surface of fluid vibration. For instance, Bezaatpour and Goharkhah [1] used a magnetic field swirling generator to increase convective heat transfer in a double-pipe mini heat exchanger. On the other hand, passive methods enhance heat transfer through modifications of the fluid flow or the heat exchanger surfaces, such as rougher surfaces, increases in the contact area, fluid additives, coiled tubes or swirl flow devices. For example, Forooghi et al. [2] added a passive insert to a flat-tube heat exchanger to increase heat transfer. Combined methods take advantage of both active and passive methods, increasing heat transfer rate with reduced pumping power.
Many studies have shown the potential of fluid additives regarding heat transfer enhancement, with Al2O3, TiO2 and CuO being recurrent ones. Sonawane et al. [3] performed an experimental study of the heat transfer characteristics of an Al2O3-water nanofluid at a 2% and 3% volume concentration in a concentric tube heat exchanger, finding an increase in heat transfer with an increase in the concentration. Bahmani et al. [4] studied the heat transfer and turbulent flow characteristics of a similar nanofluid in parallel and counter-flow double tube heat exchanger by means of a numerical code, finding that the addition of nanoparticles to water enhanced the maximum thermal efficiency and average Nusselt number in 30% and 32.7%, respectively. Experimental studies from Rao et al. [5] showed that the forced convection of an Al2O3-water nanofluid at concentrations from 0.1 to 0.4% improved the heat transfer rate by 2.5% in a turbulent regime. Yang et al. [6] compared the performance of Al2O3 and TiO2-water, finding that the Nusselt number of TiO2-water nanofluids was higher. Bajestan et al. [7] also found, experimentally and numerically, that the heat transfer characteristics of a TiO2-water nanofluid are higher than for raw water, with a maximum enhancement of 21%. CuO-water nanofluids have also shown an increase in the heat transfer coefficient up to 18–35% with respect to raw water in the work of Korpys et al. [8]. Cu- and CuO-water based nanofluids have been studied as well by Yang et al. [6] and Saeedan et al. [9]. However, it has been found that too high of concentrations of nanofluids seem to the worsen heat exchanger performance. Duangthongsuk and Wongwises [10] studied the behavior of a TiO2-water nanofluid with volume fractions from 0.2–2% in a horizontal double-tube counter-flow, finding that heat transfer coefficient was enhanced by 26% with respect to raw water in a 1% volume fraction, but it dropped by 14% with a 2% volume fraction. Other oxides have also shown good heat transfer properties: Kumar et al. [11] achieved increases of the Nusselt number up to 14.7% with Fe3O4, whereas Esfe et al. [12] reported a 21.8% increase with MgO. Likewise, other substances have been studied as fluid additives, such as carbon nanotubes. Halelfadl et al. [13] found an enhancement of 12% in heat transfer in a coaxial heat exchanger under a laminar regime. Multi-Walled Carbon Nanotubes (MWCNTs) were studied by Kumar and Chandrasekar [14], finding an increase in Nusselt numbers up to 30% for 0.6% concentration values. Nitrogen-doped graphene nanosheets have been also found to increase the heat transfer coefficient (Goodarzi et al. [15]). Heat transfer and friction factor values of a TiO2-Poly Vinyl Alcohol (PVA) nanofluid flowing in a plain tube with twisted tape were experimentally studied by Hazbehian et al. [16]. The general pattern is that nanofluids enhance the heat transfer rate and increase friction loss. Hybrid nanofluids are another option to consider. The most common are Al2O3-MgO, Cu-TiO2 and Al2O3-Ag, reaching enhancements up to 49% in the Nusselt number (Madesh et al. [17]). Finally, another option to improve the performance of the working fluid is mixing two carriers, such as water and glycol, as performed by Reddy and Rao [18]. These authors found an increase of 10.73% in the heat transfer rate with a 60–40% distilled water–glycol mixture when adding 2% TiO2 nanoparticles. The addition of stabilizers, such as cetyl trimethyl ammonium chloride (CTAC), to the mixture was also found to increase the heat exchanger performance by Korpys et al. [8], with the same effect observed by Homozi et al. [19] when adding sodium dodecyl sulfate to a hybrid Al2O3-Ag nanofluid.
Modifications of the heat exchanger geometry have also contributed to enhancing its thermal performance. Helical and longitudinal fins were studied by El Maakoul et al. [20], finding a better improvement (24%) with helical fins due to their higher surface area. Rotated inclined elliptical inserts were found to increase heat transfer rates up to 30.7% by Nakhchi et al. [21]. Perforated twisted turbulators also increase the overall heat transfer in a heat exchanger (Vaisi et al. [22]). Depending on the perforation shape (circular, square, rectangular, diamond or triangular), heat transfer increases accordingly (20.8%, 15%, 11%, 8.7%, 5%). The insertion of a V-winglet tape in the exchanger has also shown an enhancement, with the V-down configuration being more efficient than the V-up one (Promvonge et al. [23]). The effect of a trapezoidal twisted tape was studied by Murali et al. [24], finding an increase of 78.6% in the heat transfer rate with respect to a plain tube. Watel et al. [25] studied convective heat transfer from the central fin of a rotating finned tube. Finally, Aliabadi and Feizabadi [26] found an enhancement of the heat transfer coefficient of 26.3% with a twisted tape.
The combination of geometrical modifications and nanofluids seems to increase the heat exchanger performance to a higher degree. For instance, Singh and Sarkar [27] combined tapered wire coils and an Al2O3-MgO hybrid nanofluid; Karimi et al. [28] used twisted tape inserts with different pitch ratio values and an Al2O3-water nanofluid, finding promising results. Darzi et al. [29] used a helical corrugated tube and Al2O3 at a 4% concentration to increase heat transfer by a factor up to 3.31. Qi et al. [30] studied a TiO2-water nanofluid with smooth and corrugated tubes, finding an improvement in the heat transfer up to 14.8%, but at the cost of higher pressure drop values up to 6.5%. When inserting single- and double-strip helical screw tapes in a tube, Chaurasia and Sarviya [31] were able to increase the Nusselt number in 170 and 182%. Nakhchi and Esfahani [32] were also able to increase the Nusselt number and friction factor with perforated circular tubes with louvered strip vortex generators. A cone-shaped inserted double-tube heat exchanger with Al2O3 and CuO-water nanofluids was studied by Karuppasamy et al. [33], finding that Al2O3 had better performance than CuO. Nevertheless, Saedodin et al. [34] found that CuO had better performance when investigating SiO2-water, TiO2-water, Al2O3-water and CuO-water nanofluids in a circular tube with a turbulator. Mohamed et al. [35] compared Al2O3 and Cu-water nanofluids, claiming that the Cu-water nanofluid showed the best performance.
Active and passive methods may be combined to benefit from both improvements, as performed by Arzani et al. [36], who used a rotating tube with twisted tape and fins with a nanofluid. Bahiraei et al. [37] studied a rotating coaxial tube with double twisted tapes and a biological graphene nanofluid, achieving an increase of 34% in the heat transfer coefficient at a 3.5 twist ratio and 900 rpm. Nevertheless, the rotation of the tube increased the pressure drop in the exchanger. Shi and Dong [38] studied laminar convective flow in a rotating helical tube heat exchanger, finding a decrease in entropy generation due to heat transfer but an increase due to flow friction. The rotational effect was also studied by El-Maghlany et al. [39] with a Cu-water nanofluid, finding an increase in the heat exchanger effectiveness up to 30.7%. Moayedi [40] investigated double rotating cylinders in a vented cavity with a Cu-water nanofluid, finding that heat transfer was enhanced when both cylinders rotated in opposite directions, being the mean Nusselt number over 330% of its original value. Abou-Ziyan et al. [41] reported an enhancement of the Nusselt number by 7.5 times when using both fins and rotation. Ali et al. [42] also found an increase of the Nusselt number by almost 5 times with tube rotation, and Jasim et al. [43] were able to increase heat transfer up to 10.6% with an Al2O3-Cu-water hybrid nanofluid inside a vented cavity with a rotating cylinder. Although heat exchange was improved in all of these studies, the pressure drop (and hence the required pumping power) was increased.
When performing numerical simulations of heat exchangers with nanofluids, the selection of the turbulence closure is important for the accurate prediction of thermal behavior. The most employed turbulence model for this type of flow is the Renormalized Group (RNG) k-ε turbulence model (Saedodin [34]), as it adapts well to different flow regimes at low Reynolds numbers and with swirl flow. Gomaa et al. [44] were able to experimentally validate their numerical results using this model for both a double and triple concentric tube exchanger. They found that the performance of the triple exchanger was around 1.5 times higher than the double one. Abdollahzadeh et al. [45] simulated natural convection inside a channel with two parallel vertical plates, finding that k-kL-ω and k-ε models were accurate to study transitional flow. Sivashi and Jamali [46] studied a TiO2-water nanofluid flowing through an annulus with different radii ratio values using the k-ε model to verify that heat transfer performance increased with the Reynolds number. The RNG k-ε model was used by Ard and Kiatkittipong [47] to study the effect of multiple twisted tapes with different arrangements and using a TiO2 nanofluid, to find that the counter arrangement offered the best performance. This model was also used by Fattahi [48] to assess the heat transfer and pressure drop of a hybrid Al2O3-CuO-water nanofluid in a cylindrical pipe with twisted tape, modeling the fluid as a single phase. A maximum performance increase of 23% was found at a 2% concentration. YousefiMiab et al. [49] used the OpenFOAM solver to create gas pressure reducing stations utilizing an Al2O3 nanofluid in shell and tube heat exchangers, discovering that increasing the shell side Peclet number and nanoparticle volume fraction increases the total heat transfer coefficient. Increasing the shell side Peclet number and the nanoparticle volume fraction also resulted in an increase in pressure loss, which was a disadvantage of the heater’s performance. Furthermore, Dbouk et al. [50] used CFD modeling to simulate a combined Poiseuille-Taylor-Couette flow in a multifunctional heat exchanger between two rotating concentric elliptically deformed annular tubes. It was discovered that the proposed Poiseuille–Taylor–Couette flow in this heat exchanger’s elliptically deformed concentric tubes can greatly improve heat and mass transfer at the Reynolds number. Upadhya et al. [51] studied the effect of using Casson, Micropolar and Hybrid magneto-nanofluids in a suspension of cross diffusion on entropy generation. They found that the hybrid nanofluid has a higher temperature profile than micropolar and Casson fluid. The micropolar fluid shows higher entropy generation compared to the Casson and hybrid nanofluid. Ghazanfari et al. [52] investigated the influence of nanofluids on twisted tube heat exchanger efficiency using CFD. They demonstrated that using nanofluids in twisted tubes enhanced heat transfer while increasing the pressure drop. Sundar and Mouli [53] analyzed the effectiveness and number of transfer units of Fe3O4-SiO2 hybrid fluids through a plate heat exchanger. They concluded that increases in the volume concentration and Reynolds number lead to enhancements in the effectiveness and number of transfer units. Thirumalaisamy et al. [54] investigated the natural convective flow and thermal efficiency of an electroconductive ternary nanofluid-filled inclined partially heated rectangular porous cavity under the impacts of an inclined magnetic field. The results indicated that the average heat transfer rate is increased by 7.49% when augmenting nanofluids 33.3%.
As a summary, Table 1 collects the main studies found in the literature, according to the heat exchanger morphology and nanofluid employed.

Table 1.
Classification of main studies from the literature according to the heat exchanger morphology and nanofluid employed.
As it has been observed after checking the reference sources, focus has been mainly set on the flow behavior and the thermal performance of nanofluids under laminar and turbulent flow conditions. It appears that the effects of active tube rotation in the heat exchanger on its performance with different nanofluids under Reynolds numbers associated with transitional flow have not been completely discussed. Hence, in this work, the aim is set in combining both active and passive methods for the enhancement of heat transfer. After having performed experimental tests, a CFD analysis was performed to understand the involved phenomena to a higher degree. Thus, a numerical model for the simulation of transitional forced convection flow inside a horizontal rotating tube in a heat exchanger has been developed. The main objective is to understand the effects of inner tube rotation and fluid flow rate on the hydrothermal performance of the exchanger and compare the performance of Al2O3, Cu and hybrid Cu-Al2O3 water-based nanofluids. The effects of changing the tube rotational speed, as well as the nanoparticle concentration, on the effectiveness of the exchanger and the pressure drop that must be balanced by an increasing pumping power are also investigated and discussed. The development of the model might also be helpful for further optimizations, redesigning and scaling up similar heat exchangers.
2. Numerical Model
2.1. Geometry
A 3D model of the double-tube heat exchanger was developed with the aim of studying the effect of the inner tube rotation at different speeds, from 0 to 500 rpm, as well as the behavior of different working cold fluids: water, Al2O3-water nanofluid, Cu-water nanofluid and Al2O3-Cu hybrid nanofluid. Figure 1 shows a view of the geometrical model.
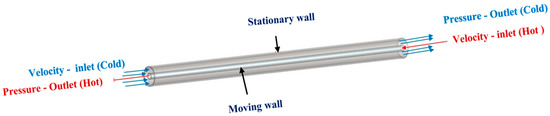
Figure 1.
Schematic view of the double-tube heat exchanger geometry and boundary conditions.
The heat exchanger length was 1200 mm. The diameters of the inner (di) and outer tubes (Di) were 25.4 and 76.2 mm, respectively. Their thickness value was 2 mm. Inner tubes were made of high-thermal-conductive copper, while the outer tube was made of transparent Plexiglass. Details of the exchanger insulation may be found in [39].
2.2. Boundary Conditions
Simulations were performed under different conditions. The Reynolds number of the circular annulus for the cold fluid Recf ranges between 2473 and 4947. This number was calculated based on the different cold fluid properties at different volume concentrations: 1, 2 and 3%. The Reynolds number of the hot fluid, hot water, flowing through the inner tube, Rehf, was fixed at 9780. Inlet temperature of nanofluids and hot water were fixed at 301 K and 333 K, respectively. The outer tube was assumed to be a stationary insulated wall. The speed of the rotating inner tube of the heat exchanger was fixed at the following values: 0, 100, 200, 300, 400 and 500 rpm, depending on each particular case. Non-slip wall conditions were applied to the surfaces of both tubes. A velocity-inlet condition was applied at the inlets of the inner tube and the annulus, with values specified depending on the flow rate. Finally, the pressure-outlet boundary condition was applied to both tube outlets. As it may be appreciated in Figure 1, the double-tube heat exchanger under study has a counter-flow configuration, with Reynolds numbers in the range of transitional flow.
2.3. Governing Equations
Forced convection flow equations were employed to study the flow and heat transfer performance of the nanofluids through the double-tube heat exchanger. The flow was considered incompressible, steady-state and homogeneous. With these assumptions, the single-phase approach for the nanofluids was adopted. The validity of this approach has been confirmed in the literature [31,37]; additionally, it reduces simulation time with a reliable accuracy compared to the two-phase approach. The finite volume method was used to discretize and solve continuity, momentum and energy equations in the computational domain based on a Reynolds-Average Navier-Stokes (RANS) model.
The continuity equation is as follows:
where xi is the Cartesian coordinate in the i-direction, ui is the mean component of velocity in the i-direction and is the fluid density.
The momentum equation is as follows:
where p is the pressure, μ is the dynamic viscosity and () are the Reynolds stresses.
The energy equation is as follows:
where is the effective conductivity , where is the turbulent thermal conductivity), is the diffusion flux of species j and h is enthalpy, and where is energy transfer due to conduction, is species diffusion and is viscous dissipation.
The turbulent viscosity was calculated as follows:
where k is the turbulent kinetic energy and ε is the dissipation rate.
The turbulent kinetic energy equation (k) is as follows:
The turbulent energy dissipation equation (ε) is as follows:
where is the generation rate of turbulent kinetic energy due to mean velocity gradients and is given as follows:
The effective turbulent viscosity is given by the following:
The constants used in the above equations were selected as in [48]:
where and are the inverse effective turbulent Prandtl numbers for k and ε.
2.4. Thermophysical Properties of Fluids
Nanofluids have been considered as incompressible fluids with constant physical properties. Their properties have been evaluated considering the different nanoparticle volume concentrations with specific correlations. Table 2 collects the thermophysical properties of pure water and the different nanoparticles studied.

Table 2.
Thermophysical properties of pure water and nanoparticles at an ambient temperature and atmospheric pressure.
The effective density of a particular nanofluid is given by Equation (10) [55]:
where ϕ is solid volume fraction.
And its specific heat is obtained from Equation (11) [55]:
The effective thermal conductivity of a nanofluid is given by Equation (12) [55]:
The effective dynamic viscosity of the nanofluid is obtained from Equation (13) for :
For hybrid nanofluids, the effective density for two-mixture nanoparticles is estimated using Equation (14) [56]:
where the volume concentration for hybrid nanofluids is calculated from Equation (15) [56]:
Consequently, the effective heat capacity of the hybrid nanofluid is estimated using Equation (16) [57]:
The effective dynamic viscosity of hybrid nanofluids is obtained from Equation (17) [57]:
And the effective thermal conductivity of a hybrid nanofluid with the modified Maxwell model is estimated using Equation (18) [57]:
Table 3 shows the thermophysical properties of the studied nanofluids at different concentration values (1, 2 and 3%). As it may be observed, the addition of nanoparticles affects the density, specific heat, conductivity and viscosity in the nanofluid. The maximum increase in density was around 24% with respect to the original (pure water) value, whereas the maximum decrease in specific heat was 19.6%. Thermal conductivity increased up to 109.2% of its original value, while dynamic viscosity was reduced to a maximum value of 8%.

Table 3.
Thermophysical properties of nanofluids for different concentrations calculated from Equations (10)–(18).
2.5. Numerical Method and Validation
The numerical model was implemented using ANSYS-FLUENT 15.0 software. The equations for momentum, turbulent kinetic energy, the turbulent dissipation rate and temperature were solved with a second-order upwind scheme. The SIMPLE algorithm was used for the pressure–velocity coupling. Thermal equilibrium was assumed between the nanoparticles and the base fluid, as well as the same velocity. This allowed for the use of a homogeneous single-phase model. The renormalized group (RNG) k-ε turbulence model was selected. According to the results from Gomaa et al. [44], the Reynolds numbers reached in this study with the rotating tube and swirl flow justify the selection of this model for the closure of turbulence, as it has been proved to be suitable for such low Reynolds numbers with swirl flow. Near-wall zone criteria with an enhanced wall treatment were considered. Finally, residual convergence criteria were set to 10−5 for continuity and momentum equations and 10−6 for the energy equation. The simulation time took around 12 h for a fixed tube case and 72 h for a rotating tube case.
2.6. Grid Independence Study
A grid independence study was performed to verify the accuracy of the numerical results. Mesh sensitivity tests were conducted for the concentric double heat exchanger with water as a base fluid at a Reynolds number Recf = 2473 and an inner tube rotational speed of 0 rpm. A combination of a hexahedral and tetrahedral cell was used to generate the mesh, as shown in Figure 2. The relevant parameters to perform the grid independence study were considered to be the number of transfer units (NTU) and the pressure drop. Figure 3 shows the results of the grid independence study. It may be appreciated that the grid with 1,835,524 cells, with an error around 0.81% for the NTU, was accurate enough for the purposes of this study.

Figure 2.
Mesh configuration of the double-tube heat exchanger.
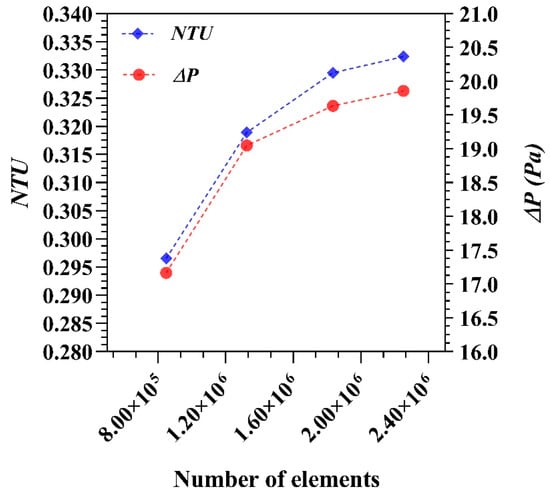
Figure 3.
Grid independence study at Recf = 2473.
2.7. Experimental Validation
Additionally, a comparison between the numerical simulations and the experimental results available for the double-tube heat exchanger was performed to validate the numerical results. The NTU, the pressure drop for water and the Cu-water nanofluid at (ϕ) = 3% transitional flow through a horizontal concentric tube heat exchanger were compared with the results from El-Maghlany et al. [39]. Figure 4 shows that the numerical results agree consistently with the experimental results, with a maximum deviation of the NTU of 4.3% and 4.88% for water and the Cu-water nanofluid, respectively, at rotational speed (0 RPM); for the pressure drop, the maximum deviations were 4% and 3.62% for water and the Cu-water nanofluid, respectively, at rotational speed (0 RPM). For rotational speed (500 RPM) at (ϕ) = 3% for the Cu-water nanofluid, the maximum deviation of NTU was 3.14%. These results confirm the suitability of the developed numerical model for the purpose of this study.
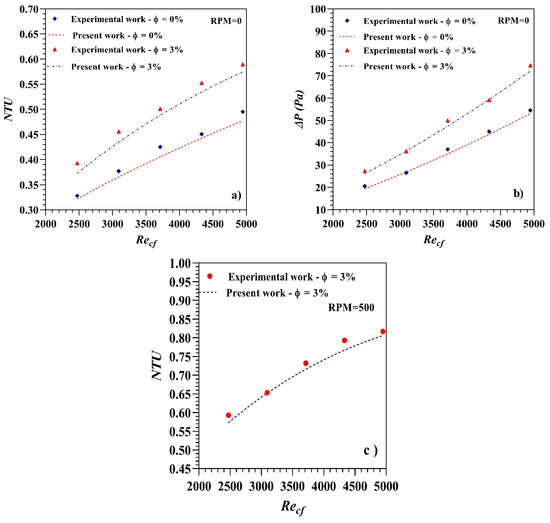
Figure 4.
Experimental validation of (a) NTU at RPM = 0, (b) pressure drop at RPM = 0 and (c) NTU at RPM = 500.
3. Data Processing
The results obtained from the simulations are processed to calculate variables of interest. The equations employed for such calculations are the following:
Heat lost from the hot fluid was obtained using Equation (19).
Heat absorbed by the cold fluid was obtained using Equation (20):
The average heat transfer rate was calculated using Equation (21):
The overall heat transfer coefficient was estimated using Equation (22):
where ΔTLMTD is the logarithmic mean temperature difference, calculated using Equation (23):
The number of transfer units, NTU, was obtained using Equation (24):
where is the smaller of the heat capacity values of the hot and cold fluids, which were calculated from Equation (25):
The effectiveness was calculated using Equation (26):
Hot and cold fluid Reynolds numbers were obtained using Equation (27):
where the hydraulic diameter was calculated using Equation (28):
Dh = Di − do
The pumping power required for the exchanger was calculated from Equation (29) [37]:
where Δp (Pa) is the pressure drop, and is the volumetric flow rate (m3/s).
4. Results and Discussion
This section presents the results obtained for the water, Al2O3-water nanofluid, Cu-water nanofluid and Al2O3-Cu hybrid nanofluid through the double-tube heat exchanger at different volume concentration values (ϕ) of 1, 2 and 3% and different inner tube rotational speeds of 0, 100, 200, 300, 400 and 500 rpm. The cold fluid Reynolds number Recf ranged between 2473 and 4947 and the hot fluid Reynolds number Rehf was fixed at 9780.
4.1. Flow Analysis
Figure 5 shows the streamlines colored by velocity magnitude at Recf = 2473 for water at different inner tube rotational speed values. In Figure 5a, the flow pattern is mainly in the axial direction, with smooth velocity streamlines at 0 RPM. However, as the rotating speed increases (Figure 5b–d), the flow has both axial and rotational components. These flow patterns are thought to enhance convective heat transfer, due to the continuous disturbance of the boundary layer and generation of swirling. Greater angular velocities change the flow direction significantly, forcing the flow to encircle the tube and resulting in longer paths, as shown in Figure 5d at 500 RPM. This increase in rotational speed leads to more turbulence and warping of the flow around the tube, a fact known to enhance heat transfer.
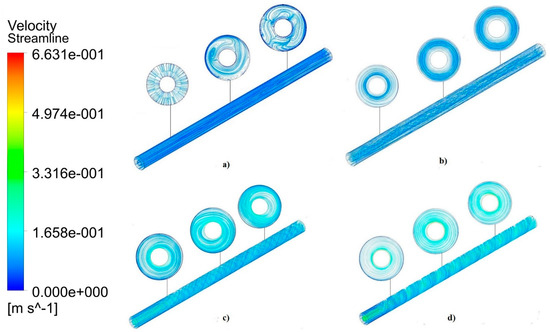
Figure 5.
3D streamlines in the double tube with different rotational speeds at Recf = 2470 (a) 0 RPM, (b) 100, (c) 300 RPM and (d) 500 RPM.
4.2. Number of Transfer Units (NTU)
Figure 6 shows the number of transfer units (NTU) as a function of the Reynolds number and rotational speed for the different nanofluid types and concentrations, obtained from Equation (24). An increase in the NTU may be found with higher Reynolds numbers and inner tube rotational speed values. Comparing the three nanofluids, the Cu-water nanofluid displays the best behavior, with the Al2O3-water nanofluid being the least effective for heat transfer. The increase in the nanoparticle concentration from 0 to 3% and the rotational speed from 0 to 500 rpm contribute to higher heat transmission values, increasing the efficiency of the heat exchanger for all nanoparticle types. The significant positive effect of the rotational speed on the convection heat transfer coefficient may be ascribed to the swirling flow that arises and is reinforced with increasing speeds. Additionally, comparing the results obtained with the different nanofluids and raw water, the benefits of incorporating nanoparticles are apparent, as the NTU increases substantially. Considering only the rotational effect, a mean increase in the NTU of around 0.146 when increasing the rotational speed from 0 to 500 rpm in pure water has been observed. When considering only the addition of nanoparticles, the mean increase in the NTU was found to be 0.078 for the addition of Cu nanoparticles at a 3% concentration. When both effects were combined, the mean increase in the NTU was found to be 0.300, hinting at possible constructive interference between the effects of the increase in rotational speed and the addition of nanoparticles to water.

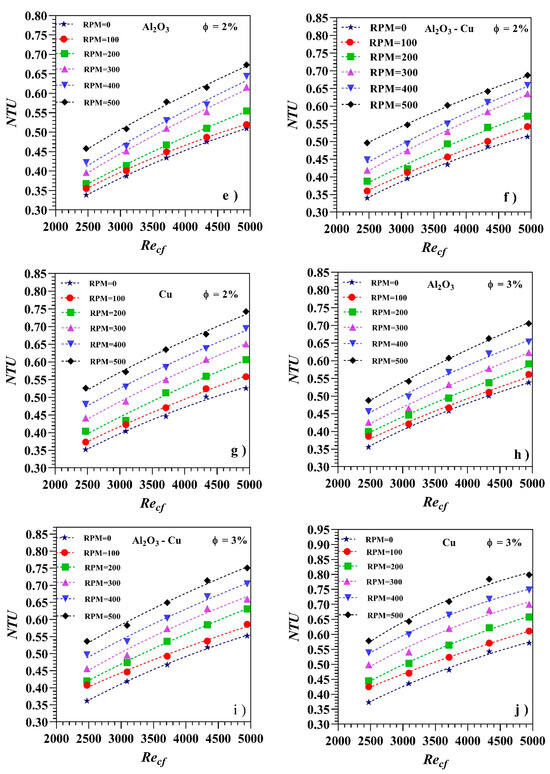
Figure 6.
NTU variation for different types of nanofluids at different concentrations (ϕ).
The NTU for the Cu-water nanofluid was higher than that for the Al2O3-Cu hybrid nanofluid and the Al2O3-water nanofluid. For instance, at a 1% volume concentration and 500 rpm, the NTU was improved by around 46.9, 43.8 and 41.5%, respectively, for the Cu-water nanofluid, the Al2O3-Cu hybrid nanofluid and the Al2O3-water nanofluid compared to raw water at 0 rpm when Recf = 2473. At Recf = 4946, the same effect was observed, with NTU being enhanced by 46.1 (Cu), 42.6 (hybrid) and 36% (Al2O3), as shown in Figure 6a–d. Figure 6e–g show an NTU enhancement of 62.4 (Cu), 53.2 (hybrid) and 41.62% (Al2O3) at Recf = 2473 at a 2% concentration and 500 rpm compared to raw water at 0 rpm. Similarly, at Recf = 4946, the maximum NTU improvement was 55.1 (Cu), 43.5 (hybrid) and 40.6% (Al2O3). As depicted in Figure 6h–j, the increase in the nanoparticle concentration to 3% and the inner tube rotation to 500 rpm achieved a maximum NTU enhancement at Recf = 4946 of 66.7 (Cu), 56.8 (hybrid) and 47.3% (Al2O3) with respect to raw water at 0 rpm. Hence, it seems that the Cu-water nanofluid was the most efficient one in terms of performance improvement. A particular detail may be commented about in Figure 6j, where it seems that Cu nanoparticles, at 500 rpm, might reach a maximum efficiency at a cold fluid Reynolds value below 5000, suggesting that further increases in its value could not result in a higher efficiency. This effect should be investigated in detail in future research.
4.3. Effectiveness
Heat exchanger effectiveness (ε) values, obtained as a function of Reynolds from Equation (26), are shown in Figure 7. Decoupling the effects of rotational speed and the addition of nanoparticles, it has been observed that the mean increase in effectiveness is around 7.5% when increasing the rotational speed from 0 to 500 rpm for pure water. The addition of Cu nanoparticles at a 3% concentration without inner tube rotation, on the other hand, causes a mean increase of around 4.2%. Constructive interference becomes apparent again, reaching mean increase values of 14.1% when both actions are combined.

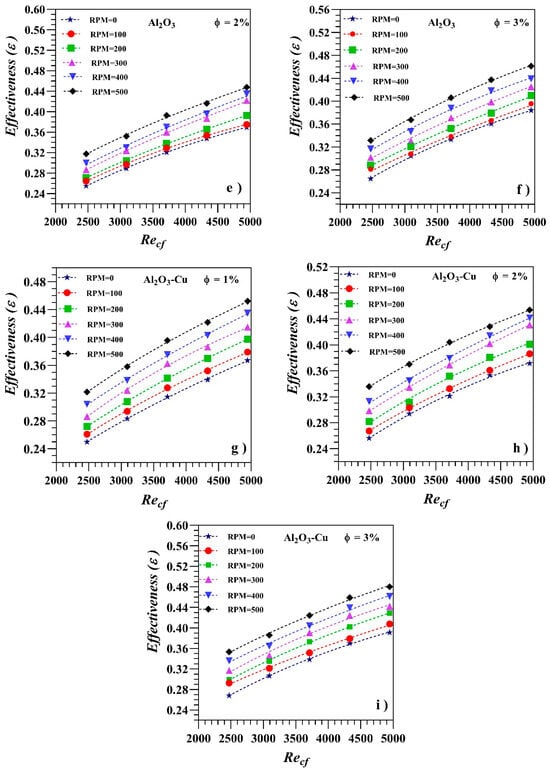
Figure 7.
Effectiveness variation for different types of nanofluids at different concentrations (ϕ).
The independent effects of both actions may be seen in Figure 7a–c, where the addition of the Cu-water nanofluid in 1, 2 and 3% concentrations improves effectiveness without any rotation of the inner tube. At Recf = 4946, the improvement was 5.2, 6.9 and 13.4%, respectively, compared with pure water. Maximum enhancement, nevertheless, arises from the combination of the nanofluid and inner tube rotation, reaching a 41.2% with a 3% concentration and 500 rpm. For the Al2O3-water nanofluid with 1, 2 and 3% concentration values at 0 rpm, as shown in Figure 7d–f, the enhancement was only 3.6, 4.5 and 8.7%, respectively. In this case, maximum enhancement occurred at a 3% concentration and 500 rpm and was equal to 30.6%. The improvement caused by the addition of the hybrid nanofluid with 1, 2 and 3% concentrations is shown in Figure 7g–i, where the enhancement at 0 rpm is equal to 3.9, 5.1 and 10.7%, respectively, when compared to raw water, reaching a maximum improvement at 500 rpm equal to 35.9%.
4.4. Effect of Rotational Speed at Higher Reynolds Numbers
It could be thought that the relative low Reynolds numbers in transitional flow, which entails low linear fluid velocities, could lead to an overestimation of the effect of rotational speed on the improvement of the heat exchanger. Hence, additional simulations at higher Reynolds numbers (10,500 and 14,000) were performed with water and the Cu-water nanofluid at a 3% concentration, to check if the effect of rotating the inner tube is still determining at those Reynolds numbers. The rotational speeds chosen were 0 and 500 rpm, to cover the range used in the previous simulations. The results, collected in Table 4, show that the increase in the Reynolds number indeed increases the effectiveness of the heat exchanger, but that the effect of increasing the rotational speed seems to be relatively independent of the Reynolds number.

Table 4.
Heat exchanger effectiveness as a function of the Reynolds number and rotational speed. Results for water and Cu-water at ϕ = 3%.
4.5. Local Heat Transfer Coefficients
Figure 8a–l shows the evolution of the local heat transfer coefficients for the inner and outer fluids. For all the studied cases, the heat transfer coefficient was higher for the hot fluid than for the cold one. It may be observed that the heat transfer coefficient becomes higher at the hot fluid inlet and then drops down as the hot fluid cools down and the cold fluid is heated up. The addition of nanoparticles increases both the heat transfer coefficients, mainly as the results of the changes in fluid properties. The effect of inner tube rotation seems to increase the heat transfer coefficients to a higher degree, mainly due to the induced turbulence by the fluid swirl motion. Again, the best performance was found when Cu-nanoparticles were added to a 3% concentration and the inner tube was rotated at 500 rpm. It may be appreciated that the thermal boundary layer is not fully developed until almost the end of the tube, considering that full development is not reached while there are still appreciable changes in the heat transfer convection coefficient. This fact hints at the idea that the heat exchanger length could be extended to profit from the relatively high heat transfer coefficient values that are reached at high rotational speeds and nanoparticle concentration values.

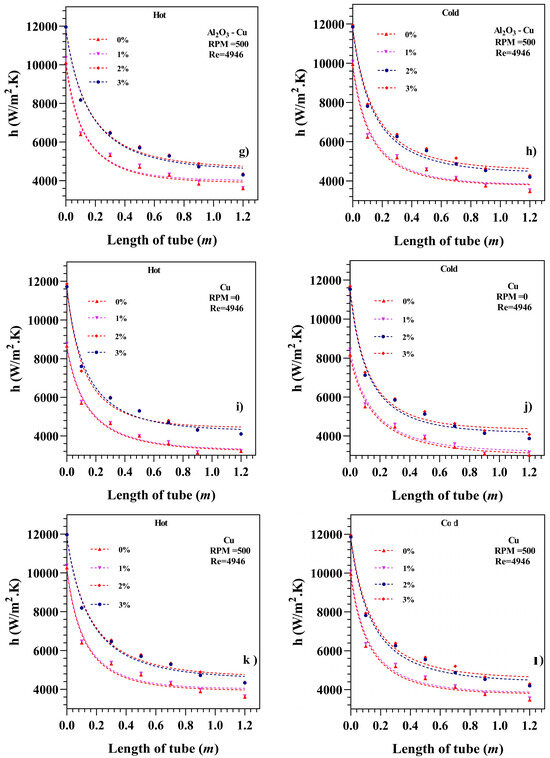
Figure 8.
Local heat transfer coefficients for the inner and outer fluids.
4.6. Pressure Drop
Furthermore, the advantages of nanofluids and inner tube rotation should not conceal their drawbacks, which should be considered when designing a heat exchanger in order to minimize energy consumption and design the most efficient exchanger. Increases in the pressure drop may lead to a waste of the beneficial effects of nanofluids and rotation. Figure 9a–i shows the pressure drop of the double-tube heat exchanger, which increases with the volume concentration of the nanofluid. The concentration increase leads to an increase in the nanofluid viscosity, resulting in an increase in friction. The ultimate consequence is the increase in the pressure drop. Additionally, as it may be appreciated in Figure 9, the increase in the inner tube rotational speed leads to an increase of the pressure drop, due to the increased fluid velocity. The magnitude of this increase may reach up to 156.3% for the Cu-water nanofluid at Recf = 4946 and a 3% concentration at 500 rpm with respect to pure water at 0 rpm, as shown in Figure 9b. Figure 9d–f show the results for the Al2O3-water nanofluid under the same conditions, where the maximum pressure drop was 104.77%. Similarly, for the hybrid nanofluid, the pressure drop increased up to 124.6%, as shown in Figure 9g–i.

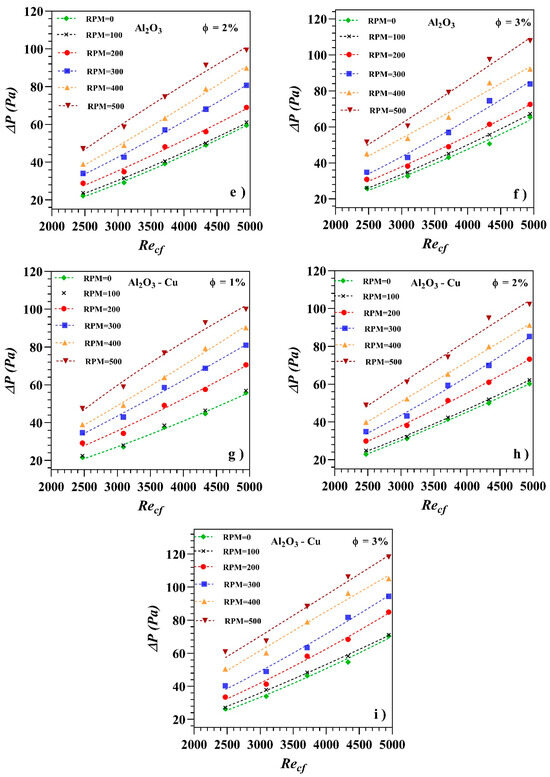
Figure 9.
Pressure drop of the double-tube heat exchanger as a function of the volume concentration and rotational speeds for different nanofluids.
The decoupled effects of tube rotation and nanoparticle addition have been studied as well, finding a mean increase of 37.71 Pa when increasing the rotational speed from 0 to 500 rpm in pure water and a mean increase of 12.70 Pa when adding Cu nanoparticles to a 3% concentration with respect to pure water. The beneficial effect of combining the two actions results here in a further increase in the pressure drop, which reaches up to an average value of 64.95 for 500 rpm and a 3% Cu nanoparticle concentration.
Finally, Figure 10 shows the pressure evolution along the exchanger tube that accounts for friction losses at the maximum rotational speed studied. This increase becomes apparent due to the changes in the fluid behavior, affected by the swirl motion, as well as fluid properties, mainly the increase in density. Nevertheless, the order of magnitude of the pressure losses is several orders below the working pressure of typical heat exchangers, so the small increases in pressure losses found do not seem to pose a serious problem for heat exchanger operation.
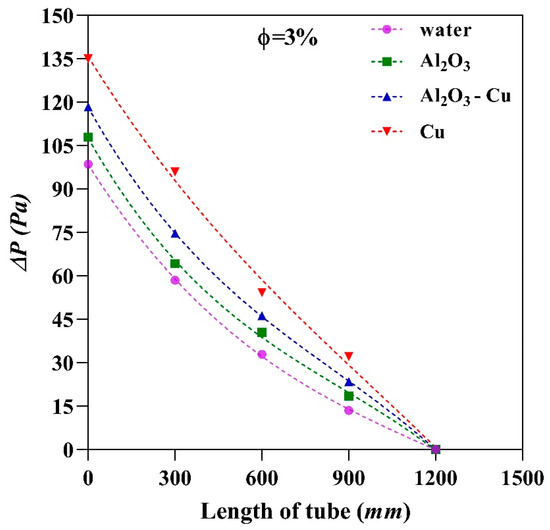
Figure 10.
Pressure drop of cold fluid in the double-tube heat exchanger at Recf = 4946 and 500 RPM along tube.
4.7. Pumping Power
As a consequence of the increase in the pressure drop, due to the nanofluids and inner tube rotation, the heat exchanger might require a higher pumping power. Equation (28) has been used to quantify the required external energy. Figure 11 shows the results of the pumping power required by the heat exchanger as a function of the nanofluid volume concentration and inner tube rotational speed at Recf = 4946 (Recf/Rehf = 0.5058) for the three nanofluids studied. It may be appreciated that the increase in the nanoparticle concentration leads to an increase in the pumping energy, mainly as a result of the increased fluid density. Meanwhile, the increase in rotational speed leads to an increase in the pumping power. However, the values of pumping power, lying in the order of magnitude of 0.1 W, should not pose a high requirement in the pumps attached to the heat exchanger.
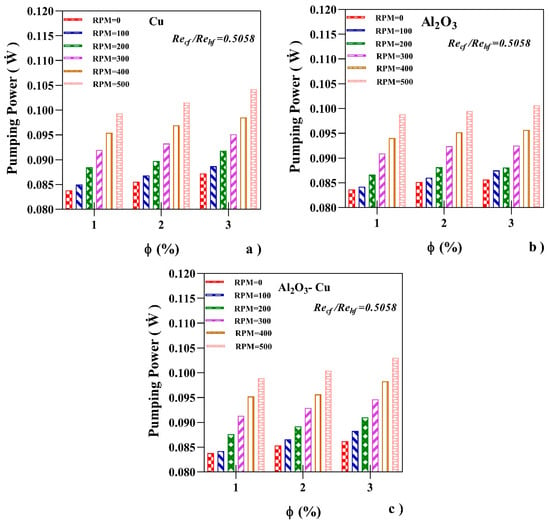
Figure 11.
Pumping power required by the double-tube heat exchanger in terms of the volume concentration for various rotational speeds at Recf = 4946 (a) Cu, (b) Al2O3, (c) Al2O3-Cu.
To provide a better insight into the improvement achieved regarding heat transfer with respect to the given pumping cost, the ratio of average heat transfer (Equation (21)) and pumping power (Equation (28)) has been plotted in Figure 12a–c. As it may be observed, the values for the Cu-nanofluid are the highest among all the nanofluids tested, obtaining higher heat transfer values per unit pumping power. An increase in the nanoparticle concentration benefits the heat transfer-to-pumping power ratio. The increase in the rotational speed, however, only increases this ratio at low rotational speed values, suggesting that speeds over 500 rpm would not be beneficial in terms of this parameter.
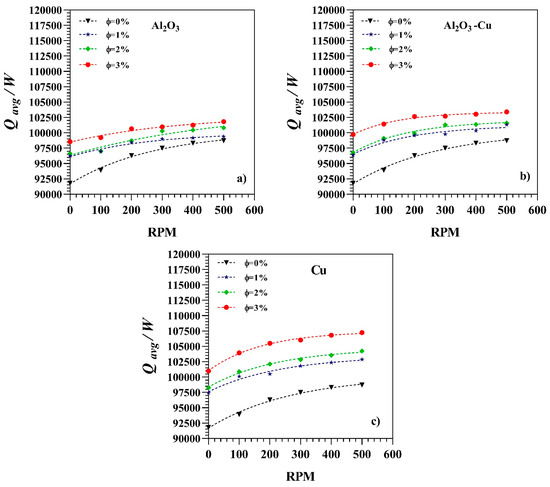
Figure 12.
Ratio of average heat transfer and pumping power (a) Al2O3, (b) Al2O3-Cu, (c) Cu.
5. Conclusions
In this work, after performing experimental tests in a horizontal double-tube heat exchanger under the transitional forced flow, a three-dimensional numerical model was developed to simulate the thermal and flow behavior, with the aim of obtaining further insight into the effects of the inner tube rotation, the fluid flow rate and the type of nanofluid employed. The different contributions from the increase in the rotational speed and the addition of nanoparticles to the change in the number of transfer units, effectiveness and pressure drop in the heat exchanger were studied. It was found that the number of transfer units and the effectiveness of the heat exchanger increased with an increase in the nanoparticle concentration (from 0 to 3%) and the rotation of the heat exchanger inner tube (from 0 to 500 rpm). Considering the type of nanoparticle employed, the Al2O3-water nanofluid showed better thermal performance values than raw water, with a maximum 12.4% improvement, but lower than the Al2O3-Cu hybrid nanofluid, with a maximum 15.34% improvement. The best performance was shown by the Cu-water nanofluid, improving the performance with respect to raw water up to 19.33%. When the rotational effect of the inner tube was added, the performance was increased by 47.3, 56.8 and 66.7% for the Al2O3, the hybrid and the Cu nanofluids at a 3% concentration, respectively, when rotating at 500 rpm. The effectiveness values were improved as well by 30.6, 35.9 and 41.2%, respectively. Nevertheless, the pressure drop along the heat exchanger was affected by these two actions, reaching maximum increase values of 104.77, 124.6 and 156.3%, respectively, compared to pure water with no rotation. This increase in the pressure drop and friction caused by the higher rotational speed and the density increase in the nanofluids, due to the higher concentration values, led to higher pumping power values required to operate the heat exchanger. Nevertheless, the maximum pumping power was found to be in the order of 0.1 W, so that should not pose great problems for normal pump operation.
The numerical model developed in this work might also help in further optimizing, redesigning and scaling up similar heat exchangers. Finally, from the results of this work, future research could consider an evaluation of the effects of different fin designs to enhance heat transfer in the exchanger. The use of multi-phase models for nanofluids with increasing concentrations could be also considered.
Author Contributions
Conceptualization, A.M.-F. and A.J.G.-T.; Data curation, M.A.E.-M.M. and A.B.; Formal analysis, M.A.E.-M.M., J.M.G.-C. and A.J.G.-T.; Funding acquisition, J.M.G.-C. and A.J.G.-T.; Investigation, M.A.E.-M.M., J.M.G.-C., A.M.-F. and A.B.; Methodology, M.A.E.-M.M. and A.M.-F.; Project administration, A.J.G.-T.; Resources, J.M.G.-C. and A.J.G.-T.; Software, M.A.E.-M.M. and A.M.-F.; Supervision, A.J.G.-T.; Validation, M.A.E.-M.M.; Visualization, A.M.-F. and A.B.; Writing—original draft, M.A.E.-M.M., A.M.-F.; Writing—review and editing, J.M.G.-C., A.B. and A.J.G.-T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article. Additional data will be provided on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| s | Heat transfer surface area: m2 |
| c | Heat capacity rate, W/K |
| cp | Specific heat capacity, J/kg K |
| D | Diameter of outer tube, m |
| d | Diameter of inside tube, m |
| Generation rate | |
| k | Thermal conductivity, W/m K |
| L | Length of concentric tube, m |
| ṁ | Mass flow rate, kg/s |
| NTU | Number of Transfer Units |
| ρ | Density, kg/m3 |
| Heat transfer rate, W | |
| Re | Reynolds number |
| T | Temperature, K |
| Logarithmic mean temperature difference, K | |
| U | Overall heat transfer coefficient, W/m2 K |
| u | Axial flow velocity, velocity component, m/s |
| Z | Direction coordinates along the tube |
| Greek symbols | |
| Inverse effective turbulent Prandtl numbers | |
| ε | Effectiveness |
| ϕ | Solid volume fraction |
| μ | Dynamic viscosity, kg/m·s |
| ρ | Density, kg/m3 |
| Subscripts | |
| avg | Average |
| cf | Cold fluid |
| eff | Effective |
| f | Fluid |
| h | Hydraulic, hybrid |
| hf | Hot fluid |
| i | Inlet, inner, direction |
| max | Maximum |
| min | Minimum |
| nf | Nanofluid |
| o | Outlet, outer |
| p | Pressure |
| s | Nanoparticle |
| t | Turbulent |
References
- Bezaatpour, M.; Goharkhah, M. Convective heat transfer enhancement in a double pipe mini heat Exchanger by magnetic field induced swirling flow. Appl. Therm. Eng. 2020, 167, 114801. [Google Scholar] [CrossRef]
- Forooghi, P.; Flory, M.; Bertsche, D.; Wetzel, T.; Frohnapfel, B. Heat transfer enhancement on the liquid side of an industrially designed flat-tube heat exchanger with passive inserts—Numerical investigation. Appl. Therm. Eng. 2017, 123, 573–583. [Google Scholar] [CrossRef]
- Sonawane, S.S.; Khedkar, R.S.; Wasewar, K.L. Study on concentric tube heat exchanger heat transfer performance using Al2O3—Water based nanofluids. Int. Commun. Heat Mass Transf. 2013, 49, 60–68. [Google Scholar] [CrossRef]
- Bahmani, M.H.; Sheikhzadeh, G.; Zarringhalam, M.; Akbari, O.A.; Alrashed, A.A.A.A.; Shabani, G.; Goodarzi, M. Investigation of turbulent heat transfer and nanofluid flow in a double pipe heat exchanger. Adv. Powder Technol. 2018, 29, 273–282. [Google Scholar] [CrossRef]
- Rao, M.S.E.; Sreeramulu, D.; Rao, C.J.; Ramana, M.V. Experimental Investigation on Forced Convective Heat Transfer Coefficient of a Nano fluid. Mater. Today Proc. 2017, 4, 8717–8723. [Google Scholar] [CrossRef]
- Yang, C.; Li, W.; Nakayama, A. Convective heat transfer of nanofluids in a concentric annulus. Int. J. Therm. Sci. 2013, 71, 249–257. [Google Scholar] [CrossRef]
- Bajestan, E.E.; Moghadam, M.C.; Niazmand, H.; Daungthongsuk, W.; Wongwises, S. Experimental and numerical investigation of nanofluids heat transfer characteristics for application in solar heat exchangers. Int. J. Heat Mass Transf. 2016, 92, 1041–1052. [Google Scholar] [CrossRef]
- Korpyś, M.; Dzido, G.; Al-Rashed, M.H.; Wojcik, J. Experimental and numerical study on heat transfer intensification in turbulent flow of CuO–water nanofluids in horizontal coil. Chem. Eng. Process. Process Intensif. 2020, 153, 107983. [Google Scholar] [CrossRef]
- Saeedan, M.; Nazar, A.R.S.; Abbasi, Y.; Karimi, R. CFD Investigation and neutral network modeling of heat transfer and pressure drop of nanofluids in double pipe helically baffled heat exchanger with a 3-D fined tube. Appl. Therm. Eng. 2016, 100, 721–729. [Google Scholar] [CrossRef]
- Duangthongsuk, W.; Wongwises, S. An experimental study on the heat transfer performance and pressure drop of TiO2-water nanofluids flowing under a turbulent flow regime. Int. J. Heat Mass Transf. 2010, 53, 334–344. [Google Scholar] [CrossRef]
- Kumar, N.T.R.; Bhramara, P.; Addis, B.M.; Sundar, L.S.; Singh, M.K.; Sousa, A.C.M. Heat transfer, friction factor and effectiveness analysis of Fe3O4/water nanofluid flow in a double pipe heat exchanger with return bend. Int. Commun. Heat Mass Transf. 2017, 81, 155–163. [Google Scholar] [CrossRef]
- Esfe, M.H.; Saedodin, S.; Mahmoodi, M. Experimental studies on the convective heat transfer performance and thermophysical properties of MgO–water nanofluid under turbulent flow. Exp. Therm. Fluid Sci. 2014, 52, 68–78. [Google Scholar] [CrossRef]
- Halelfadl, S.; Estellé, P.; Maré, T. Heat transfer properties of aqueous carbon nanotubes nanofluids in coaxial heat exchanger under laminar regime. Exp. Therm. Fluid Sci. 2014, 55, 174–180. [Google Scholar] [CrossRef]
- Kumar, P.C.M.; Chandrasekar, M. CFD analysis on heat and flow characteristics of double helically coiled tube heat exchanger handling MWCNT/water nanofluids. Heliyon 2019, 5, e02030. [Google Scholar] [CrossRef] [PubMed]
- Goodarzi, M.; Kherbeet, A.S.; Afrand, M.; Sadeghinezhadd, E.; Mehrali, M.; Zahedi, P.; Wongwises, S.; Dahari, M. Investigation of heat transfer performance and friction factor of a counter-flow double-pipe heat exchanger using nitrogen-doped, graphene-based nanofluids. Int. Commun. Heat Mass Transf. 2016, 76, 16–23. [Google Scholar] [CrossRef]
- Hazbehian, M.; Maddah, H.; Mohammadiun, H.; Alizadeh, M. Experimental investigation of heat transfer augmentation inside double pipe heat exchanger equipped with reduced width twisted tapes inserts using polymeric nanofluid. Heat Mass Transf. 2016, 52, 2515–2529. [Google Scholar] [CrossRef]
- Madhesh, D.; Parameshwaran, R.; Kalaiselvam, S. Experimental investigation on convective heat transfer and rheological characteristics of Cu–TiO2 hybrid nanofluids. Exp. Therm. Fluid Sci. 2014, 52, 104–115. [Google Scholar] [CrossRef]
- Reddy, M.C.S.; Rao, V.V. Experimental investigation of heat transfer coefficient and friction factor of ethylene glycol water based TiO2 nanofluid in double pipe heat exchanger with and without helical coil inserts. Int. Commun. Heat Mass Transf. 2014, 50, 68–76. [Google Scholar] [CrossRef]
- Hormozi, F.; ZareNezhad, B.; Allahyar, H.R. An experimental investigation on the effects of surfactants on the thermal performance of hybrid nanofluids in helical coil heat exchangers. Int. Commun. Heat Mass Transf. 2016, 78, 271–276. [Google Scholar] [CrossRef]
- El Maakoul, A.; El Metoui, M.; Abdellah, A.F.B.; Saadeddine, S.; Meziane, M. Numerical investigation of thermohydraulic performance of air to water double-pipe heat exchanger with helical fins. Appl. Therm. Eng. 2017, 127, 127–139. [Google Scholar] [CrossRef]
- Nakhchi, M.E.; Hatami, M.; Rahmati, M. Experimental evaluation of performance intensification of double-pipe heat exchangers with rotary elliptical inserts. Chem. Eng. Process. Process Intensif. 2021, 169, 108615. [Google Scholar] [CrossRef]
- Vaisi, A.; Moosavi, R.; Lashkari, M.; Soltani, M.M. Experimental investigation of perforated twisted tapes turbulator on thermal performance in double pipe heat exchangers. Chem. Eng. Process. Process Intensif. 2020, 154, 108028. [Google Scholar] [CrossRef]
- Promvonge, P.; Promthaisong, P.; Skullong, S. Experimental and numerical heat transfer study of turbulent tube flow through discrete V-winglets. Int. J. Heat Mass Transf. 2020, 151, 119351. [Google Scholar] [CrossRef]
- Murali, G.; Nagendra, B.; Jaya, J. CFD analysis on heat transfer and pressure drop characteristics of turbulent flow in a tube fitted with trapezoidal-cut twisted tape insert using Fe3O4 nano fluid. Mater. Today Proc. 2020, 21, 313–319. [Google Scholar] [CrossRef]
- Watel, B.; Harmand, S.; Desmet, B. Influence of fin spacing and rotational speed on the convective heat exchanges from a rotating finned tube. Int. J. Heat Fluid Flow 2000, 21, 221–227. [Google Scholar] [CrossRef]
- Aliabadi, M.K.; Feizabadi, A. Performance intensification of tubular heat exchangers using compound twisted-tape and twisted-tube. Chem. Eng. Process. Process Intensif. 2020, 148, 107799. [Google Scholar] [CrossRef]
- Singh, S.K.; Sarkar, J. Improving hydrothermal performance of hybrid nanofluid in double tube heat exchanger using tapered wire coil turbulator. Adv. Powder Technol. 2020, 31, 2092–2100. [Google Scholar] [CrossRef]
- Karimi, A.; Al-Rashed, A.A.A.A.; Afrand, M.; Mahian, O.; Wongwises, S.; Shahsavar, A. The effects of tape insert material on the flow and heat transfer in a nanofluid-based double tube heat exchanger: Two-phase mixture model. Int. J. Mech. Sci. 2019, 156, 397–409. [Google Scholar] [CrossRef]
- Darzi, A.A.R.; Farhadi, M.; Sedighi, K.; Aallahyari, S.; Delavar, M.A. Turbulent heat transfer of Al2O3–water nanofluid inside helically corrugated tubes: Numerical study. Int. Commun. Heat Mass Transf. 2013, 41, 68–75. [Google Scholar] [CrossRef]
- Qi, C.; Luo, T.; Liu, M.; Fan, F.; Yan, Y. Experimental study on the flow and heat transfer characteristics of nanofluids in double-tube heat exchangers based on thermal efficiency assessment. Energy Convers. Manag. 2019, 197, 111877. [Google Scholar] [CrossRef]
- Chaurasia, S.R.; Sarviya, R.M. Thermal performance analysis of CuO/water nanofluid flow in a pipe with single and double strip helical screw tape. Appl. Therm. Eng. 2020, 166, 114631. [Google Scholar] [CrossRef]
- Nakhchi, M.E.; Esfahani, J.A. CFD approach for two-phase CuO nanofluid flow through heat exchangers enhanced by double perforated louvered strip insert. Powder Technol. 2020, 367, 877–888. [Google Scholar] [CrossRef]
- Karuppasamy, M.; Saravanan, R.; Chandrasekaran, M.; Muthuraman, V. Numerical exploration of heat transfer in a heat exchanger tube with cone shape inserts and Al2O3 and CuO nanofluids. Mater. Today Proc. 2020, 21, 940–947. [Google Scholar] [CrossRef]
- Saedodin, S.; Zaboli, M.; Rostamian, S.H. Effect of twisted turbulator and various metal oxide nanofluids on the thermal performance of a straight tube: Numerical study based on experimental data. Chem. Eng. Process. Process Intensif. 2020, 158, 108106. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Trashorras, A.J.G.; Marigorta, E.B. Numerical Investigation of Heat Transfer with Nanofluids in Concentric Tube Heat Exchanger under Transitional Flow. Energy Perspect. 2020, 1, 34–56. Available online: http://globalpublisher.org/journals-1006/ (accessed on 17 January 2024).
- Arzani, H.K.; Amiri, A.; Kazi, S.N.; Chew, B.T.; Badarudin, A. Experimental and numerical investigation of thermophysical properties, heat transfer and pressure drop of covalent and noncovalent functionalized graphene nanoplatelet-based water nanofluids in an annular heat exchanger. Int. Commun. Heat Mass Transf. 2015, 68, 267–275. [Google Scholar] [CrossRef]
- Bahiraei, M.; Mazaheri, N.; Mohammadi, M.S.; Moayedi, H. Thermal performance of a new nanofluid containing biologically functionalized graphene nanoplatelets inside tubes equipped with rotating coaxial double-twisted tapes. Int. Commun. Heat Mass Transf. 2019, 108, 104305. [Google Scholar] [CrossRef]
- Shi, Z.; Dong, T. Thermodynamic investigation and optimization of laminar forced convection in a rotating helical tube heat exchanger. Energy Convers. Manag. 2014, 86, 399–409. [Google Scholar] [CrossRef]
- El-Maghlany, W.M.; Hanafy, A.A.; Hassan, A.A.; El-Magid, M.A. Experimental study of Cu–water nanofluid heat transfer and pressure drop in a horizontal double-tube heat exchanger. Exp. Therm. Fluid Sci. 2016, 78, 100–111. [Google Scholar] [CrossRef]
- Moayedi, H. Investigation of heat transfer enhancement of Cu-water nanofluid by different configurations of double rotating cylinders in a vented cavity with different inlet and outlet ports. Int. Commun. Heat Mass Transf. 2021, 126, 105432. [Google Scholar] [CrossRef]
- Abou-Ziyan, H.Z.; Helali, A.B.; Selim, M.Y.E. Enhancement of forced convection in wide cylindrical annular channel using rotating inner pipe with interrupted helical fins. Int. J. Heat Mass Transf. 2016, 95, 996–1007. [Google Scholar] [CrossRef]
- Ali, M.A.M.; El-Maghlany, W.M.; Eldrainy, Y.A.; Attia, A. Heat transfer enhancement of double pipe heat exchanger using rotating of variable eccentricity inner pipe. Alex. Eng. J. 2018, 57, 3709–3725. [Google Scholar] [CrossRef]
- Jasim, L.M.; Hamzah, H.; Canpolat, C.; Sahin, B. Mixed convection flow of hybrid nanofluid through a vented enclosure with an inner rotating cylinder. Int. Commun. Heat Mass Transf. 2021, 121, 105086. [Google Scholar] [CrossRef]
- Gomaa, A.; Halim, M.A.; Elsaid, A.M. Experimental and numerical investigations of a triple concentric-tube heat exchanger. Appl. Therm. Eng. 2016, 99, 1303–1315. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.; Esmaeilpour, M.; Vizinho, R.; Younesi, A.; Pàscoa, J.C. Assessment of RANS turbulence models for numerical study of laminar-turbulent transition in convection heat transfer. Int. J. Heat Mass Transf. 2017, 115, 1288–1308. [Google Scholar] [CrossRef]
- Siavashi, M.; Jamali, M. Heat transfer and entropy generation analysis of turbulent flow of TiO2-water nanofluid inside annuli with different radius ratios using two-phase mixture model. Appl. Therm. Eng. 2016, 100, 1149–1160. [Google Scholar] [CrossRef]
- Ard, S.E.; Kiatkittipong, K. Heat transfer enhancement by multiple twisted tape inserts and TiO2/water nanofluid. Appl. Therm. Eng. 2014, 70, 896–924. [Google Scholar] [CrossRef]
- Fattahi, A. Numerical simulation of a solar collector equipped with a twisted tape and containing a hybrid nanofluid. Sustain. Energy Technol. Assess. 2021, 45, 101200. [Google Scholar] [CrossRef]
- YousefiMiab, E.; Islami, S.B.; Gharraei, R. Feasibility assessment of using nanofluids in shell and tube heat exchanger of gas pressure reducing stations through a new developed OpenFOAM solver. Int. J. Heat Fluid Flow 2022, 96, 108985. [Google Scholar] [CrossRef]
- Dbouk, T.; Habchi, C.; Harion, J.L.; Drikakis, D. Heat transfer and mixing enhancement by Poiseuille-Taylor-Couette flow between two rotating elliptically-deformed annular tubes. Int. J. Heat Fluid Flow 2022, 96, 109011. [Google Scholar] [CrossRef]
- Upadhya, S.M.; Raju, S.V.S.R.; Raju, C.S.K.; Shah, N.A.; Chung, J.D. Importance of entropy generation on Casson, Micropolar and Hybrid magneto-nanofluids in a suspension of cross diffusion. Chin. J. Phys. 2022, 77, 1080–1101. [Google Scholar] [CrossRef]
- Ghazanfari, V.; Taheri, A.; Amini, Y.; Mansourzade, F. Enhancing heat transfer in a heat exchanger: CFD study of twisted tube and nanofluid (Al2O3, Cu, CuO, and TiO2) effects. Case Stud. Therm. Eng. 2024, 53, 103864. [Google Scholar] [CrossRef]
- Sundar, L.S.; Mouli, K.V.V.C. Effectiveness and number of transfer units of plate heat exchanger with Fe3O4–SiO2/Water hybrid nanofluids: Experimental and artificial neural network predictions. Case Stud. Therm. Eng. 2024, 53, 103949. [Google Scholar] [CrossRef]
- Thirumalaisamy, K.; Sivaraj, R.; Reddy, A.S. Fluid flow and heat transfer analysis of a ternary aqueous Fe3O4 + MWCNT + Cu/H2O magnetic nanofluid in an inclined rectangular porous cavity. J. Magn. Magn. Mater. 2024, 589, 171503. [Google Scholar] [CrossRef]
- Hatami, M.; Jing, D. Nanofluids Mathematical, Numerical, and Experimental Analysis; Academic Press: Cambridge, MA, USA, 2020; ISBN 978-0-08-102933-6. [Google Scholar]
- Siadaty, M.; Kazazi, M. Study of water based nanofluid flows in annular tubes using numerical simulation and sensitivity analysis. Heat Mass Transf. 2018, 54, 2995–3014. [Google Scholar] [CrossRef]
- Babu, J.A.R.; Kumar, K.K.; Rao, S.S. State-of-art review on hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 77, 551–565. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).