An Assessment of the Chemical Compatibility of Viton Fluoropolymers and Some Harsh Organic Liquid Mixtures

Abstract

The molecular transport of a series of industrial solvent mixtures into O-rings of Viton fluoropolymers was studied. Sorption, diffusion, and permeation of the individual liquids toluene, cyclohexane, and methanol, and their binary and ternary mixtures, were evaluated from the solvent uptake using a gravimetric method. From the sorption results, the diffusion coefficients were calculated using Fick’s equation. A numerical method was employed to calculate the liquid concentration profiles in cylinder-shaped polymers. The desorption mechanism was also evaluated. The composition dependence of sorption, diffusion, and permeation was assessed, and the results were analysed in terms of potential interactions between polymer and penetrant molecules. Observed sorption of methanol and methanol mixtures by the polymer was very high, in some cases higher than for pure liquids. In general, the amount of methanol present in the mixture determined its diffusion coefficient. Methanol showed the smallest solubility coefficient within the polymer, but due to its high mobility and permeability, it was shown to be the liquid that flows faster through Viton fluoropolymers. Flows of toluene and cyclohexane are still considerable, notwithstanding that this fluoropolymer is usually indicated as hydrocarbon resistant. This is an important fact to keep in mind when choosing sealings for applications with a mix of solvent media.

1. Introduction

Fluoropolymers have long successfully been used for industrial applications due to their exceptional chemical resistance to a high variety of harsh chemicals, low permeability to liquid and gases, and excellent strength and toughness at elevated temperatures. Among these, fluoroelastomers, designed to maintain rubber-like properties, are commonly used for sealing applications (as o-rings, seals, gaskets, and hosing) and are used in aggressive chemical environments in the main activities within the chemical processing, petrochemical, automotive, and aerospace industries [1,2,3,4,5,6]. Viton fluoroelastomer was first produced by E.I. du Pont de Nemours in 1955. The use of fluoroelastomers has increased progressively, and currently they are manufactured by a wide range of companies worldwide. Viton elastomers comprise copolymers of HFP (hexafluoropropylene) and VDF (vinylidene fluoride); terpolymers of TFE (tetrafluoroethylene), VDF, and HFP (hexafluoropropylene); and PMVE (perfluoro(methyl vinyl ether)) containing specialty additives. The fluorine content varies between 66 and 70% [7]. The superior properties presented by these polymers are due to the low polarizability and the strong electronegativity of the fluorine atom, its small Van Der Waals radius (1.32 Å), and the strong C-F bond (485 kJ mol⁻¹) [8]. This gives Viton fluoroelastomers high thermal, chemical, aging, and weather resistance, exceptional inertness to solvents, hydrocarbons, acids, and alkalis, low dielectric constants, low flammability, low refractive index, and low surface energy (remarkable oil and water repellence) and moisture absorption. As well, the presence of the strong C-F bond gives them an important influence on the high resistance to oxidation and to hydrolytic stability. Considering that the primary function of these materials is to act as barriers, knowledge of their behaviour when exposed to degrading agents is of extreme importance, because the physicochemical degradation of the fluoroelastomers directly influences their mechanical and tribological behaviour as dynamic seals. For instance, the rise in volume may increase friction in the interface seal/shaft, compromising the sealing effect and seal life. Although manufacturers perform extensive tests to provide information on the compatibility of materials and solvents, real applications require, many times, the exposure of elastomers to mixtures of industrial liquids, and, to our knowledge, there is a gap of information in that area. By studying the transport properties of liquid mixtures in polymeric materials, correlations can be obtained between diffusion parameters and the molecular structure of the material. Therefore, studies of the permeation and diffusion of organic solvents in polymeric materials are useful to describe the mechanisms of the diffusion process and the structure of the polymer [9,10,11,12].

The transport of a penetrant through a polymer usually happens through an activated diffusion process. So, the driving force for mass transport is the absence of equilibrium caused by a concentration gradient coupled with a tendency to eliminate these differences by molecular motion. The permeation process into polymers can be described with solution–diffusion models [13] that generally divide this process in three different steps: sorption of the liquid into the polymer followed by diffusion through the polymer and then desorption. The permeability coefficient, P, is a result of the liquid diffusivity coefficient through the polymer, D, and its concentration gradient, which is proportional to the liquid solubility (S) in the polymer.

$$P=DS$$

(1)

Fick’s first law [14] allows us to estimate the diffusion coefficient, D.

$$J=-D\frac{\partial c}{\partial x}$$

(2)

where J represents the one-dimensional flow (in moles or grams) per unit of area per unit of time across a reference plane, and c is the concentration in moles or grams per unit of volume. The first derivative, in respect to time, of this equation represents Fick’s second law:

$$\frac{\partial c}{\partial t}=D\left(\frac{{\partial }^{2}c}{\partial x^2}\right)$$

(3)

In practice, it is difficult to accurately determine the surface concentration in polymers, whereby it is common to express the flux per unit area, J, in terms of concentrations of external phases:

$$J=-P\frac{{\partial c}^{ext}}{\partial x}$$

(4)

where P is the permeability coefficient that determines the volume of penetrant that flows through a unit area of a polymer with a unit thickness, per unit of time, with a unit pressure across the system. The rate of permeation is governed by factors that mutually affect the diffusion coefficient and the solubility of the organic solvent in the polymer, like the temperature, the size and shape of the diffusing molecule, the cross-linking of the polymer, the crystallinity of the polymer, the nature and the amount of the filler particles in the polymer, the concentration of the diffusing species, and sometimes, the previous history of the polymer [9]. Diffusion studies in polymers can also provide information about the polymer configuration due to the movement of a penetrant through the polymer. A diffusion–sorption experiment can provide information about the configuration and flexibility of the molecular chain and the morphology of the polymer, allowing the establishment of models that relate the permeability and diffusivity in penetrant-polymer systems and connect them to the properties of the components.

The diffusion in a linked polymeric network can be associated with the solubility and permeation/permeability of the system. The equilibrium between molecules inside and outside the polymeric chain determines the solubility of a substance. The polymer may swell because, until equilibrium is attained, the polymeric chain absorbs and/or releases penetrant molecules (via diffusion) from the medium, adopting a new configuration to fit the entering molecules of the solvent (i.e., polymer sorption). When a polymer reaches its saturated state, it begins to lose solvent to its surroundings (a process known as polymer desorption), which changes the polymeric chain’s state to one that is more like when it is dry. Solvent loss through desorption is not necessarily a precise reverse of sorption, both due to the nonlinear nature of polymeric chains and the potential interactions between the polymer and the penetrant solvent. The permeation process depends on the transport molecules in the polymeric chain membrane and occurs in three different steps: the molecule dissolves at the membrane face, then diffuses until it reaches the other face, where it evaporates or is extracted [13]. In the case of an elastomeric membrane, e.g., an O-ring, a sealing is usually applied to prevent or control mass leaking; permeation due to long exposure to aggressive organic chemicals may influence the material’s structural integrity and performance [15,16]. Typically, permeation experiments are conducted by submerging the polymer sample in a pure solvent volume while maintaining a constant temperature and pressure. To simulate the real applications of polymers, the material can be immersed in solvent mixtures.

This study aims to verify the compatibility of Viton fluoroelastromers with aggressive organic liquid mixtures and our current interest arises from the fact that Viton O-rings, although designed for high resistance to individual hydrocarbons, show a noticeable permeation rate when long exposed to mixtures that can result in leakage [15,16] and/or swelling, thus leading to potential damages in industrial equipment and consequently deviations in the expected results. This is of major importance for chemical processing uses, where it is likely that a real application involves solvent mixture, but also for scientific research once instrumentation involves the manipulation of small volumes and high precision is required. Consequently, it is important to understand the behaviour of Viton elastomers in the presence of aggressive liquid mixtures composed of molecules that simulate crude oil constituents. In that sense, sorption, diffusion, and permeation of individual toluene (Tol), methanol (MeOH), and cyclohexane (Chex), together with their binary and ternary mixtures in a high range of compositions, were studied in a search to characterize the lifetime of the polymeric fluoroelastomers as a sealing material in industrial equipment, obtaining new data for the industrial and scientific community.

2. Materials and Methods

The materials employed in this study are available for purchase under the trade name Viton^® (FKM by ASTM standard) and were supplied by Sove. Toluene (99.97%) was supplied by Fisher Chemical, Cyclohexane (99.50%) by BDH Limited Poole England, and Methanol (99.50%) by ABSOLVE. All of the solvents were used without further purification.

O-ring elastomers used in this work had the following dimensions: an internal diameter of 9.25 mm and a cross-section of 3.0 mm. According to the supplier, this material presented a hardness (Shore A) of 70 and a specific gravity of 2.01 g/cm³.

Sorption experiments were performed at 298.15 K by submerging the sealing samples into screw-tight test bottles containing a 10 mL total volume of liquid mixture.

Table 1. Composition of the liquid mixtures in mass fraction (% component).

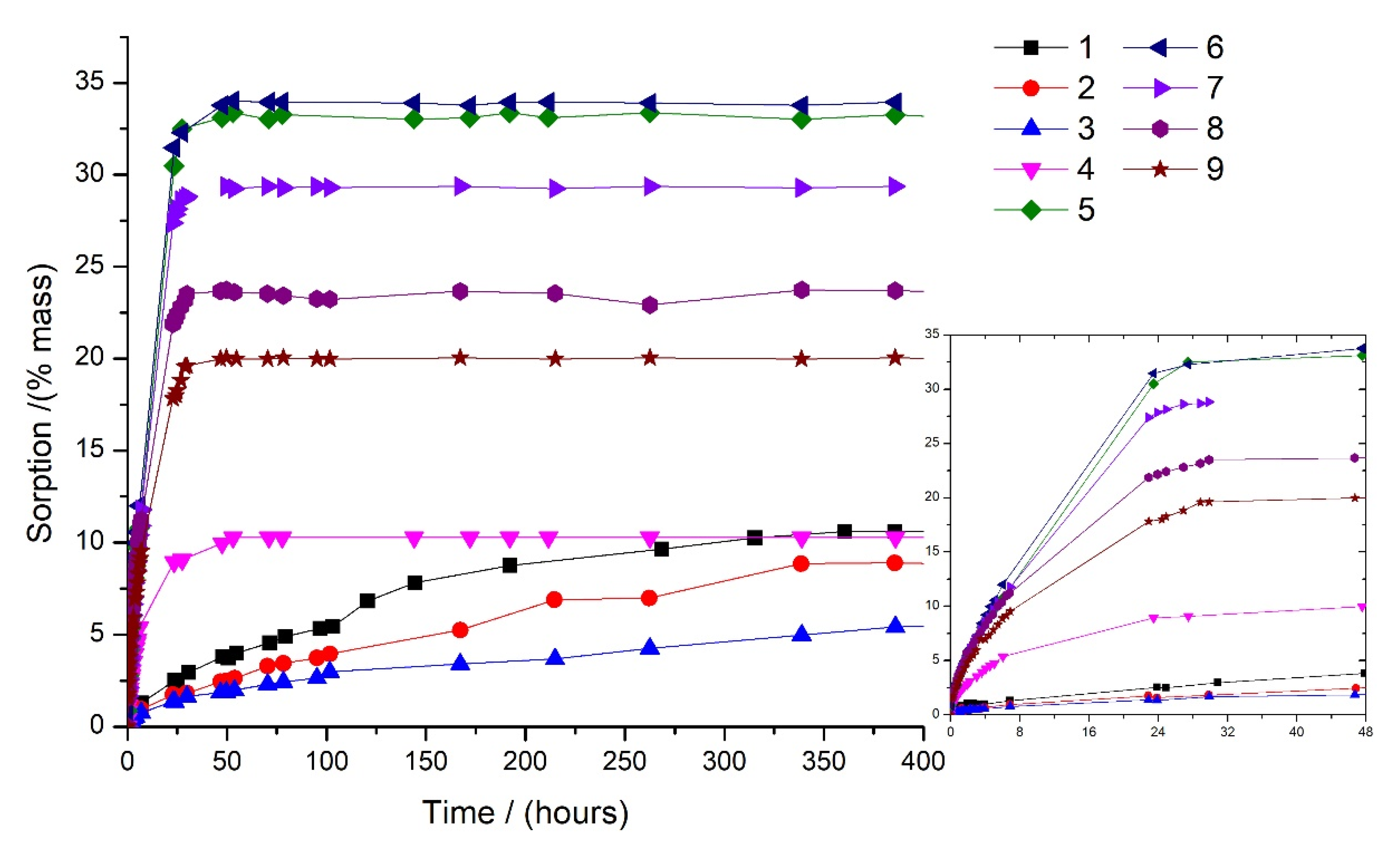
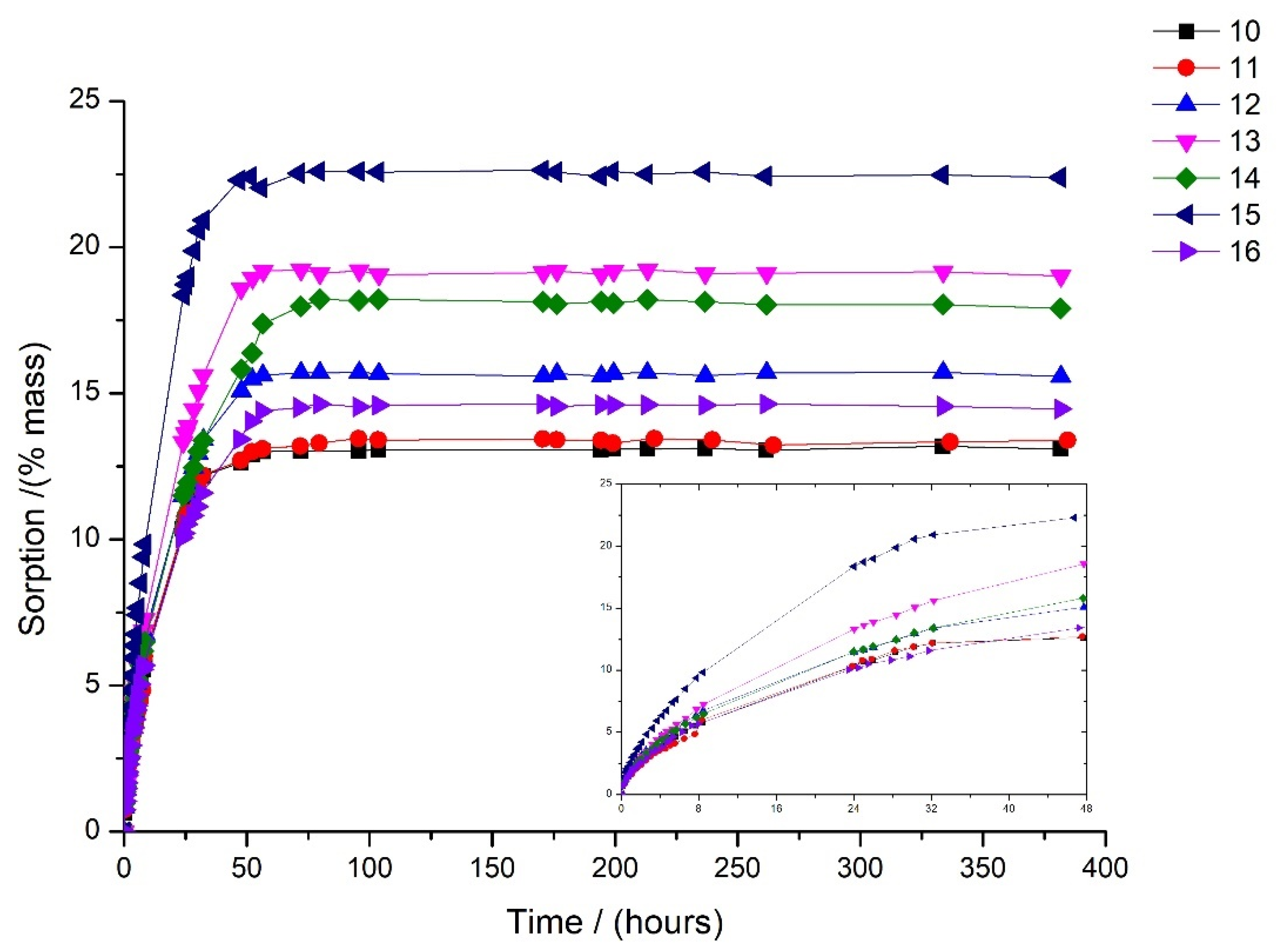
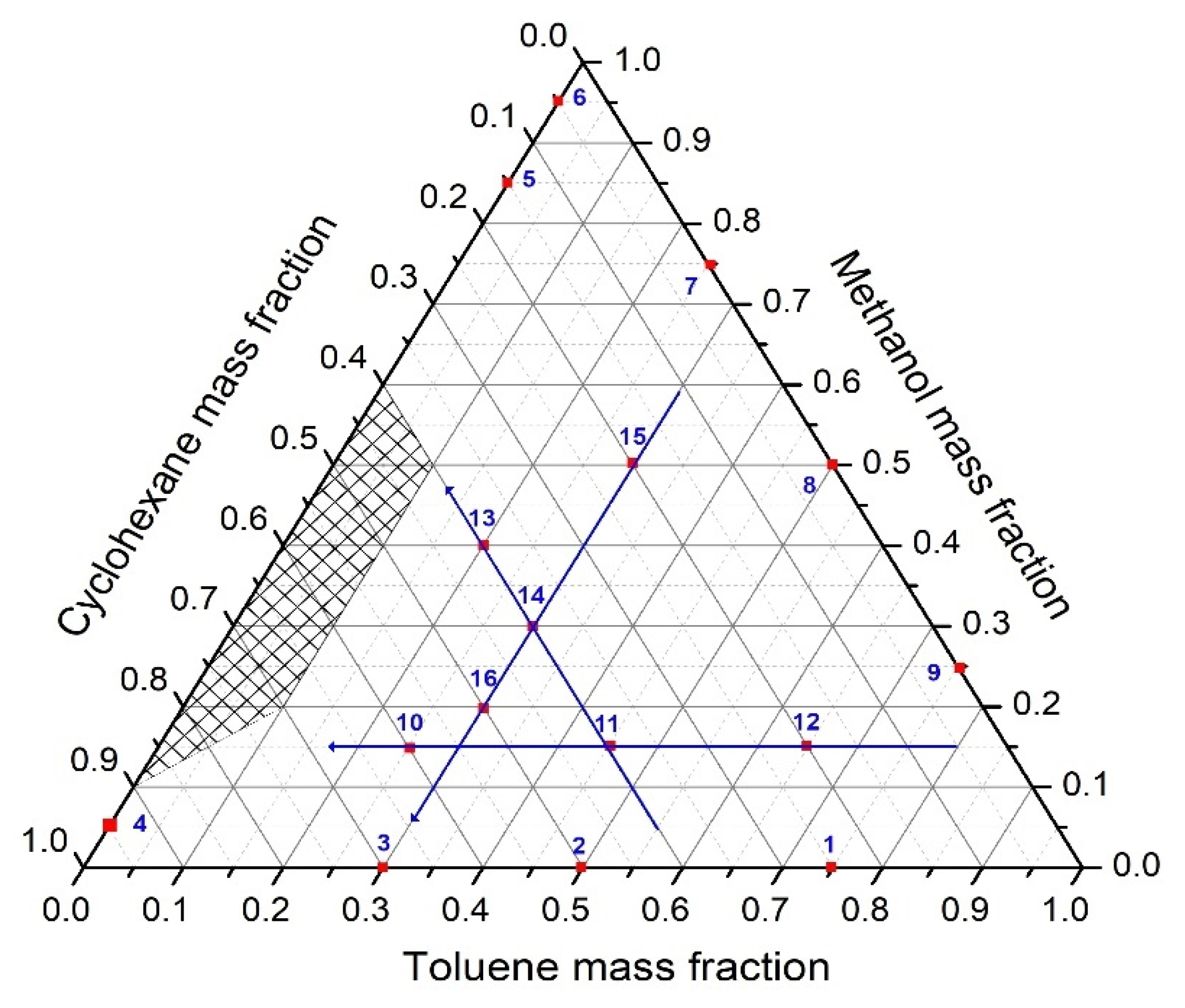
Liquid Mixtures	% Toluene	% Methanol	% Cyclohexane
1	75	0	25
2	50	0	50
3	25	0	75
4	0	5	95
5	0	85	15
6	0	95	5
7	25	75	0
8	50	50	0
9	75	25	0
10	25	15	60
11	45	15	40
12	65	15	20
13	20	40	40
14	30	30	40
15	30	50	20
16	30	20	50

presents the compositions of binary and ternary mixtures of toluene (Tol), methanol (MeOH), and cyclohexane (Chex) to which the samples were exposed. Samples were maintained in a thermostatic bath at 298.15 (±0.01) K. Samples were regularly taken from the bottle, the surface liquid was carefully removed with absorbent paper without pressing, and the sealings were weighted using a Mettler H80 digital balance with a precision of ±0.1 mg. The samples were never outside the temperature-controlled bath for more than 30 s in order to minimize the errors due to solvent evaporation. This process was repeated for at least 30 days and until the samples reached a stable weight, that is, until the variations in the weight were ±0.2 mg or less.

The desorption of the liquids was also followed using the same gravimetric method. For that, all the samples were removed from the test bottles and left in an ambient with a controlled temperature (298 (±1) K). The procedure to register the weight loss of each sample was identical to that from the sorption measurements.

The structure and molar volume of the solvents that compose the studied mixtures are presented in

Table 2. Structure and molar volume of solvents at 298.15 K.

Solvent	Structure	Vm/(cm3 mol−1)
Toluene		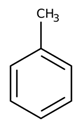106.9
Methanol		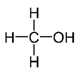40.73
Cyclohexane		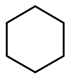108.9

.

3. Results

The initial penetration and dispersion of a solvent into a polymer is usually described by the term “sorption”. It is possible to solve the one-dimensional Fick’s diffusion equation (Equation (3)) from the sorption data, using the appropriate initial and boundary conditions, and to obtain the concentration profiles of liquids and the magnitudes of P, S, and D.

If the polymer sample is considered as a long circular cylinder in which diffusion is radial, then the diffusion equation in the cylindrical coordinate system can be solved for concentration-independent diffusivity D in two ways:

-

For sorption < 55%, also known as the short time model [17]:

$$\frac{\overline{c}\left(t\right)}{c_{\infty }}=\frac{4}{{\pi }^{\frac{1}{2}}}{\left(\frac{Dt}{r^2}\right)}^{\frac{1}{2}}$$

(5)

-

After steady sorption is attained:

$$\overline{c}\left(t\right)=c_{\infty }\left\{1-\frac{4}{r^2}{\sum }_{i=0}^{\infty }\frac{1}{{\alpha }_n^2}exp\left[-{\alpha }_n^{2}Dt\right]\right\}$$

(6)

where r is the radius of the cylinder, $\overline{c}\left(t\right)$ is the concentration in cm² s⁻¹ averaged over the radius r, t is sorption time, and α_n is the nth root of equation $J_0\left(\alpha r\right)=0$, where J₀ is the Bessel function of the first kind of order zero.

The resolution of Equations (5) and (6), transposed for sorption measurements, require the replacement of $\overline{c}\left(t\right)$, the mean concentration, by M_(t), the quantity of solvent that penetrated the rubber in time t, and the replacement of $c_{\infty }$, the equilibrium saturation concentration, by M_(∞), the quantity of solvent that penetrated the rubber after infinite time. Thus, Equation (5) becomes

$$\frac{M_t}{M_{\infty }}=K{t}^n$$

(7)

where K is a constant that depends on polymer structural features as well as how it interacts with the solvent, and the exponent, n, suggests the type of transport mechanism. Also, the resolution of Equations (5) and (6) implies the validity of the next assumptions [18]: (1) Samples are assumed to be infinite, i.e., diffusion into the polymer only occurs in the x-direction, with negligible changes in dimensions; (2) diffusivity remains constant during sorption; and (3) the solvent concentration reaches immediate equilibrium on the membrane surface.

3.1. Sorption Kinetics

Sorption isotherms for pure toluene, methanol, and cyclohexane, and binary and ternary mixtures of these solvents in Viton elastomers, were obtained at 298.15 K and are represented in Figure 1, Figure 2, and Figure 3, respectively. Detailed information on the compositions studied is presented above in Table 1. Sorption results, determined from the ratio of sorbed liquid in grams for each 100 g of the polymer, are presented in mass % in

Table 3. Sorption and estimated parameter K for Viton elastomers immersed in pure liquids and Tol/MeOH/Chex mixtures at 298.15 K.

		Sorption (Mass %)	n	103 K
Liquids	Toluene	10.51	0.49	1.72
	Methanol	31.62	0.59	0.95
	Cyclohexane	1.17	0.50	0.55
Liquid mixtures	1	10.60	0.49	1.19
	2	8.80	0.49	1.13
	3	5.56	0.45	1.03
	4	10.28	0.50	0.91
	5	33.37	0.60	0.85
	6	34.01	0.62	0.72
	7	29.37	0.54	1.60
	8	23.73	0.54	2.06
	9	20.04	0.51	2.67
	10	13.19	0.52	1.24
	11	13.45	0.50	1.61
	12	15.21	0.51	1.65
	13	19.22	0.54	1.79
	14	18.22	0.53	1.38
	15	22.59	0.55	1.39
	16	14.63	0.53	1.39

Note: n and K were calculated from Equation (7); n parameter gives information on the type of transport mechanism; K parameter reflects polymer–liquid compatibility.

. Standard deviations for the data fall between 0.01 and 0.05 g/100 g for each solvent.

The behaviour observed in the sorption isotherms for pure liquids in Viton elastomers is very dissimilar (Figure 1) and is probably the result of the different characteristics of the liquid molecules where they were immersed. While methanol presents a very high sorption coefficient in the polymer (31%), cyclohexane sorption is almost residual (1%). Binary mixtures with a higher amount of methanol present larger sorption coefficients (up to 34%) when compared with the other mixtures under study (Figure 2), and the ones containing the higher quantities of cyclohexane show the lowest sorption values (as low as 5%). This tendency is also present in ternary mixtures (Figure 3), and as expected, sorption values are higher in the mixtures that contain greater quantities of toluene and methanol in comparison to the ones with the higher composition of cyclohexane. Overall, for the generality of mixtures, the sorption coefficients are normally greater than 15%, meaning that this material shows a relatively low resistance to industrial solvents, although Viton fluoroelastomers are commonly stated by the manufacturer as providing good chemical resistance to petroleum products and solvents [4,19].

Information on the diffusion mechanism can be acquired from the analysis of sorption isotherms before 50–55% sorption (Equation (7)). Values for parameters K and n presented in Table 3 have been determined using a least square method and adjust well to a linear fitting with correlation coefficients of 0.99. Values of n are generally around 0.5, showing that the mechanism of diffusion generally respects Fick’s law, an indication that the mobility of the penetrant molecule is considerably higher than the mobility of the chains of the polymer. However, for the sealings, both submerged in pure methanol and in the binary mixtures with the highest amount of methanol (mixtures 5 and 6), a positive deviation to Fick’s law is observed, thus suggesting the existence of swelling of the polymer to some extent. Moreover, some of the ternary mixtures present a small positive deviation even if their methanol composition is small. The small size and polarity of methanol could be the reason for the observed swelling. The presence of methanol seems to have a synergetic effect in sorption, possibly through a disturbance in the polymer chains. The observed higher uptakes of liquid mixture by the elastomer when methanol is present, higher than for pure liquids, provides evidence that in the long run, the overload uptake of liquid could lead to a rupture on the polymer chain and consequently seriously affect the mechanical properties of the elastomer.

The analysis of the parameter K can provide information on the affinity between the polymer chain and the solvent or solvent mixture. Toluene and toluene-richer mixtures present a higher K, indicating that the polymer has a greater affinity for this solvent and that there are more molecular interactions between the polymer chain segments and mixtures containing this component. K is smaller for cyclohexane- and cyclohexane-rich mixtures.

3.2. Diffusion Coefficients

Table 4. Diffusion coefficients D (short time exposure), D_∞ (long time exposure) and diffusion coefficients D_d (desorption) for pure liquids and mixtures of toluene, methanol, and cyclohexane in Viton elastomers, at 298.15 K.

Liquid	D /(10−20 m2 s−1)	Dd /(10−12 m2 s−1)	D∞ /(10−12 m2 s−1)
Toluene	1.33	0.79	0.95
Methanol	4.94	0.42	4.60
Cyclohexane	0.20	0.50	0.91
1	2.64	1.10	0.83
2	1.31	1.55	0.69
3	0.94	0.83	0.80
4	0.26	0.26	5.50
5	4.78	0.45	4.58
6	4.94	0.16	4.37
7	6.38	0.33	5.98
8	9.63	2.19	5.69
9	8.43	0.37	3.94
10	6.12	0.16	2.25
11	6.56	0.02	2.39
12	7.18	0.49	2.51
13	4.32	0.01	3.95
14	4.86	0.18	3.92
15	5.26	0.20	4.13
16	4.90	0.14	3.20

Notes: D stands for diffusion coefficients for short time exposure, D_∞ stands for diffusion coefficients for long time exposure and D_d stands for diffusion coefficients for desorption, respectively. Standard deviations: S_D (D_∞, D_d) = 5 × 10⁻¹⁴ m² s⁻¹, S_D (D) = 6 × 10⁻²² m² s⁻¹.

presents the diffusion coefficients for sorption and desorption for both pure components, binary and ternary mixtures, determined at 298.15 K. Diffusion coefficients D (short time exposure) and D_∞ (long time exposure) were obtained from the resolution of Equations (5) and (6) using the sorption data for short time and longtime exposures to the liquids, respectively. The standard deviations of the values are in the range of 6 × 10⁻²² m² s⁻¹ for D (short time exposure) and 5 × 10⁻¹⁴ m² s⁻¹ for D_∞ and D_d (long time exposure and desorption, respectively).

Analysis of the observed outcomes for pure liquid diffusion into Viton elastomer reveals that the diffusion coefficients exhibit the order D_MeOH > D_Tol > D_Chex for both short and long time exposures of the polymer to the liquids. After reaching equilibrium sorption, the diffusion coefficients D_∞, calculated for a long time exposure of polymers for toluene and cyclohexane, exhibit very similar values, which is probably a result of their close molar volumes (106.9 cm³ mol⁻¹ and 108.9 cm³ mol⁻¹, respectively), while methanol, which is much smaller and has a molar volume of 40.71 cm³ mol⁻¹, presents a much higher diffusivity.

Diffusion coefficients calculated for the short time exposure of O-rings to the liquids are generally higher than the ones calculated after reaching equilibrium, which is a signal of a fast penetration mechanism in the beginning, and overall, both D and D_∞ present the same behaviour. After reaching equilibrium, that is, at a long time exposure of the polymer to the liquids or liquid mixtures, the calculated diffusion coefficients for the binary mixtures show higher values for those where the methanol composition is higher, and when the methanol is absent, the values are almost constant. In general, the variation of the diffusion coefficients with the composition shows that, at the limits, the diffusion coefficients coincide with the ones obtained for pure liquids. Regarding what concerns diffusion coefficients in ternary mixtures at sorption equilibrium, we have analysed their variation at specific composition lines for this mixture, namely at a constant mass fraction of 15% methanol (mixtures 10, 11, and 12), at a constant mass fraction of 30% toluene (mixtures 14, 15, and 16), and at a constant mass fraction of 40% cyclohexane (mixtures 11, 13, and 14). These composition lines are drawn in Figure 4 and the analysis is conducted following the compositions approaching the demixing zone presented by this mixture.

Overall, an increase in D with the increase of the methanol percentage in the mixtures is noticeable, as is a decrease in D with the decrease of methanol in the mixture composition, both for binary and ternary mixtures. Indeed, a careful analysis of these results reveals that when maintaining the toluene mass fraction constant, or cyclohexane mass fraction constant, the diffusion coefficients present a dependence on the methanol composition, increasing when methanol composition increases. At a constant methanol mass fraction, the diffusion coefficients remain almost constant (this happens not only for the ternary composition line at 15% methanol mass fraction but also in binary mixtures where the methanol is absent). This trend is also observed for other composition lines (e.g., at 25% mass fraction composition or 20% mass fraction cyclohexane). It is reasonable to assume, then, that in this mixture, methanol is the component driving the diffusion.

Concerning desorption, the calculated diffusion coefficients for pure liquids show toluene to be the fastest liquid to exit the polymer, presenting the higher D_d while methanol is shown to be the slower one. Diffusion coefficients for desorption are often lower than those for sorption, except for binary mixtures 1, 2, and 3, where methanol is not present. It is also noticeable that desorption seems to be progressively slower with the increase of components in the mixture. This can give some insights about the diffusion mechanism. Since methanol is the component showing less affinity with the polymer, and the mixtures rich in it are the ones where the desorption coefficients are smaller (e.g., mixtures 5, 6, 7, 8, and 15, where the methanol mass fraction is above 50%), this means that, as evidenced before by the sorption results, this component is affecting the chains of the polymer, not only by increasing sorption but also by possibly trapping the remaining components inside the elastomer.

3.3. Permeability and Solubility Coefficients

Calculations of permeability P in each elastomer-solvent system have been performed using the values of the solubility S (identified from the saturation stage of the sorption plot) and the diffusion coefficients at equilibrium sorption D_∞, according to the solution–diffusion model described in Equation (1). Results are presented in

Table 5. Solubility and permeability coefficients for pure liquids and for toluene, methanol, and cyclohexane mixtures through Viton elastomers.

Liquid	D∞ /(10−12 m2 s−1)	S /(10−2 kg m−3 Pa−1)	P /(10−14 kg m−1 s−1 Pa−1)
Toluene	0.95	5.16	4.89
Methanol	4.60	3.56	16.4
Cyclohexane	0.91	1.65	1.51
1	0.83	4.03	3.34
2	0.69	2.34	1.61
3	0.80	1.72	1.38
4	5.50	1.36	7.47
5	4.58	3.59	16.44
6	4.37	3.89	17.01
7	5.98	4.16	24.86
8	5.69	4.23	24.05
9	3.94	5.62	22.16
10	2.25	2.02	4.54
11	2.39	2.38	5.70
12	2.51	2.77	6.95
13	3.95	2.88	11.38
14	3.92	2.86	11.22
15	4.13	2.95	12.19
16	3.20	2.41	7.70

Notes: Standard deviations: S_D (S) = 1 × 10⁻⁴ kg.m⁻³ Pa⁻¹, S_D (P) = 2 × 10⁻¹⁶. Kg m⁻¹ s⁻¹ Pa⁻¹.

.

It makes sense that the liquid that was least compatible with the polymer would have the lowest solubility, given that solubility (S), a thermodynamic property of a polymer-permeant system, depends on the specific interaction between the liquid and the polymeric matrix. In this way, the solubility results could be related to the previous results of the affinity coefficient K. In fact, toluene is the pure liquid with both the highest solubility and the highest affinity coefficient. Toluene-rich mixtures also present higher values of solubility in comparison with the remaining mixtures. This fact suggests that the polymer matrix could be more compatible with the toluene structure, leading to the occurrence of specific interactions in the system penetrant-polymer, increasing solubility. Also, the liquid that present less compatibility with the polymer matrix (cyclohexane) presents the lowest solubility value.

A useful way of obtaining more insights on the possible polymer-permeant interactions is from the use of predictive thermodynamic models (i.e., those requiring a non-adjustable parameter), namely from the Flory–Huggins theory [20]. The Flory–Huggins parameter, χ, can provide a qualitative idea on these kind of interactions [20,21]. According to the Flory–Huggins theory, the activity of the penetrant or penetrant mixture inside the polymer can be expressed as

$$ln{a}_i=ln{\varphi }_i+\left(1-\frac{V_m}{V_p}\right){\varphi }_p+\chi {\varphi }_p^2$$

(8)

where a_i is the penetrant molecule’s activity, ϕ_i is the species’ volume fraction, and V_m and V_p are, respectively, the penetrant and polymer’s molar volume [22]. The equilibrium swelling of the membrane (mass %) can be used to compute the polymer volume fraction ϕ_p, and the χ parameter can be obtained considering the ideal solvent approximation (a_i = 1) [23]. Large values of χ (χ > 2) are typically correlated with small interactions between the selected pair polymer-solvent. On the other hand, low values of χ (χ < 2) are linked to high permeabilities and significant interactions between the polymer and the solvent. Values of χ as low as 0.5 usually mean that solvation has occurred due to the high affinity between the polymer and solvent. The calculated χ parameter for the pure liquids and toluene, methanol, and cyclohexane mixtures through Viton elastomers, obtained from Equation (8), is presented in

Table 6. Flory–Huggins parameter, molar and excess volumes for pure liquids and toluene, methanol, and cyclohexane mixtures in Viton elastomers.

Liquid	χ	Vm /cm3 mol−1	VE /cm3 mol−1
Toluene	1.27	106.90
Methanol	0.83	40.73
Cyclohexane	2.71	108.90
1	1.26	128.59	0.43
2	1.06	132.76	0.58
3	1.58	137.13	0.44
4	1.23	130.42	3.60
5	0.81	57.72	7.30
6	0.81	53.65	2.76
7	0.85	47.54	0.10
8	0.92	57.68	−0.05
9	0.99	74.03	−0.39
10	1.07	87.10	0.54
11	0.87	86.39	0.45
12	1.07	85.51	0.21
13	0.98	65.29	0.45
14	1.00	72.24	0.45
15	0.93	58.75	0.18
16	1.09	81.47	0.50

Notes: Standard deviations: S_D (ρ) = 5 × 10⁻⁶ cm³ mol⁻¹, S_D (χ) = 2 × 10⁻², S_D (V_m, V^E) = 2 × 10⁻² cm³ mol⁻¹; Density values used on calculations are from [15,24,25,26,27].

. The densities used for the calculation were collected from the literature [15,24,25,26,27].

As we can see from Table 6, for the mixtures under study, the χ parameter is generally small for all mixtures, suggesting that there are specific interactions between the polymer chain and the penetrant liquid. The sole exception is for cyclohexane, which has a high χ and thus minor interactions with the elastomer chains. According to the sorption studies above, the relatively large and nonpolar cyclohexane molecules’ unfavourable interactions with the Viton elastomer can account for their low concentration inside the polymer. An examination of the mixture’s properties, as reflected by its excess properties (for example, excess molar volume V^E), might provide additional information because the interaction between solvents in mixtures can also affect the mass transport, both in liquids and inside the polymer [28,29]. In general, all the mixtures present positive deviations from ideal behaviour, with the exception of binary methanol + toluene mixtures. Higher values are found for the binary methanol + cyclohexane mixtures, an expected behaviour for this excess property due to the proximity, in composition, to the demixing zone. The disruption of the ordered structures around the components of the mixtures, which can be due to the breaking of H-bonded associates formed between cyclohexane and methanol, can lead to an expansion in volume, hence resulting in an increase in V^E values. On the other side, the negative values of V^E can be a signal of the existence of specific dipole–dipole interactions between the components.

Interestingly, methanol does not present a high solubility within the polymer matrix but has a very high diffusivity and permeability, and the same happens for the methanol-rich mixtures. Permeability (P), which measures how easily a permeant molecule can pass through a polymer, is a parameter that takes into account both kinetic and thermodynamic aspects of the polymer-penetrant system. According to the same logic as that used for solubility, methanol should have the highest permeation coefficient if it has the highest diffusion coefficient. If we have in mind the above-mentioned molar volume of the solvents, and with methanol being much smaller than the remaining components, this behaviour can be explained by the penetrant size, as permeability generally decreases with the increasing of the penetrant size. This is indeed true for pure liquids, but in mixtures, the results show a more complex interplay. At a constant toluene mass fraction, the decrease in the methanol fraction leads to both smaller solubility and permeability in mixtures. At a constant cyclohexane mass fraction, the same is observed, except for the binary mixtures where cyclohexane is absent. When cyclohexane is absent, the increase in methanol leads to smaller solubility and higher permeability, leading us to conclude that the kinetic factor is predominant here. Toluene, on the other hand, drives the behaviour of solubility and permeability at a constant methanol fraction because both parameters decrease as the toluene fraction does. It is interesting to also notice that for the mixtures where the composition of toluene and methanol is high, a synergetic effect is observed, resulting in much higher permeabilities than those observed for pure liquids.

These findings clearly demonstrate the polymer’s aversion for cyclohexane, which is further supported by the fact that the total permeation rates calculated experimentally for mixtures of toluene and cyclohexane are up to 50% lower than the balanced average of permeation rates for pure species. The global synergy between the three components is positive for all the remaining mixtures, showing that solvents interact not only with the polymer but also with one another.

3.4. Permeation Fluxes

In view of the above results, the Viton fluoropolymer is shown to be an elastomer capable of providing an apparent resistance to the permeation of cyclohexane, but it seems to be not so effectively resistant to toluene and methanol, since the latter presents a high diffusion coefficient and a high permeability in the polymer. It is then helpful to understand the mass transfer through this selective layer. The solution–diffusion model [13] can be utilized for estimating the transport of various liquids and liquid mixtures through the elastomer if the Viton elastomer is thought of as the barrier (membrane) that separates the liquid from the outside (vapor). While the gradient of chemical potential, which is typically stated in terms of concentration differences, is what drives the transport of liquids over the membrane, in the pervorative process the driving force can be expressed in a more useful way [30], in terms of vapor pressure, as

$$J=P\frac{∆p}{l}$$

(9)

where J is the mass flux through the elastomer membrane, P is the permeability component, ∆p is the pressure difference over the membrane (driving force for permeation), and l is the membrane thickness.

Table 7. Estimated permeation fluxes (J_Toluene, J_Methanol, J_Cyclohexane and J_∑) for toluene, methanol, and cyclohexane mixtures through polymers from Equation (9).

Liquid	JToluene /(10−8 kg m−2 s−1)	JMethanol /(10−8 kg m−2 s−1)	JCyclohexane /(10−8 kg m−2 s−1)	J∑ /(10−8 kg m−2 s−1)
1	4.78		1.79	6.56
2	3.11		3.50	6.61
3	1.52		5.13	6.65
4		10.6	5.88	16.5
5		81.8	0.42	82.2
6		85.5	0.13	85.7
7	0.68	78.2		78.9
8	1.68	64.8		66.5
9	3.33	42.7		46.1
10	1.22	28.1	3.28	32.6
11	2.22	28.5	2.22	33.0
12	3.26	28.9	1.13	33.3
13	0.73	56.1	1.64	58.5
14	1.22	47.0	1.83	50.1
15	1.00	64.0	0.76	65.8
16	1.38	35.2	2.58	39.2

Notes: J_Toluene, J_Methanol, and J_Cyclohexane represent the fluxes of toluene, methanol, and cyclohexane across the polymer, respectively. J_∑ represents the global flux of liquids through the membrane.

presents the permeation fluxes assessed using Equation (9), assuming a membrane with a thickness equal to the polymer diameter and using the individual vapor pressure of the components for the estimation of the pressure difference over the membrane. In the case of mixtures, we have calculated vapor pressure using a simple additive rule. Fluxes of methanol across the elastomer are dominant in all binary and ternary mixtures where this component is present.

Indeed, from Table 7, we can verify the very small compatibility of the Viton elastomer with methanol, in view of the very high fluxes observed. Although smaller, the transport of toluene and cyclohexane is still significant when taking into account that previous resistance studies [15] demonstrate that for fluxes of these mixtures, at one order of magnitude below there are already leaking issues.

4. Conclusions

Using a gravimetric approach, the kinetics of sorption and desorption for pure liquids and binary and ternary combinations of toluene, methanol, and cyclohexane were investigated.

Methanol sorption by the polymer was found to be quite high, whereas cyclohexane sorption was nearly negligible. Binary and ternary mixtures with a high amount of methanol also presented larger sorption coefficients; in some cases, observed sorption for mixtures was higher than for individual pure liquids. Using Fick’s equation to calculate the diffusion coefficients for both short term and longterm exposure to the liquids, it was found that the diffusion coefficients were in the following order: D_MeOH > D_Tol > D_Chex, and that, in general, the amount of methanol present in the mixture determined its diffusion coefficient.

Thermodynamic parameters, such as Flory–Huggins, were determined and correlated with the sorption and solubility of liquids and liquid mixtures inside the polymer, allowing an assessment of the possible interactions of the liquids with the polymer. As the ratio of methanol in the mixture increased, the permeation coefficient also increased, while the solubility coefficient decreased. Methanol exhibited the lowest solubility coefficient within the polymer, but due to its high mobility and permeability, it was shown to be the liquid that flows the fastest through the Viton fluoropolymer. Flows of toluene and cyclohexane are still considerable, notwithstanding that this fluoropolymer is usually indicated as hydrocarbon resistant. Field engineers and technologists may find the current study valuable for carefully choosing the sealings in applications and circumstances involving mixed solvent media, particularly for these hazardous liquids and long-time exposures.