Disturbance Observer-Based Terminal Sliding Mode Tracking Control for a Class of Nonlinear SISO Systems with Input Saturation
Abstract
1. Introduction
- Input-output feedback linearization technique is applied to explicitly establish the relationship between the system output and the control input.
- Sliding mode disturbance observer is designed to estimate the lumped disturbance including the possible uncertainties, external disturbances, and input saturation, and is able to significantly reduce the chattering while keeping a certain tracking performance.
- Disturbance observer-based terminal sliding mode tracking controller with boundary layer method is further designed for the trade-off between the high-frequency chattering caused by the discontinuous function and the nonzero steady-state error caused by the continuous control within the boundary layer.
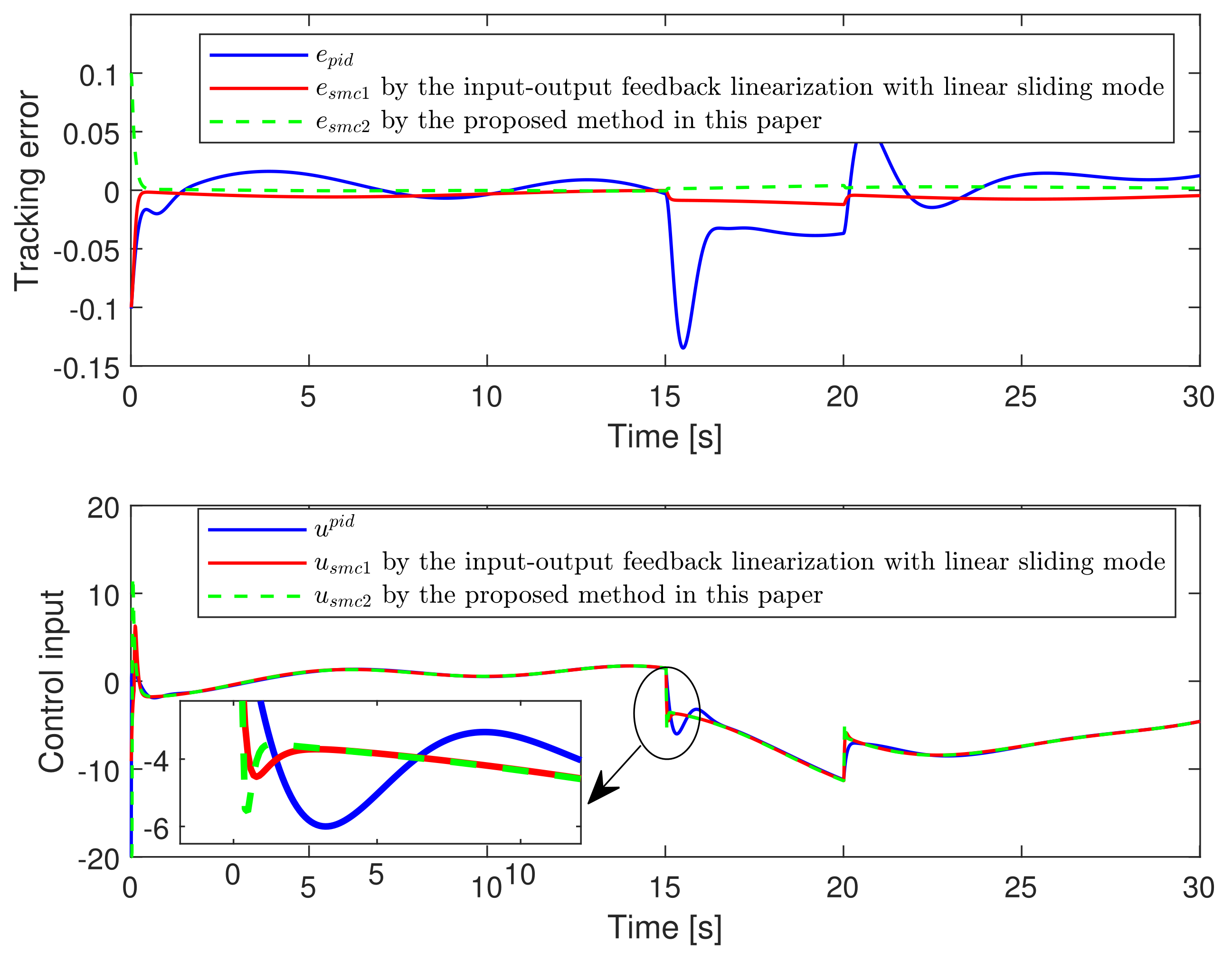
- The proposed method is evaluated by two typical nonlinear systems that are fully linearizable and partially linearizable, respectively, and compared with the state-of-the-art method in terms of tracking performance and robustness through numerical simulations.
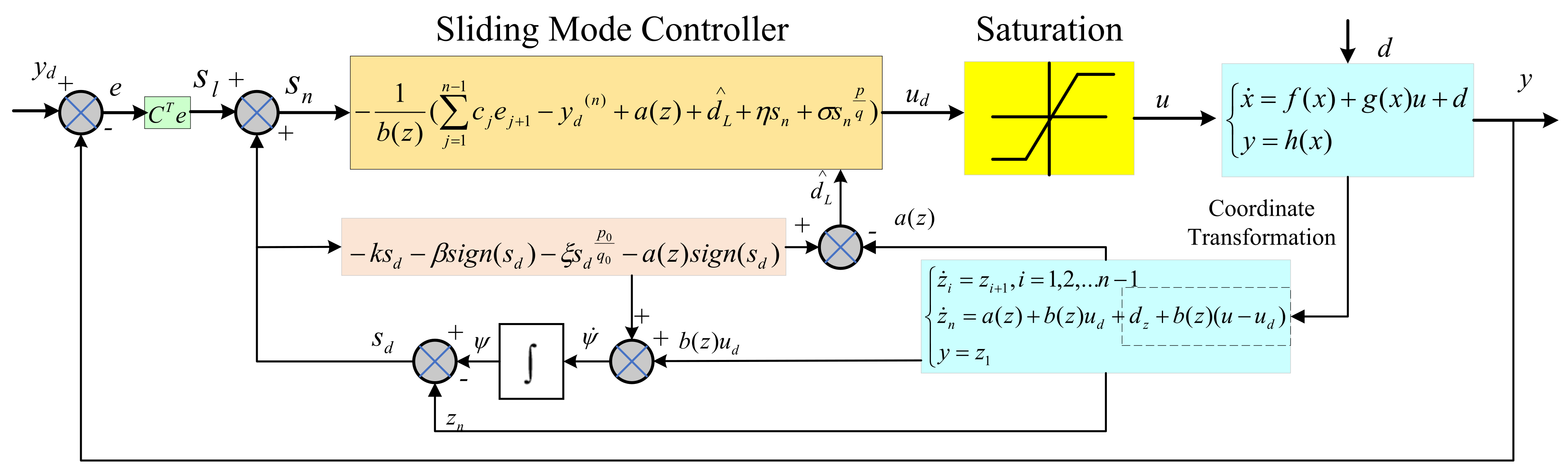
2. Problem Formulation
3. Design of Finite-Time Sliding Mode Disturbance Observer
4. Terminal Sliding Mode Control
5. Illustrative Examples
5.1. Example 1
5.2. Example 2
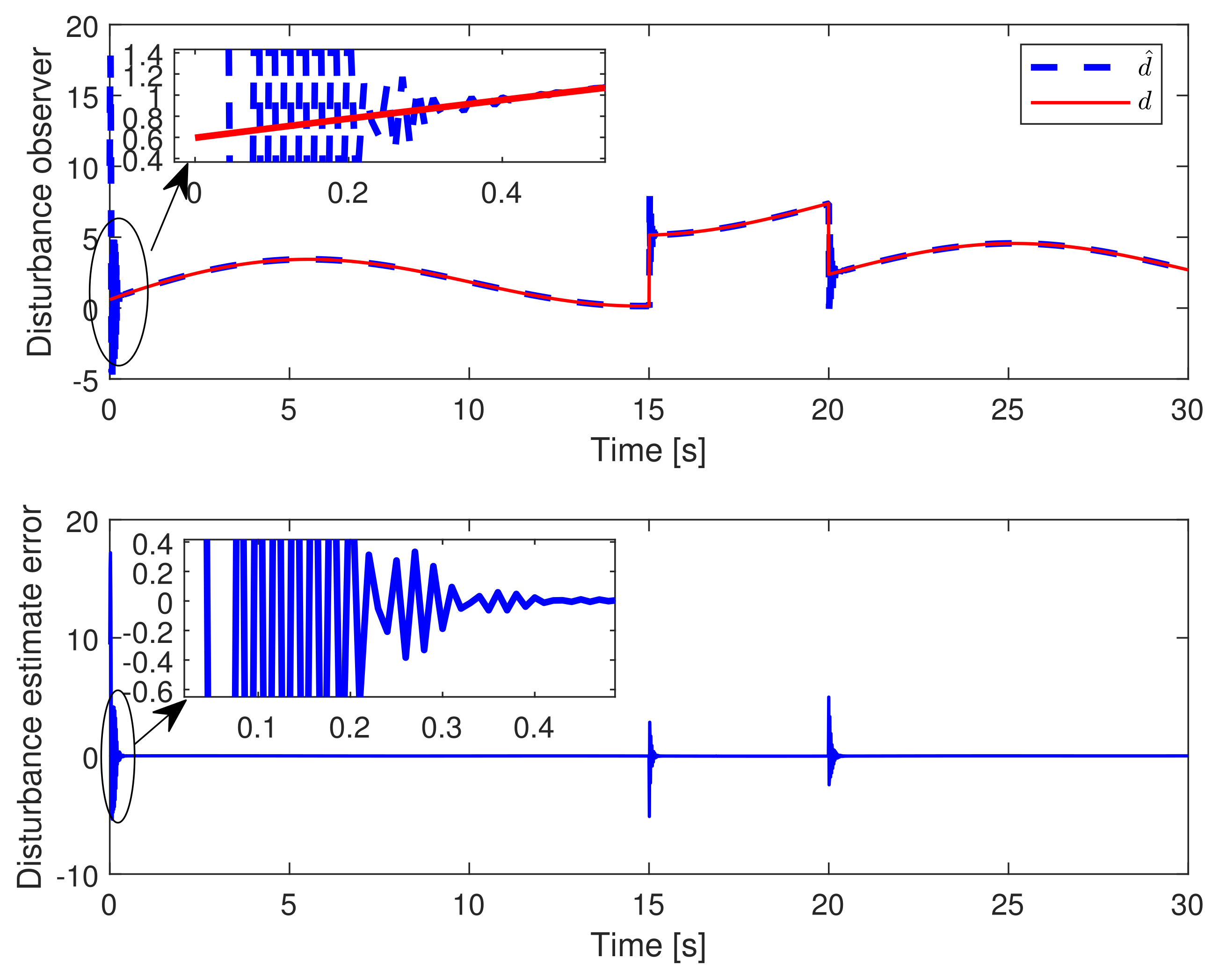
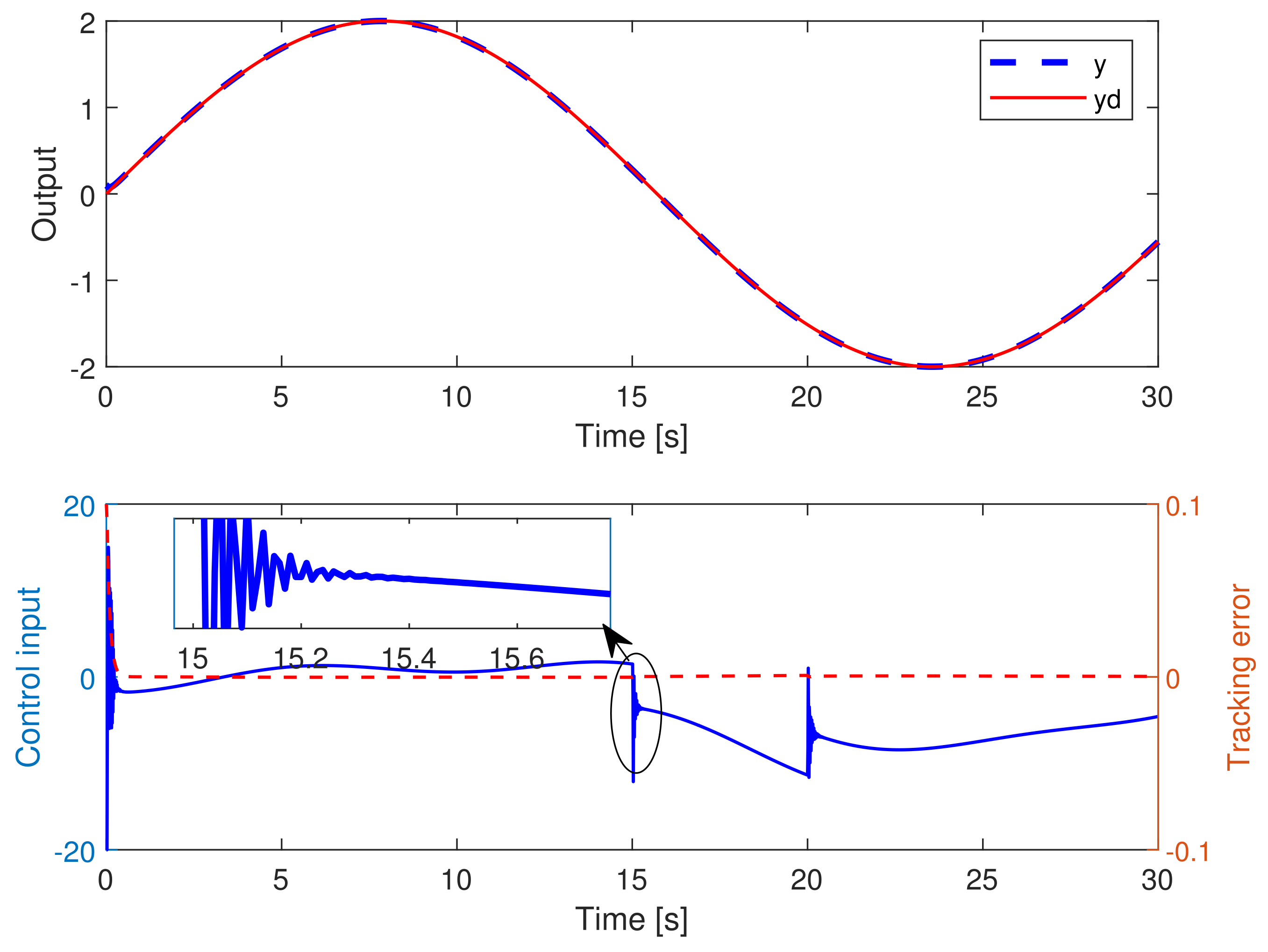
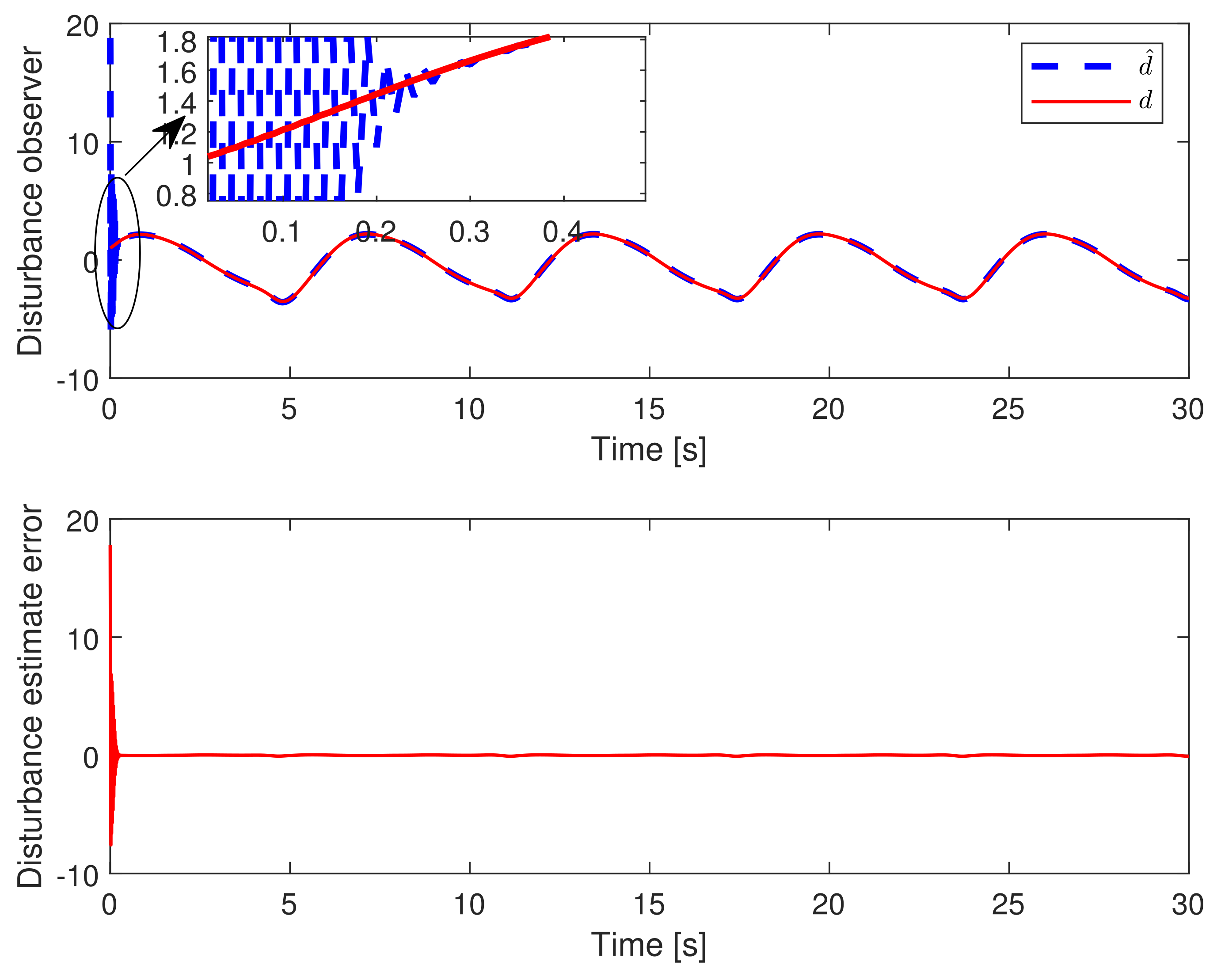
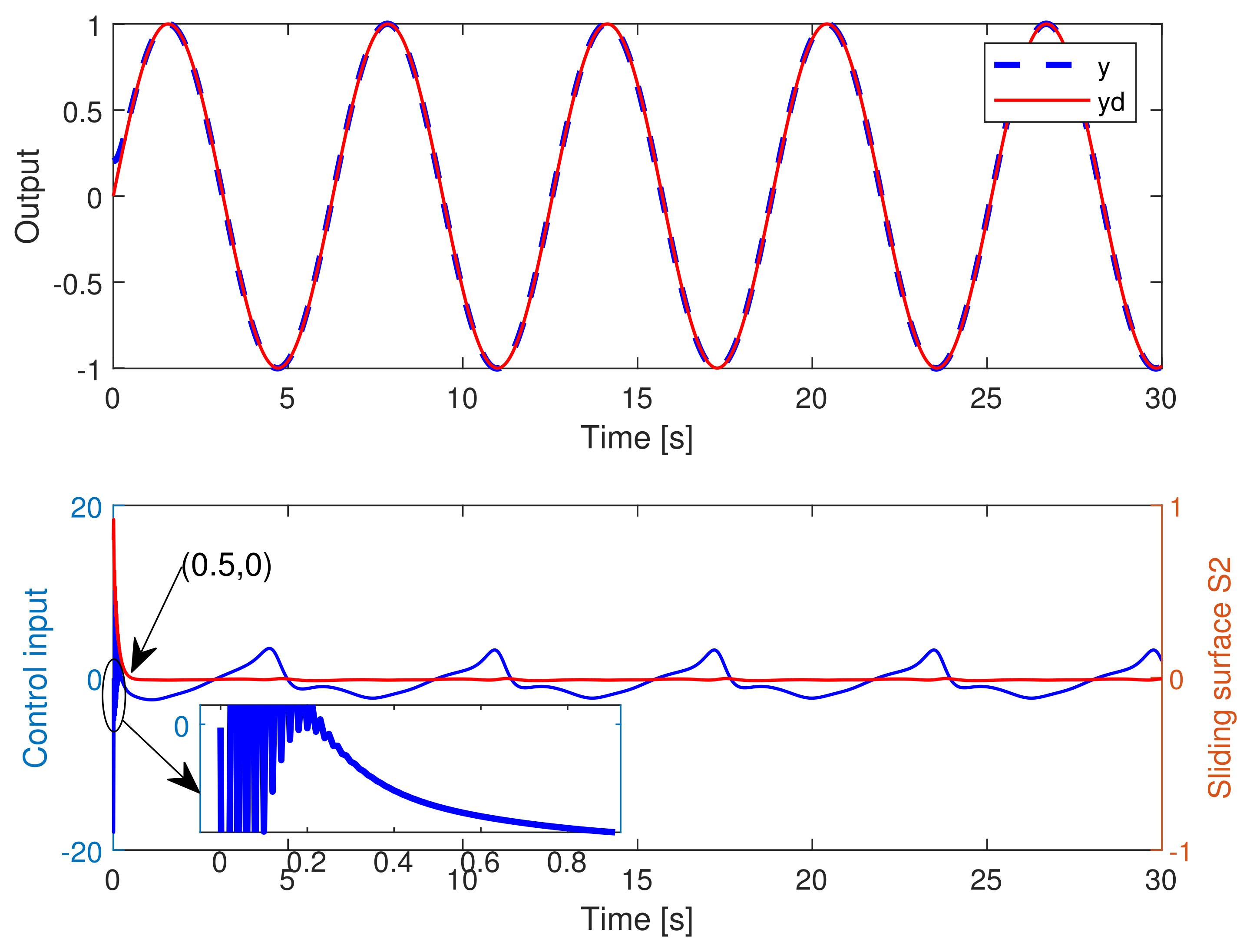
- Regarding the parameters in the terminal sliding mode control law based on the disturbance observer, is determined such that the Assumption 1 holds. The parameters are chosen such that the roots of polynomial lie in the open left half (Hurwitz) plane. The finite-time convergence of disturbance estimate error is subject to the combination of k, , , while the parameters , are selected for the finite-time convergence concerning the trajectory tracking error. In these parameters, and must hold. As for the left parameters, in general, there is no rule for the deterministic parameters tuning procedure to achieve the perfect tracking with fast convergence and without chattering. Such parameters may be determined by the trial-and-error method according to the accuracy requirement of tracking, allowable chattering frequency for the actuator, and different initial conditions.
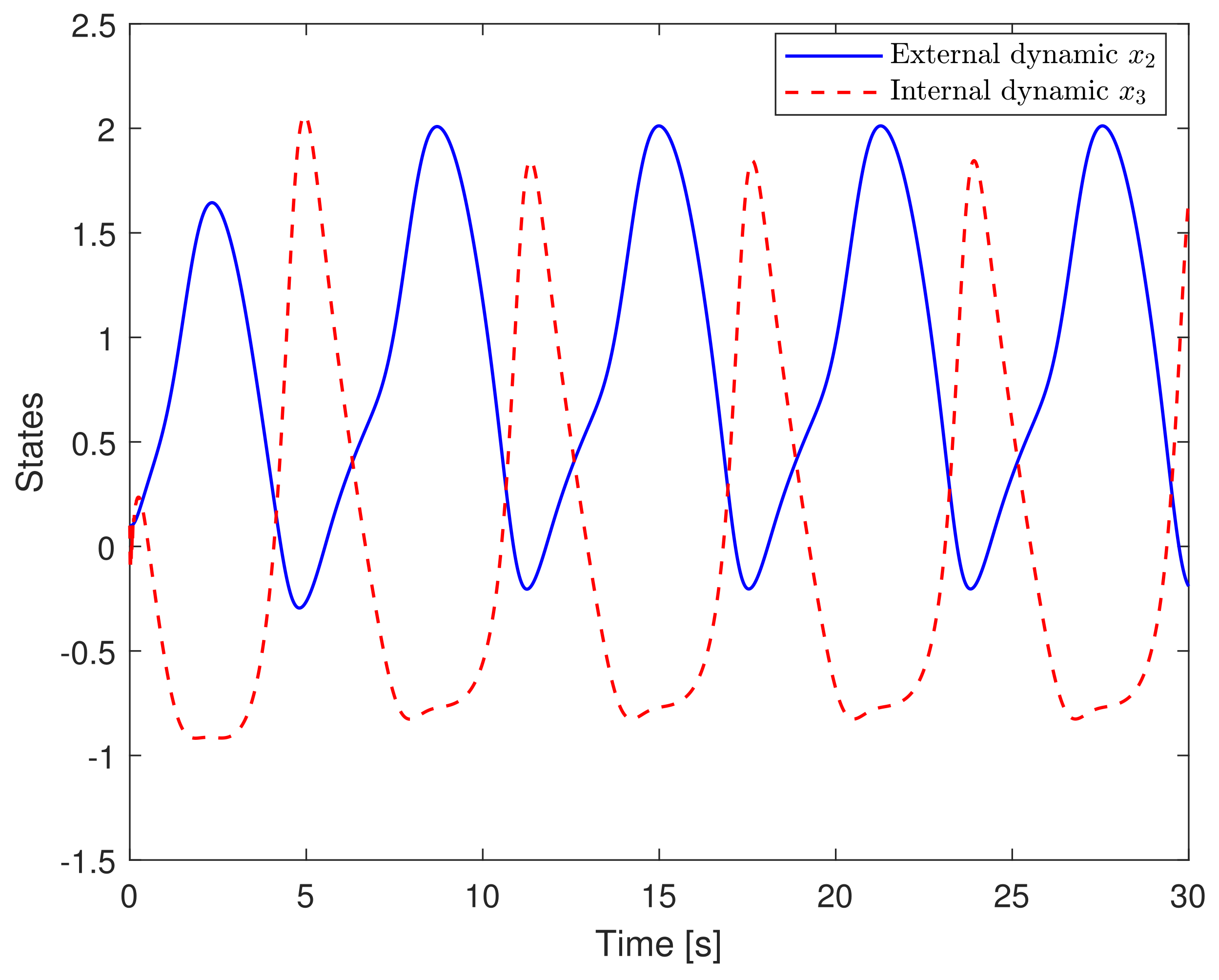
- In example 2, since the relative degree is less than the system order, there exists one unobservable state. According to Lemma 1, we choose as the new state set and utilize the method of zero dynamics analysis to keep the system output and its successive derivatives to be zero through changing control actions. In accordance with Equations (34) and (35), the stability of internal dynamics can be guaranteed when . The conclusion is verified in Figure 10 where the system output and its successive derivatives are kept at zero while the internal dynamics are bounded along with the variation of external dynamics . Further, the variations of and in the context of trajectory tracking are presented in Figure 11, where both and are bounded input bounded output (BIBO) stable.
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2008, 13, 559–576. [Google Scholar]
- Zhang, Q.; Liu, P.; Chen, Y.; Deng, Q.; Pannek, J. An improved event-triggered predictive control for capacity adjustment in reconfigurable job-shops. Int. J. Prod. Res. 2022, 2022, 1–18. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, P.; Pannek, J. Combining MPC and integer operators for capacity adjustment in job-shop systems with RMTs. Int. J. Prod. Res. 2019, 57, 2498–2513. [Google Scholar] [CrossRef]
- Marti, R.; Lucia, S.; Sarabia, D.; Paulen, R.; Engell, S.; de Prada, C. Improving scenario decomposition algorithms for robust nonlinear model predictive control. Comput. Chem. Eng. 2008, 79, 30–45. [Google Scholar] [CrossRef]
- Grüne, L.; Pannek, J. Nonlinear Model Predictive Control: Theory and Algorithms, Communications and Control Engineering; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Wang, A.; Yu, H.; Cang, S. Bio-inspired robust control of a robot arm-and-hand system based on human viscoelastic properties. J. Frankl. Inst. 2017, 354, 1759–1783. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, Q.; Wang, A.; Wen, S.; Pannek, J. Operator-Based Adaptive Tracking Capacity Control in Complex Manufacturing Processes. Appl. Sci. 2019, 13, 449. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, Q.; Pannek, J. Development of operator theory in the capacity adjustment of job shop manufacturing systems. Appl. Sci. 2019, 9, 2249. [Google Scholar] [CrossRef]
- Xia, G.; Yang, L.; Xiang, F. Event-Triggered Neural Sliding Mode Guaranteed Performance Control. Processes 2017, 10, 1742. [Google Scholar] [CrossRef]
- Plestan, F.; Shtessel, Y.; Bregeault, V.; Poznyak, A. New methodologies for adaptive sliding mode control. Int. J. Control. 2010, 83, 1907–1919. [Google Scholar] [CrossRef]
- Utkin, V.; Poznyak, A.; Orlov, Y.; Polyakov, A. Conventional and high order sliding mode control. J. Frankl. Inst. 2020, 357, 10244–10261. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Acob, J.; Pano, V. PD with sliding mode control for trajectory tracking of robotic system. Robot. Comput. Integr. Manuf. 2014, 30, 189–200. [Google Scholar] [CrossRef]
- Goel, A.; Mobayen, S. Adaptive nonsingular proportional–integral–derivative-type terminal sliding mode tracker based on rapid reaching law for nonlinear systems. J. Vib. Control. 2021, 27, 2669–2685. [Google Scholar] [CrossRef]
- Yu, X.; Zhihong, M. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I. 2002, 49, 261–264. [Google Scholar]
- Qiao, L.; Zhang, W. Trajectory tracking control of AUVs via adaptive fast nonsingular integral terminal sliding mode control. IEEE Trans. Ind. Inform. 2019, 16, 1248–1258. [Google Scholar] [CrossRef]
- Mobayen, S. Adaptive global terminal sliding mode control scheme with improved dynamic surface for uncertain nonlinear systems. Int. J. Control. Autom. Syst. 2018, 16, 1692–1700. [Google Scholar] [CrossRef]
- Lee, H.; Utkin, V.I. Chattering suppression methods in sliding mode control systems. Annu. Rev. Control. 2007, 31, 179–188. [Google Scholar] [CrossRef]
- Eker, I. Second-order sliding mode control with experimental application. ISA Trans. 2010, 49, 394–405. [Google Scholar] [CrossRef]
- Huang, Y.J.; Kuo, T.C.; Chang, S.H. Adaptive sliding-mode control for nonlinear systems with uncertain parameters. IEEE Trans. Syst. Man Cybern. B Cybern. 2008, 38, 534–539. [Google Scholar] [CrossRef]
- Shao, X.; Sun, G.; Yao, W.; Liu, J.; Wu, L. Adaptive sliding mode control for quadrotor UAVs with input saturation. IEEE ASME Trans. Mechatron. 2021, 27, 1498–1509. [Google Scholar] [CrossRef]
- Deng, M.; Wang, A. Robust non-linear control design to an ionic polymer metal composite with hysteresis using operator-based approach. IET Control. Theory Appl. 2012, 6, 2667–2675. [Google Scholar] [CrossRef]
- Huang, H.; Li, D.; Lin, Z.; Xi, Y. An improved robust model predictive control design in the presence of actuator saturation. Automatica 2011, 47, 861–864. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, H.; Wu, C.; Wang, L.; Ahn, C.K. Adaptive fuzzy control of nonlinear systems with unmodeled dynamics and input saturation using small-gain approach. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 1979–1989. [Google Scholar] [CrossRef]
- Du, J.; Hu, X.; Krstić, M.; Sun, Y. Robust dynamic positioning of ships with disturbances under input saturation. Automatica 2016, 73, 207–214. [Google Scholar] [CrossRef]
- Wen, C.; Zhou, J.; Liu, Z.; Su, H. Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance. IEEE Trans. Autom. Contr. 2011, 56, 1672–1678. [Google Scholar] [CrossRef]
- Wang, B.; Derbeli, M.; Barambones, O.; Yousefpour, A.; Jahanshahi, H.; Bekiros, S.; Aly, A.A.; Alharthi, M.M. Experimental validation of disturbance observer-based adaptive terminal sliding mode control subject to control input limitations for SISO and MIMO systems. Eur. J. Control 2022, 63, 151–163. [Google Scholar] [CrossRef]
- Matas, J.; De Vicuna, L.G.; Miret, J.; Guerrero, J.M. Feedback linearization of a single-phase active power filter via sliding mode control. IEEE Trans. Power Electron. 2008, 23, 116–125. [Google Scholar] [CrossRef]
- Chen, B.S.; Lee, C.H.; Chang, Y.C. H∞ tracking design of uncertain nonlinear SISO systems: Adaptive fuzzy approach. IEEE Trans. Fuzzy Syst. 1996, 4, 32–43. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice-Hall: New York, NY, USA, 1991; pp. 224–228. [Google Scholar]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef]
- Mahmud, M.A.; Pota, H.R.; Hossain, M.J. Dynamic stability of three-phase grid-connected photovoltaic system using zero dynamic design approach. IEEE J. Photovolt. 2004, 2, 564–571. [Google Scholar] [CrossRef]
- Isidori, A. The zero dynamics of a nonlinear system: From the origin to the latest progresses of a long successful story. Eur. J. Control 2013, 19, 369–378. [Google Scholar] [CrossRef]
- Yun, X.; Yamamoto, Y. Stability analysis of the internal dynamics of a wheeled mobile robot. J. Robot. Syst. 1997, 14, 697–709. [Google Scholar] [CrossRef]
- Shen, Y.; Huang, Y. Global finite-time stabilisation for a class of nonlinear systems. Int. J. Syst. Sci. 2012, 43, 73–78. [Google Scholar] [CrossRef]
- Yue, Y.; Geng, Y.; Wang, W. Continuous Nonsingular Fast Terminal Sliding Mode Control for Speed Tracking of PMSM Based on Finite Time Disturbance Observer. Processes 2022, 10, 1407. [Google Scholar] [CrossRef]
- Mobayen, S.; Javadi, S. Disturbance observer and finite-time tracker design of disturbed third-order nonholonomic systems using terminal sliding mode. J. Vib. Control. 2017, 23, 181–189. [Google Scholar] [CrossRef]
- Ginoya, D.; Shendge, P.D.; Phadke, S.B. Disturbance observer based sliding mode control of nonlinear mismatched uncertain systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 26, 98–107. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Z. Disturbance observer-based robust saturated control for spacecraft proximity maneuvers. IEEE Trans. Control. Syst. Technol. 2017, 26, 684–692. [Google Scholar] [CrossRef]
- Chen, M.; Shi, P.; Lim, C. C; Robust constrained control for MIMO nonlinear systems based on disturbance observer. IEEE Trans. Autom. Contr. 2015, 60, 3281–3286. [Google Scholar] [CrossRef]
- Chen, M.; Wu, Q.X.; Cui, R.X. Terminal sliding mode tracking control for a class of SISO uncertain nonlinear systems. ISA Trans. 2013, 52, 198–206. [Google Scholar] [CrossRef]
- Mobayen, S. Fast terminal sliding mode controller design for nonlinear second-order systems with time-varying uncertainties. Complexity 2015, 21, 239–244. [Google Scholar] [CrossRef]
- Xu, J.X.; Pan, Y.J.; Lee, T.H. Sliding mode control with closed-loop filtering architecture for a class of nonlinear systems. IEEE Trans. Circuits Syst. Express Briefs. 2004, 51, 168–173. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, Z.; Yuan, Y.; Huang, Y.; Li, X.; Li, W. Sliding mode controller of hydraulic generator regulating system based on the input/output feedback linearization method. Math. Comput. Simul. 2016, 119, 18–34. [Google Scholar] [CrossRef]
- Benayache, R.; Chrifi-Alaoui, L.; Bussy, P.; Castelain, J.M. Design and implementation of sliding mode controller with varying boundary layer for a coupled tanks system. In Proceedings of the 17th Mediterranean Conference on Control and Automation, Washington, DC, USA, 24–26 June 2009. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Liu, P.; Chen, Y.; Deng, Q.; Tong, A. Disturbance Observer-Based Terminal Sliding Mode Tracking Control for a Class of Nonlinear SISO Systems with Input Saturation. Processes 2023, 11, 1878. https://doi.org/10.3390/pr11071878
Zhang Q, Liu P, Chen Y, Deng Q, Tong A. Disturbance Observer-Based Terminal Sliding Mode Tracking Control for a Class of Nonlinear SISO Systems with Input Saturation. Processes. 2023; 11(7):1878. https://doi.org/10.3390/pr11071878
Chicago/Turabian StyleZhang, Qiang, Ping Liu, Yu Chen, Quan Deng, and Angxin Tong. 2023. "Disturbance Observer-Based Terminal Sliding Mode Tracking Control for a Class of Nonlinear SISO Systems with Input Saturation" Processes 11, no. 7: 1878. https://doi.org/10.3390/pr11071878
APA StyleZhang, Q., Liu, P., Chen, Y., Deng, Q., & Tong, A. (2023). Disturbance Observer-Based Terminal Sliding Mode Tracking Control for a Class of Nonlinear SISO Systems with Input Saturation. Processes, 11(7), 1878. https://doi.org/10.3390/pr11071878






