Abstract
The Industrial Internet of Things (IIoT) provides internet connectivity for instruments, digital machines, and any other manufactured object to enable intelligent industrial operations to achieve high productivity. Securing communications between IIoT devices remains a critical and challenging issue due to the resource-constrained and processing capabilities of sensing devices. Moreover, the traditional group shared key might implement complex mathematical operations that are not suitable for the limited recourse capability of the IIoT device. Furthermore, the standard Diffie–Hellman (DH) and elliptic curve Diffie–Hellman (ECDH), which are the most suited for tiny devices, only work between a pair of IIoT devices, while they are not designed to work among a group of IIoT devices. This paper proposes an authenticated group shared key (AGSK) mechanism that allows a set of industrial objects to establish a common session key over the IIoT. The proposed AGSK utilizes the combiner for the hash function and digital signature, which is implemented in IIoT devices. Additionally, the random oracle model has been used to prove the security of AGSK, while the IIoT adversary model has been used to analyze the AGSK countermeasures against cyberattacks. The results of the performance evaluation showed that the efficiency of the AGSK was reduced by 41.3% for CPU computation time, 45.7% for storage cost, and 40% less power consumption compared to the baseline group key management algorithms.
1. Introduction
The Industrial Internet of Things (IIoT) enables internet connection and communication capabilities to industrial machines, including industrial storage tanks, centrifuges, industrial mixers, electrical generators, air compressors, material handling equipment, and computer numerical control. In the IIoT platform, the Internet of Things device (i.e., called IIoT node) should be attached to industrial objects, which will enable smart productivity operations, the self-optimized performance of production lines and control centers, and improved product quality [1,2]. Unfortunately, a massive portion of the devices in the IIoT networks is susceptible to cyberattacks, such as device spoofing, denial of service, man-in-the-middle (MITM) attacks, and data leaks. As shown in Figure 1, the malicious attack can occur near the devices in the IIoT environment or between the IIoT gateway and mobile users, which causes catastrophic effects on the investments of corporate executives that decide to use IIoT. Therefore, the IIoT network should be protected by cybersecurity platforms that can identify, protect, detect, and respond to cyberattacks. Regardless of the cybersecurity mechanism (i.e., symmetric, or asymmetric) that is used in the IIoT network, the only secret information that should be prevented from disclosure is the secret key. This problem becomes increasingly wasteful when the concept of group shared key is used among the IIoT devices, sensors, actuators, gateway, and mobile devices. As a result, the IIoT network, based on the lightweight group authenticated secret key, is an essential mechanism for many youth cybersecurity protections. In industrial and manufacturing facilities, cybersecurity monitoring solutions are crucial, yet they are insufficient. Real-time protection of IIoT devices is mandatory, requiring the authentication of all devices and the protection of the information and instructions needed to control plant operations [3,4,5].
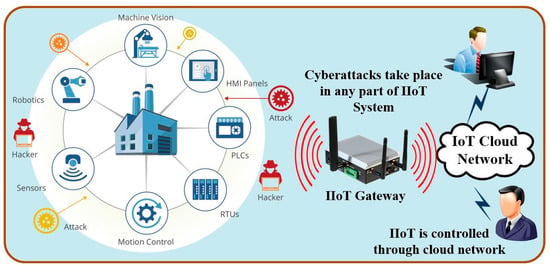
Figure 1.
Cyberattacks in IIoT system.
Group communication is becoming increasingly crucial with the emergence of shared and distributed communication applications. Using a public channel and a key establishment technique, group members can safely communicate with one another. Therefore, each member in the group communication is an essential part of creating the group shared key (GSK). The GSK mechanism consists of two parts, which are the preshared key distribution and the final key calculation. The optimal solution for the distributed preshared key is to use asymmetric (public key) cryptography with a digital signature. The source IIoT device uses asymmetric cryptography to encrypt the preshared key using its private key and the destination can confirm the identity of the sender using the public key, which is mathematically related to the private key of the sender. Furthermore, the final key calculation is implemented for each group member, simultaneously, based on the received preshared key. Nevertheless, compared to the symmetric algorithms, the implementation of asymmetric algorithms on the IIoT is more difficult and requires more complex mathematics [6,7,8]. The original shared key scheme is called Diffie–Hellman (DH) and elliptic curve Diffie–Hellman (ECDH), which can create a secret key between two parties. However, the design of DH and ECDH does not resolve the secure group communication. In an IIoT environment, the secure group shared key management is a complicated design task, with respect to both security strength and computational time, owing to resource constraints in command processing, support mathematic functions, memory limitation, microcontroller capabilities, and security issues in the IIoT transceiver [9]. Providing secure, authenticated group-shared key tasks in the IIoT network is the main challenge, and it arises from their unique characteristics, which can be explained by the following points:
- Secure communication lacking in a predisseminated shared key among a group of IIoT devices.
- Identify compromised IIoT devices and authenticate the identity of the group controller and all members. Moreover, the received data integrity must be verified at each IIoT device.
- The complicated design of the group-shared key mechanism in the resource constraints devices, such as the IIoT, which should consider both security strength and computational time.
- The dynamic supporting for join/leave members of the group.
- The optimal level of self-arrangement of the group shared key.
- The resource is constrained in terms of storage, computation, and communication power.
This paper intends to propose an effective authenticated group shared key based on the combiner for the hash functions. The summary of contributions can be described as follows:
- The proposed research builds an efficient authenticated group shared key (AGSK) among a set of industrial objects using the IIoT network platform. The common shared key over the IIoT utilizes the combiner for the geolocation hash function and the digital signature of each IIoT device.
- It proposes a key management algorithm to join and leave any group member that allows the IIoT gateway to optimize the number of required steps to dynamically change the old AGSK. Furthermore, the proposed algorithm guarantees to prevent the leaving member from using the IIoT network platform after issuing the leaving request.
- Optimal design of two-handshaking communication messages between the IIoT devices and IIoT gateway to establish the group shared key.
- The random oracle model has been used to prove the security of the AGSK and the adversary model for IIoT network that has been analyzed. In addition, countermeasures against adversary attacks have been investigated.
- Finally, the proposed method has been implemented in an emulation system, assessed (i.e., computation time, power, and storage costs), and compared with the recent baseline group shared key mechanisms.
The remaining part of this research is structured as follows: Section 2 describes the related works on the group shared key. Section 3 explains the AGSK system design algorithm. Section 4 explains the cybersecurity analysis of the AGSK algorithm. Section 5 describes the implementation and performance evaluation of the AGSK. Finally, Section 6 concludes the paper and describes future work.
3. System Design of AGSK Algorithm
Group key management and authentication algorithms invent the majority of the proposed AGSK mechanism, which would ensure elevated levels of cybersecurity defense against cyberattacks over the IIoT. The two algorithms and the process for securely transferring the group shared key amongst the IIoT devices are described in the next subsections. Table 1 lists all the notations that were applied throughout this research.

Table 1.
Frequently used notation.
3.1. Group Key Management Algorithm
The primary issue with GSK management is the exchange of the shared key among the IIoT nodes through an insecure communication channel, which leaves the IIoT devices vulnerable to several attacks. One of the practical solutions for shared key distribution is the ECDH approach, which is regarded as a suitable remedy for devices with limited resources. When compared to the Rivest–Shamir–Adleman (RSA) cryptosystem, the ECDH has a smaller key size and experiences less computation cost and power consumption. However, ECDH was not designed with the consideration of a group shared key among multidevices. Thus, the group key management is primarily proposed to exchange the shared secret keys in a secure manner among the IIoT devices to prevent spoofing attacks that impersonate the identity of the IIoT gateway. The equation of an elliptic curve is defined as follows:
where O represents an additional point on the curve at infinity; a and b are the constant coefficient of the elliptic curve equation; represents an integer finite field over a modular prime P. The elliptic curve domain parameters should be agreed upon among the IIoT gateway, wireless sensors, mobile users, etc. The parameters use P as the prime of the base finite field of the curve (modulo P), G is the generator, n is the order of G, and h is the subgroup cofactor. The proposed functions in the group key management are designed using the following presumptions, which are used throughout this paper:
- The IIoT gateway is connected at all times, which means it cannot leave the group. Furthermore, it has a strong security system that can resist any attack.
- During a programming session, the domain parameters are embedded and uploaded to all IIoT devices.
- Every IioT device has two secret keys: a public key that is accessible to all other IioT devices and a private key that is kept secret from the public.
3.1.1. Group Shared Key Generation
The group shared key has been generated using all the IIoT devices in the same group, as illustrated in Figure 2. The procedure of the proposed group shared key is performed using the following steps:
- Any IIoT device has data to be sent and it calculates the private key and the public key. The random generator function is used to select the private key d between 1, and n − 1. The scalar multiplication of d and G (e.g., Q = d × G) is used to calculate the public key Q.
- Using unicast forwarding, all public keys for the involved IIoT devices should be sent to the IIoT gateway to calculate the preshared key (PSK) for each of the IIoT devices, as follows:
- The preshared group point for the device number j () can be calculated at the gateway as follows:
- The gateway unicasts the to the device number j, which will calculate the group shared point (), while the x coordinate of will be selected as the group shared key at the device number j (), as follows:
- Finally, the gateway can calculate the GSK for the device number j, as follows:
as can be seen in Equations (4) and (5), the GSK at the gateway and any IIoT device is matching because = .
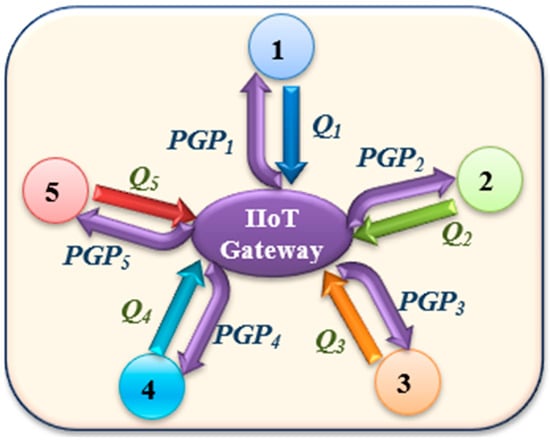
Figure 2.
Unicast message among 5 IIoT devices in the proposed group shared key.
3.1.2. Authentication Based on ECDH and Combiner for Hash Function
The proposed authentication was designed based on combiners for the hash functions, which used the geolocation information (e.g., the GPS information of the IIoT devices) and ECDH key authentication algorithms. The basic idea of the authenticated group shared key (AGSK) is illustrated in Figure 3, and it can be described as follows:
- Step 1: Digital Signature for the Digest of Public Key.
- (1)
- Each IIoT device selects the private key d and calculates the public key Q.
- (2)
- The message authentication code (MAC) is calculated for Q using the hash function-based GPS location for the IIoT device.
- (3)
- The MAC is signed with the private key d. The digital signature algorithm in our previous works [10,27,28] has been used to sign the MAC.
- (4)
- The digital signature and the Q are sent to the IIoT gateway in the same message.
- Step 2: Digital Signature Verification and Sender Authentication.
- Upon receiving the unicast messages from all IIoT groups, the gateway performs the following verification and authentication:
- (1)
- Three steps of curve-point inspection should be employed to confirm the real identity of the sender who used their signature to sign the Q: 1. Verify that Q lies on the curve. (2) Verify that Q is not equivalent to the identity element O. 3. Verify that n × Q = O.
- (2)
- Verify the sender signature using the received Q. This means that the gateway uses the Q to inverse the digital signature and it uses the stored geolocation of the sender to implement the hash function and to compare the received digest with the calculated one. If they match, the sender is legitimate, and the data are valid. Otherwise, the sender or the data are invalid, and the message is discarded.
- Step 3: Gateway Digital Signature for PGP.
- (1)
- Upon verifying and authenticating all the IIoT devices in the group, the IIoT gateway will calculate the PGP and GSK for each device.
- (2)
- The IIoT gateway creates a MAC for each PGP using GSK, and it signs the MACs using its private key.
- (3)
- The digital signature of the gateway (SG) and the PGP are sent to the corresponding IIoT device.
- Step 4: Verifying Gateway Digital Signature.
- (1)
- Upon receiving the gateway message at the IIoT sender, the true identity of the gateway is verified using three steps of curve-point inspection of PGP.
- (2)
- If the PGP is verified, it will be used to calculate the GSK using Equation (3). Furthermore, the sign−1 (QG,SG) is applied to obtain the received digest (MAC for PGP), which will be compared using the calculated digest of the IIoT device. If they matched, the gateway is legitimate, and the PGP is authenticated. Otherwise, the message will be discarded.
Algorithm 1 illustrates the previous four steps of the proposed AGSK in pseudocode details. Each line in Algorithm 1 is commented on with further details.
| Algorithm 1. AGSK pseudocode | |
| Input: Secp192r1 domain parameters p, a, b, G, n, h. | |
| Output: S, SG, GSK. | |
| Start Algorithm (AGSK) | |
| 1 | | While (new session start) do |
| 2 | | For (each IIoT device in the group) do |
| 3 | | Pick private key (dS);//1 ≤ dS ≤ n |
| 4 | | Q = (d × G); |
| Step 1: Digital Signature for the Digest of Public Key. | |
| 5 | | MAC(Q) = H(GLoc,Q); //Calculate MAC (Q) based on a hash function and key Gloc |
| 6 | | S = Sign (d,MAC);// Apply digital signature based on private key d for MAC |
| 7 | | Send_to_Gateway(S,Q);//Send public key with IIoT device signature to gateway |
| Step 2: Digital Signature Verification and Sender Authentication. | |
| 8 | | Verify_Public_key(Q);//Gateway will verify Q using the three steps of point |
| 9 | | Retrieve_Gloc(IIoT_ID); //Gateway retrieves Gloc from its database using IIoT ID |
| 10 | | if (H(Gloc,Q)==Sign−1(Q,S));/*Gateway can inverse S and obtain the received digest using Q. Furthermore, it compares calculated digest with received */ |
| 11 | | The IIoT sender is legitimate, and Q is valid. |
| 12 | | else |
| 13 | | The IIoT sender or Q is invalid; Discard_message(); |
| 14 | | End;//For loop |
| Step 3: Gateway Digital Signature for PGP. | |
| 15 | | Calculate (PGP);// Gateway calculates PGP for all IIoT devices as in Equation (2). |
| 16 | | MAC(PGP) = H(GSK,PGP); //Calculate MAC (PGP) based on a hash function and GSK |
| 17 | | SG = Sign (dG,MAC);// Apply digital signature based on private key d for MAC |
| 18 | | Send_to_IIoT(SG,PGP,QG);//Gateway sends SG,PGP,QG to the corresponding IIoT |
| Step 4: Verifying Gateway Digital Signature. | |
| 19 | | Verify_PGP();//Corresponding IIoT verifies PGP using the three steps of point |
| 20 | | Calculate (GSK); //it calculates the GSK as in Equation (3). |
| 21 | | if (H(GSK,PGP)==Sign−1(QG,SG));/*IIoT device can inverse SG and obtain received digest using QG. Moreover, it compares calculated digest with received */ |
| 22 | | The Gateway is legitimate, and PGP is valid. |
| 23 | | else |
| 24 | | The gateway or PGP is invalid; Discard_message(); |
| 25 | | End;//While loop |
| 26 | End;//Algorithm |
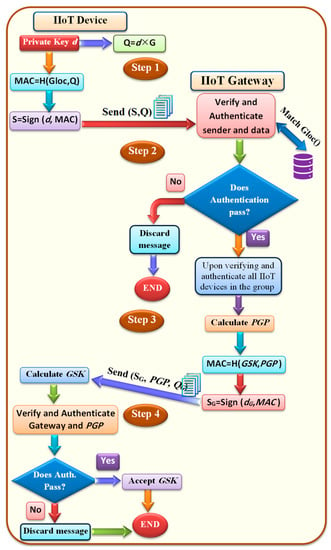
Figure 3.
Authenticated group shared key.
3.1.3. Dynamic Join and Leave in the Proposed AGSK
Since the IIoT devices are static most of the time, it is possible that one or a set of devices will want to join/leave the group. The proposed AGSK can resolve the join/leave issue based on its dynamic mechanism. This means that the IIoT devices can join/leave the group at any time based on the following security rules, which should be taken into consideration before any join/leave action. Suppose the number of nodes that want to join/leave the group is Z, the proposed dynamic algorithm will implement the following steps:
- (1)
- The new device(s) will send an authenticated unicast message that includes the public key, a digital signature, and a request to join/leave.
- (2)
- Upon the gateway receiving the join/leave request, it authenticates the sender and message data (e.g., geolocation data), recalculates the PGP, creates the digest (MAC) for the new PGP based on the new GSK, and signs the digest with its private key.
- (3)
- The gateway will specifically unicast a reply message to all IIoT devices. The reply message contents include the new PGP, the gateway digital signature, and the public key of the gateway.
- (4)
- If the IIoT node leaves the group, it will inform the gateway, which will create a new PSK between the gateway and the remaining IIoT devices. This means that the PGP will not function in the leaving node. However, if the node wants to join, it will receive the reply message and implement the four steps for the AGSK algorithm.
4. Cybersecurity Analysis
In this research, an adversary model for the IIoT network was developed to evaluate the countermeasures of AGSK against the IIoT cyberattacks, which are described in the following section.
4.1. IIoT Adversary Model
The fundamental objective of cyberattacks on the IIoT is to disturb its control function by utilizing a vulnerability that a malevolent adversary could exploit [29,30,31,32,33,34,35,36,37]. In cryptanalysis, the attacker is presumed to be able to read, transmit, and forge the AGSK on the IIoT network traffic, which could call into question the data sensed, the confidentiality of the IIoT devices, and the process control of the IIoT system. The following is a description of the most significant adversary attacks on AGSK:
- Spoofing attack: The attacker intercepts or eavesdrops on the exchange messages among the IIoT devices to determine the AGSK vulnerability and obtain access to the IIoT system information.
- A man-in-the-middle attack (MITM): The attacker eavesdrops on the traffic among the IIoT devices or between the IIoT devices and the gateway. The active MITM can manipulate or modify the packets sent to all those devices.
- A brute-force attack: The attacker attempts every available combination of letters, numbers, and symbols in the hash algorithm to obtain the hash key, which could produce the same output. This means the attacker can successfully break the AGSK even if both sides employ exceedingly difficult-to-crack domain parameters for the ECDH technique.
- An IIoT capture attack: To launch cyberattacks against the IIoT network, the attacker kidnaps an IIoT device and obtains the domain parameters and all its other credentials.
- A stolen-verifier attack: The attacker who has taken the AGSK from an IIoT device can pose for authorized access to all messages that are being exchanged among the IIoT devices. Moreover, the attacker who stole the AGSK can launch cyberattacks against the other IIoT devices to steal data or bypass the access rules.
4.2. Cryptanalysis of AGSK
The random oracle model is used to analyze the influence of the most typical cryptanalysis attacks, which can be designated as follows:
- Ciphertext-only attack: The adversary makes an effort to decipher the plaintext that was encrypted by knowing one or more ciphertexts. It is the simplest to execute in practice because all the adversary needs to do is eavesdrop on the open communication line being used to send the encrypted communications.
- Known-plaintext attack: The adversary knows some of the pairs of the ciphertext and corresponding plaintexts that share the same key. The adversary’s goal is to ascertain the encrypted plaintext to produce a different ciphertext for which the corresponding plaintext is unknown.
- Chosen plaintext attack (CPA): The ciphertexts for whatever plaintext the adversary chooses are assumed to be obtained by the adversary. The adversary can also choose the new input for encryption using the adaptive CPA (CPA2) based on an inspection of the plaintext queries that they have formerly chosen and their accompanying ciphertexts [31].
- Chosen ciphertext attack (CCA): The adversary is expected to be able to crack any ciphertext(s) of their choosing. In addition, the adaptive CCA (CCA2) enables the adversary to change the input they select for the decryption depending on an analysis of the queries they originally chose [32].
The prior four cryptanalysis attacks have been discussed in detail and the proposed cryptography, authentication, and digital signature securities have been mathematically proven in our previous works [10,27,28].
- Related-key attacks. The attacker creates a mathematical relationship between various keys, and after a session is established with those connected keys, the adversary is given access to the oracle function of the AGSK. The goal of this adversary is to obtain the genuine shared key from the AGSK. The permutation Pm (K, S(GSK)) is defined as the assortment of all the authenticated group shared keys S(GSKs) with the domain and keys pace K. Furthermore, let be a collection of functions that map K to the output of the associated key . The permitted to relate-key-deriving functions are denoted by the acronym RKD (i.e., allowed a key transformation). We can express the oracle of the related key RK(.) on the S(GSK), as an oracle that accepts two parameters ϕ ∈ and a message M ∈ S(GSK), and it returns Sϕ(k)(M). This can be written in pseudocode as:
- Oracle ERK(ϕ, k)(M) // where M ∈ S(GSK) and RK(ϕ,k) →K is a related function.
- ← ϕ (k); σ ← (M);
- return σ;
- the following is the definition of the pseudorandom permutation in relation to related-key attacks (PRP-RKA):
Definition 1.
Let S: K × M→ σ be an authentication function and let Φ be a set of allowed RKD functions over K (i.e., allowed a key transformation). Let adversary A query a restricted related-key oracle in the form of (ϕ, M), whereby M ∈ S(GSK). Hence, in a Φ-restricted related-key attack (RKA) on S, the PRP-RKA advantage of A is defined as:
The related-key attack model gives A the option of selecting a function that converts the attacked key K into the related-key as ← ϕ(k), which can be used to obtain the authenticated group shared key value on a chosen input using this transformed key. If the advantage is negligible, the AGSK is resistant to attacks using restricted related keys. On the other hand, if the advantage is substantial, A succeeds and the AGSK is not protected from Φ-restricted related-key attacks. Let us assume that the AGSK can be represented as , where L = is the key size in Secp192r1, which is equal to 192 bits.
Theorem 1.
Let S: {0, 1}L {0, 1}L{0, 1}L be an authentication function that defined (GSK, ,M) = E(GSK, M). Then, we can build a constrained PRP-RKA adversary B against S, as if the given S-PRP adversary A against , such that:
When A is used at most r key transformations and at most q times per transformation to query its oracle, B is executed at the same time as A and is used at most r key transformations (i.e., ϕ(k)) and at most q times per transformation to query its oracle.
Proof.
Consider B to be an adversary that runs A. When A issues an oracle query M, B issues an oracle query (ϕ, M), then, B provides the following response to A.
we gauge its effectiveness by identifying whether the authenticated group shared key or a random authenticated group shared key is used to answer its oracle questions. Since the following equality GSK k is a permutation on K, B computes exactly:
additionally, B responds to A by utilizing a randomly chosen permutation on 0 and 1 for each k in A’s queries to the authentication oracle. The key reason for this is that AGSK is a -collision resistance and it can be represented as = 0. Consequently, the following equality holds as well:
From Equations (7) and (8), Theorem 1 is proven. □
| Adversary |
| Run A, responding to A’s request (K, M), as follows: |
| Return |
| Until A halts returning a bit b; Return b; } |
4.3. Cyberattacks Analysis
The AGSK mechanism can provide important security features such as resistance to key compromise spoofing attacks and perfect forward secrecy (PFS). In order to offer PFS and prevent key compromising impersonation attacks, the AGSK generates a pseudorandom function (PRF) from the proposed combiner hash function, which can be utilized to provide a random oracle function.
4.3.1. Countermeasures against Replay and MITM Attacks
The AGSK security combines a multihash function that is used to authenticate the IIoT devices and the GSK. In addition, the authentication of AGSK prevents the replication of the GSK, which might be implemented by replay and MITM attacks. This is primarily due to the fact that the geolocation hash function is hard to reverse and the digital signature at the IIoT sender confirms the signer’s actual identity. Moreover, the replay attacker’s replication packet is rejected by the AGSK for the following reasons:
- Three steps must be taken by the replay and MITM attacker before they may resend the intercepted message, which are GSK determination, MAC calculation, and digital signature implementation, and these are very difficult to compromise without violating the hash function.
- The sender is authenticated based on the geolocation hash function, which is combined with the sender’s digital signature.
- The sender’s private key is used to compute the digital signature, and that key is safeguarded by another hash function.
4.3.2. Countermeasures against Brute Force Attacks
As the GSK is ephemeral and must change throughout each transmission session or when an IIoT device joins or leaves, the AGSK prevents the problem of the weak bit and complicates the brute force attacks. In fact, RFC8442 advises the use of an ephemeral GSK to provide crucial security features such as a PFS and key-compromise impersonation resilience. Moreover, a brute force attacker must solve the 0.886 k-step elliptic curve discrete logarithm problem (ECDLP). This shows that the security strength of the AGSK is 96, which means that a large amount of processing power is required [33].
4.3.3. Countermeasures against Device Capture and Stolen-Verifier Attacks
The dynamic join/leave method is used by the AGSK technique to defend against IIoT device capture and stolen-verifier attacks, which can be verified at the gateway using the geolocation data, MAC, and the built-in digital signature. The waste case is when an attacker captures the IIoT device during/after the GSK session establishment, meaning that the attacker can use the stolen device to gain access or implement any other attack. However, the GSK in our proposed system is ephemeral and must change every communication session or in the situation of the join/leave IIoT device. As a result, a stolen key will not function for all sessions without compromising the hash functions, which prevents the intruding party from accessing any of the secured data on the stolen IIoT device.
5. Implementation and Performance Evaluation of the AGSK on the IIoT
The IIoT platform’s security software should be assessed in context with the restricted computational, storage, and power resources available. As a result, AGSK employs the SECG/NIST-recommended Secp192r1 implementation of ECDH for secret key sharing [38]. The AGSK experiment and baseline protocols were implemented using a Mininet-IoT emulation environment [39]. Figure 4 illustrates an example of 50 IIoT devices in the mesh topology that were used to implement and evaluate the AGSK and baseline protocols. The key size that was used and recommended by Secp192r1 was 24 bytes (192 bits) and the maximum packet size was 127 bytes. A connection association was established between the IIoT device and the gateway using the 6LowPAN protocol (40 bytes of header data) [40]. The configuration and emulation parameters are listed in Table 2. Using the Mininet-IoT, two wireless models were installed to build a 6LowPAN protocol, which included 802.15.4 hwsim and 802.11 hwsim. The topology of emulation was chosen to be a grid with two dimensions 1000 × 900 m, and 5–50 IIoT devices were randomly distributed in the topology for each experiment. To examine the effectiveness of the AGSK, the running time of every experiment was set to 1000 s.
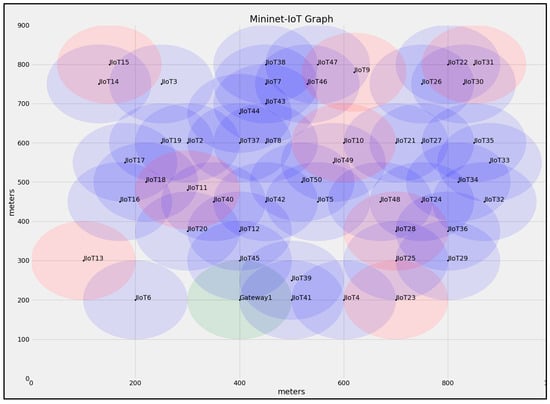
Figure 4.
An example of 50 IIoT devices in mesh topology.

Table 2.
Experiment configuration.
5.1. Comparison between AGSK and Baseline Mechanisms
The performance evaluation of the AGSK has been evaluated and compared to the baseline mechanisms in terms of CPU computation time, power consumption, and storage costs. Three baseline mechanisms were inspected which are the SGSK [10], GKA-SS [12], and NM-CHH-GKA [11]. All experiments investigated only the performance of the group key sharing without authentication and digital signature for the AGSK and baseline mechanisms. The source code for the Mininet-IoT emulator was written entirely in Python. Each testbed was repeated 10 times, while 1000 packets were exchanged between each testbed, and numerous scenarios were simulated. Finally, the confidence interval based on the average results was 95%, which means the standard deviation error was 5%. Moreover, deterministic cost profiling of the AGSK and the standard procedures was offered in the cProfile and memory profiler applications. The memory profiler application was used to estimate the computation time, memory usage, and power consumption. The number of steps per computation (s/e) and the CPU computation time for each step were multiplied to estimate the total cost of the CPU computation time. Moreover, the storage cost for each IIoT device was determined using the entire cost of the communication (packets sent or received), sensed data, and the implementation cost for each time unit. Moreover, the total energy used by each packet overhead required to run the source code was included in the predicted overall energy usage (mJ) for the IoT devices.
5.1.1. Performance Evaluation of the Group Shared Key
Figure 5 shows the performance results of AGSK and the baseline mechanisms. As illustrated in Figure 5a, the AGSK experiences, on average, 29.89% lower computation time costs compared to GKA-SS, 36.5% lower computation time compared to NM-CHH-GKA, and 41.3% lower computation time compared to SGSK. Additionally, Figure 5b depicts the storage cost for AGSK and baseline mechanisms. In this figure, AGSK experiences, on average, 24% lower storage costs compared to GKA-SS, 45.7% lower storage costs compared to NM-CHH-GKA, and 8.45% lower storage costs compared to SGSK. Furthermore, Figure 5c demonstrates the power consumption costs for AGSK and baseline mechanisms. In this figure, AGSK, on average, costs 25% less in power consumption compared to GKA-SS, 40% less compared to NM-CHH-GKA, and 6.3% less compared to SGSK.
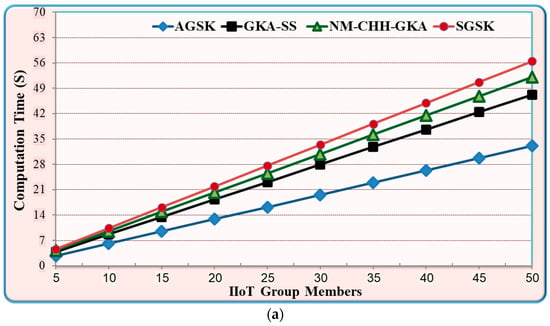
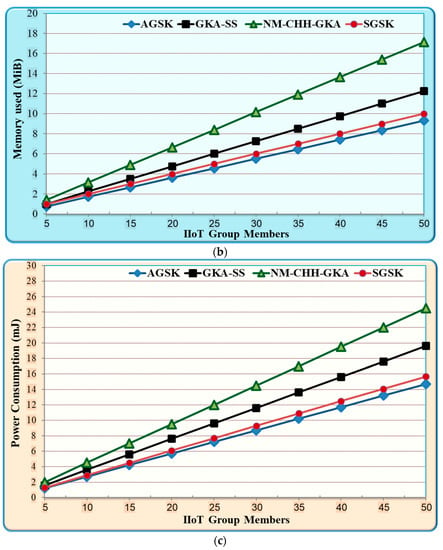
Figure 5.
Performance comparison between AGSK and baseline algorithms on IIoT (a) computation time; (b) memory cost; (c) power consumption.
- Results and Discussion
The results that are shown in Figure 5 demonstrate the performance advantage of the AGSK mechanism, which is primarily attained due to the following reasons: Firstly, AGSK uses two steps of incest, which are the public key of the IIoT device to the gateway unicast and the PGP gateway unicast to each IIoT device. In contrast, GKA-SS and NM-CHH-GKA used four steps of sending, which are three steps of broadcasting the public key and the shared key, and one step of the unicast from the gateway to each IIoT device. The reduction in the exchange of shared keys in the proposed AGSK algorithm provided fewer security risks and achieved high QoS performance. Secondly, SGSK used an extremely slow mechanism due to the token ring topology of the group-shared creation. For instance, if the group size is 1000 and each IIoT device needs 0.5 s to process the group shared key, this means that the final group shared key requires 500 s to be created. In contrast, the AGSK used a star topology and simultaneously group shared calculation, which decreased the computation time of the GSK calculation. Finally, GKA-SS and NM-CHH-GKA consumed more resources in terms of memory usage and power consumption. This was mainly due to the three times messages broadcasting between the group members and the gateway. In contrast, AGSK used two steps of unicast messages between the group members and the gateway.
5.1.2. Performance Evaluation of Join/Leave Members
Figure 6 shows the join/leave performance results of the AGSK and the baseline mechanisms. As illustrated in Figure 6a, AGSK experiences, on average, 28.6% less computation time costs compared to GKA-SS, 16.7% lower compared to NM-CHH-GKA, and 44.4% lower compared to SGSK. Furthermore, Figure 6b illustrates the storage costs for AGSK and baseline mechanisms. In this figure, AGSK experiences, on average, a reduction of 31% in storage costs compared to GKA-SS, 40% less compared to NM-CHH-GKA, and 55% less compared to SGSK. Moreover, Figure 6c depicts the power consumption costs for the AGSK and baseline mechanisms. In this figure, AGSK consumes, on average, 23.1% less power compared to GKA-SS, 33.3% less compared to NM-CHH-GKA, and 38% fewer power costs compared to SGSK.
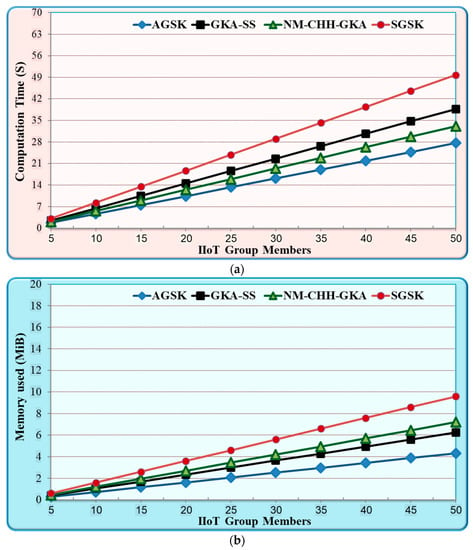
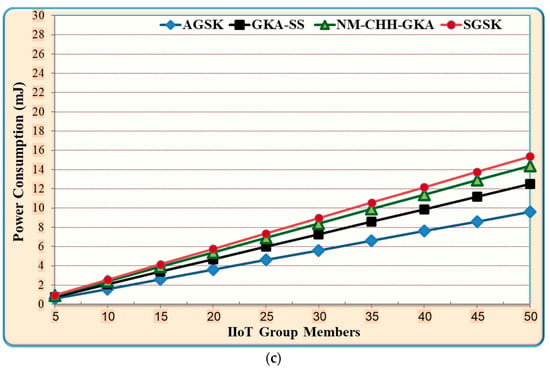
Figure 6.
Comparison between dynamic join/leave in AGSK and the baseline algorithms for the IIoT (a) computation time; (b) memory cost; (c) power consumption.
- Results and Discussion
The results shown in Figure 5 demonstrate the join/leave performance advantages of the AGSK mechanism, which are mostly attained due to the following reasons: Firstly, if some nodes join/leave the group, the gateway in the AGSK calculates the new PGP based on the remaining public keys. Afterward, the gateway will unicast the new PGP only to the involved IIoT devices. In contrast, GKA-SS and NM-CHH-GKA need to broadcast the updated message to each new member, which increases the computation time, memory cost, and power consumption. Secondly, if the join/leave nodes in the SGSK are in the beginning of the token ring, the process of the group shared key calculation needs to restart from scratch, which again increases the computation time, memory cost, and power consumption. Finally, GKA-SS and NM-CHH-GKA consume more resources in any dynamic join/leave operation. This is mainly due to the messages broadcasting between group members and the gateway. In contrast, AGSK used two steps of unicast messages between the group members and the gateway.
6. Conclusions and Future Work
This research proposed an authenticated group shared key (AGSK) algorithm over the IIoT system, to utilize a combiner for the geolocation hash function and the digital signature of each IIoT device. The security of the proposed system was proven mathematically using the random oracle model and the cybersecurity analysis for the IIoT and was explained in terms of an adversary model, and countermeasure cyberattacks. In addition, the proposed system presents the optimized dynamic join/leave algorithm, in terms of communication, storage, and computation costs, compared to the baseline group key management. The implementation of the proposed system showed that an AGSK outperformed the baseline group key management, in terms of 41.3% less CPU computation time, 45.7% less storage costs, and 40% less power consumption. The future work on this research will concentrate on proposing an efficacious digital signature and authentication system that can securely identify the true identity of legitimate IIoT devices in any IIoT environment.
Author Contributions
Conceptualization, A.A.A.; methodology, A.A.A.; software, A.A.A.; validation, A.A.A. and W.A.; formal analysis, A.A.A.; investigation, A.A.A. and W.A.; resources, W.A.; data curation, A.A.A.; writing—original draft preparation, A.A.A.; writing—review and editing, A.A.A.; visualization, W.A.; supervision, A.A.A.; project administration, W.A.; funding acquisition, W.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University (KAU), Jeddah, Saudi Arabia, grant number G-42-830-1443 and the APC was funded by G:042-830-1443.
Data Availability Statement
Not applicable.
Acknowledgments
The Deanship of Scientific Research (DSR) at King Abdulaziz University (KAU), Jeddah, Saudi Arabia has funded this Project under grant no. (G:042-830-1443).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Szymoniak, S.; Kesar, S. Key Agreement and Authentication Protocols in the Internet of Things: A Survey. Appl. Sci. 2023, 13, 404. [Google Scholar] [CrossRef]
- Sarker, I.H.; Khan, A.I.; Abushark, Y.B.; Alsolami, F. Internet of Things (IoT) Security Intelligence: A Comprehensive Overview, Machine Learning Solutions and Research Directions. Mob. Netw. Appl. 2022, 27, 1–17. [Google Scholar] [CrossRef]
- Choo, K.-K.R.; Gritzalis, S.; Park, J.H. Cryptographic Solutions for Industrial Internet-of-Things: Research Challenges and Opportunities. IEEE Trans. Ind. Inform. 2018, 14, 3567–3569. [Google Scholar] [CrossRef]
- He, D.; Ma, M.; Zeadally, S.; Kumar, N.; Liang, K. Certificateless Public Key Authenticated Encryption with Keyword Search for Industrial Internet of Things. IEEE Trans. Ind. Inform. 2018, 14, 3618–3627. [Google Scholar] [CrossRef]
- Kittur, A.S.; Pais, A.R. A trust model based batch verification of digital signatures in IoT. J. Ambient. Intell. Humaniz. Comput. 2019, 11, 313–327. [Google Scholar] [CrossRef]
- Li, S.; Zhang, T.; Yu, B.; He, K. A Provably Secure and Practical PUF-Based End-to-End Mutual Authentication and Key Exchange Protocol for IoT. IEEE Sens. J. 2021, 21, 5487–5501. [Google Scholar] [CrossRef]
- Khatoon, S.; Rahman, S.M.M.; Tso, R.; Alhamid, M.F. An efficient and secure, ID-based authenticated, asymmetric group key agreement protocol for ubiquitous pay-TV networks. J. Internet. Technol. 2020, 21, 1387–1395. [Google Scholar]
- Diro, A.A.; Chilamkurti, N.; Kumar, N. Lightweight Cybersecurity Schemes Using Elliptic Curve Cryptography in Publish-Subscribe fog Computing. Mob. Netw. Appl. 2017, 22, 848–858. [Google Scholar] [CrossRef]
- Bu, L.; Isakov, M.; Kinsy, M.A. A secure and robust scheme for sharing confidential information in IoT systems. Ad. Hoc. Netw. 2019, 92, 101762. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Barukab, O.M. Unforgeable Digital Signature Integrated into Lightweight Encryption Based on Effective ECDH for Cybersecurity Mechanism in Internet of Things. Processes 2022, 10, 2631. [Google Scholar] [CrossRef]
- Naresh, V.S.; Reddi, S.; Murthy, N.V. A provably secure cluster-based hybrid hierarchical group key agreement for large wireless ad hoc networks. Hum. Cent. Comput. Inf. Sci. 2019, 9, 26. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Z.; Qiu, F.; Li, F. A group key agreement protocol based on ecdh and short signature. J. Inf. Secur. Appl. 2023, 72, 103388. [Google Scholar] [CrossRef]
- Lo, J.W.; Wu, C.Y.; Chiou, S.F. A lightweight authentication and key agreement scheme for telecare medicine information system. J. Internet. Technol. 2020, 21, 263–272. [Google Scholar]
- Janani, V.S.; Manikandan, M.S. Enhanced security using cluster based certificate management and ECC-CRT key agreement schemes in mobile ad hoc networks. Wirel. Pers. Commun. 2017, 97, 6131–6150. [Google Scholar] [CrossRef]
- Jiang, Y.; Shen, Y.; Zhu, Q. A lightweight key agreement protocol based on Chinese remainder theorem and ECDH for smart homes. Sensors 2020, 20, 1357. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Y.; Zhang, J.; Yang, Q. A secure and efficient group key agreement scheme for VANET. Sensors 2019, 19, 482. [Google Scholar] [CrossRef]
- Rawat, A.; Deshmukh, M. Tree and elliptic curve based efficient and secure group key agreement protocol. J. Inform. Secur. Appl. 2020, 55, 102599. [Google Scholar] [CrossRef]
- Wang, Y.; Ramamurthy, B.; Zou, X. The performance of elliptic curve based group Diffie–Hellman protocols for secure group communication over ad hoc networks. In Proceedings of the 2006 IEEE International Conference on Communications, Istanbul, Turkey, 11–15 June 2006; pp. 2243–2248. [Google Scholar]
- Zhang, Q.; Zhu, L.; Li, Y.; Ma, Z.; Yuan, J.; Zheng, J.; Ai, S. A group key agreement protocol for intelligent internet of things system. Int. J. Intell. Syst. 2022, 37, 699–722. [Google Scholar] [CrossRef]
- Naresh, V.S.; Allavarpu, V.V.L.D.; Reddi, S.; Murty, P.S.R.; Raju, N.V.S.L.; Mohan, R.N.V.J. A provably secure sharding based blockchain smart contract centric hierarchical group key agreement for large wireless ad-hoc networks. Concurr. Comput. Pract. Exper. 2022, 34, e6553. [Google Scholar] [CrossRef]
- Li, X.; Yin, X. Blockchain-based group key agreement protocol for vehicular ad hoc networks. Comput. Commun. 2022, 183, 107–120. [Google Scholar] [CrossRef]
- Wu, Y.; Feng, T. An Anonymous Authentication and Key Update Mechanism for IoT Devices Based on EnOcean Protocol. Sensors 2022, 22, 6713. [Google Scholar] [CrossRef] [PubMed]
- Songshen, H.A.N.; Kaiyong, X.U.; Zhiqiang, Z.H.U.; Songhui, G.U.O.; Haidong, L.I.U.; Zuohui, L.I. Hash-Based Signature for Flexibility Authentication of IoT Devices. Wuhan Univ. J. Nat. Sci. 2022, 27, 1–10. [Google Scholar]
- Zhang, F.; Wang, H.; Zhou, L.; Xu, D.; Liu, L. A blockchain-based security and trust mechanism for AI-enabled IIoT systems. Future Gener. Comput. Syst. 2023, 147, 78–85. [Google Scholar] [CrossRef]
- Uppuluri, S.; Lakshmeeswari, G. Secure user authentication and key agreement scheme for IoT device access control based smart home communications. Wirel. Netw. 2023, 29, 1333–1354. [Google Scholar] [CrossRef]
- Rahman, H.; Haghighat, A.; Hossein, E.S. A Secure Anonymous D2D Mutual Authentication and Key Agreement Protocol for IoT. Internet Things 2022, 18, 100493. [Google Scholar]
- Ahmed, A.A.; Ahmed, W.A. An Effective Multifactor Authentication Mechanism Based on Combiners of Hash Function over Internet of Things. Sensors 2019, 19, 3663. [Google Scholar] [CrossRef]
- Ahmed, A.A. Lightweight Digital Certificate Management and Efficacious Symmetric Cryptographic Mechanism over Industrial Internet of Things. Sensors 2021, 21, 2810. [Google Scholar] [CrossRef]
- Gong, X.; Feng, T. Lightweight Anonymous Authentication and Key Agreement Protocol Based on CoAP of Internet of Things. Sensors 2022, 22, 7191. [Google Scholar] [CrossRef]
- Saleem, K.; Khalil, M.S.; Fisal, N.; Ahmed, A.A.; Orgun, M.A. Efficient random key based encryption system for data packet confidentiality in WSNs. In Proceedings of the 2013 12th IEEE International Conference on Trust, Security and Privacy in Computing and Communications, Melbourne, VIC, Australia, 16–18 July 2013; pp. 1662–1668. [Google Scholar]
- Biryukov, A. Adaptive Chosen Plaintext Attack. In Encyclopedia of Cryptography and Security; Van Tilborg, H.C.A., Jajodia, S., Eds.; Springer: Boston, MA, USA, 2011. [Google Scholar]
- Biryukov, A. Related Key Attack. In Encyclopedia of Cryptography and Security; Van Tilborg, H.C.A., Jajodia, S., Eds.; Springer: Boston, MA, USA, 2011. [Google Scholar]
- Silverma, J.H. An Introduction to the Theory of Elliptic Curves, Summer School on Computational Number Theory and Applications to Cryptography; Brown University: Providence, RI, USA, 2006. [Google Scholar]
- Vidya, R.; Prema, K.V. Lightweight hashing method for user authentication in Internet-of-Things. Ad. Hoc. Netw. 2019, 89, 97–106. [Google Scholar]
- Chuang, Y.-H.; Lo, N.-W.; Yang, C.-Y.; Tang, S.-W. A Lightweight Continuous Authentication Protocol for the Internet of Things. Sensors 2018, 18, 1104. [Google Scholar] [CrossRef]
- Riad, K.; Huang, T.; Ke, L. A dynamic and hierarchical access control for IoT in multi-authority cloud storage. J. Netw. Comput. Appl. 2020, 160, 102633. [Google Scholar] [CrossRef]
- Alamer, A. An efficient group signcryption scheme supporting batch verification for securing transmitted data in the Internet of Things. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 1–18. [Google Scholar] [CrossRef]
- Lochter, M.; Merkle, J. RFC 5639: Elliptic Curve Cryptography (ECC) Brainpool Standard Curves and Curve Generation; IETF: Fremont, CA, USA, 2010. [Google Scholar]
- Mininet-IoT Emulator of Internet of Things. Available online: https://github.com/ramonfontes/mininet-iot (accessed on 27 November 2022).
- IPv6 over Low-Power Wireless Personal Area Networks (6LoWPANs): Overview, Assumptions, Problem Statement, and Goals. Available online: http://www.ietf.org/rfc/rfc4919.txt (accessed on 27 November 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).