Abstract
Containers are used by an increasing number of Internet service providers to deploy their applications in multi-access edge computing (MEC) systems. Although container-based virtualization technologies significantly increase application availability, they may suffer expensive communication overhead and resource use imbalances. However, so far there has been a scarcity of studies to conquer these difficulties. In this paper, we design a workflow-based mathematical model for applications built upon interdependent multitasking composition, formulate a multi-objective combinatorial optimization problem composed of two subproblems—graph partitioning and multi-choice vector bin packing, and propose several joint task-containerization-and -container-placement methods to reduce communication overhead and balance multi-type computing resource utilization. The performance superiority of the proposed algorithms is demonstrated by comparison with the state-of-the-art task and container scheduling schemes.
1. Introduction
The container technique has been increasingly adopted in operating system virtualization by cloud computing and edge computing due to its high convenience and flexibility in deploying diverse applications [1]. The lightweight, scalable, and well-isolated environment provided by containers greatly increases the applications’ portability and availability [2], but at the cost of excessive communication overhead and resource utilization imbalance. Therefore, reducing communication overhead and balancing the usage of multi-type computing resources are critical design challenges for container-based multi-access edge computing (MEC).
Zhang et al. [3] studied the joint task scheduling and containerization in an edge computing system, where the tasks associated with a given application were first scheduled into processors deployed on an edge server, then an appropriate algorithm was invoked to determine the containerization scheme. As a result, multiple containers, each representing a standard unit of software for packaging code and all related dependencies, were created for executing different tasks on individual processors, while considering the time cost of inter-container communications. Workflow is a common model for describing microservice-based application’s tasks executed in containers. Bao et al. [4] presented a microservice-based workflow scheduling algorithm for minimizing the end-to-end delay of a given single application consisting of multiple microservices under a pre-specified budget constraint in a cloud, where the inter-container communication latency was considered a component of the end-to-end delay. A dual-line container placement algorithm was proposed in [5] to decide the container placement positions in a container cluster while being aware of the inter-container communication traffic. We note that all of the above contributions concentrated on reducing communication overhead while ignoring computing resource utilization problems. Naturally, allocating the containers of the same application into the same server is beneficial for reducing the cost of inter-container communications. However, this will cause serious resource utilization imbalance, since the same type of computing resource is usually used intensively by different containers of the same application, e.g., a CPU-intensive application [6]. Hence, without a proper resource-utilization balanced container scheduler, the particular server may suffer exponentially increasing response latency [7], and the total throughput of the system may be significantly reduced.
Therefore, it is important to also consider the balanced use of computing resources when designing scheduling algorithms. Since each task has a different computing resource requirement, Li et al. [8] considered the problem of scheduling microservice tasks of workflow applications to containers configured on on-demand virtual machines (VMs) and suggested a heuristic task scheduling algorithm for guaranteeing that the precedence-constrained or independent tasks are scheduled to available containers. As a benefit, the computing resources were more efficiently utilized. Ye et al. [9] explored the stochastic hybrid workflow scheduling problem to keep the cost of computing resources to the minimum, by jointly scheduling offline and online workflows. Although these contributions considerably improve the utilization efficiency of computing resources, they impose high communication overhead, because the containers of the same application have to exchange control messages and payload data. Therefore, the effectiveness of communications among containers has a significant impact on how well services are provided.
How to keep computing resource utilization balanced while reducing inter-container communication costs remains a grave challenge. In order to reduce the total inter-container communication traffic and increase the utilization efficiency of computing resources, Wu et al. [10] proposed a container placement strategy for containerized data centers, by exploiting the inter-container communication traffic pattern that obeys a Zipf-like distribution. They assumed that the major communication traffic originates from the containers that intensively communicate with each other. Each group of such containers is treated as an individual container block, which can be deployed either on the same server or on different servers, and the authors further assumed that the communication traffic between container blocks is negligible. Unfortunately, this assumption is unreasonable in the context of collaborative MEC servers. In [11], the computing resource requirements of containers are represented by a flow network, and container scheduling is formulated as a minimum-cost flow problem. To properly prioritize the execution of containers subject to a batch of concurrent requests, the proposed approach of [11] considered the average life cycle of containers as well as the affinity between the containers and the servers. Their solution took container affinity into account and placed containers with affinity on the same server. However, it is improper for scheduling container clusters with high dependencies. Lv et al. [6] studied container placement and container reassignment strategies to balance resource use in large-scale Internet data centers, where the initial container distribution is optimized further by reassigning containers among servers. However, as far as a large number of distributed MEC servers are concerned, migrating containers among these servers may incur significant communication overhead.
Furthermore, the widely used container orchestration platforms, such as Docker, only provide simple rule-based scheduling principles. Therefore, there has been a scarcity of efforts that focus on container scheduling algorithms capable of jointly reducing the communication overhead and balancing the computing resource usage in MEC.
Against the above backdrop, in this paper, our novel contributions are summarized as follows.
- We propose a task containerization and container placement optimization framework for applications running on MEC servers from a joint communication and computing perspective. The proposed framework comprises two modules. The task containerization module jointly considers low inter-container communication overhead and balanced multi-type computing resource requirements of containers. The container placement module places instantiated containers to the appropriate MEC servers by considering the balanced usage of the multi-type computing resources on MEC servers. The proposed framework is capable of achieving both low communication overhead and balanced computing resource requirement among containers, as well as balanced computing resource utilization among servers. To the best of our knowledge, our work is the first to investigate the impact of task partitioning, task containerization, and container placement on inter-container communication overhead and resource utilization balancing.
- We offer a workflow modeling method for highly interdependent tasks of an application and propose a mathematical model of the workflow to reflect the interactions among the tasks, the communication overhead, and the computing resources needed by each task. Based on the workflow model of tasks, we present a method for calculating the communication overhead and the utilization efficiency deviation of multi-type computing resources in the MEC-based computing network considered. The proposed model and methods are directly applicable to various workflow-based cloud computing and edge computing platforms.
- We evaluate the proposed task-containerization -and-container-placement algorithms in multiple aspects through extensive experiments, and compare them with state-of-the-art methods. Our experiments show that the proposed methods are capable of reducing the communication overhead by up to 74.10%, decreasing the normalized maximum load by up to 60.24%, improving the CPU utilization efficiency by up to 30.66%, and improving the memory utilization efficiency by up to 40.77% under the considered system configurations.
The rest of this paper is organized as follows. In Section 2, we present the MEC system model. In Section 3, we formulate the problem of jointly reducing the communication overhead and improving the degree of balance for multi-type computing resource utilization, which is solved by the algorithms proposed in Section 4, where the original problem is divided into two subproblems, namely the task containerization problem that is formulated as a graph partitioning problem [12], and the container placement optimization problem that is formulated as a multi-choice vector bin packing problem [13], which is a generalization of the classic vector bin packing problem. In Section 5, the proposed algorithms are compared with state-of-the-art methods by extensive simulations, and our conclusions are drawn in Section 6.
2. System Model
As shown in Figure 1, we consider the use case where Internet service providers set up and execute delay-sensitive applications in a computing network composed of multiple MEC servers. The MEC servers are deployed at the edge of a mobile network and connected to base stations (BSs). The user terminals (UTs) can access diverse delay-sensitive computing-intensive services, such as cloud gaming and cloud virtual reality (VR), provided by the MEC-based computing network through BSs. All the MEC servers are distributively connected to each other by optic fibers, so that their computing power can be shared via cooperation.
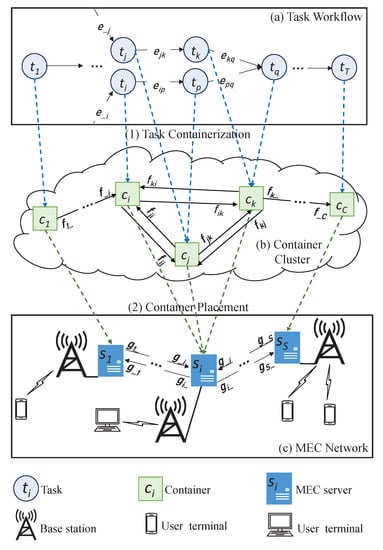
Figure 1.
A system model for user terminals to access an MEC-based computing network.
The MEC servers are represented by , where is the number of servers. In the entire MEC service process, computing resources , such as CPU, memory and disk storage, are involved, where is the number of resource types. For server , let denote the capacity of resource . We consider an application composed of multiple interdependent tasks , and the number of tasks is . Let the matrix represent dependencies between tasks, and we have
The tasks are allocated to the container cluster , which comprises containers. For container , denotes the demand for resource . For each task , let vector represent the individual volumes of various resources required by task . Note that in order to eliminate the difficulties encountered in evaluating the usage of heterogeneous resources, in this paper the volume of a specific type of resource required is normalized as the ratio of this partial volume to the total volume of the available resources of the same type across all the servers considered. The matrix represents the tasks deployment, where we have
The resource demanded by the container is the sum of the resources required by the tasks assigned to , namely
Let the matrix denote the container placement strategy, as expressed by
3. Problem Formulation
3.1. Communication Overhead
We consider the communication overhead incurred by the communications between containers within an MEC-based computing network. Typically, the life cycle of a task includes three stages: receiving data, running algorithms, and sending output data. For example, task first receives the data and stores it in memory, then it runs algorithms upon obtaining all the input information it needs. Finally, when the execution is finished, task sends the output data to related tasks, which takes a transmission time of . This is also the communication time between containers, once the tasks are assigned to containers.
Let denote the container dependency matrix. Upon assuming that the communication time between tasks assigned to the same container is negligible, the element of can be expressed as:
Similarly, we formulate the server dependency matrix as , where we have
Upon assuming that the packet size and the number of packets required in each occurrence of communication remain constant, the communication overhead in the MEC-based computing network can be modeled as the ratio of the time spent in sending data between servers to the total communication time, namely
Computing Resource Utilization Balance
The efficiency of servers is often degraded by the unbalanced use of the various computing resources deployed on the servers. The resource used by all the containers residing in the server is quantified by
Since the total available resource on the server is . Then, represents the utilization efficiency of resource on server . Typically, if a server’s consumption of different types of computing resources is relatively balanced, the server is able to host more containers and more applications. Then, the balance degree of multi-type computing resource utilization on server is given by
where is the mean utilization efficiency of all resources on server .
This metric reflects the deviation of the utilization efficiency of all resource types on a server from the average resource utilization efficiency. The total resource balance degree of the MEC-based computing network is the sum of the resource balance degree of all servers, and it is defined as
Therefore, the joint optimization of the communication overhead and the degree of resource utilization balance is formulated as a weighted-sum minimization problem of
In the above optimization problem, , , , , , , , and are all constants known a priori. Here, indicates that the transmission time of each task is non-negative; indicates that each task has a non-negative demand for each type of resource; while and specify the value range of the weights corresponding to each of the component objectives. (11b) and (11c) indicate that the optimization variables are matrices composed of binary-value elements. Equations (11d) and (11e) imply that each given task and given container have to be allocated to a single container and a single server, respectively. Furthermore, (11f) represents that the resource used by all the containers residing in the server must not exceed the capacity of the resource on the server .
It is worth noting that reducing communication overhead may lead to putting more tasks into fewer containers and packing as many containers as possible into fewer servers. However, this may result in a lower utilization efficiency of computing resources in the servers. In other words, there is a trade-off between the communication overhead and the computing resource utilization efficiency . We attempt to balance and rather than cram as many items as possible in a container or a server.
The problem is essentially a multi-objective combinatorial optimization problem involving two subproblems, namely graph partitioning [12] that is corresponding to task containerization and multi-choice vector bin packing [13] that is corresponding to container placement, as shown in Figure 1. Both of them are known NP-hard problems. Hence, the existence of any polynomial time optimal solution is ruled out unless . Furthermore, as mentioned before, the component objectives and may conflict with each other, and both of them rely on the optimization variables and . Theoretically, the optimal solution to can be found by brute-force search. However, in practice, there may be a large number of tasks, containers, and servers to deal with. Hence, the computational complexity of obtaining the optimal solution to the joint optimization problem is prohibitive. Alternatively, it is possible to solve more efficiently by using an iterative method, where at each iteration, the objective of is minimized with respect to one of the two matrix variables and while the other matrix variable is held fixed. Nevertheless, the deployment of this strategy may require a dedicated centralized computing server to run the scheduling algorithms and is not naturally aligned with the physically sequential processes of an MEC-based computing network, where the task containerization takes place first and is then followed by container placement. In other words, in practice, it is meaningful to first obtain and then obtain relying on the result of .
With this in mind, we turn our attention to a degenerate version of so that the reformulated problem is more naturally matched to the practical sequential process of deploying an application to servers. As a result, a non-iterative sequential strategy can be invoked, which is expected to find good solutions capable of optimizing both the inter-container communication overhead and the degree of resource utilization balance at the expense of lower computational complexity. More specifically, the goal of task containerization is to minimize the weighted-sum of the inter-container communication overhead and the average deviation of multi-type resource demands by each container. Thus, we have
where represents the average value of all containers’ demand for resource . As pointed out before, dividing tasks into groups and putting each group of tasks into a container can essentially be formulated as a graph partitioning problem [12]. Different from the traditional treatment of graph partitioning problems, in this paper we not only take into account the weights of edges, which represent the communication overhead but also consider the weights of vertices, which represent the resource requirements of a particular task.
Furthermore, we simplify the container placement problem without considering the communication overhead caused by inter-container communications and the communication time between servers in the objective function. This is because the servers’ geographic locations have a significant impact on the communication overhead between servers and it can be difficult to ascertain the servers’ locations. After the task containerization module obtains , the container placement module is intended to minimize the deviation of the utilization efficiency of various computing resources on the MEC servers, hence the container placement problem is formulated as:
The container placement problem is similar to the multi-choice vector bin packing problem [13]. In contrast to the traditional multidimensional vector bin packing problem, we have a set number of servers and a range of resource capacities for each server. The components of our vector set come from the containers obtained during the task containerization stage. Container values are not 0 or 1, but rather a vector of distinct forms of resource requirements as containers have different types of computing resource requirements. Our objective is more complicated—instead of minimizing the number of servers, placing containers into MEC servers requires matching the resources the containers need with what the servers can provide.
On the basis of making references to classic problems, it is vital to create solutions that are more fitting for our objectives. The fourth chapter will provide detailed explanations of the specific approach.
4. Task Containerization and Container Placement Schemes
As shown in Figure 1, the entire process of performing edge computing in an MEC-based computing network can be sequentially divided into two stages: first allocating tasks to containers, and then placing containers onto servers. To find a high-accuracy approximate solution to the problem (11), we can consider the task containerization and the container placement sequentially.
4.1. Task Containerization Method
A task containerization method is invoked to allocate tasks to containers. First of all, it is necessary to balance all types of resources needed by each container for achieving an equalized consumption of resources on each server. To this end, it is preferable to avoid grouping tasks that have a high demand for the same type of resource together. On the other hand, it is recommended to put tasks that have a large amount of data transmitted between each other into the same container and then place the containers having frequent communications with each other on the same server, in order to reduce the communication overhead.
We use workflow to describe the relationship between different tasks of an application. Workflow is an important concept for describing cloud computing and edge computing applications. It consists of multiple interdependent tasks which are bound together through data or functional dependencies. As shown in Figure 2, an application can be built as a workflow, where each task implements certain functionality and collaborates with the others. In Figure 2 the workflow is modelled, as a directed acyclic graph (DAG) . Each vertex represents a task, and the weight vector of vertex is , which represents various resources required by . The adjacency matrix of the DAG is and its elements are defined by (1), where the weights of edges are not considered. The number of edges is denoted as E, i.e., , which equals the number of nonzero elements in . Furthermore, let denote the weight of and it represents the length of communication time from task i to task j. Then, the elements of are updated as .
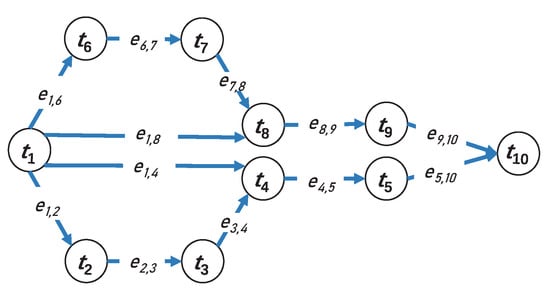
Figure 2.
An example of DAG workflow with ten tasks.
For a cluster of vertices , let denote the set of edges with all vertices in , and let represent the collection of edges connecting the two disjoint vertex sets of the graph cut . Furthermore, define a vertex set as multiple disjoint vertex sets whose union is , i.e., we have and , , . Furthermore, we denote with the demand of resource by the subset .
It has been established that the graph partitioning problem is NP-hard. For finding approximate solutions to the graph partitioning problem considered more efficiently, we propose two heuristic algorithms in this paper, i.e., the partitioning with non-critical path based initialization (P-NCPI) and the partitioning with random initialization (P-RI). The major operations of the proposed partitioning algorithms include determining the number of disjoint vertex sets, assigning one vertex to each of the disjoint vertex sets in the initial partition, and setting a scoring function for the remaining vertices. Both vertex weights and edge weights are taken into account in the scoring function, and each vertex is exclusively assigned to one of the disjoint vertex sets based on its score. Typically, these operations can be implemented in an appropriate container orchestration software, such as Kubernetes or KubeEdge. This process guarantees that the vertices are partitioned so that the edge weights between the disjoint vertex sets are minimal and that the vertex weights within the disjoint vertex sets are not excessive.
The NCPI and RI algorithms employed in our initial partition are described as follows.
- NCPI: Tasks are sorted topologically, and the critical path is chosen as the one with the highest weight. The tasks that comprise the critical path are known as essential tasks, and they determine the minimum completion time of an application. Due to the high communication overhead between essential tasks, we first select the required number of non-essential tasks and then assign each non-essential task to a different disjoint vertex set as an initial partition to reduce communication overhead between sets.
- RI: Selecting the desired tasks randomly according to the number of disjoint vertex sets and assigning each of them to a different disjoint vertex set as an initial partition.
To more conveniently describe the process of grouping the remaining vertices, we consider an alternative objective function with two components: the cost of inter-partition edge weights and the cost of intra-partition vertex weights . For each given set of vertices and a specific resource , this objective function is defined as:
where represents the sum of weights corresponding to the edges contained in the set , and we have
with representing an increasing convex function of the vertex weights in set , and being a linear function for balancing the cost of vertex weights across different sets , .
It should be noted that the optimization variable in the objective function (12a) is , while that in (14) is . Both and represent the mapping of tasks to containers, and both the expression in (12a) and the expression in (14) characterize the communication time between containers. However, the differences are: (1) in (12a) is further normalized by dividing the total communication time of all the tasks, while is a direct summation of , ; (2) in (12a) is the average deviation of multi-type resource demands by each container, while in (14) is the total demand for computing resources by all the containers. Obviously, when the demands for multi-type computing resources by the individual containers are equal, the average deviation of multi-type resource demands by each container reaches the minimum. Therefore, (12a) and (14) can be seen as different mathematical models for describing the same objective. Compared with (12a), Equation (14) directly expresses the communication time and computing resource requirements as specific analytical expressions of the variables , , thus making it more convenient to derive the solution algorithm from the graph partitioning perspective.
According to Equation (14), the task containerization method can be derived by solving the following optimization problem:
For the convex function , based on [12], we select the family of functions , where and . The parameter controls the balance degree of vertex weights between partitioned sets. The greater the value of , the greater the cost of imbalanced set weights. means that the imbalance between the demand of resource by the set , i.e., , is ignored. We choose to serve as a proper scaling factor. The optimization problem is then written as:
Furthermore, we define a function h as:
Therefore, the problem of minimizing can be solved by maximizing . For any , if , vertex t is assigned to vertex set . Based on this condition, we define a difference function
and assign vertex t to vertex set when we have . Let denote the neighbors of vertex t (i.e., the vertices directly connected to vertex t). According to Equation (19), the difference function is rewritten as:
The details of the proposed task containerization method are shown in Algorithm 1. First, tasks are selected by the RI or NCPI algorithm for initial partitioning (Lines 2–35 of Algorithm 1). Once the initial partitioning has been determined, the remaining tasks are partitioned using the scores derived from the above calculations (Lines 36–47 of Algorithm 1), thus ensuring that the communication cost and the multi-type computing resource balancing cost are minimized during the task containerization stage.
In order to measure whether the resources required for each vertex set are balanced, we define the measurement parameter as the normalized maximum load:
The balance degree of the usage of multi-type computing resources improves as approaches 1.
4.2. Container Placement Method
When tasks are divided into multiple vertex sets, each set is a container, and the resources are available to each container. We conduct a comparative study of container placement methods by using the dot product (DP) algorithm [14] and the first fit decreasing (FFD) algorithm [14] to individually solve the problem .
DP considers the demands of multi-type computing resources by each container as well as the capacities of multi-type resources on each server. Any server is listed as a candidate server for a container if it has enough multi-type resources to accommodate the container. For each container and one of its candidate servers , the dot product of multi-type resources required by the container and multi-type resources that the server can provide is denoted as . The larger the value of , the more resources server is able to supply to container . To improve computing resource utilization, we tend to place the container on the server that has the greatest amount of resources, hence we use as the matching degree between demand and supply, and for servers that are not candidates, we set the matching degree as 0. Thus we have
The procedure of the DP algorithm is shown in Algorithm 2.
FFD is a greedy algorithm in which the containers are sorted in decreasing order according to their individual weight that is determined by each container’s demands for multi-type resources, and then containers are placed sequentially in the first server that has sufficient capacity to accommodate them. As the resources required by each container are multidimensional (i.e., multi-type), the definition of dimensions and the associated weight assigned to the vector of resources required by an individual container determine the order in which the containers are placed. Containers have different resource requirements and there are multiple alternative methods for selecting an appropriate weight for each container. For example, one can calculate the weighted sum of multi-type resources required by the container as the basis for the decreasing ordering. In particular, when the weights are equal, containers are decreasingly ordered by evaluating , . Additionally, if the demands of a particular type of resource always dominate the demands of the other types of resources, one can only consider the dominant type of resource to determine the weights of containers and the decreasing order. Then, upon traversing the servers, the containers are sequentially placed on the first server that can satisfy their requirements of resources. The details of FFD are presented in Algorithm 3.
To sum up, the process of the whole task containerization and container placement scheme is as follows: An application’s tasks are first grouped by the P-NCPI or the P-RI algorithm, and then each group of tasks, denoted by , is encapsulated into a container , which is then placed on the selected server by using the DP or the FFD algorithm. In this manner, the application is eventually executed in a given number of containers and on the selected servers. As a beneficial result, the proposed scheme exhibits minimized inter-container communication cost (some containers are possibly placed on different servers), balanced resource requirements among containers, and balanced resource utilization efficiency among the selected servers.
| Algorithm 1 The proposed task containerization algorithm |
| Input: , , C, Output: ,
|
| Algorithm 2 The DP algorithm |
| Input: , , , , , Output:
|
| Algorithm 3 The FFD algorithm |
| Input: , , , , , Output:
|
4.3. Analysis of Algorithm Complexity
The task containerization method groups the tasks of the given application into multiple vertex sets, each of which is encapsulated into a single container. Then the generated containers are placed on the selected appropriate servers by using the container placement method.
More specifically, two initial partitioning algorithms, i.e., P-NCPI and P-RI, are individually employed in the task containerization method. P-RI initializes a given number of vertex sets, which are supposed to represent the task partitioning, by using the same number of randomly selected tasks (see Lines 2-5 of Algorithm 1). The time complexity of P-RI is , and the number of floating point operations is given by . P-NCPI employs the non-critical path based initialization to conduct the graph partitioning (see Lines 6-35 of Algorithm 1). Its time complexity is , and the number of floating point operations is given by .
As far as the container placement method is concerned, two bin packing algorithms are used, namely DP (see Algorithm 2) and FFD (see Algorithm 3). The time complexity of DP is and the number of floating point operations is . The time complexity of FFD is , and the number of floating point operations is .
5. Evaluation
In this section, we present simulation results to demonstrate the effectiveness of our proposed task containerization and container placement methods. The experiments were carried out on a MacBook Pro with a 4-core CPU, 8GB of RAM, and the macOS Monterey operating system. All the algorithms presented in this paper were implemented by Python 3.9.7. For the P-RI algorithm and the K-means algorithm, we took the average of 10 sets of experimental results to obtain statistically reliable results. Moreover, all the results were calculated relying on the experiments of 10 application programs, each of which is represented by a workflow composed of a different number of tasks: 5, 9, 17, 24, 30, 47, 57, 63, 91 and 93.
We considered the CPU and memory resources of a computing network comprising 10 MEC servers. The server configurations are listed in Table 1, where the volume of each type of computing resources is normalized. We set the parameters as 0.5, as 0.5, and as 1.5. The used data regarding the application tasks were obtained from the Alibaba Cloud platform [15]. Each container hosts at least one process, and each task is set up as a separate process. In general, resources allocated to a container are more than the container needs [16]. We ignored the discrepancy between the volume of resources allocated to the container and the volume of resources demanded by the container for the convenience of statistics and visualization.

Table 1.
Configuration of MEC servers.
The balance degree of utilizing computing resources is a critical performance indicator for MEC. To avoid the problem of long request delay caused by insufficient resources of the servers, the utilization of multi-type computing resources on the individual servers has to be balanced. In Figure 3, we compared the normalized maximum load (defined by Equation (22)) of the proposed task partitioning algorithms and of the benchmarking K-means clustering method. Specifically, we observe in Figure 3 that the normalized maximum load of the K-means method [17] varies greatly between 1.6 and 4. Unlike those of the K-means method, the values of for P-NCPI and P-RI remain between 1.25 and 1, indicating that the resource requirements by each group of tasks are more balanced after conducting task partitioning with our proposed algorithms (e.g., decreasing the normalized maximum load by up to 60.24% on average when using P-NCPI).

Figure 3.
Comparison of the normalized maximum load performance (defined by Equation (22)) of various task partitioning algorithms, including the proposed P-NCPI and P-RI algorithms, and the classic K-means algorithm.
In Figure 4 and Figure 5, we compared the proposed task-containerization-and-container-placement methods with the state-of-the-art strategy “Spread” [16] employed by the container orchestration tool Docker swarm, in terms of the average CPU and the memory (i.e., MEM) utilization efficiencies in the MEC-based computing network. Specifically, the average CPU utilization efficiency of the MEC-based computing network is defined as
where represents the number of servers occupied by the application, denotes the CPU utilization efficiency of server n. Similarly, the average MEM utilization efficiency of the MEC-based computing network is defined as
where represents the MEM utilization efficiency of server n.
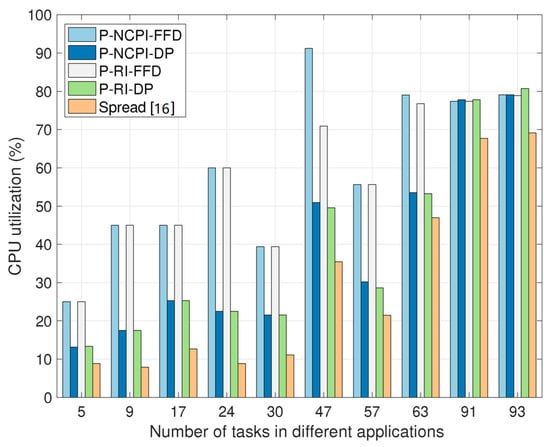
Figure 4.
Comparison of the average CPU utilization efficiency of the MEC-based computing network (defined by Equation (24)), when using the proposed four task-containerization-and-container-placement algorithms and the Spread algorithm.
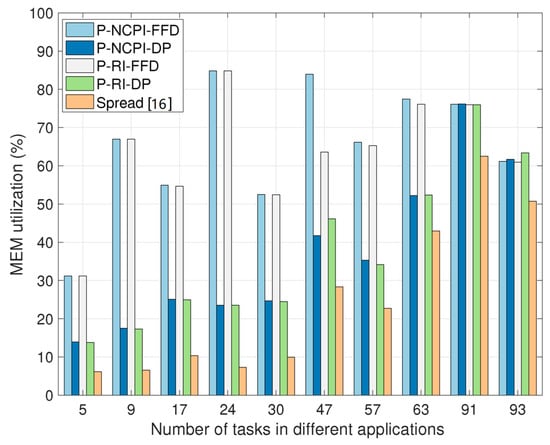
Figure 5.
Comparison of the average MEM utilization efficiency of the MEC-based computing network (defined by Equation (25)), when using the proposed four task-containerization-and-container-placement algorithms and the Spread algorithm.
We see from Figure 4 and Figure 5 that the proposed P-NCPI-FFD algorithm improves the average CPU utilization efficiency by 30.66% and the average MEM utilization efficiency by 40.77%, compared with the Spread algorithm. In general, the proposed P-NCPI-FFD algorithm achieves the highest CPU and MEM utilization efficiency among all algorithms considered. The FFD algorithm attains higher resources utilization efficiency than the DP algorithm. This phenomenon can be explained as follows. The DP algorithm focuses on finding out the largest sum product of a container’s multi-type resource requirements and the volume of multi-type resources that a server can provide, whereas FFD puts as many containers having higher resource requirements as possible on the minimum possible number of servers. Therefore, when using FFD, and in Equations (24) and (25) are larger, while is smaller, than those when employing DP. In addition, it is observed that the impact of the P-NCPI and P-RI algorithms on the results of CPU and MEM utilization is trivial.
For a given application, the metric defined by Equation (10) can reflect the extent to which different resources are used in a balanced manner. According to Figure 6, in most cases evaluated, our proposed algorithms outperform the Spread algorithm in terms of the balance degree of utilizing multi-type computing resources. Although the DP algorithm is generally inferior to the FFD algorithm in terms of the CPU and MEM utilization efficiencies (as shown by Figure 4 and Figure 5), it performs better than FFD in terms of the balance degree of utilizing multi-type computing resources across the MEC-based computing network. The P-NCPI and P-RI algorithms, which are invoked for the initial task partitioning, do not make much difference in this respect.
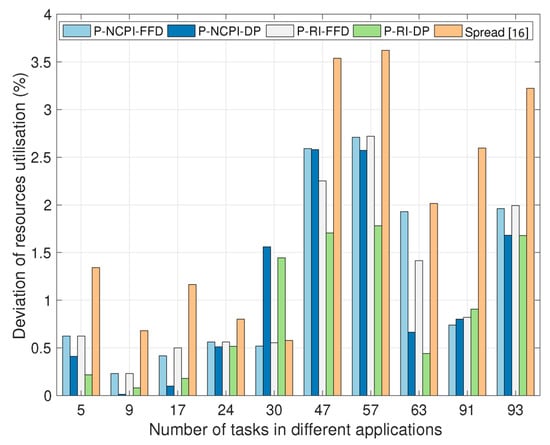
Figure 6.
Comparison of the balance degree of multi-type computing resource utilization (defined by Equation (10)), when using the proposed four task-containerization-and-container-placement algorithms and the Spread algorithm.
The running time results of all the task-containerization-and-container-placement algorithms considered are provided in Figure 7. It is observed that the running time of the P-RI algorithm is shorter than that of the P-NCPI algorithm. Additionally, when the number of tasks exceeds a particular value, the DP algorithm has a shorter running time than the FFD algorithm. Among the four algorithms we proposed, the P-RI-DP algorithm has the shortest running time, and in this regard, there is very little difference between the P-RI-DP algorithm and the Spread algorithm. Notably, the Spread algorithm always performs best in terms of the running time.
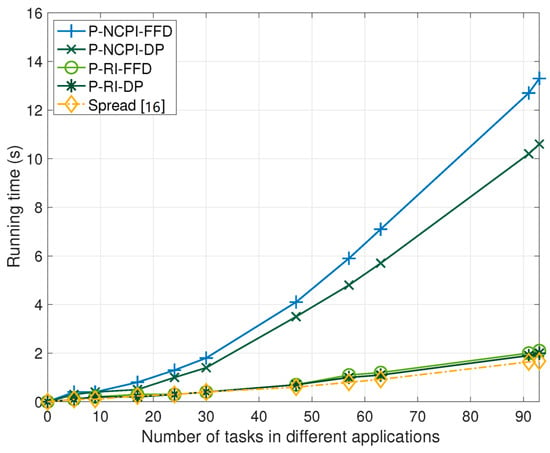
Figure 7.
Comparison of the running time of different task-containerization-and-container-placement algorithms.
Finally, the results of the communication overhead for various task-containerization-and-container-placement algorithms are shown in Figure 8. We can see that when compared with the benchmarking Spread algorithm, the P-NCPI-FFD algorithm saves 74.10% of the communication overhead, while the P-RI-FFD algorithm saves 59.32%. The communication overhead of FFD is lower than that of DP, because it does not have to consider the balance between the resource demand of containers and the resource supply of servers.
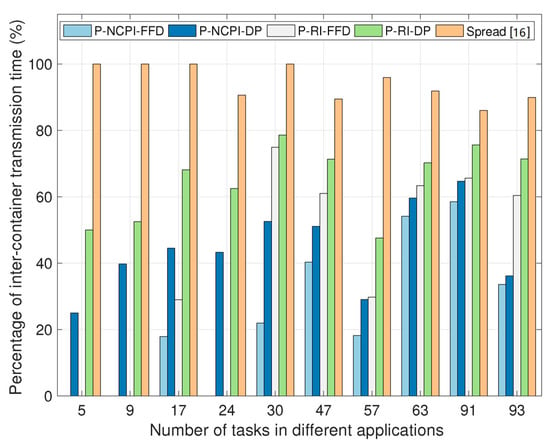
Figure 8.
The ratio of the inter-container communication overhead to the inter-task communication overhead when using different task-containerization-and-container-placement algorithms.
To sum up, our proposed task-containerization-and-container-placement algorithms outperform the existing algorithms in general. In particular, all of our proposed algorithms exhibit a more balanced resource requirements by containers, the P-NCPI-FFD algorithm achieves the highest CPU and MEM utilization efficiencies, the P-NCPI-DP and P-RI-DP algorithms achieve a higher degree of balance in utilizing multi-type computing resources, while the P-NCPI-FFD and P-RI-FFD algorithms perform better in terms of communication overhead. Additionally, different initial task partitioning algorithms, such as P-NCPI and P-RI, do not make much difference in terms of the above performance metrics.
6. Conclusions
In this paper we have proposed four task-containerization-and-container-placement algorithms to jointly reduce the inter-container communication overhead and balance the multi-type computing resource utilization in the MEC-based computing network. We establish a workflow model to reflect the interactions between interdependent tasks. As a beneficial result, the inter-task communication overhead, the inter-container communication overhead, as well as the computing resources required by each group of tasks encapsulated in a container, are conveniently characterized. Furthermore, two task containerization algorithms have been designed to reduce the inter-container communication overhead while balancing the multi-type computing resource requirements of containers. Then we proposed a pair of container placement algorithms for optimizing the utilization of multi-type computing resources across MEC servers. Extensive simulation results demonstrated that our proposed methods are capable of reducing the inter-container communication overhead by up to 74.10%, reducing the normalized maximum load by up to 60.24%, improving the CPU utilization efficiency by up to 30.66%, and improving the memory utilization efficiency by up to 40.77% in the MEC-based computing network considered.
Author Contributions
Conceptualization, S.Y. and A.L.; methodology, S.Y.; software, A.L. and J.T.; validation, A.L., J.T., Z.L. and J.S.; formal analysis, S.Y. and A.L.; investigation, A.L., J.T. and Z.L.; resources, S.Y. and H.Y.; data curation, J.T., Z.L. and J.S.; writing—original draft preparation, A.L. and S.Y.; writing—review and editing, S.Y.; visualization, A.L.; supervision, S.Y.; project administration, S.Y., T.W. and H.Y.; funding acquisition, S.Y., T.W. and H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Beijing Municipal Natural Science Foundation under Grant L202012, and in part by the BUPT-CMCC Joint Research Center under Grant A2022122.
Data Availability Statement
Restrictions apply to the availability of tasks data. Tasks data were obtained from Alibaba Group. These data are open source and available at https://github.com/alibaba/clusterdata/tree/master/cluster-trace-v2018.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Shi, W.; Cao, J.; Zhang, Q.; Li, Y.; Xu, L. Edge computing: Vision and challenges. IEEE Internet Things J. 2016, 3, 637–646. [Google Scholar] [CrossRef]
- Liu, P.; Willis, D.; Banerjee, S. Paradrop: Enabling lightweight multi-tenancy at the network’s extreme edge. In Proceedings of the IEEE/ACM Symposium on Edge Computing (SEC), Washington, DC, USA, 27–28 October 2016; pp. 1–13. [Google Scholar]
- Zhang, J.; Zhou, X.; Ge, T.; Wang, X.; Hwang, T. Joint task scheduling and containerizing for efficient edge computing. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 2086–2100. [Google Scholar] [CrossRef]
- Bao, L.; Wu, C.; Bu, X.; Ren, N.; Shen, M. Performance modeling and workflow scheduling of microservice-based applications in clouds. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 2114–2129. [Google Scholar] [CrossRef]
- Zhou, R.; Li, Z.; Wu, C. An efficient online placement scheme for cloud container clusters. IEEE J. Sel. Areas Commun. 2019, 37, 1046–1058. [Google Scholar] [CrossRef]
- Lv, L.; Zhang, Y.; Li, Y.; Xu, K.; Wang, D.; Wang, W.; Li, M.; Cao, X.; Liang, Q. Communication-aware container placement and reassignment in large-scale Internet data centers. IEEE J. Sel. Areas Commun. 2019, 37, 540–555. [Google Scholar] [CrossRef]
- Hong, Y.-J.; Thottethodi, M. Understanding and mitigating the impact of load imbalance in the memory caching tier. In Proceedings of the 4th Annual Symposium on Cloud Computing, Santa Clara, CA, USA, 1–3 October 2013; pp. 1–17. [Google Scholar]
- Li, W.; Li, X.; Ruiz, R. Scheduling microservice-based workflows to containers in on-demand cloud resources. In Proceedings of the IEEE 24th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Dalian, China, 5–7 May 2021; pp. 61–66. [Google Scholar]
- Ye, L.; Xia, Y.; Yang, L.; Yan, C. SHWS: Stochastic hybrid workflows dynamic scheduling in cloud container services. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2620–2636. [Google Scholar] [CrossRef]
- Wu, Z.; Deng, Y.; Feng, H.; Zhou, Y.; Min, G.; Zhang, Z. Blender: A container placement strategy by leveraging zipf-like distribution within containerized data centers. IEEE Trans. Netw. Serv. Manag. 2022, 19, 1382–1398. [Google Scholar] [CrossRef]
- Hu, Y.; Zhou, H.; de Laat, C.; Zhao, Z. Concurrent container scheduling on heterogeneous clusters with multi-resource constraints. Future Gener. Comput. Syst. 2020, 102, 562–573. [Google Scholar] [CrossRef]
- Tsourakakis, C.; Gkantsidis, C.; Radunovic, B.; Vojnovic, M. FENNEL: Streaming graph partitioning for massive scale graphs. In Proceedings of the 7th ACM International Conference on Web Search and Data Mining, New York, NY, USA, 24–28 February 2014; pp. 333–342. [Google Scholar]
- Patt-Shamir, B.; Rawitz, D. Vector bin packing with multiple-choice. Discret. Appl. Math. 2012, 160, 1591–1600. [Google Scholar] [CrossRef]
- Panigrahy, R.; Talwar, K.; Uyeda, L.; Wieder, U. Heuristics for Vector bin Packing. January 2011, pp. 1–14. Available online: https://www.microsoft.com/en-us/research/publication/heuristics-for-vector-bin-packing/ (accessed on 18 March 2023).
- Alibaba Cluster Trace Program. 2023. Available online: https://github.com/alibaba/clusterdata/tree/master/cluster-trace-v2018 (accessed on 18 March 2023).
- Docker. 2023. Available online: https://docs.docker.com/engine/swarm/services/ (accessed on 18 March 2023).
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-means clustering algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).