Modeling Strategies for Crude Oil-Induced Fouling in Heat Exchangers: A Review
Abstract
1. Introduction
2. Deterministic Fouling Models
3. Threshold Fouling Models
- To predict the corresponding threshold film temperature at a certain velocity using the threshold curve;
- To predict the initial fouling rate for a combination of different velocities and film temperatures.
3.1. Significance of Activation Energy
- The activation energy term lost its validity in the fouling application because of various mechanisms involved with the chemical reaction. The value used for activation energy, which is merely a factor representing the combined effect of other factors such as the solubility of precursors, fluid velocity, mass transfer limitations, etc., misrepresent its true meaning. Using the data from Ebert and Panchal, they also showed that the activation energy value varied with velocity, demonstrating it to be not true activation energy;
- The use of data fitting to estimate activation energy values from different fouling models gave different results for the same data set, as shown by Yeap et al. [45]. Also, the initial guess values in regression analysis affect the estimated parameter values. This makes activation energy no more than a fitting parameter, and dividing by gas constant in the exponential term should not have any significance;
- Using reciprocal temperature in the exponential term can be replaced with normal temperature dependence because this term becomes linear at higher temperatures (i.e., crude oil fouling range). It was shown using the data from Ebert and Panchal [40] and Petkovic and Watkinson [56] that using normal temperature in the Arrhenius plot could also give a good fitting of the data;
3.2. Prediction of Induction Period
4. Incorporation of Crude Stability/Compatibility
5. Effect of Ageing
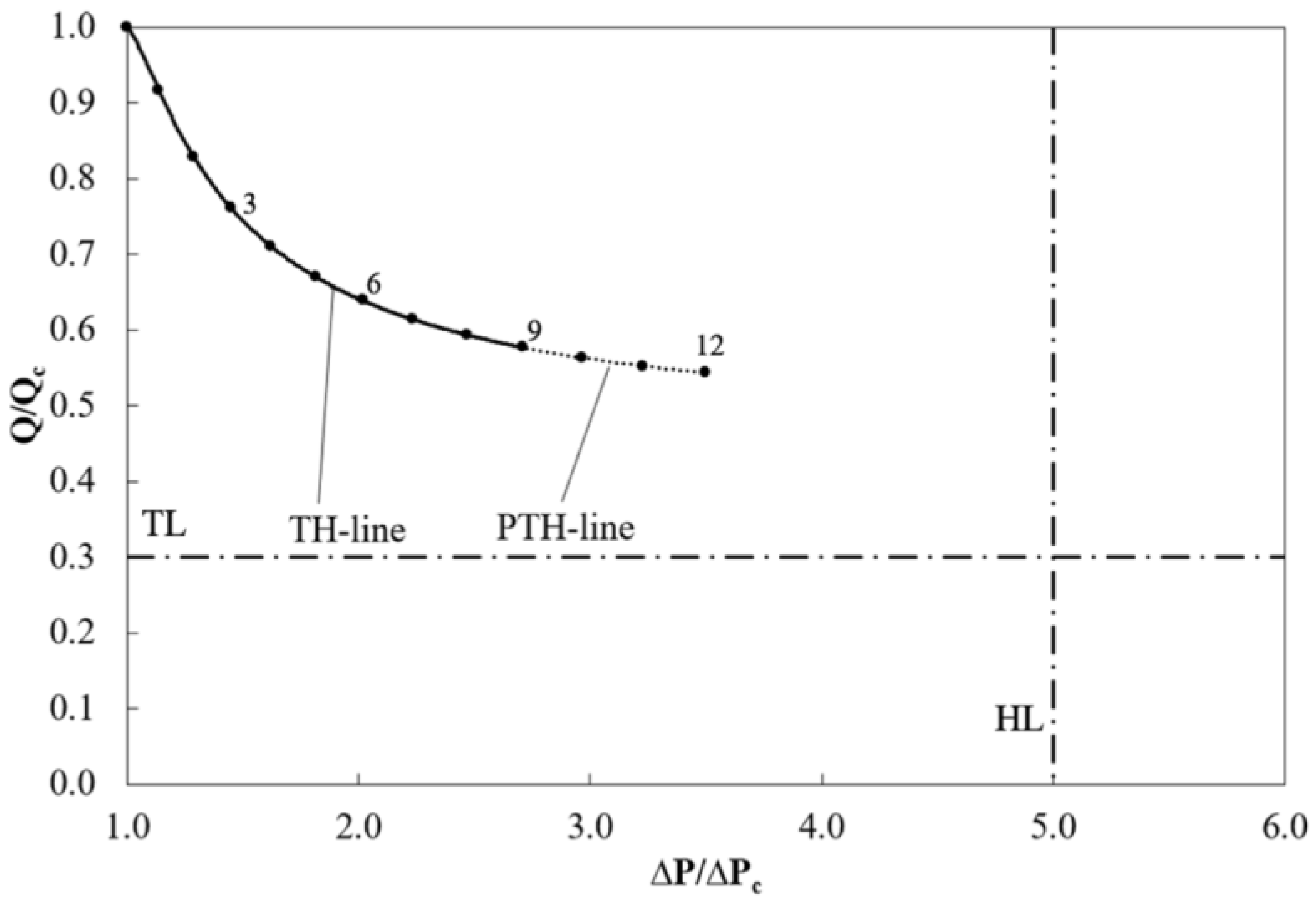
6. Thermal-Hydraulic Relationship
7. Role of Inorganic Content
8. CFD Simulations
9. Conclusions
- Using both deposition and removal terms in fouling models is criticized due to multiple empirical parameters involved. Models containing the removal parameter within the deposition term have shown comparable results and reduced fitting parameters. The removal term is highly susceptible to flow behavior, which is related to flow geometry; this emphasizes the need for a conversion factor when comparing experimental data from different geometries;
- The inclusion of the asymptotic surface coverage model is a promising approach in predicting the induction periods by combining with the fouling model to achieve a comprehensive model for longer duration;
- The activation energy in the Ebert and Panchal model has lost its validity in the Arrhenius deposition term as its value is affected by the physical processes. A better way to describe the deposition term is to introduce parameter for temperature dependency of the crude oil properties;
- The rate of asphaltenes precipitation reaction has been neglected as part of the deposition model, despite the increasing demand of opportunity crudes and blending operation. The colloidal instability parameters seem promising to incorporate in the deposition model, despite the complex dependency of asphaltenes precipitation on crude oil temperature and composition. A more practical approach would be to find the relationship between the deposition constant and the instability parameter of the crude oil or blend;
- Foulant ageing and the presence of inorganic content can cause errors in estimating the thickness of foulant layers due to an increase in foulant thermal conductivity. However, accurate prediction of fouling rate and foulant thickness can be achieved by incorporating ageing and mixing models for foulant thermal conductivity. In addition, the reduction in throughput loss near the hydraulic limit of the operation can be achieved through pressure drop measurements. Therefore, relying solely on thermal performance could lead to inaccurate estimations of fouling rate and thickness of foulant. It is, therefore, recommended to include the hydraulic performance data as necessary tool to evaluate the fouling behavior of heat exchangers;
- With difficulty in data acquisition and the long duration of experimental studies, CFD simulations can play a critical role in assessing the application of different models with a wide range of operating conditions and geometries. The application of dynamic mesh needs to be further explored to capture accurate hydraulic performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Arrhenius coefficient |
| Model constants | |
| B | Sticking Probability |
| Bi | Biot number |
| c | Concentration of foulants, kg/m3 |
| ci | Concentration of foulants at ith site, mol/m3 |
| ct,0 | total number of sites at t=0, mol/m2 |
| cA·S | sites occupied by A, mol/m2 |
| cAS | concentration of A on the surface, mol/m2 |
| CII | Colloidal instability index |
| d | tube inner diameter, m |
| E | Activation energy, J/mol |
| e | Roughness, m |
| f | fanning friction factor |
| maximum flocculation ratio | |
| G | Temperature-dependent constant, K |
| Go | Model parameter, K |
| J | mass deposition rate, kg/s |
| k1, k2 | lumped rate constants, s−1 |
| deposition constant, m4/kg2 | |
| removal constant, m2/N s | |
| L | tube length, m |
| M | molar mass, kg/kmol |
| m | mass of deposit per unit surface area, kg/m2 |
| mass flux, kg/m2 s | |
| P | Pressure, Pa |
| Po | Peptizing power of maltenes |
| Pr | Prandtl number |
| ratio of inorganic to organic deposition rate of component i | |
| Q | Heat transfer rate, Watt |
| R | Gas constant, J/mol K |
| Rf | thermal resistance, m2K/W |
| rate of fouling, m2K/J | |
| Re | Reynolds number |
| initial rate of fouling reaction, s−1 | |
| S | roughness parameter |
| Sc | Schmidt number |
| T | time, s |
| T | Temperature, K |
| U | Heat transfer coefficient, W/m2K |
| u | mean flow velocity, m/s |
| w | wettability parameter |
| mass fraction of i component | |
| x | deposit thickness, m |
| Asphaltenes content | |
| Ash content | |
| Y | Ratio of convective and conductive heat resistances |
| y | youth factor |
| Greek | |
| model fitting parameter [Equations (3) and (9)], K s2/kg | |
| β | model fitting parameter, dimensionless |
| γ | model fitting parameter [Equations (3) and (9)], m3 K s/J kg |
| ∆ | difference |
| θ | fractional surface coverage |
| thermal conductivity, W/m K | |
| μ | dynamic viscosity, Pa s |
| ρ | density, kg/m3 |
| τ | shear stress, N/m2 |
| rate of deposition, kg/m2 s | |
| model fitting parameter, dimensionless | |
| Subscripts | |
| b | Bulk fluid |
| c | crude oil |
| D | Deposition |
| eff | Effective |
| f | Film |
| F | Foulant |
| inorg | Inorganic component |
| org | Organic component |
| R | Removal |
| s | Surface |
| s0 | Surface initial |
| w | Wall |
| Superscripts | |
| o | fresh deposit |
| aged deposit |
References
- Borges, J.L.; Queiroz, E.M.; Pessoa, F.L.P.; Liporace, F.S.; Oliveira, S.G.; Costa, A.L.H. Fouling management in crude oil preheat trains through stream split optimization. Comput. Aided Chem. Eng. 2009, 27, 1587–1592. [Google Scholar] [CrossRef]
- Dai, B.; Liu, C.; Liu, S.; Wang, D.; Wang, Q.; Zou, T.; Zhou, X. Life cycle techno-enviro-economic assessment of dual-temperature evaporation transcritical CO2 high-temperature heat pump systems for industrial waste heat recovery. Appl. Therm. Eng. 2023, 219, 119570. [Google Scholar] [CrossRef]
- Van Nostrand, J.L.; Leach, W.L.J.; Haluska, S.H. Economic Penalties Associated with the Fouling of Refinery Heat transfer Equipment. In Fouling of Heat Transfer Equipment; Hemisphere Publishing: New York, NY, USA, 1981; pp. 619–643. [Google Scholar]
- Coletti, F.; Hewitt, G.F. Crude Oil Fouling Deposit Characterization, Measurements, and Modeling; Gulf Professional Publishing: Oxford, UK, 2015. [Google Scholar]
- Watkinson, A.P. Deposition from Crude Oils in Heat Exchangers. Heat Transf. Eng. 2007, 28, 177–184. [Google Scholar] [CrossRef]
- Müller-Steinhagen, H.; Malayeri, M.R.; Watkinson, A.P. Heat Exchanger Fouling: Environmental Impacts. Heat Transf. Eng. 2009, 30, 773–776. [Google Scholar] [CrossRef]
- Coletti, F.; Macchietto, S. Predicting refinery energy losses due to fouling in heat exchangers. Comput. Aided Chem. Eng. 2009, 27, 219–224. [Google Scholar] [CrossRef]
- Costa, A.L.H.; Tavares VB, G.; Borges, J.L.; Queiroz, E.M.; Pessoa FL, P.; Liporace FD, S.; de Oliveira, S.G. Parameter estimation of fouling models in crude preheat trains. Heat Transf. Eng. 2013, 34, 683–691. [Google Scholar] [CrossRef]
- Dickakian, S.; Seay, G.B. Asphaltene precipitation primary crude exchanger fouling mechanism. Oil Gas J. 1988, 86, 47–50. [Google Scholar]
- Watkinson, A.P.; Wilson, D.I. Chemical reaction fouling: A review. Exp. Therm. Fluid Sci. 1997, 14, 361–374. [Google Scholar] [CrossRef]
- Smith, A.D.; Ishiyama, E.M.; Harris, J.; Lane, M. Translating Crude Oil Fouling Testing Rig Data To The Field: A Road Map For Future Research. In Proceedings of the International Conference on Heat Exchanger Fouling and Cleaning XII, Aranjuez, Spain, 11–16 June 2017. [Google Scholar]
- Wilson, D.I.; Ishiyama, E.M.; Polley, G.T. Twenty Years of Ebert and Panchal—What Next? Heat Transf. Eng. 2017, 38, 669–680. [Google Scholar] [CrossRef]
- Diaz-Bejarano, E.; Coletti, F.; Macchietto, S. A New Dynamic Model of Crude Oil Fouling Deposits and Its Application to the Simulation of Fouling-Cleaning Cycles. AIChE J. 2016, 62, 90–107. [Google Scholar] [CrossRef]
- Diaz-Bejarano, E.; Coletti, F.; Macchietto, S. Thermo-hydraulic analysis of refinery heat exchangers undergoing fouling. AIChE J. 2017, 63, 984–1001. [Google Scholar] [CrossRef]
- Maddahian, R.; Farsani, A.T.; Ghorbani, M. Numerical investigation of asphaltene fouling growth in crude oil preheat trains using multi-fluid approach. J. Pet. Sci. Eng. 2020, 188, 106879. [Google Scholar] [CrossRef]
- Salimi, F.; Ayatollahi, S.; Seftie, M.V. Prediction of asphaltene deposition during turbulent flow using heat transfer approach. Pet. Sci. Technol. 2018, 36, 632–639. [Google Scholar] [CrossRef]
- Diaz-Bejarano, E.; Coletti, F.; Macchietto, S. Complex crude oil fouling layers: Use of model predictions to detect inorganics breakthrough. Appl. Therm. Eng. 2018, 141, 666–674. [Google Scholar] [CrossRef]
- Rammerstorfer, E.; Karner, T.; Siebenhofer, M. The kinetics and mechanisms of fouling in crude oil heat transfer. Heat Transf. Eng. 2019, 41, 691–707. [Google Scholar] [CrossRef]
- Coletti, F.; Macchietto, S.; Diaz-Bejarano, E. Beyond Fouling Factors: A Reaction Engineering Approach to Crude Oil Fouling Modelling. In Proceedings of the International Conference on Heat Exchanger Fouling and Cleaning XI, Enfield, Ireland, 7–12 June 2015; pp. 89–96. [Google Scholar]
- Rogel, E.; Hench, K.; Miao, T.; Lee, E.; Dickakian, G. Evaluation of the Compatibility of Crude Oil Blends and Its Impact on Fouling. Energy Fuels 2018, 32, 9233–9242. [Google Scholar] [CrossRef]
- Kumar, R.; Voolapalli, R.K.; Upadhyayula, S. Prediction of crude oil blends compatibility and blend optimization for increasing heavy oil processing. Fuel Process. Technol. 2018, 177, 309–327. [Google Scholar] [CrossRef]
- Patil, P.D.; Kozminski, M.; Peterson, J.; Kumar, S. Fouling Diagnosis of Pennsylvania Grade Crude Blended with Opportunity Crude Oils in a Refinery Crude Unit’s Hot Heat Exchanger Train. Ind. Eng. Chem. Res. 2019, 58, 17918–17927. [Google Scholar] [CrossRef]
- Ogbonnaya, S.; Ajayi, O. Fouling phenomenon and its effect on heat exchanger: A review. Front. Heat Mass Transf. 2017, 9, 31. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Z.; Liang, Y.; Xie, Y.; Chen, X.; Li, X. A review of experimental measurement and prediction models of crude oil fouling rate in crude refinery preheat trains. Asia-Pac. J. Chem. Eng. 2015, 10, 607–625. [Google Scholar] [CrossRef]
- Müller-Steinhagen, H. Heat transfer fouling: 50 years after the Kern and Seaton model. Heat Transf. Eng. 2011, 32, 1–13. [Google Scholar] [CrossRef]
- Deshannavar, U.; Rafeen, S.; Gounder, R.M.; Subbarao, D. Crude Oil Fouling: A Review. J. Appl. Sci. 2010, 10, 3167–3174. [Google Scholar] [CrossRef]
- Wilson, D.I.; Polley, G.; Pugh, S. Ten Years of Ebert, Panchal and The ‘Threshold Fouling’ Concept. In Proceedings of the 6th International Conference on Heat Exchanger Fouling and Cleaning—Challenges and Opportunities, Kloster Irsee, Germany, 5–10 June 2005. [Google Scholar]
- Kern, D.Q.; Seaton, R.E. A theoretical analysis of thermal surface fouling. Br. Chem. Eng. 1959, 4, 258–262. [Google Scholar]
- Watkinson, A.P. Particulate Fouling of Sensible Heat Exchangers. Ph.D. Dissertation, The University of British Columbia, Vancouver, BC, USA, 1968. [Google Scholar]
- Epstein, N. A Model of the Initial Chemical Reaction Fouling Rate for Flow within a Heated Tube and its Verfication. In Proceedings of the International Heat Transfer Conference 10, Brighton, UK, 14–18 August 1994. [Google Scholar]
- Crittenden, B.D.; Kolaczkowski, S.T.; Takemoto, T.; Phillips, D.Z. Crude Oil Fouling in a Pilot-Scale Parallel Tube Apparatus. Heat Transf. Eng. 2009, 30, 777–785. [Google Scholar] [CrossRef]
- Paterson, W.R.; Fryer, P.J. A reaction engineering approach to the analysis of fouling. Chem. Eng. Sci. 1988, 43, 1714–1717. [Google Scholar] [CrossRef]
- Chambon, A.; Ratel, M.; Anxionnaz-Minvielle, Z.; Aquino, B.; Buffet, A.; Vinet, B. Fouling in the crude oil distillation preheat train: Comparison of experimental data with model results. In Proceedings of the International Conference on Heat Exchanger Fouling and Cleaning, Enfield, Ireland, 7–12 June 2015; pp. 74–80. [Google Scholar]
- Joshi, H.M. Crude oil fouling field data and a model for pilot-plant scale data. In Proceedings of the International Conference on Heat Exchanger Fouling and Cleaning, Budapest, Hungary, 9–14 June 2013; pp. 22–26. [Google Scholar]
- Watkinson, A.P. Deposition From Crude Oils In Heat Exchangers. In Proceedings of the Heat Exchanger Fouling and Cleaning—Challenges and Opportunities, Kloster Irsee, Germany, 5–10 June 2005. [Google Scholar]
- Scarborough, C.E.; Cherrington, D.C.; Diener, R. Coking of crude oil at high heat flux levels. Chem. Eng. Prog. 1979, 75, 41–46. [Google Scholar]
- Polley, G.T.; Wilson, D.I.; Yeap, B.L.; Pugh, S.J. Evaluation of laboratory crude oil threshold fouling data for application to refinery pre-heat trains. Appl. Therm. Eng. 2002, 22, 777–788. [Google Scholar] [CrossRef]
- Yang, M.; O’meara, A.; Crittenden, B.D. Determination of Crude Oil Fouling Thresholds. In Proceedings of the International Conference on Heat Exchanger Fouling and Cleaning, Crete Island, Greece, 5–10 June 2011. [Google Scholar]
- Crittenden, B.D.; Kolaczkowski, S.T.; Downey, I.L. Fouling of crude oil preheat exchangers. Chem. Eng. Res. Des. 1992, 70, 547–557. [Google Scholar]
- Ebert, W.; Panchal, C.B. Analysis of Exxon Crude-Oil-Slip Stream Coking Data. In Fouling Mitigation of Industrial Exchange Equipment; Begell House: New York, NY, USA, 1995; pp. 451–460. [Google Scholar]
- Rodriguez, C.; Smith, R. Optimization of operating conditions for mitigating fouling in heat exchanger networks. Chem. Eng. Res. Des. 2007, 85, 839–851. [Google Scholar] [CrossRef]
- Panchal, C.B.; Kuru, W.C.; Liao, C.F.; Ebert, W.A.; Palen, J.W. Threshold Conditions for Crude Oil Fouling. In Understanding Heat Exchanger Fouling and Its Mitigation; Engineering Foundation: New York, NY, USA, 1997; pp. 273–279. [Google Scholar]
- Knudsen, J.G.; Dahcheng, L.; Ebert, W.A. The Determination of the Threshold Fouling Curve for a Crude Oil. In Understanding Heat Exchanger Fouling and Its Mitigation; Begell House: New York, NY, USA, 1999; pp. 265–272. [Google Scholar]
- Crittenden, B.; Kolaczkowski, S.T.; Hout, S.A. Modelling hydrocarbon fouling. Chem. Eng. Res. Des. 1987, 65, 171–179. [Google Scholar]
- Yeap, B.L.; Wilson, D.I.; Polley, G.T.; Pugh, S.J. Mitigation of Crude Oil Refinery Heat Exchanger Fouling Through Retrofits Based on Thermo-Hydraulic Fouling Models. Chem. Eng. Res. Des. 2004, 82, 53–71. [Google Scholar] [CrossRef]
- Nasr, M.R.J.; Givi, M.M. Modeling of crude oil fouling in preheat exchangers of refinery distillation units. Appl. Therm. Eng. 2006, 26, 1572–1577. [Google Scholar] [CrossRef]
- Saleh, Z.S.; Sheikholeslami, R.; Watkinson, A.P. Fouling characteristics of a light Australian crude oil. Heat Transf. Eng. 2005, 26, 15–22. [Google Scholar] [CrossRef]
- Shetty, N.; Deshannavar, U.B.; Marappagounder, R.; Pendyala, R. Improved threshold fouling models for crude oils. Energy 2016, 111, 453–467. [Google Scholar] [CrossRef]
- Srinivasan, M.; Watkinson, A.P. Fouling of Some Canadian Crude Oils. Heat Transf. Eng. 2005, 26, 7–14. [Google Scholar] [CrossRef]
- Polley, G.; Tamakloe, E.; Wilson, I.; Macchietto, S.; Coletti, F. Development of a model for the prediction of fouling in heat exchangers processing crude oil. In Proceedings of the 10AIChE–2010 AIChE Spring Meeting and 6th Global Congress on Process Safety, San Antonio, TX, USA, 21–25 March 2010. [Google Scholar]
- Ishiyama, E.M.; Heins, A.V.; Paterson, W.R.; Spinelli, L.; Wilson, D.I. Scheduling cleaning in a crude oil preheat train subject to fouling: Incorporating desalter control. Appl. Therm. Eng. 2010, 30, 1852–1862. [Google Scholar] [CrossRef]
- Polley, G.T.; Tamakloe, E.; Nunez, M.P.; Ishiyama, E.M.; Wilson, D.I. Applying thermo-hydraulic simulation and heat exchanger analysis to the retrofit of heat recovery systems. Appl. Therm. Eng. 2013, 51, 137–143. [Google Scholar] [CrossRef]
- Ishiyama, E.M.; Pugh, S.J.; Wilson, D.I. Incorporating Deposit Ageing into Visualisation of Crude Oil Preheat Train Fouling. Process Integr. Optim. Sustain. 2020, 4, 187–200. [Google Scholar] [CrossRef]
- Coletti, F.; Macchietto, S. A Dynamic, Distributed Model of Shell-and-Tube Heat Exchangers Undergoing Crude Oil Fouling. Ind. Eng. Chem. Res. 2011, 50, 4515–4533. [Google Scholar] [CrossRef]
- Smith, A.D.; Joshi, H.M. A Critical Look at the Use of Activation Energy in Crude Oil Fouling Models. In Proceedings of the International Conference on Heat Exchanger Fouling and Cleaning, Enfield, Ireland, 7–12 June 2015. [Google Scholar]
- Petkovic, B.; Watkinson, P. Fouling of a heated rod in a stirred tank system. Heat Transf. Eng. 2014, 35, 302–310. [Google Scholar] [CrossRef]
- Deshannavar, U.B.; Marappagounder, R. Revisiting Threshold Fouling Models for Crude Oil Fouling. Heat Transf. Eng. 2020, 42, 1–17. [Google Scholar] [CrossRef]
- Yang, M.; Young, A.; Niyetkaliyev, A.; Crittenden, B. Modelling fouling induction periods. Int. J. Therm. Sci. 2012, 51, 175–183. [Google Scholar] [CrossRef]
- Stark, J.L.; Asomaning, S. Crude Oil Blending Effects on Asphaltene Stability in Refinery Fouling. Pet. Sci. Technol. 2003, 21, 569–579. [Google Scholar] [CrossRef]
- Rashid, Z.; Wilfred, C.D.; Gnanasundaram, N.; Arunagiri, A.; Murugesan, T. A comprehensive review on the recent advances on the petroleum asphaltene aggregation. J. Pet. Sci. Eng. 2019, 176, 249–268. [Google Scholar] [CrossRef]
- Rogel, E.; Roye, M.; Vien, J.; Miao, T. Characterization of Asphaltene Fractions: Distribution, Chemical Characteristics, and Solubility Behavior. Energy Fuels 2015, 29, 2143–2152. [Google Scholar] [CrossRef]
- Gray, M.R.; Yarranton, H.W. Quantitative Modeling of Formation of Asphaltene Nanoaggregates. Energy Fuels 2019, 33, 8566–8575. [Google Scholar] [CrossRef]
- Watkinson, S.A.A.P. Petroleum Stability and Heteroatom Species Effects in Fouling of Heat Exchangers by Asphaltenes. Heat Transf. Eng. 2000, 21, 10–16. [Google Scholar] [CrossRef]
- Wiehe, I.A.; Kennedy, R.J.; Dickakian, G. Fouling of Nearly Incompatible Oils. Energy Fuels 2001, 15, 1057–1058. [Google Scholar] [CrossRef]
- Saleh, Z.; Sheikholeslami, R.; Watkinson, P. Blending Effects on Fouling of Four Crude Oils. In Proceedings of the 6th International Conference on Heat Exchanger Fouling and Cleaning—Challenges and Opportunities, Kloster Irsee, Germany, 5–10 June 2005. [Google Scholar]
- Hong, E.; Watkinson, A.P. Precipitation and Fouling in Heavy Oil-Diluent Blends. Heat Transf. Eng. 2009, 30, 786–793. [Google Scholar] [CrossRef]
- Rogel, E.; Hench, K.; Cibotti, F.; Forbes, E.; Jackowski, L. Investigation on Crude Oil Fouling Behavior. Energy Fuels 2022, 36, 818–825. [Google Scholar] [CrossRef]
- Ho, T.C. A study of crude oil fouling propensity. Int. J. Heat Mass Transf. 2016, 95, 62–68. [Google Scholar] [CrossRef]
- Wilson, D.I.; Ishiyama, E.M.; Paterson, W.R.; Watkinson, A.P. Ageing: Looking backward and looking forward. In Proceedings of the International Conference on Heat Exchanger Fouling and Cleaning VIII—2009, Schladming, Austria, 14–19 June 2009; pp. 221–230. [Google Scholar]
- Diaz-Bejarano, E.; Coletti, F.; Macchietto, S. Modeling and Prediction of Shell-Side Fouling in Shell-and-Tube Heat Exchangers. Heat Transf. Eng. 2019, 40, 845–861. [Google Scholar] [CrossRef]
- Chunangad, K.S.; Chang, R.Y.; Casebolt, R.P. Evaluation and Prediction of the Thermal and Hydraulic Impact of Crude Oil Fouling on Exchanger Performance Using Pressure Measurements. In Proceedings of the Heat Exchanger Fouling and Cleaning, Aranjuez, Spain, 11–16 June 2017; pp. 1–4. [Google Scholar]
- Ishiyama, E.A.; Coletti, F.; Macchietto, S.; Paterson, W.R.; Wilson, D.I. Impact of Deposit Ageing on Thermal Fouling: Lumped Parameter Model. AIChE J. 2009, 56, 531–545. [Google Scholar] [CrossRef]
- Fan, Z.; Watkinson, A.P. Aging of Carbonaceous Deposits from Heavy Hydrocarbon Vapors. Ind. Eng. Chem. Res. 2006, 45, 6104–6110. [Google Scholar] [CrossRef]
- Ishiyama, E.M.; Paterson, W.R.; Wilson, D.I. Exploration of alternative models for the aging of fouling deposits. AIChE J. 2011, 57, 3199–3209. [Google Scholar] [CrossRef]
- Ishiyama, E.M.; Falkeman, E.; Wilson, D.I.; Pugh, S.J. Quantifying Implications of Deposit Aging from Crude Refinery Preheat Train Data. Heat Transf. Eng. 2020, 41, 115–126. [Google Scholar] [CrossRef]
- Coletti, F.; Ishiyama, E.M.; Paterson, W.R.; Wilson, D.I.; Macchietto, S. Impact of Deposit Aging and Surface Roughness on Thermal Fouling: Distributed Model. AIChE J. 2010, 56, 3257–3273. [Google Scholar] [CrossRef]
- Mozdianfard, M.R.; Behranvand, E. A field study of fouling in CDU preheaters at Esfahan refinery. Appl. Therm. Eng. 2013, 50, 908–917. [Google Scholar] [CrossRef]
- Diaz-Bejarano, E.; Coletti, F.; MacChietto, S. A Model-Based Method for Visualization, Monitoring, and Diagnosis of Fouling in Heat Exchangers. Ind. Eng. Chem. Res. 2020, 59, 4602–4619. [Google Scholar] [CrossRef]
- Wang, W.; Watkinson, A.P. Deposition From a Sour Heavy Oil Under Incipient Coking Conditions: Effect of Surface Materials and Temperature. Heat Transf. Eng. 2015, 36, 623–631. [Google Scholar] [CrossRef]
- Diaz-Bejarano, E.; Coletti, F.; Macchietto, S. Impact of Complex Layering Structures of Organic and Inorganic Foulants on the Thermohydraulic Performance of a Single Heat Exchanger Tube: A Simulation Study. Ind. Eng. Chem. Res. 2016, 55, 10718–10734. [Google Scholar] [CrossRef]
- Diaz-Bejarano, E.; Coletti, F.; Macchietto, S. Detection of changes in fouling behavior by simultaneous monitoring of thermal and hydraulic performance of refinery heat exchangers. Comput. Aided Process Eng. 2015, 37, 1649–1654. [Google Scholar]
- Mozdianfard, M.R.; Behranvand, E. Fouling at post desalter and preflash drum heat exchangers of CDU preheat train. Appl. Therm. Eng. 2015, 89, 783–794. [Google Scholar] [CrossRef]
- Diaz-Bejarano, E.; Coletti, F.; Macchietto, S. Impact of crude oil fouling composition on the thermo-hydraulic performance of refinery heat exchangers. In Proceedings of the 11th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Skukuza, South Africa, 20–23 July 2015. [Google Scholar]
- Diaz-Bejarano, E.; Behranvand, E.; Coletti, F.; Mozdianfard, M.R.; Macchietto, S. Organic and inorganic fouling in heat exchangers—Industrial case study: Analysis of fouling state. Appl. Energy 2017, 206, 1250–1266. [Google Scholar] [CrossRef]
- Diaz-Bejarano, E.; Behranvand, E.; Coletti, F.; Mozdianfard, M.R.; Macchietto, S. Organic and Inorganic Fouling in Heat Exchangers: Industrial Case Study Analysis of Fouling Rate. Ind. Eng. Chem. Res. 2019, 58, 228–246. [Google Scholar] [CrossRef]
- Mohammadi, K.; Heidemann, W.; Müller-Steinhagen, H. Numerical Investigation of the Effect of Baffle Orientation on Heat Transfer and Pressure Drop in a Shell and Tube Heat Exchanger With Leakage Flows. Heat Transf. Eng. 2009, 30, 1123–1135. [Google Scholar] [CrossRef]
- Fahmi, B.; Wolfgang, A.; Matthias, B. Numerical Simulation of the Fouling on Structured Heat Transfer Surfaces (Fouling). In Proceedings of the Heat Exchanger Fouling and Cleaning: Fundamentals and Applications, Santa Fe, NM, USA, 18–22 May 2003. [Google Scholar]
- Svendsen, J.A. Mathematical modeling of wax deposition in oil pipeline systems. AIChE J. 1993, 39, 1377–1388. [Google Scholar] [CrossRef]
- Sileri, D.; Sahu, K.; Ding, H.; Matar, O. Mathematical modelling of asphatenes deposition and removal in crude distillation units. In Proceedings of the International Conference on Heat Exchanger Fouling and Cleaning VIII, Schladming, Austria, 14–19 June 2009; pp. 245–251. [Google Scholar]
- Yang, J.; Matar, O.; Hewitt, G.; Zheng, W.; Manchanda, P. Modelling of Fundamental Transfer Processes in Crude-Oil Fouling. In Proceedings of the International Heat Transfer Conference 15, Kyoto, Japan, 10–15 August 2014. [Google Scholar]
- Yang, J.; Serratos, M.G.J.; Fari-Arole, D.S.; Muller, E.A.; Matar, O.K. Crude Oil Fouling: Fluid Dynamics, Reactions and Phase Change. Procedia IUTAM 2015, 15, 186–193. [Google Scholar] [CrossRef]
- Bayat, M.; Aminian, J.; Bazmi, M.; Shahhosseini, S.; Sharifi, K. CFD modeling of fouling in crude oil pre-heaters. Energy Convers. Manag. 2012, 64, 344–350. [Google Scholar] [CrossRef]
- Yang, M.; Crittenden, B. Use of CFD to Determine Effect of Wire Matrix Inserts on Crude Oil Fouling Conditions. Heat Transf. Eng. 2013, 34, 769–775. [Google Scholar] [CrossRef]
- Yang, M.; Crittenden, B. Fouling thresholds in bare tubes and tubes fitted with inserts. Appl. Energy 2012, 89, 67–73. [Google Scholar] [CrossRef]
- Chambon, A.; Anxionnaz-Minvielle, Z.; Fourmigué, J.-F.; Guintrand, N.; Davaillès, A.; Ducros, F. Use of Distributed Threshold Fouling Model at Local Scale in Numerical Simulations. Ind. Eng. Chem. Res. 2019, 58, 15003–15013. [Google Scholar] [CrossRef]
- Haghshenasfard, M.; Hooman, K. CFD modeling of asphaltene deposition rate from crude oil. J. Pet. Sci. Eng. 2015, 128, 24–32. [Google Scholar] [CrossRef]
- Emani, S.; Ramasamy, M.; Shaari, K.Z.B.K. Effect of Shear Stress on Crude Oil Fouling in a Heat Exchanger Tube Through CFD Simulations. In Proceedings of the 4th International Conference on Process Engineering and Advanced Materials (ICPEAM 2016), Kuala Lumpur, Malaysia, 5–17 August 2016; Volume 148, pp. 1058–1065. [Google Scholar] [CrossRef]
- Emani, S.; Ramasamy, M.; Shaari, K.Z.K. Discrete phase-CFD simulations of asphaltenes particles deposition from crude oil in shell and tube heat exchangers. Appl. Therm. Eng. 2019, 149, 105–118. [Google Scholar] [CrossRef]
- Ghorbani, M.; Maddahian, R. Investigation of asphaltene particles size and distribution on fouling rate in the crude oil preheat train. J. Pet. Sci. Eng. 2021, 196, 107665. [Google Scholar] [CrossRef]
- Paz, C.; Suarez, E.; Conde, M.; Vence, J. Development of a Computational Fluid Dynamics Model for Predicting Fouling Process Using Dynamic Mesh Model. Heat Transf. Eng. 2020, 41, 199–207. [Google Scholar] [CrossRef]
| Model | Author (s), Year & Ref. | Fluid | Operating Parameters | Equipment | Notes |
|---|---|---|---|---|---|
| Kern & Seaton, 1959 [28] | Water | N/A | Heat exchanger | Introduced the basic concept of fouling Share based removal term | |
| Watkinson, 1968 [29] | Sour heavy gas oil | Tb = 366 K | Heated tube | Introduced sticking probability | |
| Ts = 477 K | |||||
| u = 1.7–7.4 m/s | |||||
| Patterson, 1988 [32] | Skimmed milk | Tb = 333 K | Heated tube | Assumed sub-layer as a differential chemical reactor | |
| Ts = 358–383 K | |||||
| Crittenden et al., 1992 [39] | Crude oil | Tb = 403 K | Heat exchanger | ||
| Ts = 433–553 K | |||||
| u = 0.7–2.1 m/s | |||||
| Epstein, 1994 [30] | Crude oil | N/A | Heated tube | Introduced residence time of foulant on the surface. | |
| Joshi, 2013 [34] | Crude oil | u = 0.9–2.7 m/s | Heat exchanger | Included both surface roughness and ageing parameters. | |
| Rammerstorfer, 2019 [18] | Crude oil | N/A | N/A | Determined that fouling is adsorption controlled |
| Model | Author (s), Year & Ref. | Fluid | Operating Parameters | Equipment | Notes |
|---|---|---|---|---|---|
| Ebert & Panchal, 1995 [40] | Crude oil | Tb = 505 K | Heated tube | Introduced concept of fouling threshold condition. | |
| Tf = 643–673 K | |||||
| u = 1.2–5.2 m/s | |||||
| Panchal et al., 1997 [42] | Crude oil | Tb = 477–636 K | Heat exchanger, annular flow | Introduced effect of thermal conductivity and specific heat of crude oil. | |
| Ts = 505–740 K | |||||
| u = 0.9–3.2 m/s | |||||
| Polley et al., 2002 [37] | Crude oil | Tb = 422–477 K | Annular flow | Replaced film temperature by surface temperature. Related removal term to mass transfer of turbulence. | |
| Ts = 477–602 K | |||||
| u = 0.91–3.05 m/s | |||||
| Yeap et al., 2004 [45] | Crude oil | Ts = 380–593 K | Heat exchanger | ||
| u = 0.63–3.94 m/s | |||||
| Nasr and Givi, 2006 [46] | Crude oil | Tb = 353–393 K | Annular flow | Proposed model independent of Prandtl number. | |
| Ts = 453–518 K | |||||
| u = 0.25–0.4 m/s | |||||
| Polley, 2010 [50] | Crude oil | N/A | Heat exchanger | Fewer fitting parameters than Ebert & Panchal’s model | |
| Shetty et al., 2016 [48] | Crude oil | Tb = 355–453 K | Annular flow | Incorporate the effect of dissolution of precursor with increasing bulk temperature. | |
| Ts = 516–607 K | |||||
| u = 0.35–0.5 m/s | |||||
| Deshannavar & Ramasamy, 2020 [57] | Crude oil | Tb = 353–393 K | Annular flow | Replace activation energy with temperature-dependent constant, G. | |
| Ts = 451–499 K | |||||
| u = 0.4–0.5 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, O.u.; Ramasamy, M.G.; Rozali, N.E.M.; Mahadzir, S.; Ghumman, A.S.M.; Qureshi, A.H. Modeling Strategies for Crude Oil-Induced Fouling in Heat Exchangers: A Review. Processes 2023, 11, 1036. https://doi.org/10.3390/pr11041036
Rehman Ou, Ramasamy MG, Rozali NEM, Mahadzir S, Ghumman ASM, Qureshi AH. Modeling Strategies for Crude Oil-Induced Fouling in Heat Exchangers: A Review. Processes. 2023; 11(4):1036. https://doi.org/10.3390/pr11041036
Chicago/Turabian StyleRehman, Obaid ur, Marappa Gounder Ramasamy, Nor Erniza Mohammad Rozali, Shuhaimi Mahadzir, Ali Shaan Manzoor Ghumman, and Abdul Hannan Qureshi. 2023. "Modeling Strategies for Crude Oil-Induced Fouling in Heat Exchangers: A Review" Processes 11, no. 4: 1036. https://doi.org/10.3390/pr11041036
APA StyleRehman, O. u., Ramasamy, M. G., Rozali, N. E. M., Mahadzir, S., Ghumman, A. S. M., & Qureshi, A. H. (2023). Modeling Strategies for Crude Oil-Induced Fouling in Heat Exchangers: A Review. Processes, 11(4), 1036. https://doi.org/10.3390/pr11041036