Integrated Optimization for the Coupling Network of Refinery and Synthetic Plant of Chemicals
Abstract
1. Introduction
2. Problem Description
3. Optimization Model and Solution Method
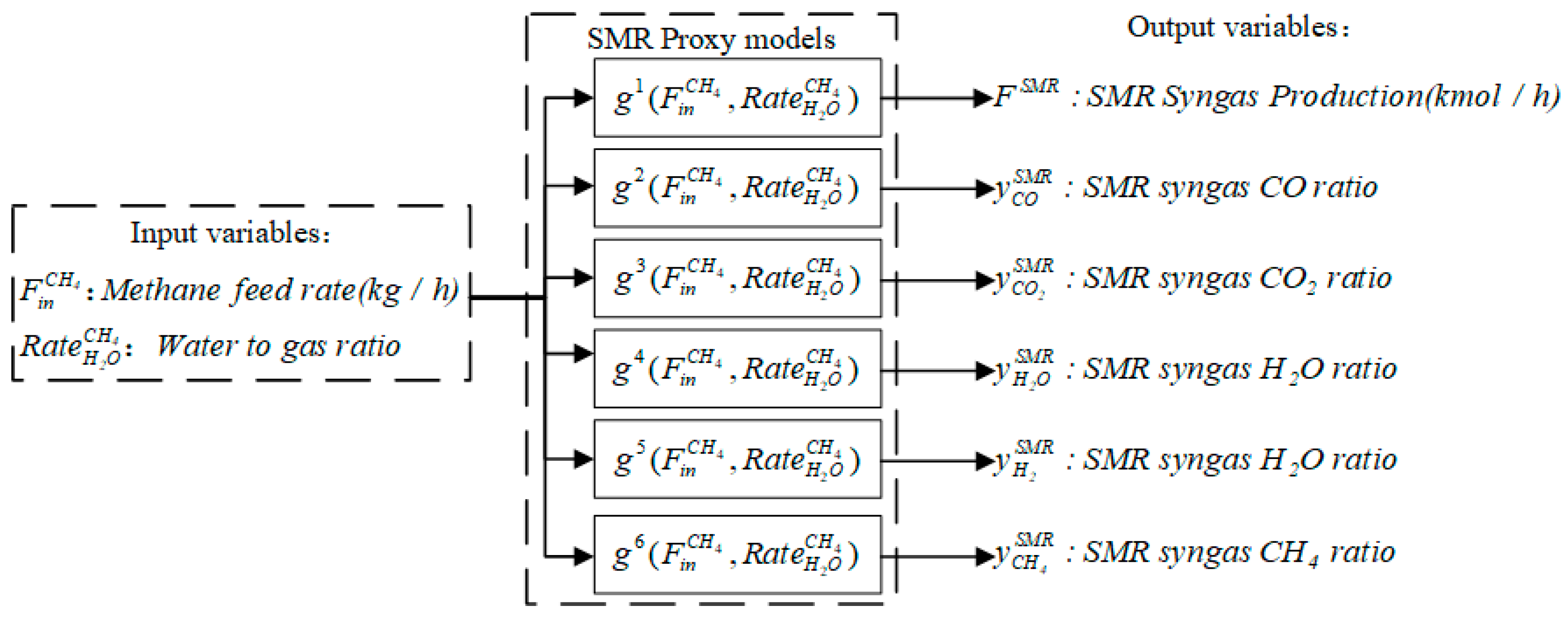
3.1. Proxy Model
3.2. Refinery-SPC Network Model
3.2.1. SPC Network
3.2.2. Hydrogen Network
3.2.3. Objective Function
4. Case Study
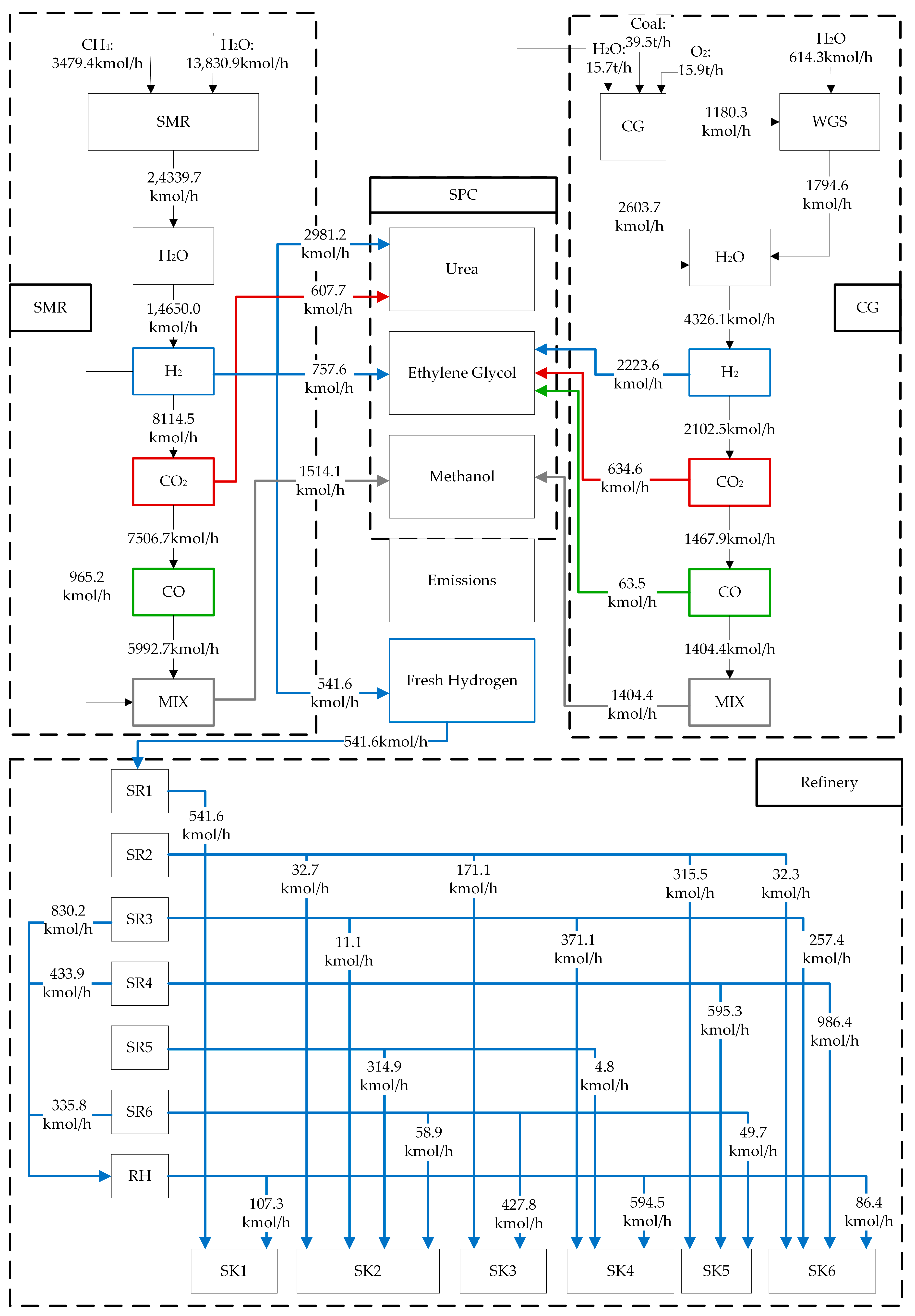
4.1. Case Data
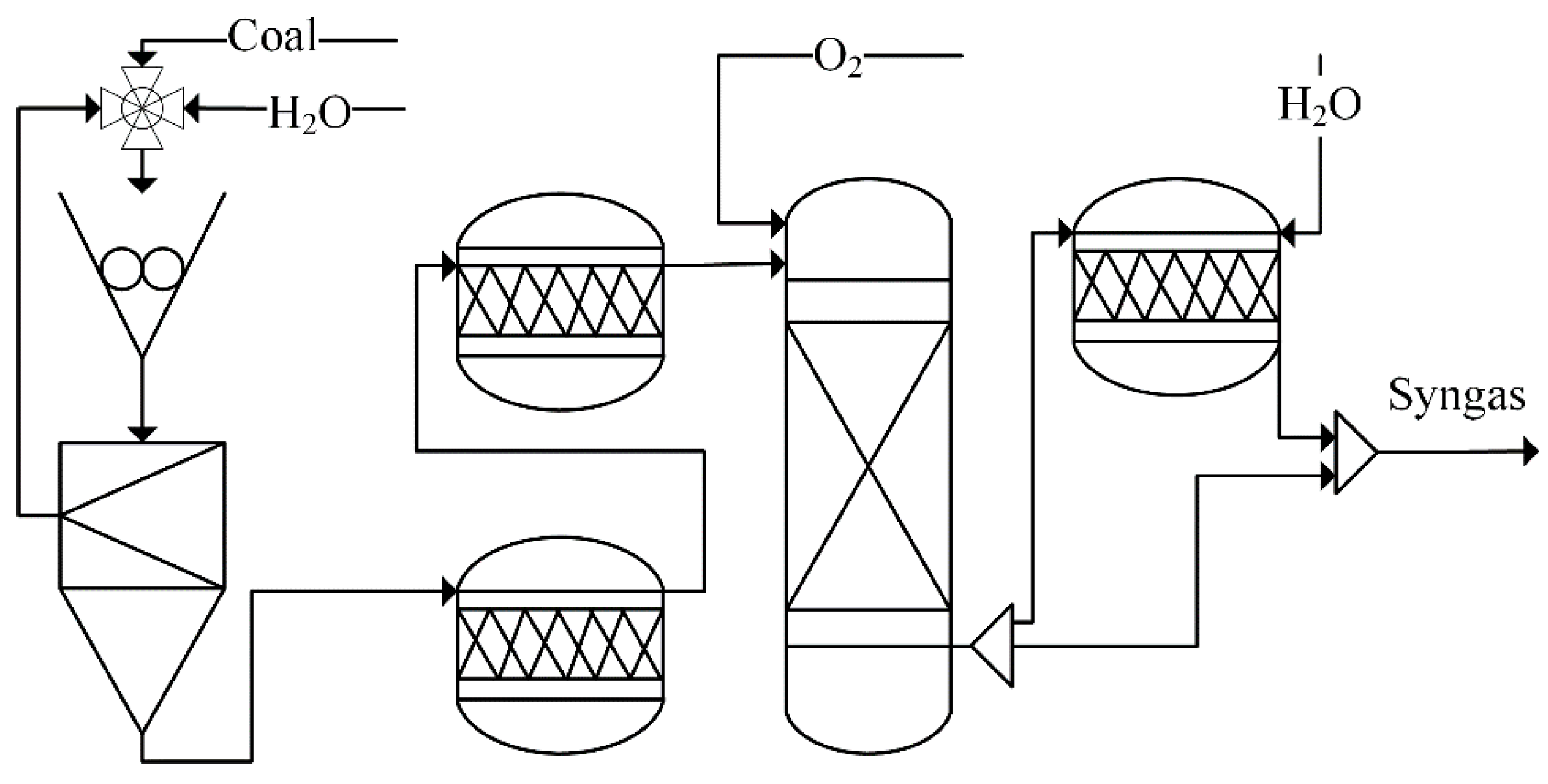
4.2. Syngas Generation
4.3. Refinery-SPC Network Integration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| F | Flow rate, kmol/h |
| H | Hydrogen flow rate, kmol/h |
| y | Component concentration |
| Rate | Gas removal rate |
| RC | Relative concentration of impurities |
| A | Set of hydrogen source |
| B | Set of hydrogen sink |
| m | Number of hydrogen sources |
| n | Number of hydrogen sinks |
| λ | Cost factor, ¥ |
| a | Subscript for hydrogen sources |
| b | Subscript for hydrogen sinks |
| k | Contaminant |
| i | Syngas routes |
| j | Components of the syngas |
| g | The proxy model function expressions of flow rate |
| f | The proxy model function expressions of components |
| sr | Hydrogen source |
| sk | Hydrogen sink |
References
- Endo, N.; Goshome, K.; Tetsuhiko, M.; Segawa, Y.; Shimoda, S.; Nozu, T. Thermal management and power saving operations for improved energy efficiency within a renewable hydrogen energy system utilizing metal hydride hydrogen storage. Int. J. Hydrogen Energy 2021, 46, 262–271. [Google Scholar] [CrossRef]
- London England British Petroleum Company. BP Statistical Review of World Energy 2021; London England British Petroleum Company: London, UK, 2021. [Google Scholar]
- Li, S.; Jin, H.; Gao, L. Cogeneration of substitute natural gas and power from coal by moderate recycle of the chemical unconverted gas. Energy 2013, 55, 658–667. [Google Scholar] [CrossRef]
- Huang, H.; Yang, S. Design concept for coal-based poly generation processes of chemicals and power with the lowest energy consumption for CO2 capture. Comput. Aided Chem. Eng. 2018, 44, 1381–1386. [Google Scholar]
- Qin, Z.; Bhattacharya, S.; Tang, K.; Zhang, Z. Effects of gasification condition on the overall performance of methanol-electricity poly generation system. Energy Convers. Manag. 2019, 184, 362–373. [Google Scholar] [CrossRef]
- Li, Y.; Veser, G. Methane and Natural Gas Utilization. Energy Technol. 2020, 8, 2000460. [Google Scholar] [CrossRef]
- London England British Petroleum Company. Statistical Review of World Energy 2020; London England British Petroleum Company: London, UK, 2020. [Google Scholar]
- Morgan, N.N.; Elsabbagh, M. Hydrogen Production from Methane Through Pulsed DC Plasma. Plasma Chem. Plasma Process 2017, 37, 1375–1392. [Google Scholar] [CrossRef]
- Chen, L.; Sreekanth, P.; Balamurali, N.; Lengyel, I.; Baek, B.; Wu, C.; Retheesh, V.M.; West, D. Experimental and numerical study of a two-stage natural gas combustion pyrolysis reactor for acetylene production: The role of delayed mixing. Proc. Combust. Inst. 2018, 37, 5715–5722. [Google Scholar] [CrossRef]
- Gambo, Y.; Jalil, A.A.; Triwahyono, S.; Abdulrasheed, A.A. Recent advances and future prospect in catalysts for oxidative coupling of methane to ethylene: A review. J. Ind. Eng. Chem. 2018, 59, 218–229. [Google Scholar] [CrossRef]
- Brady, C.; Debruyne, Q.; Majumder, A.; Goodfellow, B.; Lobo, R.; Calverley, T.; Xu, B. An integrated methane dehydroaromatization and chemical looping process. Chem. Eng. J. 2021, 406, 127168. [Google Scholar] [CrossRef]
- Li, K.; Wang, H.; Wei, Y. Syngas Generation from Methane Using a Chemical-Looping Concept: A Review of Oxygen Carriers. J. Chem. 2013, 2013, 294817. [Google Scholar] [CrossRef]
- Zhou, L.; Hu, S.; Li, Y.; Zhou, Q. Study on co-feed and co-production system based on coal and natural gas for producing DME and electricity. Chem. Eng. J.-Lausanne 2008, 136, 31–40. [Google Scholar] [CrossRef]
- Yu, B.Y.; Chien, I.L. Design and economic evaluation of a coal-based poly generation process to coproduce synthetic natural gas and ammonia. Ind. Eng. Chem. Res. 2015, 54, 10073–10087. [Google Scholar] [CrossRef]
- Gu, J.; Yang, S.; Kokossis, A. Modeling and analysis of coal-based Lurgi gasification for LNG and methanol coproduction process. Processes 2019, 7, 688. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, D.; Chen, Q.; Tang, Z. Techno-economic analysis of green methanol plant with optimal design of renewable hydrogen production: A case study in China. Int. J. Hydrogen Energy 2022, 8, 47. [Google Scholar] [CrossRef]
- Joao, A. Analysis and Design of Refinery Hydrogen Distribution Systems; University of Manchester: Manchester, UK, 1999. [Google Scholar]
- El-Halwagi, M.M.; Gabriel, F.; Harell, D. Rigorous Graphical Targeting for Resource Conservation via Material Recycle/Reuse Networks. Ind. Eng. Chem. Res. 2003, 42, 4319–4328. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, G.; Feng, X. New Graphical Method for The Integration of Hydrogen Distribution Systems. Ind. Eng. Chem. Res. 2006, 45, 6512–6517. [Google Scholar] [CrossRef]
- Foo, D.C.Y.; Manan, Z.A. Setting the Minimum Utility Gas Flow Rate Targets Using Cascade Analysis Technique. Ind. Eng. Chem. Res. 2006, 45, 5986–5995. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, M.; Liu, G.; Feng, X. Relative Concentration Based Pinch Analysis for Targeting and Design of Hydrogen and Water Networks with Single Contaminant. J. Clean. Prod. 2016, 112, 4799–4814. [Google Scholar]
- Yang, M.; Feng, X.; Liu, G. Algebraic Approach for The Integration of The Hydrogen Network with A Single Impurity. Ind. Eng. Chem. Res. 2016, 55, 615–623. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Q.; Yang, M.; Liu, G. A Graphical Method for Optimization of Hydrogen Networks Considering Impurity Removal Through Chemical Absorption. Chem. Eng. Trans. 2018, 70, 1159–1164. [Google Scholar]
- Hallale, N.; Liu, F. Refinery Hydrogen Management for Clean Fuels Production. Adv. Environ. Res. 2001, 6, 81–98. [Google Scholar] [CrossRef]
- Zhang, Q.; Song, H.; Liu, G.; Shi, G. Relative Concentration-Based Mathematical Optimization for The Fluctuant Analysis of Multi-Impurity Hydrogen Networks. Ind. Eng. Chem. Res. 2016, 55, 10344–10354. [Google Scholar] [CrossRef]
- Jia, X.; Liu, G. Optimization of Hydrogen Networks with Multiple Impurities and Impurity Removal. Chin. J. Chem. Eng. 2016, 24, 1236–1242. [Google Scholar] [CrossRef]
- Liao, Z.; Tu, G.; Lou, J.; Jiang, B.; Wang, J.; Yang, Y. The Influence of Purifier Models on Hydrogen Network Optimization: Insights from A Case Study. Int. J. Hydrogen Energy 2016, 41, 5243–5249. [Google Scholar] [CrossRef]
- Hu, L.; Jin, H.; Lin, G.; Han, W. Economic Analysis of Coal-Based Polygene Ration System for Methanol and Power Production. Energy 2010, 35, 858–863. [Google Scholar]
- Bose, A.; Jana, K.; Mitra, D.; De, S. Co-production of Power and Urea from Coal with CO2 Capture: Performance Assessment. Clean Technol. Environ. Policy 2015, 17, 1271–1280. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Y.; Lei, K.; Ye, B.; Cao, J.; Liu, D. Thermodynamic and Economic Analyses of a Novel Coal Pyrolysis-Gasification-Combustion Staged Conversion Utilization Polygene Ration System. Asia-Pac. J. Chem. Eng. 2018, 13, 2171. [Google Scholar] [CrossRef]
- Chen, Y.; Adams, T.A.; Barton, P.I. Optimal Design and Operation of Static Energy Polygene Ration Systems. Ind. Eng. Chem. Res. 2011, 50, 5099–5113. [Google Scholar] [CrossRef]
- Thomas, I.; Barton, P.I. Combining Coal Gasification and Natural Gas Reforming for Efficient Polygene Ration—ScienceDirect. Fuel Process. Technol. 2011, 92, 639–655. [Google Scholar]
- Yang, S.; Yang, Q.; Yi, M.; Xiang, D.; Qian, Y. Conceptual Design and Analysis of a Natural Gas Assisted Coal-to-Olefins Process for CO2 Reuse. Ind. Eng. Chem. Res. 2013, 52, 14406–14414. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, X.; Zhu, S.; Huang, W.; Zhang, D. Efficient Utilization of CO2 In a Coal to Ethylene Glycol Process Integrated with Dry/Steam-Mixed Reforming: Conceptual Design and Techno-Economic Analysis. Acs Sustain. Chem. Eng. 2019, 7, 3496–3510. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, Y.; Feng, X.; Yang, M.; Zhao, L. The Integration of Hybrid Hydrogen Networks for Refinery and Synthetic Plant of Chemicals. Int. J. Hydrogen Energy 2020, 46, 1473–1487. [Google Scholar] [CrossRef]




| Reaction | Output t/h | Feed Gas Flow Rate kmol·h−1 | ||
|---|---|---|---|---|
| CO | CO2 | H2 | ||
| Ethylene glycol | 36.94 | 1578 | 0 | 2981 |
| Methanol | 73.49 | 0 | 1242 | 4271 |
| Urea | 73.02 | 2664 | 91.9 | 5603 |
| Hydrogen Source | Molar Flow kmol·h−1 | Relative Concentration of Impurities | ||
|---|---|---|---|---|
| S | N | C | ||
| sr1 | 2901.79 | 0.0000 | 0.0000 | 0.0001 |
| sr2 | 892.53 | 0.0115 | 0.0264 | 0.1089 |
| sr3 | 1205.98 | 0.0147 | 0.0170 | 0.0995 |
| sr4 | 1189.67 | 0.0180 | 0.0159 | 0.0276 |
| sr5 | 883.43 | 0.0067 | 0.0552 | 0.0112 |
| sr6 | 999.40 | 0.0271 | 0.0627 | 0.1092 |
| Hydrogen Sink | Molar Flow kmol·h−1 | Relative Concentration of Impurities | ||
|---|---|---|---|---|
| S | N | C | ||
| sk1 | 785.71 | 0.0226 | 0.0769 | 0.0769 |
| sk2 | 457.14 | 0.0131 | 0.0559 | 0.0559 |
| sk3 | 687.14 | 0.0154 | 0.0162 | 0.0162 |
| sk4 | 1002.56 | 0.0075 | 0.0085 | 0.0085 |
| sk5 | 1134.38 | 0.0354 | 0.1311 | 0.1311 |
| sk6 | 1409.38 | 0.0132 | 0.0518 | 0.0518 |
| Device | Output Variables | RMSE | R2 | Device | Output Variables | RMSE | R2 |
|---|---|---|---|---|---|---|---|
| SMR | 101.8 | 0.9999 | CG | 5.619 | 0.9999 | ||
| 0.001444 | 0.9999 | 0.0000461 | 0.9999 | ||||
| 0.000835 | 0.9995 | 0.0000131 | 0.9999 | ||||
| 0.000251 | 0.9989 | 0.0000095 | 0.9999 | ||||
| 0.001319 | 0.9999 | 0.0000235 | 0.9999 | ||||
| 0.000734 | 0.9912 | ||||||
| Items | Raw Material Consumption | H2 Discharge kmol/h | CO2 Discharge kmol/h | CO Discharge kmol/h | Cost 104 ¥/y | |
|---|---|---|---|---|---|---|
| Coal to ethylene glycol | 48.8 t/h | 0 | 1006.0 | 0 | 80,359 | |
| Natural gas to urea | 1264.0 kmol/h | 804.0 | 0 | 35.3 | 117,391 | |
| Natural gas to methanol | 2836.6 kmol/h | 2914.6 | 29.7 | 11.9 | 193,251 | |
| Natural Gas to Hydrogen (Refinery) | 315.4 kmol/h | 0 | 325.9 | 9.4 | 30,398 | |
| Total | Coal Natural gas | 48.8 t/h 4415.9 kmol/h | 3718.6 | 1361.6 | 103.6 | 421,184 |
| Items | Raw Material Consumption | H2 Discharge kmol/h | CO2 Discharge kmol/h | CO Discharge kmol/h | Cost 104 ¥/y | |
|---|---|---|---|---|---|---|
| Original situation | Coal Methane | 48.8 t/h 4415.9 kmol/h | 3718.6 | 1361.576 | 103.62 | 421,184 |
| Optimization results | Coal Methane | 39.5 t/h 3479.4 kmol/h | 0 | 0 | 0 | 322,547 |
| Reduction | Coal Methane | 19.1% 21.2% | 100% | 100% | 100% | 23.46% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Zhang, Q.; Feng, X. Integrated Optimization for the Coupling Network of Refinery and Synthetic Plant of Chemicals. Processes 2023, 11, 789. https://doi.org/10.3390/pr11030789
Yang S, Zhang Q, Feng X. Integrated Optimization for the Coupling Network of Refinery and Synthetic Plant of Chemicals. Processes. 2023; 11(3):789. https://doi.org/10.3390/pr11030789
Chicago/Turabian StyleYang, Sen, Qiao Zhang, and Xiao Feng. 2023. "Integrated Optimization for the Coupling Network of Refinery and Synthetic Plant of Chemicals" Processes 11, no. 3: 789. https://doi.org/10.3390/pr11030789
APA StyleYang, S., Zhang, Q., & Feng, X. (2023). Integrated Optimization for the Coupling Network of Refinery and Synthetic Plant of Chemicals. Processes, 11(3), 789. https://doi.org/10.3390/pr11030789







