A Gas Emission Prediction Model Based on Feature Selection and Improved Machine Learning
Abstract
1. Introduction
2. Data Processing for Gas Emission Prediction
2.1. Initial Index System of Gas Emission Prediction
2.2. Data Standardization Processing
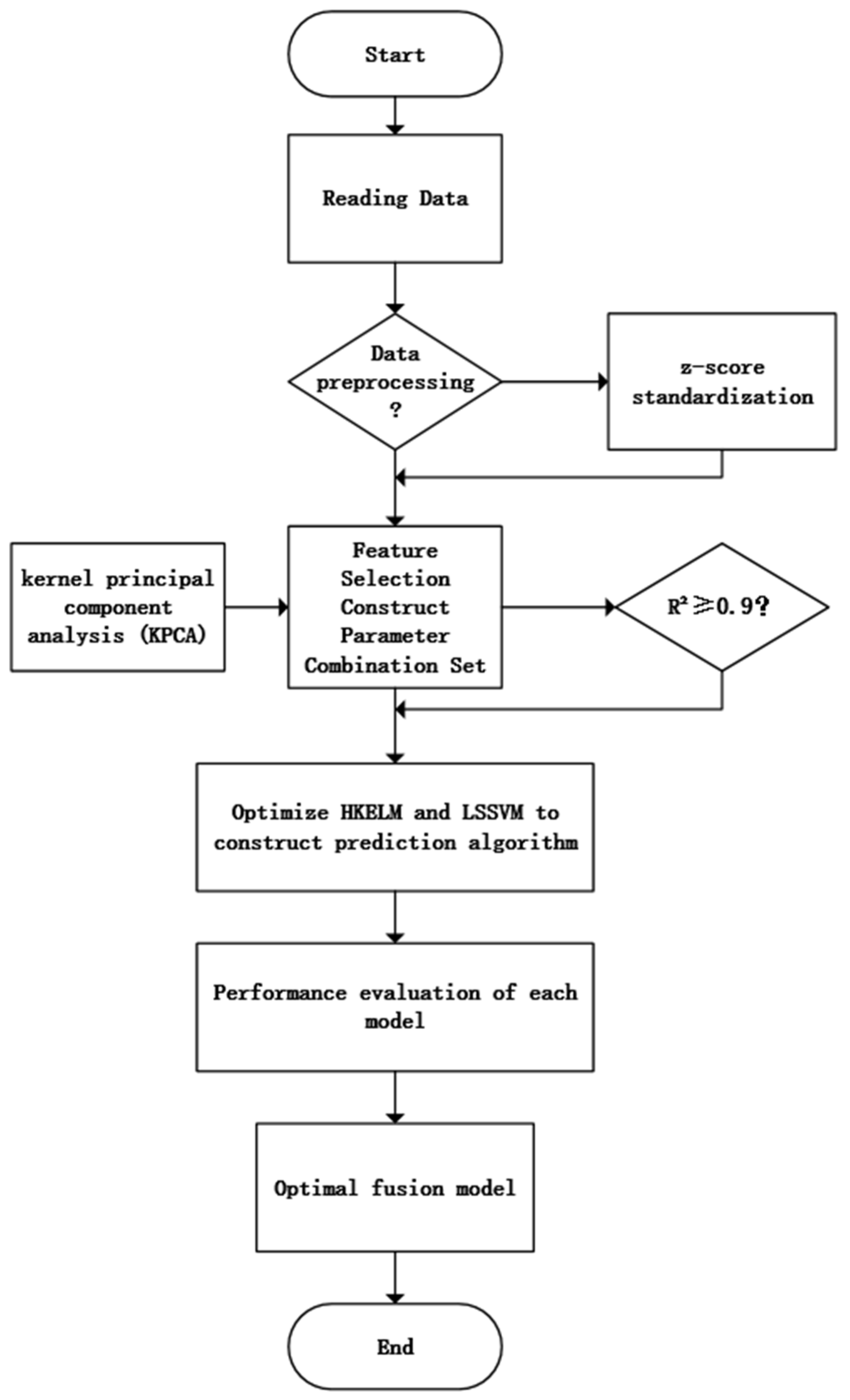
3. Construction of the Mine Gas Emission Prediction Model
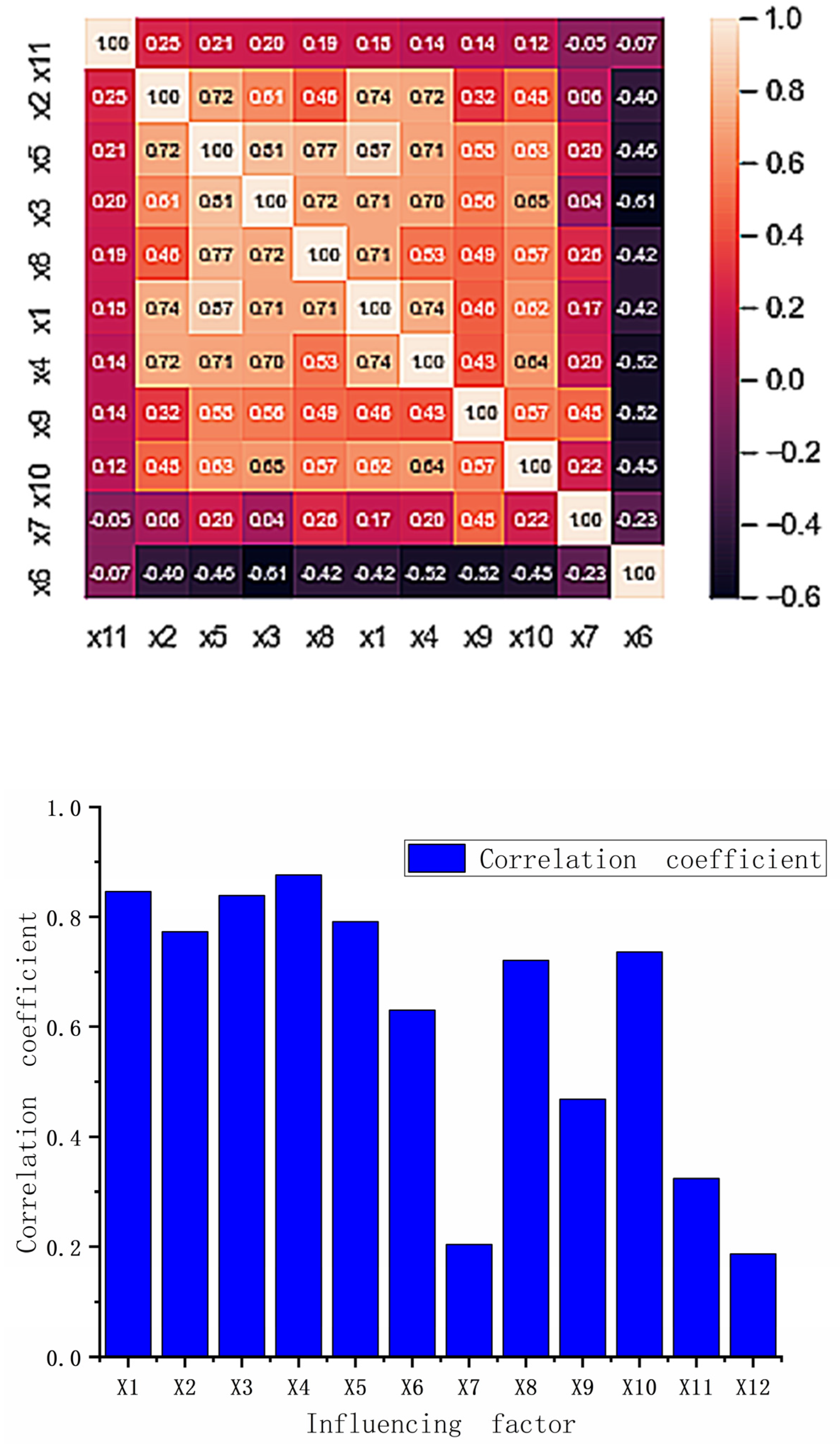
3.1. Determination of Characteristic Parameter Sets for Gas Emission Prediction
3.1.1. Total Subset Regression
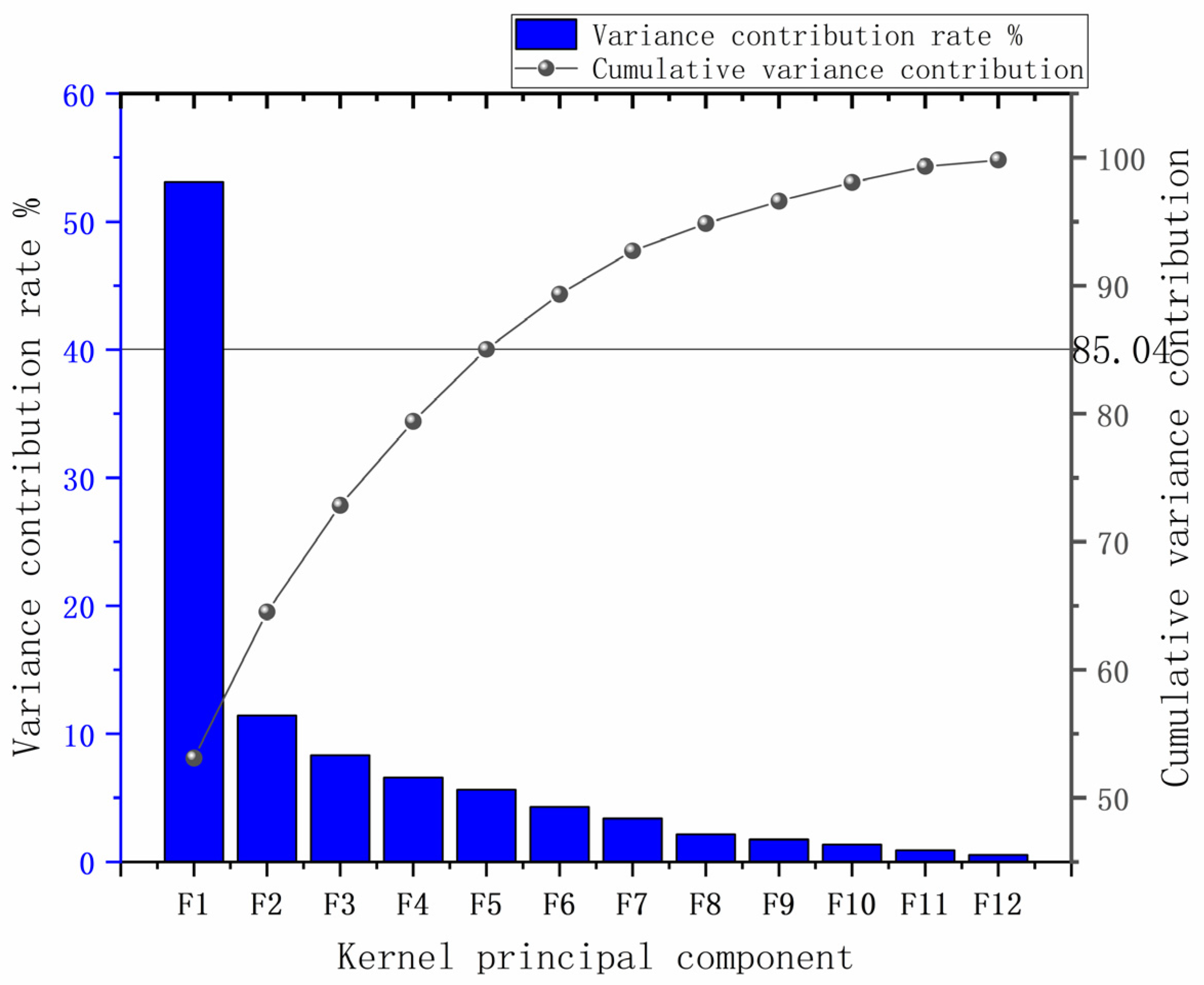
3.1.2. Kernel Principal Component Analysis (KPCA)
3.2. A Selection of Gas Emission Prediction Algorithms
4. Optimal Fusion Model Selection
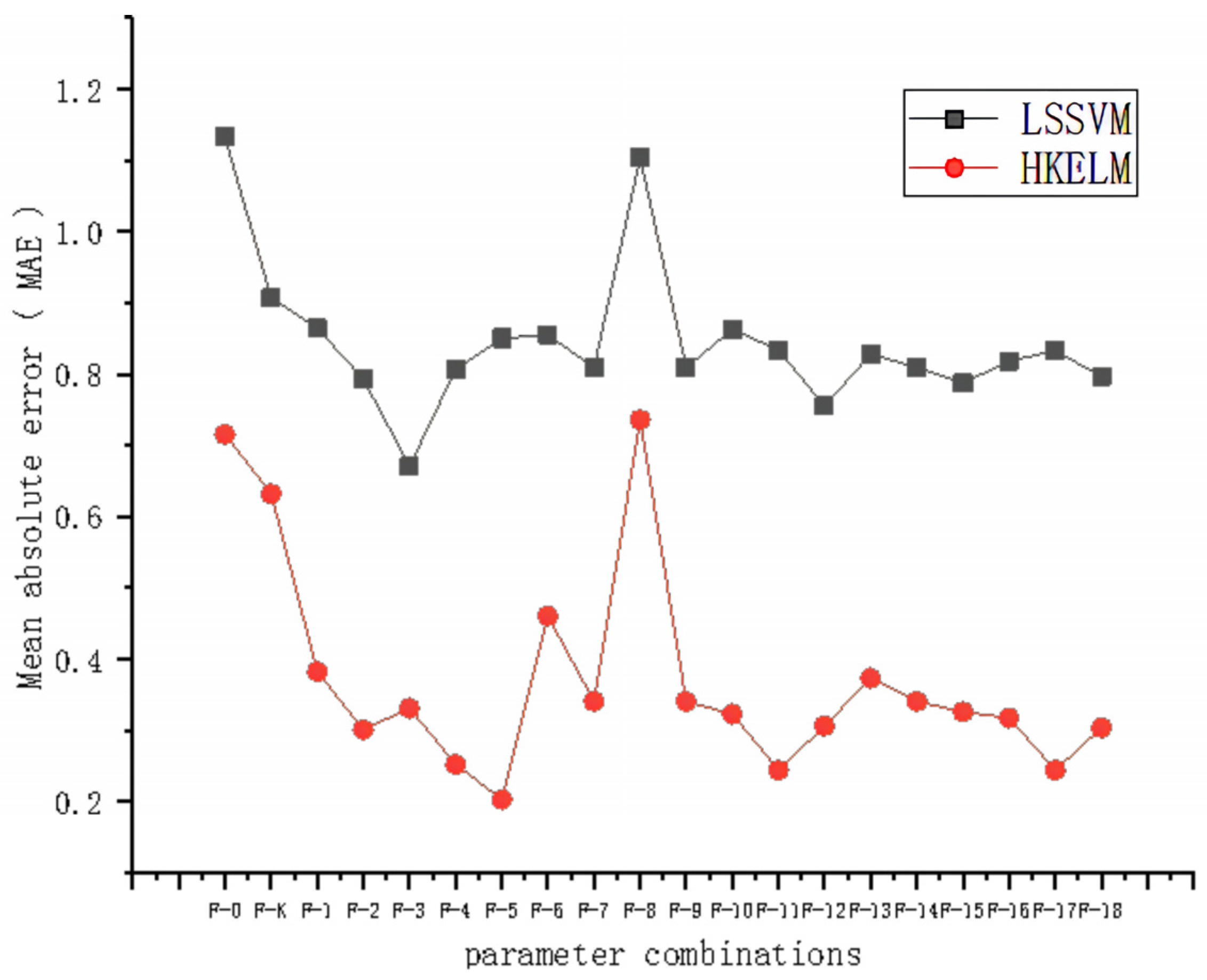
4.1. Determination of the Optimal Parameter Set
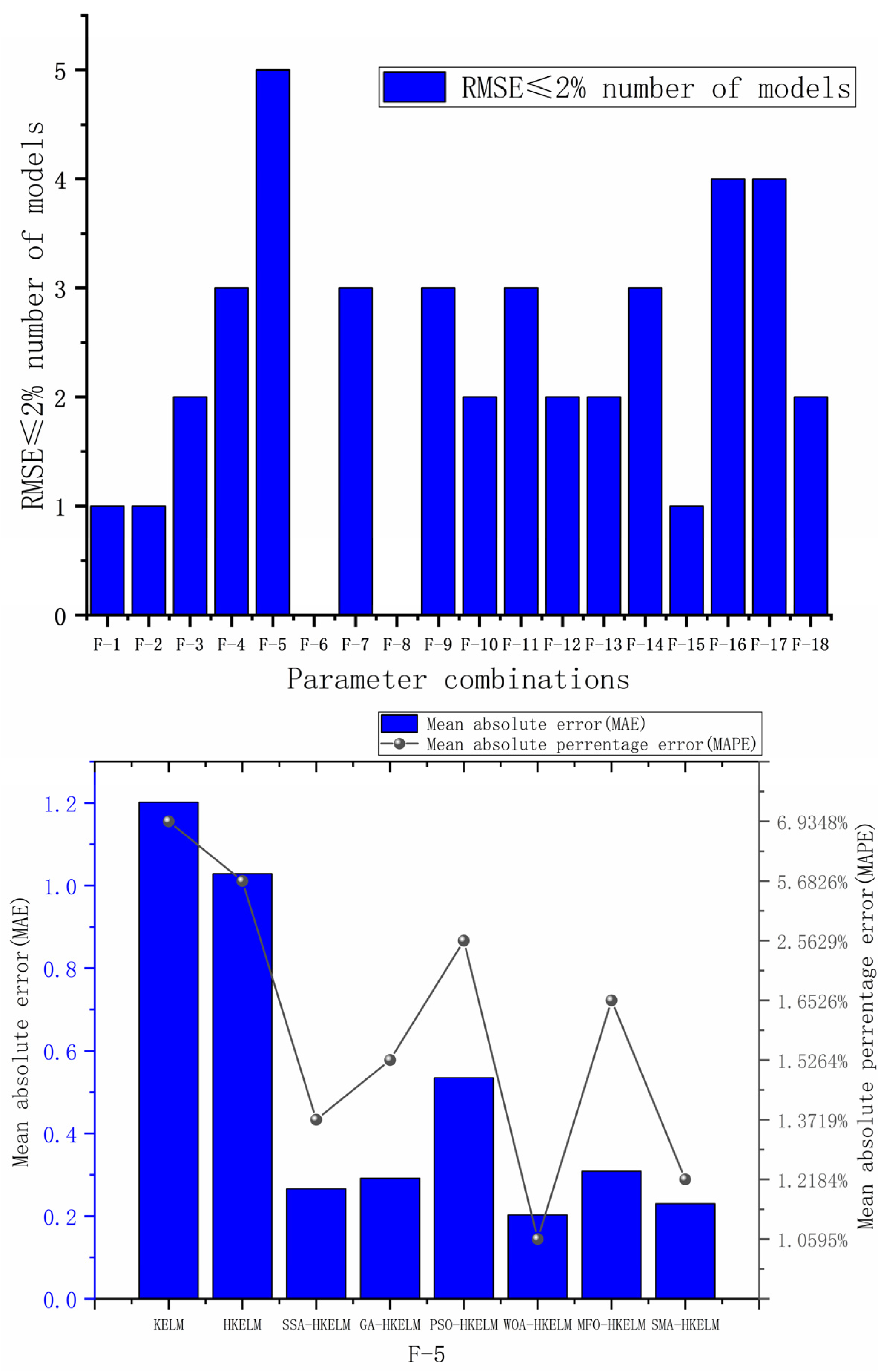
4.2. Determination of the Optimal Improved Machine Learning Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Qin, Y.J.; Su, W.W.; Jiang, W.Z.; Chen, Y.P. Mine gas emission prediction technology in China. Research progress and development direction of coal mine safety, ploidy of 2020. 52–59. [CrossRef]
- Xie, H.P.; Zhou, H.W.; Xu, D.J.; Wang, H.W.; Zhang, R.; Gao, F. Research and consideration on deep coal mining and critical mining depth. J. China Coal Soc. 2012, 37, 535–542. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Q. Weighted grey target decision method to predict coal and gas outburst dangerous study. J. Saf. Environ. Eng. 2021, 28, 61–66. [Google Scholar] [CrossRef]
- Qin, Y.; Su, W.; Jiang, W.; Chen, Y. Research progress and development direction of mine gas emission prediction technology in China. Coal Mine Saf. 2020, 51, 52–59. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, J.; Huang, Z. Numerical study on cavitation-vortex-noise correlation mechanism and dynamic mode decomposition of a hydrofoil. Phys. Fluids 2022, 34, 125105. [Google Scholar] [CrossRef]
- Guo, B.; Wang, Y.; Zhou, H.; Hu, F. Can environmental tax reform promote carbon abatement of resource-based cities? Evidence from a quasi-natural experiment in China. Environ. Sci. Pollut. Res. 2022, 1–13. [Google Scholar] [CrossRef]
- Lu, S.; Guo, J.; Liu, S.; Yang, B.; Liu, M.; Yin, L.; Zheng, W. An improved algorithm of drift compensation for olfactory sensors. Appl. Sci. 2022, 12, 9529. [Google Scholar] [CrossRef]
- Qin, X.; Liu, Z.; Liu, Y.; Liu, S.; Yang, B.; Yin, L.; Liu, M.; Zheng, W. User OCEAN personality model construction method using a bp neural network. Electronics 2022, 11, 3022. [Google Scholar] [CrossRef]
- Wang, Y.; Zhan, G.; Fu, H.; Wang, S. Gas emission prediction based on variational mode decomposition and deep integrated combination model. Control Eng. 2022, 1–12. [Google Scholar] [CrossRef]
- Dai, W.; Fu, H.; Ji, C.P.; Wang, Y.J. Prediction method of VMD-DE-RVM interval for gas emission in mining face. China Saf. Sci. J. 2018, 28, 109–115. [Google Scholar] [CrossRef]
- Li, B.; Zhang, C.H.; Li, X.J.; Wang, X.F. Prediction of mine gas emission based on PCA-ELM. World Sci. Res. Dev. 2016, 38, 49–53. (In Chinese) [Google Scholar] [CrossRef]
- Xiao, P.; Xie, X.; Shuang, H.; Liu, C.; Wang, H.; Xu, J. Prediction of gas emission based on KPCA-CMGANN algorithm. China Saf. Sci. J. 2020, 30, 39–47. [Google Scholar] [CrossRef]
- Wen, T.; Sun, X.; Kong, X.; Tian, H. Sub-source prediction of gas emission based on PSOBP-AdaBoost model. China Saf. Sci. J. 2016, 26, 94–98. [Google Scholar] [CrossRef]
- Chen, W.H.; Yan, X.H.; Fu, H. Application of improved Elman neural network in gas emission prediction. J. Saf. Environ. 2015, 15, 19–24. [Google Scholar] [CrossRef]
- Peng, X.H.; Liu, L.Q. Wavelet packet neural network prediction method in the application of gas emission. J. Microelectron. Comput. 2016, 114, 129–133. [Google Scholar] [CrossRef]
- Xu, Y.; Qi, C.; Feng, S. Prediction model of gas emission based on IGSA-BP network. J. Electron. Meas. Instrum. 2019, 33, 111–117. [Google Scholar] [CrossRef]
- Ma, S.; Li, X. Improved BP neural network prediction model for coal mine gas emission. Min. Res. Dev. 2019, 39, 138–142. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Han, Q.; Li, Y.; Zhou, C. Prediction of gas emission in mining face based on PCA-BO-XGBoost. J. Xi’an Univ. Sci. Technol. 2022, 42, 371–379. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, L. Prediction of gas emission in Mining face based on LASSO-LARS. Coal Sci. Technol. 2022, 50, 171–176. [Google Scholar] [CrossRef]
- Lin, H.; Zhou, J.; Gao, F.; Jin, H.; Yang, Z.; Liu, S. Coal seam gas content prediction based on feature selection and machine learning fusion. Coal Sci. Technol. 2021, 49, 44–51. [Google Scholar] [CrossRef]
- Chen, J.; Wang, S.; Liu, X.; Zheng, S.; Wang, G.; Sun, L. Study on influencing factors of gas emission from horizontal sublevel mining face in steeply inclined extra-thick coal seam. Coal Sci. Technol. 2022, 50, 127–135. [Google Scholar] [CrossRef]
- Xiong, Y.; Cheng, J.; Duan, Z. Gas emission prediction model of coal mine based on CSBP algorithm. ITM Web Conf. 2016, 7, 09006. [Google Scholar] [CrossRef]
- Cao, L.Y.; Fan, Q.Q.; Huang, J.Y. Intraoperative hypothermia prediction based on feature selection and XGBoost optimization. Data Acquis. Process. 2022, 37, 134–146. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Liu, Z.; Qi, J. Research on gas emission prediction model based on IABC-LSSVM. Sens. Microsyst. 2022, 41, 34–38. [Google Scholar] [CrossRef]
- Shi, Y.S.; Li, J.; Ren, J.R.; Zhang, K. Prediction of residual service life of lithiumion batteries based on WOA-XGBoost. Energy Storage Sci. Technol. 2022, 11, 3354–3363. (In Chinese) [Google Scholar] [CrossRef]
- Jia, J.; Ke, D.; Chen, Y. Prediction of coal mine gas emission based on orthogonal test-multiple regression. J. Saf. Environ. 2021, 21, 2037–2044. [Google Scholar] [CrossRef]
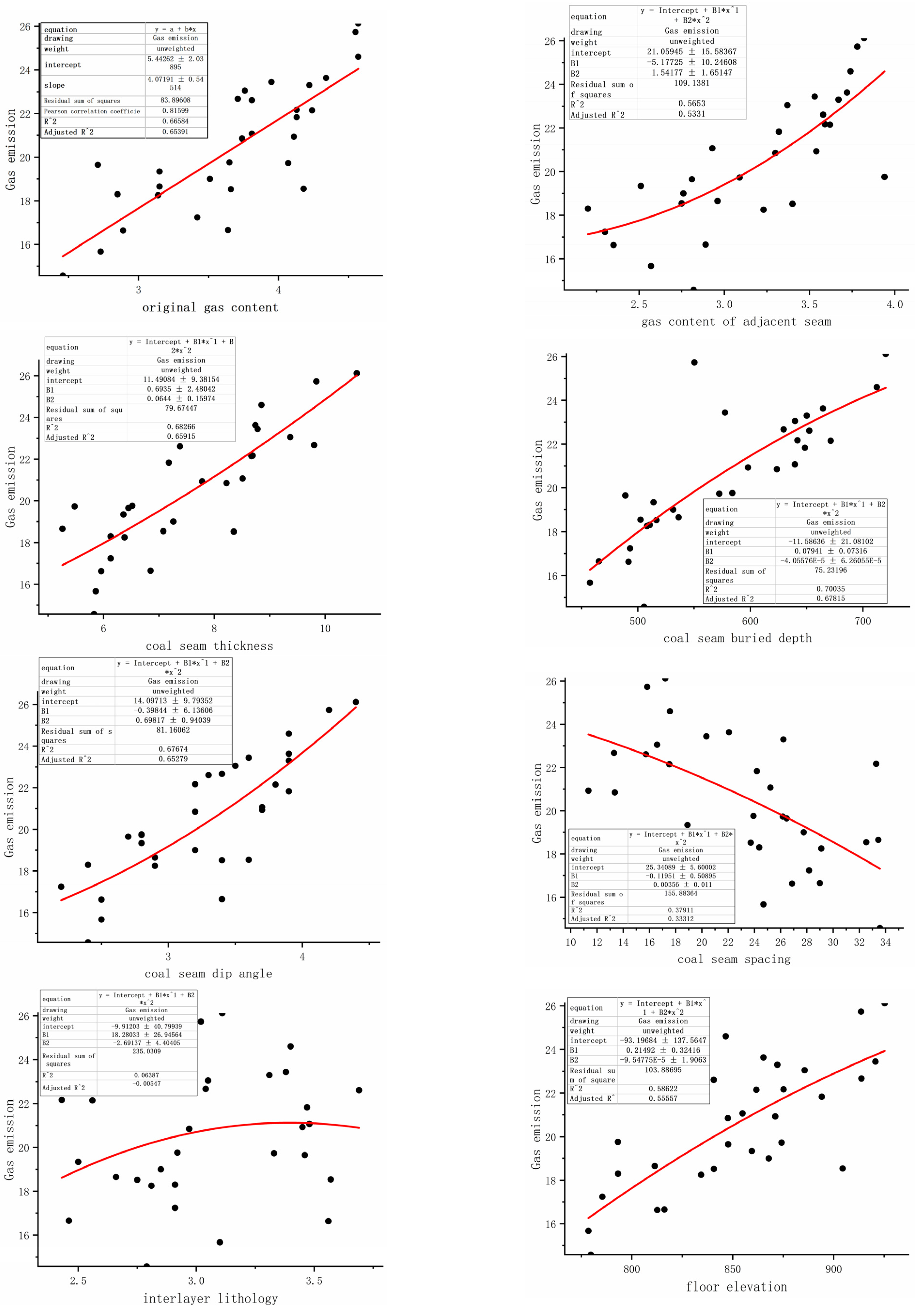


| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | Y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.55 | 3.78 | 9.84 | 550.32 | 4.20 | 15.83 | 3.02 | 913.54 | 7.40 | 0.35 | 4.80 | 1 | 25.73 |
| 2 | 3.95 | 3.53 | 8.78 | 577.5 | 3.60 | 20.34 | 3.38 | 920.65 | 7.20 | 0.32 | 4.67 | 1 | 23.44 |
| 3 | 2.85 | 2.2 | 6.13 | 510.58 | 2.40 | 24.37 | 2.91 | 793.20 | 6.70 | 0.25 | 4.50 | 1 | 18.30 |
| 4 | 3.81 | 2.93 | 8.51 | 639.53 | 3.70 | 25.22 | 3.48 | 854.84 | 7.30 | 0.27 | 3.72 | 1 | 21.07 |
| 5 | 4.22 | 3.67 | 7.54 | 650.12 | 3.90 | 26.21 | 3.31 | 872.09 | 7.10 | 0.23 | 4.04 | 1 | 23.30 |
| 6 | 4.13 | 3.59 | 8.69 | 641.82 | 3.20 | 33.28 | 2.43 | 875.15 | 6.50 | 0.33 | 3.35 | 1 | 22.17 |
| 7 | 4.34 | 3.72 | 8.74 | 664.48 | 3.90 | 22.06 | 2.90 | 865.18 | 7.20 | 0.35 | 3.11 | 1 | 23.63 |
| 8 | 4.57 | 3.82 | 10.57 | 720.22 | 4.40 | 17.21 | 3.11 | 925.24 | 7.50 | 0.36 | 3.79 | 1 | 26.12 |
| 9 | 3.81 | 3.58 | 7.38 | 652.35 | 3.30 | 15.73 | 3.69 | 840.59 | 7.30 | 0.28 | 3.22 | 1 | 22.61 |
| 10 | 2.89 | 2.35 | 5.96 | 491.75 | 2.50 | 26.87 | 3.56 | 812.59 | 7.40 | 0.29 | 3.01 | 1 | 16.63 |
| 11 | 3.14 | 3.23 | 6.38 | 508.17 | 2.90 | 29.10 | 2.81 | 834.33 | 6.90 | 0.23 | 3.19 | 1 | 18.25 |
| 12 | 4.57 | 3.74 | 8.85 | 712.25 | 3.90 | 17.56 | 3.40 | 846.53 | 7.40 | 0.33 | 2.49 | 1 | 24.60 |
| 13 | 3.51 | 2.76 | 7.26 | 531.35 | 3.20 | 27.76 | 2.85 | 867.83 | 6.80 | 0.28 | 2.50 | 1 | 19.00 |
| 14 | 3.71 | 2.84 | 9.8 | 629.55 | 3.40 | 13.30 | 3.04 | 913.71 | 7.30 | 0.30 | 3.48 | 1 | 22.67 |
| 15 | 3.76 | 3.37 | 9.37 | 639.67 | 3.50 | 16.58 | 3.05 | 885.61 | 7.20 | 0.26 | 3.17 | 1 | 23.05 |
| 16 | 3.15 | 2.51 | 6.36 | 514.03 | 2.80 | 18.90 | 2.50 | 859.43 | 6.80 | 0.22 | 2.89 | 1 | 19.34 |
| 17 | 4.11 | 3.54 | 7.78 | 597.87 | 3.70 | 11.35 | 3.45 | 871.07 | 6.90 | 0.33 | 2.50 | 1 | 20.93 |
| 18 | 4.18 | 2.75 | 7.08 | 502.45 | 3.60 | 32.53 | 3.57 | 904.41 | 6.90 | 0.18 | 3.00 | 1 | 18.54 |
| 19 | 2.71 | 2.81 | 6.45 | 488.96 | 2.70 | 26.46 | 3.46 | 847.72 | 6.80 | 0.15 | 3.30 | 1 | 19.65 |
| 20 | 3.64 | 2.89 | 6.85 | 465.42 | 3.40 | 28.99 | 2.46 | 816.14 | 6.60 | 0.18 | 3.36 | 1 | 16.65 |
| 21 | 3.66 | 3.40 | 8.35 | 516.57 | 3.40 | 23.72 | 2.75 | 840.67 | 7.40 | 0.17 | 3.70 | 1 | 18.52 |
| 22 | 4.07 | 3.09 | 5.48 | 572.34 | 2.80 | 26.16 | 3.33 | 874.15 | 7.00 | 0.20 | 3.64 | 1 | 19.73 |
| 23 | 3.74 | 3.30 | 8.22 | 623.52 | 3.20 | 13.36 | 2.97 | 847.57 | 6.60 | 0.18 | 3.51 | 1 | 20.85 |
| 24 | 2.73 | 2.57 | 5.86 | 457.53 | 2.50 | 24.69 | 3.10 | 778.53 | 7.30 | 0.21 | 2.98 | 1 | 15.67 |
| 25 | 3.42 | 2.30 | 6.13 | 493.20 | 2.20 | 28.17 | 2.91 | 785.41 | 6.60 | 0.20 | 3.29 | 1 | 17.24 |
| 26 | 3.65 | 3.94 | 6.52 | 584.00 | 2.80 | 23.93 | 2.92 | 793.10 | 6.60 | 0.22 | 4.08 | 1 | 19.76 |
| 27 | 3.15 | 2.96 | 5.26 | 536.24 | 2.90 | 33.45 | 2.66 | 811.35 | 6.50 | 0.18 | 3.27 | 1 | 18.65 |
| 28 | 4.13 | 3.32 | 7.18 | 648.45 | 3.90 | 24.19 | 3.47 | 894.11 | 7.30 | 0.34 | 4.52 | 1 | 21.83 |
| 29 | 4.24 | 3.62 | 8.67 | 671.30 | 3.80 | 17.52 | 2.56 | 861.71 | 7.30 | 0.27 | 4.48 | 1 | 22.15 |
| 30 | 2.46 | 2.82 | 5.83 | 505.57 | 2.40 | 33.57 | 2.79 | 779.70 | 6.30 | 0.14 | 3.73 | 1 | 14.57 |
| Influencing Factor | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F-0 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ |
| F-1 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | |||||
| F-2 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | |||||
| F-3 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | |||||
| F-4 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | |||||
| F-5 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | |||||
| F-6 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ||||||
| F-7 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ||||||
| F-8 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ||||||
| F-9 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ||||||
| F-10 | ☆ | ☆ | ☆ | ☆ | ☆ | |||||||
| F-11 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ||||||
| F-12 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ||||||
| F-13 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ||||||
| F-14 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ||||||
| F-15 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ||||||
| F-16 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | |||||
| F-17 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ | |||||
| F-18 | ☆ | ☆ | ☆ | ☆ | ☆ | ☆ |
| Kernel Principal Component | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| variance contribution rate % | 53.11 | 11.41 | 8.31 | 6.57 | 5.63 | 4.30 | 3.38 | 2.14 | 1.75 | 1.35 | 0.90 | 0.52 |
| Parameter Combinations | Improved Algorithm | RMSE | MAE | MAPE | R2 | NSE |
|---|---|---|---|---|---|---|
| F-0 | GA-HKELM | 0.93431 | 0.63198 | 3.8216% | 0.88091 | 0.87333 |
| F-K | SSA-HKELM | 1.02890 | 0.71577 | 4.2977% | 0.88348 | 0.84639 |
| F-4 | WOA-HKELM | 0.28456 | 0.25234 | 1.3347% | 0.98987 | 0.98825 |
| F-5 | SSA-HKELM | 0.37306 | 0.26626 | 1.3719% | 0.99184 | 0.97980 |
| F-5 | SMA-HKELM | 0.25932 | 0.23025 | 1.2184% | 0.99194 | 0.99024 |
| F-5 | WOA-HKELM | 0.22865 | 0.20306 | 1.0595% | 0.99395 | 0.99241 |
| F-11 | SSA-HKELM | 0.37306 | 0.26626 | 1.3719% | 0.99184 | 0.97980 |
| F-11 | MFO-HKELM | 0.31620 | 0.24417 | 1.2260% | 0.99592 | 0.98549 |
| F-11 | WOA-HKELM | 0.31637 | 0.24134 | 1.2068% | 0.99594 | 0.98548 |
| F-17 | MFO-HKELM | 0.31620 | 0.24417 | 1.2260% | 0.99592 | 0.98549 |
| F-17 | WOA-HKELM | 0.31637 | 0.24134 | 1.2068% | 0.99594 | 0.98548 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, L.; Zhang, K. A Gas Emission Prediction Model Based on Feature Selection and Improved Machine Learning. Processes 2023, 11, 883. https://doi.org/10.3390/pr11030883
Shao L, Zhang K. A Gas Emission Prediction Model Based on Feature Selection and Improved Machine Learning. Processes. 2023; 11(3):883. https://doi.org/10.3390/pr11030883
Chicago/Turabian StyleShao, Liangshan, and Kun Zhang. 2023. "A Gas Emission Prediction Model Based on Feature Selection and Improved Machine Learning" Processes 11, no. 3: 883. https://doi.org/10.3390/pr11030883
APA StyleShao, L., & Zhang, K. (2023). A Gas Emission Prediction Model Based on Feature Selection and Improved Machine Learning. Processes, 11(3), 883. https://doi.org/10.3390/pr11030883






