Abstract
This paper proposes a methodology based on a genetic algorithms (GA) to calibrate the parameters of a chlorine decay model in a water distribution system (WDS). The proposed methodology first contemplates that a GA is implemented using historical measurements of chlorine concentration at some sensed nodes to calibrate the unknown values corresponding to both the bulk and wall reaction coefficients. Once both parameters are estimated, the optimal-fit chlorine decay model is used to predict the decay of chlorine concentration in the water at each node for any concentration input at the pumping station. Then, a second GA-based algorithm is implemented to obtain the minimal chlorine concentration needed at the input to ensure that every node in the system meets the official normativity requirements for free chlorine in a WDS. The proposed methodology performed satisfactorily for a WDS simulated in EPANET with a GA implemented in MATLAB, both for the estimation of the reaction coefficients and the optimization of the required chlorine concentration at the input. Simulation results illustrate the performance of the proposed algorithm.
1. Introduction
Water management companies focus on meeting water demand and ensuring chlorine concentration requirements. In recent decades, water pollution has unfortunately increased worldwide and as a result, continuous monitoring to maintain the integrity of drinking water has gained increasing importance. Water quality is a broad term that is related to many aspects of both the physics and the chemistry of drinking water. According to [1], the quality of the water is closely related to parameters such as turbidity, temperature, color, taste, solids in suspension, pH, and the concentration of many elements (such as nitrogen, fluoride and other heavy metals) and substances such as chlorine residual (Cl2). From all of the abovementioned parameters, chlorine residual is typically the most addressed. Even if chlorine does not exist naturally in water, it is added to it for disinfection purposes, specially in the case of drinking and waste water. In [2] it is stated that the residual chlorine concentration maintained in the distribution system ensures a good sanitary quality of the water being distributed, which makes it one of the most important parameters to monitor to make certain the quality of the water in a distribution system.
As stated in [3], both laboratory and online measurements are necessary to account for chlorine concentration monitoring. Typically, bacteriological measurements (e.g., the number of Escherichia coli bacteria) are among the typical laboratory measurements in a water distribution system (WDS). However, laboratory testing cannot be performed online for obvious reasons and this delays the time in which the quality of the water being distributed is known. As a result, water agencies rely on online measurements to estimate the water quality in the WDS. In this way, adequate levels of chlorine allow immediate elimination of harmful bacteria and viruses and provide a protective residual throughout the drinking water distribution network [4]. However, because drinking water systems are complex, it is not easy to ensure that residuals are maintained throughout the distribution network under permissible levels. On the one hand, excessive chlorine dosages may consequently lead to formation of chlorine by-products, some of which are carcinogenic and may also cause birth-related problems such as low birth weight and genetic malformations [5]. On the other hand, an insufficient chlorine residual could cause the multiplication of pathogenic bacteria, which in turn could trigger public health problems with severe consequences.
Since chlorine reacts with organic matter found in water, its concentration decreases over time. Thus residual chlorine decay models can predict this decrease, including chlorine levels to comply with the normative standard that establishes the lower and upper bounds in which free chlorine can be found. The World Health Organization (WHO) indicates that to adequately treat drinking water, a minimal chlorine concentration of /L should be maintained right to the point of consumer delivery, and that to avoid harmful effects to public health, it should not be found in concentrations higher than 5 /L [6]. In particular, this paper will address the indications given by the the Mexican norm NOM-127-SSA1-1994 [7], which indicates that free chlorine in a WDS must not be found in concentrations lower than 0.2 or higher than 1.5 .
In the literature, several approaches that analytically describe and predict the decay of free chlorine concentration in drinking WDS have been reported. In [8] a sequential steady-state approach compared to field-measured data was reported. In the same way, a mass-transfer-based model approach was presented in [9]. The authors highlighted that such an approach takes into consideration first-order reactions of chlorine that take place in both the bulk flow and in the pipe wall, demonstrating how higher decay rates of chlorine are associated with smaller pipe diameters and higher flow velocities. The effect of fluid velocity and pipe inner radius in chlorine propagation was studied in [10]. Here an EPANET model of the WDS was used, and it was shown how the same variables that affect the propagation of residual chlorine levels can potentially affect disinfection performance. Following this direction, in [11] a computational scheme was proposed to accurately and efficiently treat kinetic processes in chlorine concentration models. It was observed that both a higher accuracy and a better computational efficiency were achieved when comparing it with similar schemes. The effect of water temperature in chlorine decay was also addressed in [12]. It was evidenced how chlorine concentration experiences a faster decay rate in fresh samples than in those re-chlorinated with sodium hipochlorite. Moreover, a combined first- and second-order model was presented in [12]. This approach showed a more accurate model behavior compared with a conventional first-order model. It was pointed out that chlorine decay is mainly influenced by its initial concentration, which explains why chlorine decays faster during the initial stages of the propagation process. An inverse-model-based technique to estimate the input chlorine concentration needed to meet a specified value at a desired node in the WDS was explored in [13]. Results evidenced an excellent agreement between the inverse method and the direct simulation technique. Interval state observers were also used in [3] to model the decay of chlorine concentration, showing sufficient numerical efficiency for on-line implementations of the proposed method.
Computational models have also been used to simulate this chemical phenomena. In [14], a computer model was used to predict the spatial and temporal distribution of a residual constituent with first-order reaction rate in a pipe network under variable unsteady flow conditions. Even if a good agreement with results from a standard extended-period simulation during the initial stages was obtained, the chlorine concentration at different nodes in the network presented deviation when the flow regime became more unsteady. The main issue noted about computational models of chlorine concentration and decay was that simulation environments commonly require to know the bulk reaction coefficient and wall reaction coefficient with accuracy. In the last decades, the well-known EPANET software has been used to simulate, besides hydraulic behavior, the decay and diffusion of substances such as chlorine in a WDS. In particular, the Multi-Species eXtension (EPANET-MSX) allows for the consideration of multiple interacting species in the bulk flow and on the pipe walls. This capability has been incorporated into both a stand-alone executable program and a toolkit library of functions that programmers can use to build customized applications. Several contributions have been reported by using this approach, as in [15], where the performance of the proposed model as well as an nth-order decay kinetics was tested for the full-scale modeling of chlorine concentration in a WDS. It was shown how a similar level of accuracy can be achieved with the tested models, provided that there is a good calibration of the decay reaction coefficients. Following this direction, a new model of chlorine-wall reaction for simulation of the chlorine concentration in a WDS was proposed in [16], which provides the accurate chlorine modeling required to improve disinfection strategies in a WDS when implemented in EPANET-MSX (or similar simulation software). Alternative simulation software environments have also been used to model the decay of chlorine concentration, such as the work presented in [17], where the authors presented an alternative methodology based on AQUASIM to model chlorine concentration in a distribution network; however, the authors stated that further evaluation of the methodology on a larger scale WDS is needed. In [18], a methodology to efficiently calibrate chlorine decay models was proposed and applied to a part of the Barcelona drinking water distribution network. Measurements and simulated chlorine concentrations at nodes with a sensor were compared to calibrate the chlorine bulk reaction coefficient. From the artificial-intelligence (AI)-based approach, a work was presented in [19] where a genetic algorithm (GA) was used in a real WDS together with particle swarm optimization (PSO) and a hybrid GA-PSO as three different AI-based approaches to calibrate the wall reaction coefficient while minimizing the residuals for chlorine concentrations. The obtained results clearly demonstrated that the hybrid GA-PSO outperformed the other two algorithms when considering only one decision variable (the wall reaction coefficient).
Based on the abovementioned research and since water quality monitoring has become more and more important worldwide for its inherent impact on public health, the development of more efficient water quality monitoring techniques remains in challenge nowadays. For this reason the main contribution presented in this paper is an alternative method based on a GA for the estimation of both the bulk and wall reaction coefficients in a WDS by using a reduced number of chlorine meters. This approach allows the chlorine concentration along the WDS to be estimated with accuracy, which in turn aids the water management staff to adopt a better feed-chlorine strategy. To the best of our knowledge, no previous investigations have focused on the estimation of both the bulk and wall reaction coefficients simultaneously by means of a GA.
This paper is organized as follows: Section 2 and Section 3 provide with the theoretical background on the genetic algorithm and the reactions within a pipe involved in the decay of chlorine concentration in water, respectively. Section 4 explains in depth the proposed methodology for the GA-driven calibration of the bulk and wall reaction coefficients and the estimation of the minimal required chlorine concentration at the input. Section 5 illustrates the obtained simulation results, and finally Section 6 discusses conclusions and future work proposals.
2. The Genetic Algorithm
This paper proposes the use of the genetic algorithm (GA) to calibrate the unknown parameters of the chlorine-decay model in EPANET for the WDS under study. The steps followed by the GA to perform the calibration of the desired parameters are:
- Creation: An initial population is created and distributed as uniformly as possible across a pre-defined search area.
- Selection: A selection mechanism is used to assign a probability for each individual in the population that their genes will prevail to the next generation. This selection mechanism is commonly a fitness/cost function computed for each individual, where the fittest individuals are awarded a higher probability.
- Cross-over: Once the fittest individuals are selected, the cross-over stage takes place to create the following generation. For this purpose, the genes of two parent solutions are recombined to create two new offspring solutions.
- Mutation: The last evolutionary stage is the random mutation of some of the genes in the newly-created population. This random mutation serves two purposes: (1) it stops the population from becoming uniform and helps maintain some level of diversity in the individuals; (2) it prevents the algorithm from failing to find locally-optimal solutions instead of the desired global optimal.
This process takes place during a pre-set number of generations or while the mean performance of the newly created population is significantly better than the previous one. Once any termination criteria are met, the GA provides the best-performing solution. The entire process is represented graphically in Figure 1, which is designed on the basis of [20,21].
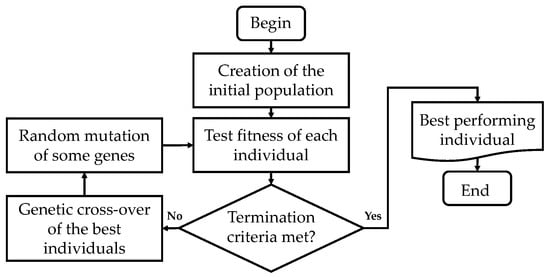
Figure 1.
The genetic algorithm process as a block diagram.
3. Reaction Zones within a Pipeline
The decay of a substance by reaction as it travels through a water distribution system is an important topic of study. To model this decay, the rate at which this substance reacts and the relation between this reaction and the substance concentration must be known. According to [22], the reaction can occur in two different ways: (1) within the bulk flow; and (2) with the material along the pipe wall. The two ways in which reaction of a substance can occur are visualized in Figure 2, where free chlorine (HOCL) reacts with natural organic matter (NOM) in the bulk flow to produce the disinfectant by-product (DBP), and is also transported through the boundary layer of the pipe wall to oxidize the iron (Fe) released from through-wall corrosion.
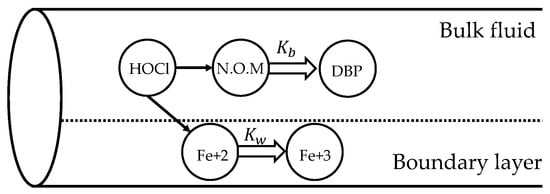
Figure 2.
Reaction zones within a pipeline.
3.1. Bulk Reactions
Reaction occurring in the bulk flow is modeled with n-th order kinetics, where the instantaneous rate of reaction R (mass/volume/time) is assumed to be concentration-dependent, according to [22] as:
where is known as the bulk reaction coefficient, C is the reactant concentration (mass/ volume) and n is the reaction order. The units of are concentration raised to the (1 − n) power divided by time, and its value is positive for the case of growth reactions and negative for decay reactions. Cases where a limiting concentration exists in the ultimate growth or loss of the substance can also be considered, where Equation (1) is expressed as:
where is the limiting concentration of the substance. Some cases of well-known kinetic models are provided in Table 1.

Table 1.
Different kinetic models.
The diffusion of chlorine in a WDS is an example of a first-order decay reaction, and thus for first-order reactions () has units of 1/day. Even if an experimental estimation of can be performed, the reliability of the estimated value depends on the careful measurement of the reactant concentration at each sampling time (which is prone to human mistake) as well as taking into consideration the effects of temperature in the decay of the substance. This is a strong argument to use a computer-based estimation of this parameter.
3.2. Wall Reactions
The rate at which chlorine concentration decay reactions take place near the wall of the pipe can be considered to be dependent on the concentration in the bulk flow by the expression:
where is known as the wall reaction coefficient and is the surface area per unit volume within a pipe segment. This latter term converts the mass reacting per unit of wall area to a per unit volume basis. Typically, values range from 0 to 1.5 m/day. The value of should be adjusted to consider any mass-transfer limitation in moving reactants and products between the bulk flow and the wall. The wall reaction coefficient depends on the temperature and can also be affected by the age of the pipe, since the increase of encrustation, tuberculation or corrosion produces a higher roughness coefficient, resulting in a greater head-loss through the pipe. Some evidence has shown that the same processes that impact the roughness coefficient in a pipe also tend to increase the reactivity of the inner wall with some types of chemical species, in particular chlorine and other types of disinfectants. The value of can be modeled as a function of the coefficient used to describe the roughness of the pipeline (this is, the chosen head-loss model) as shown in Table 2.

Table 2.
Wall reaction formulas related to head-loss.
In the table, C is the Hazen–Williams C-factor, is the absolute roughness of the pipe, D is the pipe diameter and n is the Manning roughness coefficient. The coefficient F should be developed according to site-specific field measurements and it will have different values and units depending on the head-loss equation used.
4. Proposed Methodology
4.1. Estimation of and
Considering the availability of sensors in practice is always a limitation, the idea is to estimate the chlorine concentration in the whole WDS (all nodes) at any time regardless of the reduced number of chlorine sensors. To do that, the proposed methodology considers a few chlorine measurements at some nodes. It is also considered that those measurements are obtained for a duration of at least two days, i.e., 48 h. The performance of the proposed methodology is tested using synthetic data generated via a simulation. To do that, initial conditions of the sourced chlorine at the pumping station and initial chlorine concentration at the nodes are assumed to be known, whereas the bulk and wall reaction coefficients are considered as unknown variables. Then, for every node, the chlorine concentration value at each sampling time is obtained by performing a simulation process through the well-known EPANET-MATLAB Toolkit [23].
This methodology relies on a WDS model with an input format (.inp) suitable for the EPANET software, for which the hydraulic parameters roughness coefficient and minor loss coefficient K are well-adjusted such that it is reliable in terms of hydraulic behavior (see [22]). Let us now consider that n denotes a reduced number of chlorine sensors installed along the WDS and their measurements are recorded and stored in a matrix where m denotes the number of samples. Then, the GA-driven calibration process begins as follows: a population of solution vectors is created where is selected as the population size and each solution vector is structured as:
where is the i-th candidate bulk reaction coefficient and is the i-th candidate wall reaction coefficient, such that:
with and denoting the lower and upper bounds, respectively. Then, the candidate set of and values are assigned into the .inp EPANET file as the bulk and wall reaction coefficients of each pipe, and thus a 24 h simulation is performed to compute the chlorine concentration along the WDS. The software-driven simulation provides the estimation of the chlorine concentration at each node in the network, where attention should be directed to those nodes with a sensor. Next, let us denote that is a matrix containing the estimations of chlorine concentration at nodes for which the corresponding chlorine measurements are also available such that an error matrix can be computed as follows:
where column 1 of e contains the estimation error for the first measured node and column 2 contains the estimation error for the second measured node, and so on. For each node the mean squared estimation error (mse) can be computed as:
Finally, the global mean squared error () containing the overall estimation error is computed as:
where is set as the optimization goal for the GA, that is, a proposed vector is found that contains the optimal values for and that minimize the value of . It is not expected that a single generation will provide the optimal values and thus the best-performing vectors are selected for the cross-over and mutation stages, which are repeated iteratively until a satisfying match is found. The methodology presented in this paper is programmed with the aid of the OpenWater Analytics EPANET-MATLAB Toolkit [23], which is an open-source software used for interfacing the EPANET tools in a MATLAB programming environment. As a pseudocode, this process is summarized as follows:
| Pseudocode 1: GA-driven calibration for and reaction coefficients |
| INPUT: Array : |
| where columns , , …, contain the chlorine concentration at nodes with a sensor and m denotes the number of samples. |
| LOAD into memory the .inp file of the WDS. |
| SET the quality time-step in the .inp file for simulation as the sampling rate of the measurements. |
| CREATE the array of sensed nodes . |
| DECLARE the GA parameters: population size , maximum generations , minimum tolerance , |
| lower and upper search area bounds. |
| CREATE the initial population ; |
| IF |
| FOR each |
| SET and in the .inp file. |
| COMPUTE the water-quality time series with help of the EPANET-MATLAB Toolkit |
| BUILD the array similarly as . |
| FOR |
| FOR |
| = |
| END FOR |
| END FOR |
| INITIALIZE mse |
| FOR |
| = |
| END FOR |
| END FOR |
| CHOOSE the values that provide the lowest . |
| IF lowest |
| CREATE new population , and CONTINUE. |
| ELSE |
| END ALGORITHM |
| END IF |
| ELSE |
| END ALGORITHM |
| END IF |
| OUTPUT: Values for and that minimize . |
4.2. Analysis of the Minimal Chlorine Concentration in the WDS
Once a set of and values that minimize the overall error have been calibrated, the minimal required input chlorine must be determined. For this, let us denote , where denotes the total number of nodes in the WDS and is a matrix containing the m simulated values for the chlorine concentration at every node. From , a vector can be built such that . It is now safe to state that the minimal value in corresponds to the overall minimal value for the experiment time. Let us denote this overall minimal value as . To meet the official normativity requirements for the WDS, ideally, this must be contained between the lower and upper bounds (0.2 to 1.5 listed in the official norm [7]. Please note that at this point it is unknown which chlorine concentration is needed at the input to ensure that a chlorine concentration of at least of 0.2 is met at each node in the WDS anytime. Since [7] also provides a maximum permitted value of 1.5 it is not possible to simply add chlorine at the input of the WDS until the minimal value is met at the expense of exceeding the permitted upper bound. Under said conditions, the problem now turns into finding the optimal chlorine concentration between the stated lower and upper bounds at the input to ensure that the minimal normativity value is met. This analysis will also contemplate the possibility that the WDS will require a re-design if it is not possible to meet the normativity requirements under the permitted source chlorine concentration input.
The proposed optimization process is explained as follows:
- First, the calibrated and values are set into an .inp file as the actual bulk and wall reaction coefficients of the pipeline.
- Then, a GA is set to minimize the value corresponding to the chlorine concentration at the input as a restriction is also satisfied: that , where is the overall minimal required chlorine concentration in the WDS.
- By setting a proposed value to the model and performing the simulation of the chlorine decay, matrix and vector are obtained as previously explained.
- Then, the fitness of a given value is defined as follows:
- (a)
- If then a very low fitness is assigned to ;
- (b)
- If then the fitness of is defined as the difference between the two values.
- The search process continues until a ( value is found that minimizes the difference between and .
As a pseudocode, this process is described as follows:
| Pseudocode 2: GA-driven calibration for minimal required value |
| INPUT: |
| LOAD into memory the .inp file with the previously calibrated and values. |
| DEFINE the population size , the maximum generations and the minimum tolerance . |
| DEFINE the lower () and upper bound () for the search area as stated by the normativity. |
| CREATE the initial population ; |
| IF |
| FOR each |
| ASSIGN to the model. |
| PERFORM the water-quality simulation with help of the EPANET-MATLAB Toolkit |
| CREATE matrix . |
| IF |
| Error (Very high value) |
| ELSE IF |
| Error |
| END IF |
| END FOR |
| CHOOSE the values that provide the lowest Error. |
| IF lowest Error . |
| CREATE new population , and CONTINUE. |
| ELSE |
| END ALGORITHM |
| ELSE |
| END ALGORITHM |
| END IF |
| OUTPUT: Optimal value for that ensures . |
5. Simulation Results
To demonstrate the performance of the proposed methodology, data from a simulation environment will be used. In Figure 3 the system under study is presented, whereas its general topology is presented in Figure 4.
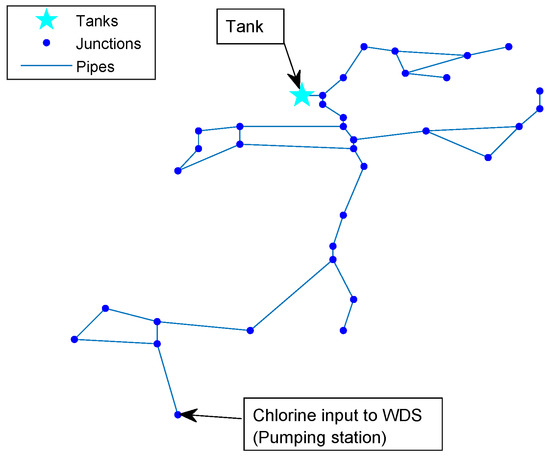
Figure 3.
WDS under study.
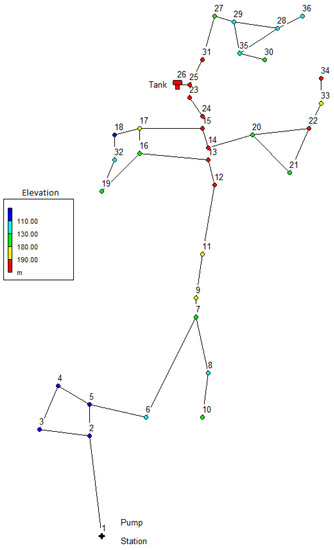
Figure 4.
General topology of the WDS under study.
The system is made up of 1 pumping station (node ) that is also the input node for chlorine, 1 tank (node ), 34 connection nodes, and 40 pipe segments. It is assumed that only nodes , , , , and have chlorine concentration meters installed; thus the EPANET-simulated chlorine concentration values at said nodes will be used as the reference value for calibration, while in experimental applications of this methodology these values can be replaced by physical measurements without major changes. At the pumping station, the input chlorine concentration is 0.8 and also the initial chlorine concentration condition at the entire WDS is 0.5 . Note that the values corresponding to and are still unknown. Figure 5 shows the evolution of the chlorine concentration value as simulated by EPANET for nodes , , , , and for a period of 198,000 s = 55 h.
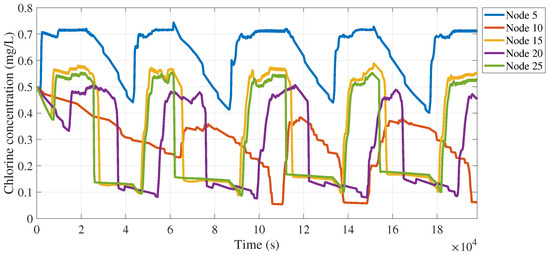
Figure 5.
Historical evolution of chlorine concentration.
The chlorine concentrations illustrated in Figure 5 will be considered as the calibration objective and thus the GA-based methodology will try to adjust the values of the and coefficients in the .inp file of the system that when set as the actual bulk and wall reaction coefficients provide a low-error fit between the EPANET-simulated values (obtained with the real and coefficients) and the GA-fitted-model estimated chlorine concentrations. After the calibration process was finished, the obtained results for and are:
Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 show the comparison between the EPANET-simulated and the GA-fitted-model chlorine concentration values in nodes 5, 10, 15, 20, and 25 respectively.
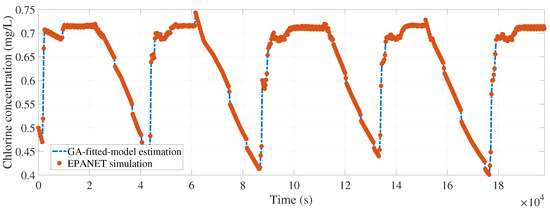
Figure 6.
Calibrated model fitting for node 5 (rmse = 2.0835 ).
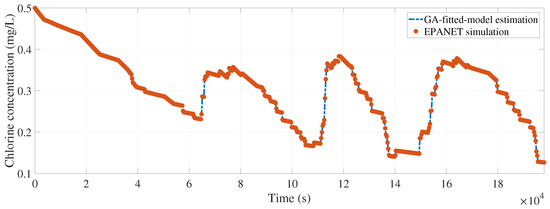
Figure 7.
Calibrated model fitting for node 10 (rmse = 7.2047 ).
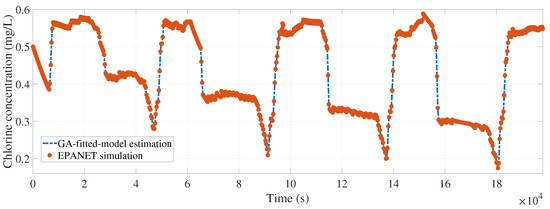
Figure 8.
Calibrated model fitting for node 15 (rmse = 2.7089 ).
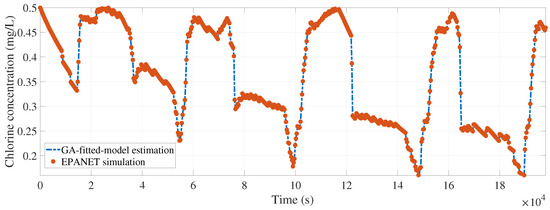
Figure 9.
Calibrated model fitting for node 20 (rmse = 1.0999 ).
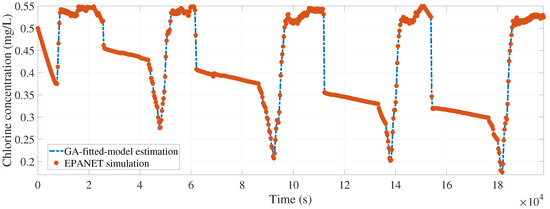
Figure 10.
Calibrated model fitting for node 25 (rmse = 4.0421 ).
Given that for each tested node the calibrated model provides an estimation that closely matches the real behavior, it is safe to ensure that the calibrated and values will estimate with accuracy the chlorine concentration at any other node. Even if Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 represent the evolution of chlorine concentration for a total time of 55 only for the tested nodes, with the new well-calibrated chlorine-decay model it is possible to determine the chlorine concentration evolution at any other node in the system. Moreover, knowing the minimal concentration in the entire WDS for the duration of the simulation is now possible. It should be noted that the evolution shown in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 considers 0.8 as the source chlorine concentration at the input node () ( in Figure 3), as well as an initial chlorine concentration () at each node of 0.5 . Even if both initial and source chlorine concentration values are contained within the range indicated by the official norm, it is not safe to say that normativity values will be met at each node in the WDS. After performing a chlorine-decay simulation using the calibrated model, Figure 11 provides the minimal overall chlorine concentration at each node.
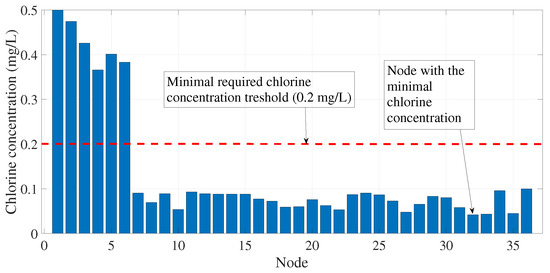
Figure 11.
Minimal chlorine concentration at each node when 0.8 and is 0.5 .
From Figure 11 it is clear that only nodes 1 to 6 comply with the normativity requirements with every other node dropping to a minimal chlorine concentration below 0.1 . This indicates that a higher chlorine concentration (still within the official normativity requirements) needs to be sourced to the WDS to meet the requirements. It will be assumed that chlorine is sourced to the WDS as a constant concentration at the input node (N1). It is also theorized that to minimize the amount of sourced chlorine, the initial concentration needs to be the highest possible value. Calibration of is performed through the GA-based methodology proposed in Section 4.2, while considering a value of 1.5 (upper permitted bound according to the official norm). After applying the proposed methodology, the obtained minimal value that ensures that at all times with at least 0.2 of chlorine concentration are met for any point in the system is:
Please note that it was assumed that the initial concentration at each node in the system is already at its highest possible value of 1.5 . This condition is assumed only because in a simulated environment it is possible to freely manipulate this value, while for experimental implementations only the initial chlorine concentration at nodes with chlorine meters can be known, and thus their initial concentration values shall be included as calibration variables in the GA-based algorithm. Figure 12 shows the minimal chlorine concentration at each node when = 1.271229 and = 1.5 .
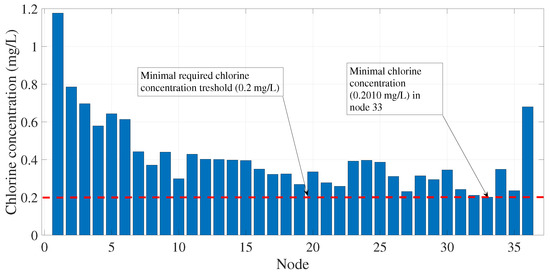
Figure 12.
Minimal chlorine concentration at each node when 1.271229 and is 1.5 .
In Figure 13 the evolution of the chlorine concentration at every measured node is illustrated. It is shown how during the simulated 55 h chlorine concentration remains always within the established limits of 0.2 and 1.5 .
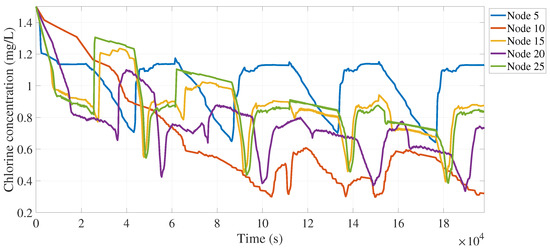
Figure 13.
Evolution of measured chlorine concentration with 1.271229 and is 1.5 .
Discussion of the Results
Application of the proposed methodology allowed for calibration of the required chlorine concentration at the input node to ensure that the minimal normativity-required value was met for every node in the network. The first calibration process to estimate the values of and coefficients was performed under an input chlorine concentration of and an initial chlorine concentration of . Actually, once the and parameters are calibrated, it is possible to perform a quality simulation at the uppermost condition for the initial chlorine concentration ( ), which yields that the minimal chlorine concentration threshold is not met, since many nodes are still under the required 0.2 concentration, as shown in Figure 14.
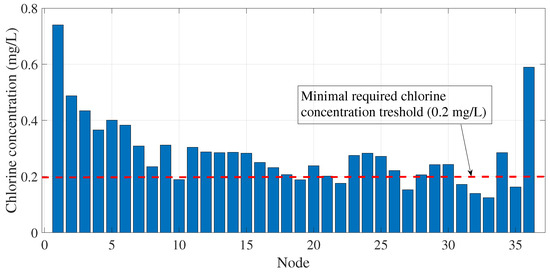
Figure 14.
Minimal chlorine concentration at each node when 0.8 and is 1.5 .
The importance of the calibrated model now relies on the fact that simulation of any what-if scenario is possible, and furthermore the re-design of input conditions ensures the required chlorine concentration no matter the time of day or the analyzed node. As shown previously, the calibrated chlorine-decay model is able to compute chlorine concentrations for every node at every time interval, which makes it a powerful tool in analyzing already existing networks as well as during the design and implementation stages in the creation of a new WDS. Following this line, it could be possible that even if the chlorine decay has already been finely adjusted, an value cannot be found to ensure that a chlorine concentration within the official norm is met for every node (e.g., the required for ). Models not converging to a satisfactory solution may require the adjustment of some physical parameters of the WDS as well as analyzing the possibility of sourcing chlorine at more than one node to ensure that the normative standard is met in the entire system. For example, in Figure 12 it can be inferred that for the initial chlorine concentration value for each node lower than 1.5 the required would be slightly higher than the calibrated 1.271 and thus a point will be reached where even if (its theoretical highest possible), it would be impossible to meet the minimal required chlorine concentration value as stated by the normativity. In other words, the re-design of the network should be performed to allow chlorine input in many different nodes since only one input node did not allow to meet the normativity requirements. For the particular WDS tested in this study, it was not possible to achieve a [] when and thus it was decided to run the simulation at however in experimental implementations of this work this initial condition may not be able to be achieved and further alternatives should be analyzed. It should be noted that even if the results presented in this paper considered that the permitted chlorine concentration values range according to the mexican NOM-127-SSA1-1994, the algorithm can be adjusted to meet the requirements given by a different normativity framework (e.g., the WHO recommendations).
It is important to note that the tested methodology proposes an alternative approach to most of the state-of-the-art investigations, where the major part of the related work addresses the issue of modeling of chlorine decay in a WDS while not exactly focusing on the calibration of the bulk and wall reaction coefficients, which is the main objective of the proposed methodology. Following this line, in [9], aside from the wall reaction coefficient, the initial conditions of the simulation were also considered as calibration variables (the bulk reaction coefficient was determined independently in a laboratory), while in [19] a hybrid PSO-GA demonstrated a better performance than a pure GA in finding an optimal match between observed and simulated chlorine concentration when the only calibration variable considered was the wall reaction coefficient. Moreover, both [9,19] took into consideration data from a real WDS. Even if not directly comparable, the authors stated that the methodology proposed in this paper can demonstrate an improvement from previous related studies since this work also contemplated calibration of the bulk reaction coefficient (not addressed by previous research) as well as the estimation of the minimal required source-chlorine concentration to meet normativity requirements. The performed study can be extended in future implementations by considering as well the unknown initial conditions as a calibration variable once this method is tested with non-synthetic data.
6. Conclusions
This work presented an efficient methodology on the basis of genetic algorithms for both the calibration of the bulk coefficient and wall reaction coefficient in the chlorine-decay model of a WDS. Moreover, this approach allowed to determine if the input chlorine concentration dosage ensures the compliance of the normative along the whole WDS. Simulation results illustrate a good performance in obtaining a calibrated chlorine-decay model that is able to estimate the chlorine concentration at those nodes without sensors considering the availability of a reduced number of chlorine sensors. The relevance of the presented work relies on the fact that water agencies require precise knowledge on the quality of water delivered to consumers from a healthcare perspective as well as to ensure compliance with the applicable official normativity. On the other hand, this research work expanded upon the results obtained in previous investigations by considering both the bulk and wall reaction coefficients as decision variables during the optimization process. Additionally, such a GA-based approach provided a good performance in simultaneously calibrating both variables no matter the reduced availability of chlorine sensors. It also expanded the state-of-the-art by presenting an application of the calibrated model in which the chlorine concentration rationed at the pumping station is optimized to ensure the compliance of official normativity for public health purposes. Finally, the presented methodology was shown to be a useful tool for the analysis of WDS encountered in practice as well as the re-design of a WDS that does not meet the applicable official normative. Implementation of this methodology in a real WDS will be part of future developments.
Author Contributions
Conceptualization, L.G.-C. and J.A.D.-A.; Data curation, L.G.-C.; Formal analysis, J.A.D.-A.; Methodology, L.G.-C. and J.A.D.-A.; Project administration, J.A.D.-A.; Software, L.G.-C.; Supervision, J.A.D.-A.; Validation, L.G.-C.; Visualization, I.S.-R. and A.N.-D.; Writing—original draft, L.G.-C., J.A.D.-A., I.S.-R. and A.N.-D.; Writing—review and editing, L.G.-C., J.A.D.-A., I.S.-R. and A.N.-D. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Tecnológico de Monterrey.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by Tecnológico de Monterrey through APC funding, by CONACyT through a scholarship for the first author under grant 801871, by Tecnológico Nacional de México (TecNM), and achieved during a research stay of the first author at CIIDETEC-UVM Guadalajara. Second author would like to thank Ing. Gómez for his significant achievement in this short-research stay, Santos-Ruiz and Adrián “El Gallo Claudio” Navarro-Díaz for fruitful interactions in recent collaborations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Omer, N.H. Water quality parameters. Water-Qual.-Sci. Assess. Policy 2019, 18, 1–34. [Google Scholar]
- Davis, M.L. Water and Wastewater Engineering: Design Principles and Practice; McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Langowski, R.; Brdys, M. Monitoring of chlorine concentration in drinking water distribution systems using an interval estimator. Int. J. Appl. Math. Comput. Sci. 2007, 17, 199. [Google Scholar] [CrossRef]
- García-Ávila, F.; Avilés-Añazco, A.; Ordoñez-Jara, J.; Guanuchi-Quezada, C.; del Pino, L.F.; Ramos-Fernández, L. Modeling of residual chlorine in a drinking water network in times of pandemic of the SARS-CoV-2 (COVID-19). Sustain. Environ. Res. 2021, 31, 1–15. [Google Scholar] [CrossRef]
- Nono, D.; Odirile, P.T.; Basupi, I.; Parida, B.P. Assessment of probable causes of chlorine decay in water distribution systems of Gaborone city, Botswana. Water SA 2019, 45, 190–198. [Google Scholar] [CrossRef]
- World Health Organization. Principles and Practices of Drinking-Water Chlorination: A Guide to Strengthening Chlorination Practices in Small-to Medium Sized Water Supplies. 2017. Available online: https://apps.who.int/iris/handle/10665/255145 (accessed on 11 January 2023).
- Secretaría de Gobernación, México. NOM-127-SSA1-1994, Salud Ambiental. Agua Para Uso y Consumo Humano. Límites Permisibles de Calidad y Tratamientos a Que debe Someterse el Agua Para su Potabilización. Diario Oficial de la Federación. 2000. Available online: https://www.dof.gob.mx/nota_detalle.php?codigo=2063863&fecha=31/12/1969#gsc.tab=0 (accessed on 11 January 2023).
- Males, R.M.; Grayman, W.M.; Clark, R.M. Modeling water quality in distribution systems. J. Water Resour. Plan. Manag. 1988, 114, 197–209. [Google Scholar] [CrossRef]
- Rossman, L.A.; Clark, R.M.; Grayman, W.M. Modeling chlorine residuals in drinking-water distribution systems. J. Environ. Eng. 1994, 120, 803–820. [Google Scholar] [CrossRef]
- Clark, R.M.; Rossman, L.A.; Wymer, L.J. Modeling distribution system water quality: Regulatory implications. J. Water Resour. Plan. Manag. 1995, 121, 423–428. [Google Scholar] [CrossRef]
- Park, K.; Kuo, A.Y. A multi-step computation scheme: Decoupling kinetic processes from physical transport in water quality models. Water Res. 1996, 30, 2255–2264. [Google Scholar] [CrossRef]
- Hua, F.; West, J.; Barker, R.; Forster, C. Modelling of chlorine decay in municipal water supplies. Water Res. 1999, 33, 2735–2746. [Google Scholar] [CrossRef]
- Islam, M.R.; Chaudhry, M.H.; Clark, R.M. Inverse modeling of chlorine concentration in pipe networks under dynamic condition. J. Environ. Eng. 1997, 123, 1033–1040. [Google Scholar] [CrossRef]
- Islam, M.R.; Chaudhry, M.H. Modeling of constituent transport in unsteady flows in pipe networks. J. Hydraul. Eng. 1998, 124, 1115–1124. [Google Scholar] [CrossRef]
- Monteiro, L.; Figueiredo, D.; Dias, S.; Freitas, R.; Covas, D.; Menaia, J.; Coelho, S. Modeling of chlorine decay in drinking water supply systems using EPANET MSX. Procedia Eng. 2014, 70, 1192–1200. [Google Scholar] [CrossRef]
- Fisher, I.; Kastl, G.; Sathasivan, A. New model of chlorine-wall reaction for simulating chlorine concentration in drinking water distribution systems. Water Res. 2017, 125, 427–437. [Google Scholar] [CrossRef] [PubMed]
- Madzivhandila, V.A.; Chirwa, E. Modeling chlorine decay in drinking water distribution systems using aquasim. Chem. Eng. Trans. 2017, 57, 1–6. [Google Scholar]
- Nejjari, F.; Puig, V.; Pérez, R.; Quevedo, J.; Cuguero, M.; Sanz, G.; Mirats, J. Chlorine decay model calibration and comparison: Application to a real water network. Procedia Eng. 2014, 70, 1221–1230. [Google Scholar] [CrossRef]
- Minaee, R.P.; Afsharnia, M.; Moghaddam, A.; Ebrahimi, A.A.; Askarishahi, M.; Mokhtari, M. Calibration of water quality model for distribution networks using genetic algorithm, particle swarm optimization, and hybrid methods. MethodsX 2019, 6, 540–548. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 43–55. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Rossman, L.A.; Woo, H.; Tryby, M.; Shang, F.; Janke, R.; Haxton, T. EPANET 2.2 User Manual; Technical Report EPA/600/R-20/133; U.S. Environmental Protection Agency: Washington, DC, USA, 2020. [Google Scholar]
- Eliades, D.G.; Kyriakou, M.; Vrachimis, S.; Polycarpou, M.M. EPANET-MATLAB Toolkit: An Open-Source Software for Interfacing EPANET with MATLAB. In Proceedings of the 14th International Conference on Computing and Control for the Water Industry (CCWI), Amsterdam, The Netherlands, 7–9 November 2016. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).