Multi-Objective Bus Timetable Coordination Considering Travel Time Uncertainty
Abstract
:1. Introduction
1.1. Related Studies
1.2. Objective and Contributions
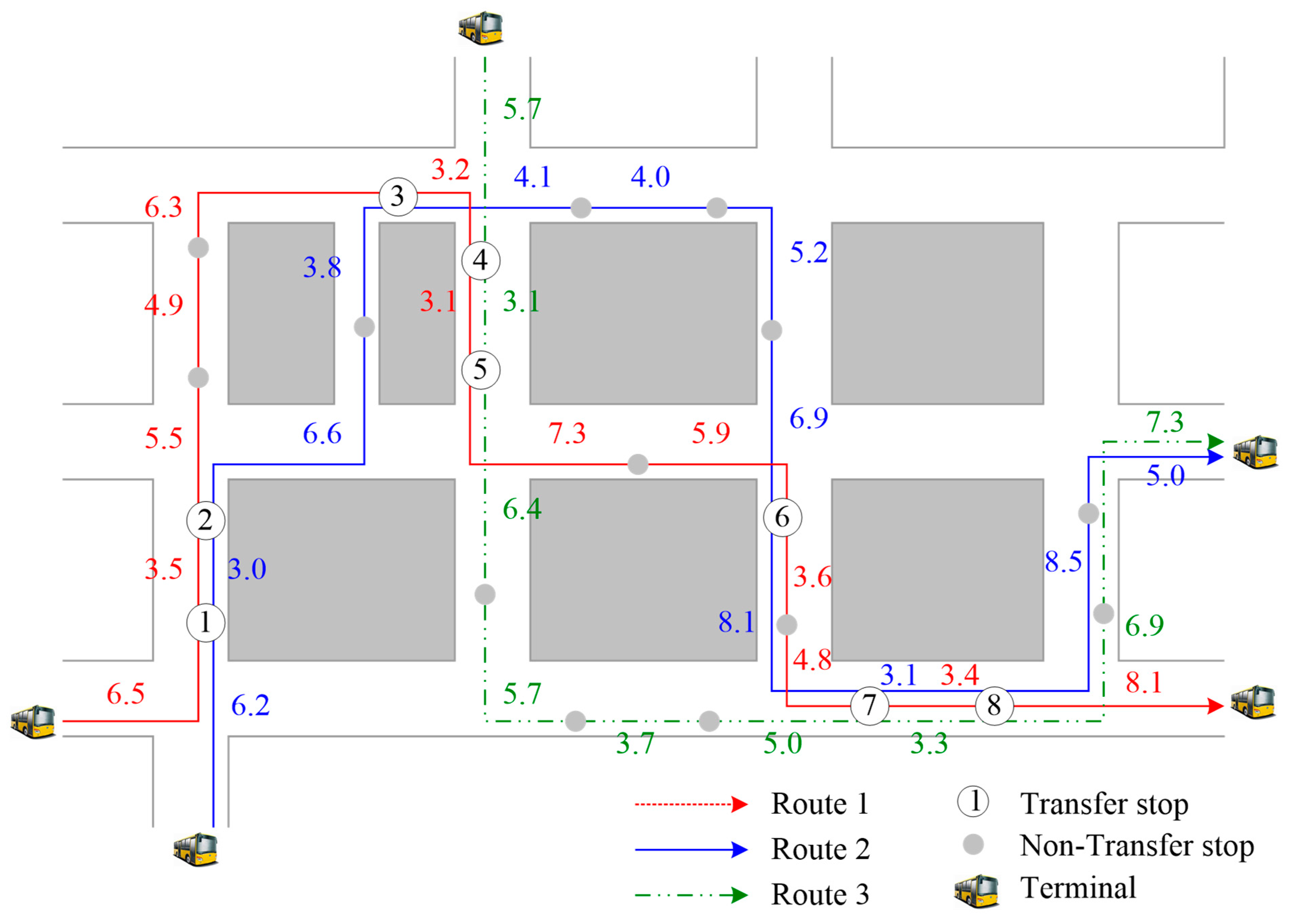
2. Problem Description
3. Model Formulation
3.1. Transfer Waiting Time
- If and (i.e., and ), bus of route is obviously not the connecting bus of bus of route for scenario . As and , then . In effect, due to the minimization objective function (detailed in Section 3.3), will be forced to be zero in this case.
- If and (i.e., and ), bus of route is the connecting bus of bus of route . As and , then . Due to the minimization objective function, will be forced to be in this case, which is the practical waiting time of transfer passengers from bus of route .
- If and (i.e., and ), bus of route is obviously not the connecting bus of bus of route for scenario . As and , then . In effect, due to the minimization objective function, will be forced to be zeros in this case.
3.2. Initial Waiting Time
3.3. Mixed-Integer Linear Programming Model
3.4. Constraints for First-Bus Transfer Problem
4. Solution Method
- [MILP]
| Objective: | Equation (18) |
| Subject to: | Equations (3)–(9), (11)–(17), (20), and (21) |
5. Numerical Experiments
5.1. Parameter Setting
5.2. Optimization Results
5.3. Common Sub-Routes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Land Transport Authority of Singapore. Public Transport Ridership. 2020. Available online: https://www.lta.gov.sg/content/dam/ltagov/who_we_are/statistics_and_publications/statistics/pdf/PT_Ridership_2015_2019.pdf (accessed on 17 June 2022).
- Espino, R.; Román, C. Valuation of transfer for bus users: The case of Gran Canaria. Transp. Res. Part A Policy Pract. 2020, 137, 131–144. [Google Scholar] [CrossRef]
- Wu, W.; Liu, R.; Jin, W.; Ma, C. Stochastic bus schedule coordination considering demand assignment and rerouting of passengers. Transp. Res. Part B Methodol. 2019, 121, 275–303. [Google Scholar] [CrossRef]
- Liu, T.; Ceder, A. Integrated public transport timetable synchronization and vehicle scheduling with demand assignment: A bi-objective bi-level model using deficit function approach. Transp. Res. Part B Methodol. 2018, 117, 935–955. [Google Scholar] [CrossRef]
- Klemt, W.D.; Stemme, W. Schedule synchronization for public transit networks. In Computer-Aided Transit Scheduling; Springer: Berlin/Heidelberg, Germany, 1988; pp. 327–335. [Google Scholar]
- Schröder, M.; Solchenbach, I. Optimization of Transfer Quality in Regional Public Transit; Berichte des Fraunhofer ITWM: Kaiserslautern, Germany, 2006. [Google Scholar]
- Khani, A.; Shafahi, Y. Transfer optimization in transit networks: Headway and departure time coordination. In Proceedings of the 14th International IEEE Conference on Intelligent Transportation Systems, Washington, DC, USA, 5–7 October 2011. [Google Scholar] [CrossRef]
- Parbo, J.; Nielsen, O.A.; Prato, C.G. User perspectives in public transport timetable optimization. Transp. Res. Part C Emerg. Technol. 2014, 48, 269–284. [Google Scholar] [CrossRef]
- Shafahi, Y.; Khani, A. A practical model for transfer optimization in a transit network: Model formulations and solutions. Transp. Res. Part A Policy Pract. 2010, 44, 377–389. [Google Scholar] [CrossRef]
- Saharidis, K.D.G.; Dimitropoulos, C.; Skordilis, E. Minimizing waiting times at transitional nodes for public bus transportation in Greece. Oper. Res. 2014, 14, 341–359. [Google Scholar] [CrossRef]
- Abdolmaleki, M.; Masoud, N.; Yin, Y. Transit timetable synchronization for transfer time minimization. Transp. Res. Part B Methodol. 2020, 131, 143–159. [Google Scholar] [CrossRef]
- Chakroborty, P.; Deb, K.; Subrahmanyam, P.S. Optimal scheduling of urban transit system using genetic algorithms. J. Transp. Eng. 1995, 121, 544–553. [Google Scholar] [CrossRef]
- Chen, C.; Yan, S.; Tseng, C. Inter-city bus scheduling for allied carriers. Transportmetrica 2010, 6, 161–185. [Google Scholar] [CrossRef]
- Chu, J.C.; Korsesthakarn, K.; Hsu, Y.-T.; Wu, H.Y. Model and a solution algorithm for planning transfer synchronization of bus timetables. Transp. Res. Part E Logist. Transp. Rev. 2019, 131, 247–266. [Google Scholar] [CrossRef]
- Ceder, A.; Tal, O. Designing synchronization into bus timetables. Transp. Res. Rec. 2001, 1760, 28–33. [Google Scholar] [CrossRef]
- Ibarra-Rojas, J.; Rios-Solis, Y.A. Synchronization of bus timetabling. Transp. Res. Part B Methodol. 2012, 46, 599–614. [Google Scholar] [CrossRef]
- Ibarra-Rojas, J.; López-Irarragorri, F.; Rios-Solis, Y.A. Multiperiod bus timetabling. Transp. Sci. 2015, 50, 805–822. [Google Scholar] [CrossRef]
- Bookbinder, J.H.; Désilets, A. Transfer optimization in a transit network. Transp. Sci. 1992, 26, 106–118. [Google Scholar] [CrossRef]
- Cevallos, F.; Zhao, F. Minimizing transfer times in a public transit network with a genetic algorithm. Transp. Res. Rec. 2006, 1971, 74–79. [Google Scholar] [CrossRef]
- Wu, Y.; Tang, J.; Yu, Y.; Pan, Z. A stochastic optimization model for transit network timetable design to mitigate the randomness of travelling time by adding slack time. Transp. Res. Part C Emerg. Technol. 2015, 52, 15–31. [Google Scholar] [CrossRef]
- Kim, M.; Schonfeld, P. Integration of conventional and flexible bus services with timed transfers. Transp. Res. Part B Methodol. 2014, 68, 76–97. [Google Scholar] [CrossRef]
- Gong, M.; Hu, Y.; Chen, Z.; Li, X. Transfer-based customized modular bus system design with passenger-route assignment optimization. Transp. Res. Part E Logist. Transp. Rev. 2021, 153, 102422. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, Y.; Yan, X. Autonomous bus timetable synchronization for maximizing smooth transfers with passenger assignment. Expert Syst. Appl. 2022, 193, 116430. [Google Scholar] [CrossRef]
- Guo, X.; Wu, J.; Sun, H.; Liu, R.; Gao, Z. Timetable coordination of first trains in urban railway network: A case study of Beijing. Appl. Math. Model. 2016, 40, 8048–8066. [Google Scholar] [CrossRef]
- Kang, L.; Zhu, X. A simulated annealing algorithm for first train transfer problem in urban railway networks. Appl. Math. Model. 2016, 40, 419–435. [Google Scholar] [CrossRef]
- Kang, L.; Zhu, X.; Sun, H.; Puchinger, J.; Ruthmair, M.; Hu, B. Modeling the first train timetabling problem with minimal missed trains and synchronization time differences in subway networks. Transp. Res. Part B Methodol. 2016, 93, 17–36. [Google Scholar] [CrossRef]
- Kang, L.; Li, H.; Sun, H.; Wu, J.; Cao, Z.; Buhigiro, N. First train timetabling and bus service bridging in intermodal bus-and-train transit networks. Transp. Res. Part B Methodol. 2021, 149, 443–462. [Google Scholar] [CrossRef]
- Liu, T.; Cats, O.; Gkiotsalitis, K. A review of public transport transfer coordination at the tactical planning phase. Transp. Res. Part C Emerg. Technol. 2021, 133, 103450. [Google Scholar] [CrossRef]
- Gkiotsalitis, K.; Cats, O.; Liu, T. A review of public transport transfer synchronisation at the real-time control phase. Transp. Rev. 2023, 43, 88–107. [Google Scholar] [CrossRef]
- Ceder, A.; Marguier, P.H.J. Passenger waiting time at transit stops. Traffic Eng. Control 1985, 26, 327–329. [Google Scholar]
- Mak, W.K.; Morton, D.P.; Wood, R.K. Monte Carlo bounding techniques for determining solution quality in stochastic programs. Oper. Res. Lett. 1999, 24, 47–56. [Google Scholar] [CrossRef]
- Ma, Z.; Ferreira, L.; Mesbah, M.; Zhu, S. Modeling distribution of travel time variability for bus operations. J. Adv. Transp. 2016, 50, 6–24. [Google Scholar] [CrossRef]
- Löfberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 26 April–1 May 2004. [Google Scholar] [CrossRef]

| 1 | 06:01:00 | 06:14:00 | 06:27:00 | NA | −6 | 6 |
| 2 | 06:02:00 | 06:14:00 | 06:26:00 | NA | −5 | 5 |
| 3 | 06:00:00 | 06:10:00 | 06:20:00 | 06:30:00 | −4 | 4 |
| Scenario | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0 | 1 | 3 | 5 | |
| −0.8048 | −0.7815 | −0.7379 | −0.7155 | |
| −0.2238 | −0. 2238 | −0. 2238 | −0.2238 | |
| −0.5143 | −0.5027 | −0.4809 | −0.4696 | |
| 0.0317 | 0.0199 | 0.0066 | 0.0036 |
| Scenario | 1 | 2 | 3 | 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 3 | 5 | |||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| 4 | 5 | 4 | 4 | 5 | 4 | 4 | 5 | 4 | 4 | 5 | 4 | |
| 6 | 1 | −4 | 6 | 2 | −4 | 6 | 2 | −4 | 6 | 2 | −4 | |
| −6 | −5 | −4 | −6 | −5 | −4 | −6 | −5 | −4 | −6 | −5 | 2 | |
| NA | NA | −4 | NA | NA | −4 | NA | NA | −4 | NA | NA | −4 | |
| Scenario | 4 | 5 | 6 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 5 | 5 | |||||||
| 0.5 | 0.75 | 1 | |||||||
| −0.7155 | −0.7112 | −0.7168 | |||||||
| −0.2238 | −0. 2238 | −0.1832 | |||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| 4 | 5 | 4 | 4 | 5 | 4 | 4 | 5 | 3 | |
| 6 | 2 | −4 | 6 | 2 | −4 | 6 | 2 | 2 | |
| −6 | −5 | 2 | −6 | −5 | −4 | −2 | −5 | 4 | |
| NA | NA | −4 | NA | NA | −4 | NA | NA | −4 | |
| Scenario | 7 | 8 | 9 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 5 | 5 | |||||||
| 0.5 | 0.75 | 1 | |||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| 4 | 5 | 4 | 4 | 5 | 4 | 4 | 5 | 3 | |
| 6 | 2 | −4 | 6 | 2 | −4 | 6 | 2 | 2 | |
| −6 | −5 | 1 | −6 | −5 | 0 | −3 | −5 | 3 | |
| NA | NA | −4 | NA | NA | −4 | NA | NA | −4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, X.; Li, T. Multi-Objective Bus Timetable Coordination Considering Travel Time Uncertainty. Processes 2023, 11, 574. https://doi.org/10.3390/pr11020574
Dou X, Li T. Multi-Objective Bus Timetable Coordination Considering Travel Time Uncertainty. Processes. 2023; 11(2):574. https://doi.org/10.3390/pr11020574
Chicago/Turabian StyleDou, Xueping, and Tongfei Li. 2023. "Multi-Objective Bus Timetable Coordination Considering Travel Time Uncertainty" Processes 11, no. 2: 574. https://doi.org/10.3390/pr11020574
APA StyleDou, X., & Li, T. (2023). Multi-Objective Bus Timetable Coordination Considering Travel Time Uncertainty. Processes, 11(2), 574. https://doi.org/10.3390/pr11020574






