Abstract
Liquid–liquid extraction has proven to be an aid in biologics manufacturing for cell and component separation. Because distribution coefficients and separation factors can be appropriately adjusted via phase screening, especially in aqueous two-phase systems, one stage is frequently feasible. For biologics separation, aqueous two-phase systems have proven to be feasible and efficient. The simple mixer–settler equipment type is still not standard in biologics manufacturing operations. Therefore, a scalable digital twin would be of aid for operator training, process design under the regulatory demanded quality by design approach for risk analysis, design and control space definition, and predictive maintenance. Autonomous operation is achieved with the aid of process analytical technology to update the digital twin to real time events and to allow process control near any optimal operation point. Autonomous operation is first demonstrated with an experimental feasibility study based on an industrial type example of pDNA manufacturing via lysis from E. coli with and without cell separation performance.
1. Introduction
1.1. Liquid–Liquid Extraction and Aqueous Two-Phase Systems for Biologics
Liquid–liquid extraction (LLE) is a widely used process in the chemical industry for the preparation and purification of metal ions, aromatics, and other organic substances [1,2,3]. Other developments of the process in the pharmaceutical industry include biopharmaceutical products such as antibiotics and enzymes [4]. New applications are also emerging in the clarification of alkaline lysis of Escherichia coli (E. coli) for the production of plasmid DNA (pDNA) [5]. In the context of quality by design (QbD) process development, aqueous two-phase extraction (ATPE) will be considered.
To identify an optimal ATPE substance system for the extraction of pDNA, a series of screening experiments is performed. This substance system will be used to develop a continuous process. For this purpose, a model and a model parameter determination concept are created to describe the continuous horizontal settler. This is validated using a procedure published several times in the literature [6,7,8]. With the help of the model, an analysis of the risk potentials of the process is carried out in order to develop an effective control strategy.
This is to be realized by implementing the model as a digital twin (DT). Digital twins mirror real processes in real time and can make predictions about the behavior of a process in the future using current measurement data. This can be used for quality monitoring and process control, as desired states of the process can be targeted using the predictive model [9,10].
The aim of this work is to demonstrate continuous phase separation in a horizontal separator using a validated digital twin. For this purpose, a suitable ATPE system in a DN50 separator is used to evaluate the effort and benefit of autonomous operation.
1.2. Quality by Design and Digital Twins
Quality by Design is a process development principle aimed at ensuring product quality. This is particularly important for pharmaceutical products, which are subject to strict regulatory requirements. The focus is on the identification of risk factors and the quantitative influence of these on the defined quality criteria. From these, a comprehensive control strategy is developed [11].
For the risk factors, areas where the quality criteria are within the previously defined target can be determined These areas are called design spaces and can be used for process development and optimization. This is also shown in Figure 1. The number of parameters in a process engineering process makes the experimental creation of these a considerable effort. The number of experiments to be performed multiplies. The modeling of the processes is essential here [12].
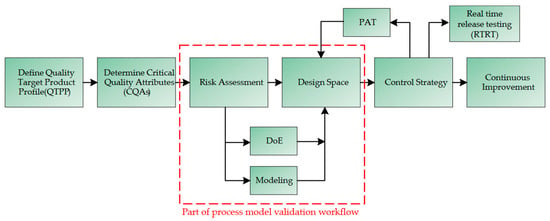
Figure 1.
Presentation of the risk analysis and regulation within the framework of the QbD [13].
In simulation studies, design spaces can be created with less effort because parameters in simulations can be changed independently of each other in a validated range in small step sizes. This requires a validated model of the process [13].
Part of the control strategy can be the use of DT. DT are a product of the industry 4.0 transformation. Their goal is to digitally map real processes. This is achieved by modeling reality and establishing interfaces from the process to the DT. The main tasks of the DT are in process engineering in the active control of a process and the prediction of the yield/purity of products. Furthermore, tasks in the area of maintenance and business planning are conceivable [10].
Figure 2 shows the development stages of a model from a stationary model to a DT. The ability to represent dynamic processes must be given. The model is validated to be able to represent the reality of the process. Afterwards, interfaces between the model and the measuring points of the process are established. The model is called a “shadow twin” if it can independently simulate the operations of the process in real time. Only one interface in the direction of the model is necessary. The last stage is the predictive control of the process from the DT, where the interface must exist in both directions. To establish the DT as a process control strategy a dynamic, valid and scalable process model is required [9]. The DT does not need to start from a stationary model, to speed up development, this step can be skipped. Although most literature models have been developed as steady state models, due to their task of process development and scale up and the constraint of computing power [14].
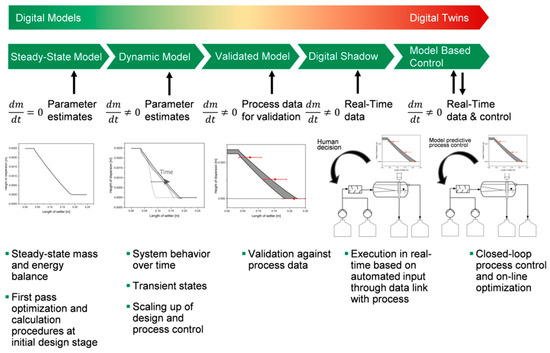
Figure 2.
Schematic and qualitive illustration of the development path from a stationary model to a digital twin with the example of the mixer–settler [9].
For the model to be used as a DT, the computing time must be faster than the time it takes for the modeled process to transition states. Otherwise, real-time control is not achievable. To this end, reduced-order models have been used in the literature before [15,16].
2. Review of Physiochemical Fundamentals for Scalable Digital Twin Modelling of Mixer–Settlers for Liquid–Liquid Extraction Process
Liquid–liquid extraction fundamentals have already been reviewed in [1,2,3]. Aside from mixer–settler modeling for pulsed and agitated columns, different modeling depths have been obtained using Redrop Monte-Carlo-simulation-based [17,18], CFD, and population balances [19,20,21,22] as well as axial dispersion models, which were used for the first time in 1984 [23]. Therefore, special fluid dynamic basis is only pointed out regarding fluid dynamics of mixer–settler modelling comprehension.
2.1. Fluid Dynamics
The hold-up is defined as the volume fraction of the disperse phase, shown here in Equation (1). This has an influence on mass transfer in LLE systems. Furthermore, it has a hydrodynamic influence on the settling behavior [2,24].
The droplet size has a large influence on the sinking behavior, coalescence, and mass transfer behavior in the LLE. For models that do not represent a droplet size distribution over a population balance, the Sauter diameter is generally used. This represents a characteristic droplet by dividing the sum of the volume of a droplet collective by its surface area. This is shown in Formula (2) [24].
The coalescence of a droplet of the dispersion at the interface is shown in Figure 3. This process consists of three steps. First, the droplet approaches the interface due to the buoyancy force. This step is determined by the density difference between the phases and the drag force determined by the droplet size. The largest resistance of coalescence is the film between a droplet and the interface. This drainage is driven by the density difference of the phases. However, this is opposed by the deformation of both phase boundaries. The film drainage is the velocity determining step in the model consideration of coalescence. The third step is the so-called film rupture. This occurs when the film reaches a critical thickness; it tears and the droplet flows together with the disperse phase. The film break is the fastest part of the entire process [25].
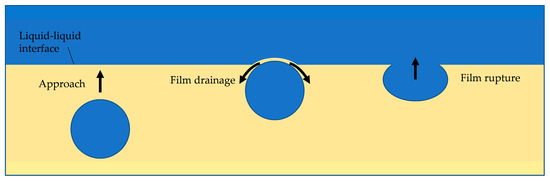
Figure 3.
Schematic representation of the coalescence of a droplet with the phase boundary [25].
Figure 4 shows the sedimentation behavior of a droplet swarm. It can be clearly seen that the sedimentation is completed first. After some time , the dispersion consists only of the most densely packed layer. This is temporally constrained by the film drainage. The droplets in a droplet swarm also coalesce with each other, resulting in a growth of the droplet diameter. This accelerates the coalescence until a final monolayer of droplets is present [26].
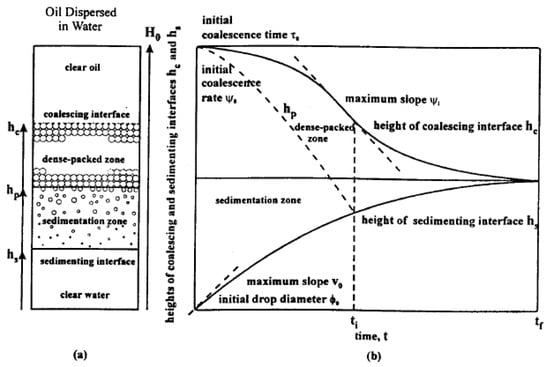
Figure 4.
Schematic representation of the settling behavior of a water/oil system (a) and the sedimentation and coalescence curve over time (b) [26].
A dispersion wedge or a dispersion band can form in a horizontal continuously operated settler. In a dispersion wedge, elongated vortices form in the coherent phases. These are induced on the inside by the inflow of dispersion. When a dispersion band is formed, this wedge collides with the back wall of the settler, and the dispersion accumulates in the settler until the band is approximately the same height along the separator. In contrast to the wedge, a higher flow velocity of the coherent phases than of the dispersion is observed here at the center of the settler [14].
2.2. Continuous Settler Equipment
The simplest implementation of LLE is the mixer–settler, shown in Figure 5, which consists of an agitated or static mixer and a settling section. In the mixer section, the mass transfer is accelerated by the splitting of the droplets, and in the settling section, the phases are passively separated by gravity [27]. Important factors are the properties of the fluids, such as the density difference, the kinetics of mass transfer, and the required throughput of the process [28,29].
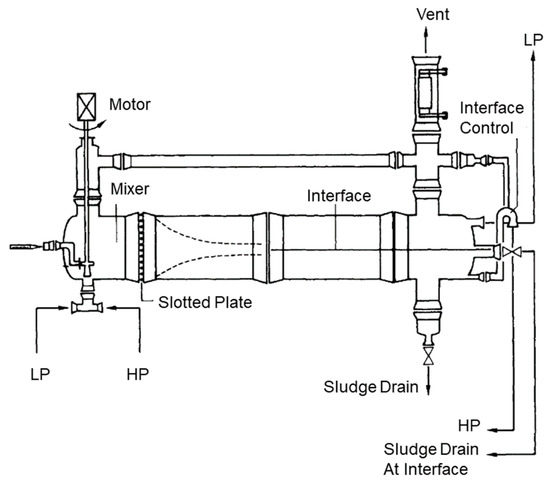
Figure 5.
Schematic drawing of a mixer–separator [28].
An important control parameter for separators is the phase height. This is determined by the back pressure of the heavy phase effluent. To adjust this, a dip tube or overflow valve can be used, which is open at the lower end into the separator and upwards against the atmospheric pressure. The height can thus be adjusted to the desired phase height using Bernoulli’s equation [1]. Since dynamic effects usually affect the phase boundary level, a control system is used for this purpose. In this case, the sensor unit depends on the substance system used. In ATPE, the heavy phase has a high conductivity and the light phase a low one. This means that the phase boundary level can be determined from the conductivity at different heights of the separator [5,30].
In smaller pharmaceutical processes, there are further advantages for the mixer-settler. The simple design of the apparatus results in a high degree of flexibility. The mode of operation can be quickly and easily adapted to the feed provided. Since there is no need for any internals in the mixer–separator, the apparatus can be sterilized with less labor and chemical consumption [31].
2.3. Settler Models
2.3.1. Modelling Depth
Mathematical models are developed for process engineering to design apparatus more efficiently and with fewer preliminary tests. Other applications are cost estimation and process control via conventional controls or digital twins. The level of detail of the models varies widely, as shown in Figure 6. In black box models, no real chemicophysical processes are represented, while in computer fluid dynamic (CFD) models, the space of the apparatus is discredited three-dimensionally to represent flow behavior and mass transfer at high resolution. It should be noted that with increasing model depth, the required computing power and the effort of model generation increase [1,32].
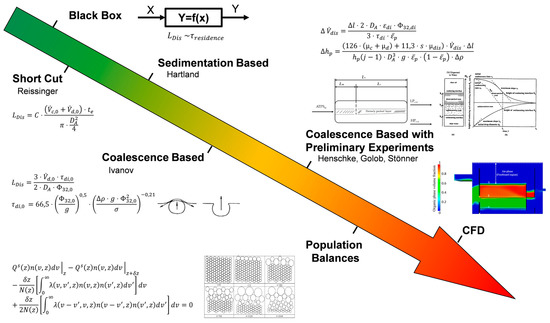
Figure 6.
Schematic representation of increasing model depth with examples [26,30,32,33,34,35,36,37].
Several models have been designed for the separator in the past. These can be divided into models with and without preliminary experiments [14]. Other categories of settler models are sedimentation models and coalescence models. Sedimentation models consider dispersion sedimentation and droplet–interface coalescence, while coalescence models also describe droplet growth via droplet–droplet coalescence [33].
A typical model without preliminary experiments is Reisinger’s model. In this model, the settling time of a dispersion is directly correlated with the length of the dispersion wedge (), see Equation (3). The “dynamic settling time” is derived graphically or from the material properties [35].
A well-known model that takes coalescence into account was developed by Hartland [36]. The starting point for this semi-empirical wedge model is the assumption that the decrease of the dispersion wedge is equal to the decrease of the volume of the droplets coalesced with the interface. The growth rate of the droplets via droplet–droplet coalescence is considered. Here, the derivation of the final equations is performed using integration along wedge length, as shown in Equation (4), with the droplet interface coalescence time . Here, the growth in the vertical direction is neglected. A mean hold-up in the dispersion was assumed to be 0.8 [36].
In the model of Stönner and Wöhler [38], the settling process is broken down into two partial steps: the coalescing of droplets from the mixing process in the dispersion area and the combining of these newly formed droplets with the disperse phase. This results in a dependence on the overall process due to the limiting first step of coalescence. This can be described for the settling experiment by the differential Equation (5). Here, ΔH is the height difference between the sedimentation and coalescence curves. Here, the preliminary experiments determine the exact course of the settling behavior and not the time until complete separation of the phases [38].
2.3.2. Henschke Model
Henschke’s model is a semi-empirical model with preliminary experiments. A model of the coalescence and sedimentation of the settling test is developed. This is used to calculate the coalescence parameter . The course of the settling curve and the settling time are considered here [14].
A sedimentation model and a coalescence model are implemented in the settling model. Both droplet growth and droplet–interface coalescence are modeled.
The horizontal settling model uses the same coalescence models as the sedimentation model. Sedimentation does not occur here as it does in the settling test. Instead, an inlet length is calculated where sedimentation is completed. In addition, the turbulence caused by the diameter change at the inlet is reduced in the inlet region [14].
To represent the large-scale flow in the separator, the settling behavior and three-phase flow were simulated using a CFD model. The forward pressure along the length of the separator in the dispersion was analyzed. With the results of the simulations, this was modeled by an empirical equation. This is shown in Equation (6). Through the relationship from Equation (8), the height of the dispersion is discretely related to the forward pressure. This results in the decrease of the dispersion height in a length discrete [14].
The coalescence model of asymmetric film drainage is shown in Equations (9)–(13). The following assumptions and simplifications are made [14]:
- The vertical velocity in the film is neglected because the change in film thickness is very small compared to distance from the center of the film.
- The continuous phase is treated in the dispersion as an incompressible Newtonian fluid with constant viscosity.
- Gravity is negligible compared to the pressure due to the droplet packing.
- The film is considered to be two-dimensional.
- The spherical curvature of the film is neglected in the coalescence.
The wedge is additionally discretized in the vertical direction to represent the droplet growth. Thus, the droplet diameter and the coalescence time at the interfaces and are calculated. These determine the decrease in dispersion volume, shown in Equation (14) [14].
The model assumes a constant hold-up of the densely packed layer of the dispersion of . This is based on the hold-up of the most densely packed layer after sedimentation is complete. The inlet length, where the settling behavior is governed by sedimentation and no coalescence is present, is calculated using Equation (15). This was derived using dimensional analysis and the exponents were fitted to experimental values [14].
The viscosity of the dispersion () is calculated from the model of Yaron and Gal-Or [39]. This is based on a statistical approximation method, the cell model [39]. The viscosity influence of surface-active substances () is assumed to be zero in the case of liquid–liquid mixtures [14].
2.3.3. Computational Fluid Dynamics
In computational fluid dynamics simulations, the interior of the apparatus under study is discretized in all three spatial dimensions. The Navier–Stokes equation and the continuity equation are solved for each discrete. Thus, flow phenomena can be represented at high resolution. This can be done stationary and dynamic. However, this requires high computational power [40,41].
For the separator, these simulations have been performed for transition states of hydrometallurgical LLE processes [42,43,44]. Due to the particular flow behaviors, these simulations are useful for separators with internals, such as grids or walls [45,46,47].
2.3.4. Distributed Plug Flow Model
The distributed plug flow model (DPF) is based on a discretized view of the flow conditions in a piston flow. In the ideal plug flow, the radial concentration distribution along the tube remains constant. By means of the axial dispersion coefficient , the backmixing—and thus the real behavior of the fluid dynamics—can be represented, as shown in Figure 7. All factors that can cause backmixing—such as diffusion, wall friction, and internal friction—are combined in this dispersion coefficient [48].
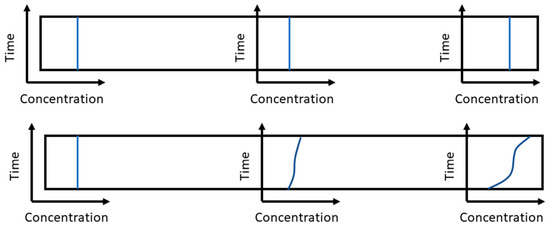
Figure 7.
Schematic representation of the radial concentration distribution of ideal and real plug flow [48].
The following model concepts and assumptions apply to this model:
- There is no concentration or velocity gradient in the radial direction.
- The model is one-dimensional.
- The convective transport is superimposed by a dispersive one.
- In the axial direction, material values, axial dispersion coefficient, and the geometric dimensions are assumed to be constant.
- A transient mass transport can be represented.
Equation (16) shows the axial dispersion model for the concentration. Here, the mass accumulation equals the transport by convection plus the opposite transport by dispersion and the source/sink term .
Either an ideal laminar flow (Equation (20)) or an open system (Equation (21)) can be assumed as the local boundary condition [48,49].
3. Material and Methods
3.1. Process Analytical Technologies
Process monitoring and product quality assurance are implemented using a wide range of measuring sensors. These are grouped under the term process analytical technologies (PAT).
During the optical analysis, images of the droplet swarm are taken with a high-resolution macro-capable camera. These are analyzed using appropriate software. Typically, algorithms based on intensity thresholding or double thresholding are used in conjunction with filtering methods to improve the contours of the objects to be evaluated [50].
3.2. Experimental Setup
3.2.1. Batch Settling Experiments
Settling experiments are carried out to quantify the coalescence properties of the liquid–liquid mixtures used. For this purpose, defined volumes of the two phases are placed in a double-walled glass container (3 × 18 cm). These should be mutually saturated before the experiment to prevent falsification of the results. The phases are mixed for a defined time with a stand motor (VWR, VOS 16) and a stirrer (inclined blade rotor, 3 cm diameter). For a more precise evaluation, the separator is filmed with a suitable camera. Especially in case of very fast or very slow settling of the phases, this allows a more precise evaluation. After the mixing time, the stirrer is quickly removed from the fluid, and a stopwatch is started at the same time.
At regular intervals, the heights of the interfaces on both sides of the dispersion are read. In addition, the time of complete phase separation is recorded.
The aim of the evaluation is to calculate the coalescence parameter . This is calculated using parameter estimation of a settling model [14,51]. A Python® script is written and used to implement the model.
3.2.2. Continuous Horizontal Settler
Figure 8 shows the flow diagram of the process level. The process consists of a static mixer (StaMixCo, New York, NY, USA) and a horizontal continuous separator (glass, 5 × 30 cm). These are fed from two pumps (Fisher Scientific, Hampton, NH, USA) with fluid from two different reservoirs. The pumps are controlled by two mass flow sensors (Bronkhorst, Germany). These also continuously measure density and temperature; these data are also recorded. Monitoring and control is implemented digitally on a Siemens S7-1200 (Siemens, Germany) (PLC; Programmable Logic Controller).
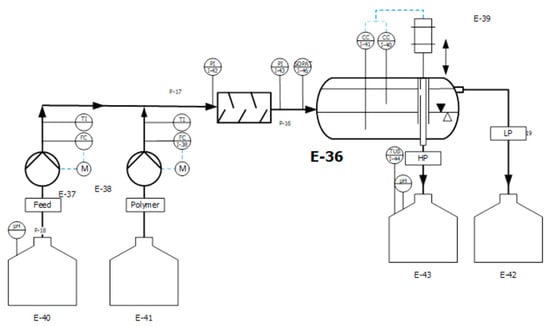
Figure 8.
Illustration of the structure of the continuous settler.
Furthermore, process monitoring is supported by pressure sensors (Autosen, AP016, Essen, Germany) before and after the static mixer and an optical sensor (SOPAT GmbH, PA). The latter has a resolution range of 15 to 2300 µm. In addition, two conductivity sensors (Conducell 4UxF Arc; Hamilton, NH, USA) are mounted at different heights in the static mixer. These are used to control the interface level. This is implemented on the PLC and is implemented by a step motor (ADI Trinamic, PD60-4-1161, Hamburg, Germany). The step motor adjusts the height of the dip tube, which influences the phase level in the separator via the back pressure of the discharge.
A pH probe (Endress + Hauser, Orbisint CP511D-7AA21, Reinach, Switzerland) is installed in the feed tank (E-40) and in the product tank (E-43). A turbidity probe (Excel 231; Exner, Germany) is also located in the product tank.
3.2.3. Alkaline Lysis and ATPE
The goal of alkaline lysis is to disrupt the cell and release the pDNA. The subsequent ATPE is to constrict the product phase and remove the cell debris.
The following solutions are needed for this:
The resuspension buffer (P1) consists of tris(hydroxymethyl)aminomethane hydrochloride (TrisHCl) and ethylenediaminetetraacetic acid (EDTA). The lysis buffer (P2) consists of sodium lauryl sulfate (SDS) and NaOH. The neutralization buffer (P3) is made from citrate solution, which was adjusted to the desired pH with a citric acid solution. As part of the ATPE, polyethylene glycol (PEG) is added to an aqueous solution. The weight fraction of PEG depends on the molecular weight of the PEG.
For alkaline lysis, wet cell paste (WCP) of an E. coli bacterium is resuspended in eight times the mass of P1 with vigorous stirring. P2 is added to the resuspended WCP in a defined amount and shaken manually for a certain time. To terminate lysis, P3 cooled to 4 °C is added and stirred with the remaining solution. For ATPE, a defined amount of PEG solution is added and mixed. Phase separation is performed via centrifuge for small scales. On large scales the mixing of the neutralized with the PEG solution is performed immediately before the settler in a static mixer.
For evaluation, a 0.5 mL sample is drawn from the heavy phase and neutralized. This is cleaned of suspended solids through a 0.2 µm cellulose acetate filter and measured by an appropriate chromatographic analysis method. The concentration of pDNA in the sample is determined [52].
3.3. Continous Settler Process Model
For modeling the dispersion in the separator, the distributed plug flow approach is chosen. In this model, the dispersion is considered a densely packed layer after the sedimentation in the inlet area is completed. The volume of the three phases is described as the subject of the equation. A separate DPF equation is used for all three phases (continuous, dispersion, and dispersed). These are shown in Equation (22) through (24). A separate axial dispersion coefficient is determined for all phases since the phases differ in density and viscosity. The DPF equation divides into a convective, a dispersive, and a source/sink term. The convective term in this model view depends on the axial change in volume, as well as the change in velocity. The axial velocity is different in the phases when the height of the phase boundary in the separator is different from the hold-up of the feed stream.
The source/sink term describes the droplet–interface coalescence. For the DPF term of the dispersion, this is a sink term, which is linked to the DPF equations of the continuous and dispersed phases via the hold-up of the dispersion (). The hold-up of the dispersion () is assumed to be constant with the value 0.9 in this model and the hold-up at the interface () as 1. With representing as the length of a discrete, the diameter of the settler and the flow velocity of the phase.
The volume of dispersion at the beginning of the separator depends on the dispersion formation parameter . This model parameter describes the relative proportion of dispersion depending on the maximum possible. The maximum volume of dispersion occurs when the entire disperse phase is dispersed in the continuous. The model parameter is introduced to describe the real dispersion that arises and can be adjusted in the parameter estimation to map the experimental wedge length. In Equation (25), this is formally represented, and in Equation (22), it is implemented as a boundary condition for the DPF term of the dispersion phase.
A DPF approach is also adopted for droplet growth and droplet interface coalescence. The coalescence rates are described by the asymmetric film drainage model. Equation (27) describes the growth, convection, and dispersion of the droplets. The convective velocity is equal to that of dispersion. The source and sink terms describe the droplet–droplet coalescence as growth and the droplet–interface coalescence as the sink term of the droplet size. These are dependent on the coalescence times described in Equations (12) and (13).
This model computes the length of the dispersion wedge in the continuous settler by finding the point where the dispersion volume equals zero. To this the length of the inlet zone from Equation (15) is added.
4. Results
4.1. Implementation of the Digital Twin
The essential interface for the implementation is OPC Unified Architecture (OPC-UA). Two servers are set up: one on the computer to which the SOPAT probe is connected and one on the computer to which the PLC is connected. Via these interfaces, the process parameters are passed on to a third computer, on which the digital twin is implemented.
The main values of the process are the incoming volume flow and the phase ratio in it. Furthermore, the densities of the flows are also passed on to the digital twin. From the image evaluation of the SOPAT probe, the Sauter diameter is passed on to the DT.
For product quality assurance, the temperatures of the feed streams from the mass flow sensors can be recorded. In addition, the turbidity and pH values of the feeds and the product in the respective reservoirs are measured. The pressure difference between the inlet and outlet of the static mixer is measured to estimate the degree of mixing. The flow chart of the lab scale plant is shown in Figure 9.
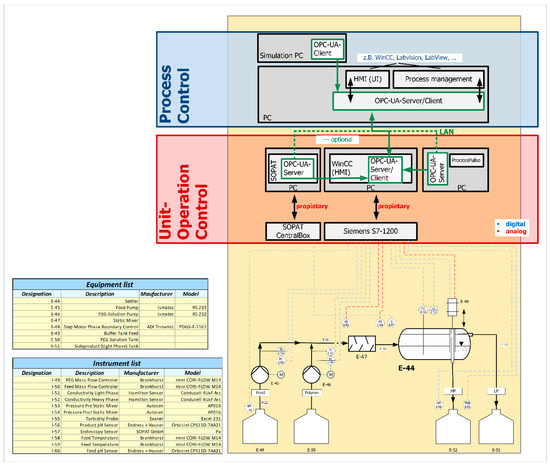
Figure 9.
Process and instruments flow diagram of the separator and control level.
The model is simulated at specifiable time intervals using actual parameters. For the experiments described here, this interval was chosen to be 30 s. The model has a computation time of about 10 s, and in addition the values have to be transferred to the interface used. In this time the model is able to compute the dynamic process of 2500 s. This means that real-time computation is achieved. Furthermore, it was observed in previous experiments that the time until a steady state is established in the separator is about 5 min. This depends on the substance system; this time is valid for the ATPE. A reduced-order model is therefore not necessary to achieve real-time control of the process.
The algorithm supporting the DT runs as shown in Figure 10. The model parameters (coalescence parameter and separator geometry) determined before operation, as well as the quantities known from the offline analysis, are made available to the algorithm. These are used with the quantities from the online measurement to determine the model parameters ( and ). With all parameters set, the expected wedge length is now simulated in DT. If this is shorter the volume flow can be increased. If it is longer than the separator, the volume flow is reduced.
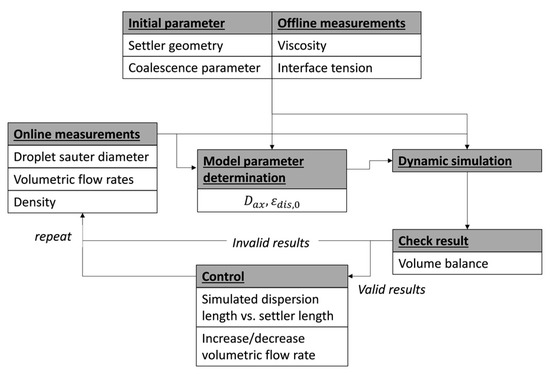
Figure 10.
Flowchart of the digital twin operation.
4.2. Model Parameter Determination
The model parameters to be determined for the model are divided into the following groups: coalescence kinetics, phase equilibrium, and fluid dynamics. These are supplemented by offline and online measurements of material parameters and operating parameters. The summary of the concept is shown in Figure 11.
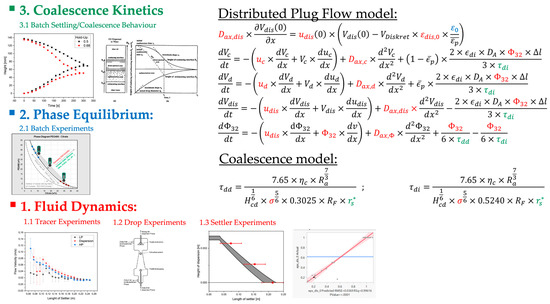
Figure 11.
Summary of the model parameter determination concept and qualitive examples of the experimental data used [3,26,28].
The substance parameters are determined in the respective off-line measurements. A rotational viscometer (Viscotester 550, Thermo Scientific, Waltham, MA, USA) is used to measure the viscosity of the phases. For the densities, a flexural oscillator is used. The surface tension is determined by experiments in a rotational tensiometer. Online measurements are possible for the observation of the droplet diameter via optical analysis. Furthermore, the densities and the operating parameter volume flow are determined online.
The coalescence parameter significantly determines the coalescence rate. This is determined by settling tests, as described in Section 3.2.1.
The dispersion evolution parameter is determined by a regression over the remaining operating and stock parameters. For this regression, tests are carried out with different stock systems in the continuous settler. The wedge length of the dispersion in the separator is measured. To determine the model parameter , parameter estimation is performed with the model. The regression is performed by OLS, with all material and operating parameters as input variables. A part of the data set is retained for validation.
The axial dispersion coefficient is usually determined by tracer tests. A pulse of an easily detectable substance is added to a constant volume flow. At the output of the apparatus is a detector which records the output signal. From the residence time and the temporal distortion of the signal, an axial dispersion coefficient can be determined [53].
For the determination of the coalescence parameter , four settling tests are performed with a citrate/PEG ATPE as described in Section 3.2.1. This is performed twice each for hold-ups of 0.5 and 0.68, respectively. The settling curves of the experiments are plotted including the statistical errors in Figure 12. The difference in settling time is very small for both experiments. Using Henschke’s settling model, a coalescence parameter of 0.1 is determined. The error of the settling curves is very small; therefore, the error of the coalescence parameter is negligible here.
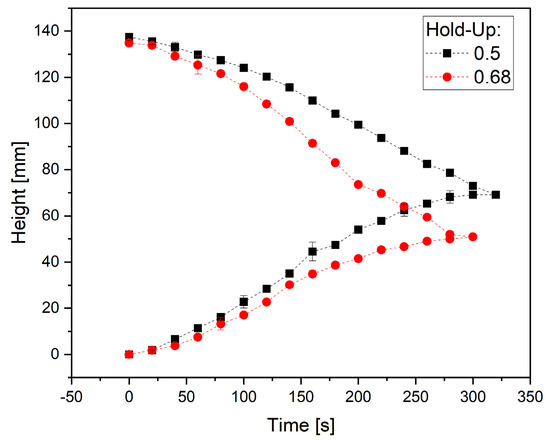
Figure 12.
Settling curves of the ATPE settling test for two different hold-ups.
For the determination of the regression of the dispersion formation parameter simulations of 29 experiments in the continuous settler with 8 input parameters are used. A least squares method is used for the regression via the JMP™ Pro statistical program. Seventeen percent of the results are retained to check the validity of the regression. The regression quality of fit achieved in this process is . From the results of the validation set, the regression quality is . Thus, the regression can be used to determine this model parameter. For the axial dispersion parameter , the regression of Trivedi and Vasudeva is used for laminar flows in noncurved pipes [54].
4.3. Validation of the Process Model
Figure 13 shows the workflow of model validation. This consists of four stages or “decision criteria”. These represent the following attributes of the model: plausibility, sensitivity, accuracy, and precision. In order to achieve these, various methods and simulation studies are shown in Figure 13, which must be run through. For this, it must be proven that the model calculates plausible results without errors of the mass/volume balance (Decision criteria 1). In the second stage, the sensitivity of individual factors is determined from a one-factor-at-a-time (OFAT) simulation study. In order to determine the interactions of the factors, a multi-factors-at-a-time (MFAT) simulation is performed. Here, the parameters of the model are varied in a statistical experimental design. The amplitude of the variation depends on the knowledge gained from the OFAT study. The results of these studies are statistically evaluated and qualitatively compared with literature, experiments and empirical values. If the results are plausible here as well, this stage is considered completed.
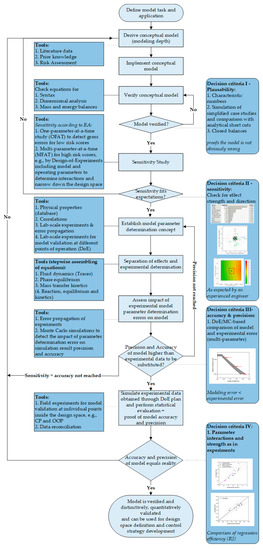
Figure 13.
Schematic representation of the model validation workflow [55].
In the third stage, the precision of the simulations is determined via a simulative Monte Carlo study. For this purpose, the factors within a plausible space are randomly varied in a large number of simulations. A plausible space represents the statistical errors of all input factors in the model. The error calculated from the Monte Carlo simulation is compared with the experimental error. This is calculated from an experimental study. If these errors are similar, the model is considered accurate.
For the final validation, an experimental DoE is performed. Here, the most important input variables are varied. These experiments are simulated with the created model. If the results of the experiments and simulations are within the specified error limits of each other, the model is validated.
4.3.1. Plausibility
The majority (97.5%) of the simulations have a volume balance error below 2.5%. Below the 1% error of the volume balance are 87.7% of the simulations, and 75.5% of the simulations have a lower error of 0.5%.
To prove the plausibility of the model, the calculated flow conditions in the settler and inlet are compared with examples from the literature. For this purpose, the dimensionless numbers of Equations (28)–(31) are used. Dimensionless numbers are generally used for scale-up to describe behavior independent of the size of an apparatus. For this reason, they are suitable here to make a statement about the plausibility of the model [49].
The Reynolds number compares the forces of internal friction with the inertial forces of a flow. When a critical Reynolds number of 2300 is exceeded in a pipe, the flow can be considered turbulent [56]. Both the inlet and the separator itself have a pipe geometry. Laminar flow is expected in the separator, while turbulent flow can occur in the inlet. The Weber number is used as an estimate of the deformation of droplets in two-phase mixtures, it is composed of the inertial forces and the surface tension. Values less than 1 constitute a valid range for liquid–liquid dispersion [57]. The Bond number is defined by the gravitational forces and the surface tension. It can be used to describe the drop shape. Here, values less than 1 are expected [58]. The Archimedes number can be used to determine the maximum sinking velocity of droplets or particles. It compares the buoyancy force with viscous friction. In addition, the Archimedes number is used in the determination of droplet size in batch settling experiments. Here, values greater than 1 are expected [51].
Table 1 shows the results of the simulations of the separator with the substance systems n-butanol/water, water/cyclohexanone, water/n-hexane, and cyclohexane/water. For the simulations, the characteristic numbers were calculated from Equations (28)–(31). The Weber numbers of the simulations are in the valid range. According to the estimation of the Reynolds numbers, turbulent flow may exist in the narrow inlet of the separator, while laminar flow exists in the separator in any case. This was to be expected and agrees with observations from experiments. The Archimedes number is also above the value 1 in every case and thus within the valid range of the Pilhofer–Mewes model [59] for droplet sedimentation velocities.

Table 1.
Representation of dimensionless ratios from simulations of a horizontal continuous settler.
Thus, the model can be considered plausible and the first “decision criteria” of the model validation is completed.
4.3.2. Sensitivity
To establish the sensitivity of the model, an OFAT simulation study was performed. The selected center point represents the operating point for the ATPE of pDNA. Here, 11 parameters were varied in four steps (by 50%, 75%, 125%, and 150% of the center point). The results are shown in Figure 14. The dots represent the simulation results of the wedge length. These are connected by the dashed line. All lines pass through the selected center point. This shows that the model does not exhibit discontinuity when parameters are varied.
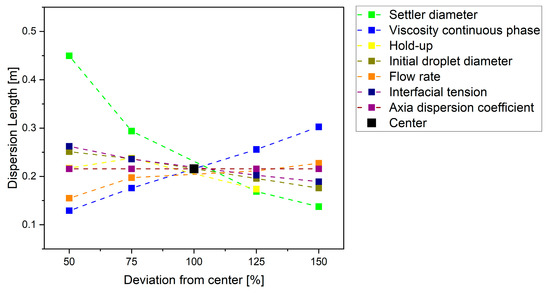
Figure 14.
Presentation of the results of OFAT with wide parameter variation.
The wedge length in the separator correlates negatively with the diameter of the separator. This is plausible with the accompanying reduction of the retention time in the separator. The high slope of the graph signals a high sensitivity of the parameter in the investigated range of values. A positive correlation with the wedge length has the viscosity of the continuous phase. This parameter also has a high sensitivity. A very low sensitivity could be assigned to the axial dispersion parameter of the droplets in the OFAT study. This confirms the assumption made in Section 4.2 of this parameter being constant.
For the density of the two phases, as well as for the viscosity of the disperse phase and coalescence parameter, a finer simulation study was performed in the range +/− 10% of the center point. These parameters are either very sensitive or show a non-linear progression around the center point. The results of this are shown in Figure 15.
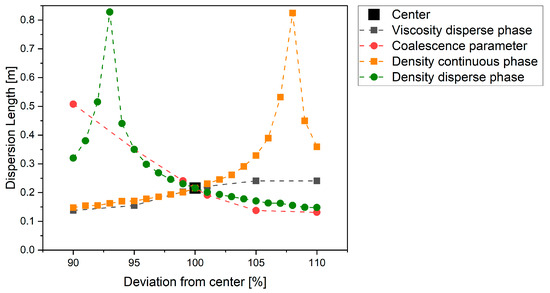
Figure 15.
Plot of OFAT results with fine parameter variation.
The densities of the two phases show a nonlinear correlation. Here, the wedge length is maximized when the density difference is reduced. This is a very sensitive parameter of the model. The coalescence parameter is also very sensitive and correlates negatively with the wedge length in the separator.
From the OFAT study, the sensitivities of individual parameters of the model were determined. In order to also determine the interactions of the parameters with each other, an MFAT study is carried out. For this purpose, the sensitive parameters of the OFAT study are used. Additionally, the diameter of the separator is not used as a parameter because it is assumed to be constant. The range of values of the parameters is coupled to the experimentally realizable or observed values. These are presented in Table 2. A statistical experimental design was created for the implementation of the study. In this, a partial factorial design with 129 simulations including midpoint is selected and carried out.

Table 2.
Parameters and value range of the MFAT simulation study.
The results of the simulations are statistically analyzed. In this process, a regression analysis of the results is evaluated through an OLS analysis. Additionally, the results are evaluated by a PLS and an ANN regression.
The results of the OLS regression are shown in Figure 16. On the left side, the quality of the regression is shown, and it has a coefficient of determination of 0.92. Thus, the MFAT results can be sufficiently well represented by the OLS and further conclusions can be drawn from the OLS regression. On the right side of Figure 16, the p-values of the respective factors and interactions are shown. In the range of values investigated, the volume flow rate and the coalescence parameter have the greatest influence on the wedge length. For the coalescence parameter, the statement of the OFAT study is confirmed. The strong correlation of the volume flow with the wedge length is due to the wide range of values of this parameter.

Figure 16.
Illustration of the regression quality of the OLS regression (a) and parameter sensitivities of the MFAT simulations (b).
The coalescence parameter and the droplet size have a high number of interactions with other parameters and with each other. This is especially the case with other coalescence parameters such as surface tension and volume flow.
Figure 17 shows the regression quality and the correlation of the input parameters with the output variable. The regression quality of 0.59 indicates a slight correlation between the model and the actual value.
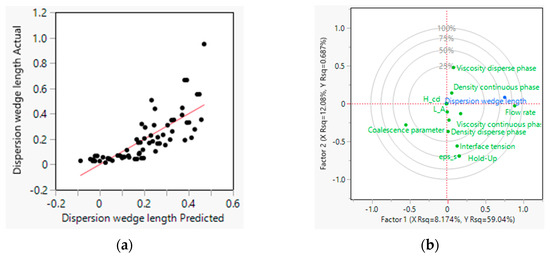
Figure 17.
Plot of model quality of fit (a) and correlation loading plot of PLS analysis from MFAT results (b).
From the correlation-loading plot of the PLS regression, the correlations of the input variable with the output variable can be determined. As from the OLS regression, a strong positive correlation of the volumetric flow rate with the wedge length, and a strong negative correlation of the coalescence parameter with the wedge length can be seen. This is consistent with the results of the OFAT simulation study and the OLS analysis. Therefore, an error not of the sensitivity study can be excluded by the regression used.
The OLS regression was used to create a high-resolution design space. In doing so, within the range of values covered by the MFAT simulation study, the wedge length was calculated for all parameter combinations. These are dependent on the volume flow rate, as shown in Figure 18. The areas within the error limits of the measuring instruments and parameter determinations have been marked in black. These are the normal operating points of the ATPE for pDNA extraction investigated here. The control areas are marked in red. In these areas, separation of the phases in the separator has been demonstrated by modeling and can be performed without loss of productivity.
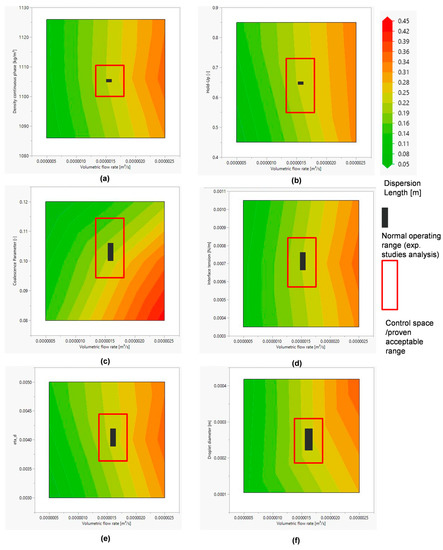
Figure 18.
Illustration of the design spaces for density continuous phase (a), hold-up (b), coalescence parameter (c), interface tension (d), viscosity disperse phase (e), and droplet diameter (f) from the OLS analysis of the MFAT simulation study.
The trajectories of these design spaces qualitatively reflect the expectations for a real ATPE separator. For example, the wedge length correlates positively with the volumetric flow rate and negatively with the coalescence parameter. At a higher coalescence parameter, the dispersion settles faster, so the wedge becomes shorter. In contrast, the wedge becomes longer when the dispersion flows faster through the apparatus due to the increased volumetric flow rate. The generated results reflect the expected effects. Thus, the sensitivity analysis of the model is successfully completed.
4.3.3. Precision
A Monte Carlo simulation is performed to determine the expected error of the model. Here, the input variables are varied randomly within the normal operating point. In total, 150 simulations of the model are performed with these operating parameters.
From these simulations, a mean value of the wedge length of 0.2134 m with a standard deviation of 0.0087 m was calculated. The 95% confidence interval is 0.0144 m. This value corresponds to a relative deviation from the mean of +/− 6.74%. This is the expected error or precision of the simulation.
For validation, experiments are performed with the ATPE in the continuous settler. For this purpose, a statistical experimental design is created. Here, full-factorial variation is made in the volumetric flow rate, hold-up, and length of the static mixer. Some experiments are performed in duplicate or triplicate to determine an experimental error. The length of the resulting wedge is measured. For the subsequent simulation, the Sauter diameter is determined by the installed SOPAT probe. Since the evaluation is not performed in parallel with the measurement, a large amount of data (120 images) is recorded in order to be able to make a well-founded statement about the droplet diameter.
The standard deviation of the repeat tests is 0.0152 m, the 95% confidence interval is thus 0.0360 m. This corresponds to a relative error of 16.8%. Thus, it can be stated that the model is more accurate than the experiments. The experimental error of 16.8% is of a comparable size to the error of the model of 6.7%. Thus, the model can be considered precise.
4.3.4. Accuracy and Validation
To determine the accuracy, the experiments from Section 4.3.3 are simulated with the model. The results of the simulation are shown depending on the experimentally determined wedge length in Figure 19. Furthermore, the results from simulations of separators of four other material systems are shown. The experimental values and operating parameters of the experiments were taken from the work of [14].
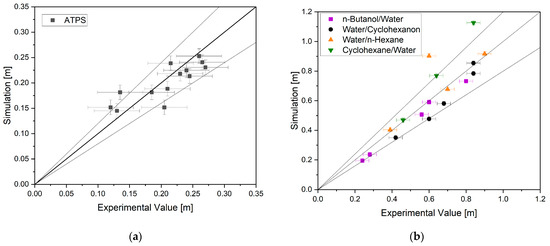
Figure 19.
Representation of wedge length from experiments and simulations from ATPE (a), n-butanol/water, water/cyclohexanone, water/n-hexanes, and cyclohexane/water material systems (b).
The simulations of the ATPE experiments have a coefficient of determination R² of 0.72, the simulations of the other material systems one of R² = 0.79. This estimation of the model quality does not consider the experimental and simulative errors. As can be seen in Figure 19, the range of simulations and experiments coincides. Thus, the model is sufficiently accurate and validated.
4.4. Risk Analysis
Figure 20 lists the parameters that have an influence on the purity, yield and error-free continuous performance of ATPE. Here, the volumetric flow rate, hold-up, Sauter diameter of the droplets, coalescence parameters, surface tension, densities and viscosities of the phases, the axial dispersion coefficient, and the separator geometry are examined in more detail. Since these are the factors that the model created can represent.
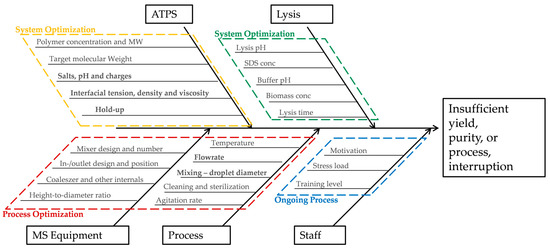
Figure 20.
Ishikawa diagram of the possible process disturbances of ATPE and lysis.
In order to consider these risk parameters quantitatively, two critical quality characteristics of the ATPE were defined. The first is the length of the dispersion wedge; if this is too long, the purity of the product will be negatively affected. In addition, contamination of the heavy phase may occur, requiring parts of the product to be discarded. Thus, the yield is also affected. A second characteristic of ATPE is the space-time yield (STY).
From the OFAT study conducted in Section 4.3.2, the most sensitive main effects were identified. These were evaluated in Figure 21. The most sensitive main effects are the coalescence parameter, the surface tension and the diameter of the separator. The sensitivity of the interactions was evaluated using the MFAT study. Here, the strongest effects are volumetric flow rate, Sauter diameter, and coalescence parameter. By multiplying the score of the main and interaction effect, the severity of the parameters is captured. Here, the Sauter diameter of the droplets and the coalescence parameter are at the top of the list. Thus, these are the parameters with the highest risk potential. These must be monitored to ensure the quality of the product. In contrast, the axial dispersion coefficient and the viscosity of the phases are not sensitive and can be varied within the tested value range without much influence on the wedge length.
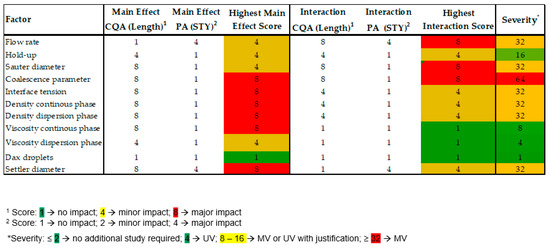
Figure 21.
Quantitative risk assessment from OFAT and MFAT simulation study.
The risky parameters and their severity are plotted against the relative frequency of their occurrence in Figure 22. The droplet diameter and hold-up were assigned the highest probability of occurrence. The droplet diameter is dependent on many factors, such as the composition of the ATPE and the volume flow, due to the use of the static mixer. The hold-up in the feed stream is more dependent on the behavior of the pumps in the ATPE since depending on the volume of PEG solution and salt solution, a different mixing point can occur, which affects the phase ratio. This can also influence the settling behavior and thus the coalescence parameter. In the experiments with biomass, it is often observed that the biomass forms a layer on the interface. This can be a barrier for the heavy phase and thus limit the usable diameter of the separator. For this reason, the risk of the usable separator geometry was assigned a higher probability.
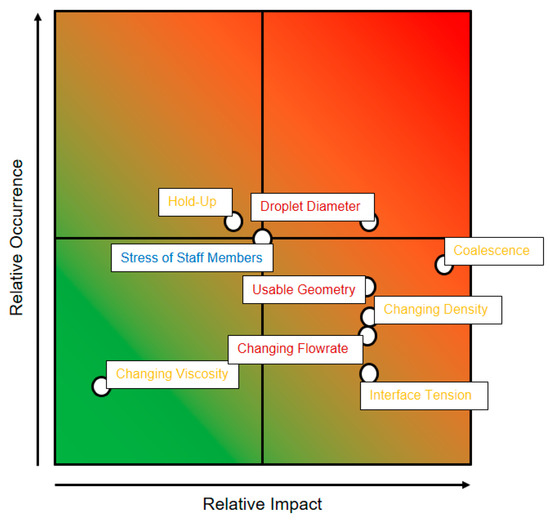
Figure 22.
Representation of the effects and relative probability of the studied disturbances of the process.
Combining the probability and the severity, the important risk factors are to be identified. These can be found in the red area in Figure 22. Particularly noteworthy here are the droplet diameter and the coalescence parameter. These must be monitored particularly closely in the process. For the droplet diameter, an online measurement can be performed via endoscopy, and thus, the control range of this parameter can be monitored. The coalescence parameter depends on many parameters, but most of them can be monitored online. These include the densities of the phases and the hold-up. Thus, the parameter can be monitored. Less important is the constant control of the viscosity and the surface tension.
4.5. Experimental Feasibility by Autonomous Operation Study
For the demonstration of the DT, an aqueous (without biomass) ATPE was first selected. An operating point is selected with a volume flow of 60 mL/min of the saline phase and the corresponding volume flow of the PEG solution. As described in Section 4.1, the measured densities, volumetric flows, and Sauter diameters are passed to the model. These are shown with the simulated and observed wedge lengths in Figure 23 for the experiment.
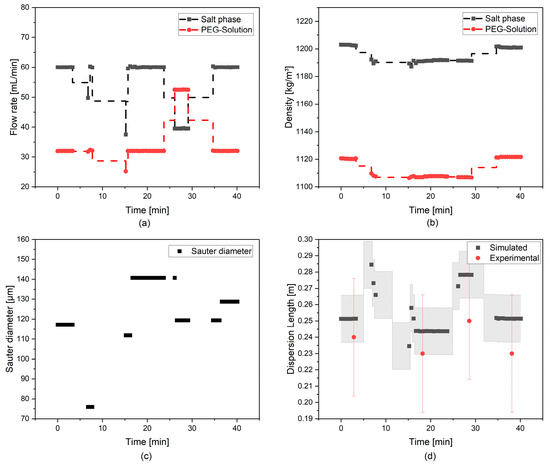
Figure 23.
Plot of measured volumetric flow rate (a), density (b), Sauter diameter (c), and simulated and measured wedge length from aqueous ATPE experiment (d).
After minute 25, this is varied somewhat to test the response of the DT. The response of the model here is much faster than the behavior in the separator. This allows active control of the operating parameters to ensure complete separation of the phases. The significant variations in the simulation result can further be explained by the variations in the analysis of the SOPAT probe images. The smaller the calculated Sauter diameter, the longer the dispersion wedge in the separator.
A reading error of 1.56 cm was determined for the observed wedge lengths from previous experiments (Section 4.3.3). It can be seen in Figure 23 that the simulation does not continuously calculate results. This is due to two factors, firstly the computation time of the model varies and secondly a software error can occur due to the licensing of the OPC-UA interface. This has to be fixed manually at the moment. The varying convergence times of the model occur when the solution approaches a singularity. The reason for this is the possibility of the model to calculate a negative value for the height due to the discrediting. The change of the calculation rule can delay the iteration time here.
An anticipated problem in the implementation of the developed DT into the real system of ATPE with biomass is the measurement of the operating parameters. Especially when determining the droplet diameter, the biomass flocs can block the optical sensor. As an example, recording and evaluation of the droplet size, consider Figure 24. This is generated during the biomass experiment. As described in Section 2.3.1, the SOPAT algorithm identifies the droplets by their sphericity. This means that for larger droplets, the detection is not very accurate. This is not the case here. However, a high computational effort is required for the algorithm, which is why the evaluation of the images takes between 2 and 10 min. A high security of the data is achieved for offline measurements by a large amount of data.
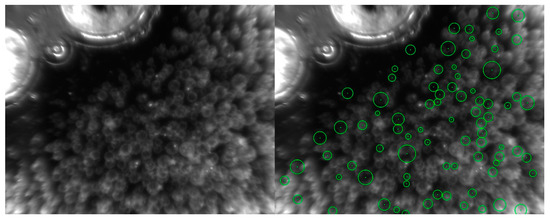
Figure 24.
Acquisition of the droplets (left) and evaluation of the image (right) by the SOPAT-PA probe and the SOPAT algorithm.
Figure 25 shows the summarized evaluation of all 1108 recorded droplets from the biomass test as a histogram and as a cumulative distribution. An accumulation of small droplets with diameters of about 25 µm and a flatter but wider distribution around 100 µm can be observed. Here, not only the actual drop size distribution but also the ability of the algorithm to identify them influences the generated value. A blocking of the sensor could not be detected even through a manual evaluation. Therefore, the droplet size data is used for the demonstration of the DT in the biomass experiment.
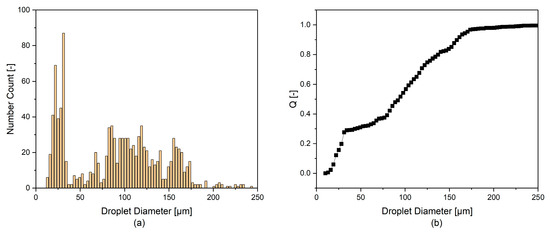
Figure 25.
Histogram of Sauter diameters (a) and cumulative distribution (b) of all images from the SOPAT probe of the biomass experiment.
Figure 26 shows the test data for the test with biomass. The same volume flow rates are selected as for the previous experiment. These are 60 mL/min for the neutralization and 32 mL/min of the PEG solution, which correspond to an average residence time of 6.4 min. Here, too, this is varied during the experiment in order to compare the model response with the real system. An increase in the Sauter diameter, from 123 µm on average in the aqueous test to 139 µm in the test with biomass, can be observed. As a result, the simulated wedge is shorter than in the aqueous test.
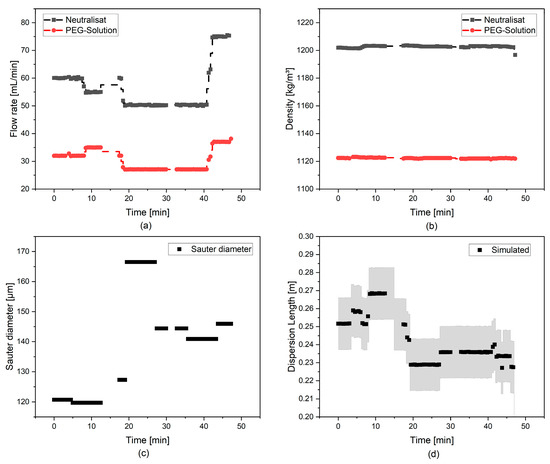
Figure 26.
Plot of measured volumetric flow rate (a), density (b), Sauter diameter (c), and simulated and measured dispersion wedge length (d) from the biomass igneous ATPE test.
Due to the biomass in the separator, no dispersion wedge can be observed optically. This can also be seen in Figure 27. As evidence of the complete separation of the phases, the light phase is settled batch wise in a 2 L separating funnel. In this process, 250 mL of heavy phase is recovered from 3850 mL of light polymer-containing phase formed. From the continuous settler, 1550 mL of heavy phase is collected. Thus, a yield of 86% is achieved. The reason for the loss of heavy phase is biomass in the separator. It could be observed visually that this formed a blanket on the heavy phase. This is more difficult to be penetrated by the heavy phase present in the dispersion. This effect occurs especially in the rear part of the separator. Another effect can also be observed in the ATPE, with biomass operated in a heap. Here, a fast but not complete phase separation can be observed in the 2 L separator. The last 10% of the heavy phase is recovered through centrifugation of the biomass, as in Section 4.1. A theoretical reason for the effect is that the biomass flocs are wetted by the heavy phase, resulting in the observed yield loss.

Figure 27.
Photograph of continuously operated lying settler at ATPE trial with biomass.
From the tests with the aqueous ATPE, a coefficient of determination of 0.816 can be calculated between the simulated and experimentally determined wedge lengths. For the experiments with biomass, no quantitative assessment of DT can be determined due to the biomass. However, all simulated results of the wedge length are smaller than the separator length. Therefore, complete phase separation at the end of the separator can be assumed. No significant amount of heavy phase is found in the light phase reservoirs, which cannot be explained by the effect of biomass. Thus, the use of the DT to monitor and control the separator can be considered useful.
5. Conclusions and Discussion
A digital twin has been successfully established, validated, and integrated for the first time with process analytical technology operated autonomously for biologics manufacturing, as exemplified on alkaline pDNA lysis of E. coli using ATPE with and without cell debris separation. An operation point with about 20% higher throughput has been successfully operated at process variations. Such an autonomous operation was conducted for the first time.
For this purpose, a model was developed from flow and coalescence models. Furthermore, a model parameter determination concept was prepared for this model. A validation was carried out for both: In 97.5% of the simulations, the difference in volume balance was less than +/− 2.5%. A one-factor-at-a-time and a multiple-factor-at-a-time simulation study were performed to analyze the sensitivity of the model, material, and operating parameters. As expected, the most sensitive parameters are the densities of the phases, the volumetric flow rate, the coalescence parameter, and the diameter of the separator. A Monte Carlo simulation study was performed to determine the error of the simulations with respect to the separator zone length: 0.0144 m (+/− 6.47%). The experimental error was determined to be 0.0360 m (+/− 16.8%). This indicates that the model is sufficiently accurate to be used for separator design and monitoring. The ATPE experiments were simulated using the model to determine accuracy. A coefficient of determination R² of 0.72 was obtained for the ATPE and 0.79 for other two-phase systems from the literature n-butanol/water, water/cyclohexanone, water/n-hexanes, and cyclohexane/water. Thus, the model validation has been successfully completed.
As part of the QbD based process development, a risk analysis was performed using the model. The parameters with the highest risk were identified as the coalescence properties, the hold-up and the droplet diameter. In ATPE, the hold-up has an influence on the coalescence properties of the dispersion, since it affects the composition and thus the material properties of the resulting phase.
For monitoring and control of the continuously operated horizontal separator, the model created was implemented as a digital twin. OPC-UA interfaces between the model and the plant were used for this purpose. For monitoring, a control concept consisting of optical measurement of the droplet diameter (SOPAT), mass flow sensors, and conductivity measurement was developed.
In the experimental feasibility studies, by supporting the digital twin, the residence time in the DN50 separator was reduced from 10 min with the phase level conductivity control to 6.4 min with the digital twin. As a result, an increase in throughput can be achieved: The digital twin does not need the conductivity information. However, it is conceivable to use a hybrid control system in which the conductivity probes are placed at critical points in the separator to reliably prevent product loss even in the event of any malfunction. In the case of no control, an operator crew would have to permanently monitor the phase boundary level and complete phase separation. Assuming a length premium of 20% for the design of a separator, 20% more throughput could be achieved for the same separator controlled by the digital twin.
In this work, it was shown that the digital twin can serve for risk analysis (sensitivity) as well as for the determination of design spaces and optimal control spaces. In addition, the digital twin was used at the institute directly for real-time process control for the first time, which means that for the first time, a validated digital twin is available for ATPE from process development up to process control.
This methodology opens up a new frontier for ATPE in biologics manufacturing as most industries are not yet familiar with such chemistry and equipment. The digital twin concept enables operator training, process design in accordance with regulatory requirements and with design and control space definition, scaled up and predictive maintenance, and even real-time release testing with autonomous cleaning and cleaning validation. The digital twins of settler and columns [3] open up in combination any autonomous operation of integrated processes for fractionation with extraction, wash, and scrub [2].
The concept will be transferred to all other unit operations and proven via experimental feasibility studies. Parallel industrialization projects are supported.
Author Contributions
Conceptualization, J.S.; methodology, A.U.; validation, A.U. and A.S.; investigation, A.U.; writing—original draft preparation, J.S. and A.U.; writing—review and editing, A.S. and M.W.H.; supervision, J.S. and M.W.H.; project administration, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors want to gratefully acknowledge the Bundesministerium für Wirtschaft und Klimaschutz (BMWK), especially Michael Gahr (Projektträger FZ Jülich), for funding the scientific work.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the whole institute‘s team, especially Mourad Mouellef and Thomas Knebel for their endless automation efforts; laboratory head Frank Steinhäuser for his full-time troubleshooting and total support; Martin Tegtmeier as a qualified person for his regulatory guidance and supervision; and Werner Bäcker, formerly Bayer AG Central Technology Leverkusen, for his contagious liquid–liquid extraction enthusiasm. The authors acknowledge financial support by Open Access Publishing Fund of Clausthal University of Technology.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goedecke, R. Fluidverfahrenstechnik: Grundlagen, Methodik, Technik, Praxis; Wiley-VCH: Weinheim, Germany, 2006; ISBN 978-3-527-31198-9. [Google Scholar]
- Schmidt, A.; Strube, J. Application and Fundamentals of Liquid-Liquid Extraction Processes: Purification of Biologicals, Botanicals, and Strategic Metals. In Kirk-Othmer Encyclopedia of Chemical Technology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000; pp. 1–52. ISBN 9780471238966. [Google Scholar]
- Schmidt, A. Prozessintegration Mittels Validierter Digitaler Zwillinge von Flüssig-Flüssig-Extraktionsprozessen zur Gewinnung von Metallischen, Pflanzlichen und …; Shaker Verlag: Düren, Germany, 2021. [Google Scholar]
- dos Santos, N.V.; Carvalho Santos-Ebinuma, V.D.; Pessoa Junior, A.; Pereira, J.F.B. Liquid-liquid extraction of biopharmaceuticals from fermented broth: Trends and future prospects. J. Chem. Technol. Biotechnol. 2018, 93, 1845–1863. [Google Scholar] [CrossRef]
- Richter, M.C.; Rudolph, F.; Schmidt, A.; Strube, J. Verfahren zum reinigen und anreichern von proteinen, nukleinsäuren oder viren unter verwendung eines wässrigen zwei-phasen-systems. Patent WO2022157365A1, 28 June 2022. [Google Scholar]
- Helgers, H.; Hengelbrock, A.; Schmidt, A.; Vetter, F.L.; Juckers, A.; Strube, J. Digital Twins for scFv Production in Escherichia coli. Processes 2022, 10, 809. [Google Scholar] [CrossRef]
- Hengelbrock, A.; Helgers, H.; Schmidt, A.; Vetter, F.L.; Juckers, A.; Rosengarten, J.F.; Stitz, J.; Strube, J. Digital Twin for HIV-Gag VLP Production in HEK293 Cells. Processes 2022, 10, 866. [Google Scholar] [CrossRef]
- Schmidt, A.; Helgers, H.; Lohmann, L.J.; Vetter, F.; Juckers, A.; Mouellef, M.; Zobel-Roos, S.; Strube, J. Process analytical technology as key-enabler for digital twins in continuous biomanufacturing. J. Chem. Technol. Biotechnol. 2022, 97, 2336–2346. [Google Scholar] [CrossRef]
- Helgers, H.; Hengelbrock, A.; Schmidt, A.; Strube, J. Digital Twins for Continuous mRNA Production. Processes 2021, 9, 1967. [Google Scholar] [CrossRef]
- Kritzinger, W.; Karner, M.; Traar, G.; Henjes, J.; Sihn, W. Digital Twin in manufacturing: A categorical literature review and classification. IFAC-PapersOnLine 2018, 51, 1016–1022. [Google Scholar] [CrossRef]
- Sixt, M. Methoden zur Systematischen Gesamtprozessentwicklung und Prozessintensivierung von Extraktions-und Trennprozessen zur Gewinnung Pflanzlicher Wertkomponenten; Shaker Verlag: Düren, Germany, 2018. [Google Scholar]
- Pharmaceutical Development Q8(R2): International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use; ICH: Geneva, Switzerland, 2009.
- Uhlenbrock, L.; Sixt, M.; Strube, J. Quality-by-Design (QbD) process evaluation for phytopharmaceuticals on the example of 10-deacetylbaccatin III from yew. Resou.-Eff. Technol. 2017, 3, 137–143. [Google Scholar] [CrossRef]
- Henschke, M. Dimensionierung Liegender Flüssig-Flüssig-Abscheider Anhand Diskontinuierlicher Absetzversuche; Zugl.: Aachen, Techn. Hochsch., Diss., 1994, Als Ms. gedr; VDI-Verl.: Düsseldorf, Germany, 1995; ISBN 3-18-337903-1. [Google Scholar]
- Narasingam, A.; Kwon, J.S.-I. Development of local dynamic mode decomposition with control: Application to model predictive control of hydraulic fracturing. Comput. Chem. Eng. 2017, 106, 501–511. [Google Scholar] [CrossRef]
- Shi, D.; Mhaskar, P.; El-Farra, N.H.; Christofides, P.D. Predictive control of crystal size distribution in protein crystallization. Nanotechnology 2005, 16, S562–S574. [Google Scholar] [CrossRef] [PubMed]
- Henschke, M.; Pfennig, A. Simulation of Packed Extraction Columns with the REDROP Model; Czech Society of Chemical Engineering: Praha, Tsjechië, 1996; ISBN 80-02-01106-6 1130. [Google Scholar]
- Ayesterán, J.; Kopriwa, N.; Buchbender, F.; Kalem, M.; Pfennig, A. ReDrop–A Simulation Tool for the Design of Extraction Columns Based on Single-Drop Experiments. Chem. Eng. Technol. 2015, 38, 1894–1900. [Google Scholar] [CrossRef]
- Hlawitschka, M.W.; Schäfer, J.; Hummel, M.; Garth, C.; Bart, H.-J. Populationsbilanzmodellierung mit einem Mehrphasen-CFD-Code und vergleichende Visualisierung. Chem. Ingenieur Tech. 2016, 88, 1480–1491. [Google Scholar] [CrossRef]
- Hlawitschka, M.W.; Jaradat, M.; Chen, F.; Attarakih, M.M.; Kuhnert, J.; Bart, H.-J. A CFD-Population Balance Model for the Simulation of Kühni Extraction Column. In 21st European Symposium on Computer Aided Process Engineering; Elsevier: Amsterdam, The Netherlands, 2011; pp. 66–70. ISBN 9780444538956. [Google Scholar]
- Drumm, C.; Attarakih, M.; Hlawitschka, M.W.; Bart, H.-J. One-Group Reduced Population Balance Model for CFD Simulation of a Pilot-Plant Extraction Column. Ind. Eng. Chem. Res. 2010, 49, 3442–3451. [Google Scholar] [CrossRef]
- Mühlbauer, A.; Hlawitschka, M.W.; Bart, H.-J. Models for the Numerical Simulation of Bubble Columns: A Review. Chem. Ingenieur Tech. 2019, 91, 1747–1765. [Google Scholar] [CrossRef]
- Casamatta, G.; Vogelpohl, A. Modellierung der Fluiddynamik und des Stoffübergangs in Extraktionskolonnen. Chem. Ingenieur Tech. 1984, 56, 230–231. [Google Scholar] [CrossRef]
- Lohrengel, B. Thermische Trennverfahren: Trennung von Gas-, Dampf-und Flüssigkeitsgemischen, 3rd ed.; De Gruyter Oldenbourg: Berlin, Germany, 2017; ISBN 978-3-11-047321-6. [Google Scholar]
- Rommel, W.; Meon, W.; Blass, E. Hydrodynamic Modeling of Droplet Coalescence at Liquid-Liquid Interfaces. Sep. Sci. Technol. 1992, 27, 129–159. [Google Scholar] [CrossRef]
- Jeelani, S.A.K.; Hartland, S. Effect of Dispersion Properties on the Separation of Batch Liquid−Liquid Dispersions. Ind. Eng. Chem. Res. 1998, 37, 547–554. [Google Scholar] [CrossRef]
- Mersmann, A.; Stichlmair, J.; Kind, M. Thermische Verfahrenstechnik: Grundlagen und Methoden; 2., wesentlich erweiterte and aktualisierte Auflage; Springer: Berlin, Germany, 2005; ISBN 3540280529. [Google Scholar]
- Sattler, K. Thermische Trennverfahren: Grundlagen, Auslegung, Apparate; 3., überarb. u. erw. Aufl., [Nachdr.]; Wiley-VCH: Weinheim, Germany, 2007; ISBN 9783527302437. [Google Scholar]
- Brandt, H.W.; Reissinger, K.-H.; Schröter, J. Moderne Flüssig/Flüssig-Extraktoren-Übersicht und Auswahlkriterien. Chem. Ingenieur Tech. 1978, 50, 345–354. [Google Scholar] [CrossRef]
- Schmidt, A.; Richter, M.; Rudolph, F.; Strube, J. Integration of Aqueous Two-Phase Extraction as Cell Harvest and Capture Operation in the Manufacturing Process of Monoclonal Antibodies. Antibodies 2017, 6, 21. [Google Scholar] [CrossRef]
- Hui, Y.H.; Bruinsma, B. (Eds.) Food Plant Sanitation; Dekker: New York, NY, USA, 2003; ISBN 0824707931. [Google Scholar]
- Strube, J.; Schulte, M. Thermische Trennverfahren als Schlüsseltechnologie in den Life Sciences. Chem. Ingenieur Tech. 2003, 75, 1071–1072. [Google Scholar] [CrossRef]
- Frising, T.; Noïk, C.; Dalmazzone, C. The Liquid/Liquid Sedimentation Process: From Droplet Coalescence to Technologically Enhanced Water/Oil Emulsion Gravity Separators: A Review. J. Dispers. Sci. Technol. 2006, 27, 1035–1057. [Google Scholar] [CrossRef]
- Ruiz, M.C.; Padilla, R. Separation of liquid-liquid dispersions in a deep-layer gravity settler: Part II. Mathematical modeling of the settler. Hydrometallurgy 1996, 42, 281–291. [Google Scholar] [CrossRef]
- Reissinger, K.-H.; Schröter, J.; Bäcker, W. Möglichkeiten und Probleme bei der Auslegung von Extraktoren. Chem. Ingenieur Tech. 1981, 53, 607–614. [Google Scholar] [CrossRef]
- Hartland, S. Koaleszenz in dichtgepackten Gas/Flüssig-und Flüssig/Flüssig-Dispersionen. Ber. Der Bunsenges. Für Physikalische Chem. 1981, 85, 851–863. [Google Scholar] [CrossRef]
- Panda, S.K.; Buwa, V.V. Effects of Geometry and Internals of a Continuous Gravity Settler on Liquid–Liquid Separation. Ind. Eng. Chem. Res. 2017, 56, 13929–13944. [Google Scholar] [CrossRef]
- Stönner, H.M. Proceedings of the Mathematisches Modell für den Flüssig-Flüssig-Abscheide-Vorgang (am Beispiel der dichtgepackten Dispersion): Vortrag Anlässlich der Sitzung des Extraktionsgremiums, Frankfurt/Main, Duitsland, 20 March 1981.
- Yaron, I.; Gal-Or, B. On viscous flow and effective viscosity of concentrated suspensions and emulsions. Rheol. Acta 1972, 11, 241–252. [Google Scholar] [CrossRef]
- Ferziger, J.H. Numerische Strömungsmechanik; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-68228-8. [Google Scholar]
- Singh, K.K.; Sarkar, S.; Sen, N.; Mukhopadhyay, S.; Shenoy, K.T. Computational fluid dynamics modelling of solvent extraction equipment: A review. BARC Newslett. 2021, 379, 45–55. [Google Scholar]
- Panda, S.K.; Singh, K.K.; Shenoy, K.T.; Buwa, V.V. Numerical simulations of liquid-liquid flow in a continuous gravity settler using OpenFOAM and experimental verification. Chem. Eng. J. 2017, 310, 120–133. [Google Scholar] [CrossRef]
- Shabani, M.O.; Mazahery, A.; Alizadeh, M.; Tofigh, A.A.; Rahimipour, M.R.; Razavi, M.; Kolahi, A. Computational fluid dynamics (CFD) simulation of effect of baffles on separation in mixer settler. Int. J. Min. Sci. Technol 2012, 22, 703–706. [Google Scholar] [CrossRef]
- Schmidt, A.; Montenegro, V.; Wehinger, G.D. Transient CFD Modeling of Matte Settling Behavior and Coalescence in an Industrial Copper Flash Smelting Furnace Settler. Metall. Mater. Trans. B 2021, 52, 405–413. [Google Scholar] [CrossRef]
- Shabani, M.; Mazahery, A. Computational Fluid Dynamics (CFD) Simulation of Liquid-Liquid Mixing in Mixer Settler. Arch. Metall. Mat. 2012, 57, 173–178. [Google Scholar] [CrossRef]
- Kankaanpää, T. CFD Procedure for Studying Dispersion Flows and Design Optimization of the Solvent Extraction Settler; Helsinki University of Technology, Laboratory of Materials Processing and Powder Metallurgy: Espoo, Finland, 2007; ISBN 1795-0074. [Google Scholar]
- Hlawitschka, M. ERNA—Effiziente Tropfenabscheidung in Flüssig-Flüssig-Systemen an Gestricken: Schlussbericht; 2021. Schlussbericht zu IGF-Vorhaben 19743 N/1: Berichtszeitraum: 01.10.2017–30.06.2020. Available online: https://books.google.ro/books/about/ERNA_Effiziente_Tropfenabscheidung_in_Fl.html?id=3CbyzgEACAAJ&redir_esc=y (accessed on 6 January 2023).
- Danckwerts, P.V. Continuous flow systems. Chem. Eng. Sci. 1953, 2, 1–13. [Google Scholar] [CrossRef]
- Güttel, R.; Turek, T. Chemische Reaktionstechnik; 1. Aufl. 2021; Springer: Berlin/Heidelberg, Germany, 2021; ISBN 9783662631508. [Google Scholar]
- Emmerich, J.; Tang, Q.; Wang, Y.; Neubauer, P.; Junne, S.; Maaß, S. Optical inline analysis and monitoring of particle size and shape distributions for multiple applications: Scientific and industrial relevance. Chin. J. Chem. Eng. 2019, 27, 257–277. [Google Scholar] [CrossRef]
- Henschke, M. Determination of a coalescence parameter from batch-settling experiments. Chem. Eng. J. 2002, 85, 369–378. [Google Scholar] [CrossRef]
- Urthaler, J.; Buchinger, W.; Necina, R. Improved downstream process for the production of plasmid DNA for gene therapy. Acta Biochim. Pol. 2005, 52, 703–711. [Google Scholar] [CrossRef] [PubMed]
- Levenspiel. Chemical Reaction Engineering; John Wiley and Sons Inc: Hoboken, NJ, USA, 1999. [Google Scholar]
- Trivedi, R.N.; Vasudeva, K. Axial dispersion in laminar flow in helical coils. Chem. Eng. Sci. 1975, 30, 317–325. [Google Scholar] [CrossRef]
- Sixt, M.; Uhlenbrock, L.; Strube, J. Toward a Distinct and Quantitative Validation Method for Predictive Process Modelling—On the Example of Solid-Liquid Extraction Processes of Complex Plant Extracts. Processes 2018, 6, 66. [Google Scholar] [CrossRef]
- Reynolds, O. XXIX. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. R. Soc. 1883, 174, 935–982. [Google Scholar] [CrossRef]
- Dessimoz, A.-L.; Cavin, L.; Renken, A.; Kiwi-Minsker, L. Liquid–liquid two-phase flow patterns and mass transfer characteristics in rectangular glass microreactors. Chem. Eng. Sci. 2008, 63, 4035–4044. [Google Scholar] [CrossRef]
- Kralj, S.; Eeuwema, W.; Eckhardt, T.H.; Dijkhuizen, L. Role of asparagine 1134 in glucosidic bond and transglycosylation specificity of reuteransucrase from Lactobacillus reuteri 121. FEBS J. 2006, 273, 3735–3742. [Google Scholar] [CrossRef]
- Mewes, D.; Pilhofer, T. Vorausberechnung der fluiddynamischen Eigenschaften von Siebbodenextraktionskolonnen ohne Pulsation. Chem. Ingenieur Tech. 1978, 50, 203–211. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).