Analysis via 3D FEM of the Passing Capacity of Pipeline Inspection Gauges in Bends with Different Curvatures
Abstract
:1. Introduction
2. Simulation Strategy
2.1. FEM of the PIG in the Bend
2.2. Grid Independence and Boundary Conditions
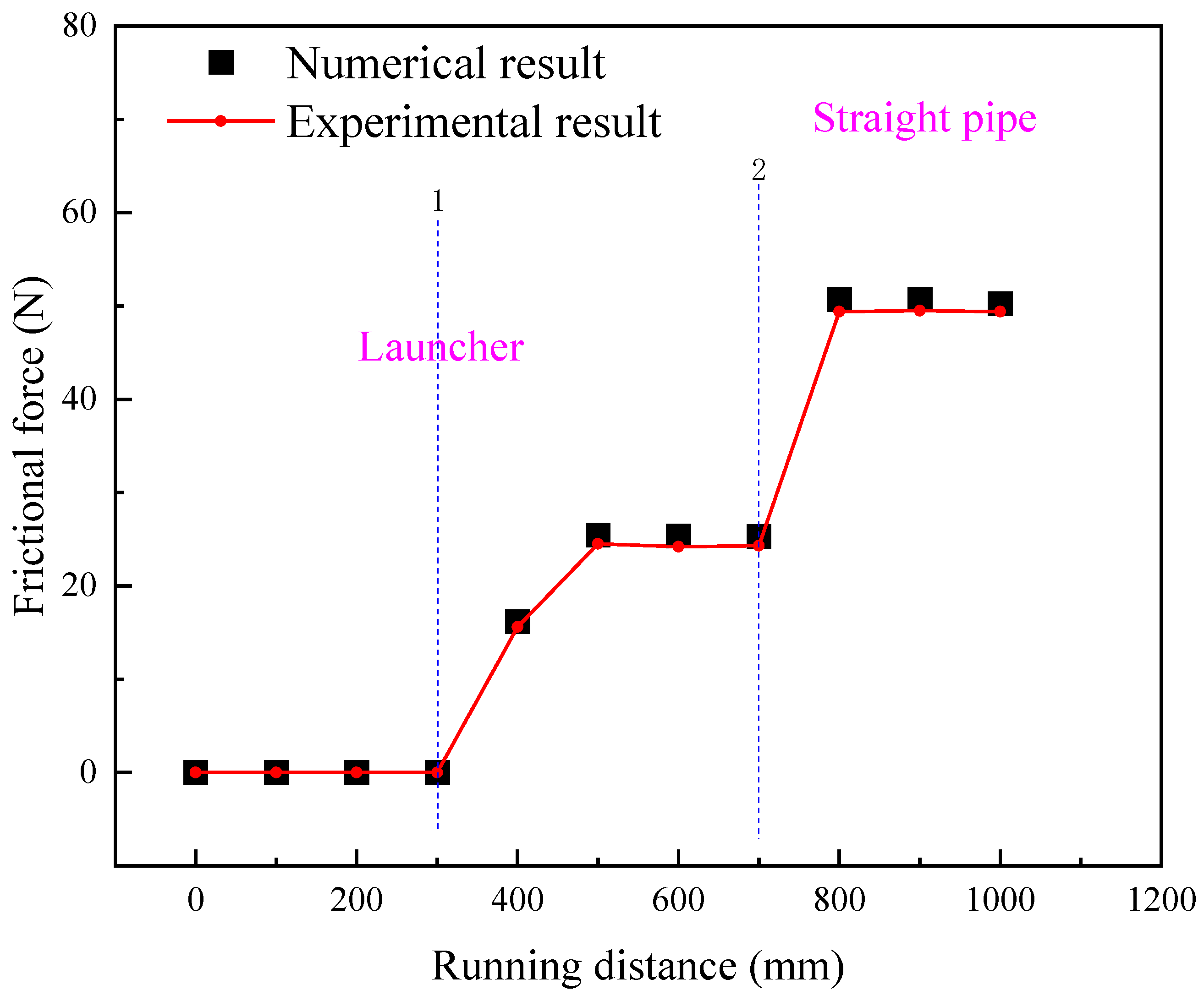
2.3. Verification of the 3D FE Model
3. Results and Discussion
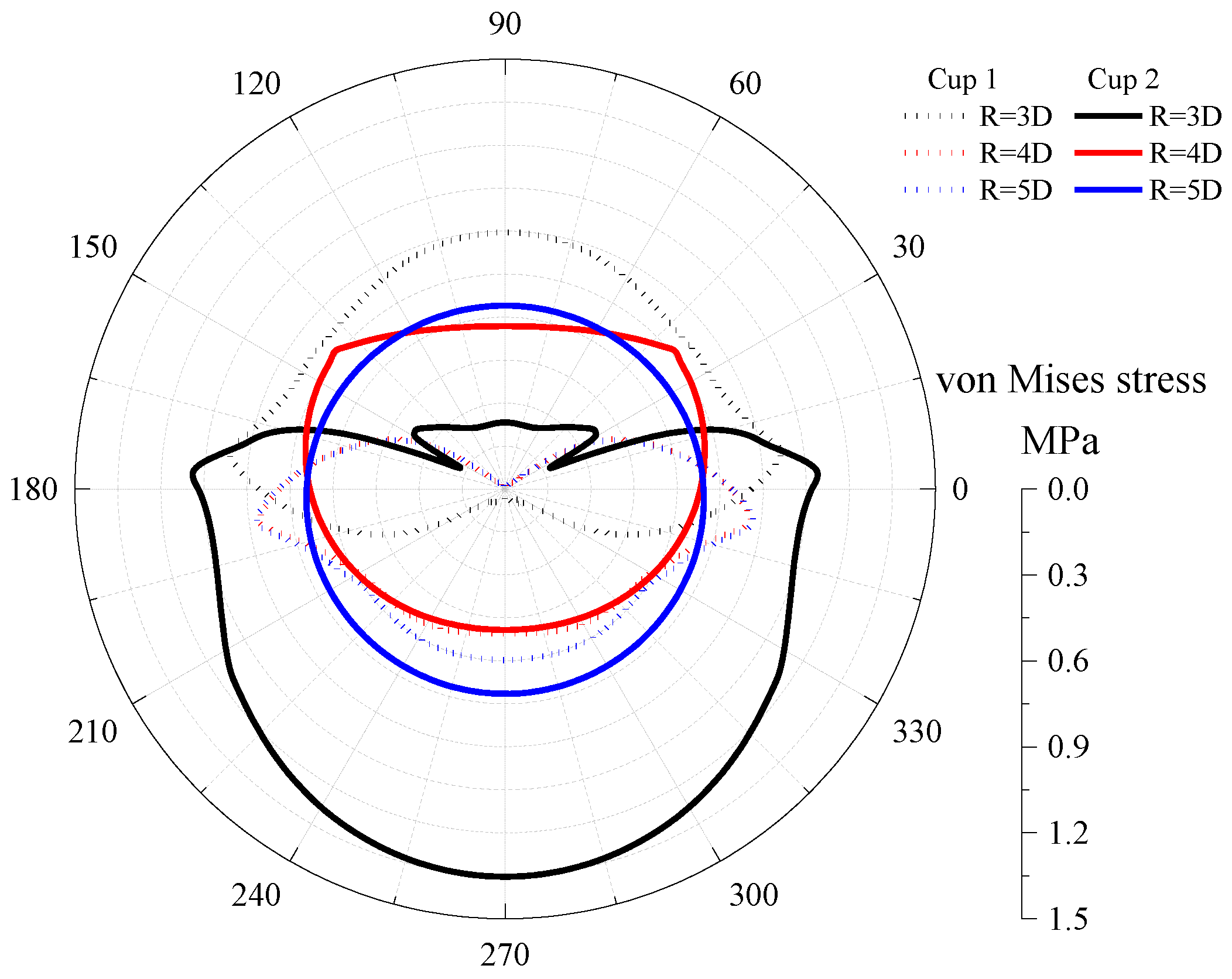
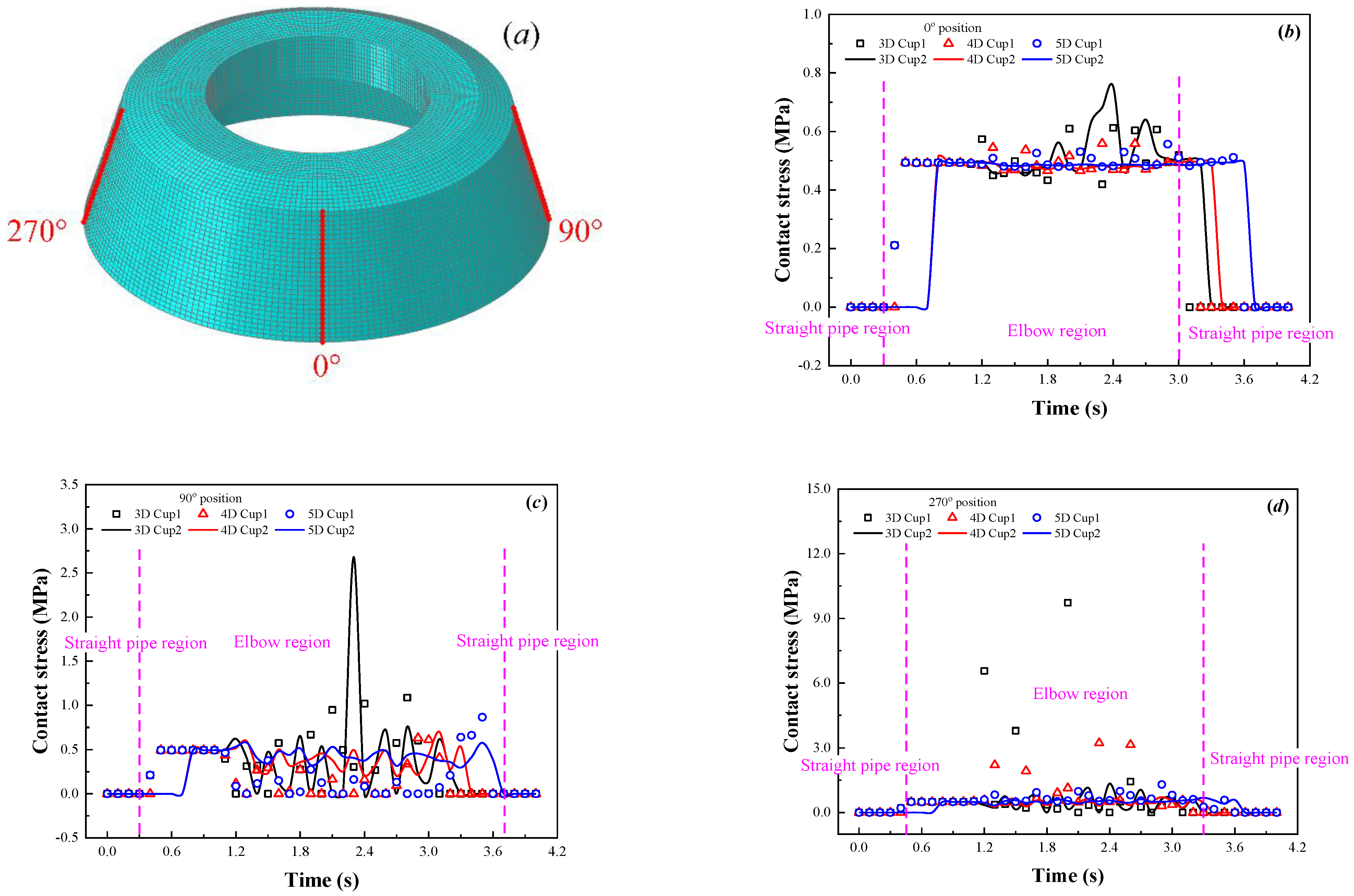
3.1. Analysis of the Safe Application Performance of the PIG
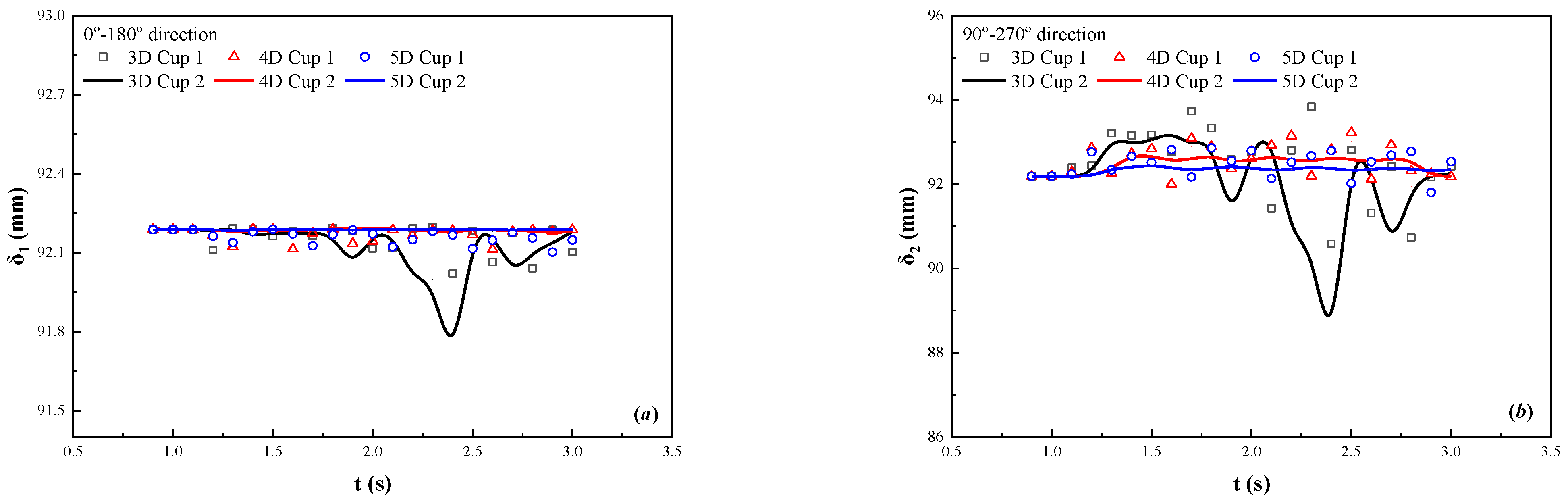
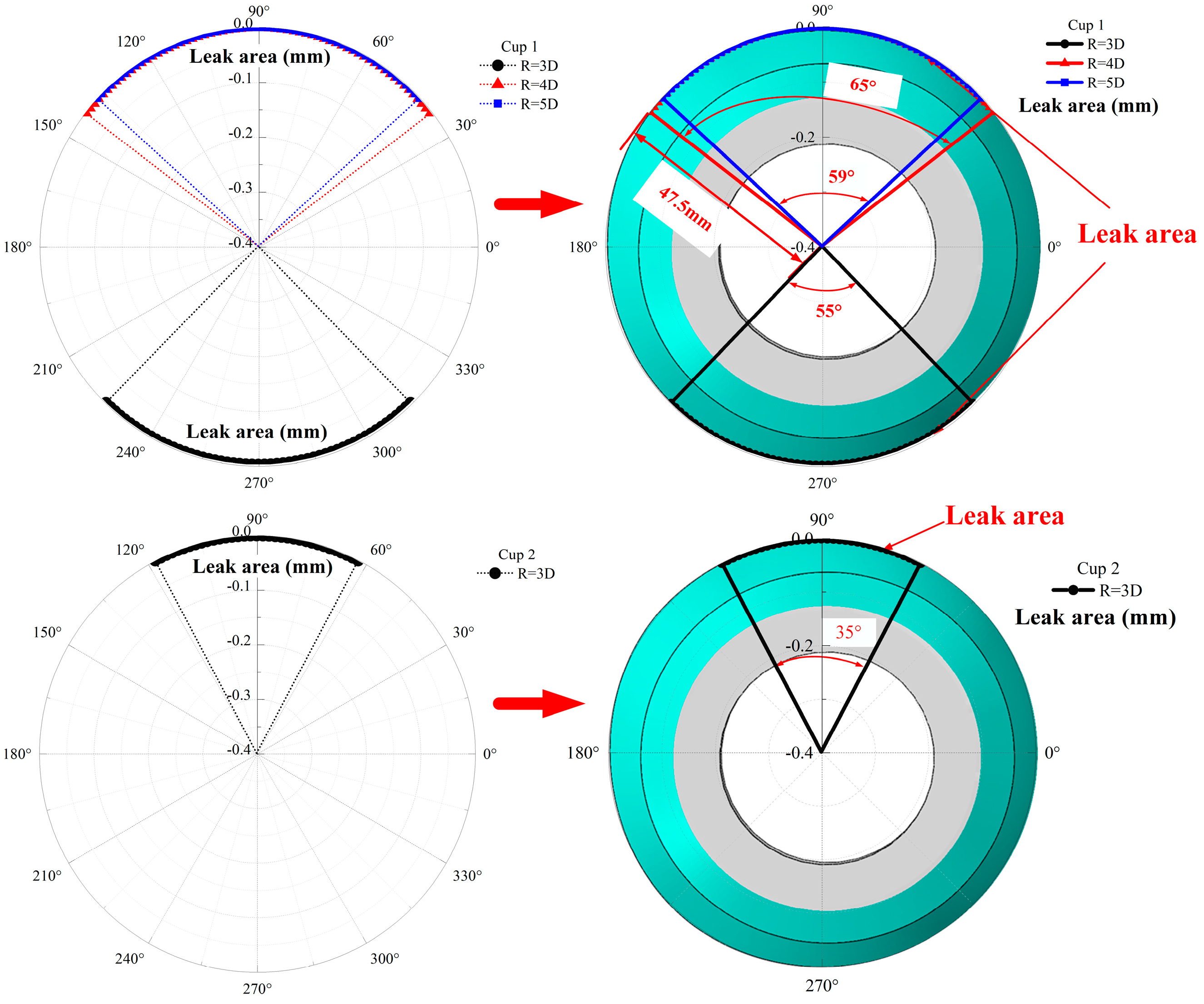
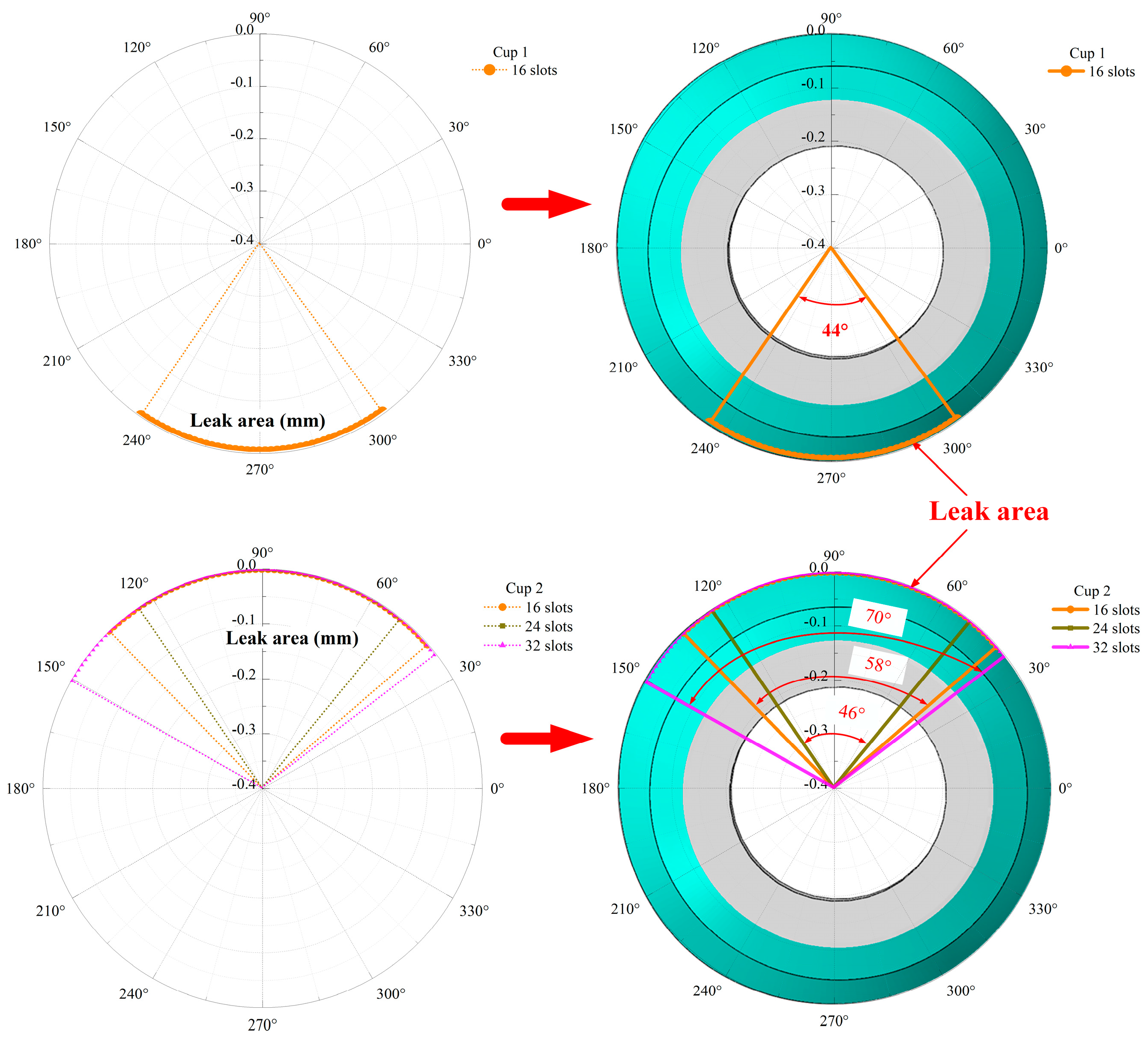
3.2. Sealing Performance of the PIG
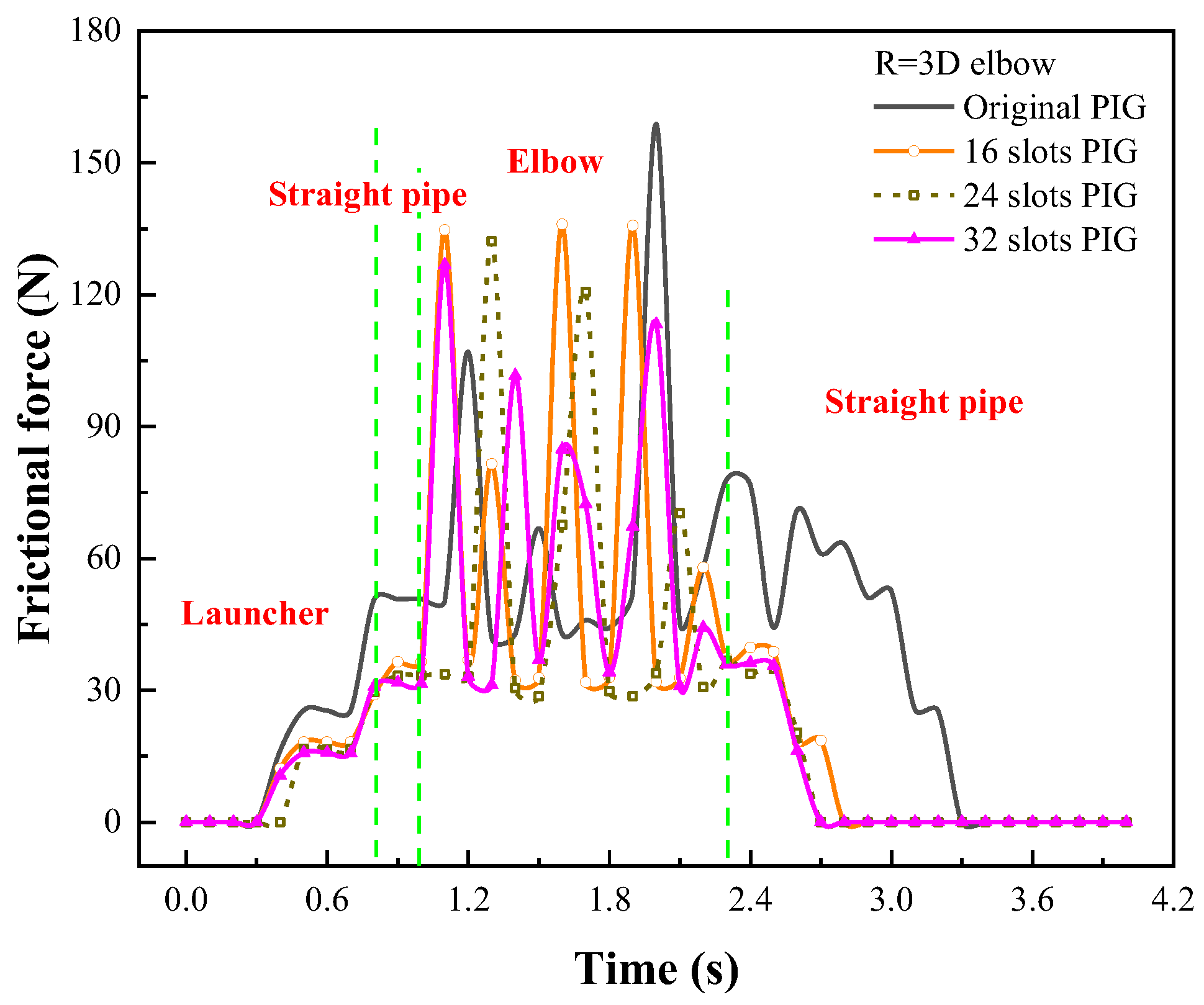
3.3. Driving Performance of the PIG
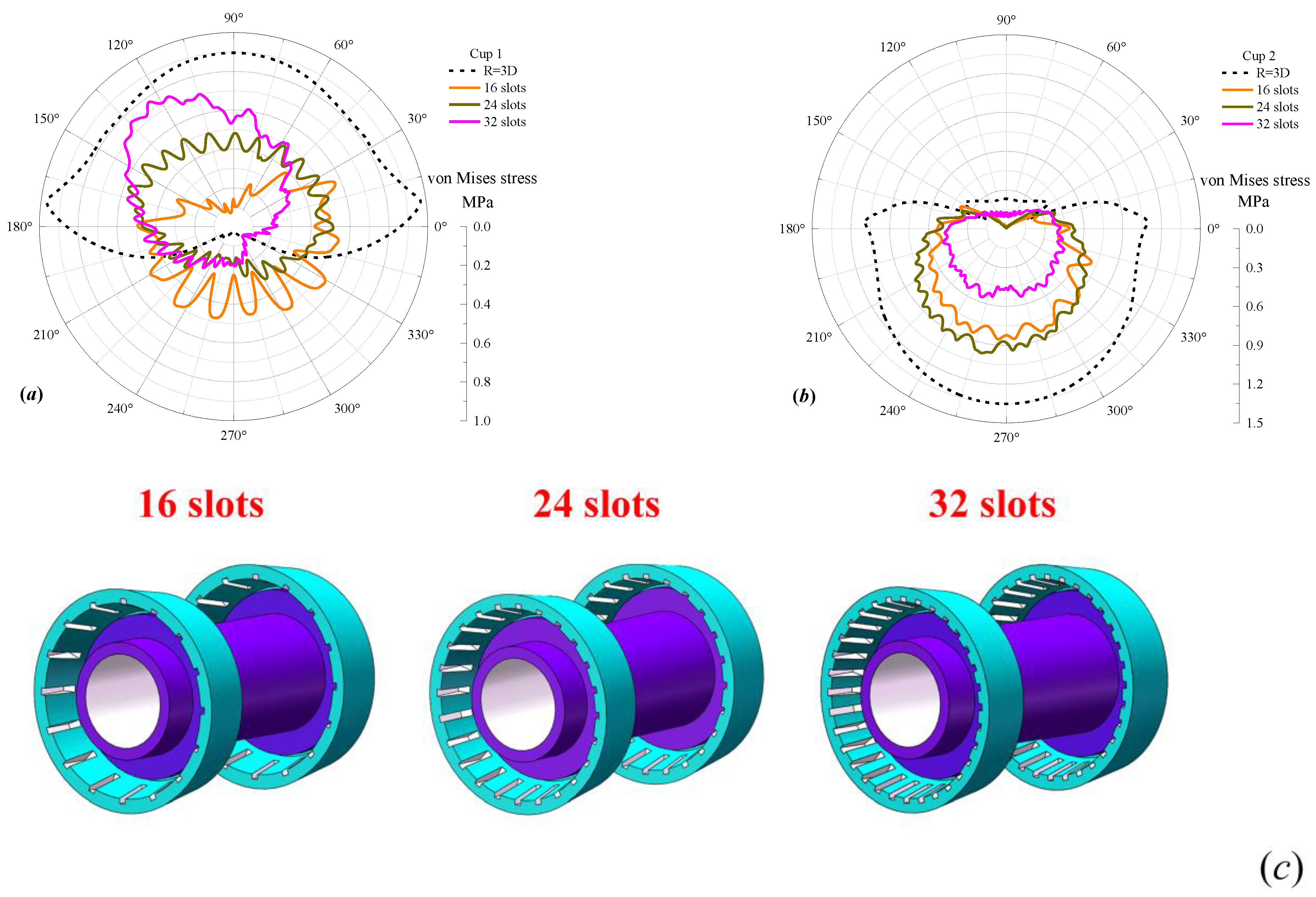
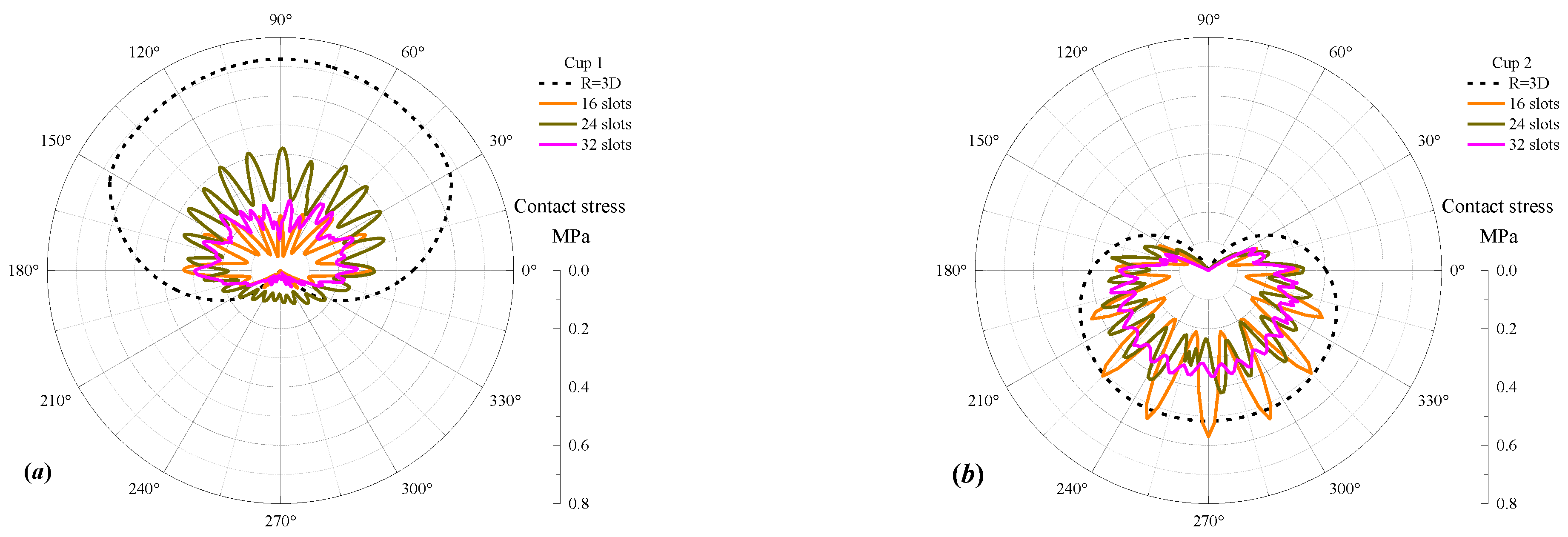
3.4. Optimization Analysis of Passing Capacity
4. Conclusions
- (1)
- The maximum von Mises stress on the cup can be used as a measure to characterize the safety performance of PIG application. The calculation shows that the safe application performance of the PIG can be improved by 47.4% when the bend’s radius of curvature increases from 3D to 5D.
- (2)
- The two cups on the PIG have the poorest sealing performance at a 48° curvature of the bend. The sealing performance of the PIG is defined by the leakage area ratio while the PIG is leaking. As the radius of curvature increases from 3D to 5D, the leakage area ratio decreases from 25% to 16.4%, resulting in an 8.6% improvement in sealing performance.
- (3)
- The minimum driving differential pressure can be used to evaluate the driving performance, which can be improved by 65.2% when the ratio R = 3D increases to 5D.
- (4)
- Considering safe application performance, sealing performance, and driving performance, it is most appropriate to introduce 24 grooves to the cup in order to optimize the passing capacity of the PIG. Compared to the worst passing capacity performance in the case of R = 3D, creating 24 grooves can improve the safe application performance by 40.8%, improve the sealing performance by 12.22%, and improve the driving performance by 17%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guan, L.W.; Cong, X.D.; Sun, Y.L.; Gao, Y.B.; Iqbal, U.; Noureldin, A. Enhanced MEMS SINS Aided Pipeline Surveying System by Pipeline Junction Detection in Small Diameter Pipeline. IFAC-PapersOnLine 2017, 50, 3560–3565. [Google Scholar] [CrossRef]
- Glisic, B. 14-Sensing solutions for assessing and monitoring pipeline systems. In Sensor Technologies for Civil Infrastructures, 1st ed.; Wang, M.L., Lynch, J.P., Sohn, H., Eds.; Woodhead Publishing: Cambridge, UK, 2014; Volume 56, pp. 422–460. ISBN 978-1-78242-242-6. [Google Scholar]
- An, Z.T.; Tang, Q.; Huang, Y.F.; Li, H. Time-dependent analysis of buried high-density polyethylene (PE100) pipelines with a scratch defect subjected to touchdown impact loading of blasting collapsed body. Int. J. Pres. Ves. Pip 2022, 195, 104605. [Google Scholar] [CrossRef]
- Rastogi, A.; Fan, Y.L. Experimental and modeling study of onset of liquid accumulation. J. Nat. Gas Sci. Eng. 2020, 73, 103064. [Google Scholar] [CrossRef]
- Bagheri, M.; Sari, A. Study of natural gas emission from a hole on underground pipelines using optimal design-based CFD simulations: Developing comprehensive soil classified leakage models. J. Nat. Gas Sci. Eng. 2022, 102, 104583. [Google Scholar] [CrossRef]
- Yan, Y.T.; Dong, X.Q.; Li, J.M. Experimental study of methane diffusion in soil for an underground gas pipe leak. J. Nat. Gas Sci. Eng. 2015, 27, 82–89. [Google Scholar] [CrossRef]
- Askari, M.; Aliofkhazraei, M.; Afroukhteh, S. A comprehensive review on internal corrosion and cracking of oil and gas pipelines. J. Nat. Gas Sci. Eng. 2019, 71, 102971. [Google Scholar] [CrossRef]
- Liu, C.; Cao, Y.G.; Chen, J.Z.; Dai, C.L.; He, R.Y.; Zhou, Z.G. The blockage risk in the bend of the Bi-directional pig used for submarine pipeline based on the modified Burgers-Frenkel (MB-F) model. Ocean Eng. 2023, 268, 113508. [Google Scholar] [CrossRef]
- Coramik, M.; Ege, Y. Discontinuity inspection in pipelines: A comparison review. Measurement 2017, 111, 359–373. [Google Scholar] [CrossRef]
- Sampath, S.; Chaurasiya, L.K.; Aryan, P.; Bhattacharya, B. An innovative approach towards defect detection and localization in gas pipelines using integrated in-line inspection methods. J. Nat. Gas Sci. Eng. 2021, 90, 103933. [Google Scholar] [CrossRef]
- Song, H.D.; Yang, L.; Liu, G.H.; Tian, G.Y.; Ona, D.; Song, Y.P.; Li, S.Q. Comparative Analysis of In-line Inspection Equipments and Technologies. IOP Conf. Ser. Mater. Sci. Eng. 2018, 382, 032021. [Google Scholar] [CrossRef]
- Liu, C.; Wei, Y.G.; Cao, Y.G.; Zhang, S.H.; Sun, Y.T. Traveling ability of pipeline inspection gauge (PIG) in bend under different friction coefficients by 3D FEM. J. Nat. Gas Sci. Eng. 2020, 75, 103134. [Google Scholar] [CrossRef]
- Zhang, H.X.; Qin, M.; Liao, K.X.; Wang, K.; He, G.X. Pipe-soil vibration characteristics of natural gas pipelines during the pigging process. J. Nat. Gas Sci. Eng. 2021, 95, 104148. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, S.M.; Liu, S.H.; Wang, Y. Collisional vibration of PIGs (pipeline inspection gauges) passing through girth welds in pipelines. J. Nat. Gas Sci. Eng. 2017, 37, 15–28. [Google Scholar] [CrossRef]
- Miao, X.Y.; Zhao, H.; Gao, B.X.; Ma, Y.H.; Hou, Y.G.; Song, F.L. Motion analysis and control of the pipeline robot passing through girth weld and inclination in natural gas pipeline. J. Nat. Gas Sci. Eng. 2022, 104, 104662. [Google Scholar] [CrossRef]
- Kim, S.; Jeong, J.; Yoo, K.; Yoo, H.; Seo, Y. Experimental investigation on speed excursion of PIG due to friction variation in natural gas pipeline. J. Nat. Gas Sci. Eng. 2022, 104, 104659. [Google Scholar] [CrossRef]
- Bernasconi, G.; Giunta, G. Acoustic detection and tracking of a pipeline inspection gauge. J. Pet. Sci. Eng. 2020, 194, 107549. [Google Scholar] [CrossRef]
- Zhao, J.G.; Wang, J.; Liu, Q.Y.; Luo, X.; Dong, X.C. A review of mechanical model, structure, and prospect for long-distance pipeline pig and robot. Robotica 2022, 40, 4271–4307. [Google Scholar] [CrossRef]
- Lee, D.H.; Moon, H.; Koo, J.C.; Choi, H.R. Map building method for urban gas pipelines based on landmark detection. Int. J. Control Autom. Syst 2013, 11, 127–135. [Google Scholar] [CrossRef]
- Shi, M.; Yang, L.J.; Gao, S.W.; Wang, G.Q. Small-Diameter Tube Wall Damage-Detection Method Based on TE01 Mode Microwave. Sensors 2022, 22, 6476. [Google Scholar] [CrossRef]
- Davoudi, M.; Heidari, Y.; Mansoori, S.A.A. Field experience and evaluation of the South Pars sea line pigging, based on dynamic simulations. J. Nat. Gas Sci. Eng. 2014, 18, 210–218. [Google Scholar] [CrossRef]
- Soorgee, M.H. A numerical study on differential pressure needed for ball pig motion in pipelines based on nonlinear hyperelastic material model. J. Nat. Gas Sci. Eng. 2018, 59, 466–472. [Google Scholar] [CrossRef]
- Naeini, H.S.; Soorgee, M.H. Experimental investigation on sphere pig movement in multiple thickness pipe. J. Nat. Gas Sci. Eng. 2021, 95, 104152. [Google Scholar] [CrossRef]
- Cao, Y.G.; Liu, C.; Tian, H.J.; Zhang, S.H. Prediction of the driving force for a cup pig based on the distribution of contact stress. J. Nat. Gas Sci. Eng. 2020, 81, 103415. [Google Scholar] [CrossRef]
- Cao, Y.G.; Zhang, L.; Liu, C.; Li, X.Y.; Wei, Y.G.; Sun, Y.T. Prediction of the Driving Force for the Bidirectional Pig Based on the Cantilever-Kelvin Combination Model. J. Pipeline. Syst. Eng. 2021, 12, 04021004. [Google Scholar] [CrossRef]
- Zhu, X.X.; Zhang, S.M.; Li, X.L.; Wang, D.G.; Yu, D. Numerical simulation of contact force on bi-directional pig in gas pipeline: At the early stage of pigging. J. Nat. Gas Sci. Eng. 2015, 23, 127–138. [Google Scholar] [CrossRef]
- Zhu, X.X.; Wang, W.; Zhang, S.M.; Liu, S.H. Experimental Research on the Frictional Resistance of Fluid-Driven Pipeline Robot with Small Size in Gas Pipeline. Tribol. Lett 2017, 65, 49. [Google Scholar] [CrossRef]
- Hendrix, M.H.W.; Graafland, C.M.; van Ostayen, R.A.J. Frictional forces for disc-type pigging of pipelines. J. Pet. Sci. Eng. 2018, 171, 905–918. [Google Scholar] [CrossRef]
- Hendrix, M.; den Heijer, A.; Breugem, W.-P.; Henkes, R.A.W.M. Frictional forces during pigging of multiphase pipelines. In Proceedings of the 10th North American Conference on Multiphase Technology, Banff, AB, Canada, 8–10 June 2016. BHR: 2016–2103. [Google Scholar]
- Zhang, H.; Zhang, S.M.; Liu, S.H.; Wang, Y.; Lin, L. Measurement and analysis of friction and dynamic characteristics of PIG’s sealing disc passing through girth weld in oil and gas pipeline. Measurement 2015, 64, 112–122. [Google Scholar] [CrossRef]
- Wang, S.; Yao, X.F.; Yang, H.; Huang, S.H. Measurement and evaluation on contact stress at the rubber contact interface. Measurement 2019, 146, 856–867. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, X.Y.; Yang, L.L. Deformation and stress analysis of cup on pipeline inspection gauge based on reverse measurement. Energy Sci. Eng. 2022, 10, 2509–2526. [Google Scholar] [CrossRef]
- Chen, S.T.; Xia, L.; Wang, X.L.; Teng, K.; Zhang, Y.B.; Zhang, M.Y.; Gong, Y.J. Motion Law and Mechanical Properties of PIGs When Passing through a Pipe Bend. Machines 2022, 10, 963. [Google Scholar] [CrossRef]
- Zhang, H.; Dong, J.H.; Cui, C.; Liu, S.H. Stress and strain analysis of spherical sealing cups of fluid-driven pipeline robot in dented oil and gas pipeline. Eng. Failure Anal. 2020, 108, 104294. [Google Scholar] [CrossRef]
- Jiang, J.X.; Zhang, H.; Ji, B.L.; Yi, F.N.; Yan, F.; Liu, X.B. Numerical investigation on sealing performance of drainage pipeline inspection gauge crossing pipeline bends. Energy Sci. Eng. 2021, 9, 1858–1871. [Google Scholar] [CrossRef]
- Zheng, C.; Zheng, X.F.; Qin, J.; Liu, P.; Aibaibu, A.; Liu, Y.H. Nonlinear finite element analysis on the sealing performance of rubber packer for hydraulic fracturing. J. Nat. Gas Sci. Eng. 2021, 85, 103711. [Google Scholar] [CrossRef]
- Zhu, X.X.; Wang, W.; Zhang, S.M.; Wang, C. The Pig gravity impact on its frictional force in oil and gas pipeline. In Proceedings of the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25 June 2017; pp. 140–144. [Google Scholar]
- Cao, Y.G.; Zhen, Y.; Shi, Y.J.; Zhang, S.H.; Sun, Y.T.; Nie, W.J. Stress Distribution of the Power Section Cup of Pipeline Inspection Gauges by Finite Element Method. J. Pipeline. Syst. Eng. 2018, 9, 04017039. [Google Scholar] [CrossRef]
- Rashid, M.Z.A.; Yakub, M.F.M.; Salim, S.A.Z.S.; Mamat, N.; Putra, S.M.S.M.; Roslan, S.A. Modeling of the in-pipe inspection robot: A comprehensive review. Ocean Eng. 2020, 203, 107206. [Google Scholar] [CrossRef]
- Kim, S.; Yoo, K.; Yoo, B.; Kim, D.; Yoo, H.; Seo, Y. Speed excursion simulation of PIG using improved friction models. J. Nat. Gas Sci. Eng. 2022, 97, 104371. [Google Scholar] [CrossRef]
- Dong, J.H.; Zhang, H.; Liu, S.H. 3D printed bio-inspired sealing disc of pipeline inspection gauges (PIGs) in small diameter pipeline. J. Nat. Gas Sci. Eng. 2019, 61, 344–356. [Google Scholar] [CrossRef]
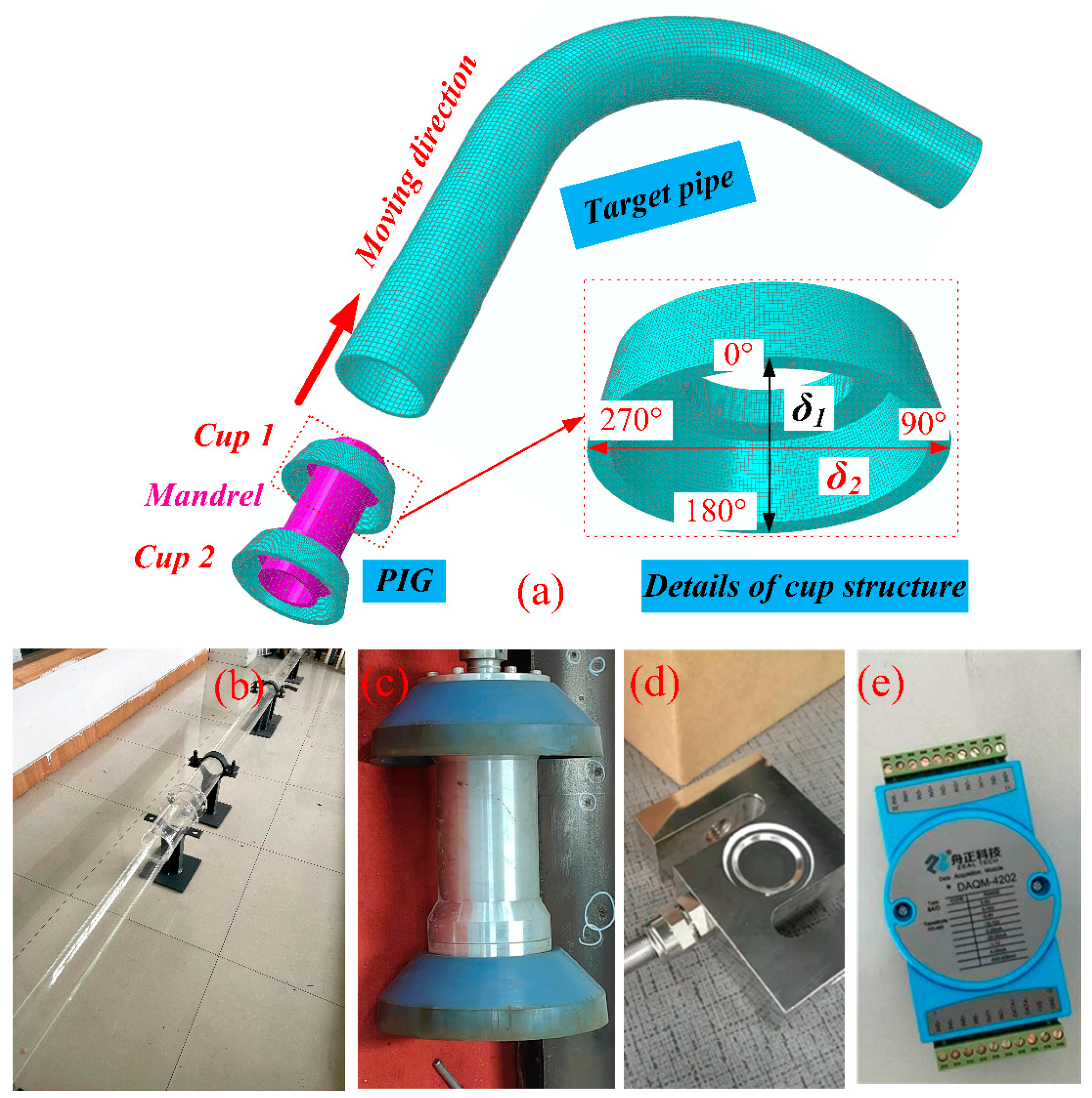



| Parameter | Value |
|---|---|
| Length of PIG | 132 mm |
| Outer diameter of the cup | 97.85 mm |
| Thickness of the cup | 6 mm |
| Diameter of the mandrel | 50 mm |
| Diameter of the flange | 65 mm |
| Hardness of the cup | 78 HA |
| Elastic modulus of the cup | 8.34 MPa |
| C10 | 1.42 |
| C01 | 0.36 |
| Mesh of pipe | C3D20H |
| Mesh of cup | C3D8H |
| Mesh of mandrel and flange | C3D10M |
| Boundary conditions of pipe | Constant |
| Boundary conditions of the cup, mandrel, and flange | Bound |
| Mesh of Cup | Size (mm) | N Grid | True Strain | Error (%) | Contact Area (mm2) | Error (%) |
|---|---|---|---|---|---|---|
| coarser | 1.75 | 15360 | 10.85 | - | 0.76 | - |
| coarse | 1.35 | 35690 | 11.03 | 1.66 | 0.69 | 9.21 |
| original | 1 | 88256 | 11.06 | 0.27 | 0.68 | 1.44 |
| refined | 0.7 | 254720 | 11.10 | 0.36 | 0.65 | 4.41 |
| more refined | 0.55 | 544680 | 11.17 | 0.63 | 0.63 | 3.08 |
| Curvature Radius (mm) | Average Friction Force on Straight Pipe (n) | Maximum Friction Force in the Bend (N) | Minimum Required Drive Differential Pressure (MPa) |
|---|---|---|---|
| 3D | 24.56 | 158.8 | 0.0224 |
| 4D | 23.33 | 71.2 | 0.0100 |
| 5D | 24.59 | 55.5 | 0.0078 |
| Number of Grooves | Maximum Friction Force in Bend (N) | Minimum Required Drive Differential Pressure (MPa) |
|---|---|---|
| 0 | 158.80 | 0.0224 |
| 16 | 136.04 | 0.0192 |
| 24 | 132.13 | 0.0186 |
| 32 | 126.77 | 0.0180 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F.; Lin, H.; Zhang, Y.; Zhao, S.; Fu, S.; Zhang, H. Analysis via 3D FEM of the Passing Capacity of Pipeline Inspection Gauges in Bends with Different Curvatures. Processes 2023, 11, 3288. https://doi.org/10.3390/pr11123288
Zhou F, Lin H, Zhang Y, Zhao S, Fu S, Zhang H. Analysis via 3D FEM of the Passing Capacity of Pipeline Inspection Gauges in Bends with Different Curvatures. Processes. 2023; 11(12):3288. https://doi.org/10.3390/pr11123288
Chicago/Turabian StyleZhou, Faqi, Haoye Lin, Ying Zhang, Suyang Zhao, Shuangcheng Fu, and Hui Zhang. 2023. "Analysis via 3D FEM of the Passing Capacity of Pipeline Inspection Gauges in Bends with Different Curvatures" Processes 11, no. 12: 3288. https://doi.org/10.3390/pr11123288
APA StyleZhou, F., Lin, H., Zhang, Y., Zhao, S., Fu, S., & Zhang, H. (2023). Analysis via 3D FEM of the Passing Capacity of Pipeline Inspection Gauges in Bends with Different Curvatures. Processes, 11(12), 3288. https://doi.org/10.3390/pr11123288












