Effect of Non-Uniform Minerals Distribution on Hydraulic Fracture Evolution during Unconventional Geoenergy Exploration
Abstract
:1. Introduction
2. Basic Principles of Mineral Non-Uniform Distribution Model Construction
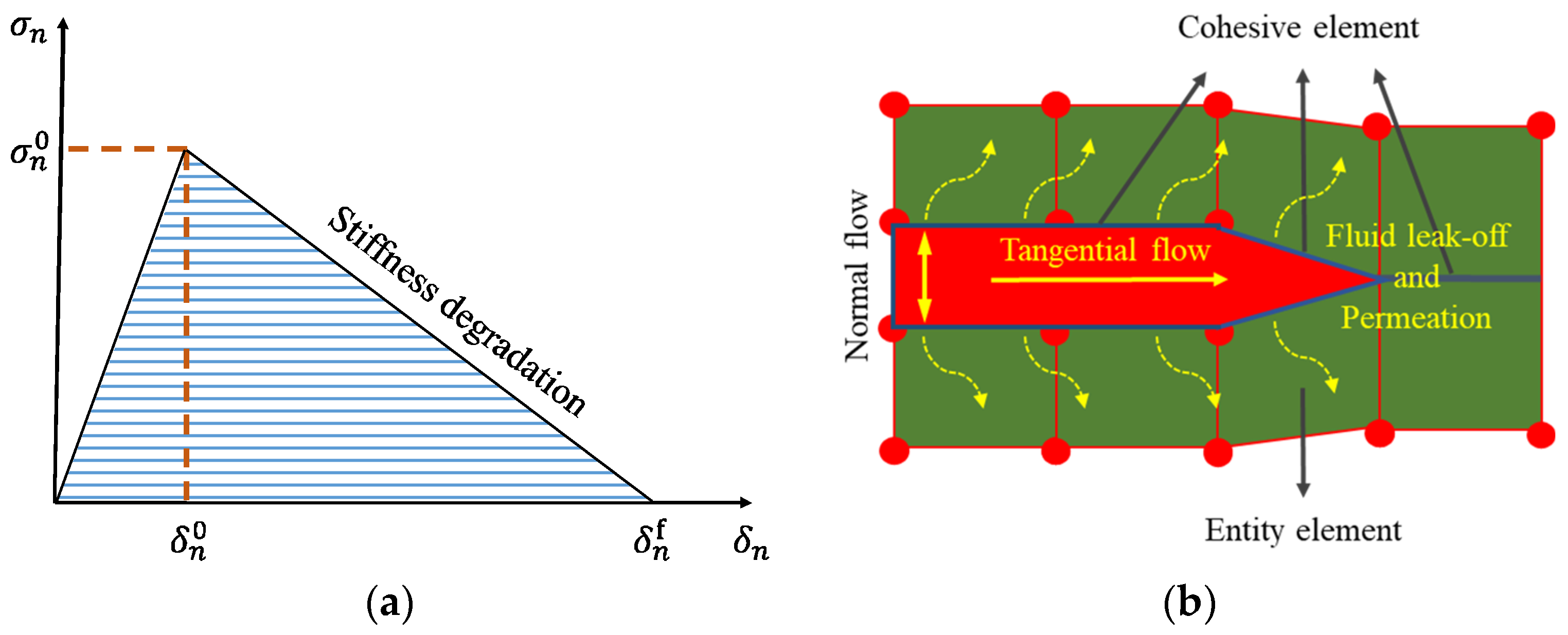
2.1. Global Cohesive Element Embedding Principle
2.2. Methods for Implementing Non-Uniform Distribution of Minerals
2.3. Model Design
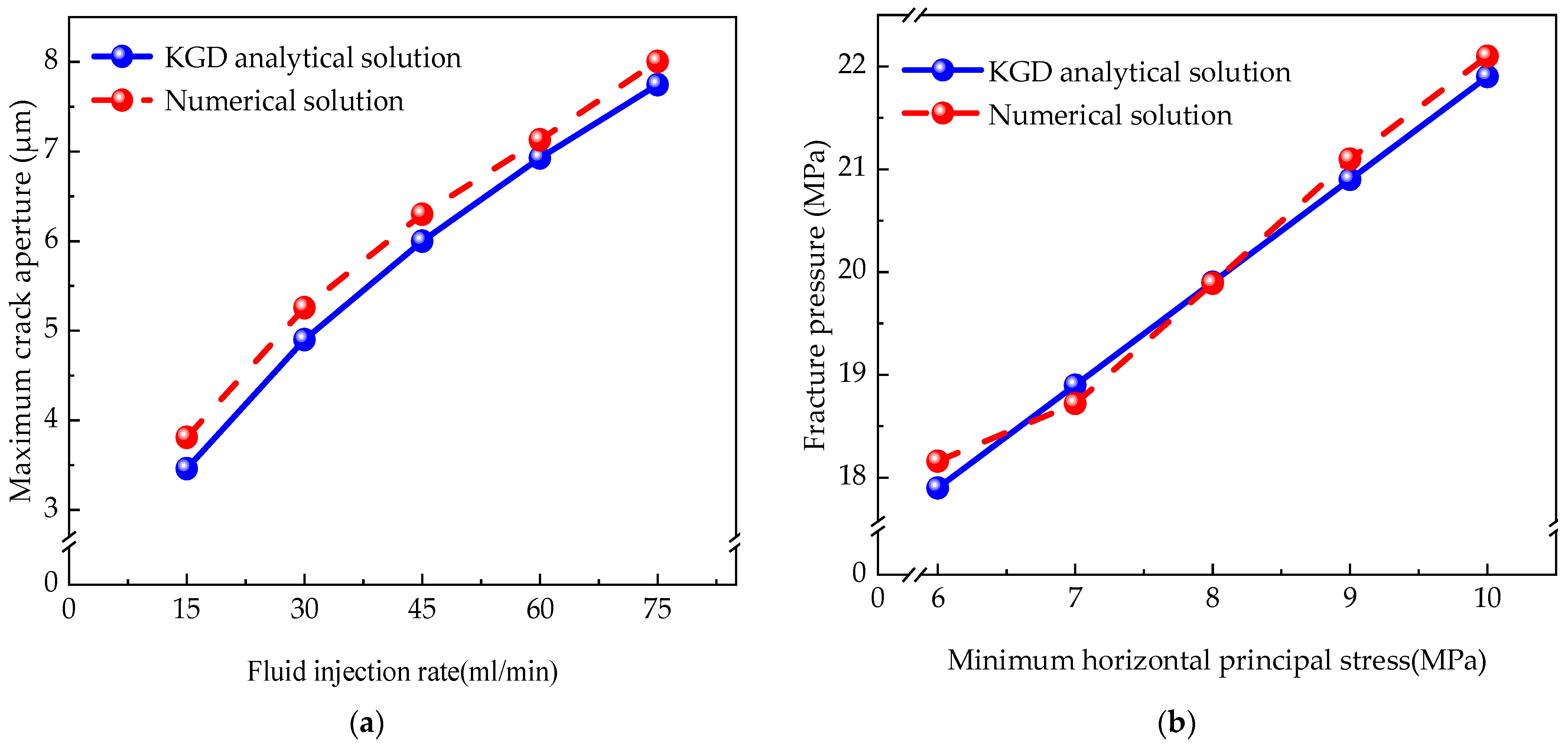
2.4. Model Validity Verification
3. Numerical Results and Analysis
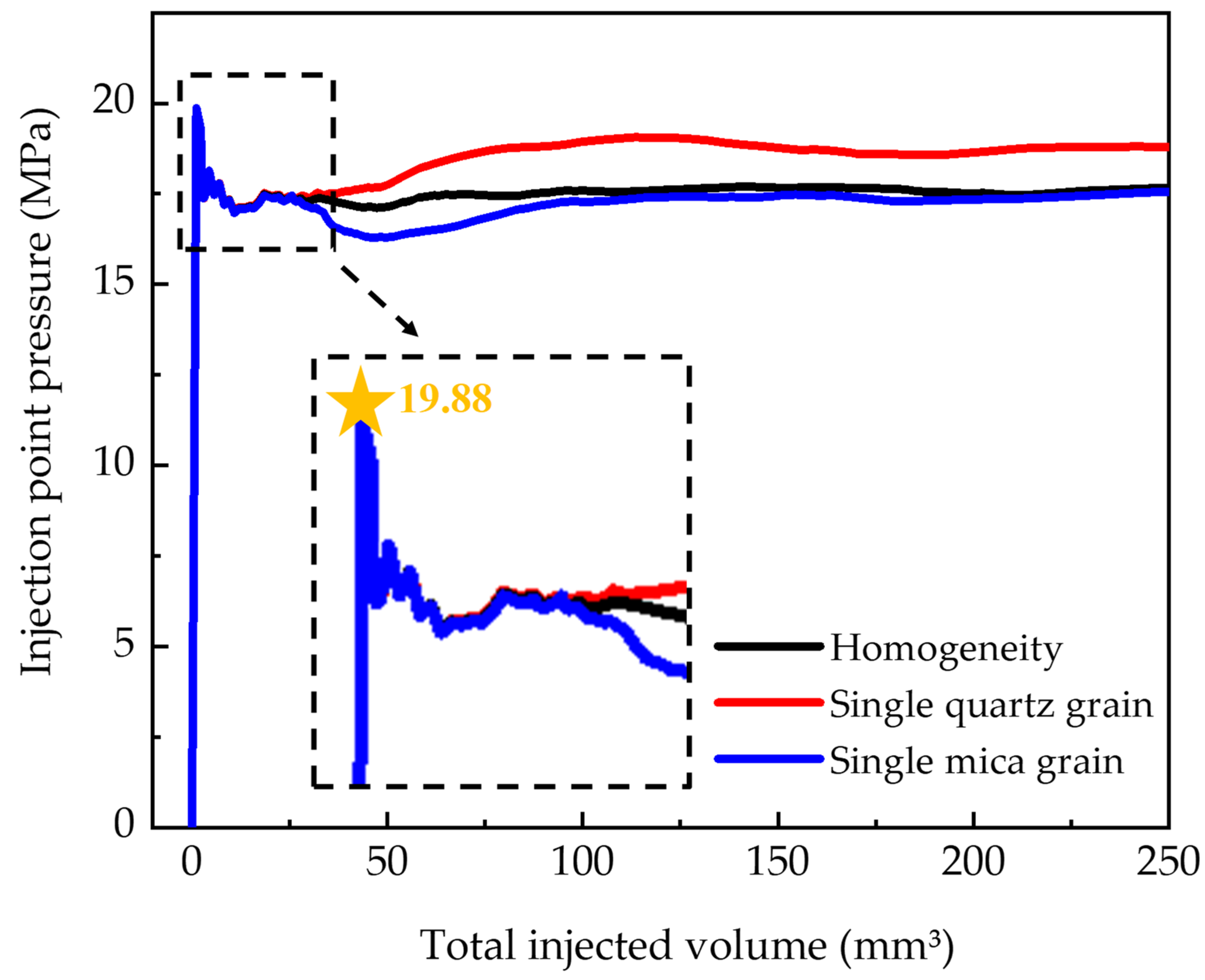
3.1. The Influence of Single Mineral
3.2. Effects of Particle Size, Composition, and Spatial Arrangement under Mineral Mixing
3.2.1. Fracture Morphology
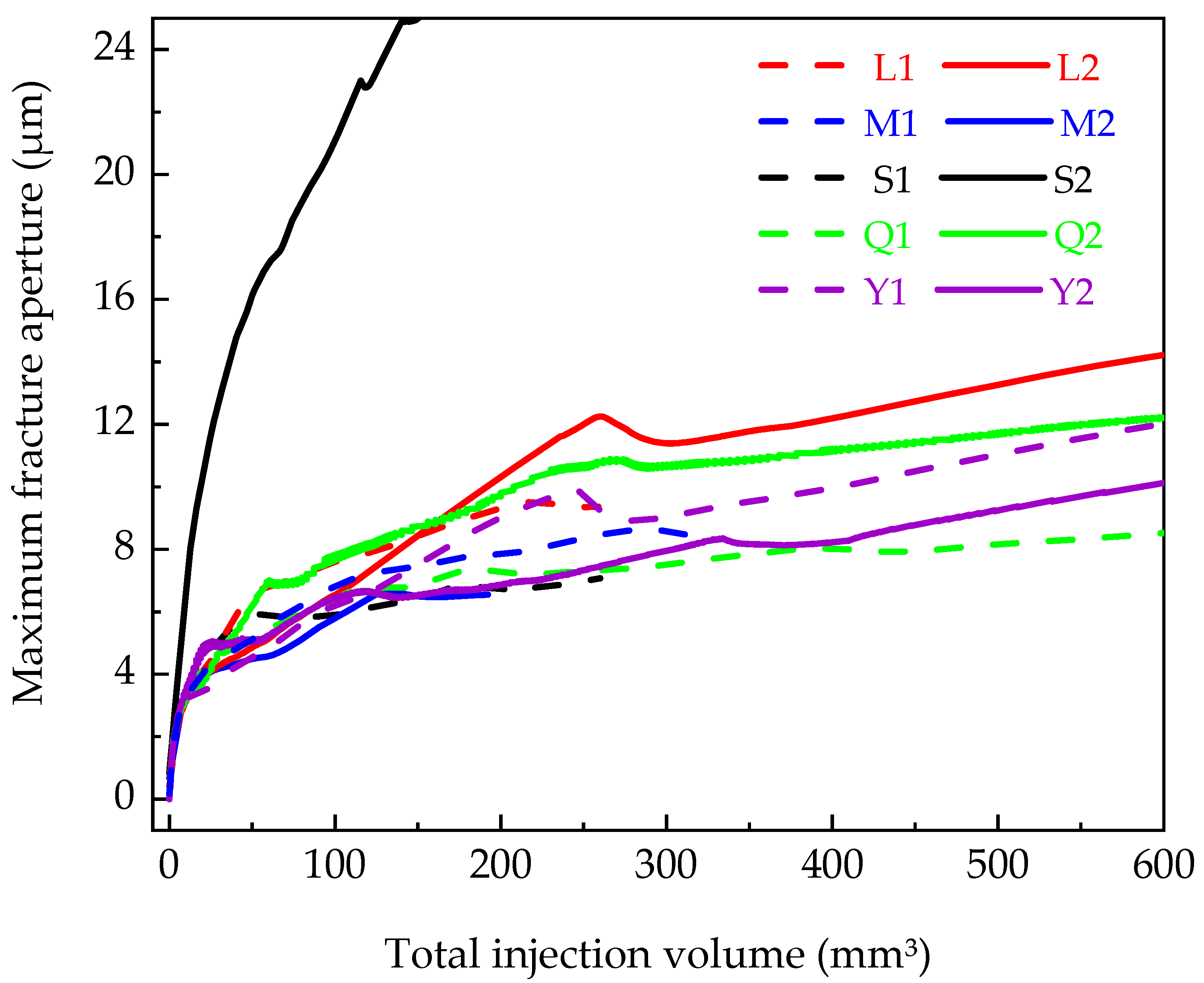
3.2.2. Maximum Fracture Aperture
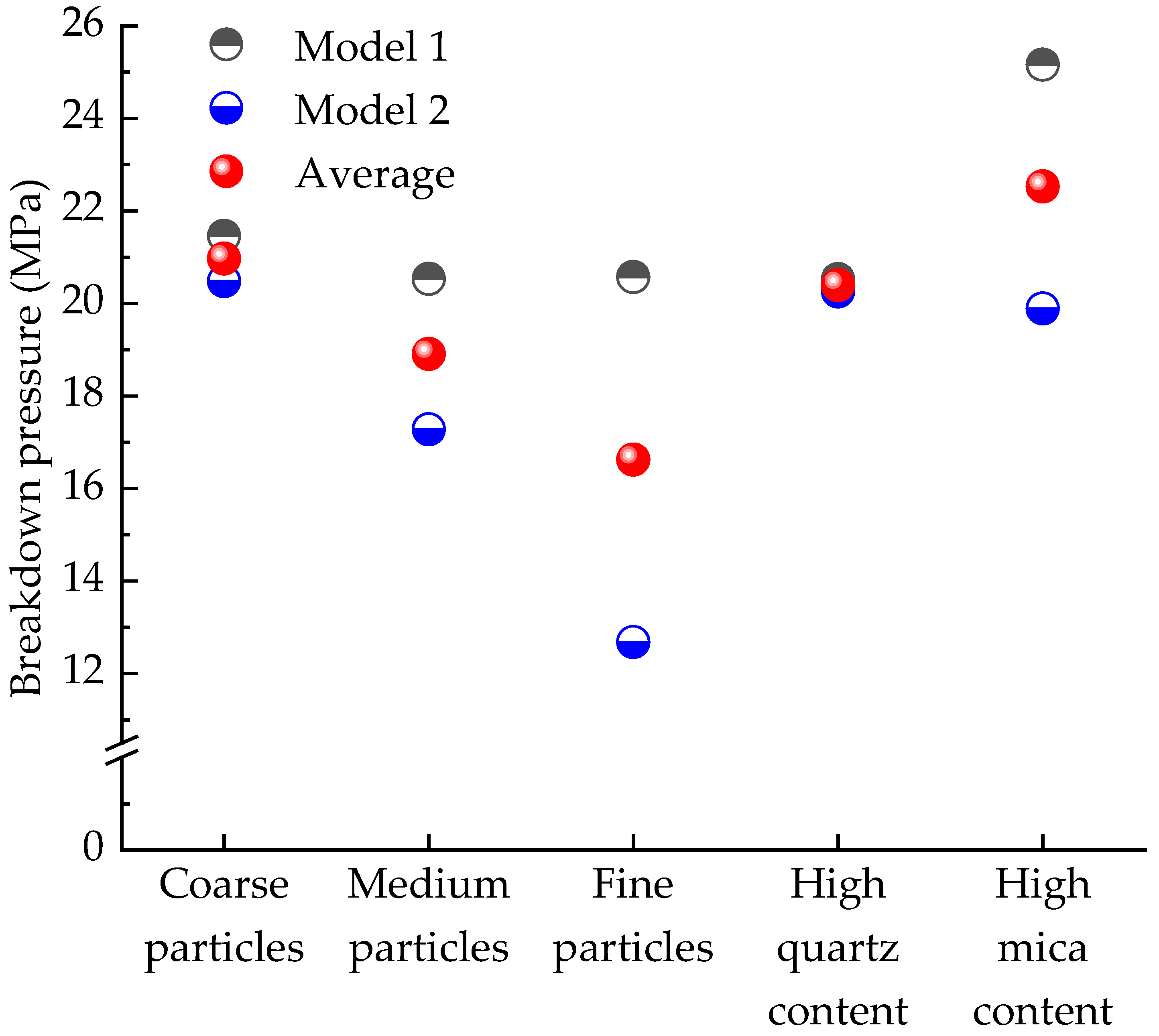
3.2.3. Breakdown Pressure
4. Sensitivity Analysis of Fracturing Parameters for Heterogeneous Granite
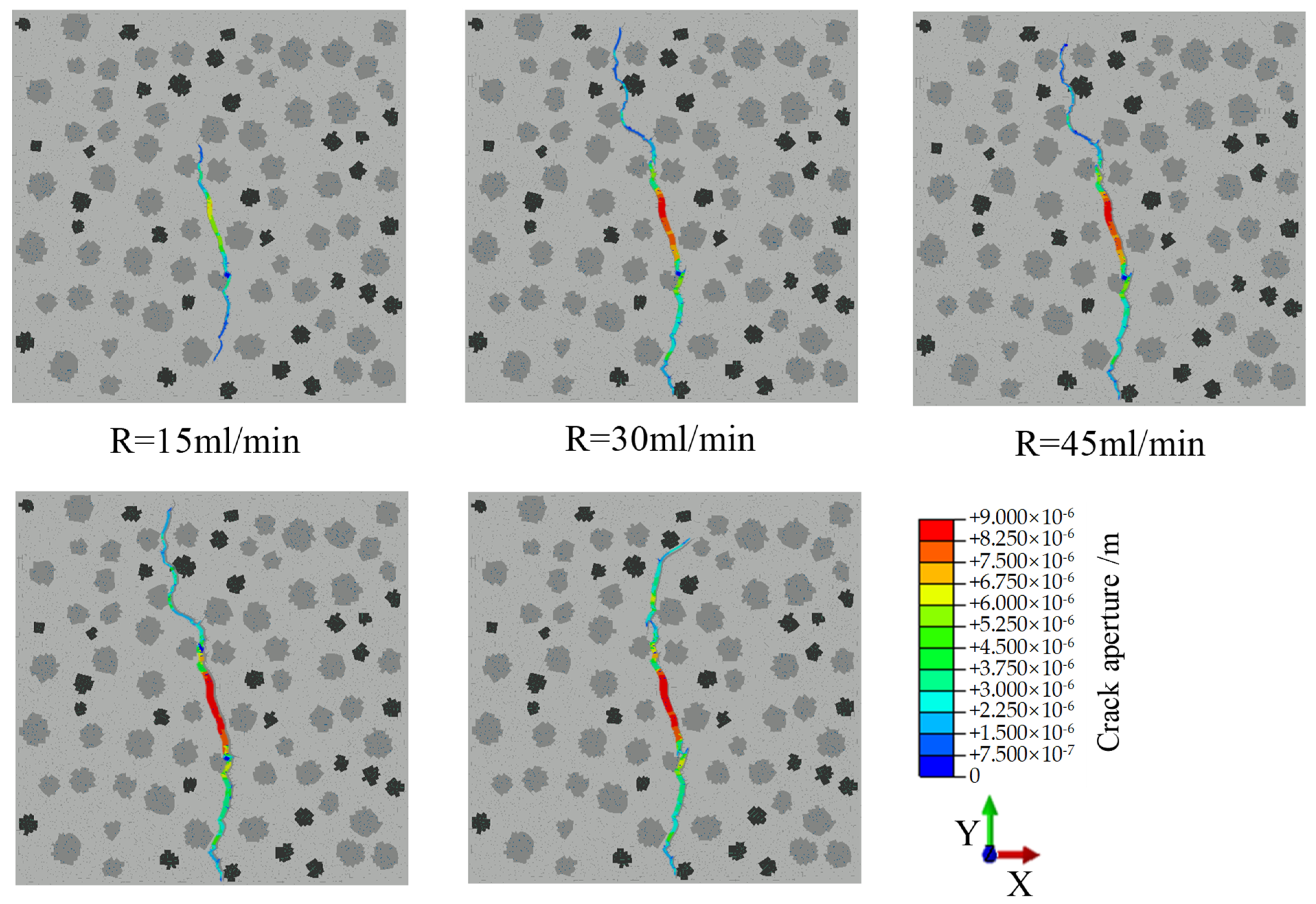
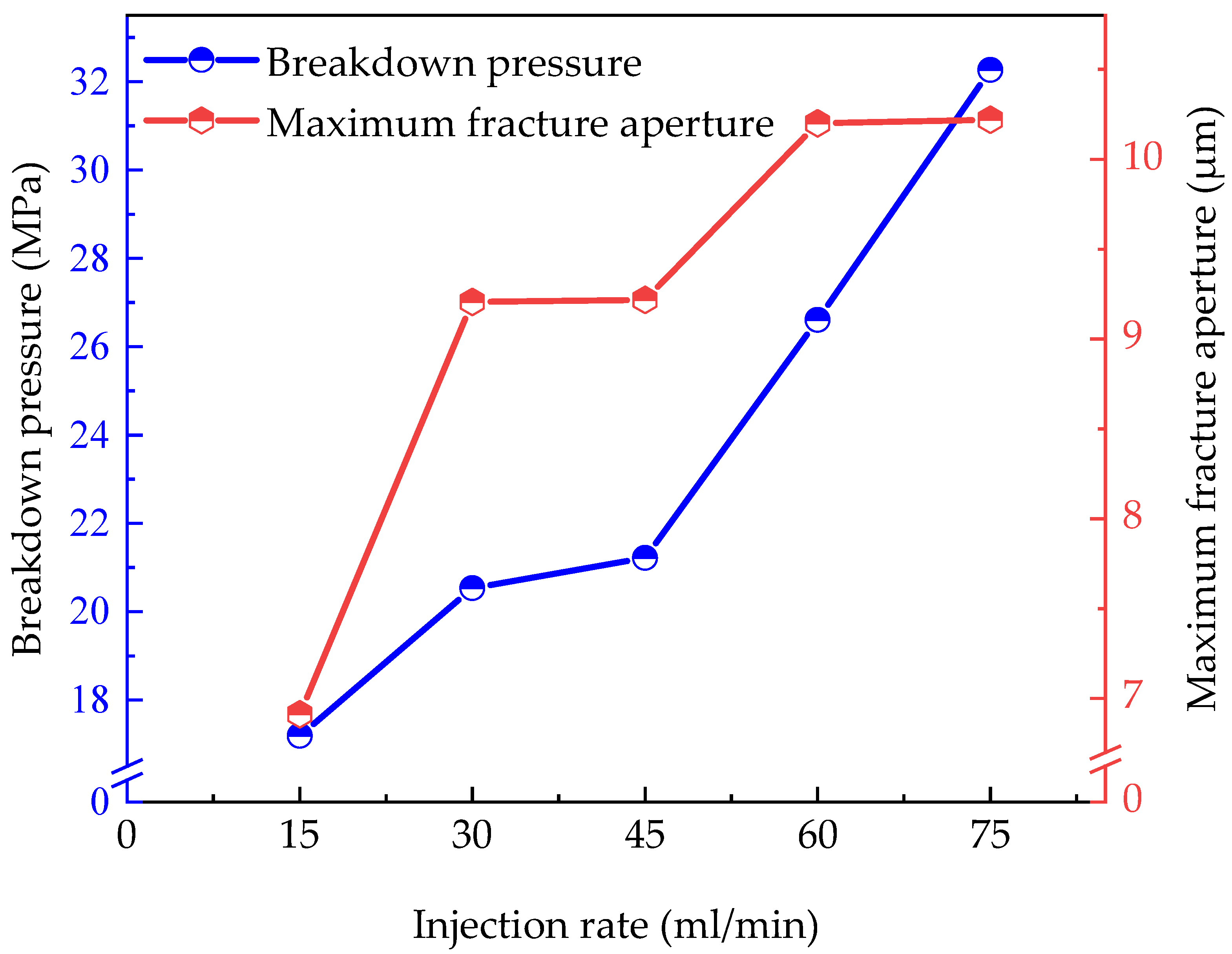
4.1. Injection Rate
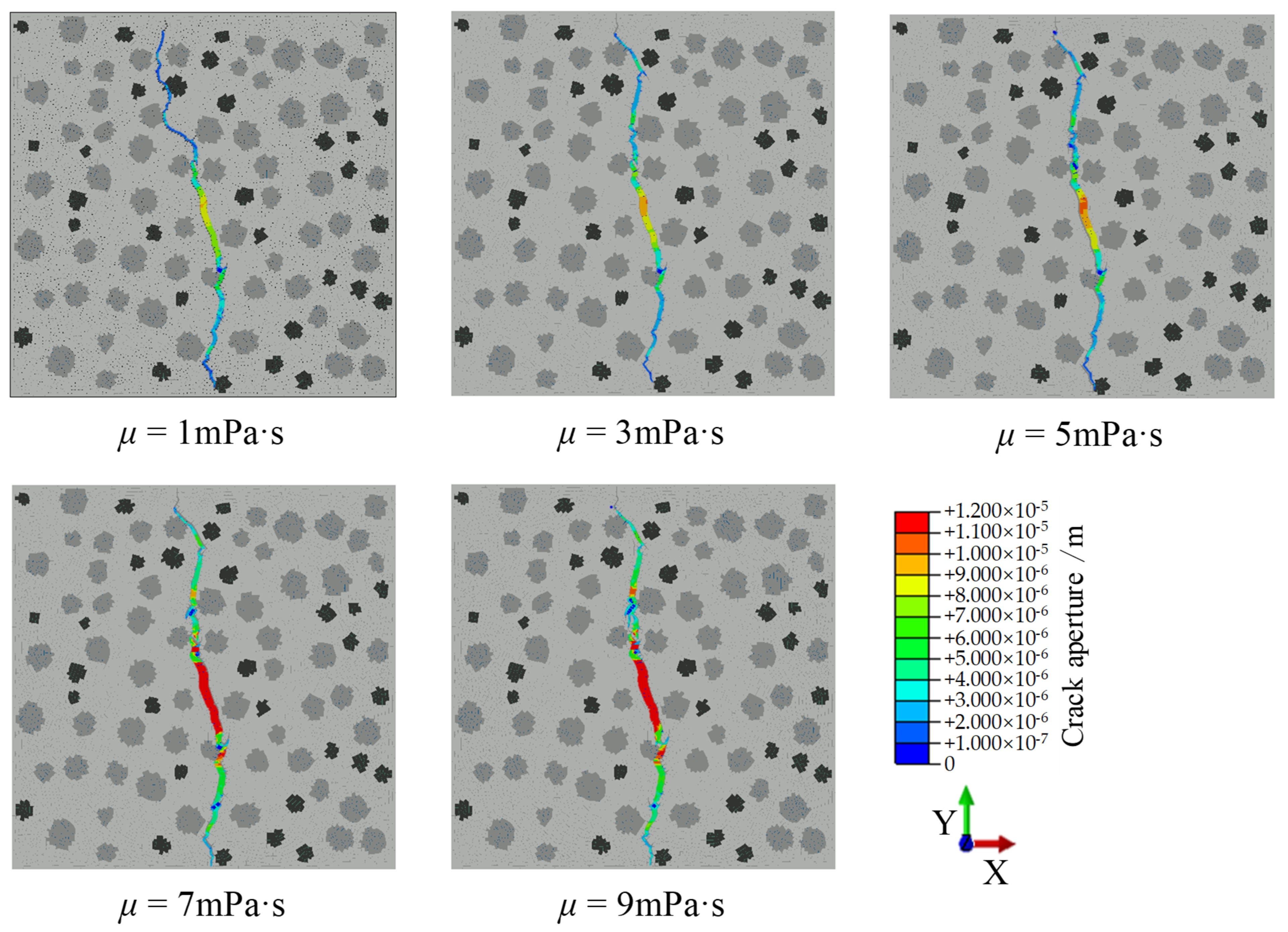
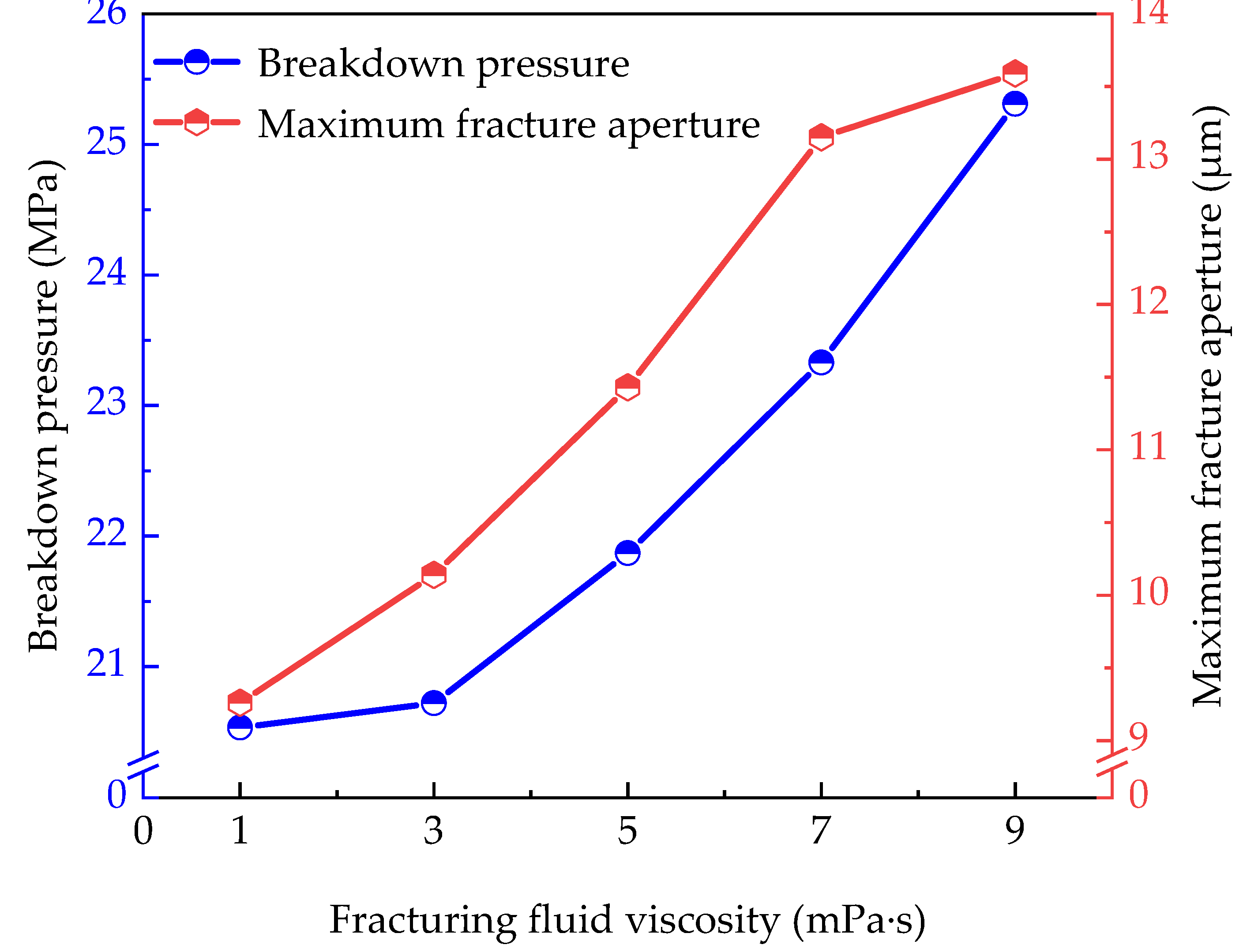
4.2. Fracturing Fluid Viscosity
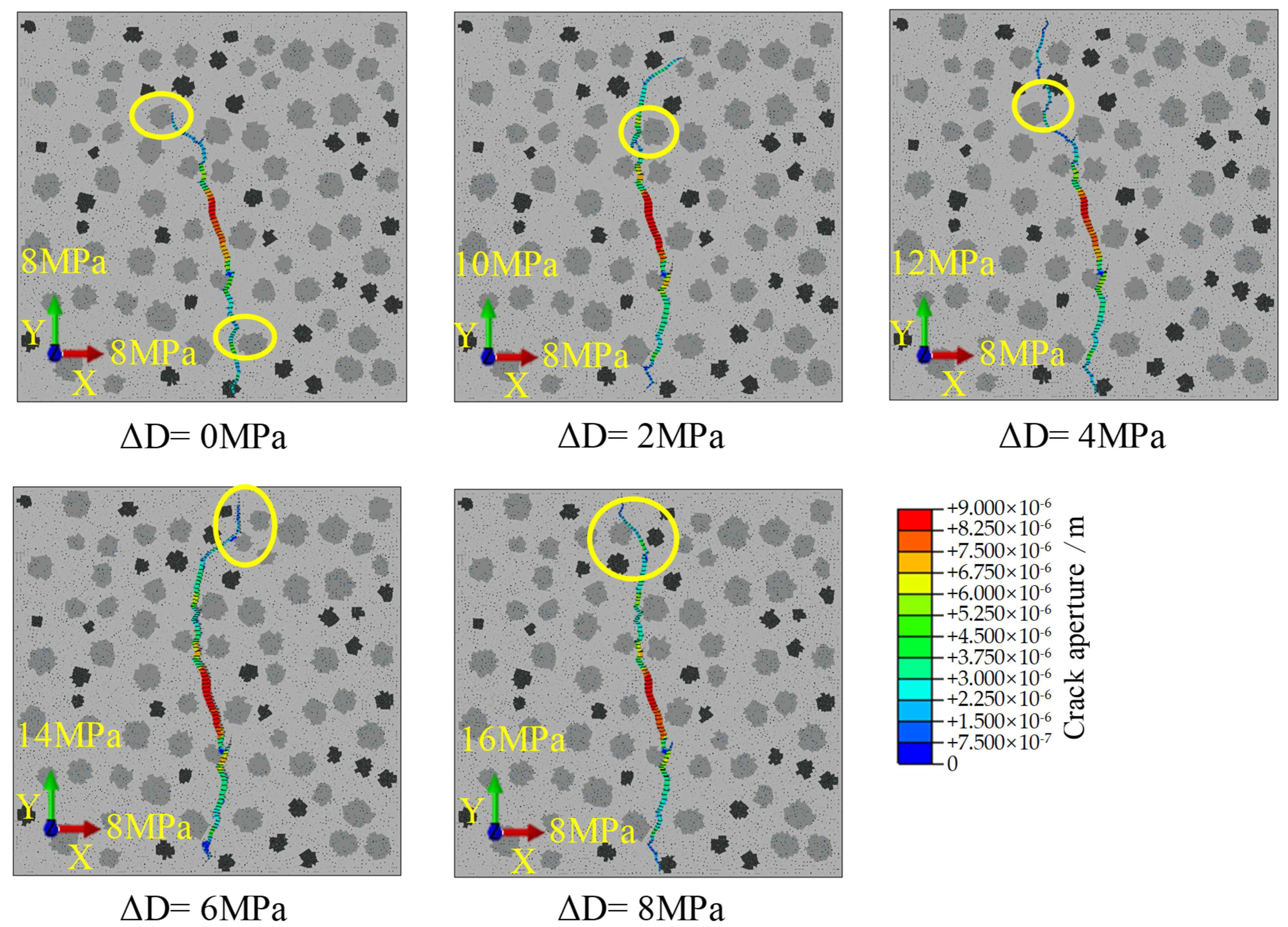
4.3. Horizontal Stress Difference
5. Conclusions
- (1)
- The existence of hard mineral—quartz, in the crack propagation path, changes the direction of the crack and easily results in branch cracks. On the contrary, the crack can directly penetrate the weak mineral—mica. In addition, at the crack tip, the crack bypassing quartz tends to increase the extension pressure, while the crack passing through mica generates a lower extension pressure.
- (2)
- Coarse-grained granite has the widest range of crack deflection, while medium-grained granite is easier to lengthen and warp cracks. The failure result of fine-grained granite is determined by the spatial arrangement of minerals. Furthermore, the fractures in granite with a high content of quartz are more complex, and the hydraulic fractures in rock with a high content of mica clearly expand toward mica.
- (3)
- In granite with a non-uniform distribution of minerals, BP and MFA increase versus the IR and FFV increase. The morphology of hydraulic fractures is significantly influenced by the HSD. When cracks bypass quartz during their propagation, driven by high stress differences, they clearly expand in the direction of the maximum principal stress. In contrast, under low stress differences, cracks tend to expand laterally.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, Y.; Hou, M.Z.; Liu, H.; Li, C. Anisotropic time-dependent behaviors of shale under direct shearing and associated empirical creep models. J. Rock Mech. Geotech. Eng. 2023, in press. [Google Scholar] [CrossRef]
- Siddhamshetty, P.; Mao, S.; Wu, K.; Kwon, J.S.-I. Multi-Size Proppant Pumping Schedule of Hydraulic Fracturing: Application to a MP-PIC Model of Unconventional Reservoir for Enhanced Gas Production. Processes 2020, 8, 570. [Google Scholar] [CrossRef]
- Guanhua, N.; Kai, D.; Shang, L.; Qian, S. Gas desorption characteristics effected by the pulsating hydraulic fracturing in coal. Fuel 2019, 236, 190–200. [Google Scholar] [CrossRef]
- Li, N.; Xie, H.; Hu, J.; Li, C. A critical review of the experimental and theoretical research on cyclic hydraulic fracturing for geothermal reservoir stimulation. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 8, 7. [Google Scholar] [CrossRef]
- Wu, X.; Guo, Y.; Chang, X.; Bi, Z.; Zhao, G.; Yang, H.; Guo, W. Experimental Study on Cyclic Hydraulic Fracturing of Tight Sandstone under In-Situ Stress. Processes 2023, 11, 875. [Google Scholar] [CrossRef]
- Li, C.; Caner, F.C.; Chau, V.T.; Bažant, Z.P. Spherocylindrical microplane constitutive model for shale and other anisotropic rocks. J. Mech. Phys. Solids 2017, 103, 155–178. [Google Scholar] [CrossRef]
- Kong, L.; Xie, H.; Li, C. Coupled microplane and micromechanics model for describing the damage and plasticity evolution of quasi-brittle material. Int. J. Plast. 2023, 162, 103549. [Google Scholar] [CrossRef]
- Zhuang, L.; Zang, A. Laboratory hydraulic fracturing experiments on crystalline rock for geothermal purposes. Earth-Sci. Rev. 2021, 216, 103580. [Google Scholar] [CrossRef]
- Li, C.; Xie, H.; Wang, J. Anisotropic characteristics of crack initiation and crack damage thresholds for shale. Int. J. Rock Mech. Min. Sci. 2020, 126, 104178. [Google Scholar] [CrossRef]
- Zhou, C.; Xie, H.; Wang, Z.; Zhou, T.; Zhu, J. A novel fractal-statistical scaling model of rocks considering strain rate. J. Rock Mech. Geotech. Eng. 2023, 15, 2831–2841. [Google Scholar] [CrossRef]
- Hu, J.; Xie, H.; Sun, Q.; Li, C.; Liu, G. Changes in the thermodynamic properties of alkaline granite after cyclic quenching following high temperature action. Int. J. Min. Sci. Technol. 2021, 31, 843–852. [Google Scholar] [CrossRef]
- Coggan, J.S.; Stead, D.; Howe, J.H.; Faulks, C.I. Mineralogical controls on the engineering behavior of hydrothermally altered granites under uniaxial compression. Eng. Geol. 2013, 160, 89–102. [Google Scholar] [CrossRef]
- Zhenhua, H.; Luqing, Z.; Jian, Z.; Guangxiang, Y.; Pengjiao, W. Uniaxial compression test and numerical studies of grain size effect on mechanical properties of granite. J. Eng. Geol. 2019, 27, 497–504. [Google Scholar] [CrossRef]
- Ghasemi, S.; Khamehchiyan, M.; Taheri, A.; Nikudel, M.R.; Zalooli, A. Crack Evolution in Damage Stress Thresholds in Different Minerals of Granite Rock. Rock Mech. Rock Eng. 2019, 53, 1163–1178. [Google Scholar] [CrossRef]
- Feng, Z.-j.; Zhao, Y.-s.; Liu, D.-n. Permeability Evolution of Thermally Cracked Granite with Different Grain Sizes. Rock Mech. Rock Eng. 2021, 54, 1953–1967. [Google Scholar] [CrossRef]
- Yin, W.; Feng, Z.; Zhao, Y. Effect of Grain Size on the Mechanical Behaviour of Granite Under High Temperature and Triaxial Stresses. Rock Mech. Rock Eng. 2020, 54, 745–758. [Google Scholar] [CrossRef]
- Saadat, M.; Taheri, A. A numerical approach to investigate the effects of rock texture on the damage and crack propagation of a pre-cracked granite. Comput. Geotech. 2019, 111, 89–111. [Google Scholar] [CrossRef]
- He, C.; Mishra, B.; Shi, Q.; Zhao, Y.; Lin, D.; Wang, X. Correlations between mineral composition and mechanical properties of granite using digital image processing and discrete element method. Int. J. Min. Sci. Technol. 2023, 33, 949–962. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Peng, J.; Teh, C.I. Numerical investigation of mineralogical composition effect on strength and micro-cracking behavior of crystalline rocks. J. Nat. Gas Sci. Eng. 2018, 53, 191–203. [Google Scholar] [CrossRef]
- Chen, S.; Yue, Z.Q.; Tham, L.G. Digital image-based numerical modeling method for prediction of inhomogeneous rock failure. Int. J. Rock Mech. Min. Sci. 2004, 41, 939–957. [Google Scholar] [CrossRef]
- Zhuang, L.; Zang, A.; Jung, S. Grain-scale analysis of fracture paths from high-cycle hydraulic fatigue experiments in granites and sandstone. Int. J. Rock Mech. Min. Sci. 2022, 157, 105177. [Google Scholar] [CrossRef]
- Hu, J.; Xie, H.; Gao, M.; Li, C.; Sun, Q. Damage mechanism and heat transfer characteristics of limestone after thermal shock cycle treatments based on geothermal development. Int. J. Rock Mech. Min. Sci. 2022, 160, 105269. [Google Scholar] [CrossRef]
- Li, N.; Xie, H.; Gao, Z.; Li, C. Study on the Hydraulic Fracturing Failure Behaviour of Granite and Its Comparison with Gas Fracturing. Sustainability 2022, 14, 4593. [Google Scholar] [CrossRef]
- Zhou, C.; Xu, C.; Karakus, M.; Shen, J. A particle mechanics approach for the dynamic strength model of the jointed rock mass considering the joint orientation. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 2797–2815. [Google Scholar] [CrossRef]
- Chen, B.; Barboza, B.R.; Sun, Y.; Bai, J.; Thomas, H.R.; Dutko, M.; Cottrell, M.; Li, C. A Review of Hydraulic Fracturing Simulation. Arch. Comput. Methods Eng. 2021, 29, 1–58. [Google Scholar] [CrossRef]
- Gupta, P.; Duarte, C.A. Simulation of non-planar three-dimensional hydraulic fracture propagation. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1397–1430. [Google Scholar] [CrossRef]
- Deb, P.; Salimzadeh, S.; Vogler, D.; Düber, S.; Clauser, C.; Settgast, R.R. Verification of Coupled Hydraulic Fracturing Simulators Using Laboratory-Scale Experiments. Rock Mech. Rock Eng. 2021, 54, 2881–2902. [Google Scholar] [CrossRef]
- Farkas, M.P.; Hofmann, H.; Zimmermann, G.; Zang, A.; Zhuang, L.; Kim, K.Y. Numerical investigation of laboratory hydraulic fracturing tests in Pocheon granite. Acta Geotech. 2022, 18, 2011–2038. [Google Scholar] [CrossRef]
- Paluszny, A.; Thomas, R.N.; Saceanu, M.C.; Zimmerman, R.W. Hydro-mechanical interaction effects and channelling in three-dimensional fracture networks undergoing growth and nucleation. J. Rock Mech. Geotech. Eng. 2020, 12, 707–719. [Google Scholar] [CrossRef]
- Guo, T.; Tang, S.; Liu, S.; Liu, X.; Zhang, W.; Qu, G. Numerical simulation of hydraulic fracturing of hot dry rock under thermal stress. Eng. Fract. Mech. 2020, 240, 107350. [Google Scholar] [CrossRef]
- Chen, W.; Konietzky, H.; Liu, C.; Tan, X. Hydraulic fracturing simulation for heterogeneous granite by discrete element method. Comput. Geotech. 2018, 95, 1–15. [Google Scholar] [CrossRef]
- Kong, L.; Ranjith, P.G.; Li, B.Q. Fluid-driven micro-cracking behaviour of crystalline rock using a coupled hydro-grain-based discrete element method. Int. J. Rock Mech. Min. Sci. 2021, 144, 104766. [Google Scholar] [CrossRef]
- Li, M.; Zhang, F.; Zhuang, L. Micromechanical analysis of hydraulic fracturing in granite with a grain-based DEM coupled with pore network model. In Proceedings of the ARMA/DGS/SEG International Geomechanics Symposium, Virtual, 1–4 November 2021; p. ARMA–IGS-21-089. [Google Scholar]
- Wu, M.Y.; Zhang, D.M.; Wang, W.S.; Li, M.H.; Liu, S.M.; Lu, J.; Gao, H. Numerical simulation of hydraulic fracturing based on two-dimensional surface fracture morphology reconstruction and combined finite-discrete element method. J. Nat. Gas Sci. Eng. 2020, 82, 103479. [Google Scholar] [CrossRef]
- Wu, M.; Wang, W.; Song, Z.; Liu, B.; Feng, C. Exploring the influence of heterogeneity on hydraulic fracturing based on the combined finite–discrete method. Eng. Fract. Mech. 2021, 252, 107835. [Google Scholar] [CrossRef]
- Wang, S.; Li, H.; Li, D. Numerical Simulation of Hydraulic Fracture Propagation in Coal Seams with Discontinuous Natural Fracture Networks. Processes 2018, 6, 113. [Google Scholar] [CrossRef]
- Ma, W.; Wang, Y.; Wu, X.; Liu, G. Hot dry rock (HDR) hydraulic fracturing propagation and impact factors assessment via sensitivity indicator. Renew. Energy 2020, 146, 2716–2723. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, X.; Liu, Z.; Yan, Y.; Yang, H. Investigation on the hydraulic fracture propagation of multilayers-commingled fracturing in coal measures. J. Pet. Sci. Eng. 2018, 167, 774–784. [Google Scholar] [CrossRef]
- Zhang, G.M.; Liu, H.; Zhang, J.; Wu, H.A.; Wang, X.X. Three-dimensional finite element simulation and parametric study for horizontal well hydraulic fracture. J. Pet. Sci. Eng. 2010, 72, 310–317. [Google Scholar] [CrossRef]
- Ben, W.; Hong, W.; Zhiqiang, Z.; Mengjiao, Z. Mesoscopic modeling method of concrete aggregates with arbitrary shapes based on mesh generation. Chin. J. Comput. Mech. 2017, 34, 591–596. [Google Scholar] [CrossRef]
- Guo, P.; Zhang, P.; Bu, M.; Wang, J.; Zheng, X.; He, M. Microcracking behavior and damage mechanism of granite subjected to high temperature based on CT-GBM numerical simulation. Comput. Geotech. 2023, 159, 105385. [Google Scholar] [CrossRef]
- Li, M.; Wu, Z.; Weng, L.; Liu, Q.; Chu, Z. Quantitative relationships between the mineral composition and macro mechanical behaviors of granite under different temperatures: Insights from mesostructure-based DEM investigations. Comput. Geotech. 2022, 148, 104838. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, L.; Azzam, R.; Zhou, J.; Wang, S. A statistical index indicating the degree and mechanical effects of grain size heterogeneity in rocks. Eng. Geol. 2021, 293, 106292. [Google Scholar] [CrossRef]
- Xie, H.-h.; Yu, T.-f.; Lin, P.; Wang, Z.-y.; Xu, Z.-h. Effect of petrographic characteristics on uniaxial compressive strength of granitic rocks from Xinjiang, China. J. Cent. South Univ. 2023, 30, 2340–2359. [Google Scholar] [CrossRef]
- Taleghani, A.D.; Gonzalez-Chavez, M.; Yu, H.; Asala, H. Numerical simulation of hydraulic fracture propagation in naturally fractured formations using the cohesive zone model. J. Pet. Sci. Eng. 2018, 165, 42–57. [Google Scholar] [CrossRef]
- Carrier, B.; Granet, S. Numerical modeling of hydraulic fracture problem in permeable medium using cohesive zone model. Eng. Fract. Mech. 2012, 79, 312–328. [Google Scholar] [CrossRef]
- Khristianovic, S.; Zheltov, Y.P. Formation of vertical fractures by means of highly viscous liquid. In Proceedings of the World Petroleum Congress Proceedings, Rome, Italy, 6–15 June 1955; pp. 579–586. [Google Scholar]
- Geertsma, J.; De Klerk, F. A rapid method of predicting width and extent of hydraulically induced fractures. J. Pet. Technol. 1969, 21, 1571–1581. [Google Scholar] [CrossRef]
- Sobhaniaragh, B.; Trevelyan, J.; Mansur, W.J.; Peters, F.C. Numerical simulation of MZF design with non-planar hydraulic fracturing from multi-lateral horizontal wells. J. Nat. Gas Sci. Eng. 2017, 46, 93–107. [Google Scholar] [CrossRef]
- Xie, L.; Min, K.-B.; Shen, B. Simulation of hydraulic fracturing and its interactions with a pre-existing fracture using displacement discontinuity method. J. Nat. Gas Sci. Eng. 2016, 36, 1284–1294. [Google Scholar] [CrossRef]
- Zhai, C.; Li, M.; Sun, C.; Zhang, J.; Yang, W.; Li, Q. Guiding-controlling technology of coal seam hydraulic fracturing fractures extension. Int. J. Min. Sci. Technol. 2012, 22, 831–836. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Yuan, B.; Yin, S. In-situ stresses controlling hydraulic fracture propagation and fracture breakdown pressure. J. Pet. Sci. Eng. 2018, 164, 164–173. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, J.; Li, B.; Zhu, C. Crack propagation patterns and factors controlling complex crack network formation in coal bodies during tri-axial supercritical carbon dioxide fracturing. Fuel 2021, 286, 119381. [Google Scholar] [CrossRef]
- Li, C.; Gao, C.; Xie, H.; Li, N. Experimental investigation of anisotropic fatigue characteristics of shale under uniaxial cyclic loading. Int. J. Rock Mech. Min. Sci. 2020, 130, 104314. [Google Scholar] [CrossRef]
- Feng, F.; Wang, X.; Guo, B.; Ai, C. Mathematical model of fracture complexity indicator in multistage hydraulic fracturing. J. Nat. Gas Sci. Eng. 2017, 38, 39–49. [Google Scholar] [CrossRef]
- He, J.; Li, X.; Yin, C.; Zhang, Y.; Lin, C. Propagation and characterization of the micro cracks induced by hydraulic fracturing in shale. Energy 2020, 191, 116449. [Google Scholar] [CrossRef]
- Lei, B.; Zuo, J.; Massimo, C.; Wu, G.; Liu, H.; Yu, X. Experimental and numerical investigation on meso-fracture behavior of Beishan granite subjected to grain size heterogeneity. Eng. Fract. Mech. 2023, 292, 109623. [Google Scholar] [CrossRef]
- Hu, J.; Xie, H.; Li, C.; Liu, G. Evolution mechanism of permeability of hot dry rock under coupled effect of thermal fatigue and seawater interaction during coastal geothermal development. Renew. Sustain. Energy Rev. 2023. [CrossRef]
- Zhuang, L.; Kim, K.Y.; Jung, S.G.; Diaz, M.; Min, K.-B. Effect of Water Infiltration, Injection Rate and Anisotropy on Hydraulic Fracturing Behavior of Granite. Rock Mech. Rock Eng. 2018, 52, 575–589. [Google Scholar] [CrossRef]
- Long, X.; Xie, H.; Liu, J.; Li, N.; Li, C. Gas fracturing behavior and breakdown pressure prediction model for granite under different confining pressure and injection rate. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 76. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, W.; Qu, Z.; Guo, T.; Sun, Y.; Rabiei, M.; Cao, Q. Feasibility evaluation of hydraulic fracturing in hydrate-bearing sediments based on analytic hierarchy process-entropy method (AHP-EM). J. Nat. Gas Sci. Eng. 2020, 81, 103434. [Google Scholar] [CrossRef]
- Cong, Z.; Li, Y.; Tang, J.; Martyushev, D.A.; Yang, F. Numerical simulation of hydraulic fracture height layer-through propagation based on three-dimensional lattice method. Eng. Fract. Mech. 2022, 264, 108331. [Google Scholar] [CrossRef]
- Zhang, R.; Hou, B.; Han, H.; Fan, M.; Chen, M. Experimental investigation on fracture morphology in laminated shale formation by hydraulic fracturing. J. Pet. Sci. Eng. 2019, 177, 442–451. [Google Scholar] [CrossRef]

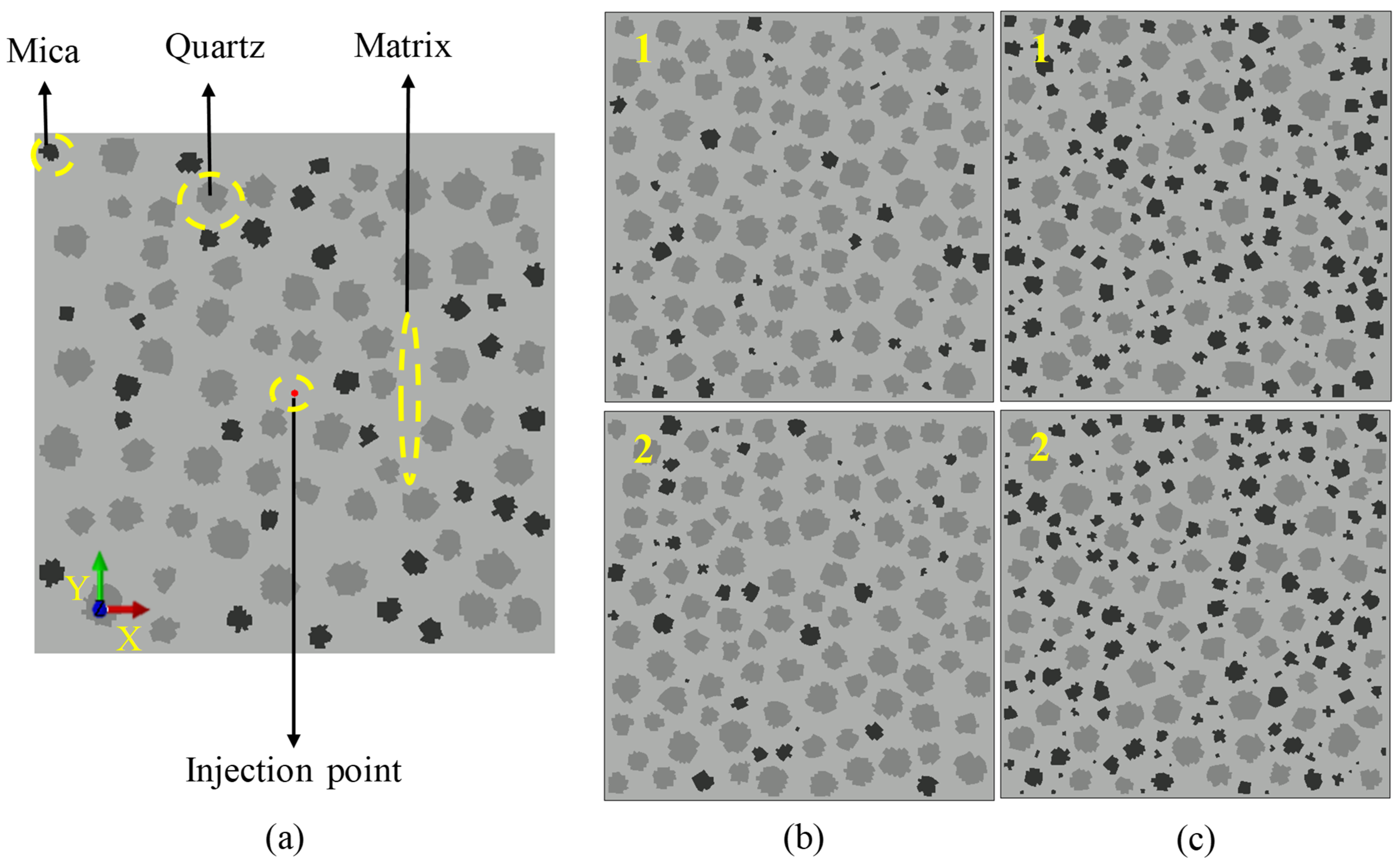




| Category | Mineral Types | Particle Size (mm) | Content |
|---|---|---|---|
| Coarse-grained | Quartz | 6–9 | 25% |
| Mica | 5–7 | 5% | |
| Medium-grained | Quartz | 3–5 | 25% |
| Mica | 2–3.5 | 5% | |
| Fine-grained | Quartz | 1–2 | 25% |
| Mica | 0.5–1.5 | 5% | |
| High quartz content | Quartz | 3–5 | 40% |
| Mica | 2–3.5 | 5% | |
| High mica content | Quartz | 3–5 | 25% |
| Mica | 2–3.5 | 20% |
| Input Parameter | Value | Input Parameter | Value |
|---|---|---|---|
| Model dimensions (mm2) | 50 × 50 | Porosity | 0.001 |
| Matrix elastic modulus (GPa) | 60 | Matrix Poisson’s ratio | 0.2 |
| Matrix permeability coefficient (m/s) | 1 × 10−10 | Matrix tensile strength (MPa) | 10 |
| Matrix cohesive elastic modulus (GPa) | 60 | Matrix leak-off coefficient (m/(Pa·s)) | 1 × 10−14 |
| Quartz elastic modulus (GPa) | 72 | Quartz Poisson’s ratio | 0.17 |
| Quartz permeability coefficient (m/s) | 1 × 10−12 | Quartz tensile strength (MPa) | 50 |
| Quartz cohesive elastic modulus (GPa) | 72 | Quartz leak-off coefficient (m/(Pa·s)) | 1 × 10−15 |
| Mica elastic modulus (GPa) | 30 | Mica Poisson’s ratio | 0.22 |
| Mica permeability coefficient (m/s) | 1 × 10−8 | Mica tensile strength (MPa) | 8 |
| Mica cohesive elastic modulus (GPa) | 30 | Mica leak-off coefficient (m/(Pa·s)) | 1 × 10−13 |
| Fluid specific gravity (kg/m3) | 9800 | Fluid dynamic viscosity (Pa·s) | 1 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Li, N.; Tu, J.; Yang, L. Effect of Non-Uniform Minerals Distribution on Hydraulic Fracture Evolution during Unconventional Geoenergy Exploration. Processes 2023, 11, 3200. https://doi.org/10.3390/pr11113200
Gao Z, Li N, Tu J, Yang L. Effect of Non-Uniform Minerals Distribution on Hydraulic Fracture Evolution during Unconventional Geoenergy Exploration. Processes. 2023; 11(11):3200. https://doi.org/10.3390/pr11113200
Chicago/Turabian StyleGao, Ziqi, Ning Li, Jiahui Tu, and Liu Yang. 2023. "Effect of Non-Uniform Minerals Distribution on Hydraulic Fracture Evolution during Unconventional Geoenergy Exploration" Processes 11, no. 11: 3200. https://doi.org/10.3390/pr11113200
APA StyleGao, Z., Li, N., Tu, J., & Yang, L. (2023). Effect of Non-Uniform Minerals Distribution on Hydraulic Fracture Evolution during Unconventional Geoenergy Exploration. Processes, 11(11), 3200. https://doi.org/10.3390/pr11113200







