Deep Neural Network Model for Determination of Coal Cutting Resistance and Performance of Bucket-Wheel Excavator Based on the Environmental Properties and Excavation Parameters
Abstract
:1. Introduction
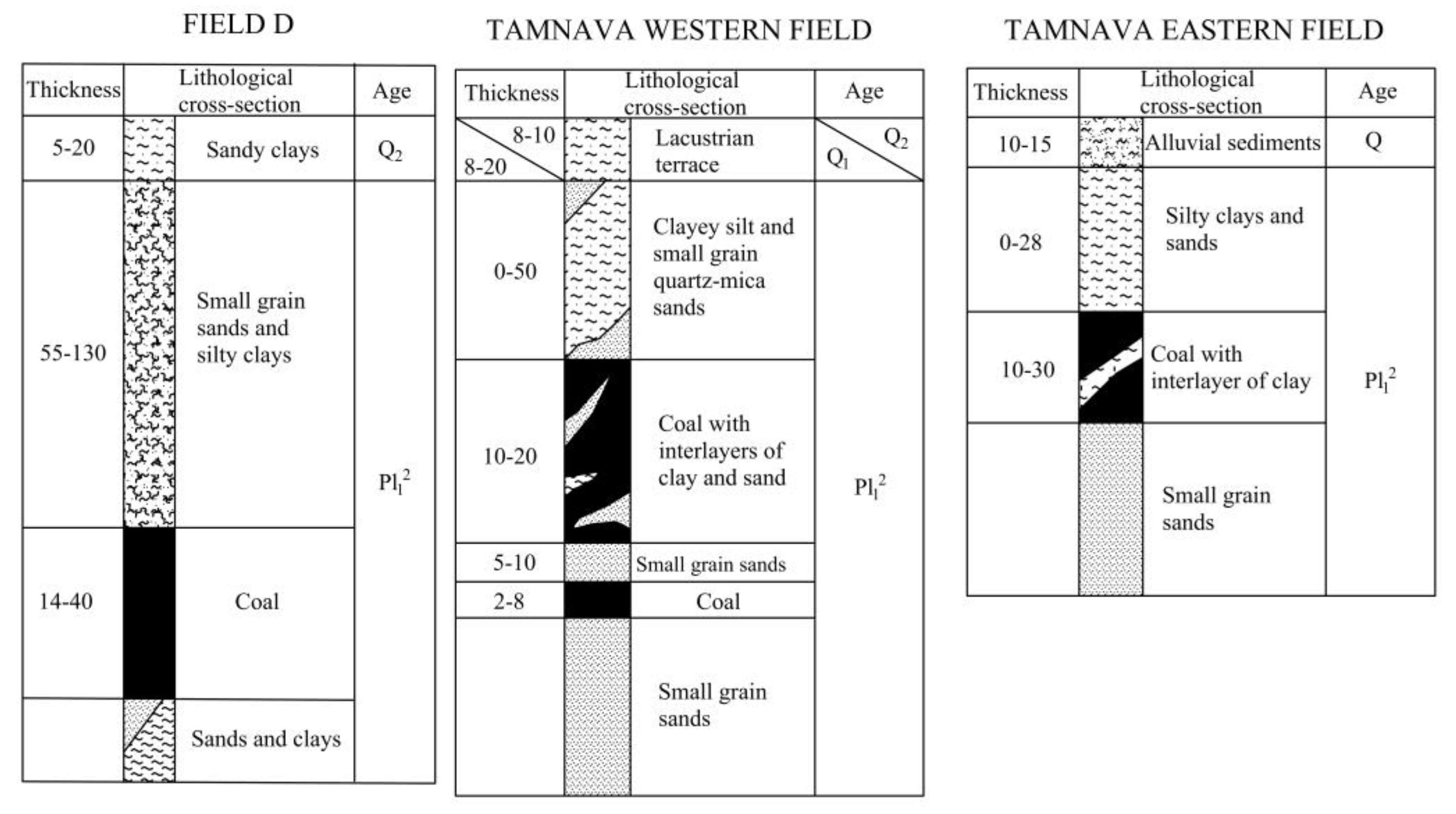
2. Methodology and Data Analyzed
- Installed power for rotary wheel engine: 2 × 500 kW (at Tamnava Western Field) and 2 × 375 kW (at Tamnava Eastern Field and Field D)
- Bucket volume: 630 L
- Number of buckets: 20
- Number of buckets emptied: 162 per min
- Angular distance between buckets: 18°
- Rotary wheel diameter: 10 m
- Length of rotary arrow: 35 m
- Wheel velocity: 4.24 m/s
- Parameter ReduceLROnPlateau, which reduces the learning rate if no accuracy on the validation dataset is improved for 35 epochs.
- Parameter EarlyStopping, which interrupts training if no accuracy is improved on the validation dataset for 45 epochs.
3. Dependence of Each Output Factor on Controlling Parameters
3.1. Performance of Bucket-Wheel Excavator
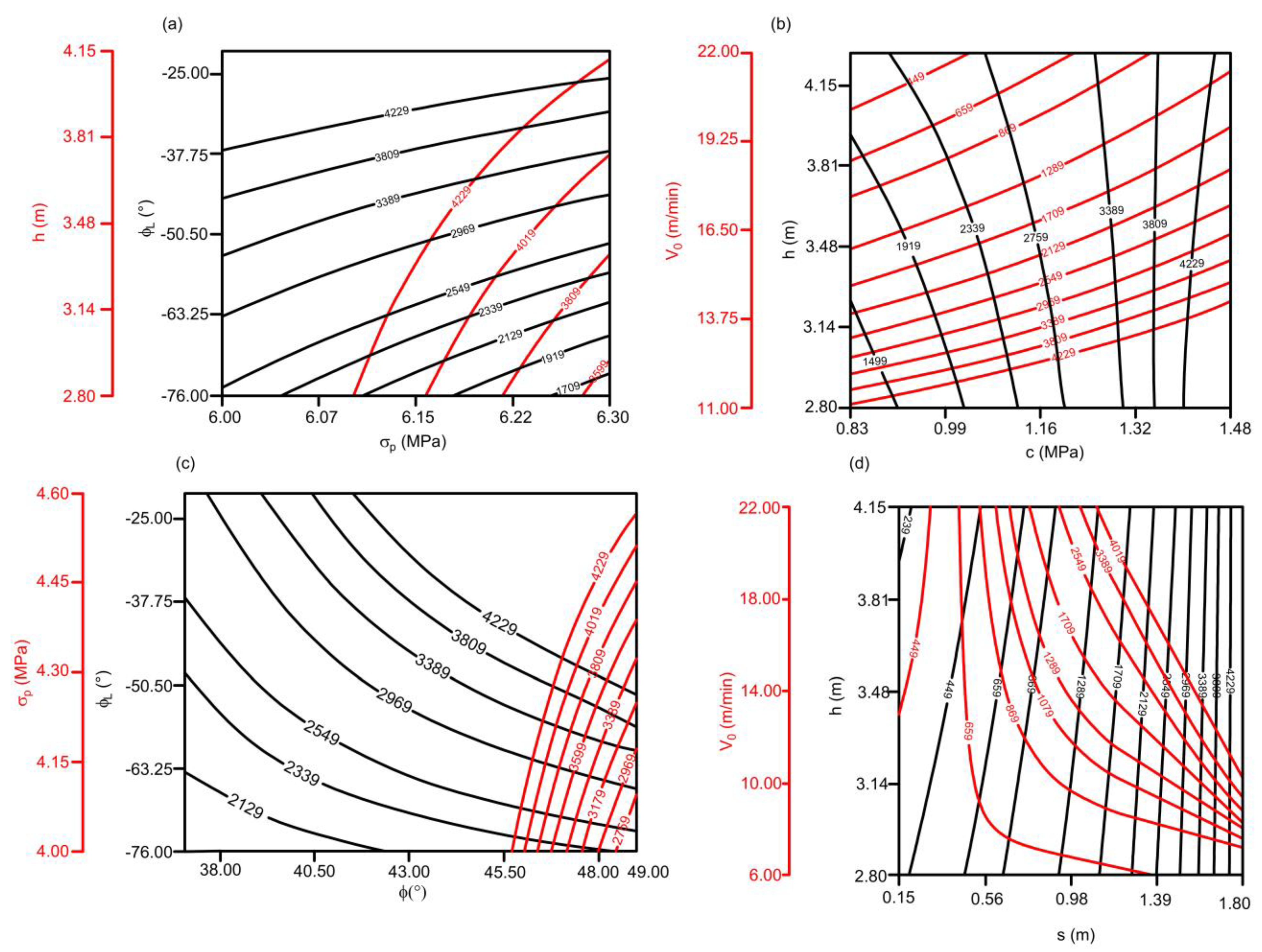
3.1.1. Excavator Capacity Qef
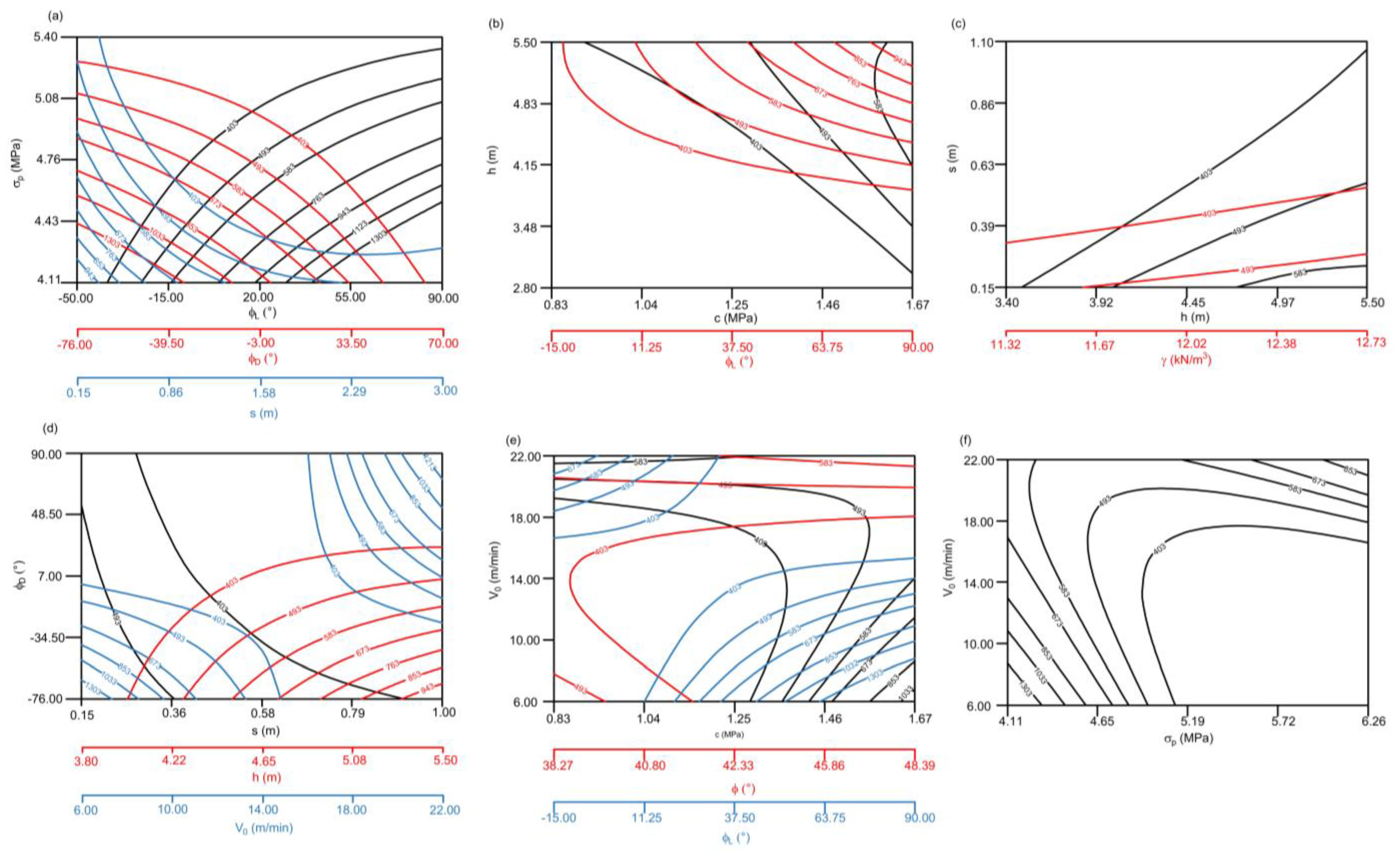
- Coal uniaxial compressive strength σp: It appears that σp has a variable effect on Qef, depending on the type of the parameter in the interaction. When σp is in interaction with the slice height (h) and the excavator movement angle in the left direction (φL), σp has a negative (decreasing) effect on Qef, meaning that excavator capacity decreases with the increase in σp (Figure 4a), which is expected. Such effect is obtained for the upper range of values of σp (6.00–6.30 MPa). However, when σp is in interaction with the coal friction angle φ, it appears that it has a positive effect on Qef (Figure 4c). This interesting finding could indicate that for high values of coal friction angles (above 45.5°), an increase in σp leads to increase in Qef. One should note that this is achieved for the lower range of values of σp (4.00–4.60 MPa).
- Coal cohesion (c): It has a positive effect on Qef (Figure 4b), indicating that Qef increases as c increases. One should note that such an effect is captured for a relatively narrow range of values for cohesion (0.83–1.48 MPa).
- Coal friction angle (φ): For medium values of σp (around 5 MPa), φ has a positive effect on Qef (Figure 4c). However, for low values of σp (4.00–4.30 MPa), φ has a negative effect on Qef (Figure 4c). However, one should note that the results of the ANOVA test indicate that the individual effect of the coal friction angle is statistically insignificant (p-value = 0.6374), so Figure 4c should be observed as relevant only for φL and σp: an increase in φL leads to an increase in Qef for all examined values of φ, while the increase in σp leads to an increase in Qef only for very high values of φ (>45.5°).
- Slice thickness (s): Similar to slice height, s also has a positive effect on Qef in all statistically significant interactions: h and V0 (Figure 4d).
3.1.2. Current Consumption Imax
- Coal unit weight (γ): γ has a different effect on Imax depending on the parameter in co-action. When γ is interacting with c and V0, γ has a positive effect on Imax (Figure 5a). However, when γ is interacting with s, for lower values of s, the increase in γ has almost no effect on Imax. For higher values of s, the increase in γ leads to the decrease in Imax.
- Excavator movement angle: It has an opposite effect on Imax, depending on the excavation direction and coal compressive strength, which indicates specific geometry constraints and sedimentation conditions, which are favorable in the right direction of excavation for zones of coal with higher values of σp and in the left direction for zones of coal with lower values of σp:
- ○
- Excavator movement angle in the left direction (φL): φL has different effects for lower and medium-to-high values of σp (Figure 5b). For lower values of σp, φL has a negative effect on Imax. However, φL has a positive effect on Imax for medium-to-high values of σp.
- ○
- Excavator movement angle in the right direction (φD): φD has different effects for lower and medium-to-high values of σp (Figure 5b). For lower values of σp, φD has a positive effect on Imax. However, φD has a negative effect on Imax for medium-to-high values of σp.
- Coal compressive strength (σp): σp has a different effect on Imax depending on the parameters in interaction and their values. When interacting with φD, σp has a positive effect on Imax for medium-to-lower values of φD, while σp has a negative effect on Imax for higher values of φD (Figure 5b). When interacting with φL, σp has a negative effect on Imax for medium-to-lower values of φL, while σp has a positive effect on Imax for higher values of φL. From the viewpoint of geomechanics, the relevant impact of σp is for the excavation angle in the left direction for σp higher than 5 MPa, where the increase in σp leads to the increase in Imax.
- Coal angle of internal friction (φ): The effect of φ on Imax depends on the type of parameter in interaction and its values. For lower values of slice height h, φ has a positive effect on Imax, while φ has a negative effect on Imax for medium-to-high values of h (Figure 5c). On the other hand, for medium-to-lower values of V0, φ has a negative effect on Imax, while φ has a positive effect on Imax for higher values of V0 (Figure 5c). However, according to the results of the ANOVA test, the individual effect of φ is statistically insignificant (p-value = 0.5541), so Figure 5 should be considered as relevant only for V0 and h, meaning that for all examined values of φ, an increase in V0 leads to an increase in Imax, while an increase in h leads to a decrease in Imax.
- Slice height (h): h has a negative effect on Imax (Figure 5c,d). In particular, current consumption is lower for the higher values of slice height.
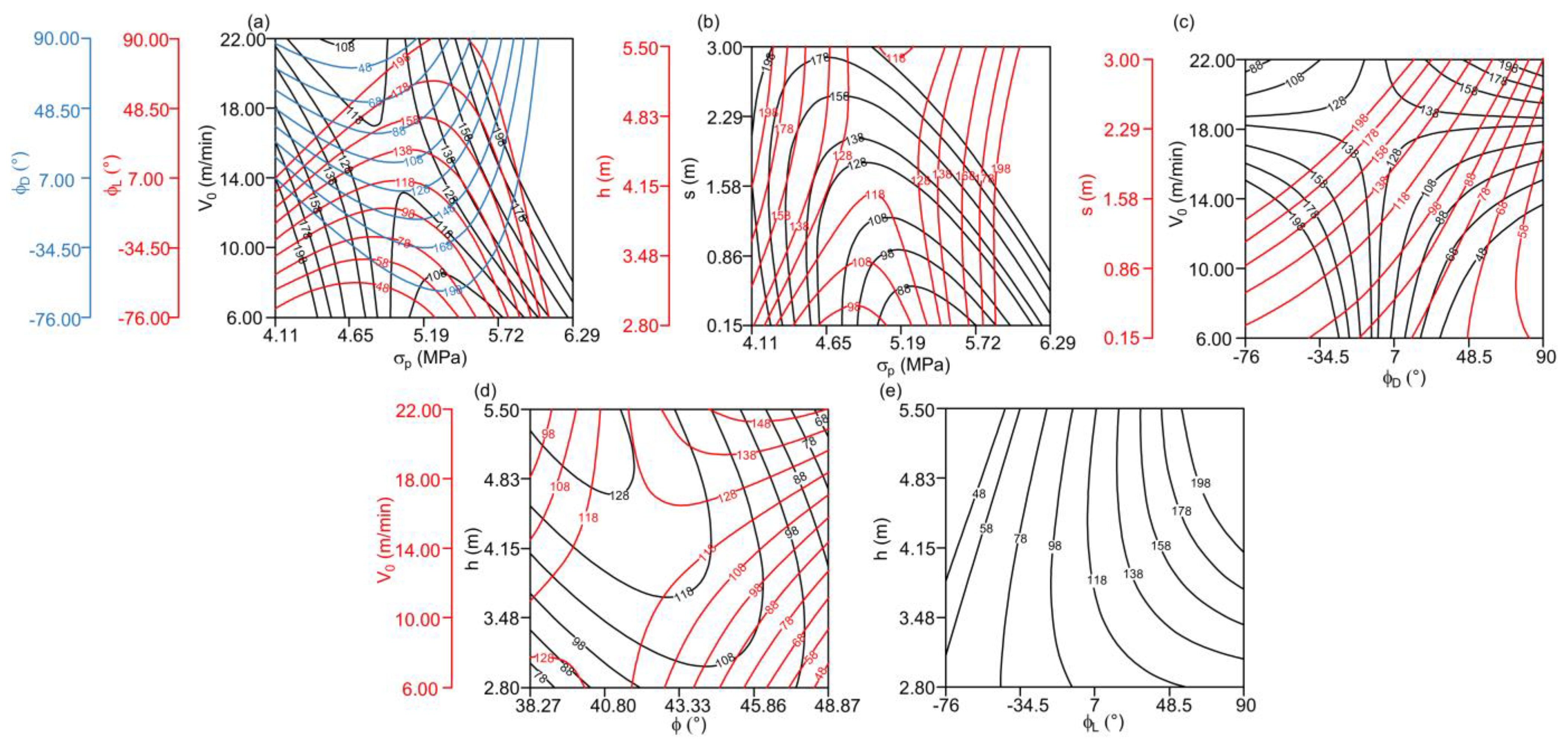
3.1.3. Power Consumption Nmax
- Velocity of the rotary movement of the excavator (V0): V0 has a positive effect on Nmax (Figure 6c). Such a relationship is expected, indicating that the increase in V0 requires an increase in power consumption.
- Slice thickness (s): s has a positive effect on Nmax, regardless of the type of parameter in interaction (Figure 6a). In particular, an increase in slice thickness leads to an increase in Nmax.
- Excavator movement angle in the left (φL) and right (φD) direction: It has a negative effect on Nmax, regardless of the type of parameter in interaction (Figure 6b,c), which could be interpreted as a product of a specific geometry of the coal seam.
- Coal compressive strength (σp): σp has a positive effect on Nmax (Figure 6a), which indicates that the increase in σp leads to an increase in Nmax.
- Coal cohesion (c): c has a positive effect on Nmax, regardless of the type of parameter in interaction (Figure 6b). In particular, an increase in coal cohesion leads to an increase in Nmax.
- Coal angle of internal friction (φ): φ has a negative effect on Nmax, regardless of the type of parameter in interaction (Figure 6a,c). However, the ANOVA test indicated the statistically insignificant individual effect of φ (p-value = 0.0041). Therefore, Figure 6a,c should be considered as relevant only for s and V0, meaning that Nmax increases with the increase in V0 and s for all the examined values of coal friction angle.
- Slice height (h): h has a negative effect on Nmax, regardless of the type of parameter in interaction (Figure 6a,b). However, results of the ANOVA test indicate that h has statistically insignificant individual influence (p-value = 0.124), so the two-factor interactions should be considered as relevant only for c, meaning that an increase in cohesion leads to an increase in Nmax for all the examined values of slice height.
3.1.4. Force Consumption Pmax
- Velocity of the rotary movement of the excavator (V0): The effect of V0 on Pmax depends on the type of parameter in interaction and its values. For lower values of σp, φD, and φ, an increase in V0 leads to a decrease in Pmax (Figure 7a,c,d). However, for medium-to-high values of σp, φD, and φ, V0 has a positive effect on Pmax.
- Slice thickness (s): s has a positive effect on Pmax, regardless of the parameter in interaction (Figure 7b,c). Such influence is expected because the increase in slice thickness should lead to an increase in Pmax.
- Excavator movement angle: It has an opposite effect on Pmax, depending on the excavation direction, which identifies specific geometry constraints and sedimentation conditions, which are favorable in the right direction of excavation:
- Coal compressive strength (σp): An increase in σp from lower-to-medium values leads to a decrease in Pmax in all interactions (Figure 7a,b). However, a further increase in σp from medium-to-high values leads to an increase in Pmax. Therefore, one could conclude that relevant values of σp are higher than approximately 5 MPa.
- Coal angle of internal friction (φ): An increase in φ from lower-to-medium values leads to an increase in Pmax in interaction with h (Figure 7d). However, an increase in φ for lower-to-medium values of V0 leads to a decrease in Pmax (Figure 7d). A further increase in φ for higher values of V0 leads to an increase in Pmax (Figure 7d). One should note that according to the ANOVA test, the individual effect of the coal friction angle on Pmax is statistically insignificant (p-value = 0.2113). However, the influence of two-factor interaction φ × V0 is statistically significant (p-value = 0.005), while the impact of φ × h should be taken with caution (p-value = 0.0587). Concerning this, one should consider the effect of the coal friction angle on Pmax as relevant only for the lower values of φ (38–41°).
- Slice height (h): for lower values of σp, an increase in h leads to an increase in Pmax. For higher values of σp, an increase in h has almost no effect on Pmax (Figure 7b). For lower-to-medium values of φ, h has a positive effect on Pmax, while h has a negative effect on Pmax for higher values of φ (Figure 7d). For lower-to-medium values of φL, an increase in h leads to a decrease in Pmax, while h has a positive effect on Pmax for higher values of φL (Figure 7e).
3.1.5. Energy Consumption Emax
- Velocity of the rotary movement of the excavator (V0): V0 has a negative effect on Emax, for all parameters in interaction, except for slice height, where a positive effect of V0 on Emax is recorded, for the medium-to-high values of V0 and medium-to-high values of slice height (Figure 8b).
- Slice thickness (s): s has a negative effect on Emax, regardless of the parameters in interaction (Figure 8a,b). This means that the increase in slice thickness leads to a decrease in Emax. One should note that such an effect is obtained only for the range of s = 0.15–0.64 m, while for the higher values of s (0.64–1.20 m), slice thickness does not affect Emax.
- Excavator movement angle in the right direction (φD): φD has a negative effect on Emax, regardless of the parameters in interaction. This means that an increase in the excavator movement angle in the right direction leads to a decrease in Emax, which could be due to the specific geometry of the coal seam and/or particular sedimentation conditions.
- Slice height (h): h has a positive effect on Emax, regardless of the parameters in interaction (Figure 8a,b). In particular, an increase in slice height leads to an increase in Emax, which is physically possible and expected.
3.2. Cutting Resistance
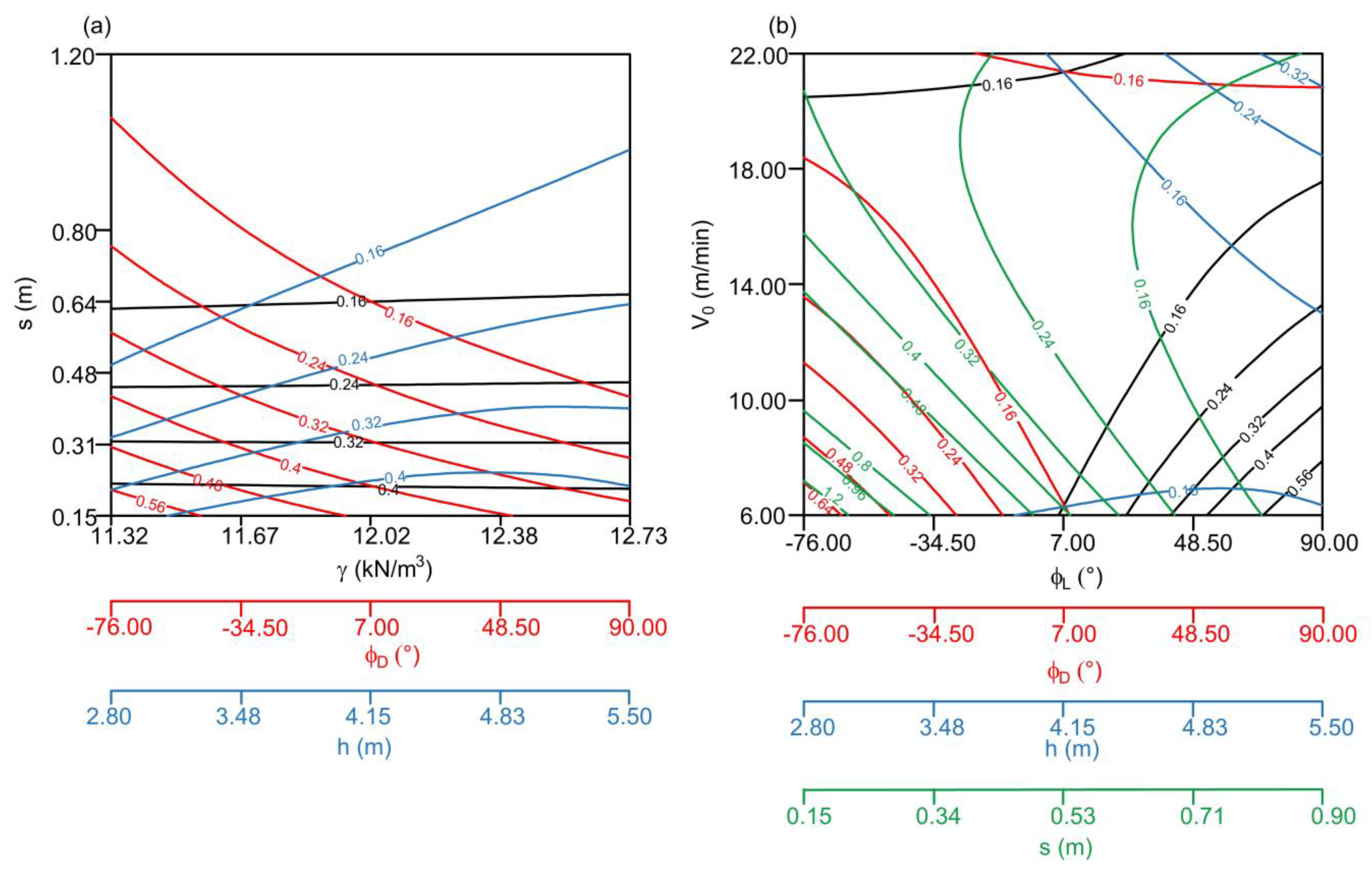
3.2.1. Linear Cutting Resistance KLmax
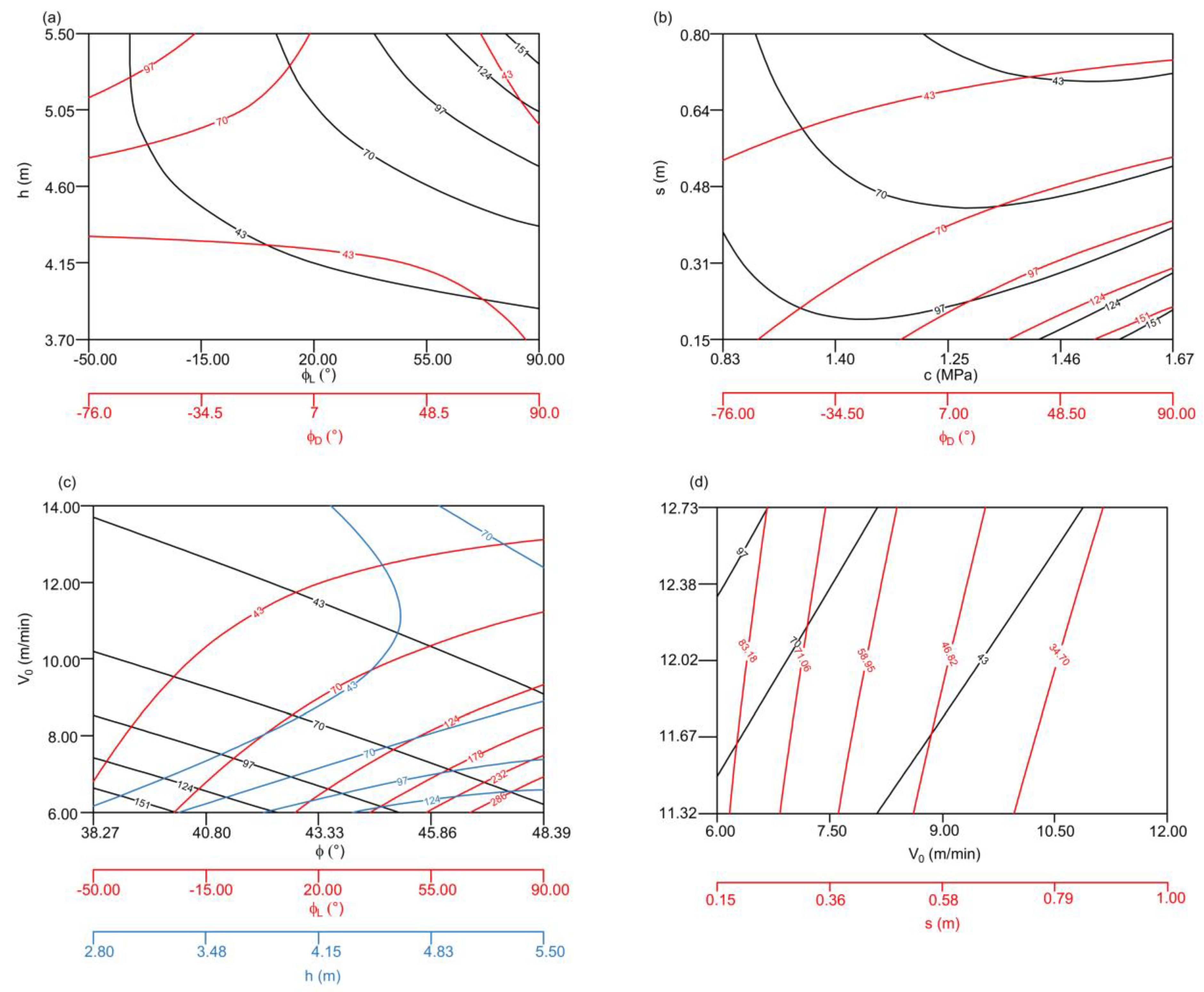
- Velocity of the rotary movement of the excavator (V0): For low φD and σp, V0 has a negative effect on KLmax (Figure 9d,f). For medium-to-high values of φD, an increase in V0 leads to an increase in KLmax. On the other hand, for low-to-medium values of cohesion c and φL, an increase in V0 leads to an increase in KLmax (Figure 9e), while for higher values of c, V0 has a negative effect on KLmax. There is a positive effect of V0 on KLmax for all values of the coal friction angle φ, except for very low values of φ, where an increase in V0 from low-to-medium values leads to a decrease in KLmax.
- Slice thickness (s): s has a negative effect on KLmax, regardless of the parameters in interaction (Figure 9a,c). This means that an increase in slice thickness leads to a decrease in linear cutting resistance. However, if one takes a closer look at Figure 8a,c, it is clear that such an effect is captured only for low values of slice thickness. In particular, such effect is captured only for s = 0.15–1.5 m and σp = 4.11–4.43 MPa (Figure 9a); for higher values of s, slice thickness does not affect KLmax. Additionally, for higher values of h (Figure 9c), there is a negative effect on KLmax. However, one could say that in both figures, s predominantly does not affect KLmax.
- Coal unit weight (γ): Unit weight has a positive effect on KLmax for lower values of c (Figure 9c). For higher values of c, unit weight does not affect KLmax. Indeed, an increase in unit weight should lead to an increase in linear cutting resistance.
- Excavator movement angle: It has an opposite effect on KLmax, depending on the excavation direction, which indicates specific geometry constraints and sedimentation conditions, which are favorable in the right direction of excavation:
- Coal compressive strength (σp): σp has a negative effect on KLmax for all parameters in interaction (Figure 9a,f), except for a very high value of V0 (Figure 9f) when σp has a positive effect on KLmax. The effect of compressive strength is apparently physically possible only for the higher values of V0 because the increase in compressive strength should lead to the increase in KLmax;
- Coal cohesion (c): c has a positive effect on KLmax, regardless of the parameters in interaction (Figure 9b,e). Such an effect is expected—an increase in cohesion should lead to an increase in KLmax.
- Slice height (h): h has a positive effect on KLmax, regardless of the parameters in interaction (Figure 9b–d), except for the high values of φD when h does not affect KLmax. In particular, the increase in the slice height requires higher excavation power, which, further, reduces the cutting resistance.
3.2.2. Areal Cutting Resistance KFmax
- Velocity of the rotary movement of the excavator (V0): V0 has a negative effect on KFmax, regardless of the parameters in interaction (Figure 10c,d). Such an effect is expected, because the increased wheel velocity indicates higher power and, thus, lower cutting resistance.
- Slice thickness (s): s has a negative effect on KFmax, regardless of the parameters in interaction (Figure 10b,d). This means that the increase in slice thickness leads to a decrease in areal cutting resistance. However, one should note that such an effect is observed only for low values of slice thickness (below 1 m), so it could be said that predominantly s has no effect on KFmax.
- Coal unit weight (γ): γ has a positive effect on KFmax (Figure 10d). From a geomechanical viewpoint, such an effect is expected: the increase in unit weight leads to the increased cutting resistance.
- Excavator movement angle in the left direction (φL): φL has a positive effect on KFmax, regardless of the parameters in interaction (Figure 10a,c). In a particular case, it means that the increase in the movement angle in the left direction leads to the increase in cutting resistance, which could be ascribed to the specific geometry of the coal seam and inherent sedimentation conditions.
- Excavator movement angle in the right direction (φD): φD has a different effect on KFmax, depending on the type of parameter in interaction. In interaction with σp and h, φD has a negative effect on KFmax. In particular, for higher values of h (4.60–5.50 m), an increase in φD leads to a decrease in KFmax. This effect is the same for lower values of σp (4.11–4.81 MPa). In interaction with s, φD has a positive effect on KFmax, which is identical to the influence in the case of φL.
- Coal cohesion (c): c has a positive effect on KFmax (Figure 10b). Such effect is expected because the increase in cohesion of the coal indeed leads to the increase in the areal cutting resistance.
- Coal angle of internal friction (φ): φ has a negative effect on KFmax (Figure 10c). One would expect that because cohesion has a positive effect on KFmax, such influence is expected also for the friction angle. However, resistance to failure during the cutting is obviously determined by cohesion, while, once the failure is achieved during the cutting process, shear strength does not affect KFmax. Figure 10c should be observed as relevant only for wheel velocity V0, meaning that the increase in V0 for any value of φ leads to a decrease in KFmax. This is further proven by the ANOVA test, which indicates a much smaller p-value for V0 (0.0096) compared to the p-value for φ (0.0631). The p-value of V0×φ is also relatively high (0.0614).
- Slice height (h): h has a positive effect on KFmax, regardless of the parameters in interaction (Figure 10a,c). In particular, the increase in the slice height requires higher excavation power, which, further, reduces the cutting resistance.
3.3. Analysis of the Most Significant Factors
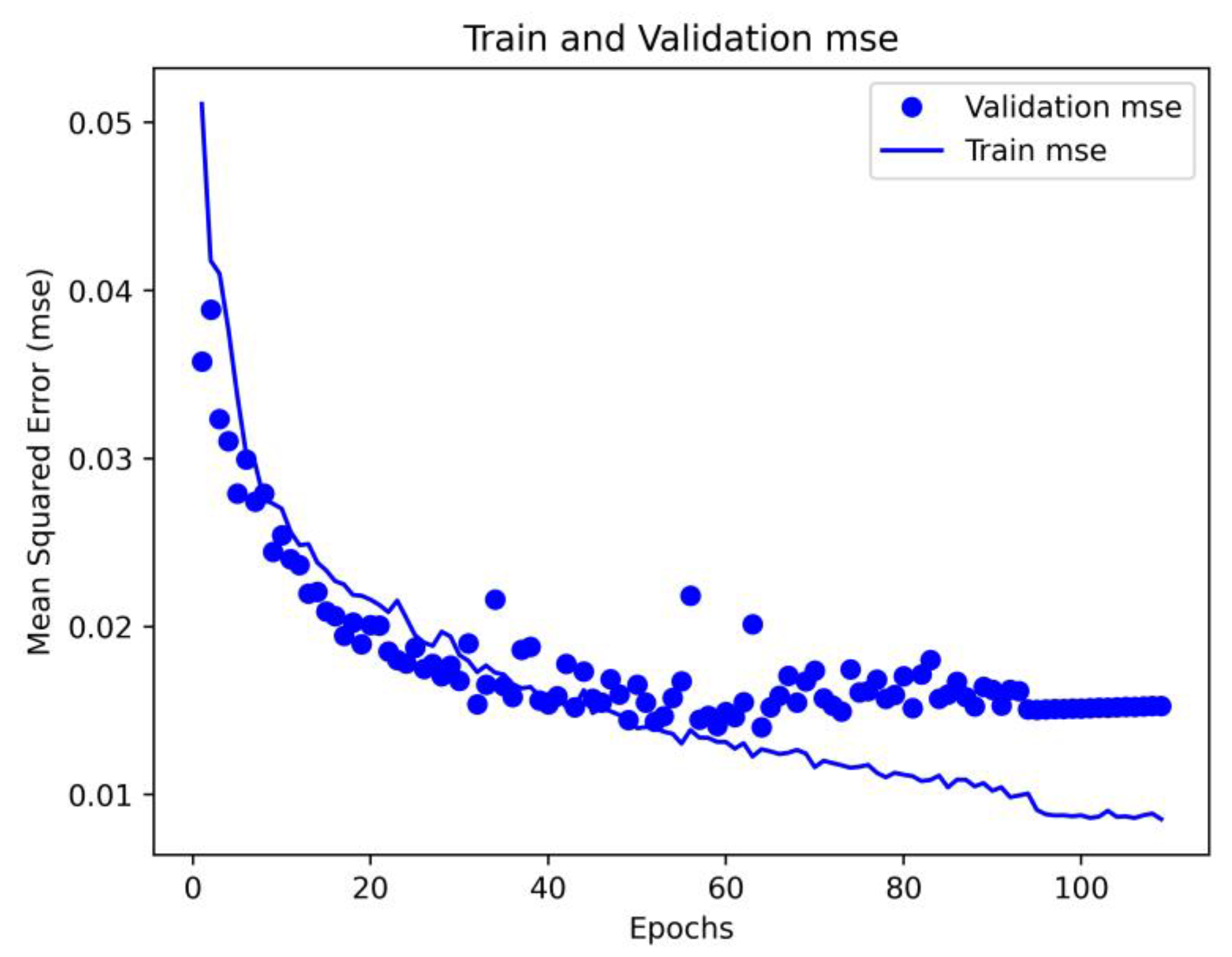
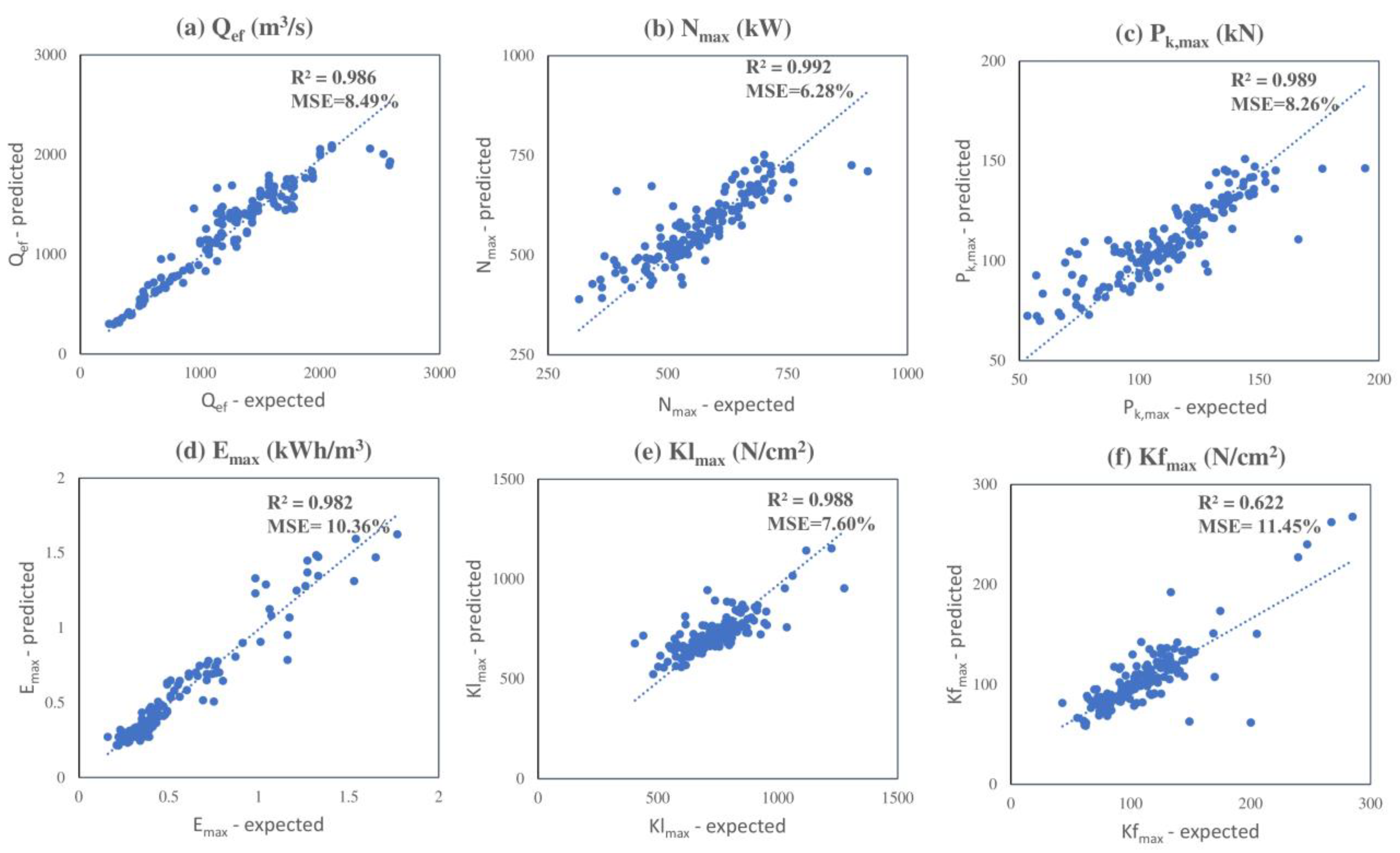
4. Development of a Model Based on Deep Neural Networks
5. Conclusions
- Coal unit weight γ has a statistically significant effect only for the current consumption Imax, areal cutting resistance KFmax, and for the linear cutting resistance KLmax for low values of coal cohesion. For all the rest of the output factors, γ does not have a statistically significant influence.
- Coal cohesion c has a statistically significant effect only for the excavator capacity Qef, power consumption Nmax, and linear and areal cutting resistance of coal, KLmax and KFmax.
- Coal angle of internal friction φ does not have a statistically significant effect on energy consumption Emax and linear cutting resistance KLmax.
- Coal compressive strength σp does not have a statistically significant influence on energy consumption Emax and areal cutting resistance KFmax.
- Excavator movement angle in the right direction (φD) does not have a statistically significant influence on excavator capacity Qef.
- Velocity of the rotary movement of the excavator (V0):
- ○
- V0 has a negative effect (meaning that the output parameter decreases as V0 increases) on (1) Qef in interaction with c and s; (2) Pmax, for lower values of σp, φD, and φ; (3) Emax, for all parameters in interaction, except for moderate-to-high values of slice height; (4) KLmax, for low-to-medium values of cohesion c and φL, and for higher values of c and V0 and very low values of φ; and (5) KFmax;
- ○
- V0 has a positive effect (meaning that the output parameter increases as V0 increases) on (1) Imax; (2) Nmax; (2) Pmax, for medium-to-high values of σp, φD, and φ; (3) Emax, for medium-to-high values of slice height; and (4) KLmax, for low-to-medium values of cohesion c and φL.
- Slice thickness (s):
- ○
- s has a negative effect (meaning that the output parameter decreases as s increases) on Emax, KLmax, and KFmax;
- ○
- s has a positive effect (meaning that the output parameter increases as s increases) on Qef, Imax, Nmax, and Pmax.
- Coal unit weight (γ):
- ○
- γ has a negative effect (meaning that the output parameter decreases as γ increases) on Imax, for higher values of slice thickness s;
- ○
- γ has a positive effect (meaning that output parameter increases as γ increases) on (1) Imax, except for the higher values of s; (2) KLmax, for lower values of cohesion; and (3) KFmax.
- Excavator movement angle in the left direction (φL):
- ○
- φL has a negative effect (meaning that the output parameter decreases as φL increases) on (1) Imax, for lower values of σp, and (2) Nmax;
- ○
- φL has a positive effect (meaning that the output parameter increases as φL increases) on Qef, Imax (for moderate to high values of σp), Pmax, KLmax, and KFmax.
- Excavator movement angle in the right direction (φD):
- ○
- φD has a negative effect (meaning that the output parameter decreases as φD increases) on Imax (for medium-to-high values of σp), Nmax, Pmax, Emax, KLmax, and KFmax (in interaction with σp and h);
- ○
- φD has a positive effect (meaning that the output parameter increases as φD increases) on Imax (for lower values of σp) and KFmax (in interaction with s).
- Coal compressive strength (σp):
- ○
- σp has a negative effect (meaning that the output parameter decreases as σp increases) on (1) Qef, in interaction with slice height (h) and excavator movement angle in the left direction (φL); (2) Imax, for higher values of φD and for medium-to-lower values of φL; (3) Pmax, for lower-to-medium values of σp; and (4) KLmax, except for very high values of V0;
- ○
- σp has a positive effect (meaning that the output parameter increases as σp increases) on (1) Qef, in interaction with friction angle, for a lower range of values of σp (4.00–4.60 MPa); (2) Imax, for medium-to-lower values of φD and for higher values of φL; (3) Nmax; (4) Pmax, for moderate-to-high values of σp; and (5) KLmax, for very high values of V0.
- Coal cohesion (c):
- ○
- c has no negative effect on the output parameters;
- ○
- c has a positive effect (meaning that the output parameter increases as c increases) on Qef, Nmax, KLmax, and KFmax.
- Coal angle of internal friction (φ):
- ○
- φ has a negative effect (meaning that the output parameter decreases as φ increases) on (1) Qef, for low values of σp (4.00–4.30 MPa); (2) Imax, for medium-to-high values of h and for medium-to-lower values of V0; (3) Nmax; (4) Pmax, for lower-to-medium values of V0; and (5) KFmax;
- ○
- φ has a positive effect (meaning that the output parameter increases as φ increases) on (1) Qef, for medium values of σp (around 5 MPa); (2) Imax, for lower values of slice height h and higher values of V0; and (3) Pmax, for lower-to-medium values of φ and for higher values of V0.
- Slice height (h):
- ○
- h has a negative effect (meaning that the output parameter decreases as h increases) on Imax, Nmax, and Pmax (for higher values of φ and for lower-to-medium values of φL);
- ○
- h has a positive effect (meaning that the output parameter decreases as h increases) on Qef; Pmax (for lower values of σp and for lower-to-medium values of φ, and for higher values of φL); Emax; KLmax, except for the high values of φD; and KFmax.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gordon, L.R. World Coal. Economics, Policies and Prospects; Cambridge University Press: London, UK, 1987. [Google Scholar]
- Available online: https://ember-climate.org/data-catalogue/yearly-electricity-data/ (accessed on 15 August 2023).
- Available online: https://ember-climate.org/insights/research/european-electricity-review-2022/ (accessed on 15 August 2023).
- Available online: https://www.energyinst.org/statistical-review/ (accessed on 15 August 2023).
- Ritchie, H. The Death of UK Coal in Five Charts. Available online: https://ourworldindata.org/death-uk-coal (accessed on 8 August 2023).
- Liu, X.; Li, L.; Yang, Y. Development status of coal mining in China. J. South. African Inst. Min. Metal. 2023, 123, 19–28. [Google Scholar] [CrossRef]
- Vujić, S. (Ed.) Serbian Mining and Geology in the Second Half of the XX Century; Academy of Engineering Science of Serbia, Matica Srpska and Mining Institute: Belgrade, Serbia, 2014. (In Serbian) [Google Scholar]
- Andraș, A.; Radu, S.M.; Brînaș, I.; Popescu, F.D.; Budilică, D.I.; Korozsi, E.B. Prediction of Material Failure Time for a Bucket Wheel Excavator Boom Using Computer Simulation. Materials 2021, 14, 7897. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Liao, G.; Zhu, S.; Hu, Y. Investigation on Cutting Resistance Characteristic of Bucket Wheel Excavator Using DEM and DOE Methods. Simul. Model. Pract. Theory 2021, 111, 102339. [Google Scholar]
- Popescu, F.D.; Radu, S.M.; Kotwica, K.; Andraș, A.; Kertesz, I. Simulation of the Time Response of the ERc 1400-30/7 Bucket Wheel Excavator’s Boom during the Excavation Process. Sustainability 2019, 11, 4357. [Google Scholar] [CrossRef]
- Sowała, M.; Strempski, A.; Woźniak, J.; Pactwa, K. Impact of the Length of Manoeuvering Roads of a Bucket Wheel Excavator for Working Times in the Shortwall. J. Min. Sci. 2019, 55, 603–609. [Google Scholar] [CrossRef]
- Machniak, L.; Kozioł, W. Method of assessment of hard rock workability using bucket wheel excavators. Arch. Min. Sci. 2017, 62, 73–82. [Google Scholar] [CrossRef]
- Bolukbasi, N.; Koncagul, O.; Pasamehmetoglu, A.G. Material diggability studies for the assessment of bucket wheel excavator performance. Min. Sci. Technol. 1991, 13, 271–277. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Y. Determination and analysis of the theoretical production of a bucket wheel excavator. Arch. Min. Sci. 2014, 59, 283–291. [Google Scholar]
- Xiang, Y.; Mutschler, S.; Brix, N.; Brach, C.; Geimer, M. Optimization of Operation Strategy for Primary Torque based Hydrostatic Drivetrain using Artificial Intelligence. arXiv 2020, arXiv:2003.10011. [Google Scholar]
- Xiang, Y.; Tang, T.; Su, T.; Brach, C.; Liu, L.; Mao, S.S.; Geimer, M. Fast CRDNN: Towards on Site Training of Mobile Construction Machines. IEEE Access 2021, 9, 124253–124267. [Google Scholar] [CrossRef]
- Kostić, S.; Trivan, J. Optimization of coal overburden excavation considering variable geomechanical properties and states of excavator teeth. Arch. Min. Sci. 2022, 67, 123–142. [Google Scholar]
- Ignjatović, D. Study on Optimization of the Construction of Buckets of the Buecket-Wheel Excavator in Order to Increase the Capacity of the Excavator; University of Belgrade Faculty of Mining and Geology: Belgrade, Serbia, 2003; p. 218. (In Serbian) [Google Scholar]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363, eaau032. [Google Scholar] [CrossRef] [PubMed]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Mignan, A.; Broccardo, M. Neural network applications in earthquake prediction (1994–2019): Meta-analytic and statistical insights on their limitations. Seismol. Res. Lett. 2020, 91, 2330–2342. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, Sardinia, Italy, 13 May 2010; pp. 249–256. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Zeiler, M.D. Adadelta: An adaptive learning rate method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the COMPSTAT’2010: 19th International Conference on Computational Statistics, Paris, France, 22–27 August 2010; Keynote, Invited and Contributed Papers. pp. 177–186. [Google Scholar]




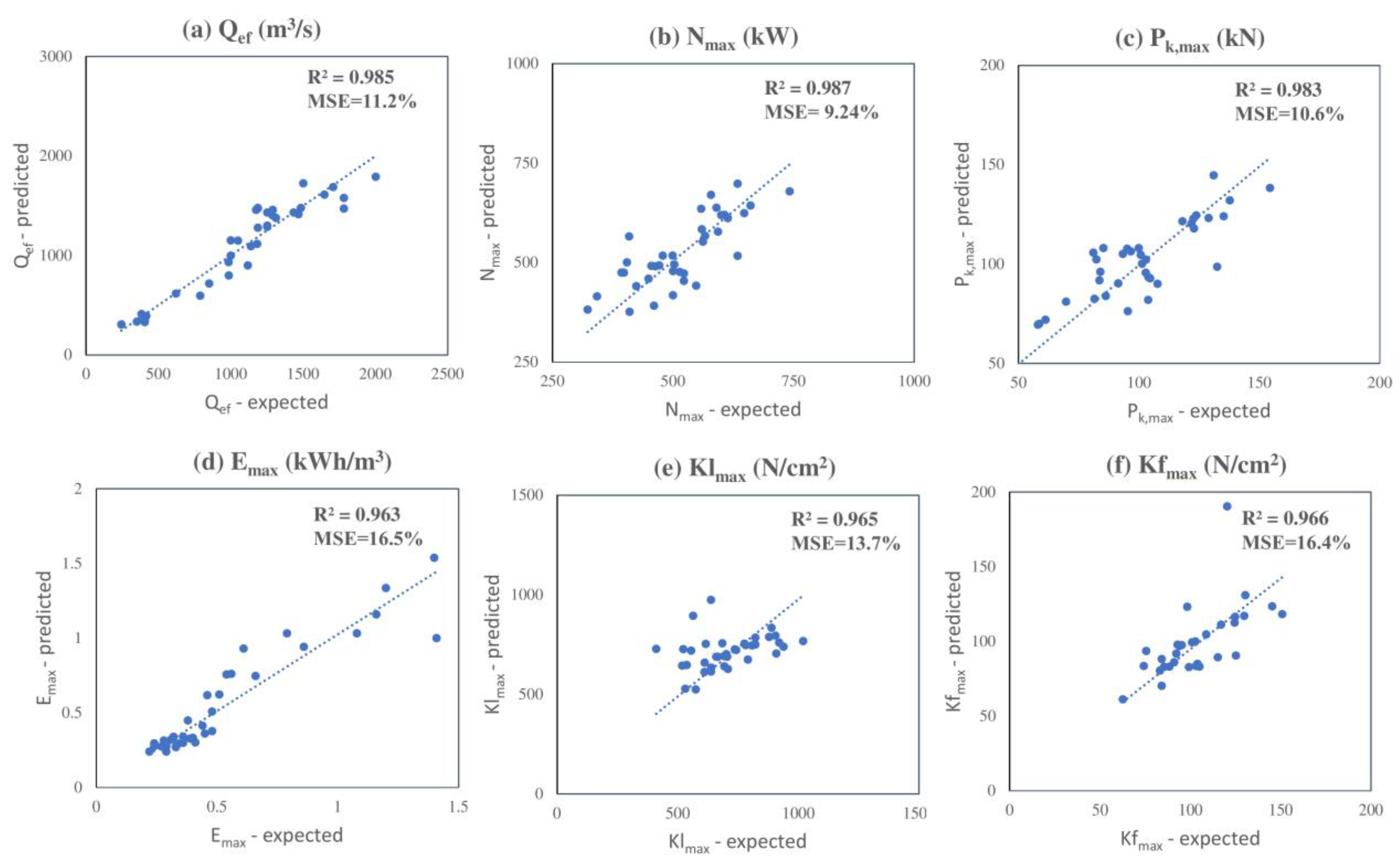
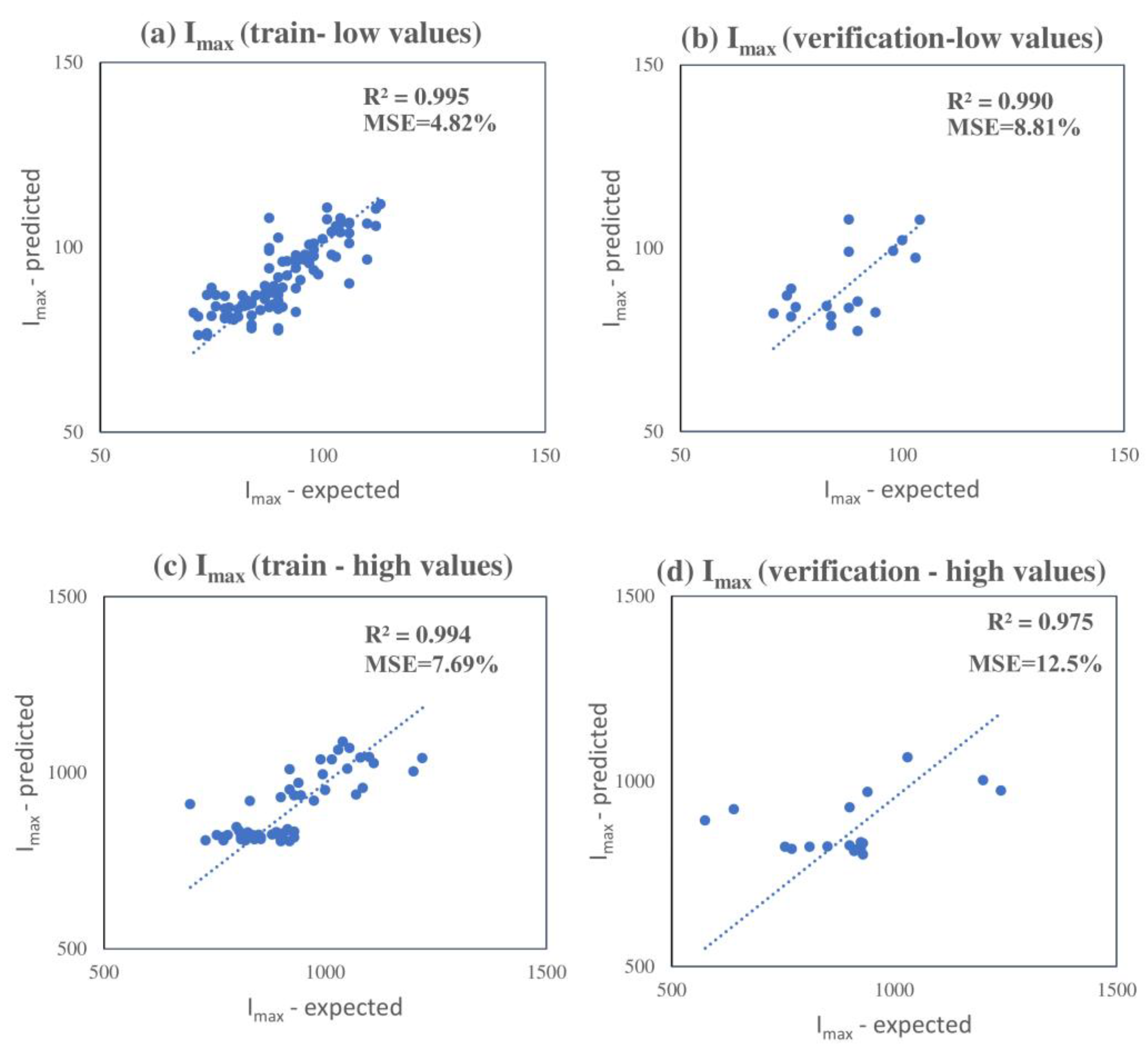
| Output Factors | Range of Values |
| Qef, effective capacity (m3/h) | 239.3–1782 |
| Imax, maximum current consumption (A) | 25–1335 |
| Nmax, maximum power consumption (kW) | 314.8–755.5 |
| Pmax, maximum force consumption (kN) | 48.1–176.4 |
| Emax, maximum energy consumption (kWh/m3) | 0.16–1.77 |
| KLmax, maximum linear cutting resistance (N/cm) | 403.7–1276.7 |
| KFmax, maximum areal cutting resistance (N/cm2) | 43–285 |
| Input Factors | Range of Values |
| γ, coal unit weight (kN/m3) | 11.32–12.73 |
| σp, coal compressive strength (MPa) | 4.11–6.26 |
| c, coal cohesion (Mpa) | 0.83–1.67 |
| φ, coal angle of internal friction (°) | 38.27–48.39 |
| φL, excavator movement angle in the left direction (°) | −76–90 |
| φD, excavator movement angle in the right direction (°) | −76–90 |
| h, slice height (m) | 2.8–5.5 |
| s, slice thickness (m) | 0.15–3.0 |
| V0, velocity of the rotary movement of the excavator (m/min) | 6–22 |
| Significant Input Factors (p < 0.0001) | Output Factors |
|---|---|
| φL × V0 | Nmax, Pmax, Emax, KLmax |
| φD× V0 | Nmax, Emax, KLmax, Pmax |
| σp × φL | Qef, Imax, KLmax |
| φL × φD | Qef, Emax |
| c × h | Imax, KLmax |
| φD× h | KLmax, KFmax |
| σp × φD | Imax |
| φD× s, h × s, s × V0 | Emax |
| c × V0 | KLmax |
| σp × V0 | KFmax |
| Optimization Algorithm | MSE (Training) | MSE (Test) |
|---|---|---|
| Adam [26] | 0.0121 | 0.0191 |
| AdaDelta [25] | 0.0434 | 0.0432 |
| SDG [27] | 0.0425 | 0.0431 |
| Model Configuration | MSE (Training) | MSE (Test) |
|---|---|---|
| 512, 256, 128, Adam | 0.0142 | 0.0206 |
| 256, 128, 64, Adam | 0.0121 | 0.0192 |
| 128, 64, 32, Adam | 0.0113 | 0.0198 |
| 64, 32, 16, Adam | 0.0210 | 0.0199 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kostić, S.; Stojković, M.; Ilić, V.; Trivan, J. Deep Neural Network Model for Determination of Coal Cutting Resistance and Performance of Bucket-Wheel Excavator Based on the Environmental Properties and Excavation Parameters. Processes 2023, 11, 3067. https://doi.org/10.3390/pr11113067
Kostić S, Stojković M, Ilić V, Trivan J. Deep Neural Network Model for Determination of Coal Cutting Resistance and Performance of Bucket-Wheel Excavator Based on the Environmental Properties and Excavation Parameters. Processes. 2023; 11(11):3067. https://doi.org/10.3390/pr11113067
Chicago/Turabian StyleKostić, Srđan, Milan Stojković, Velibor Ilić, and Jelena Trivan. 2023. "Deep Neural Network Model for Determination of Coal Cutting Resistance and Performance of Bucket-Wheel Excavator Based on the Environmental Properties and Excavation Parameters" Processes 11, no. 11: 3067. https://doi.org/10.3390/pr11113067
APA StyleKostić, S., Stojković, M., Ilić, V., & Trivan, J. (2023). Deep Neural Network Model for Determination of Coal Cutting Resistance and Performance of Bucket-Wheel Excavator Based on the Environmental Properties and Excavation Parameters. Processes, 11(11), 3067. https://doi.org/10.3390/pr11113067






