A Design Method for Improving the Effect of Shale Interlaced with Limestone Reservoir Reconstruction
Abstract
:1. Introduction
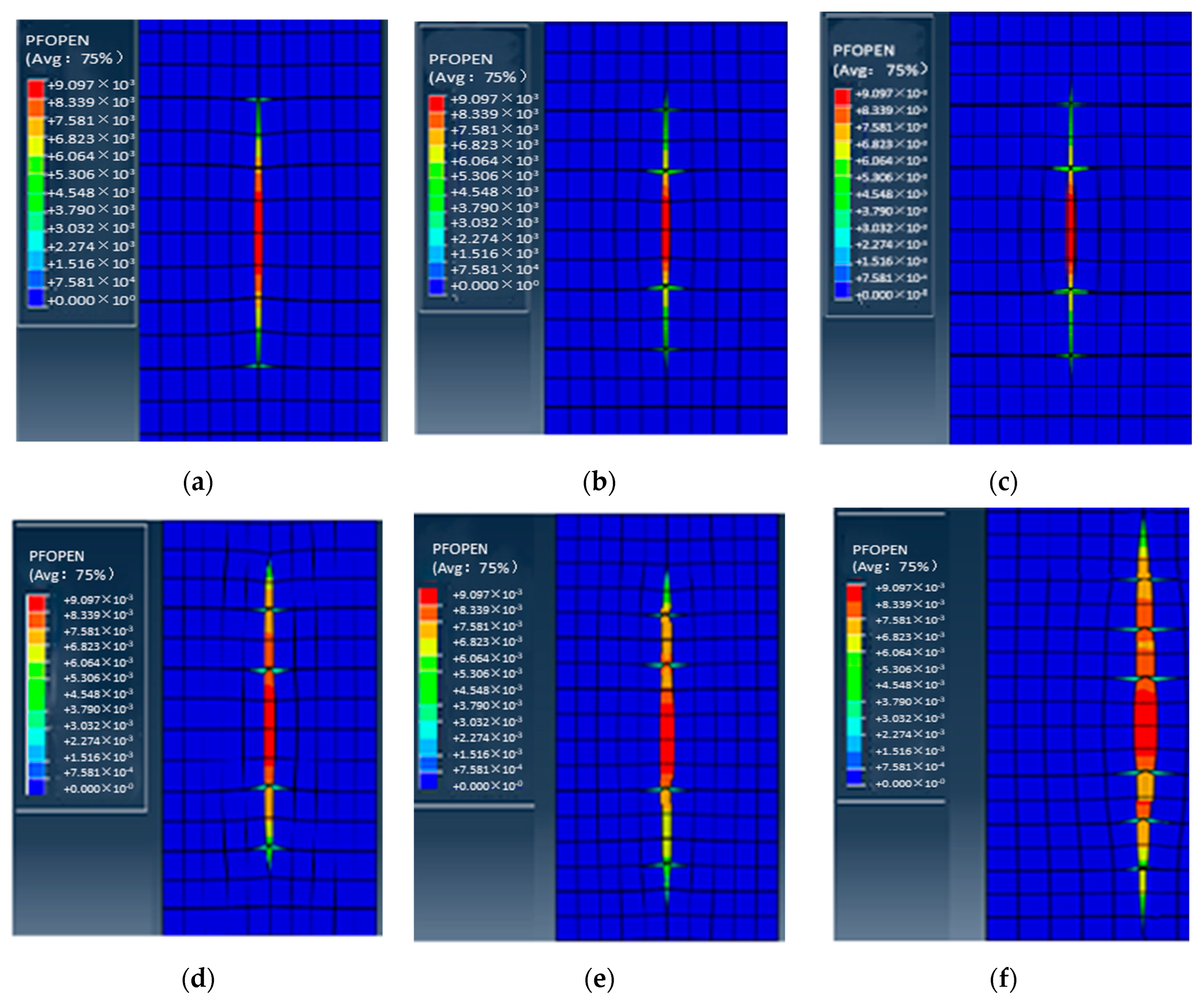
2. Numerical Simulation of Crack Height Expansion
2.1. Geological Factor
2.1.1. Shear Strength of Interlayer Interface
2.1.2. Vertical Stress Difference
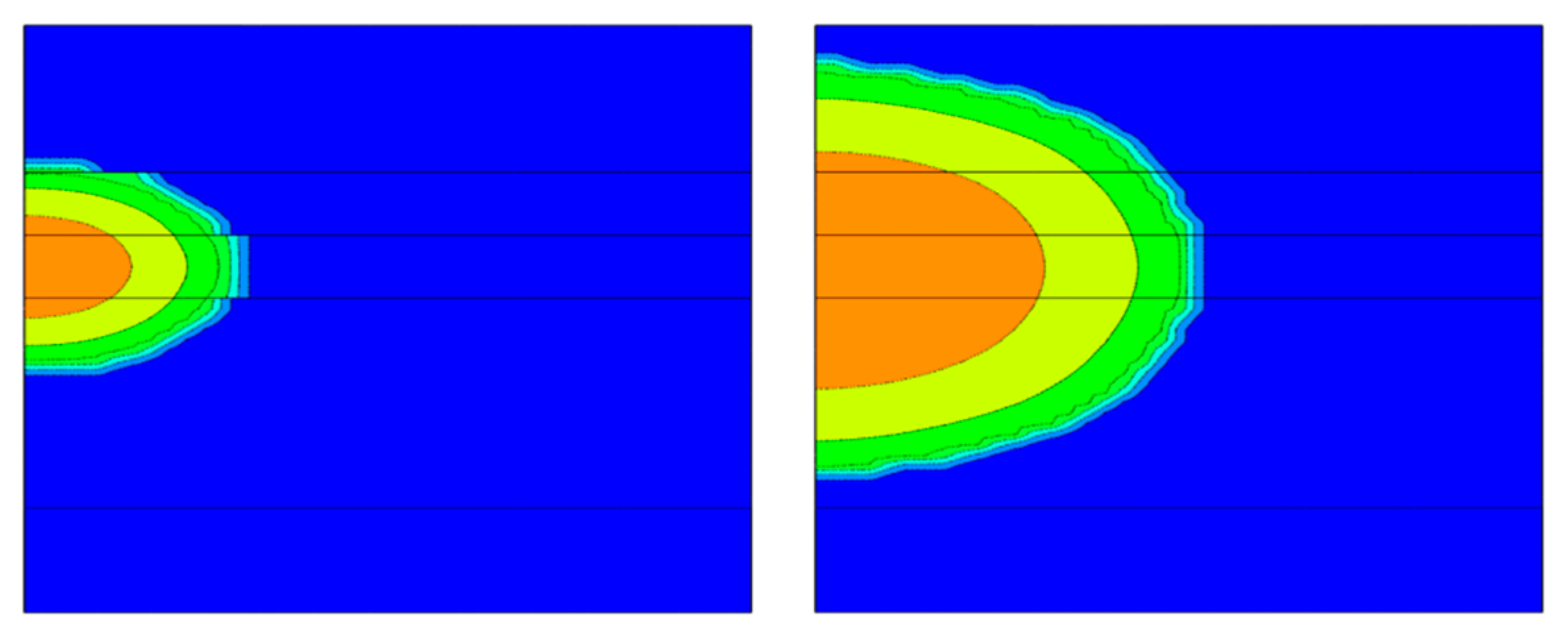
2.1.3. Interlayer Stress Difference
2.1.4. Tensile Strength Difference
2.1.5. Factor Weight
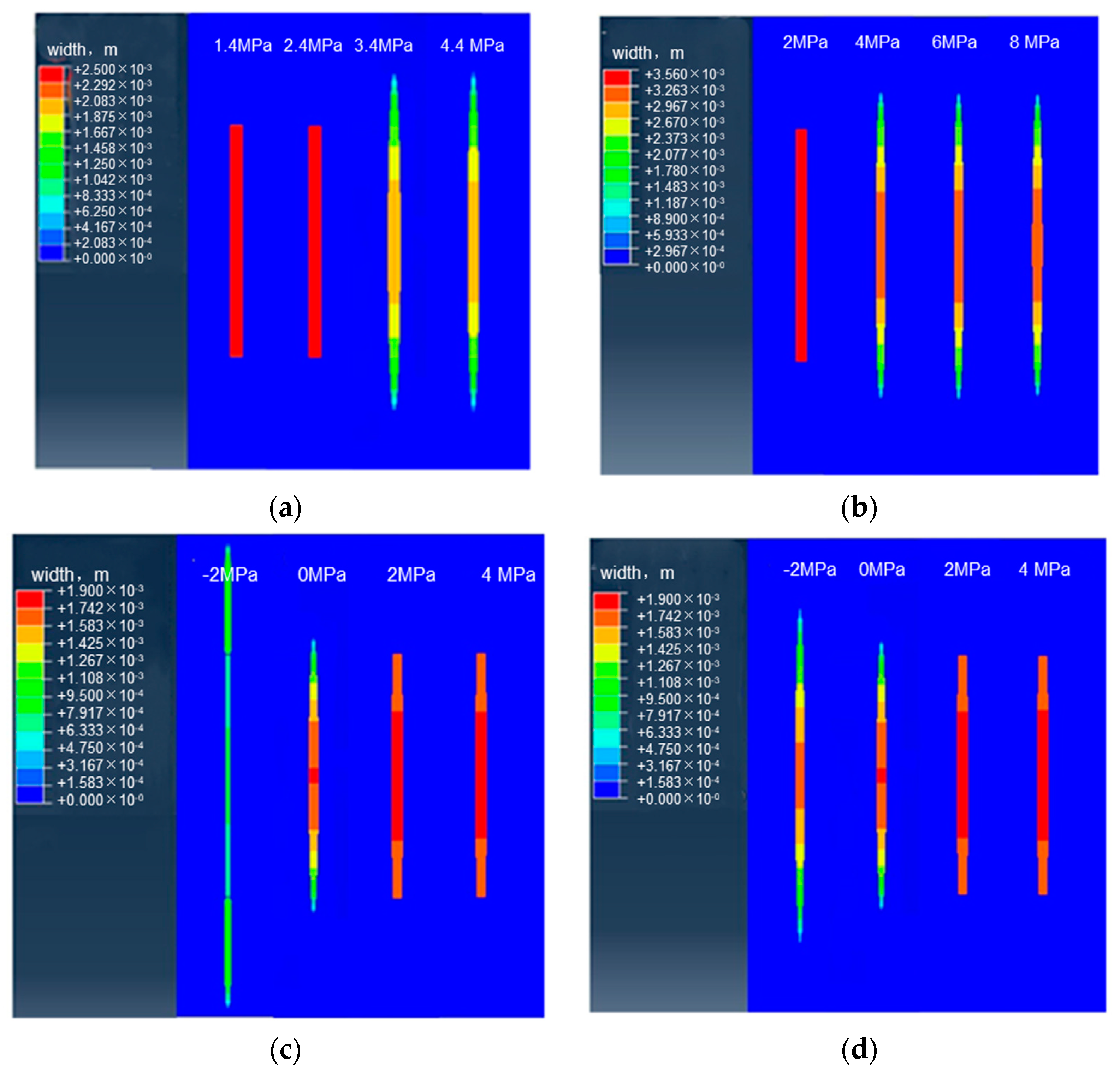
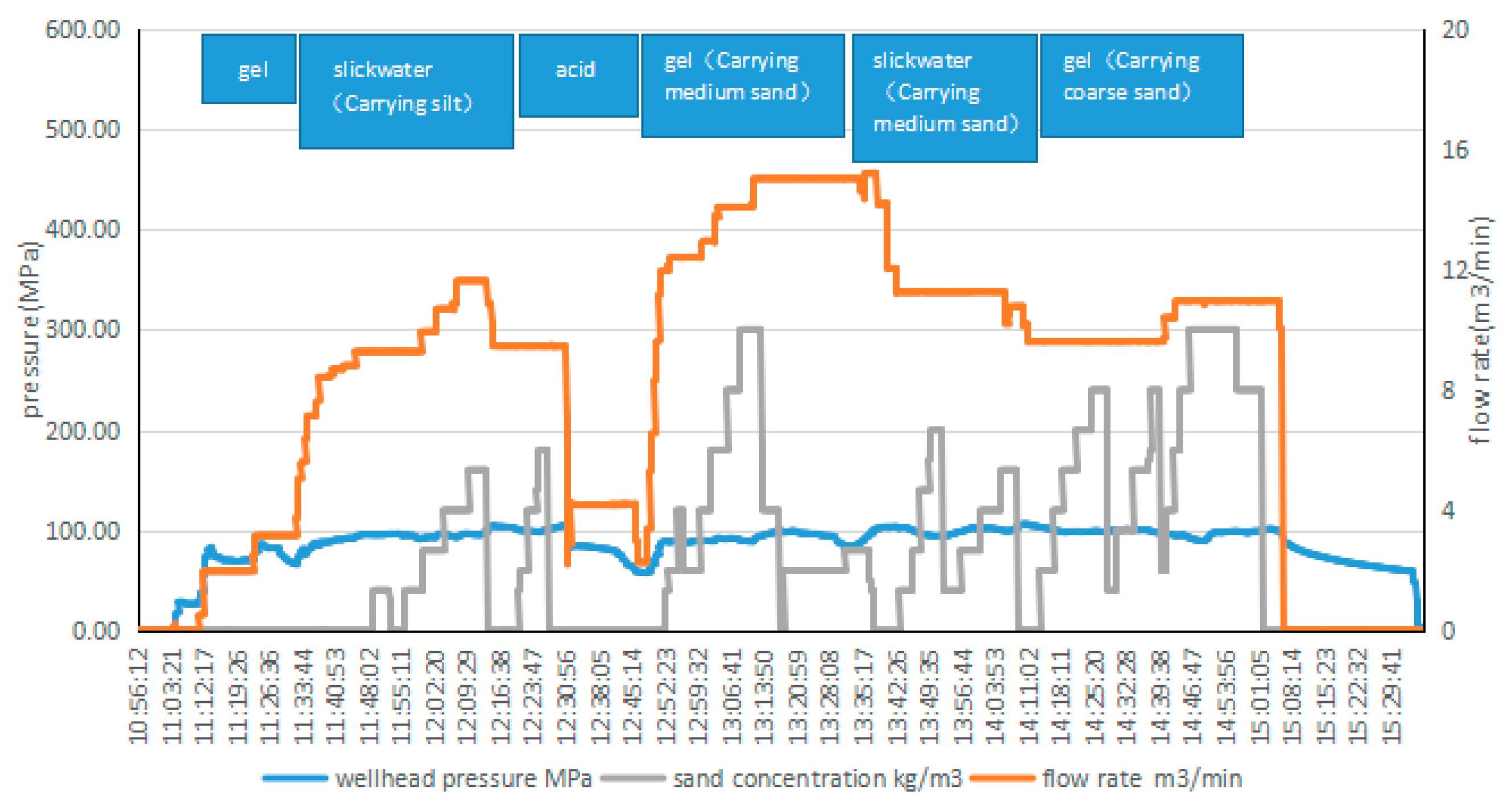
2.2. Construction Displacement
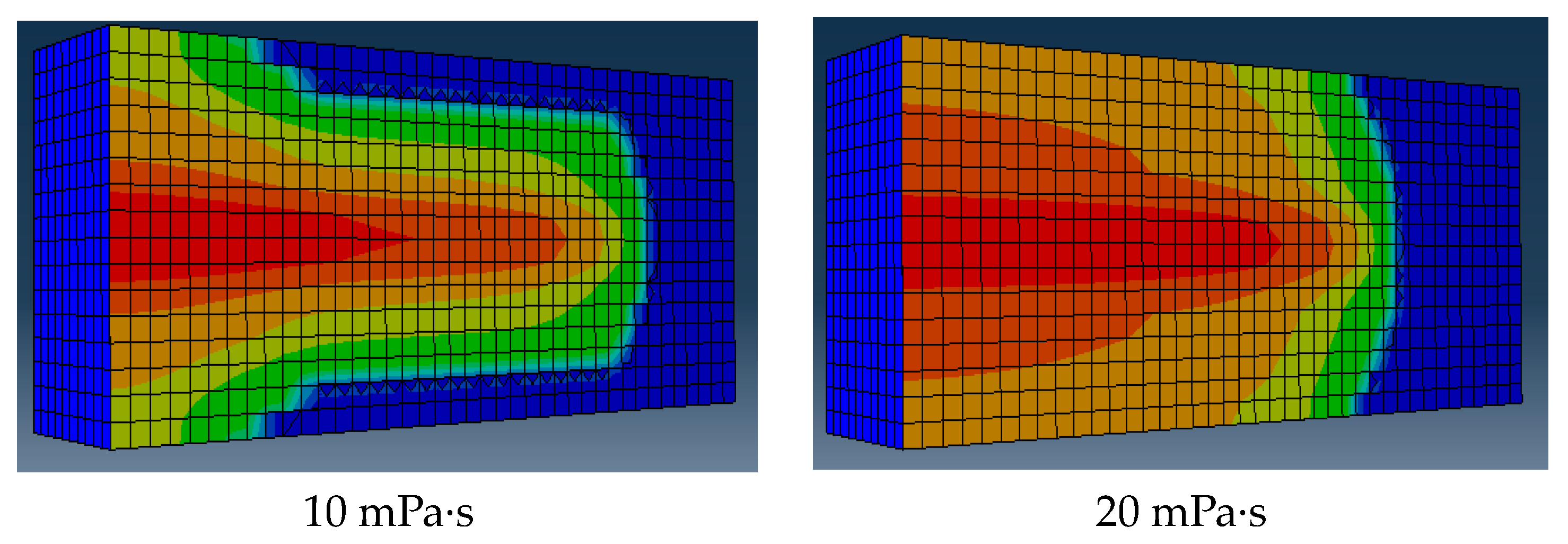
2.3. The Viscosity of Fracturing Fluid
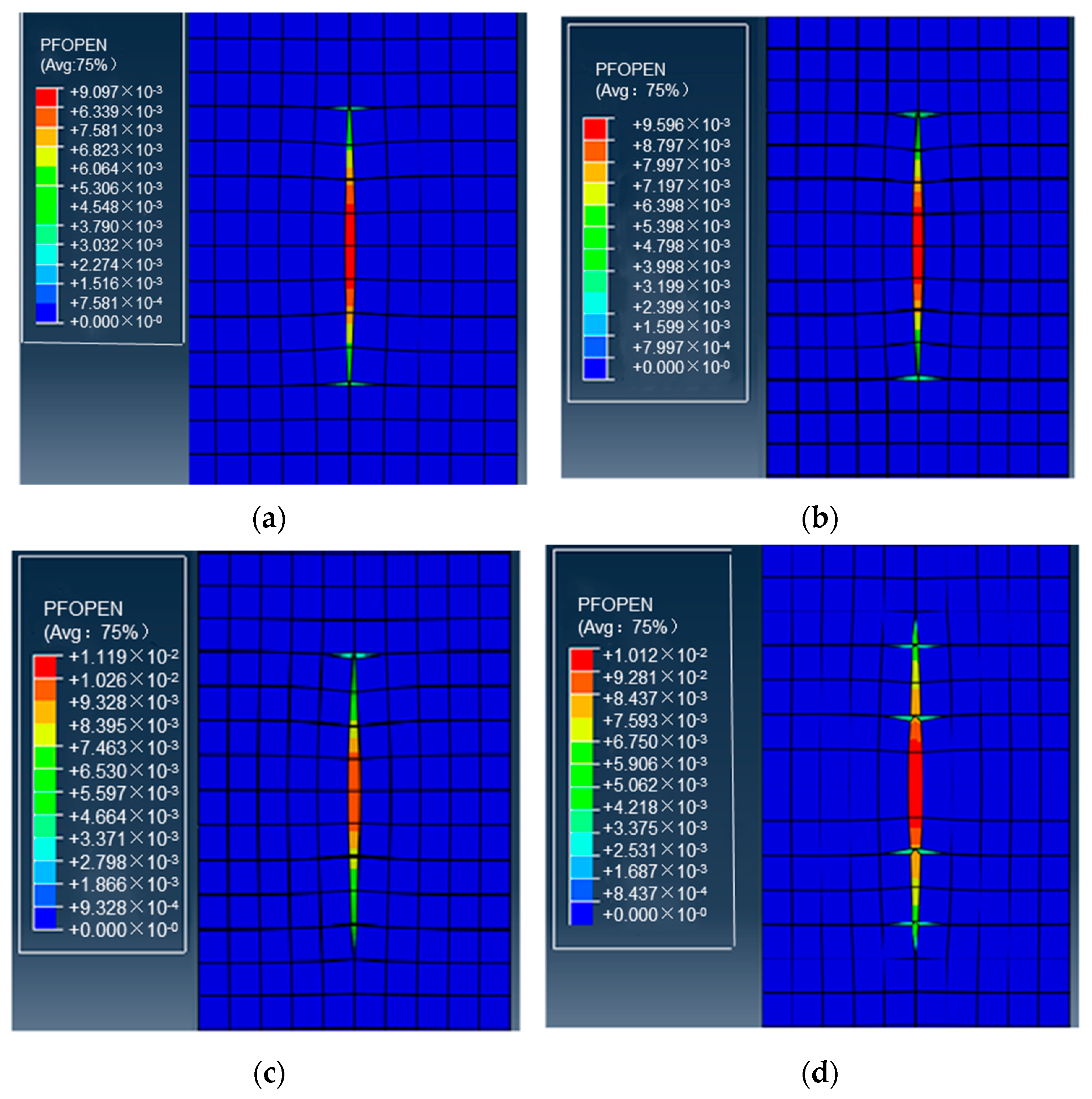
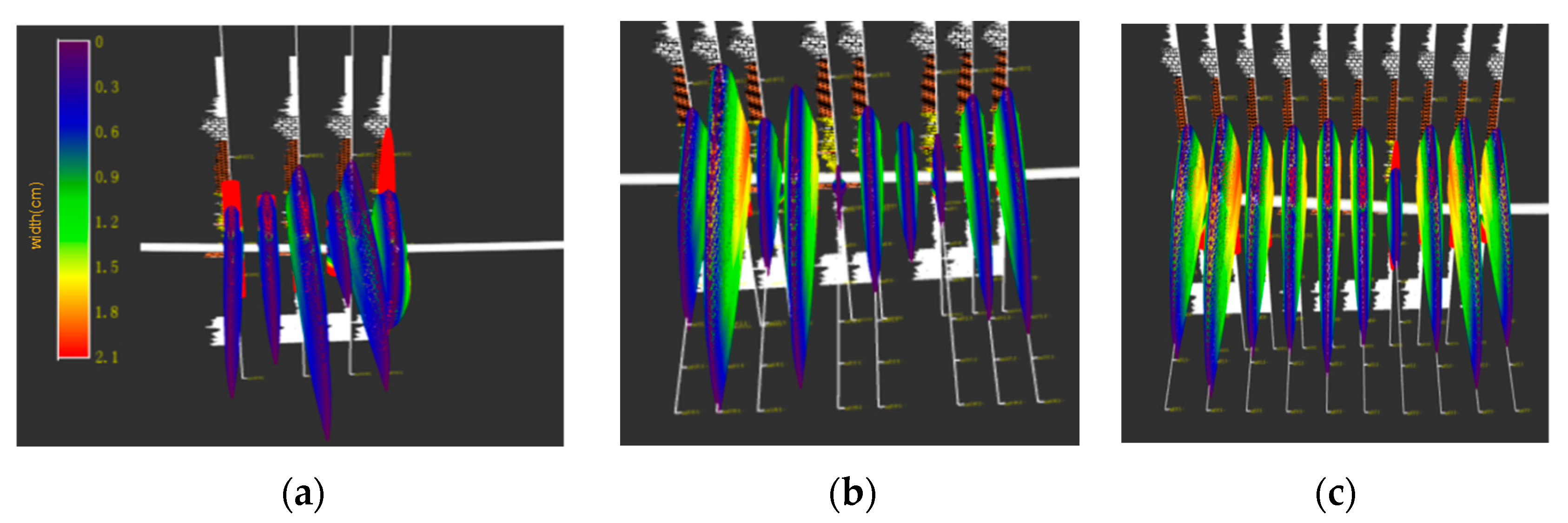
2.4. Simulation of Temporary Blocking and Turning to Fracturing in Horizontal Wells
2.4.1. Simulation of Temporarily Blocked Clusters
2.4.2. Stress Difference Simulation
3. Results
4. Discussion
- (1)
- By employing finite element numerical simulation, this investigation has unveiled the primary factors influencing the longitudinal propagation of interactive lithology, specifically interlayer interface strength and interlayer stress disparity. These findings possess significant implications for comprehending hydraulic fracture propagation in intricate lithological formations.
- (2)
- Currently, the exploration and development of continental shale oil is experiencing a significant surge, but it will encounter numerous challenges in terms of reconstructing intricate lithologic reservoir layers. Therefore, this study holds substantial practical significance.
- (3)
- The propagation of longitudinal fractures in shale oil reservoirs containing interbedded shale and limestone formations is highly intricate. The author strongly advocates for further comprehensive research, combined with large-scale model experiments, to delve more deeply into this complex phenomenon.
- (4)
- This study aims to optimize the parameters for temporary plugging through numerical simulation. However, it is important to note that the temporary plugging process requires a more systematic investigation. Further research on the temporary plugging machine and evaluation of its effectiveness are necessary.
5. Conclusions
- (1)
- The reservoir consisted of shale and limestone, with the Young’s modulus and stress of the limestone layer being notably higher than those of the shale layer. In the initial stage, a slack-water volume fracturing process was employed, resulting in significant inhibition of the fracture height.
- (2)
- Finite element numerical simulation revealed that the longitudinal propagation of hydraulic fractures is influenced by interlayer interface strength, interlayer stress differential, fracturing displacement, and viscosity.
- (3)
- The results of the numerical simulation demonstrated the indispensability of employing a combination of substantial displacement and pre-viscous liquid in order to accomplish longitudinal penetration.
- (4)
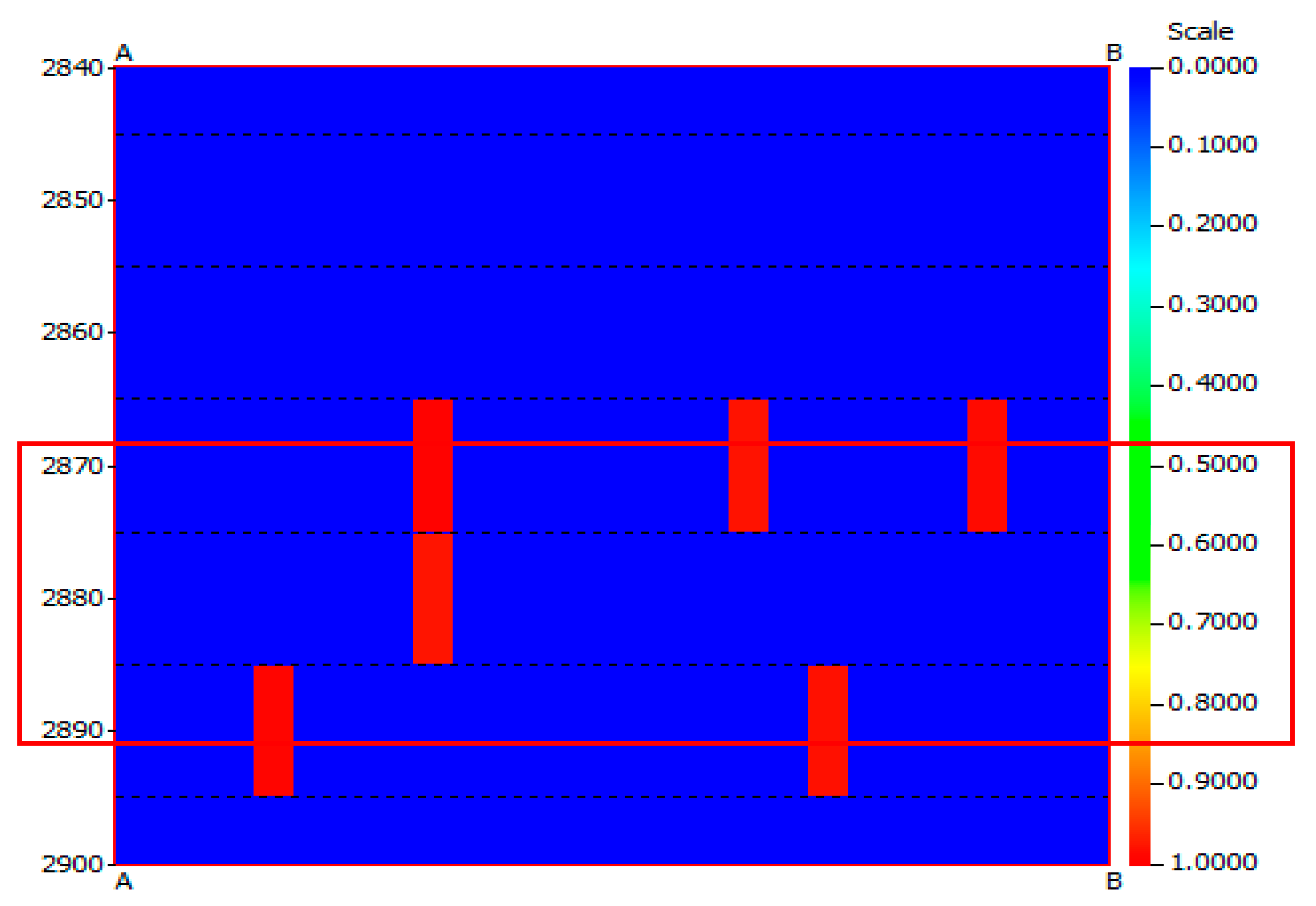
- Horizontal wells exhibit significant heterogeneity, posing challenges in terms of achieving uniform hydraulic fracture propagation. Through the implementation of a temporary plugging process, approximately 40% of the perforations were effectively obstructed, facilitating the even expansion of multiple fracture clusters.
- (5)
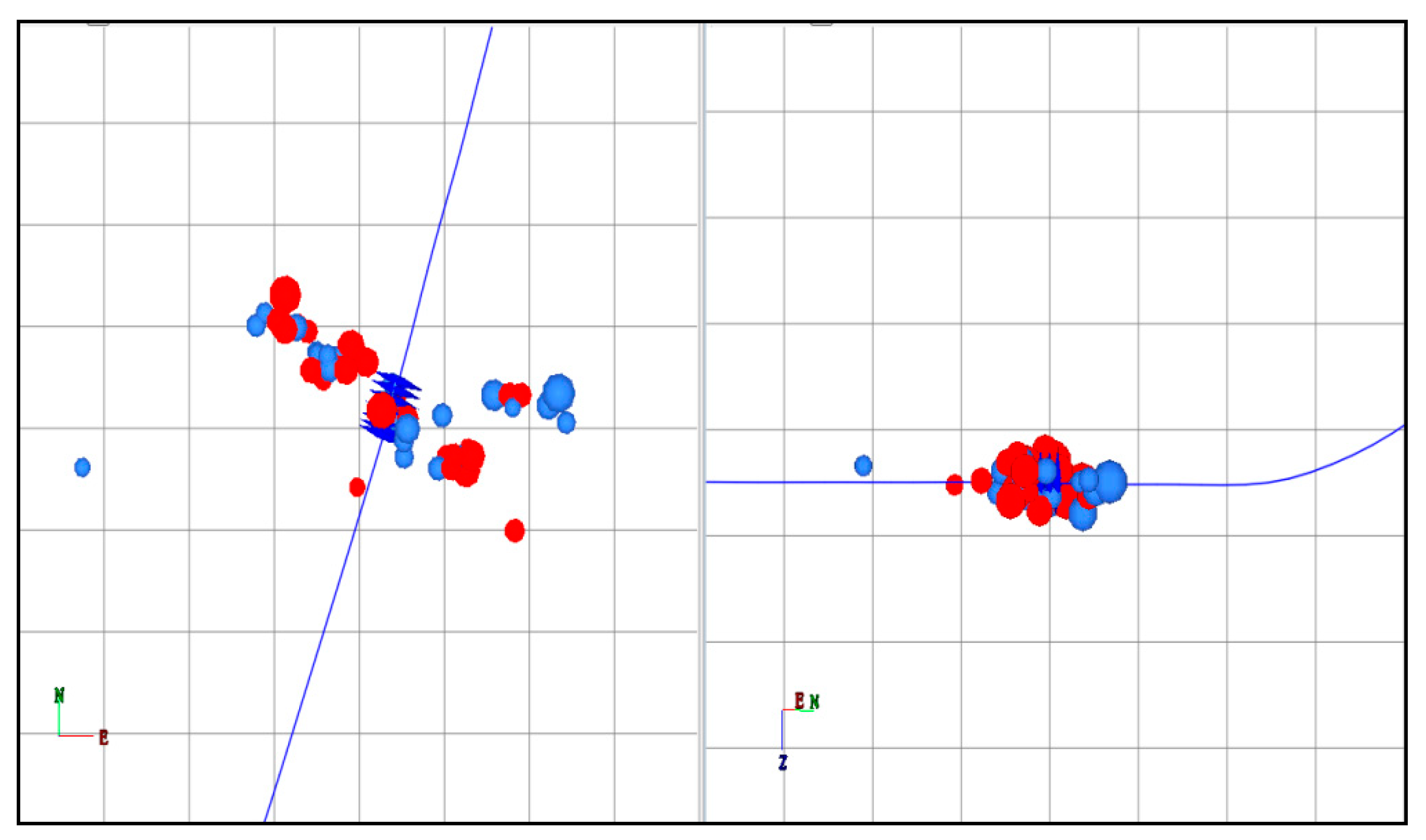
- The application results demonstrated the successful implementation of the perforating fracturing process in the Qiulin 22 well. The monitoring results confirmed the effectiveness of this recommended procedure, thereby validating its reliability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, Y.; Zhang, S.; Ma, X.; Zhang, X.; Zhang, S. Hydraulic fracture morphology and conductivity of continental shale under the true-triaxial stress conditions. Fuel 2023, 352, 129056. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Hou, B.; Yuan, L.; Xiong, Z. Experimental investigation of hydraulic fracturing for multi-type unconventional gas co-exploitation in Ordos basin. Arab. J. Sci. Eng. 2019, 44, 10503–10511. [Google Scholar] [CrossRef]
- Hou, B.; Wu, A.; Chang, Z.; You, Y.; Kou, X.; Zhang, F. Experimental study on vertical propagation of fractures of multi-sweet of spots shale oil reservoir. Chin. J. Geotech. Eng. 2021, 43, 1322–1330. [Google Scholar]
- Wang, Y.; Hou, B.; Wang, D.; Jia, Z. Features of fracture height propagation in cross-layer fracturing of shale oil reservoirs. Pet. Explor. Dev. 2021, 48, 469–479. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Y.; Wang, S.; Jiang, Y.; Zhang, L. Simulation of complex fracture networks influenced by natural fractures in shale gas reservoir. Nat. Gas Ind. B 2014, 1, 89–95. [Google Scholar]
- Guo, J.; Luo, B.; Lu, C.; Lai, J.; Ren, J. Numerical investigation of hydraulic fracture propagation in a layered reservoir using the cohesive zone method. Eng. Fract. Mech. 2017, 186, 195–207. [Google Scholar] [CrossRef]
- Huang, L.; Liu, J.; Zhang, F.; Dontsov, E.; Damjanac, B. Exploring the influence of rock inherent heterogeneity and grain size on hydraulic fracturing using discrete element modeling. Int. J. Solids Struct. 2019, 176, 207–220. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Sheng, Q.; Fu, X.D. Numerical simulation of fracture propagation of heterogeneous material. Appl. Mech. Mater. 2012, 170, 581–584. [Google Scholar] [CrossRef]
- Paluszny, A.; Zimmerman, R.W. Numerical simulation of multiple 3D fracture propagation using arbitrary meshes. Comput. Methods Appl. Mech. Eng. 2011, 200, 953–966. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, Z. Composite stimulation technology for improving fracture length and conductivity of unconventional reservoirs. Front. Phys. 2023, 11, 1181302. [Google Scholar] [CrossRef]
- Li, J.; Dong, S.; Hua, W.; Li, X.; Pan, X. Numerical investigation of hydraulic fracture propagation based on cohesive zone model in naturally fractured formations. Processes 2019, 7, 28. [Google Scholar] [CrossRef]
- Shi, X.; Qin, Y.; Xu, H.; Xu, H.; Feng, Q.; Wang, S.; Xu, P.; Han, S. Numerical simulation of hydraulic fracture propagation in conglomerate reservoirs. Eng. Fract. Mech. 2021, 248, 107738. [Google Scholar] [CrossRef]
- Shou, Y.; Zhou, X.; Berto, F. 3D numerical simulation of initiation, propagation and coalescence of cracks using the extended non-ordinary state-based peridynamics. Theor. Appl. Fract. Mech. 2019, 101, 254–268. [Google Scholar] [CrossRef]
- Fei, Y. Rock fracture toughness during hydraulic fracture extension. J. Rock Mech. Eng. 2004, 14, 2346–2350. [Google Scholar]
- Jiang, T. Research and application prospect of fracture complexity index for shale oil and gas horizontal wells. Pet. Drill. Technol. 2013, 2, 7–12. [Google Scholar]
- Chen, M.; Pang, F.; Jin, Y. Simulation and analysis of large-scale true triaxial hydraulic fracturing. J. Rock Mech. Eng. 2000, z1, 868–872. [Google Scholar]
- Hou, Z.; Cheng, H.; Sun, S.; Chen, J.; Qi, D.; Liu, Z. Study on hydraulic fracturing and fracture propagation law in rocks with different lithology. Appl. Geophys. 2019, 2, 243–251+255. [Google Scholar] [CrossRef]
- Zhou, T.; Wang, H.; Li, F.; Li, Y.; Zou, Y.; Zhang, C. Numerical simulation of hydraulic fracture propagation in laminated shale reservoirs. Pet. Explor. Dev. 2020, 47, 1117–1130. [Google Scholar] [CrossRef]
- Yang, W.; Geng, Y.; Zhou, Z.; Li, L.P.; Gao, C.L.; Wang, M.X.; Zhang, D.S. DEM numerical simulation study on fracture propagation of synchronous fracturing in a double fracture rock mass. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 39. [Google Scholar] [CrossRef]
- Taleghani, A.D.; Gonzalez-Chavez, M.; Yu, H.; Asala, H. Numerical simulation of hydraulic fracture propagation in naturally fractured formations using the cohesive zone model. J. Pet. Sci. Eng. 2018, 165, 42–57. [Google Scholar] [CrossRef]
- Wang, S.; Li, H.; Li, D. Numerical simulation of hydraulic fracture propagation in coal seams with discontinuous natural fracture networks. Processes 2018, 6, 113. [Google Scholar] [CrossRef]
- Zhang, B.; Ji, B.; Liu, W. The study on mechanics of hydraulic fracture propagation direction in shale and numerical simulation. Geomech. Geophys. Geo-Energy Geo-Resour. 2018, 4, 119–127. [Google Scholar] [CrossRef]
- Liu, W.; Zeng, Q.; Yao, J. Numerical simulation of elasto-plastic hydraulic fracture propagation in deep reservoir coupled with temperature field. J. Pet. Sci. Eng. 2018, 171, 115–126. [Google Scholar] [CrossRef]
- Sun, C.; Zheng, H.; Liu, W.D.; Lu, W. Numerical simulation analysis of vertical propagation of hydraulic fracture in bedding plane. Eng. Fract. Mech. 2020, 232, 107056. [Google Scholar] [CrossRef]
- Bakhshi, E.; Golsanami, N.; Chen, L. Numerical modeling and lattice method for characterizing hydraulic fracture propagation: A review of the numerical, experimental, and field studies. Arch. Comput. Methods Eng. 2021, 28, 3329–3360. [Google Scholar] [CrossRef]
- Hossain, M.M.; Rahman, M.K. Numerical simulation of complex fracture growth during tight reservoir stimulation by hydraulic fracturing. J. Pet. Sci. Eng. 2008, 60, 86–104. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J. Numerical simulation of fracture network generation in naturally fractured reservoirs. J. Nat. Gas Sci. Eng. 2016, 30, 430–443. [Google Scholar] [CrossRef]
- Sanchez, E.C.M.; Cordero, J.A.R.; Roehl, D. Numerical simulation of three-dimensional fracture interaction. Comput. Geotech. 2020, 122, 103528. [Google Scholar] [CrossRef]
- Wen, M.; Huang, H.; Hou, Z.; Wang, F.; Qiu, H.; Ma, N.; Zhou, S. Numerical simulation of the non-Newtonian fracturing fluid influences on the fracture propagation. Energy Sci. Eng. 2022, 10, 404–413. [Google Scholar] [CrossRef]
- Guo, T.; Qu, Z.; Gong, F.; Wang, X. Numerical simulation of hydraulic fracture propagation guided by single radial boreholes. Energies 2017, 10, 1680. [Google Scholar] [CrossRef]
- Ju, Y.; Wang, Y.; Xu, B.; Chen, J.; Yang, Y. Numerical analysis of the effects of bedded interfaces on hydraulic fracture propagation in tight multilayered reservoirs considering hydro-mechanical coupling. J. Pet. Sci. Eng. 2019, 178, 356–375. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, Y.; Yu, Z.; Hu, Z.; Yang, Y. An investigation on hydraulic fracturing characteristics in granite geothermal reservoir. Eng. Fract. Mech. 2020, 237, 107252. [Google Scholar] [CrossRef]

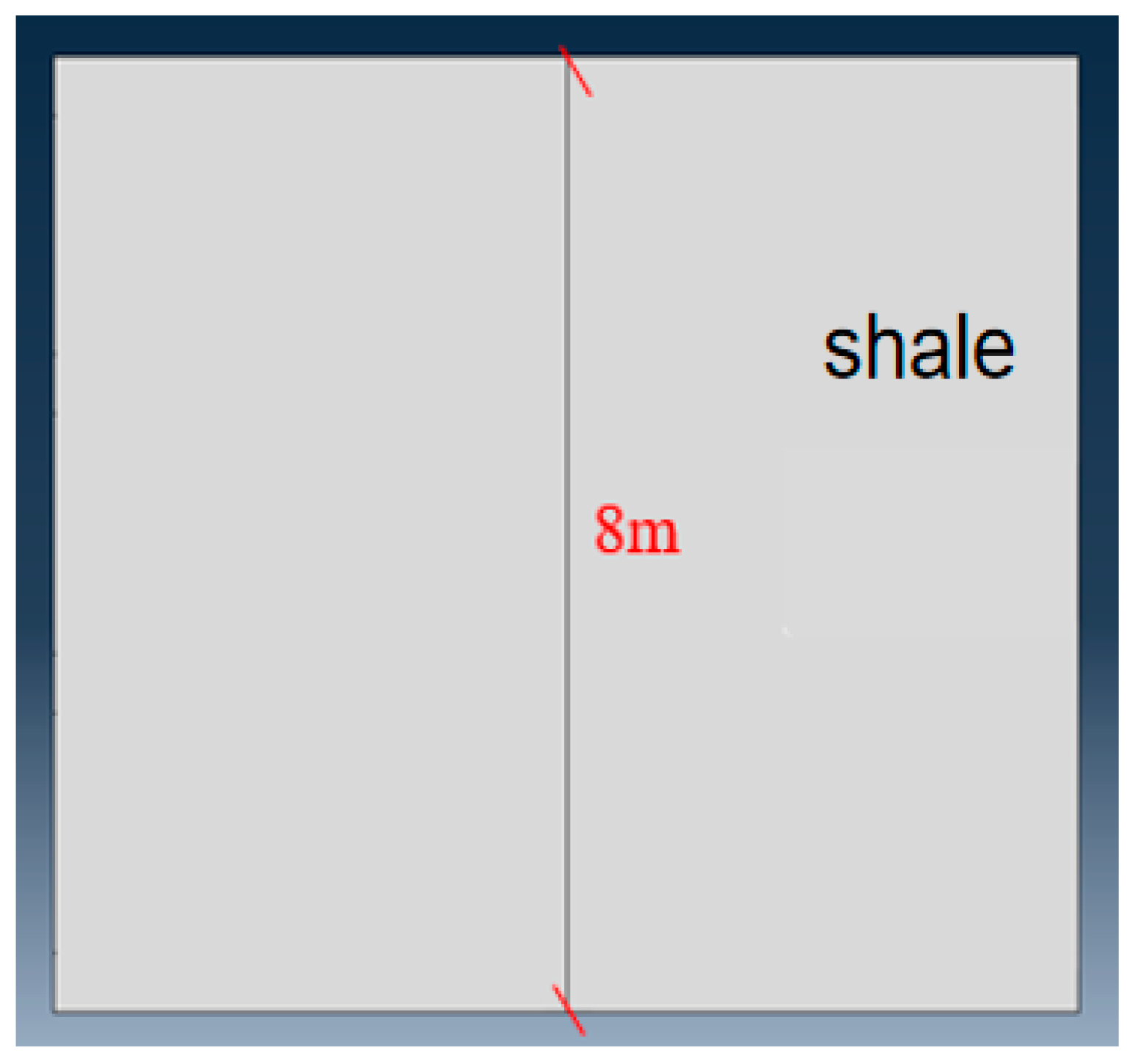

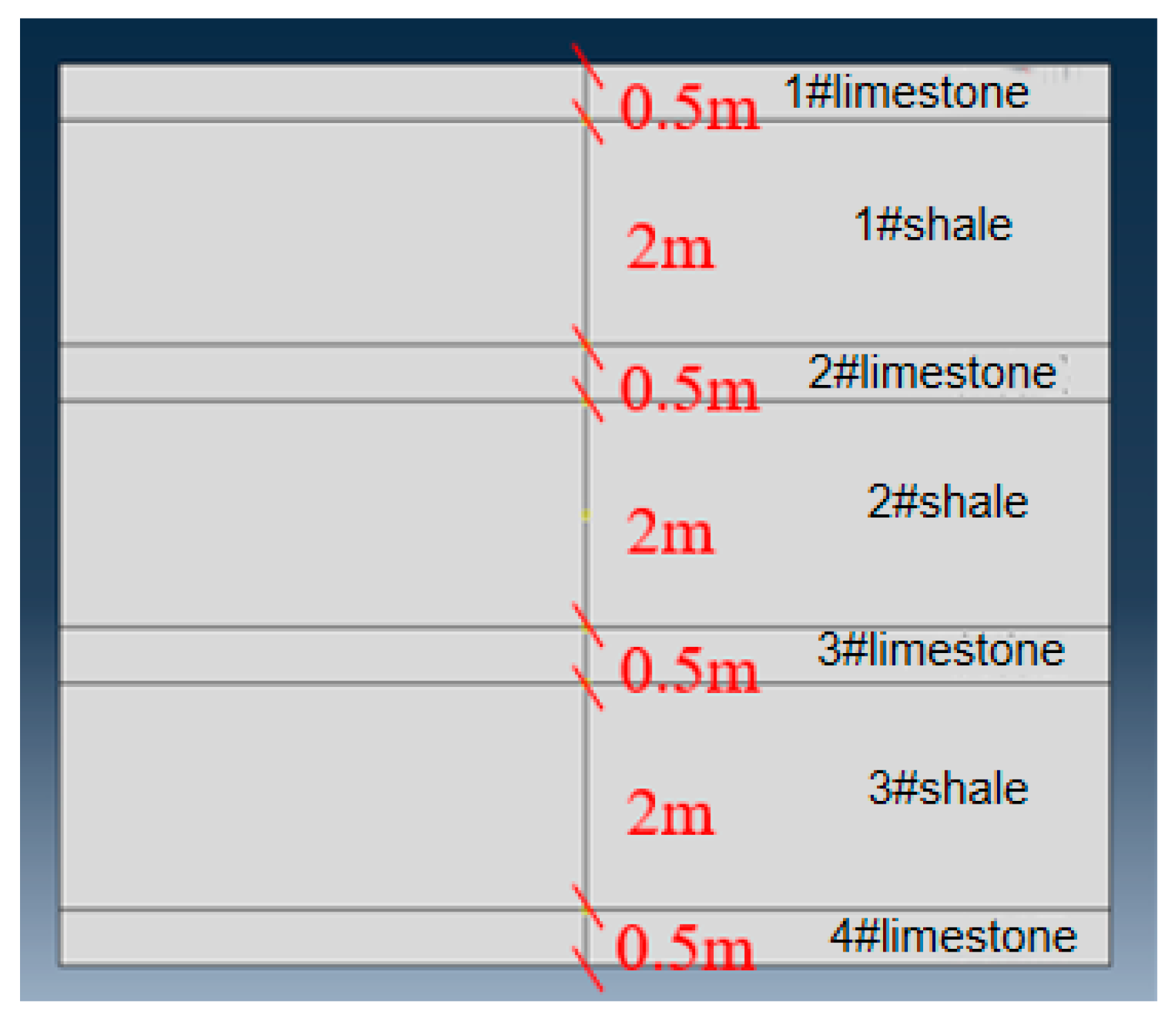
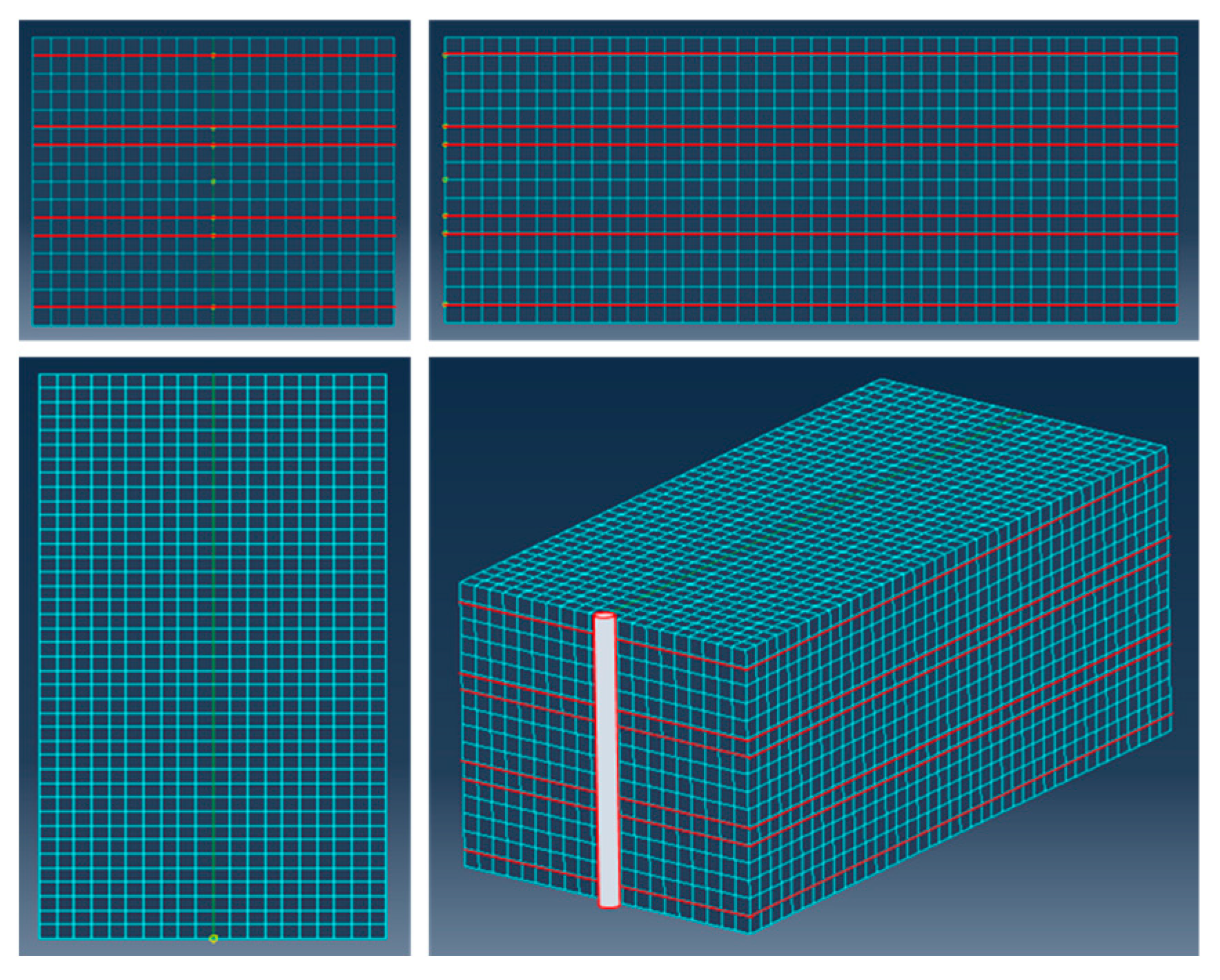
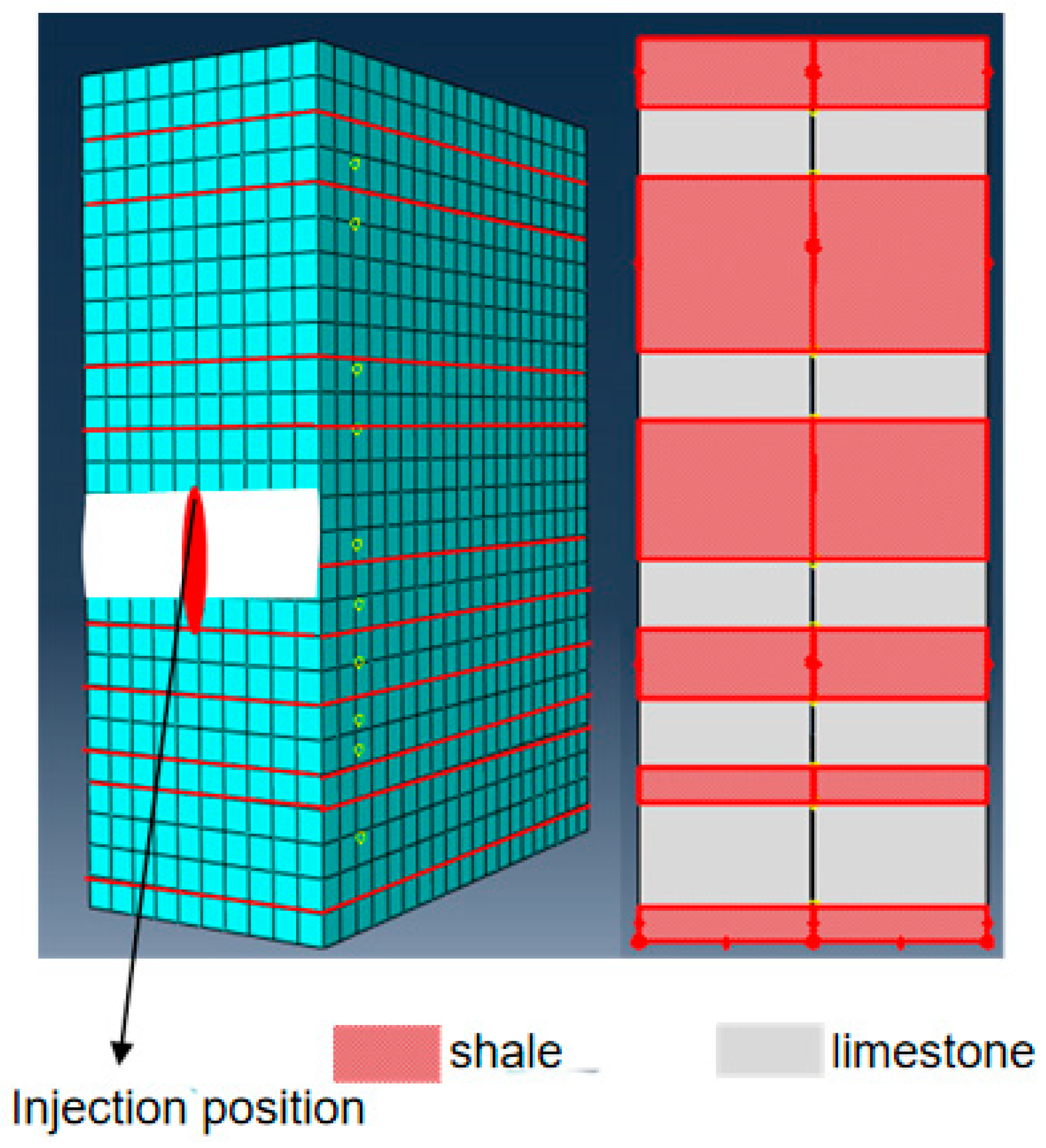





| Well | Lithology | Maximum Horizontal Principal Stress MPa | Minimum Horizontal Principal Stress MPa | Vertical Stress MPa | Coefficient of Stress Difference |
|---|---|---|---|---|---|
| Nanchong 2H | Shale | 74.7 | 62.23 | 64.22 | 0.2 |
| Longan1 | Shale | 81.6 | 71.98 | 89.05 | 0.13 |
| limestone | 94.2 | 81.5 | 89.6 | 0.16 | |
| Renan1 | Shale | 51.74 | 43.7 | 62.7 | 0.18 |
| limestone | 67.05 | 56.2 | 62.8 | 0.19 |
| Well | Lithology | Depth m | Compressive Strength MPa | Young’s Modulus 104 MPa | Poisson’s Ratio |
|---|---|---|---|---|---|
| Longan1 | limestone | 3485.72~3485.95 | 325.1 | 4.74 | 0.28 |
| Shale | 3505.58~3505.68 | 214.8 | 2.25 | 0.23 | |
| limestone | 3508.17~3508.33 | 187.4 | 2.92 | 0.2 | |
| 3514.27~3514.45 | 210.1 | 4.29 | 0.31 | ||
| Renan1 | Shale | 2453.13~2453.44 | 130.84 | 2.236 | 0.182 |
| Shale | 2456.69~2456.90 | 140.03 | 2.005 | 0.234 | |
| 141.88 | 2.137 | 0.329 | |||
| Shale | 2459.72~2459.84 | 169.15 | 2.4 | 0.208 | |
| limestone | 2465.12~2465.26 | 281.79 | 4.257 | 0.256 | |
| 274.05 | 3.679 | 0.26 | |||
| limestone | 2474.43~2474.59 | 184.99 | 3.556 | 0.333 | |
| 196.85 | 4.091 | 0.288 |
| Depth m | Lithology | Compressive Strength MPa | Young’s Modulus 104 MPa | Poisson’s Ratio |
|---|---|---|---|---|
| 3639.00~3639.18 | Limestone | 399.52 | 6.318 | 0.364 |
| Shale | 404.96 | 5.092 | 0.277 | |
| 3673.95~3674.15 | Shale | 208.97 | 2.233 | 0.11 |
| Shale interbedded with limestone | 291.03 | 3.444 | 0.21 | |
| Limestone | 212.8 | 2.574 | 0.195 | |
| Limestone and shale interbedded | 266.52 | 4.294 | 0.294 | |
| 210.9 | 2.702 | 0.271 |
| Serial Number | Top Depth m | Bottom Depth m | Thickness m | TOC % | Total Gas Content m3/t | POR % | SW % | PERM mD |
|---|---|---|---|---|---|---|---|---|
| 1 | 3627 | 3652.4 | 25.4 | 1.4 | 1.5 | 6.4 | 62.1 | 0.34 |
| 2 | 3652.4 | 3666.4 | 14 | 1.4 | 1.3 | 4.5 | 58.4 | 0.122 |
| 3 | 3666.4 | 3690.5 | 24.1 | 1.3 | 1.2 | 4.8 | 69.8 | 0.138 |
| Shale Porosity, % | 5.5 | Porosity of Shell Limestone Layer, % | 1.9 |
| Shale permeability, nD | 90 | Permeability of shell limestone layer, mD | 0.01 |
| Young’s modulus of shale formation, GPa | 24 | Young’s modulus of shell limestone, GPa | 38 |
| Poisson’s ratio of shale beds, dimensionless | 0.26 | Poisson’s ratio of shell limestone, dimensionless | 0.31 |
| Injection rate, m3/min | 8.0~14.0 | Working fluid viscosity, mPa·s | 1~20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Z.; Chen, W.; Wang, Y.; He, R.; Liu, F.; Li, S. A Design Method for Improving the Effect of Shale Interlaced with Limestone Reservoir Reconstruction. Processes 2023, 11, 3190. https://doi.org/10.3390/pr11113190
Lv Z, Chen W, Wang Y, He R, Liu F, Li S. A Design Method for Improving the Effect of Shale Interlaced with Limestone Reservoir Reconstruction. Processes. 2023; 11(11):3190. https://doi.org/10.3390/pr11113190
Chicago/Turabian StyleLv, Zefei, Weihua Chen, Yang Wang, Rui He, Fei Liu, and Song Li. 2023. "A Design Method for Improving the Effect of Shale Interlaced with Limestone Reservoir Reconstruction" Processes 11, no. 11: 3190. https://doi.org/10.3390/pr11113190
APA StyleLv, Z., Chen, W., Wang, Y., He, R., Liu, F., & Li, S. (2023). A Design Method for Improving the Effect of Shale Interlaced with Limestone Reservoir Reconstruction. Processes, 11(11), 3190. https://doi.org/10.3390/pr11113190









