MK-DCCA-Based Fault Diagnosis for Incipient Faults in Nonlinear Dynamic Processes
Abstract
:1. Introduction
2. Methodological Theory
2.1. Kernel Principal Component Analysis
2.2. Dynamic Canonical Correlation Analysis
2.3. Contribution-Based Fault Identification
2.3.1. Q-Based Contribution
2.3.2. -Based Contribution
2.3.3. -Based Contribution
3. MK-DCCA Method
4. Case Study
4.1. Case I: Case Study Using Randomly Generated Data
4.1.1. Model Introduction
| Algorithm 1 Generation of Fault-Free and Faulty Data |
Input: coefficient matrix and , bias vector , number of fault-free data samples , number of faulty data samples , magnitude of additive fault , Gaussian noise and , sensor fault vector , process fault matrix Output: input data matrix , output data matrix , faulty input data matrix , faulty output data matrix
− Calculate as . − if j is greater than half of then Add an actuator fault as follows: * Calculate as . * Calculate as . Or add a sensor falut as follows: * Calculate as . * Calculate as . * Calculate as . − else don’t add faults − end if − Append to . − Append to . • end for Return U, Y,, and |
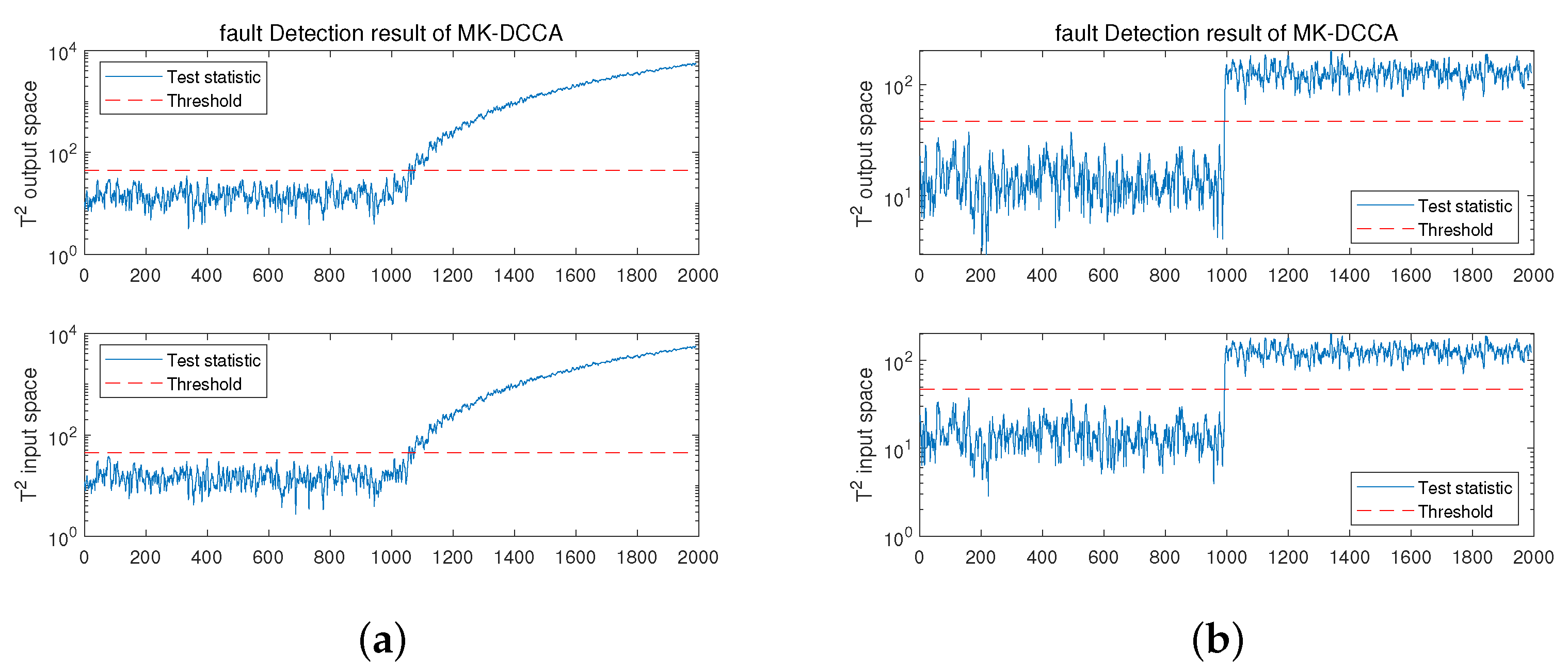
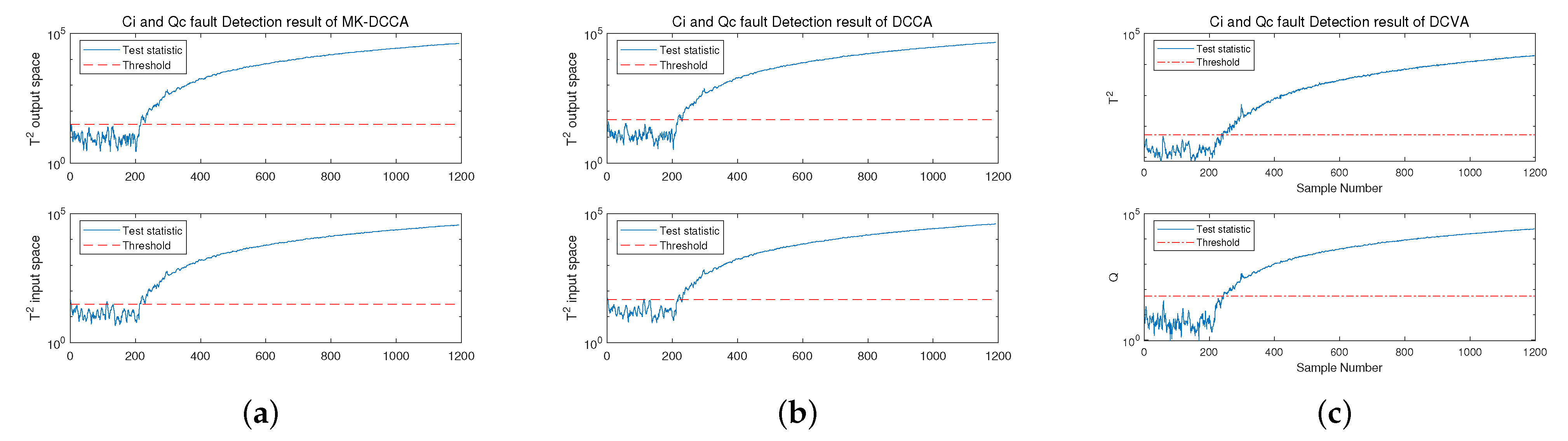
4.1.2. Process Monitoring
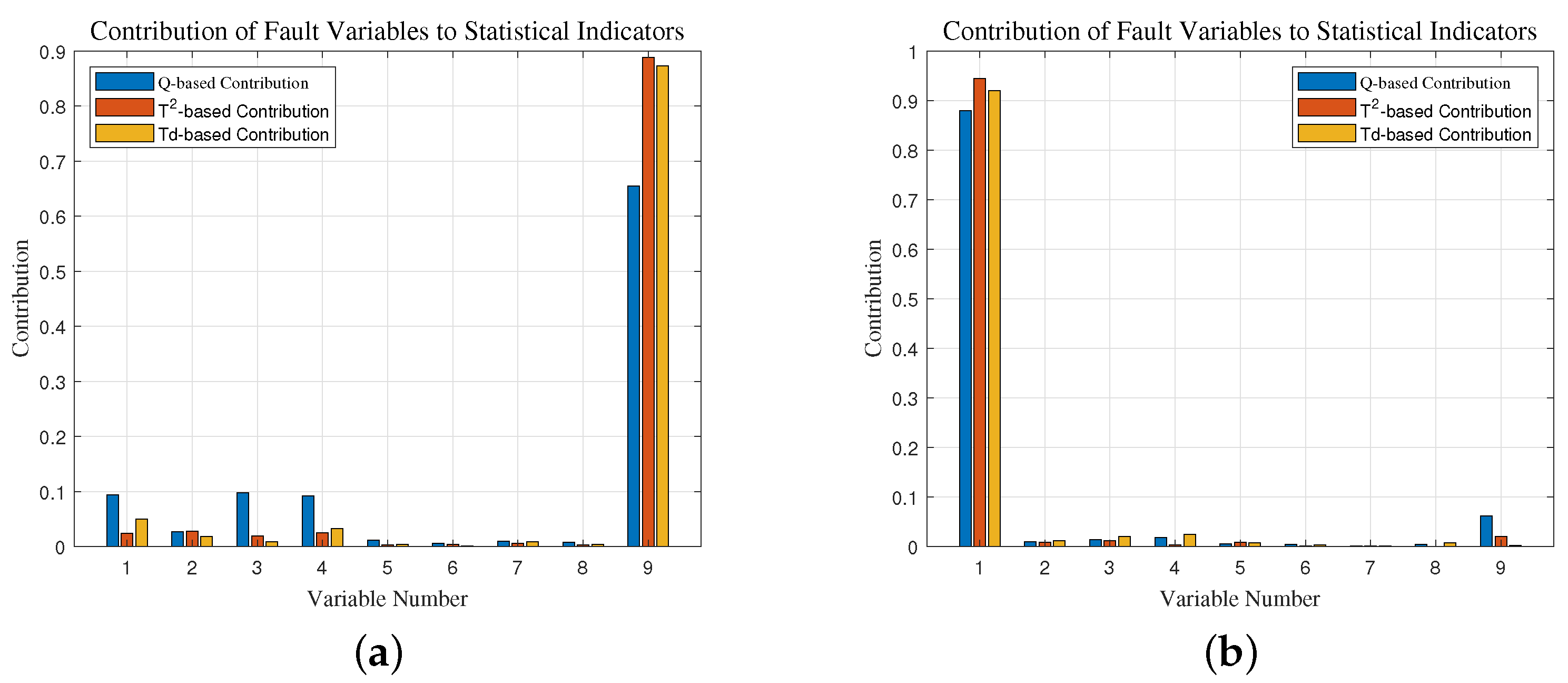
4.1.3. Fault Identification
4.2. Case II: Case Analysis of CSTR Simulation Model
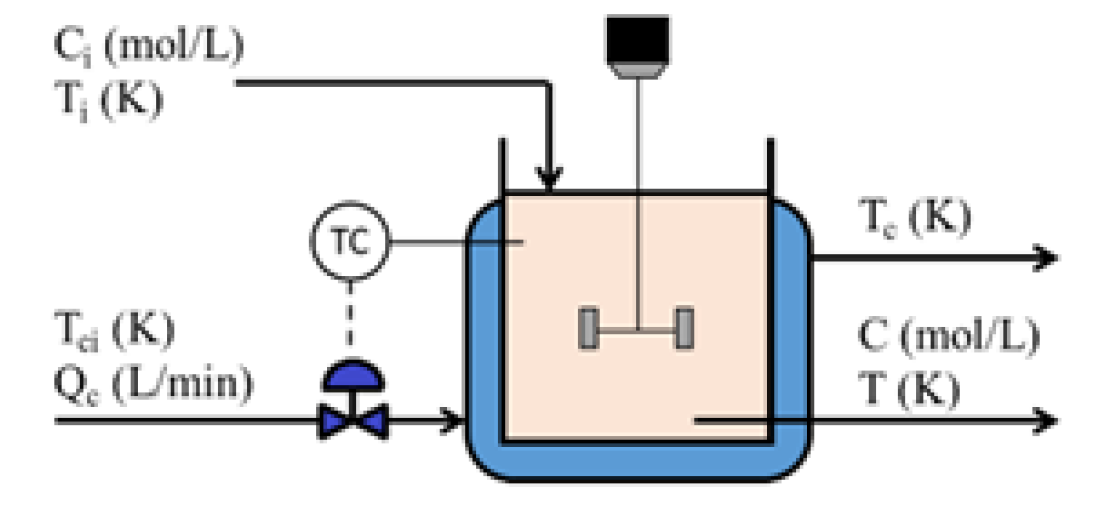
4.2.1. Model Introduction
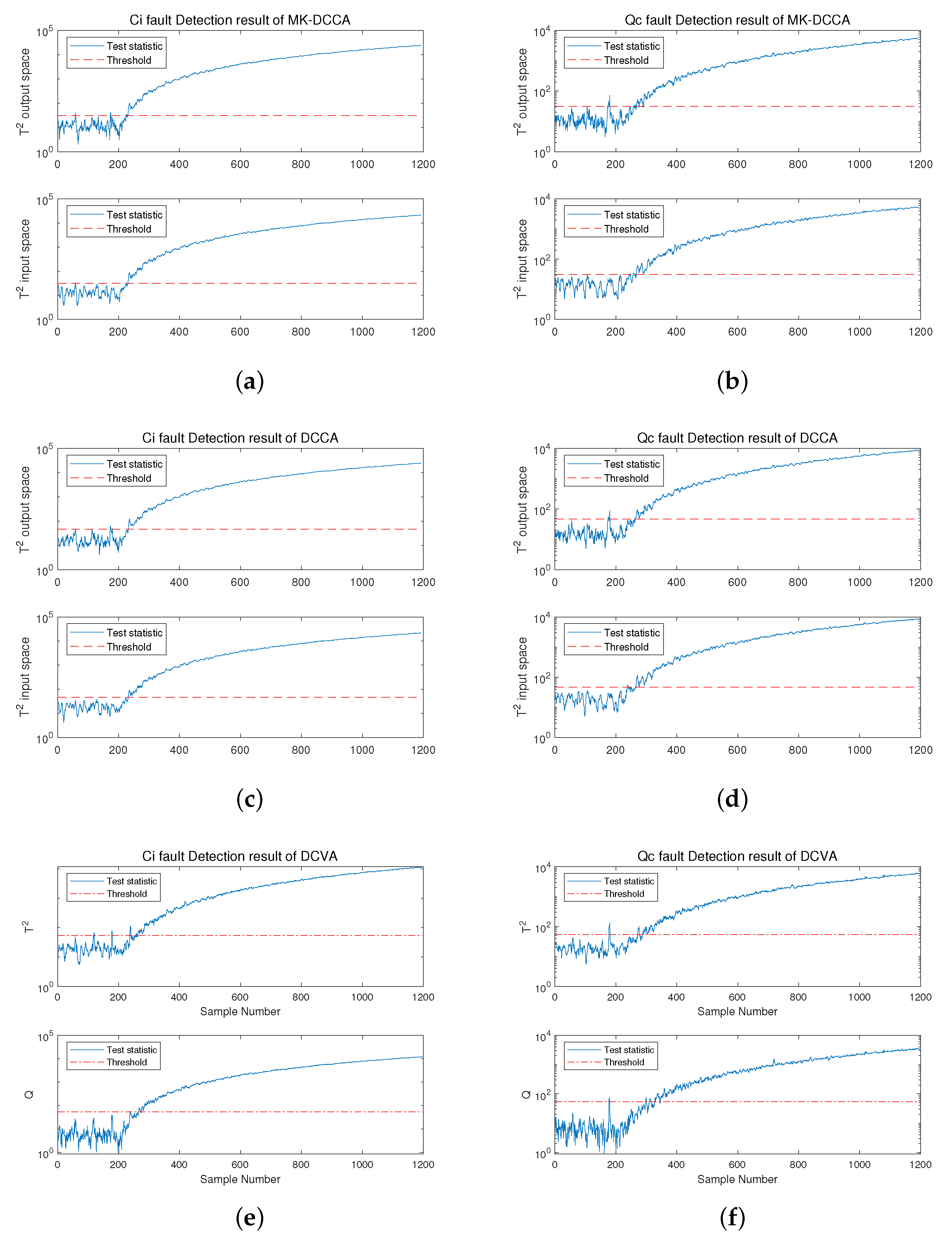
4.2.2. Process Monitoring
4.2.3. Fault Identification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, M.; Yang, C.; Gui, W. Fault detection based on cost-sensitive support vector machine for alumina evaporation process. Control. Eng. China 2011, 18, 645–649. [Google Scholar]
- Qin, S.J. Survey on data-driven industrial process monitoring and diagnosis. Annu. Rev. Control. 2012, 36, 220–234. [Google Scholar] [CrossRef]
- Wise, B.M.; Gallagher, N.B. The process chemometrics approach to process monitoring and fault detection. J. Process. Control 1996, 6, 329–348. [Google Scholar] [CrossRef]
- Tessier, J.; Duchesne, C.; Tarcy, G.; Gauthier, C.; Dufour, G. Analysis of a potroom performance drift, from a multivariate point of view. In Proceedings of the Light Metals-Warrendale-Proceedings—TMS, New Orleans, LO, USA, 9–13 March 2008; Volume 2008, p. 319. [Google Scholar]
- Abd Majid, N.A.; Taylor, M.P.; Chen, J.J.; Stam, M.A.; Mulder, A.; Young, B.R. Aluminium process fault detection by multiway principal component analysis. Control. Eng. Pract. 2011, 19, 367–379. [Google Scholar] [CrossRef]
- Ding, S.X.; Yin, S.; Peng, K.; Hao, H.; Shen, B. A novel scheme for key performance indicator prediction and diagnosis with application to an industrial hot strip mill. IEEE Trans. Ind. Inform. 2012, 9, 2239–2247. [Google Scholar] [CrossRef]
- Harkat, M.F.; Mansouri, M.; Nounou, M.N.; Nounou, H.N. Fault detection of uncertain chemical processes using interval partial least squares-based generalized likelihood ratio test. Inf. Sci. 2019, 490, 265–284. [Google Scholar]
- Ruiz-Cárcel, C.; Cao, Y.; Mba, D.; Lao, L.; Samuel, R. Statistical process monitoring of a multiphase flow facility. Control. Eng. Pract. 2015, 42, 74–88. [Google Scholar] [CrossRef]
- Pilario, K.E.S.; Cao, Y. Canonical variate dissimilarity analysis for process incipient fault detection. IEEE Trans. Ind. Inform. 2018, 14, 5308–5315. [Google Scholar] [CrossRef]
- Pilario, K.E.S.; Cao, Y.; Shafiee, M. Mixed kernel canonical variate dissimilarity analysis for incipient fault monitoring in nonlinear dynamic processes. Comput. Chem. Eng. 2019, 123, 143–154. [Google Scholar] [CrossRef]
- Pilario, K.E.S.; Cao, Y.; Shafiee, M. Incipient Fault Detection, Diagnosis, and Prognosis using Canonical Variate Dissimilarity Analysis. Comput. Aided Chem. Eng. 2019, 46, 1195–1200. [Google Scholar]
- Chen, Z.; Ding, S.X.; Zhang, K.; Li, Z.; Hu, Z. Canonical correlation analysis-based fault detection methods with application to alumina evaporation process. Control. Eng. Pract. 2016, 46, 51–58. [Google Scholar] [CrossRef]
- Chen, Z.; Deng, Q.; Zhao, Z.; Tang, P.; Luo, W.; Liu, Q. Application of just-in-time-learning CCA to the health monitoring of a real cold source system. IFAC-PapersOnLine 2022, 55, 23–30. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, K.; Ding, S.X.; Shardt, Y.A.; Hu, Z. Improved canonical correlation analysis-based fault detection methods for industrial processes. J. Process. Control 2016, 41, 26–34. [Google Scholar] [CrossRef]
- Gao, L.; Li, D.; Yao, L.; Gao, Y. Sensor drift fault diagnosis for chiller system using deep recurrent canonical correlation analysis and k-nearest neighbor classifier. ISA Trans. 2022, 122, 232–246. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, Y.; Tang, B.; Qin, Y.; Zhang, G. Canonical correlation analysis of dimension reduced degradation feature space for machinery condition monitoring. Mech. Syst. Signal Process. 2023, 182, 109603. [Google Scholar] [CrossRef]
- Chen, Z.; Liang, K. Canonical correlation analysis–based fault diagnosis method for dynamic processes. In Fault Diagnosis and Prognosis Techniques for Complex Engineering Systems; Elsevier: London, UK, 2021; pp. 51–88. [Google Scholar]
- Pilario, K.E.; Shafiee, M.; Cao, Y.; Lao, L.; Yang, S.H. A Review of Kernel Methods for Feature Extraction in Nonlinear Process Monitoring. Processes 2020, 8, 24. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, Y.; Huang, D.; Cai, B.; Wang, Q. Rebooting kernel CCA method for nonlinear quality-relevant fault detection in process industries. Process. Saf. Environ. Prot. 2021, 149, 619–630. [Google Scholar] [CrossRef]
- Cheng, H.; Wu, J.; Huang, D.; Liu, Y.; Wang, Q. Robust adaptive boosted canonical correlation analysis for quality-relevant process monitoring of wastewater treatment. ISA Trans. 2021, 117, 210–220. [Google Scholar] [CrossRef]
- Liu, Q.; Zhu, Q.; Qin, S.J.; Chai, T. Dynamic concurrent kernel CCA for strip-thickness relevant fault diagnosis of continuous annealing processes. J. Process. Control 2018, 67, 12–22. [Google Scholar] [CrossRef]
- Yu, J.; Yang, Z.; Zhou, L.; Ye, L.; Song, Z. A Novel Dynamic Baysian Canonical Correlation Analysis Method for Fault Detection. IFAC-PapersOnLine 2020, 53, 13707–13712. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Y. Key-performance-indicator-related state monitoring based on kernel canonical correlation analysis. Control. Eng. Pract. 2021, 107, 104692. [Google Scholar] [CrossRef]
- Zhu, Q.; Liu, Q.; Qin, S.J. Concurrent monitoring and diagnosis of process and quality faults with canonical correlation analysis. IFAC-PapersOnLine 2017, 50, 7999–8004. [Google Scholar] [CrossRef]
- Huang, Z.-J.; Yuan, S.-J.; Li, D.-S.; Li, H.-N. A kernel canonical correlation analysis approach for removing environmental and operational variations for structural damage identification. J. Sound Vib. 2023, 548, 117516. [Google Scholar] [CrossRef]
- Amorosi, L.; Padellini, T.; Puerto, J.; Valverde, C. A Mathematical Programming Approach to Sparse Canonical Correlation Analysis. Expert Syst. Appl. 2024, 237, 121293. [Google Scholar] [CrossRef]
- Luo, L.; Wang, W.; Bao, S.; Peng, X.; Peng, Y. Robust and sparse canonical correlation analysis for fault detection and diagnosis using training data with outliers. Expert Syst. Appl. 2024, 236, 121434. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Smola, A.; Ovári, Z.; Williamson, R.C. Regularization with dot-product kernels. Adv. Neural Inf. Process. Syst. 2000, 13, l308–1314. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Negiz, A.; Çlinar, A. Statistical monitoring of multivariable dynamic processes with state-space models. AIChE J. 1997, 43, 2002–2020. [Google Scholar] [CrossRef]
- Li, X.; Mba, D.; Diallo, D.; Delpha, C. Canonical variate residuals-based fault diagnosis for slowly evolving faults. Energies 2019, 12, 726. [Google Scholar] [CrossRef]
- Jiang, B.; Huang, D.; Zhu, X.; Yang, F.; Braatz, R.D. Canonical variate analysis-based contributions for fault identification. J. Process. Control 2015, 26, 17–25. [Google Scholar] [CrossRef]
- Jordaan, E. Development of Robust Inferential Sensors: Industrial Applications of Support Vector Machines for Regression. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, Holland, 2002. [Google Scholar] [CrossRef]
- Vairo, T.; Pettinato, M.; Reverberi, A.P.; Milazzo, M.F.; Fabiano, B. An approach towards the implementation of a reliable resilience model based on machine learning. Process. Saf. Environ. Prot. 2023, 172, 632–641. [Google Scholar] [CrossRef]

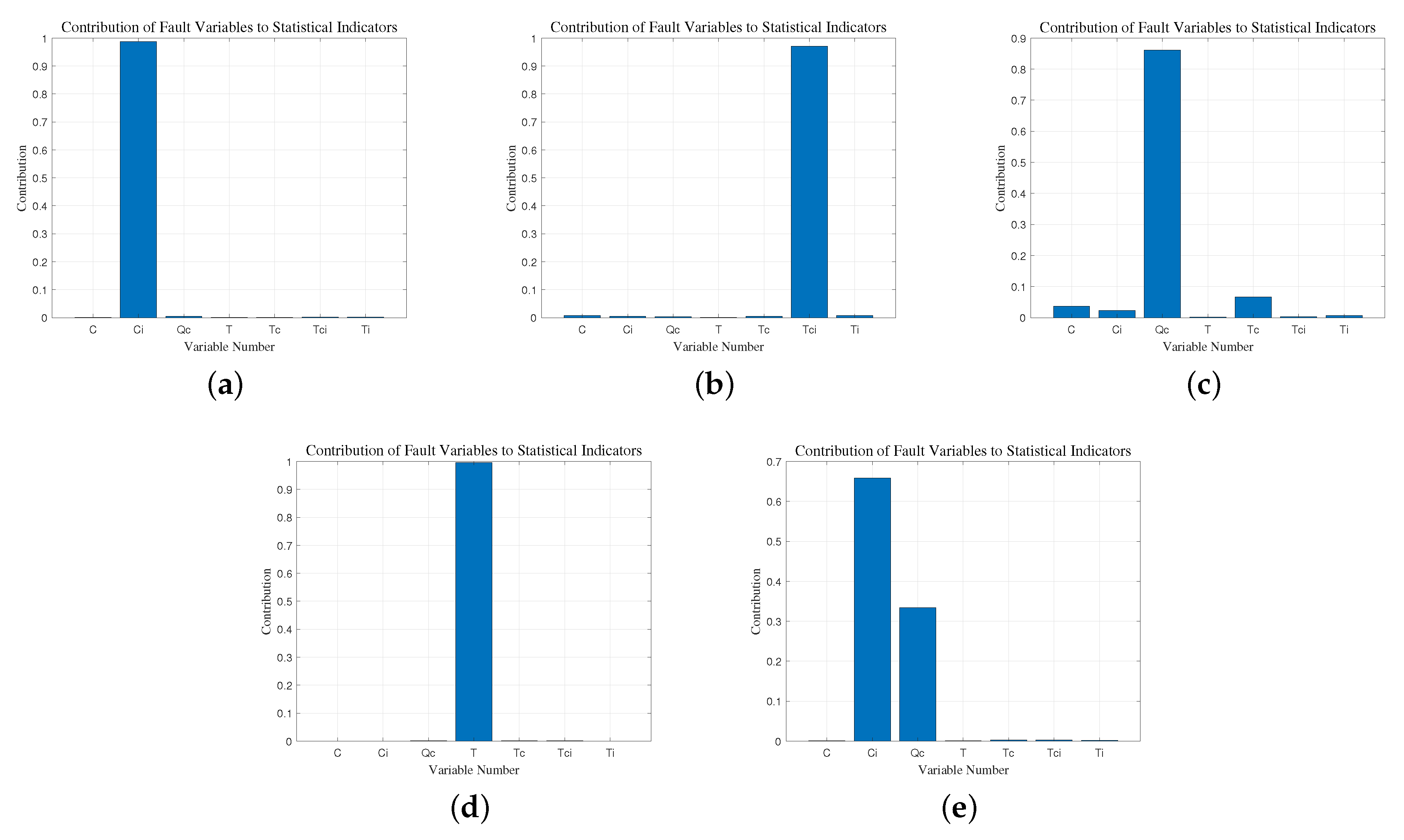
| Fault Index | Fault Location | Fault Category | Fault Variables | Sample Count | Feature Count | Introduction Time (s) |
|---|---|---|---|---|---|---|
| Fault-Free | / | / | / | 2000 | 6 | / |
| Fault 1 | Sensor | Incipient | 9th | 2000 | 6 | 1000 |
| Fault 2 | Actuator | Abrupt | 1st | 2000 | 6 | 1000 |
| Fault Index | Statistical Metrics | FDR(%) | FAR(%) | MDR(%) | FDT(s) |
|---|---|---|---|---|---|
| Fault 1 | 91.9 | 0 | 8.1 | 1054 | |
| 92.5 | 0 | 7.5 | 1054 | ||
| Fault 2 | 99.9 | 0 | 0.1 | 1000 | |
| 99.9 | 0.1 | 0.1 | 1000 |
| Variable Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Variable Name | C | T | 1 |
| Fault Index | Simulated Fault Scenario | Fault Variables | Fault Category | Introduction Time (s) | Associated Subspace |
|---|---|---|---|---|---|
| Fault 1 | Feed valve malfunction | Incipient | 200 | Input | |
| Fault 2 | High coolant temperature | Abrupt | 200 | Input | |
| Fault 3 | Coolant leakage | Incipient | 200 | Output | |
| Fault 4 | High reactor temperature | T | Abrupt | 200 | Output |
| Fault 5 | Both 1 and 3 | , | Incipient | 200 | / |
| Fault Index | Method | Statistical Metrics | FDR(%) | FAR(%) | MDR(%) | FDT(s) |
|---|---|---|---|---|---|---|
| Fault 2 | MK-DCCA | 99.8 | 0 | 0.2 | 202 | |
| 100 | 0 | 0 | 200 | |||
| DCCA | 99.9 | 0 | 0.1 | 201 | ||
| 100 | 3.14 | 0 | 200 | |||
| DCVA | Q | 99.5 | 1.05 | 0.5 | 205 | |
| 99.5 | 2.1 | 0.5 | 205 | |||
| Fault 4 | MK-DCCA | 100 | 1.05 | 0 | 200 | |
| 100 | 2.62 | 0 | 200 | |||
| DCCA | 100 | 2.62 | 0 | 200 | ||
| 100 | 6.81 | 0 | 200 | |||
| DCVA | Q | 99.5 | 3.66 | 0.5 | 205 | |
| 99.5 | 5.24 | 0.5 | 205 |
| Fault Index | Method | Statistical Metrics | FDR(%) | FAR(%) | MDR(%) | FDT(s) |
|---|---|---|---|---|---|---|
| Fault 1 | MK-DCCA | 96.204 | 5.24 | 3.80 | 223 | |
| 96.304 | 1.57 | 3.70 | 225 | |||
| DCCA | 96.004 | 0 | 4.0 | 231 | ||
| 96.004 | 3.14 | 4.0 | 231 | |||
| DCVA | Q | 92.607 | 0 | 7.40 | 237 | |
| 93.506 | 3.14 | 6.50 | 236 | |||
| Fault 3 | MK-DCCA | 93.007 | 0 | 7.0 | 246 | |
| 92.408 | 3.14 | 7.60 | 259 | |||
| DCCA | 92.907 | 0 | 7.10 | 238 | ||
| 92.907 | 2.62 | 7.10 | 260 | |||
| DCVA | Q | 87.013 | 1.57 | 12.99 | 297 | |
| 91.009 | 2.09 | 8.99 | 271 |
| Method | Statistical Metrics | FDR(%) | FAR(%) | MDR(%) | FDT(s) |
|---|---|---|---|---|---|
| MK-DCCA | 97.203 | 1.04 | 2.80 | 215 | |
| 97.403 | 0 | 2.60 | 216 | ||
| DCCA | 97.103 | 1.05 | 2.90 | 215 | |
| 97.303 | 0 | 2.70 | 216 | ||
| DCVA | Q | 94.805 | 0 | 5.19 | 243 |
| 95.105 | 0 | 4.90 | 237 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Zhang, M.; Chen, L. MK-DCCA-Based Fault Diagnosis for Incipient Faults in Nonlinear Dynamic Processes. Processes 2023, 11, 2927. https://doi.org/10.3390/pr11102927
Wu J, Zhang M, Chen L. MK-DCCA-Based Fault Diagnosis for Incipient Faults in Nonlinear Dynamic Processes. Processes. 2023; 11(10):2927. https://doi.org/10.3390/pr11102927
Chicago/Turabian StyleWu, Junzhou, Mei Zhang, and Lingxiao Chen. 2023. "MK-DCCA-Based Fault Diagnosis for Incipient Faults in Nonlinear Dynamic Processes" Processes 11, no. 10: 2927. https://doi.org/10.3390/pr11102927
APA StyleWu, J., Zhang, M., & Chen, L. (2023). MK-DCCA-Based Fault Diagnosis for Incipient Faults in Nonlinear Dynamic Processes. Processes, 11(10), 2927. https://doi.org/10.3390/pr11102927








