1. Introduction
The gas pipeline is an essential infrastructure in modern life. In order to ensure the safety of transportation, the gas pipeline is usually wired in the buried way. As the underground conditions are complex and the metal pipe is buried for a long time, it is easy to be corroded and cause defects [
1], which increases the maintenance cost of the pipeline and is not conducive to safe transportation. With the improvement of material technology, polyethylene (PE) has been used as a gas pipeline, which has the characteristics of low cost, corrosion resistance, and lightweight [
2]. And it has gradually replaced metal pipelines with buried gas pipelines. However, due to the insulation and magnetic isolation characteristics of the PE pipeline, conventional metal pipe detection equipment cannot detect the location of the PE pipeline [
3]. As the location of the gas pipeline cannot be accurately detected, it is easy to cause accidents and unnecessary losses [
4]. How to accurately and quickly locate the location of the gas PE pipeline has become a key problem.
The efficient positioning technology of buried gas pipelines is of great significance to ensure the safe operation of gas pipelines, but most of the existing research are pipe mechanics under external load [
5]. According to the acoustic emission characteristics of buried pipelines, the stress-strain relationships have been studied and obtained the under-vibration response of buried pipelines [
6,
7]. Some research studied the positioning of high-pressure pipelines based on the acoustic emission method and the characteristics of acoustic emission in the time domain and frequency domain, believing that energy attenuation could be used as a method for acoustic emission location [
8,
9,
10,
11,
12]. Others analyzed the characteristics of non-metallic buried gas pipelines and proposed electromagnetic wave acoustic waves as the means of pipeline positioning and detection. The electromagnetic detection method does not require direct contact with the ground, easily affected by surface buildings, vehicles and other human interference, the impact on the environment is small, and with the increase in depth, the signal strength will weaken. Compared with the electromagnetic detection method, the magnetic gradient method is less affected by electromagnetic interference, but it is affected by magnetic substances. The induced seismicity method can provide a large depth range of information, has high cost and complexity, and has safety risks. In order to solve the problem of non-metallic pipe positioning, it proposed a pipeline positioning method based on RFID technology, pressure sensors, and laser. Different technologies have different implementation methods. The voice signal is used to inject a certain frequency of sound signal into the pipeline.
RFID technology realizes label identification, pipeline positioning, and information storage [
13,
14]. Laser is used to monitor gas pipelines [
15]. The pressure sensors collect the difference between the arrival time and the corresponding frequency to obtain the position of the pipeline [
16]. According to the current research status, pipeline positioning technology still needs to be improved where acoustic positioning technology has been the focus of research. The voice signal is used to inject a certain frequency of sound signal into the pipeline. As the gas in the pipeline has flow rate and pressure, the acoustic signal propagates along the pipeline. Acoustic signals of corresponding frequency can be detected by signal acquisition instruments to complete pipeline positioning.
In this paper, vibration characteristics of buried PE pipelines are studied on the basis of existing research. Firstly, combined with the working conditions of the buried gas pipeline, it analyzes the vibration characteristics of the buried gas pipeline and establishes the numerical calculation theoretical model. Then, the model is calculated through the given input parameters, obtaining the results of vibration characteristics of buried pipelines under pulse excitation. Finally, through the experimental test of a buried gas pipeline under pulse excitation, it compared the theoretical solution with experimental test results to verify the validity of the numerical calculation model. Therefore, the research on vibration characteristics of buried gas pipelines has theoretical research value and can also provide theoretical support for efficient positioning technology of buried gas pipelines.
2. Analysis Model
As the buried pipeline has elbow, tee and other structures, the internal cross-sectional area of the joint will change. Due to the viscosity and absorption of gas, the acoustic signal will attenuate. Combined with the working conditions of the PE gas pipeline, it is made the following assumptions to ensure that the research results are more realistic and generic. (1) The pressure in the pipeline is stable and does not decay with time: it is assumed that the gas pressure inside the pipeline remains stable during the experiment and will not decay with time. (2) The medium around the pipeline is uniform medium and the buried depth of the pipeline does not change: assuming that the medium around the pipeline is uniform, there will be no changes in density, speed, etc., and the buried depth of the pipeline will not change during the experiment. (3) External excitation is stable, and the frequency and power of sound waves do not change during the experiment: it is assumed that the acoustic wave excitation applied externally to the pipeline is stable during the experiment, and its frequency and power will not change. (4) The pressure at the input end of the test area has random fluctuations, and its spectral function is almost white: if the pressure at the input end of the test area has random fluctuations, the spectral function of this random fluctuation is approximately white noise, that is, it has similar energy at each frequency. (5) The pressure in and near the contraction zone of the test area can be measured with a pressure detector: it is assumed that the pressure in and near the contraction zone of the test area can be accurately measured with a pressure detector. Through the above assumptions, we can better simulate the actual working conditions, obtain more realistic and universal research results, and provide a more reliable theoretical basis for the application of buried pipeline acoustic measurement.
Assumption (1) indicates that the gas transport is a strictly compressible flow and the pipe wall is thin enough that there is no attenuation to the signal. Since the flow resistance or power used to transport the gas is proportional to the gas flow velocity, there is always an economically optimal gas flow velocity, which is determined by the diameter and length of the pipe and the nature of the gas. The optimal velocity of gas flow in commercial pipelines, 10–20 m/s, is not high relative to the speed of sound except in pipelines for special purposes.
Assumption (2) is made to avoid the obvious feature that different depths of the pipeline could influence the location and also make the theoretical development easier. As a single pipeline usually has only one cross-sectional area for long distances.
Assumption (3) is necessary because the position of the pipeline is measured by the amplitude of the acquired acoustic waves at a particular frequency. Therefore, the frequency and amplitude of sound waves are directly related to the validity of positioning
Assumption (4) is required. If the noise generated by the compressor and/or turbulence occurs near the input and has a wide spectrum, the noise will interfere with the test results.
Assumption (5) means that pipeline location depends on the characteristics of the band of the acoustic wave measured at the input and output area. We must consider the frequency band of the detector as a limiting factor and study its effect on the location of the leak.
When an acoustic wave travels through an ideal medium, the influence of heat conduction and viscosity on propagation can be ignored. According to the difference of acoustic wave front in the pipeline, the acoustic wave in the cylindrical pipeline is a plane wave, and the plane wave equation is a one-dimensional equation, which is expressed as follows.
where
is the initial amplitude of the acoustic wave.
is the frequency of acoustic wave.
x is the propagation distance.
k is the wave number of undamped waves,
.
is the propagation speed of acoustic wave.
In non-ideal media, energy conversion and attenuation occur when sound waves propagate, and viscosity is an important factor. The viscosity causes sound waves to convert sound energy into heat energy, and it gradually weakens as the distance it travels increases. In the actual oil and gas pipeline, due to the long length of the pipeline, we need to consider damping effects, including viscous absorption and heat conduction. It is also necessary to consider the viscosity, viscous force, and heat conduction factors to accurately describe the attenuation characteristics of sound waves in non-ideal media. This facilitates more accurate modeling and analysis of acoustic transmission in the pipeline. When the velocity of adjacent particles in the medium is inconsistent, viscous force is generated. The presence of viscous force will cause the sound wave to lose energy during the propagation process and cause the attenuation of the sound wave intensity. At the same time, heat conduction will further promote the conversion of sound wave energy into heat energy, thus intensifying the attenuation phenomenon of sound wave. The viscous force can be expressed as:
where
v is the velocity of sound wave,
η is the viscosity coefficient, which is mainly composed of shear viscosity coefficient
η’ and capacitive viscosity coefficient
η″.
Sound pressure
p can be expressed as.
where
Ks is the volume elastic coefficient and
is displacement.
The motion equation of viscous gas in the medium is as follows.
where
is the density of the gas medium.
Taking into account that the viscous force is in the opposite direction of the pressure increment, substitute Equations (2) and (4) into Equation (5). The wave equation of acoustic wave in viscous gas can be written as.
For one-dimensional plane waves, the solution to the equation is
, and substitute it into the Equation (6).
where
k is the wave number of the acoustic wave, and
. Introducing the absorption coefficient
,
k can be expressed as.
Hypothesis
, where
. Substitute
and Equation (8) into
, then it is obtained the following equations after squaring.
The solution of the above equations is as follows.
From the attenuation coefficient formula of sound waves in non-ideal media, it can be found that high-frequency sound waves decay faster than low-frequency sound waves, and low-frequency sound waves can travel longer distances and reflect and scatter less in the pipe, so they can provide more accurate position information. Therefore, it is more effective to use low-frequency sound waves as a carrier when measuring pipe position. The vibration of a pipeline system can essentially be regarded as the vibration of a system with infinite degrees of freedom. Different piping systems can be transformed into systems with limited degrees of freedom [
17]. For a given piping system, it can be thought of as a system with n degrees of freedom. By solving this set of vibration equations, the vibration modes of the pipeline system and the corresponding vibration frequencies and modes can be obtained. This can help us understand the natural vibration characteristics of the pipeline system, and carry out related analysis and design. Studying the vibration mode and frequency of pipeline systems can help us understand the structural characteristics of pipeline systems, predict the vibration response and resonance characteristics of pipeline systems, and effectively reduce the failure probability of pipeline systems. In addition, by optimizing the natural vibration characteristics of the pipeline system, the noise and vibration levels of the pipeline system can be reduced, and its working efficiency and reliability can be improved. Therefore, it is necessary to deeply study and analyze the vibration characteristics of the pipeline system. According to solid mechanics, when the effect of damping is ignored, its vibration equation is as follows.
where
is the total mass matrix of the pipeline system.
is the total stiffness matrix of the pipeline system.
is the force load vector of the pipeline system.
is the vibration displacement vector.
is the vibration acceleration vector.
In general, Equation (11) is an n-dimensional coupled equation where the matrix H is not a diagonal matrix. In order to solve the n-dimensional equations in a relatively simplified way, the coordinate transformation method can be used to transform the coupling of the equations into decoupling. In particular, variables in the original coordinate system can be converted to variables in the new coordinate system by a suitable linear transformation, such that the new system of equations becomes a diagonal system. In this way, in the new coordinate system, the solution of the system can be decomposed into the solution of n-independent solutions. It is taken the several main mode vectors,
, of the pipeline as the basis and the geometric coordinates,
, are expressed as the linear combination of the basis, which expressions are as follows.
It decomposes the displacement vector
x according to each main vibration mode, and the expansion form of the Equation (12) is as follows.
Equation (13) can also be expressed as
. Substitute it into Equation (10) and multiply it by
. Then, Equation (11) can be expressed as follows
where
is the generalized mass matrix,
.
is a generalized stiffness matrix,
.
is the generalized load,
. And
are
diagonal matrices, so the Equation (14) has become a pair form, including
n-independent equations as follows.
where
i = 1,2, …,
n.
is the element of the
i-th row of
.
is the element of the
i-th row of
.
Divide both sides of Equation (15) by
, then it gets the following equation.
where the vibration frequency of the pipeline is expressed as
. Under the condition of the initial displacement and initial velocity are zero, Equation (16) can be solved by Duhamel integral (18). Its result is as follows.
If the initial displacement and the initial velocity are
and
. And
and
satisfy the following equation.
So the values of
and
are shown below.
Therefore, the solution of pipeline vibration displacement can be written as follows.
3. Numerical Calculation and Experimental Study
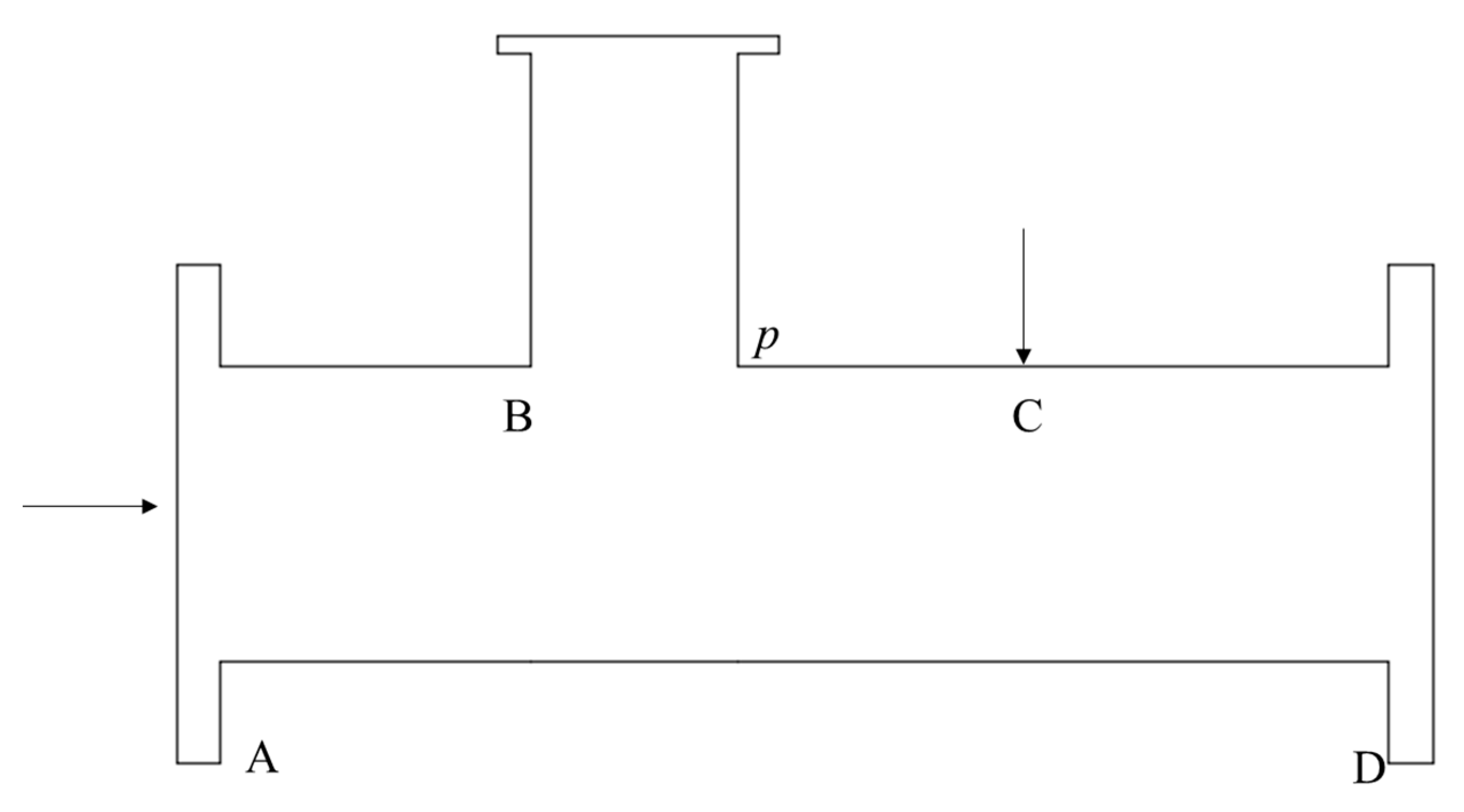
Supposing at some point, the gas flows from the main pipe to the branch pipe and produces an impact force at point 1 in a gas pipe filled with a certain pressure. If the pressure is constant at both ends of pipeline AD and it ignores the friction loss of airflow in the pipeline, the dynamic analysis of the airflow shows that the pressure at point B soon reaches constant, which value is
p. In order to analyze the vibration characteristics of the pipeline, it is assumed that the freedom of vibration is 2, the length of the pipeline is
L, the elastic modulus of the pipe is
E, and the moment of inertia of the section is
I. The distance from point B to point A and point C to point D is
L/3. The schematic diagram of vibration simplification is shown in
Figure 1.
According to the analysis, the natural vibration frequencies at point 1 and point 2 are as follows, respectively.
The main mode matrix of the pipeline is as follows.
The transformation of coordinates is as follows.
Therefore, the vibration displacement of the pipeline is expressed as follows.
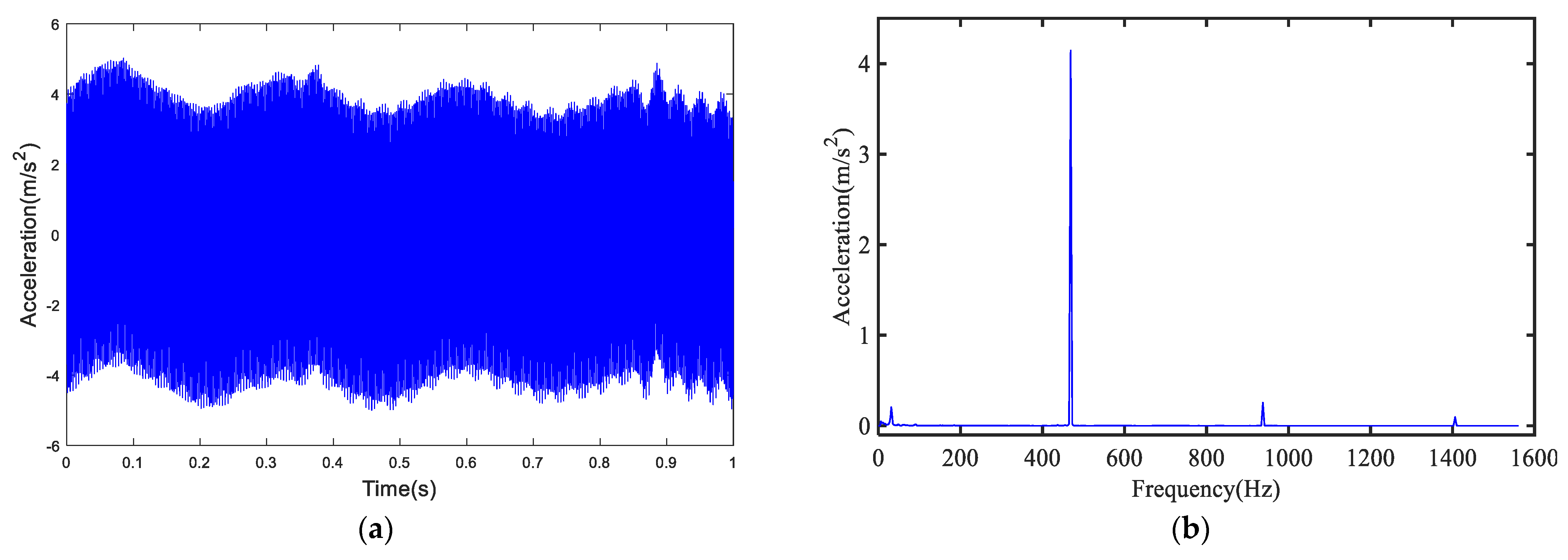
As the transmission of acoustic waves will be affected by many factors, such as the material of the pipe, the gas in the pipe and the surrounding medium. Therefore it carried out the ground experiment with the same type of pipe. Before the experiment, it installs the pulse signal generator on the pipeline and checks the sealing performance of the pipeline. Selecting the input power and frequency of the pulse source requires comprehensive consideration of equipment requirements, load requirements, system efficiency, noise, and interference, as well as available resources and other factors to ensure the normal operation of the equipment, performance optimization, and efficient use of energy. At the same time, according to the above analysis model, we set the input power of the pulse source to 20 W and the input power to 470 HZ. After digital filtering, the acceleration-time curve is shown in
Figure 2a. Since there is no stratum medium, the acoustic wave does not show attenuation. It carries out the spectrum analysis of the acceleration time curve, obtaining the spectrum graph with acceleration as ordinate and frequency as abscissa in
Figure 2b. In the 470 Hz signal band, the peak does not attenuate. According to the above analysis, it is carried out field experiments to verify the validity of positioning buried pipelines by acoustic wave.
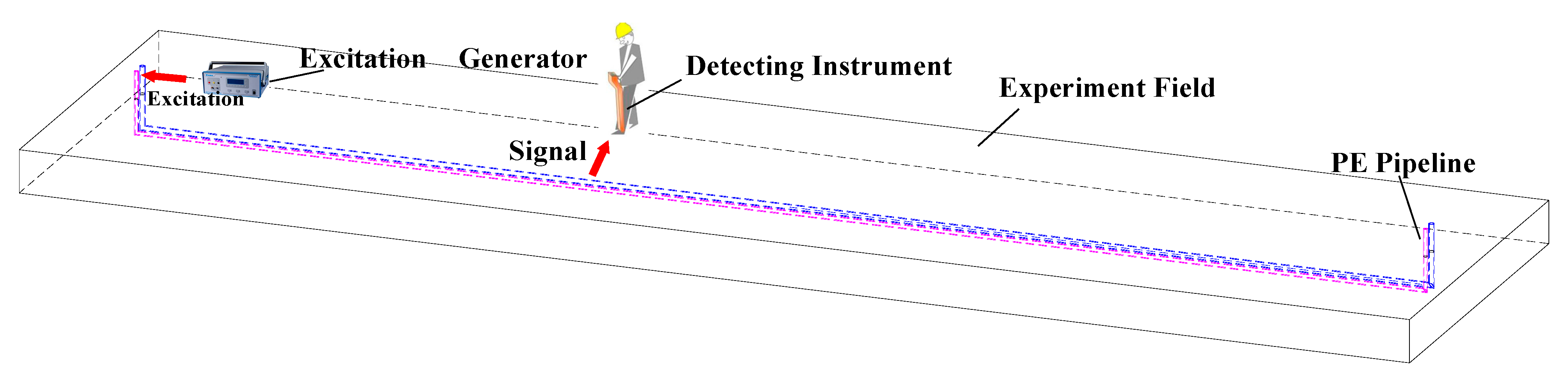
The excitation generator is connected to the gas pipeline through the connecting port of the regulating pressure box. Taking the gas in the PE pipeline as a medium, the excitation generator generates an acoustic signal with a special frequency and it transmits in the pipeline. The acoustic signal transmits in the PE pipeline and travels through the soil to the surface. The test diagram is shown in
Figure 3.
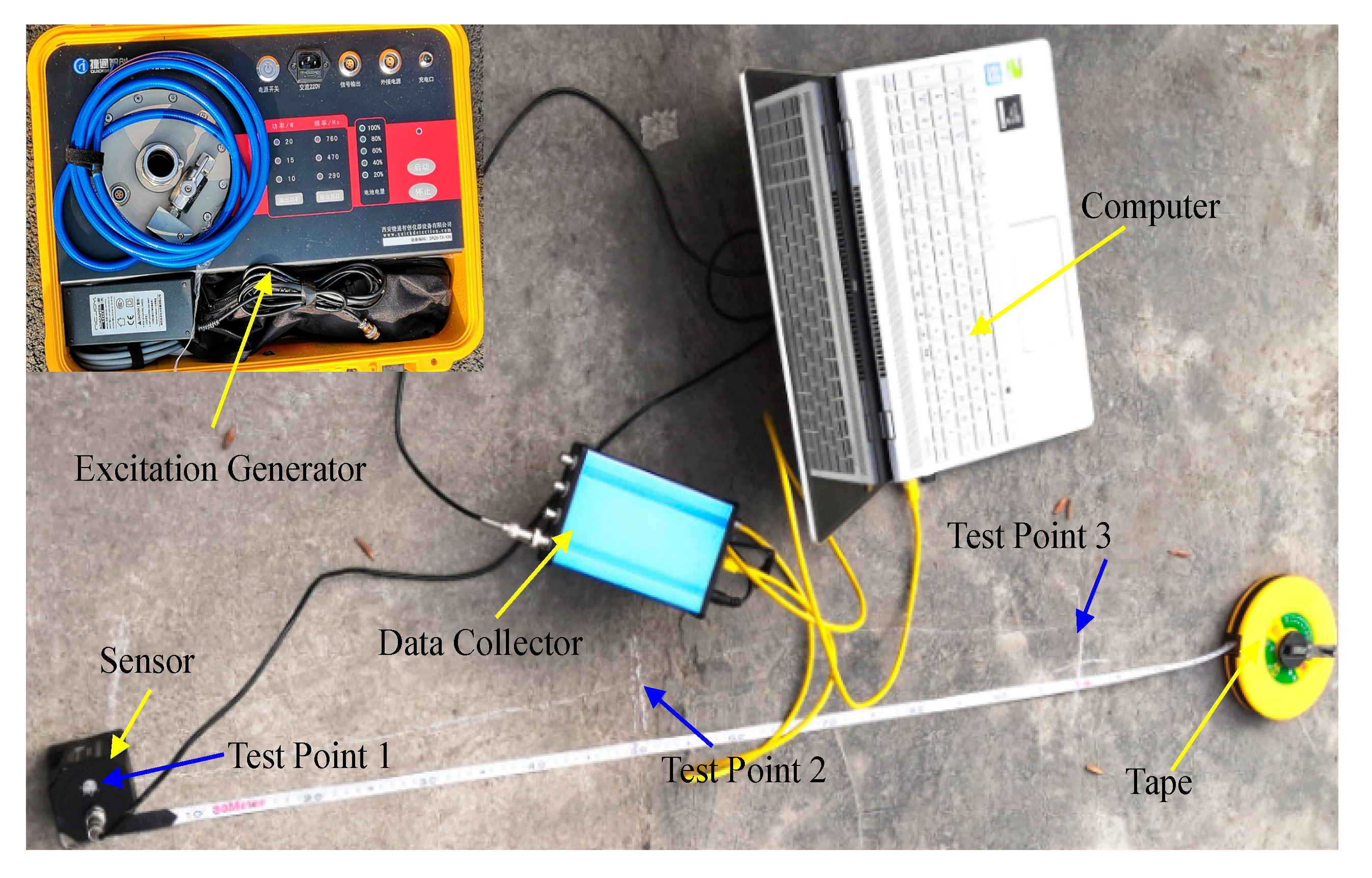
The experiment pipeline is a medium-pressure pipe with an outer diameter of
Φ 160 mm, the wall thickness of 14.6 mm, the inner pressure of 0.2 MPa, and burial depth of 80 cm. The experimental test site and test instruments are shown in
Figure 4. Test point 1 is located directly above the pipeline, test point 2 and test point 3 are separated from test point 1 by 50 cm and 100 cm, respectively.
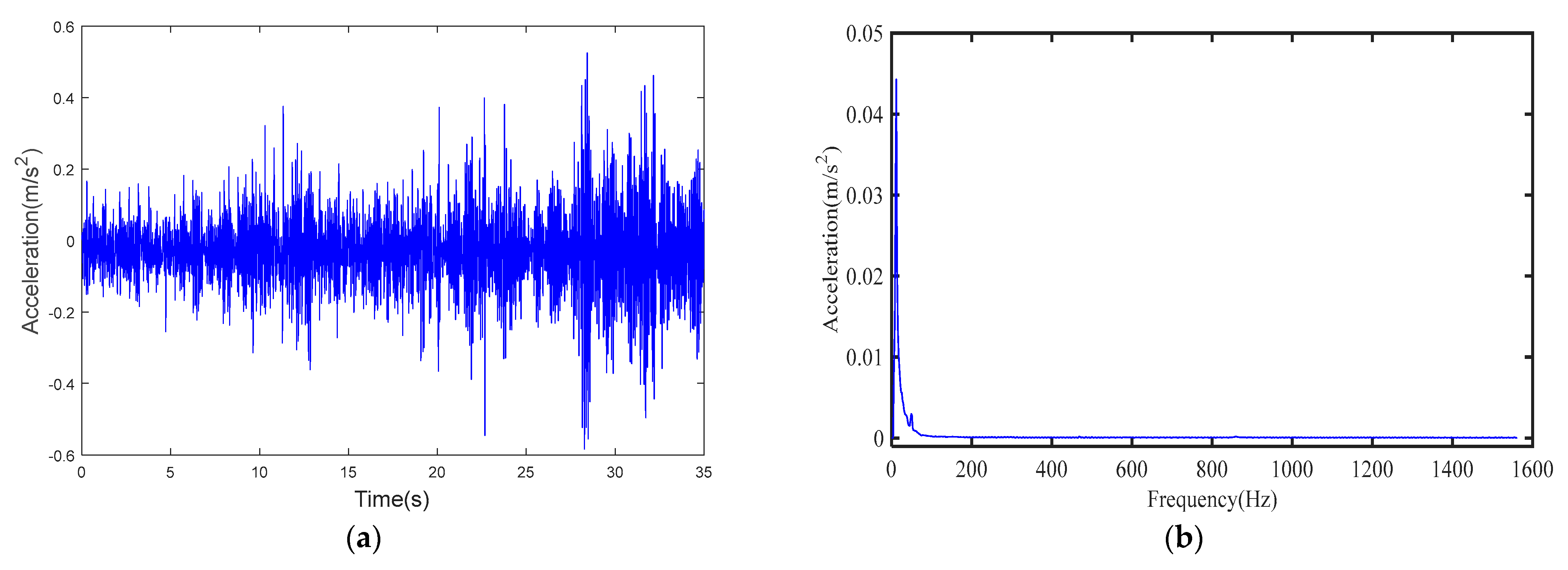
In order to ensure the validity of experimental results, it needs to eliminate the interference of background noise. The range of sensor acoustic spectrum analysis and positioning depends on a number of factors, including sensor type, pipe material, environmental conditions, etc. Generally speaking, the sensor acoustic spectrum analysis and positioning can realize the rough location of abnormal sounds or leakage sources inside the pipeline. The error range of positioning can reach a few meters to about ten meters. According to the test points selected above, it collects the surrounding sound signals without applying the test carrier wave in the pipeline, obtaining the acceleration time curve, and acquiring the spectral diagram by Fourier transform. They are shown in
Figure 5a,b. According to the results of the spectrum diagram, it can be seen that the low-frequency acoustic signal exists in the test environment. Considering that the test environment is outdoor, the interaction between the gas inside the pipe and the pipe wall will also produce low-frequency acoustic signals. Therefore, these acoustic signals are the background noise in the environment. The frequency of the acoustic signal used in this test is 470 Hz, which can be well distinguished from the ambient noise. Therefore, the environmental noise will not interfere with the experimental results.
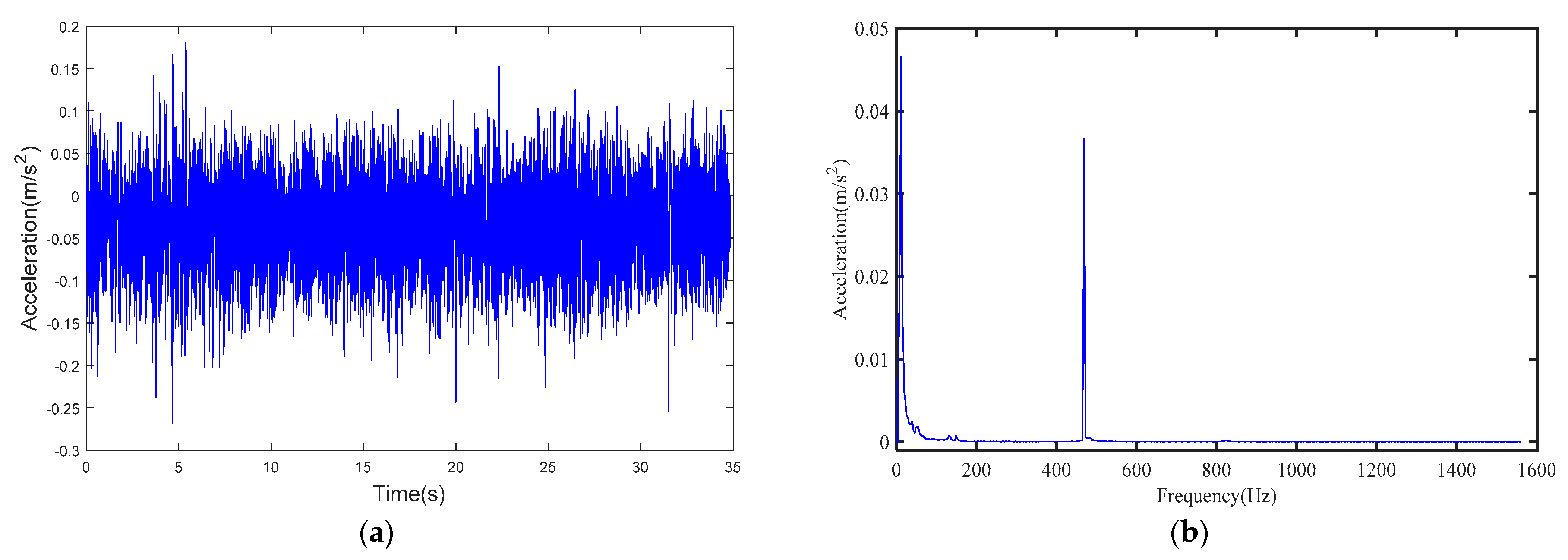
The sensor was placed at test point 1 and it obtained the acceleration-time curve shown in
Figure 6a. Compared with the air-pipe test results, the amplitude of the acoustic signal attenuated. Similarly, spectrum analysis was carried out on the time-history curve, obtaining the spectrum curve as shown in
Figure 6b. There is an obvious peak near 470 Hz, meaning that it collects the signal in the PE pipeline. Due to the influence of the stratum, the signal peak value attenuated, which is consistent with the result of the acceleration-time curve. Compared with the ground experiment, the amplitude attenuation of the acoustic signal reaches 99% at a depth of 80 cm.
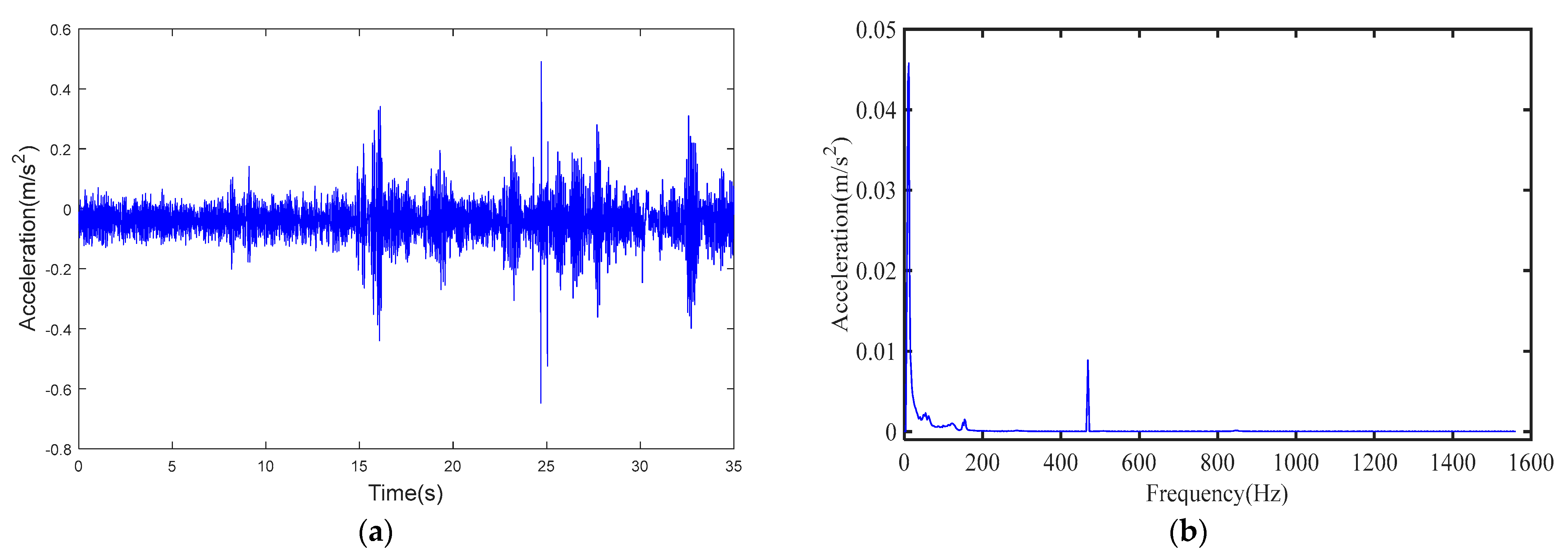
The sensor was placed at test point 2, and the acceleration-time curve as shown in
Figure 7a was obtained. Again, the amplitude of the acceleration decreases. Spectral analysis was performed on the time-history curve, and the spectral curve as shown in
Figure 7b was obtained. Compared with the spectrum diagram of test point 1, a new amplitude also appears at 470 HZ, but the signal amplitude of test point 2 is reduced, indicating that test point 2 is far away from the pipeline. Compared with test point 1, the amplitude attenuation of the acoustic signal reaches 75%.
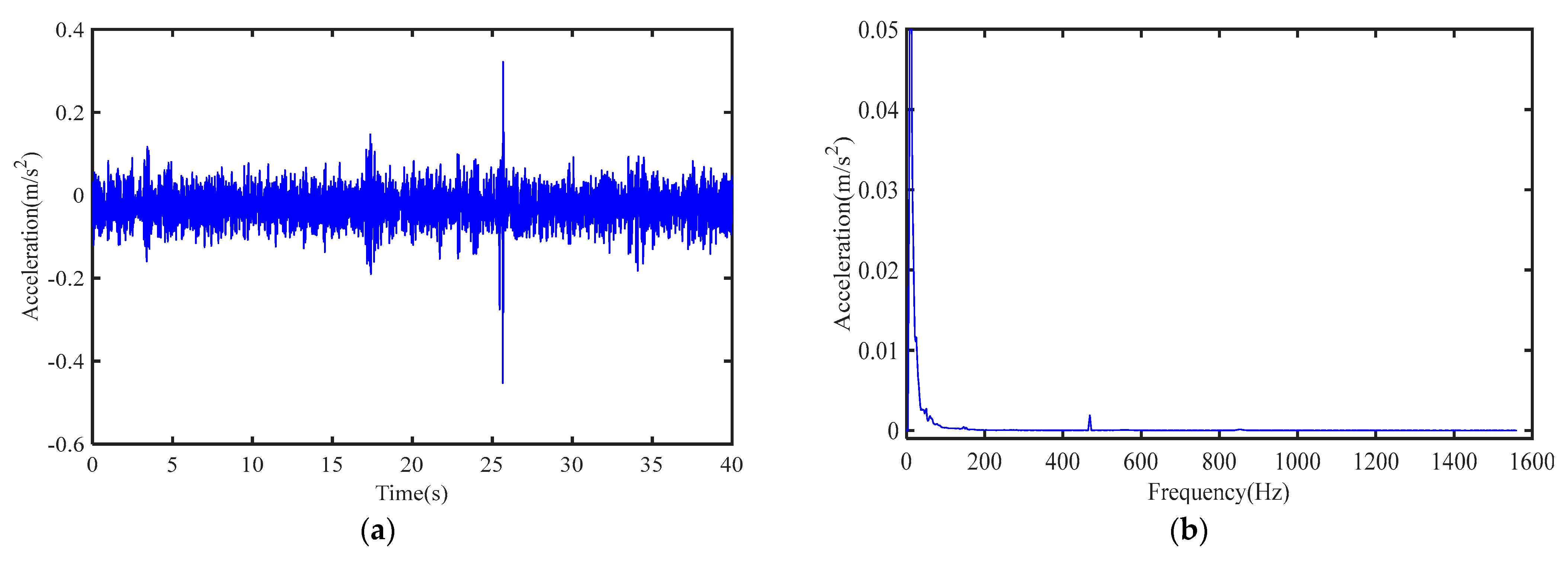
A sensor was placed at test point 3, and the acceleration-time curve was obtained, as shown in
Figure 8a. By comparing the time curve of test point 1 and test point 2, it is found that the amplitude of signal change is small at test point 3. Further spectrum analysis was carried out on the time history curve of test point 3, and the spectrum curve was obtained, as shown in
Figure 8b. As can be seen from the figure, the amplitude of the signal is weak, which indicates that test point 3 is farthest from the pipeline. Compared with test point 1, the amplitude attenuation of the acoustic signal reaches 87.5%. Therefore, based on these analysis results, we can determine the location of the pipeline at test point 1.
4. Results
In order to locate the PE pipe accurately, we establish the attenuation model of sound waves in a non-ideal medium and deduce the absorption coefficient and attenuation characteristic equation of sound waves, according to the propagation characteristics of sound waves. We found that sound decays faster and faster as the frequency increases. In order to study the vibration characteristics of the pipeline more deeply, we set up the coordinate system of the pipeline and give the vibration characteristics of the pipeline under pulse excitation with the help of the knowledge of solid mechanics.
Based on the theoretical model, the vibration characteristics of the pipeline under pulse excitation are analyzed and verified by ground test. The experimental results and the corresponding acceleration-time curve spectra show that the amplitude attenuation is very weak when the pulse propagates if it does not pass through the soil, which further confirms the effectiveness of sound waves in locating the location of the pipeline.
In the design of pipeline location, it is necessary to consider many factors such as pipeline vibration and environmental noise. In order to eliminate the interference of these factors on the test results, the field background noise was detected before the test began. Through the spectrogram of the test results, we find that there is low-frequency noise in the surrounding environment. According to the results of pipeline vibration analysis, we determine that the pipeline noise is caused by the interaction between gas and pipe wall. In this test, we chose a carrier frequency of 470 Hz, which is greater than the background noise frequency of the environment. Therefore, these noises do not affect the test results and the judgment of the results. Based on the test results measured in the field, we can confirm that these results are valid. It should be noted that for different environments and vibration and noise frequencies, we should use different carrier signals to test to ensure accuracy.
According to the working conditions of the PE pipeline, we put forward a reasonable test scheme and carried out the test on-site. Fourier transform is applied to the acceleration-time curve of the acoustic signal to obtain the spectrum diagram, where the horizontal coordinate is the frequency and the vertical coordinate is the acceleration. Due to the attenuation effect of the ground, the amplitude attenuation of the acoustic signal is large. By comparing the acceleration-time curves and spectrograms of the three measuring points, we find that the acceleration-time curves of measuring points 2 and 3 have a higher peak value, which indicates that the geological layer at measuring point 2 has a weak influence on signal attenuation. In the spectrum diagram, the amplitude of the 470 Hz frequency curve at test point 1 is higher than that at test points 2 and 3. This indicates that the formation signal at test point 1 has a greater attenuation, but is closer to the PE pipe in the vertical direction. Therefore, in the project, we can choose the test point in the other direction to further determine the precise position of the pipeline. It is very helpful for the positioning of pipelines in subsequent projects.