Abstract
The surface areas of the materials are generally the most vulnerable parts since they are directly exposed to different stresses such as wear, fatigue, and corrosion. On the other hand, the successive impact of the droplets finds numerous applications in additive manufacturing technologies such as 3D printing and liquid metal projection. The lamella state formed by the impact and spreading of the first particle represents the target for the second; however, its molten state or fragmented state, bouncing or a slide, interacts thermally and dynamically to allow or not allow stacking. The deposition, deformation, and solidification of the droplets are the constituent steps of the process which determine the final result, as the topography of the substrate not only conditions the mechanical adhesion of the drop to the substrate but also affects the wettability of the surfaces. The objective of this work was to model by numerical simulation the impact of successive and simultaneous droplets with solidification and simultaneous deformation in the presence of an oxide layer on the substrate, which presents different topography, in order to fix the knowledge on the behavior of the impact, the spreading, or the splashing with solidification. However, a peak diameter greater than 5% of the particle diameter causes the formation of concave roughness which directly infects the mechanical adhering and subsequently the formation of an ordinary lamella.
1. Introduction
The phenomenon of particle-oxidized substrate interaction is studied by several researchers, such as Saubole et al. [1], who investigated the effect of oxidation on the dynamics of powder particle flattening and the development of particle–substrate interactions during thermal spraying and presented analytical formulas for estimating these processes. Analytical results take into account substrate roughness, spatter solidification, wetting, and spatter. It was found that a decrease in particle diameter leads to an increase in the size of oxidized particles and the thickness of an oxidized layer. To decrease the particle size, it is necessary to have a narrow size distribution of the powder particles with a relatively large average value. Oxidation causes an increase in the thickness of the splinter and a decrease in the splint of the radius. Additionally, the oxidation decreases the pressure on the droplet, which is harmful to the contact between the substrate and the splash.
Xue et al. [2] proposed an analytical model of the true contact surface between molten metal and a solid, rough surface. The analytical model was incorporated into a three-dimensional time-dependent numerical model of free-surface flows and heat transfer. It was used to simulate the impact, spreading, and solidification of molten metal droplets on a solid surface while calculating contact resistance distributions at the liquid–solid inter-face. It was found that a surface oxide or other contaminants are likely to produce additional changes in contact resistance that cannot be predicted from surface roughness alone.
Sanjeev Chandra et al. [3] discussed the techniques for defining the substrate and characterizing both chemical (oxide layers) and physical (surface topography and adsorbed and condensed pollutants) characteristics. The findings of the current study on the production of solid lamellae by the impact of particles from thermal spraying on solid surfaces were reviewed. Recent research on the impact of thermal spray particles were reviewed, and methodologies for photographing the impact and quantifying cooling rates were provided.
Ortega-Casanova et al. [4] presented a numerical simulation of heat transfer from a heated plate with the surface variation of an impact jet. All these suggestions were limited to the range of parameters used in their study. The results and the findings presented in their article may be of interest, in particular for future research in device cooling processes where temperature has an important role in their working behavior. Studies included simulating the impact of molten and semi-molten nickel particles in an atmospheric plasma spray (APS) process.
Alavi et al. [5] studied the effects of various parameters, such as solid particle core diameter, initial velocity, and temperature. Simulations showed that the size of the solid core has a large effect on the number of particles splashing upon impact. The results demonstrated that a solid bump forms as a result of the solid core in the final spalt shape. The effects of impact velocity and solid core size on particle impact were also investigated. Impact characteristics, including spatter, bump size, and amount of spreading on the substrate, depend on particle velocity and solid core size. It was found that the main effects of initial velocity were on the number of splat particles, splat thickness, and vortex deformations. The size of the solid core, however, affected the final bump size, spatter spread, and amount of spatter.
In the same line of research, the realization of numerical experiments by the finite element method is proposed in this study through an investigation of the impact, the spreading, and the solidification of an alumina particle on a rigid substrate, where the Eulerian volume of fluid (VOF) technique of two-phase flow was applied for boundary tracking. However, during the coating process, the impact of a partially melted particle on an oxidized substrate having asperities on an industrial scale was always present and was a source of an undesirable coating defect, and with the objective to better understand the interaction of the presence of the particle fusion state, the oxidation and the surface roughness of the substrate were studied by numerical simulations, and we consequently proposed solutions validated experimentally [2].
2. Modeling
In a Cartesian coordinate system, the Newtonian, incompressible, and viscous flows are quantified by the equations defined in the paragraphs below.
2.1. The Continuity Equation
This equation relates to the principle of conservation of mass in an element. It ex-presses the equality between the variation of the element mass and the difference between the quantity of fluid which enters and that which leaves at the same time [6].
The global continuity equation is given by Equation (1) [6].
In a Cartesian coordinate system, the speed is and ρ is the density. Therefore, the previous equation becomes Equation (2) [6].
2.2. The Momentum Equation
In fluid mechanics, the Navier–Stokes Equation (3) is a nonlinear partial differential equation that describes the motion of fluids in the continuum approximation. For example, the movements of air in the atmosphere, ocean currents, the flow of water in a pipe, the movement of air in rooms, and many other fluid flow phenomena are governed and are named after two 19th century physicists, Claude Navier and George Stokes [6].
where:
ρ: the density considered variable with time.
μ: dynamic viscosity is also variable.
P: pressure.
g: gravity.
2.3. Two-Phase Liquid/Solid Modeling
Many experimental and numerical investigations have focused on the study of spreading and cooling mechanisms during the impact of a single particle [6,7,8,9]. These numerical studies are divided into two distinct categories. First, the particle is modeled as part of the fluid using a method known as volume of fluid (VOF) [7], from where a domain Ω made up of two phases is considered, one liquid and the other solid, occupying the sub-domains Ω1 and Ω2, respectively. It is assumed that the medium is saturated, which implies that only these two phases are present. According to the framework of the theory of mixtures, the volume fraction of the liquid phase α is defined by [7].
2.4. Thermal Model
T: temperature.
q: volume source.
One-dimensional heat transfer models coupled with models that describe the spread of matter on the substrate treat the cooling and solidification of lamellae as purely thermal problems. These are simple models compared to models of the flow of the fluid phase, such as those developed by Xue et al. [2], which treat the formation of lamellae in a very broad way to predict their morphology as well as the effect of the various parameters [2,8].
Through this study, the physical models have been necessary for the study of the coupled phenomenon of the spread and solidification of particles, metallic or ceramic, during a thermal spraying process. The first publications on phase change date back to Stefan [10]. This is why the denomination “Stefan problem” for a phase change is always used, even for more complex formulations than the initial problem. In Stefan’s problem, the phase change is considered an instantaneous isothermal transformation. For twenty years, multiple numerical methods have been proposed in the literature to solve Stefan’s problem [11]. In general, these methods seek to approximate the position of the solidification or fusion front over time and are then divided into two main categories: mobile or deformable grid methods, also called front tracking methods; and fixed spatial grid methods, which include, for example, the equivalent specific heat method, the fictitious heat source method, and the method enthalpy. For technical and numerical reasons, the formulation opts for an equivalent heat capacity, which consists of taking into account the latent heat directly in the heat capacity cp [9]. Thus, if the solidification path is only a function of the temperature, an equivalent specific heat Equation (5) can be formally defined by [8].
The equivalent specific heat is defined as follows by Equation (6) [8].
This method makes it possible to express the thermal problem in terms of temperature by solving Equation (7) [8].
The phase change is then treated as a nonlinearity of physical properties.
2.5. The Thermal Model Used
The heat transfer model that we adopted is based on a formulation with equivalent specific heat of a moving fluid, which therefore makes it possible to control the energy conversions in the system. The equivalent specific heat transfer model is particularly well-suited to fixed domain models since they do not require the explicit imposition of the phase change condition at the solid–liquid interface. On the other hand, it is also the most suitable Formulation (8) for the numerical resolution of isothermal phase change problems [8].
3. Results and Discussions
In this numerical study, we were interested in aluminum particles melted in a plasma jet and projected onto a steel substrate. The composition and thickness of the oxide layer grow on the surface and its growth progresses with the preheating temperature of the substrate, and subsequently, the role that it plays is concretized in the process of lamella formation. The thermo-physical properties of the materials are given in Table 1.

Table 1.
Properties of the materials used [2,12].
3.1. Identification
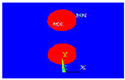
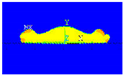
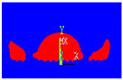
For identification, where the objective is to justify the model used (see Figure 1), we proposed to compare our simulation results of drop impact on a substrate under identical conditions to the numerical and experimental work of Xue et al. [2] in this first portion of our effort.
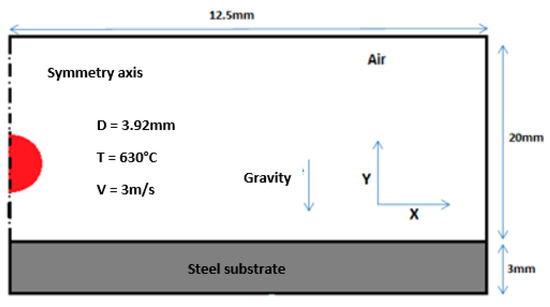
Figure 1.
Geometric configuration and spreading conditions for identification.
The effect of a completely molten aluminum particle:
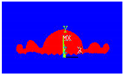
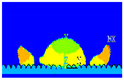
Figure 2 represents the simulation results of the impact of an aluminum particle with a diameter of 3.92 mm, initially at a temperature of 630 °C and at a speed of 3 m/s on a steel substrate that was initially at 200 °C. The droplet began to propagate at 0.1 ms. The liquid followed the topography of the surface. During droplet impact or the heat transfer model, it was used to observe that the “fingers” at the lamella periphery recently formed solidified and settled on rough asperities of the substrate. This is due to the radial flow and the high speed separation of the main lamella edge (splat) which was distributed above the asperities of the substrate; numerical results also indicated that the center of a lamella (splat) typically conformed well to the underlying substrate topography due to the stagnation pressure and shear rate of the flow which was directed steeply toward the surface, encouraging fluid to flow into the exterior cavities.
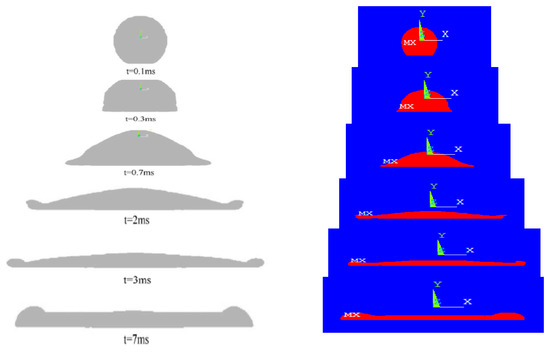
Figure 2.
Sequential impact of a 3.92 mm diameter aluminum particle with an initial speed of 3 m/s and a temperature of 630 °C on a steel substrate.
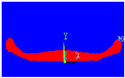
Figure 3, which is a qualitative representation of the quantitative comparison of the impact and spreading of the particle on a smooth substrate shown in Figure 2, shows the spreading factor of the alumina drop in the proposed model, where the effect of solidification on the viscous forces before spreading was considered numerically and corrected after each time step under the effect of heat transfer in the particle, compared to the experimental results of Xue et al. [2]. During the impact, the dispersion and form of the drop were comparable. The decrease stabilized at t = 0.7 ms and acquired the shape of the final spread.
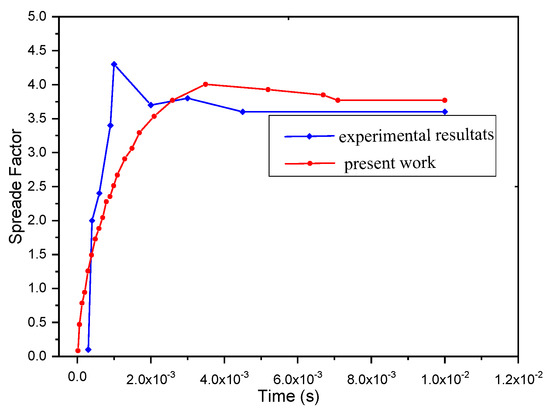
Figure 3.
Comparison between spreading factors under the same conditions.
3.2. Oxidation of the Surface of Metal Substrates
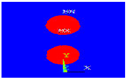
The Figure 4 show the formation of an oxide layer, composed mainly of Fe2O3, on the surface of the steel substrate was taken into account in this study in two different ways by modifying the thickness of the layer with additional thermal contact resistance.
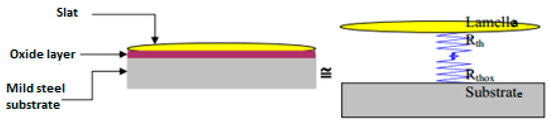
Figure 4.
Diagram showing the lamella–substrate contact after the oxidation of the surface.
The formation of an oxide layer of thickness eox was assumed to contribute to increasing the lamella–substrate contact thermal resistance by an amount equal to (Equation (9))
where kox is the thermal conductivity of the oxide formed at the surface of the substrate and eox is the thickness of this layer. eox is of the order of 0.01 mm and the thermal conductivity kox of this layer is equal to 2.9 W/m.K, a low value compared to the thermal conductivity of steel (26 W/m.K).
Rthox = eox/kox
The thermal conductivity of the iron oxide Fe2O3 was used as the value for the oxide layer thermal conductivity which is predominant in this layer. Its physical properties used in the calculations are shown in Table 1.
3.2.1. Configuration and Spreading Conditions with an Oxidation Layer
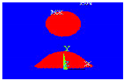
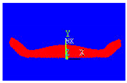
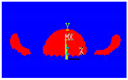
In this numerical part, the formation of an oxide layer was taken into account after preheating the Fe2O3 iron oxide on the surface of the steel beyond the transition temperature. The oxide layer indeed increased in thickness when the substrates were preheated. This thickness was of the order of 0.01 to 0.03 mm in the case of the preheated steel substrate at 630 °C, and of the order of 0.1 mm in that of the steel (see Figure 5). This oxide layer was introduced into the solidification calculations of the projected aluminum slats on metal substrates, where the initial conditions were:
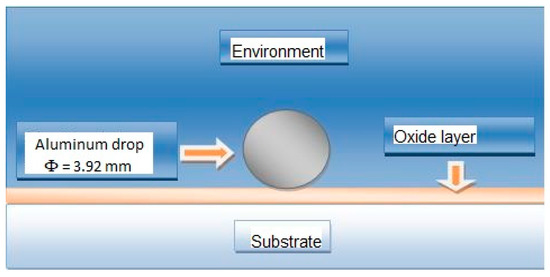
Figure 5.
Geometric configuration and spreading conditions with the presence of an oxidation layer.
- The initial temperature of the droplet considering an aluminum particle t = 630 °C.
- The initial temperature of the substrate T = 200 °C.
- Speed of the 3 m/s droplet.
3.2.2. Description of the Field of Application
In this study, by proposing to simulate and study the cooling and the dynamics of the impact and the spreading of two and more aluminum particles on an oxidized substrate with different shapes, where the high temperature in the presence of oxygen gives rise by chemical reaction of the metallic surface in contact [13] to the formation of a thin surface layer of oxide even under a controlled environment, the morphology of the spreading of a particle can be modified. Consequently, adding a thermal resistance due to the oxide layer, hence the possibility of the arrival of the second particle, by impacting on a wet target can be advantageous for the stack or disadvantageous according to the thickness of the oxide layer formed. In addition to the harsh trajectory and the duration of the particle in the jet, it gives the possibility of formation of partially molten particles; on the other hand, the roughness of the substrate promotes mechanical attachment under the effect of the speed of solidification of the spread particles. A digital tool was proposed to study the interaction of the physically possible three phenomena at the same time to better understand the sources of defect of the coatings metallics.
3.2.3. Different Pick Sizes
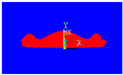
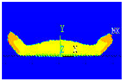
The cooling and dynamics of impact were proposed to simulate and compare the effect of peak diameter on the spreading of two aluminum particles on an oxidized substrate with varied peak sizes in this study (see Figure 6).
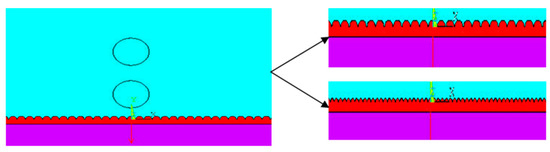
Figure 6.
Geometric configuration of the impact of two aluminum drops of 3.92 mm in diameter on a substrate at 200 °C with d = 0. 2 mm and d = 0. 4 mm.
Figure 7 shows the successive impact of two aluminum particles on an oxidized substrate which has roughness with a diameter of 0.2 mm and 0.4 mm.
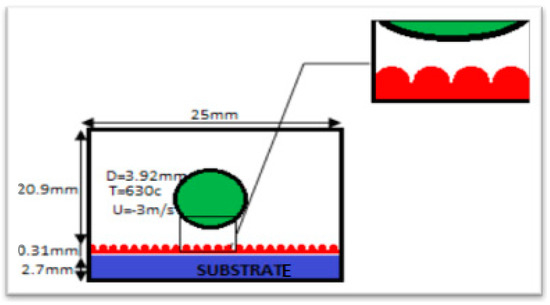
Figure 7.
Geometric configuration of the impact of two aluminum drops of 3.92 mm in diameter on a roughness substrate of 200 °C.
We made comparison of the findings from Figure 8 and Figure 9, which depict temperature differences at various substrate-level locations and provide information on the amount of heat evacuated during the cooling and solidification of impacting particles in the two research scenarios. The initial finding was that the second particle touched the first before it solidified, which means that their internal energies added up and that the density of the particles in the jet functioned as a control parameter for anything from stacking canapés to a covering. It is also important to note that when D = 0.2 mm, the substrate’s temperature was higher than when D = 0.4 mm, increasing the infected zone for small asperities. This fact helps to explain why coverslips form when the diameter of the peaks is small, increasing the surface area of the spread particle/substrate. On the other hand, the volume left over after the spreading in the asperities (Table 2) assumed a concave shape for the minor peaks, concentrating the tensions and acting as a suction cup for the lamella to enhance grip.
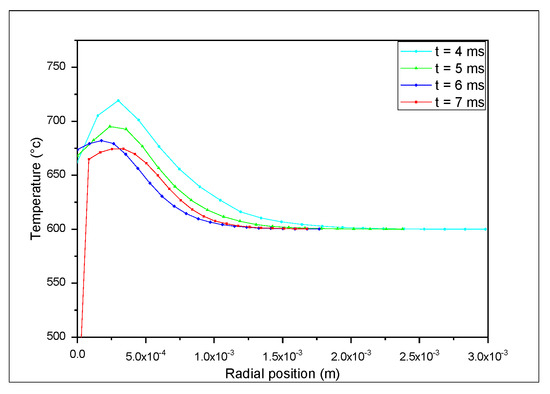
Figure 8.
Time−sequential temperature profile for D = 0.2 mm.
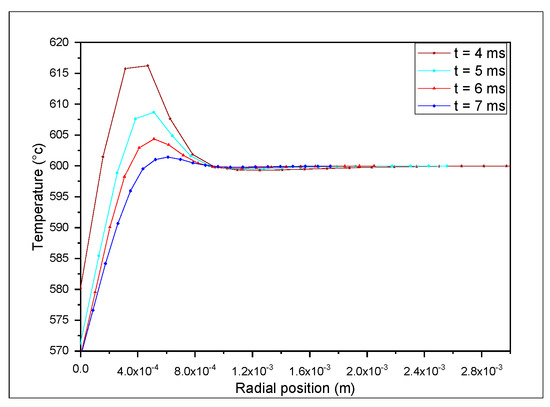
Figure 9.
Time−sequential temperature profile for D = 0.4 mm.

Table 2.
The results of the drops’ smearing of the first experiment.
Figure 10 and Figure 11’s sequential pressures clearly depict the same behavior for both scenarios with an impact pressure that favors attachment.
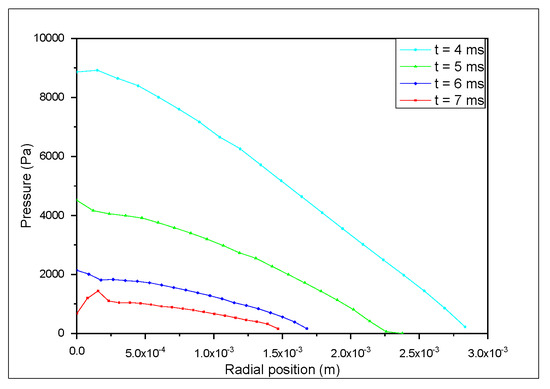
Figure 10.
Time−sequential pressure profile for D = 0.2 mm.
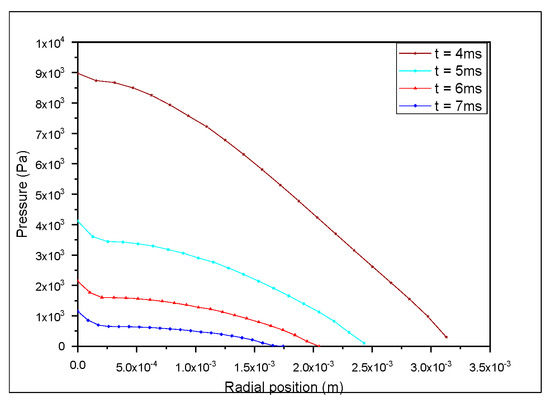
Figure 11.
Time−sequential pressure profile for D = 0.4 mm.
Figure 12 and Figure 13 show how the pressure of impact of the two particles changed over time, showing that the particle produced a high pressure that is both necessary and sufficient for a good mechanical attachment, particularly at the initial point of impact particle-substrate, which was minimized over time. This pressure also allowed for good adhesion of the lamella on the oxidized substrate. Due to the viscosity and elasticity of the two particles, it increased once more as the second particle collided with the first; however, at a lesser pressure than the first impact.
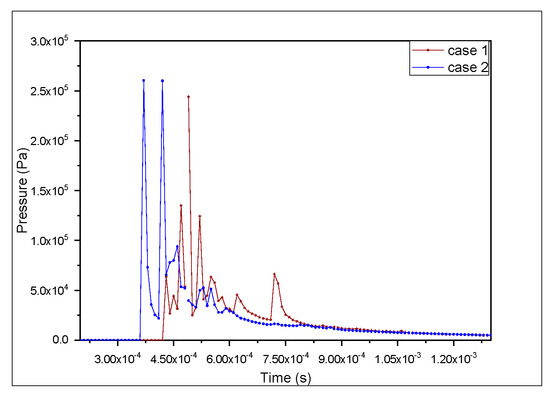
Figure 12.
The variation in impact pressure at the particle–substrate interface over time for D = 0.2 mm.
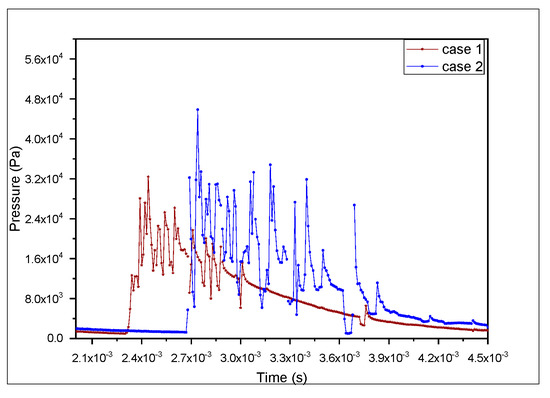
Figure 13.
The variation in impact pressure at the particle–particle interface over time for D = 0.2 mm.
The regions of excellent and unsatisfactory contact at the particle–substrate interface are depicted in Figure 14. This graphic shows the temperature profile for four locations in the substrate. It is seen that the substrate temperature rose for the four spots in each of the two situations, and that the second case’s cooling rate was slower than the first, leading to particle splashing.
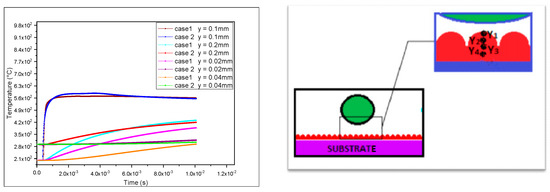
Figure 14.
Profile of temperature as a function of time for four positions along substrates vertically for the two cases.
The effect of the substrate’s topography on the spreading of the drops for D = 0.2 mm and D = 0.4 mm is shown in Figure 15. In the first instance, the spreading was nearly flawless and the gaps were filled, demonstrating strong mechanical attachment. However, in the second instance, the roughness might hinder the drop from making close contact with the substrate and as a result, damage the surface’s wettability. It should be noted that the concave and void filling forms are advantageous for a decent hanging in both situations.
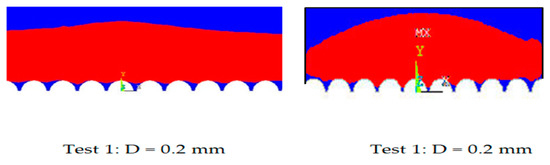
Figure 15.
The influence of the substrate’s topography on the drops’ spread in the two cases.
Figure 16 depicts the pressure distribution at the contact for the two case studies and for a spreading time series. The pressure distribution on the spreading surface exhibited negative values alternated with other positive values with a significant difference in the case of greater peaks, promoting tearing, which adequately supports the earlier observations. On the other hand, the pressure was always positive for asperities that were minimal.
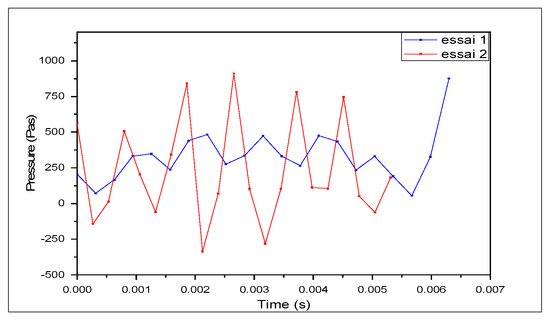
Figure 16.
A sequential pressure profile along the substrate over time.
The figures in Table 2 show the temperature distribution as a result of the two drops striking a steel substrate initially at a temperature of 630 °C. The increase in peak size promoted transverse thermal diffusion, which produced the splash in the second example, where the heat transfer model utilized detected that the lamella’s ends recorded a delay in cooling and solidification [14].
4. Conclusions
The goal of the work was to understand the mechanisms connected to the production of lamellae and therefore to regulate the defects of coatings carried out by layer stacking, which has a direct influence on the surface treatment industry and the accompanying academic research. Our results from a numerical model with a low computational cost and a high environmental cost clearly demonstrated that:
- ➢
- The adherence of the particle to the substrate determined its impact pressure, which was why the pressure that the particles produced was rather high.
- ➢
- There was a larger pressure at the place of impact (under the sipe), which led to good adhesion. The diameter of the peaks had a significant impact on adhesion, which in turn affected the final shape of the lamella formation.
- ➢
- The asperities at the level of the lamella–substrate contact were important, taking into account the oxide layer that formed automatically on the surface of metal substrates during preheating.
The model utilized in this work for the numerical experiments of impact, spreading, and solidification was based on the treatment of flows of immiscible two-phase fluid, allowing us to regulate the phenomena of attachment by thermal and dynamic factors such as temperature and pressure. In order to better understand and interpret the numerical findings, a fluid structure interaction model for inquiry was provided, which highlights the results of computations in the form of mechanical characteristics such as stress concentrations and interfacial deformations.
Author Contributions
Conceptualization, S.T. and M.Z.; methodology, O.L.; software, Y.C.; validation, O.L., S.T. and M.Z.; formal analysis, O.L.; investigation, M.Z.; resources, Y.C.; data curation, O.L.; writing—original draft preparation, S.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sobolev, V.V.; Guilemany, J.M. Effect of oxidation on droplet flattening and splat-substrate interaction in thermal spraying. J. Therm. Spray Technol. 1999, 8, 523–530. [Google Scholar] [CrossRef]
- Xue, M.; Heichal, Y.; Chandra, S.; Mostaghimi, J. Modeling the impact of a mol-ten metal droplet on a solid surface using variable interfacial thermal contact resistance. J. Mater. Sci. 2007, 42, 9–18. [Google Scholar] [CrossRef] [Green Version]
- Chandra, S.; Fauchais, P. Formation of solid splats during thermal spray deposition. J. Therm. Spray Technol. 2009, 18, 148–180. [Google Scholar] [CrossRef]
- Ortega-Casanova, J.; Granados-Ortiz, F.J. Numerical simulation of the heat transfer from a heated plate with surface variations to an impinging jet. Int. J. Heat Mass Transf. 2014, 76, 128–143. [Google Scholar] [CrossRef]
- Alavi, S.; Passandideh-Fard, M.; Mostaghimi, J. Simulation of semi-molten particle impacts including heat transfer and phase change. J. Therm. Spray Technol. 2012, 21, 1278–1293. [Google Scholar] [CrossRef]
- Zirari, M.; Abdellah El-Hadj, A.; Bacha, N. Numerical analysis of partially molten splat during thermal spray process using the finite element method. Appl. Surf. Sci. 2010, 256, 3581–3585. [Google Scholar] [CrossRef]
- Tahar, S.; Zirari, M.; Benzerdjeb, A.; Hanini, S. Numerical simulation EF/VOF to study the influence of the surface condition of the formation of the slats of a nickel deposit produced by plasma spraying. Ann. Chim. Sci. Matériaux 2018, 42, 165–180. [Google Scholar]
- Abdellah El-Hadj, A.; Zirari, M.; Bacha, N. Numerical analysis of the effect of the gas temperature on splat formation during thermal spray process. Appl. Surf. Sci. 2011, 257, 1643–1648. [Google Scholar] [CrossRef]
- Zirari, M.; Tahar, S.; Chandra, S.; Bacha, N. Numerical analysis of the dynamics and the rapid solidification on splat formation during thermal spray process using the finite element method. In Proceedings of the 21ème Congrès Français de Mécanique, Bordeaux, France, 26–30 August 2013. [Google Scholar]
- Ghafouri-Azar, R.; Mostaghimi, J.; Chandra, S.; Charmchi, M. A stochastic model to simulate the formation of a thermal spray coating. J. Therm. Spray Technol. 2003, 12, 53–69. [Google Scholar] [CrossRef]
- Voller, V.R. Fast implicit finite-difference method for the analysis of phase change problems. Numer. Heat Transf. 1990, 17, 155–169. [Google Scholar] [CrossRef]
- Shinde, S.S.; Bansode, R.A.; Bhosale, C.H.; Rajpure, K.Y. Physical properties of hematite α-Fe2O3 thin films: Application to photoelectrochemical solar cells. J. Semicond. 2011, 32, 013001. [Google Scholar] [CrossRef]
- Maitre, A.; Denoirjean, A.; Fauchaisb, P.; Lefortb, P. Plasma-jet coating of preoxidized XC38 steel: Influence of the nature of the oxide layer. J. Phys. Chem. Chem. Phys. 2002, 4, 3887–3893. [Google Scholar] [CrossRef]
- Le Bot, C.; Vincent, S.; Meillot, E.; Sarret, F.; Caltagirone, J.P.; Bianchi, L. Numerical simulation of several impacting ceramic droplets with liquid/solid phase change. Surf. Coat. Technol. 2015, 268, 272–277. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).