Evaluation of Weighted Mean of Vectors Algorithm for Identification of Solar Cell Parameters
Abstract
:1. Introduction
- A novel optimization method (INFO) is applied to estimate the variables of three models of solar cell: the three-diode model of solar cell (TDMSC), double-diode model of solar cell (DDMSC), and single-diode model of solar cell (SDMSC).
- The fitness function of the identification work is to minimize the RSME between the measured data of current and the data of simulated current based on the parameters identified from the algorithms.
- The INFO technique is compared with another seven methods: Harris hawk optimization, tunicate swarm algorithm, sine–cosine algorithm, moth–flame optimizer, grey wolf optimization, chimp optimization algorithm, and Runge–Kutta Optimization.
- The statistical analysis is applied to measure and assess the performance of the proposed RUN algorithm along with all competing algorithms. The analysis contains several points, such as the mean, minimum, maximum, and standard deviation for the objective function over 30 independent runs.
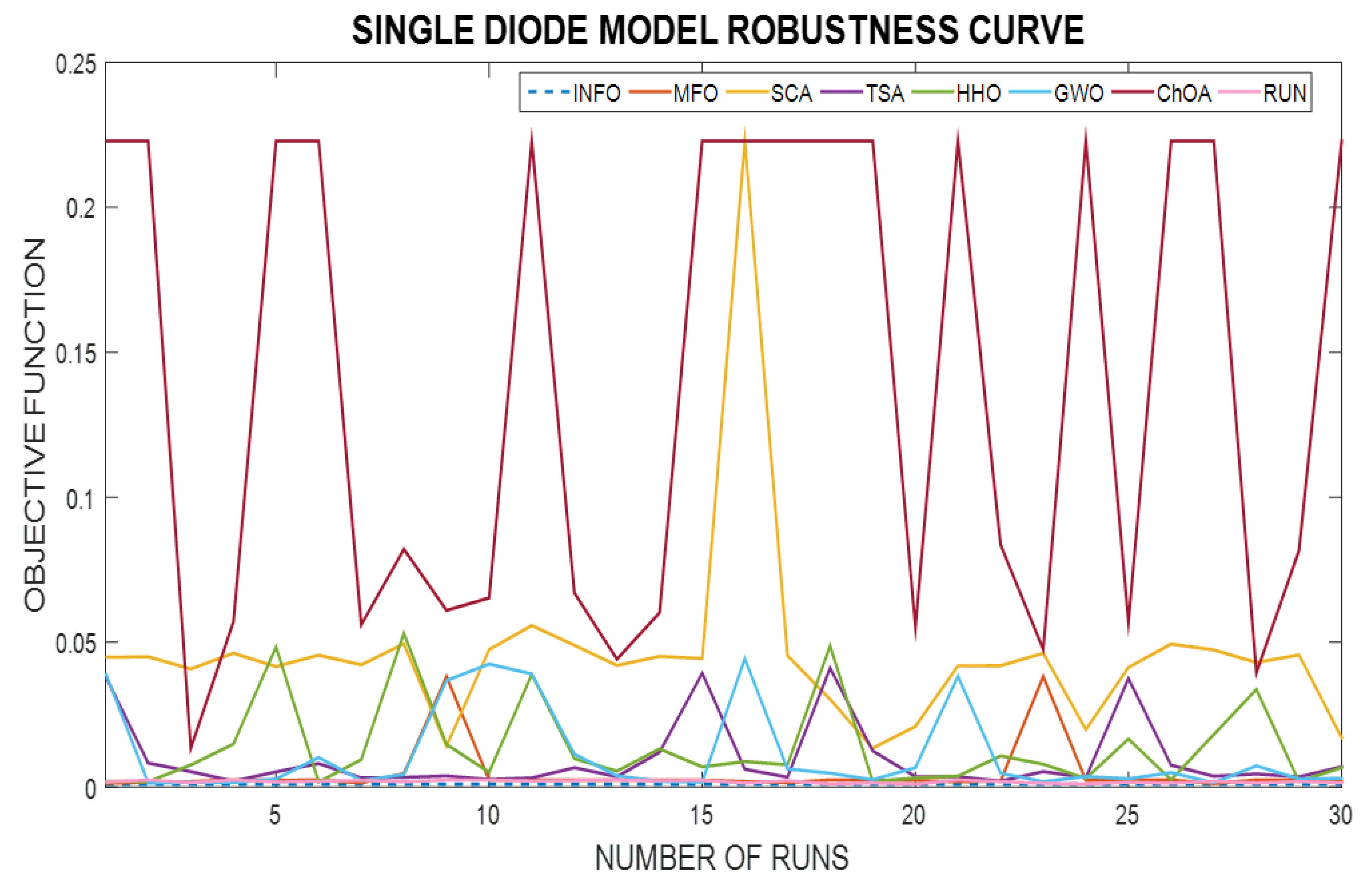
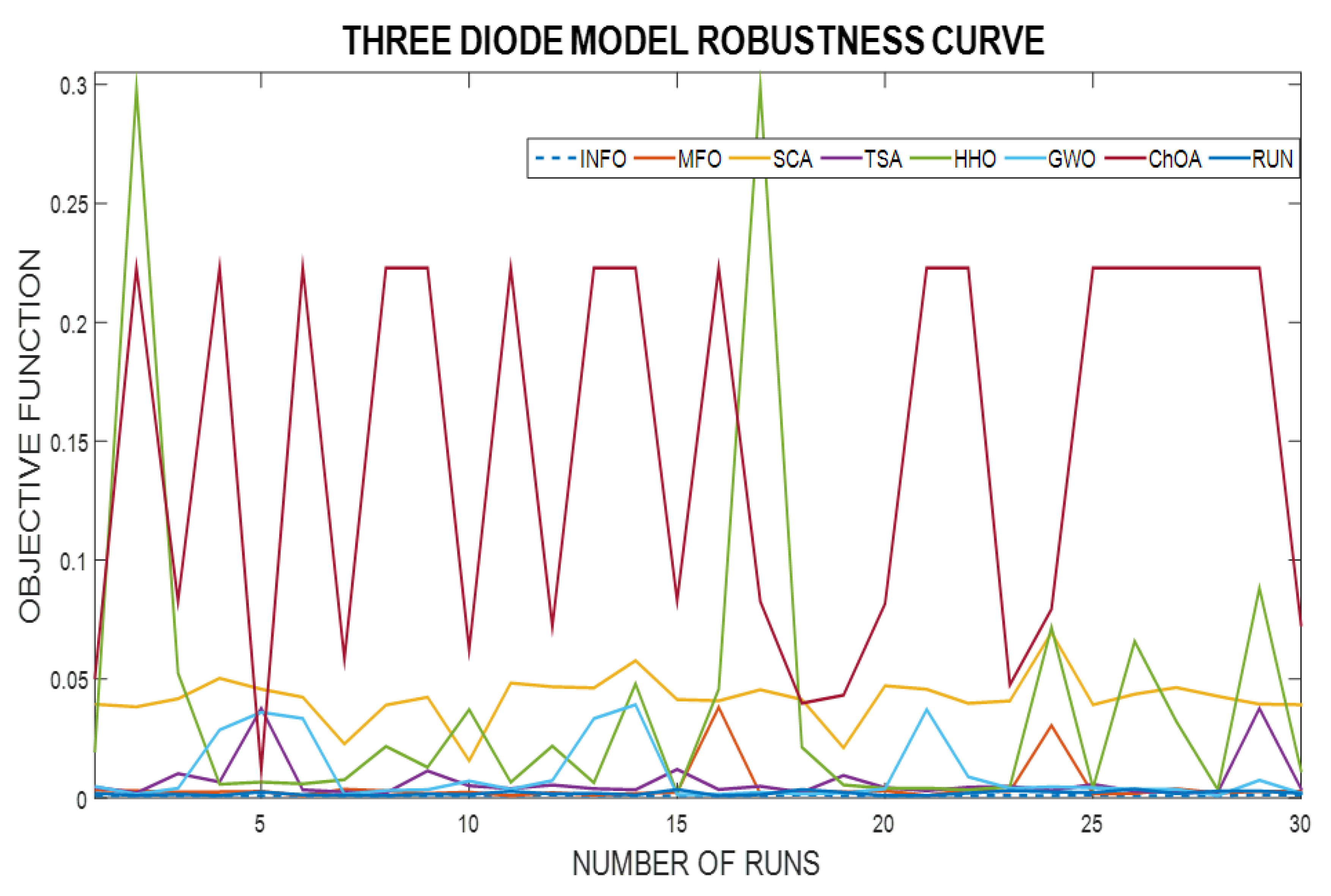
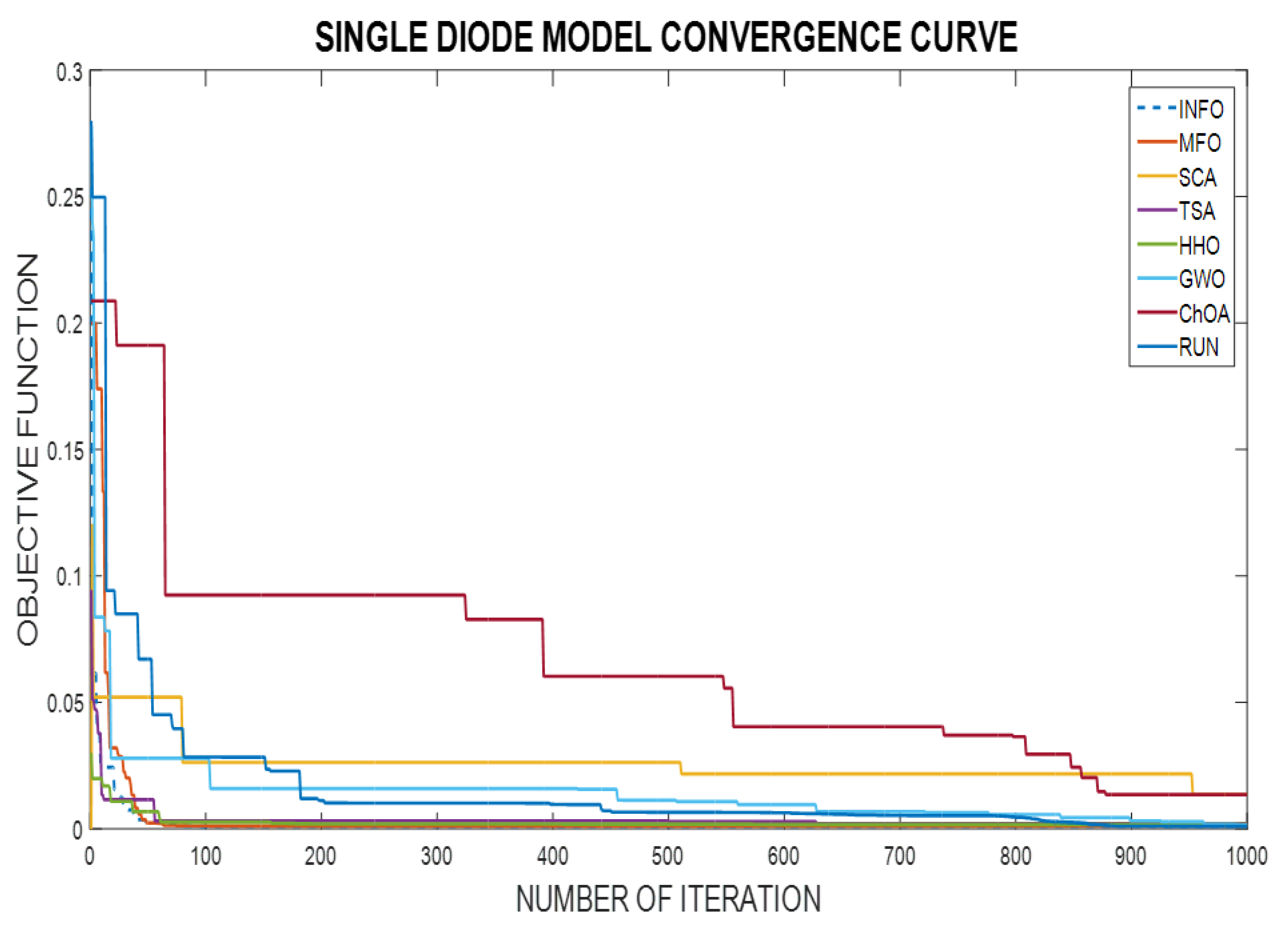
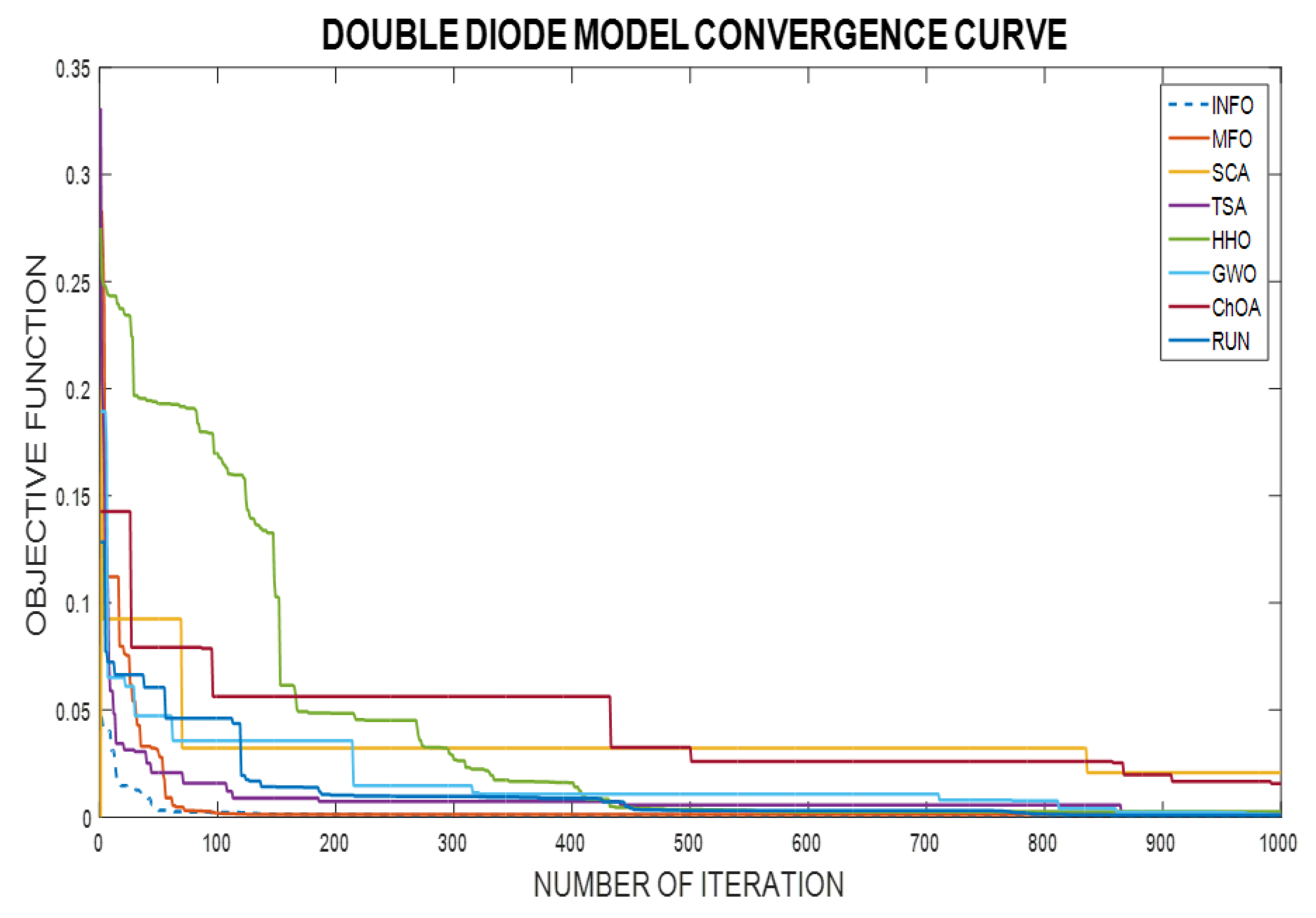
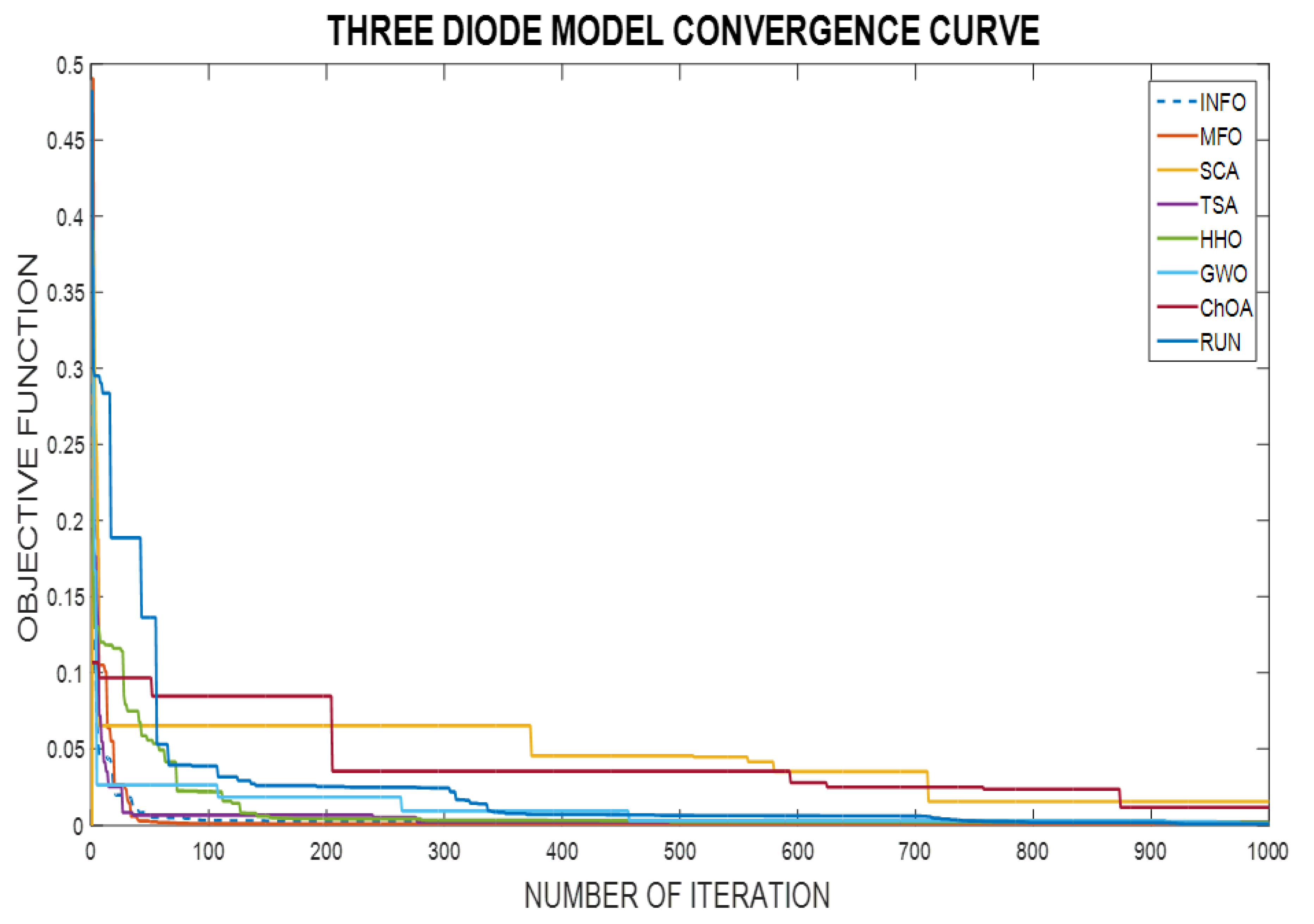
- The fastest and most reliable algorithm is determined according to the convergence and robustness curves for all algorithms.
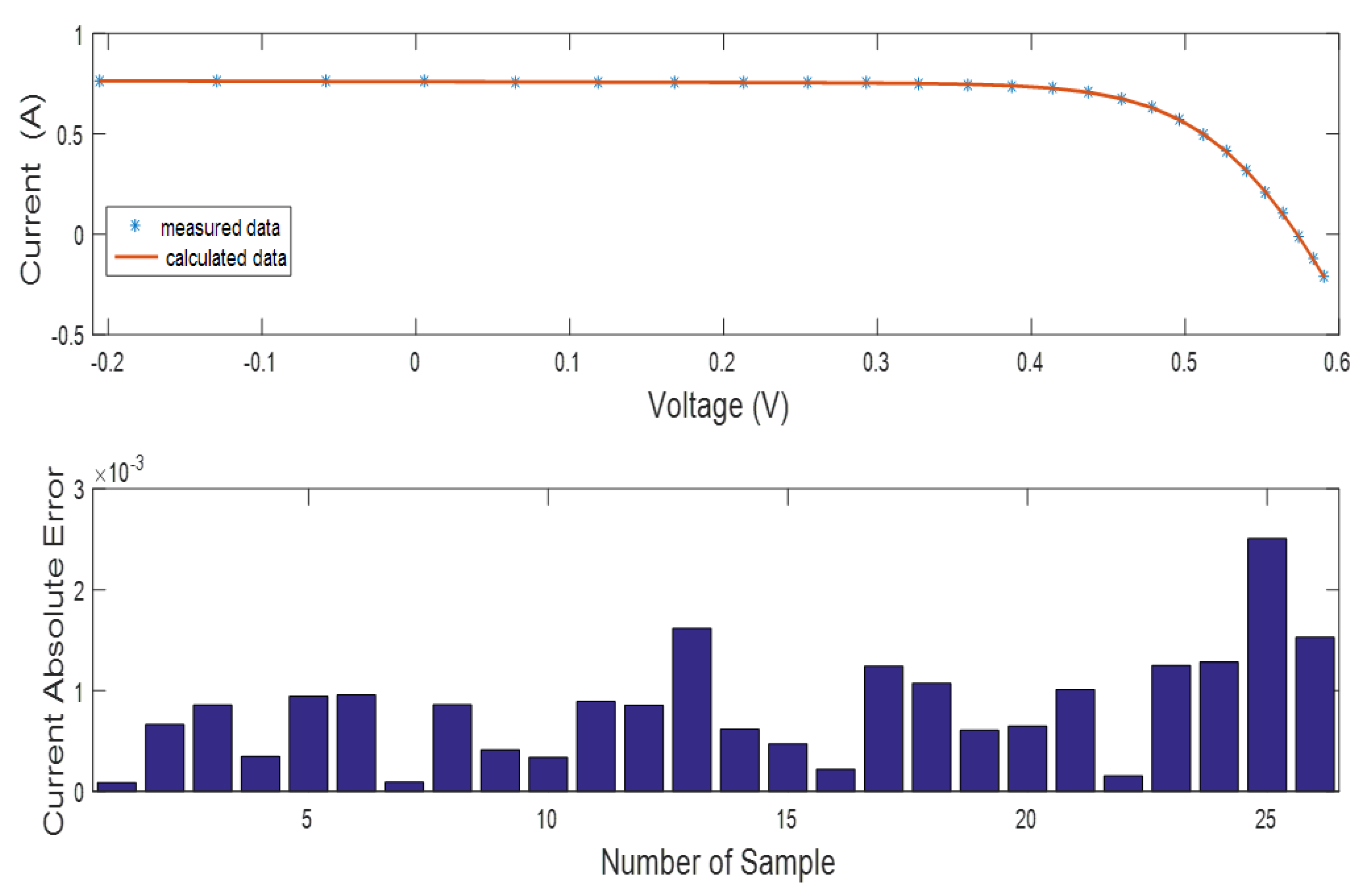
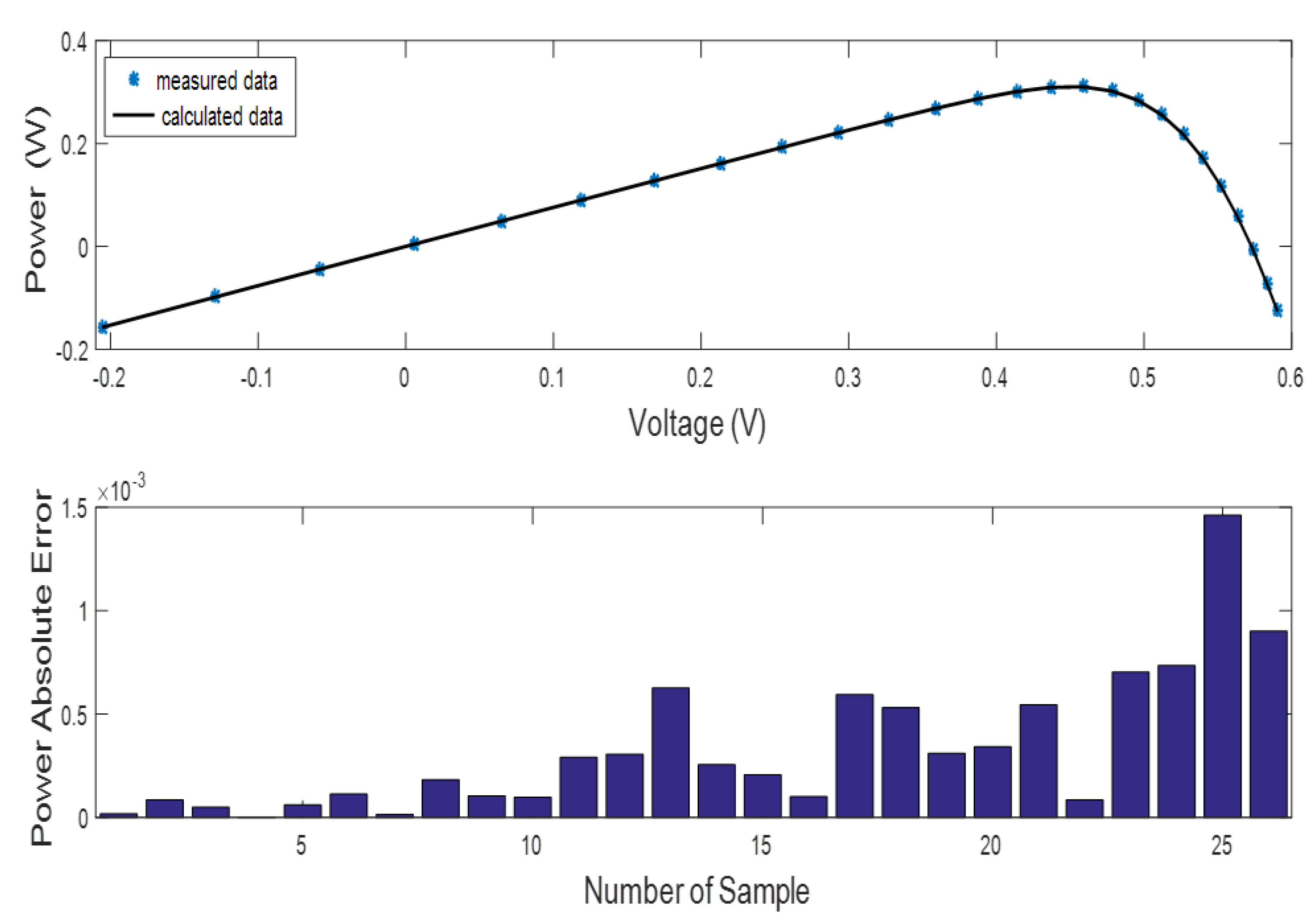
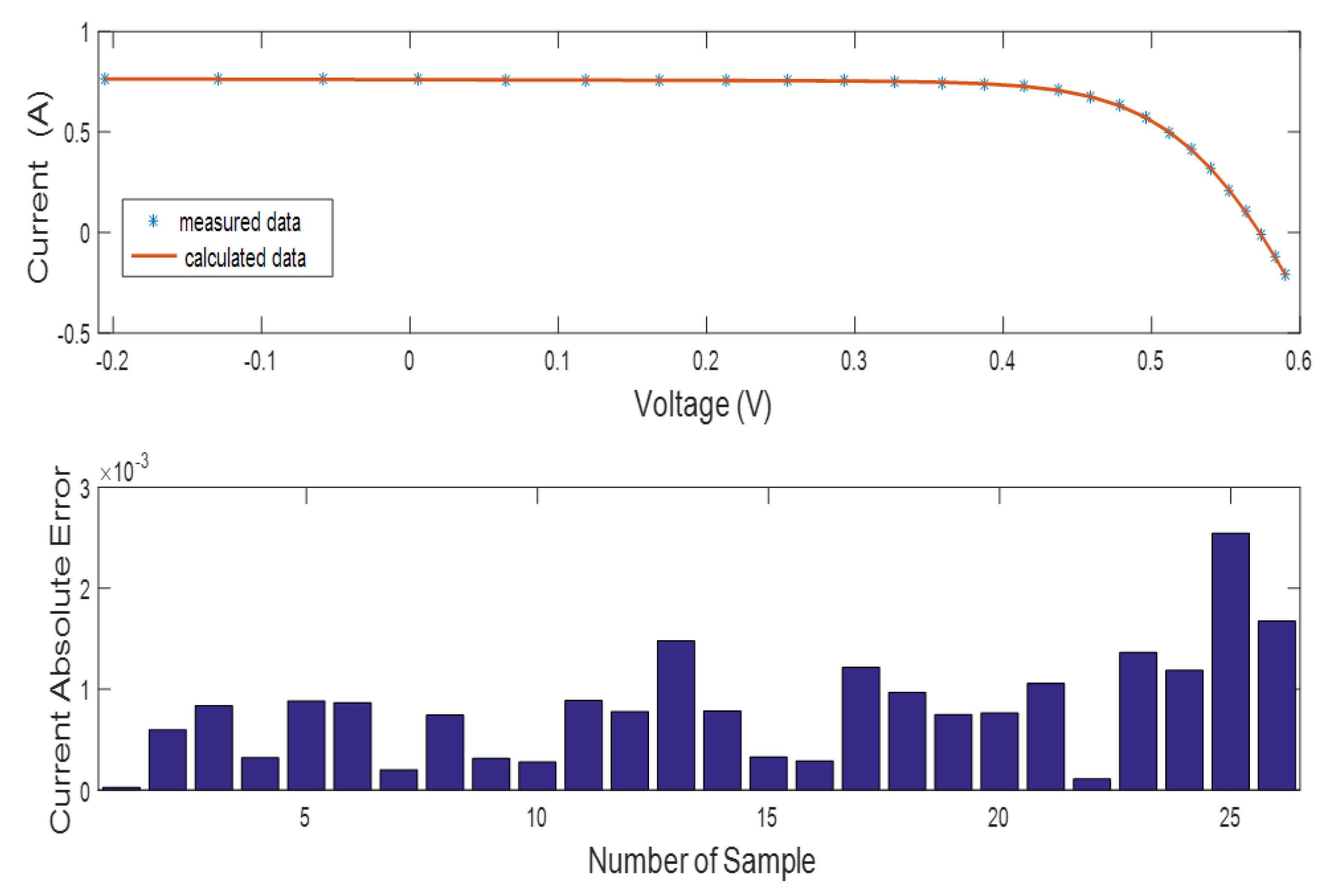
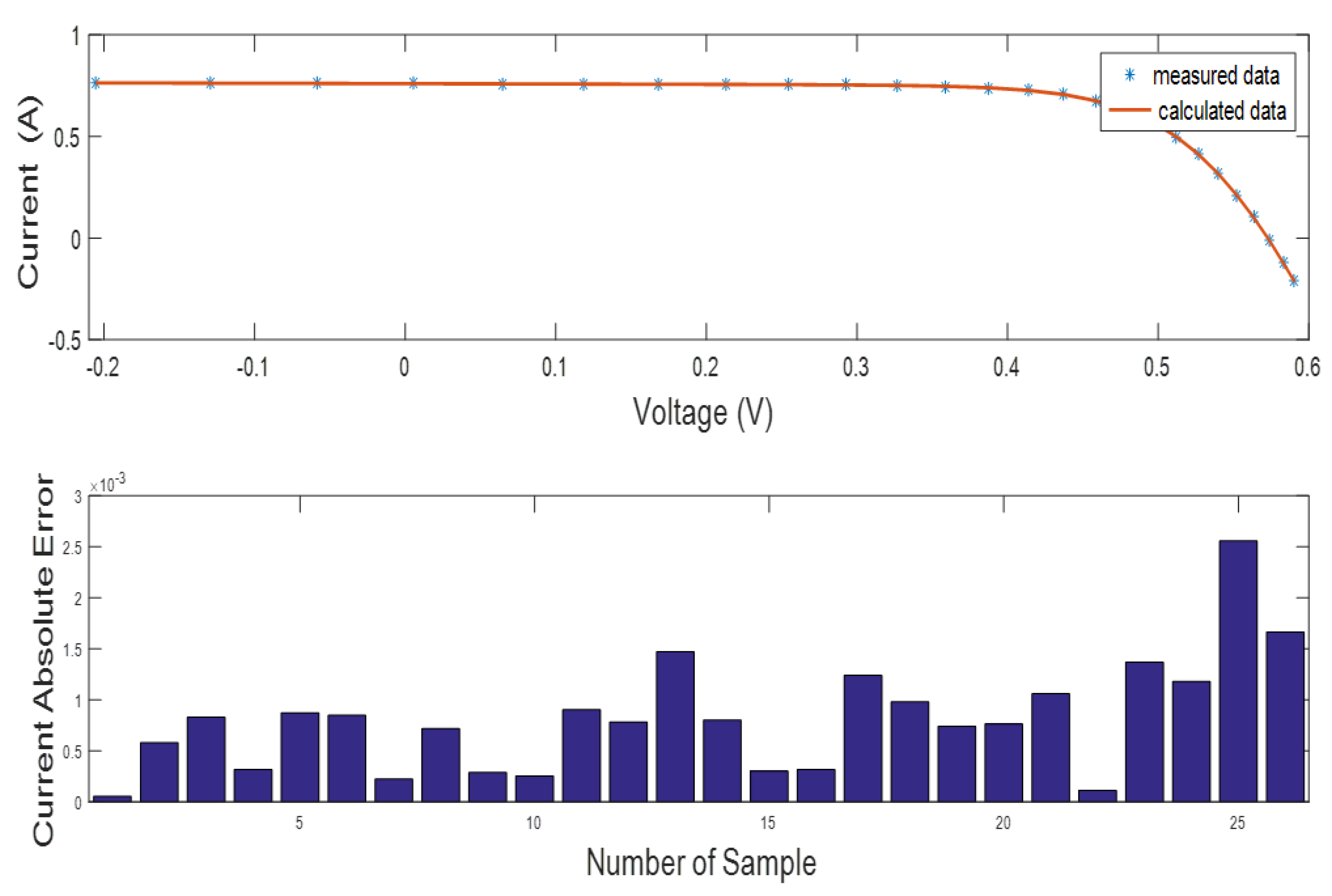
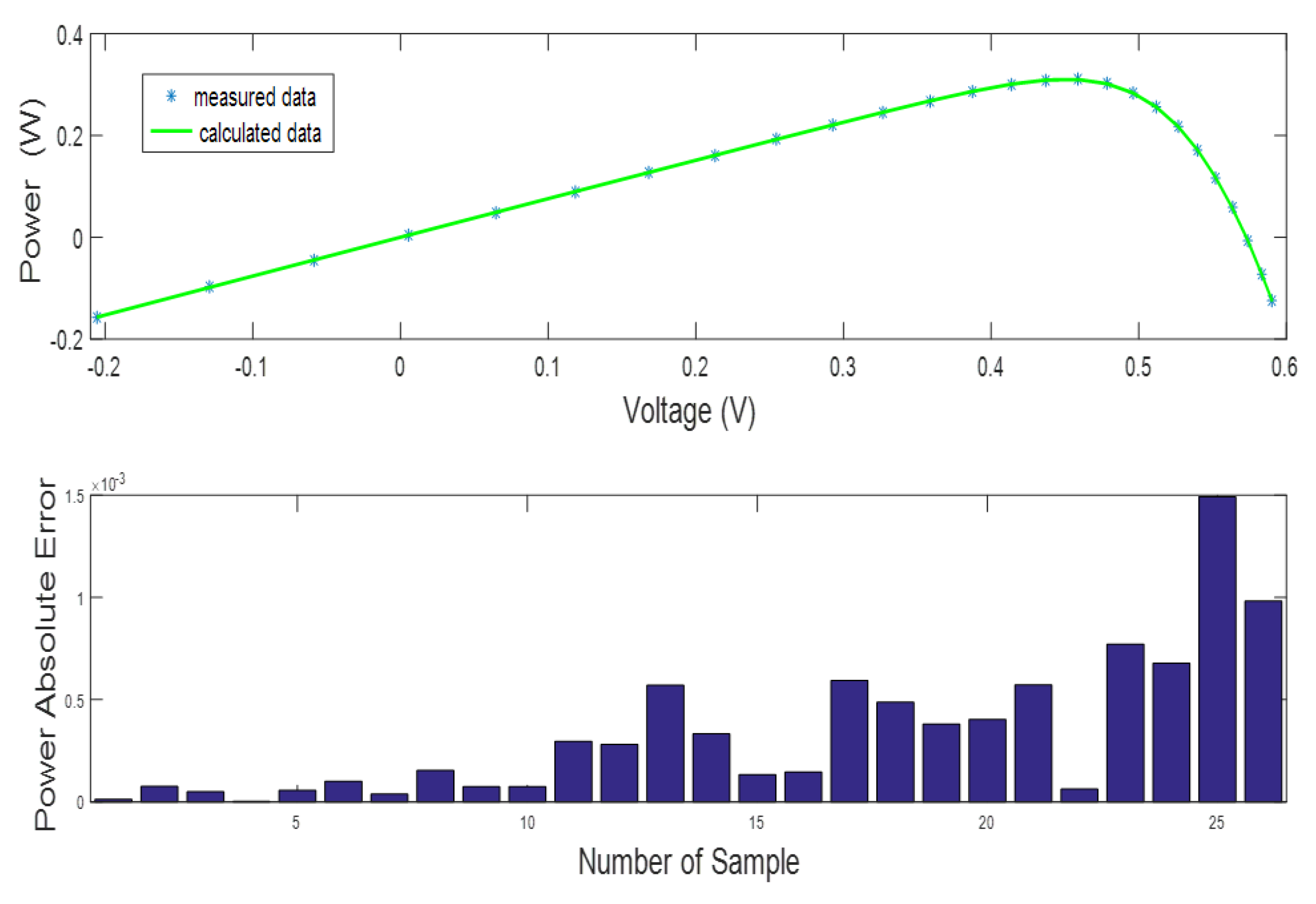
- The efficiency of the INFO method is also determined based on the absolute error values of current and power among both measured and simulated data.
2. Problem Formulation of Solar Cell Models
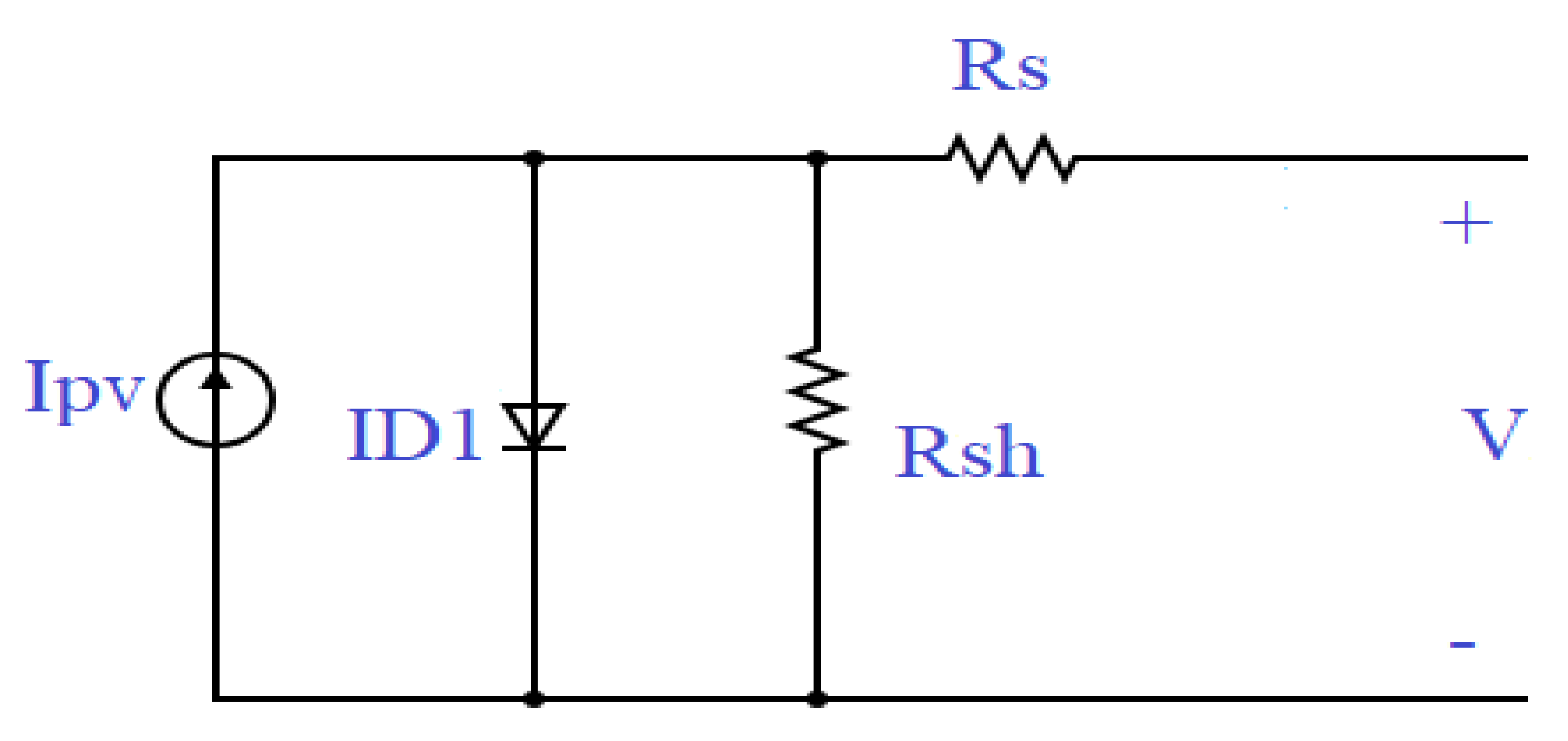
2.1. Analysis of SDMCS
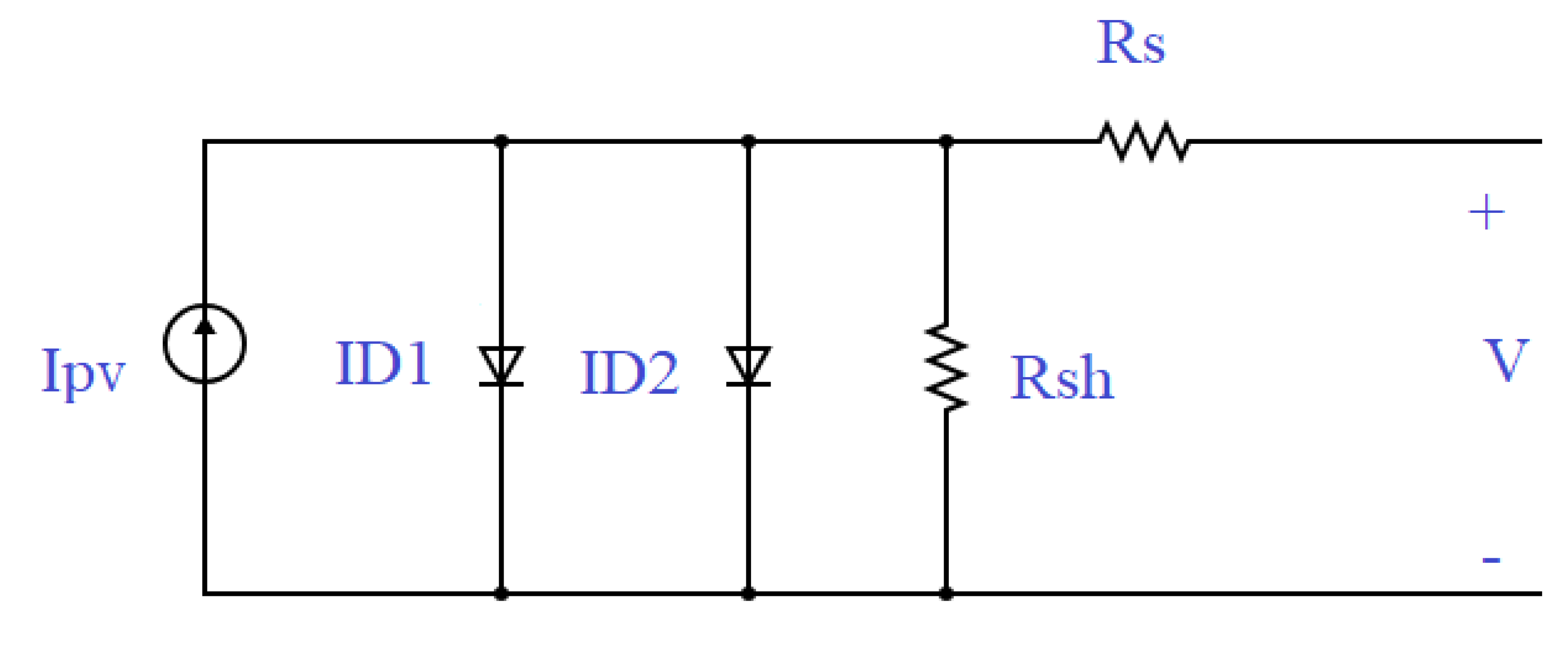
2.2. Analysis of DDMSC
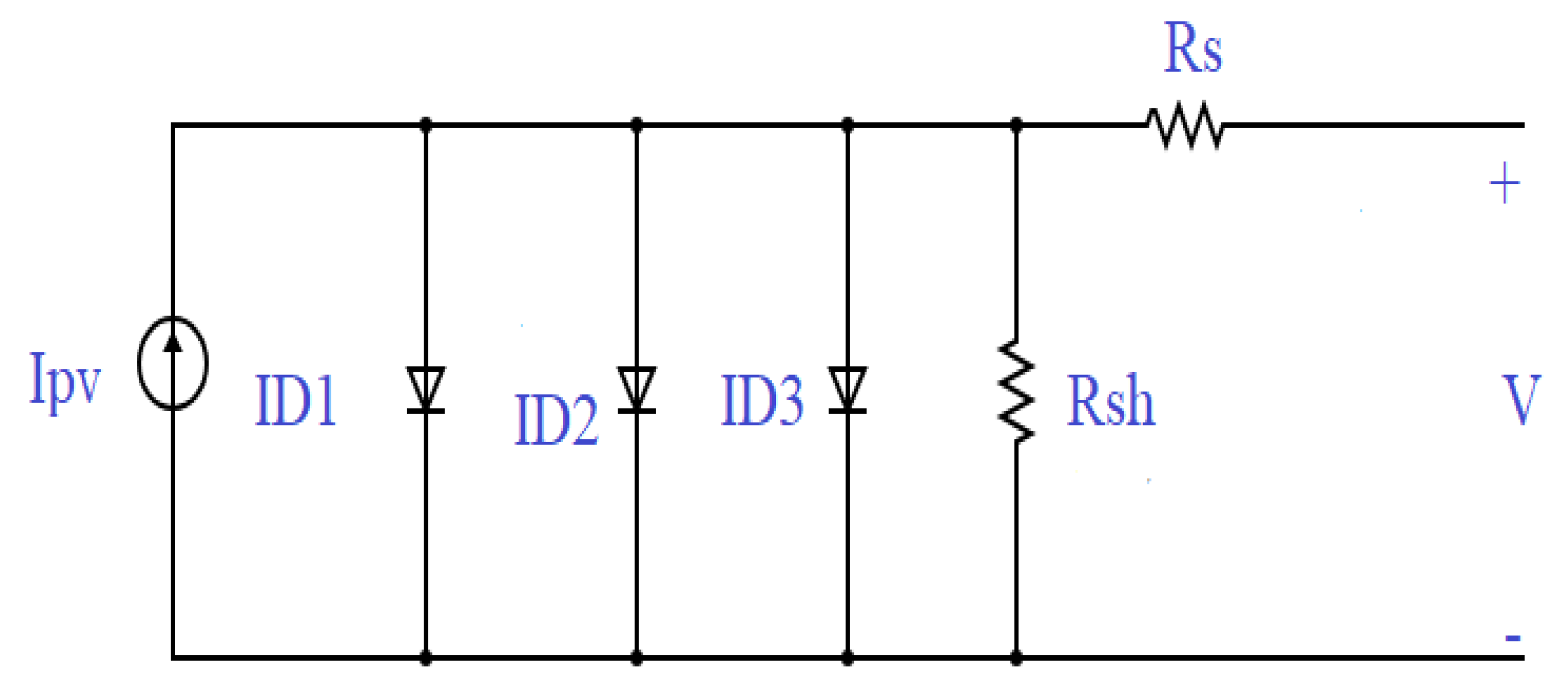
2.3. Analysis of TDMSC
3. Fitness Function for Identifying the Parameters of the Solar Cell
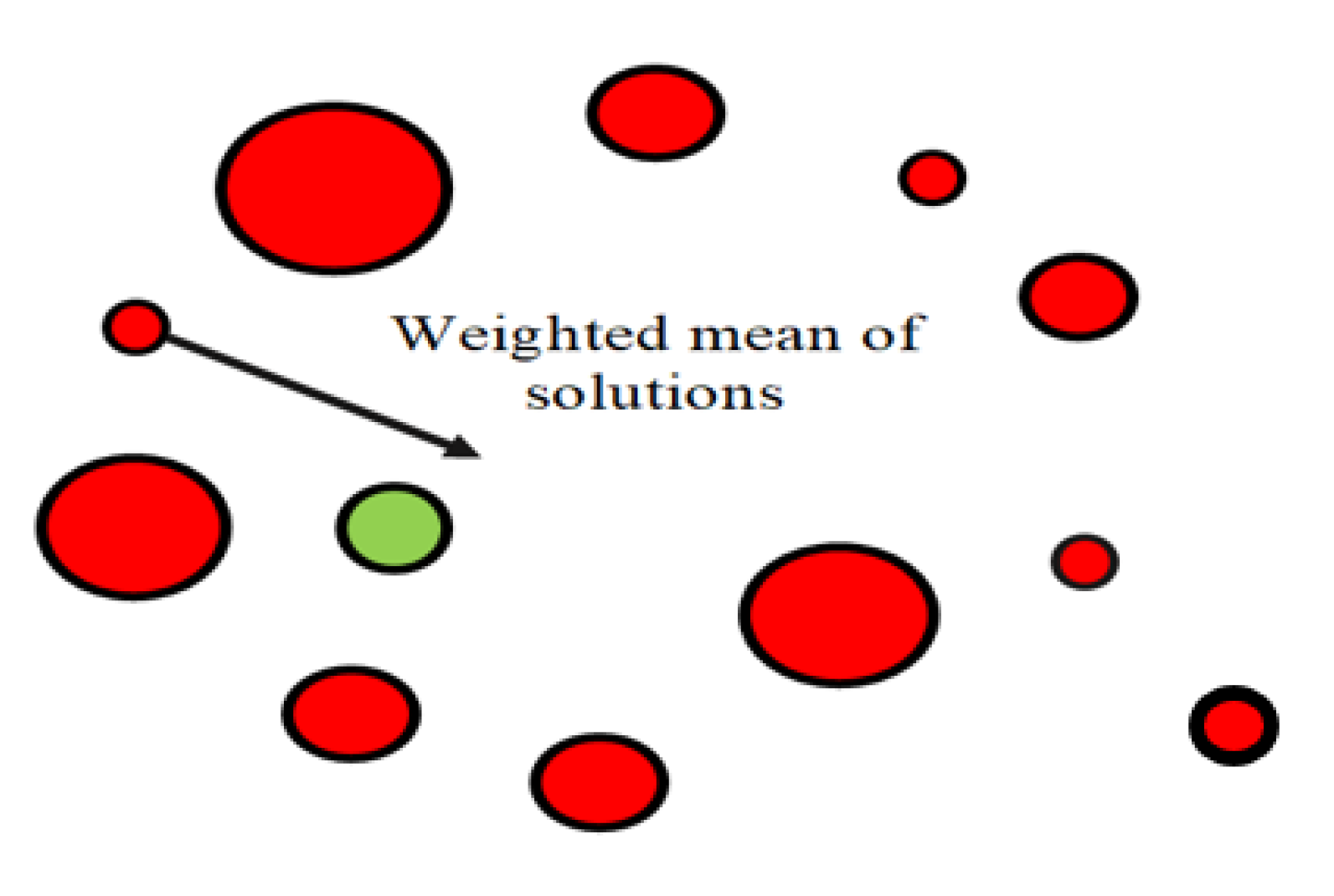
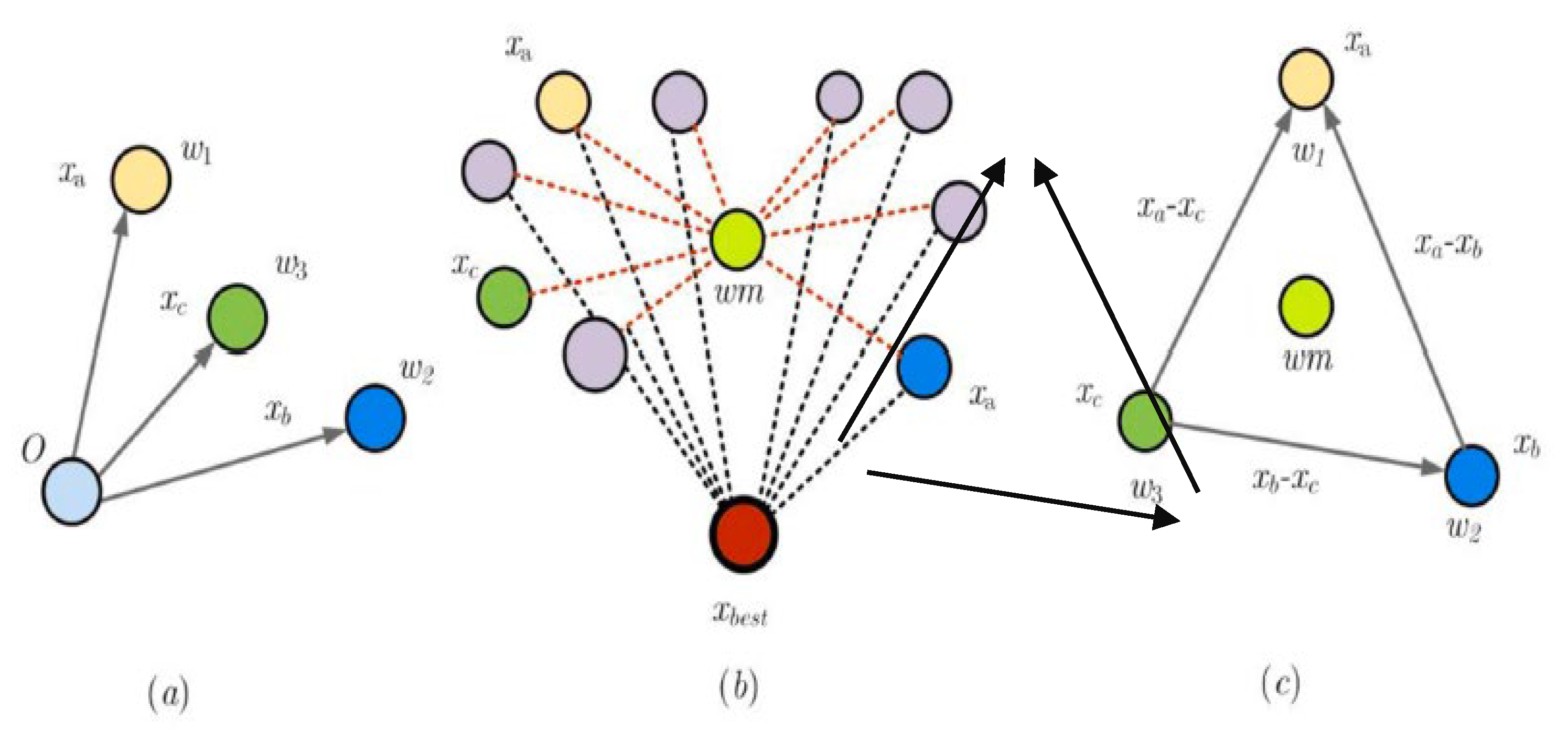
4. Weighted Mean Definition
Weighted Mean Definition from a Mathematical Point of View
5. The Weighted Mean from Vectors Algorithm
- Phase 1: Updating rules;
- Phase 2: Vector combination;
- Phase 3: Local search.
5.1. The Initialization Phase
5.2. The Rule-Updating Phase
5.3. The Vector-Combining Phase
5.4. The Local Search Phase
| Algorithm 1: The pseudocode for the INFO algorithm |
| Set the parameters of and Produce the initial population Compute an objective function value from each vector: . Determine the optimal vector . Do { Choose randomly in the range . Compute by using Equations (10)–(12) and (15)–(17). Update by using Equation (19) and with Equation (24). Compute the solutions and using Equation (23). Compute by using Equation (26). Compute by using Equation (27). Compute by using Equation (27). Compute by using Equation (29). Compute by using Equation (30). Compute the value of objective function, . = Update the optimal vector . } Return the vector as a final solution. |
6. Numerical Analysis of Results
6.1. SDMSC Extracted Results
6.2. DDMSC Extracted Results
6.3. TDMSC Extracted Results
6.4. Statistical Analysis of the Three Solar Cell Models
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RE | Renewable energy |
| SE | Solar energy |
| PV | Photovoltaic |
| SD | Single-diode |
| DD | Double-diode |
| TD | Triple-diode |
| INFO | Weighted mean of vectors |
| HHO | Harris hawk optimization |
| TSA | Tunicate swarm algorithm |
| SCA | Sine–cosine algorithm |
| MFO | Moth–flame optimizer |
| GWO | Grey wolf optimization |
| ChOA | Chimp optimization algorithm |
| RUN | Runge–Kutta optimization |
| TDMSC | Three-diode model of solar cell |
| DDMSC | Double-diode model of solar cell |
| SDMSC | Single-diode model of solar cell |
| RMSE | Root-mean-square error |
References
- Chenouard, R.; El-Sehiemy, R.A. An interval branch and bound global optimization algorithm for parameter estimation of three photovoltaic models. Energy Convers. Manag. 2020, 205, 112400. [Google Scholar] [CrossRef]
- Ghasemiasl, R.; Abhari, M.K.; Javadi, M.A.; Ghomashi, H. 4E investigating of a combined power plant and converting it to a multigeneration system to reduce environmental pollutant production and sustainable development. Energy Convers. Manag. 2021, 245, 114468. [Google Scholar] [CrossRef]
- Javadi, M.A.; Najafi, N.J.; Abhari, M.K.; Jabery, R.; Pourtaba, H. 4E analysis of three different configurations of a combined cycle power plant integrated with a solar power tower system. J. Sustain. Energy Technol. Assess. 2021, 48, 101599. [Google Scholar] [CrossRef]
- Ismaeel, A.A.; Houssein, E.H.; Oliva, D.; Said, M. Gradient-based optimizer for parameter extraction in photovoltaic models. IEEE Access 2021, 9, 13403–13416. [Google Scholar] [CrossRef]
- Yousri, D.; Abd Elaziz, M.; Oliva, D.; Abualigah, L.; Al-qaness, M.A.; Ewees, A.A. Reliable applied objective for identifying simple and detailed photovoltaic models using modern metaheuristics: Comparative study. Energy Convers. Manag. 2020, 223, 113279. [Google Scholar] [CrossRef]
- Jordehi, A.R. Enhanced leader particle swarm optimization (ELPSO): An ef_cient algorithm for parameter estimation of photovoltaic (PV) cells and modules. Sol. Energy 2018, 159, 78–87. [Google Scholar] [CrossRef]
- El-Negamy, M.; Eteiba, M.; El-Bayoumi, G. Modeling and simulation of Egyptsat-1 satellite system powered by photovoltaic module. J. Am. Sci. 2013, 9, 110–116. [Google Scholar]
- Mostafa, M.; Abdullah, H.M.; Mohamed, M.A. Modeling and experimental investigation of solar stills for enhancing water desalination process. IEEE Access 2020, 8, 219457–219472. [Google Scholar] [CrossRef]
- Javadia, M.A.; Khalajia, M.; Ghasemiasl, R. Exergoeconomic and environmental analysis of a combined power and water desalination plant with parabolic solar collector. Desalination Water Treat. 2020, 193, 212–223. [Google Scholar] [CrossRef]
- Mahdavi, S.; Sarhaddi, F.; Hedayatizadeh, M. Energy/exergy basedevaluation of heating/cooling potential of PV/T and earth-air heat exchanger integration into a solar greenhouse. Appl. Thermal Eng. 2019, 149, 996–1007. [Google Scholar] [CrossRef]
- Said, M.; Shaheen, A.M.; Ginidi, A.R.; El-Sehiemy, R.A.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Estimating Parameters of Photovoltaic Models Using Accurate Turbulent Flow of Water Optimizer. Processes 2021, 9, 627. [Google Scholar] [CrossRef]
- Shaban, H.; Houssein, E.H.; Pérez-Cisneros, M.; Oliva, D.; Hassan, A.Y.; Ismaeel, A.A.; AbdElminaam, D.S.; Deb, S.; Said, M. Identification of Parameters in Photovoltaic Models through a Runge Kutta Optimizer. Mathematics 2021, 9, 2313. [Google Scholar] [CrossRef]
- Ahmad, W.; Liu, D.; Wu, J.; Ahmad, W.; Wang, Y.; Zhang, P.; Zhang, T.; Zheng, H.; Chen, L.; Chen, Z.D.; et al. Enhanced Electrons Extraction of Lithium-Doped SnO2_{2} Nanoparticles for Efficient Planar Perovskite Solar Cells. IEEE J. Photovolt. 2019, 9, 1273–1279. [Google Scholar] [CrossRef]
- Abdelminaam, D.S.; Said, M.; Houssein, E.H. Turbulent flow of water-based optimization using new objective function for parameter extraction of six photovoltaic models. IEEE Access 2021, 9, 35382–35398. [Google Scholar] [CrossRef]
- AbdElminaam, D.S.; Houssein, E.H.; Said, M.; Oliva, D.; Nabil, A. An Efficient Heap-Based Optimizer for Parameters Identification of Modified Photovoltaic Models. Ain Shams Eng. J. 2022, 13, 101728. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Arefifar, S.A.; Paz, F.; Ordonez, M. Improving Solar Power PV Plants Using Multivariate Design Optimization. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 638–650. [Google Scholar] [CrossRef]
- Kumar, N.; Saha, T.K.; Dey, J. Sliding-Mode Control of PWM Dual Inverter-Based Grid-Connected PV System: Modeling and Performance Analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 435–444. [Google Scholar] [CrossRef]
- Lun, S.; Wang, S.; Yang, G.; Guo, T. A new explicit double-diode modeling method based on Lambert W-function for photovoltaic arrays. Sol. Energy 2015, 116, 69–82. [Google Scholar] [CrossRef]
- Ayang, A.; Wamkeue, R.; Ouhrouche, M.; Djongyang, N.; Salomé, N.E.; Pombe, J.K.; Ekemb, G. Maximum likelihood parameters estimation of single-diode model of photovoltaic generator. Renew. Energy 2019, 130, 111–121. [Google Scholar] [CrossRef]
- Toledo, F.J.; Blanes, J.M.; Galiano, V. Two-Step Linear Least-Squares Method for Photovoltaic Single-Diode Model Parameters Extraction. IEEE Trans. Ind. Electron. 2018, 65, 6301–6308. [Google Scholar] [CrossRef]
- Et-Torabi, K.; Nassar-eddine, I.; Obbadi, A.; Errami, Y.; Rmaily, R.; Sahnoun, S.; El Fajri, A.; Agunaou, M. Parameters estimation of the single and double diode photovoltaic models using a Gauss–Seidel algorithm and analytical method: A comparative study. Energy Convers. Manag. 2017, 148, 1041–1054. [Google Scholar] [CrossRef]
- Ma, X.; Huang, W.H.; Schnabel, E.; Köhl, M.; Brynjarsdóttir, J.; Braid, J.L.; French, R.H. Data-Driven II–VV Feature Extraction for Photovoltaic Modules. IEEE J. Photovolt. 2019, 9, 1405–1412. [Google Scholar] [CrossRef] [Green Version]
- Saleem, H.; Karmalkar, S. An Analytical Method to Extract the Physical Parameters of a Solar Cell From Four Points on the Illuminated I-V Curve. IEEE Electron Device Lett. 2009, 30, 349–352. [Google Scholar] [CrossRef]
- Soeriyadi, A.H.; Wang, L.; Conrad, B.; Li, D.; Lochtefeld, A.; Gerger, A.; Barnett, A.; Perez-Wurfl, I. Extraction of Essential Solar Cell Parameters of Subcells in a Tandem Structure With a Novel Three-Terminal Measurement Technique. IEEE J. Photovolt. 2018, 8, 327–332. [Google Scholar] [CrossRef]
- Houssein, E.H.; Deb, S.; Oliva, D.; Rezk, H.; Alhumade, H.; Said, M. Performance of gradient-based optimizer on charging station placement problem. Mathematics 2021, 9, 2821. [Google Scholar] [CrossRef]
- Ismaeel, A.A.; Houssein, E.H.; Hassan, A.Y.; Said, M. Performance of gradient-based optimizer for optimumwind cube design. Comput., Mater. Contin. 2022, 71, 339–353. [Google Scholar]
- Houssein, E.H.; Helmy, B.E.D.; Rezk, H.; Nassef, A.M. An enhanced Archimedes optimization algorithm based on Local escaping operator and Orthogonal learning for PEM fuel cell parameter identification. Eng. Appl. Artif. Intell. 2021, 103, 104309. [Google Scholar] [CrossRef]
- Said, M.; Houssein, E.H.; Deb, S.; Alhussan, A.A.; Ghoniem, R.M. A Novel Gradient Based Optimizer for Solving Unit Commitment Problem. IEEE Access 2022, 10, 18081–18092. [Google Scholar] [CrossRef]
- Deb, S.; Abdelminaam, D.S.; Said, M.; Houssein, E.H. Recent methodology-based gradient-based optimizer for economic load dispatch problem. IEEE Access 2021, 9, 44322–44338. [Google Scholar] [CrossRef]
- Abido, M.A.; Sheraz, K.M. Seven-parameter PV model estimation using differential evolution. Electr. Eng. 2017, 100, 971–981. [Google Scholar] [CrossRef]
- Rajasekar, N.; Kumar, N.K.; Venugopalan, R. Bacterial foraging algorithm based solar PV parameter estimation. Sol. Energy 2013, 97, 255–265. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Artificial bee swarm optimization algorithm for parameters identification of solar cell models. Appl. Energy 2013, 102, 943–949. [Google Scholar] [CrossRef]
- Chen, X.; Yu, K.; Du, W.; Zhao, W.; Liu, G. Parameters identification of solar cell models using generalized oppositional teaching learning based optimization. Energy 2016, 99, 170–180. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mughal, M.A.; Ma, Q.; Xiao, C. Photovoltaic cell parameter estimation using hybrid particle swarm optimization and simulated annealing. Energies 2017, 10, 1213. [Google Scholar] [CrossRef] [Green Version]
- Hamid, N.F.A.; Rahim, N.A.; Selvaraj, J. Solar cell parameters identification using hybrid Nelder-Mead and modified particle swarm optimization. J. Renew. Sustain. Energy 2016, 8, 015502. [Google Scholar] [CrossRef]
- Kiani, A.T.; Nadeem, M.F.; Ahmed, A.; Sajjad, I.A.; Raza, A.; Khan, I.A. Chaotic inertia weight particle swarm optimization (CIWPSO): An efficient technique for solar cell parameter estimation. In Proceedings of the 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sindh, Pakistan, 29–30 January 2020; pp. 1–6. [Google Scholar]
- Guo, L.; Meng, Z.; Sun, Y.; Wang, L. Parameter identification and sensitivity analysis of solar cell models with cat swarm optimization algorithm. Energy Convers. Manag. 2016, 108, 520–528. [Google Scholar] [CrossRef]
- Derick, M.; Rani, C.; Rajesh, M.; Farrag, M.E.; Wang, Y.; Busawon, K. An improved optimization technique for estimation of solar photovoltaic parameters. Sol. Energy 2017, 157, 116–124. [Google Scholar] [CrossRef]
- Jervase, J.A.; Bourdoucen, H.; Al-Lawati, A. Solar cell parameter extraction using genetic algorithms. Meas. Sci. Technol. 2001, 12, 1922–1925. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Ting, T.O.; Man, K.L.; Zhang, N.; Guan, S.-U.; Wong, P.W.H. Parameter estimation of photovoltaic models via cuckoo search. J. Appl. Math. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Gong, W.; Cai, Z. Parameter extraction of solar cell models using repaired adaptive differential evolution. Sol. Energy 2013, 94, 209–220. [Google Scholar] [CrossRef]
- El-Naggar, K.M.; AlRashidi, M.R.; AlHajri, M.F.; Al-Othman, A.K. Simulated annealing algorithm for photovoltaic parameters identification. Sol. Energy 2012, 86, 266–274. [Google Scholar] [CrossRef]
- AlHajri, M.; El-Naggar, K.; AlRashidi, M.R.; Al-Othman, A.K. Optimal extraction of solar cell parameters using pattern search. Renew. Energy 2012, 44, 238–245. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Noshadian, S.; Chen, H.; Gandomi, A.H. INFO: An efficient optimization algorithm based on weighted mean of vectors. Expert Syst. Appl. 2022, 195, 116516. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 1–26. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN Beyond the Metaphor: An Efficient Optimization Algorithm Based on Runge–Kutta Method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]



| Parameters | Lower Bound | Upper Bound |
|---|---|---|
| 0 | 1 | |
| 0 | 0.5 | |
| 0 | 1 | |
| 1 | 2 | |
| 0 | 100 |
| Algorithm | Parameter Setting |
|---|---|
| INFO | c = 2, d = 4 (Default) |
| HHO | E0 ∈ [−1, 1], β = 1.5 (Default) |
| TSA | Pmin = 1 and Pmax = 4 (Default) |
| RUN | a = 20 and b = 12 (Default) |
| GWO | Control parameter (a) linearly decreases from 2 to 0 (default) |
| MFO | b = 1 and a linearly decreases from −1 to −2 (default) |
| SCA | A = 2 (default) |
| ChOA | Control parameter (a) linearly decreases from 2 to 0 (default) |
| Method | RMSE | |||||
|---|---|---|---|---|---|---|
| INFO | 0.760775531 | 3.23 × 10−7 | 1.481183583 | 0.036377093 | 53.71852003 | 0.000986022 |
| MFO | 0.760610259 | 4.66 × 10−7 | 1.519075084 | 0.034885349 | 66.30741592 | 0.001211865 |
| SCA | 0.756072108 | 5.75 × 10−7 | 1.542488704 | 0.026028415 | 35.73635426 | 0.01342705 |
| TSA | 0.7601137 | 6.18 × 10−7 | 1.549825146 | 0.03367546 | 63.2081264 | 0.002027996 |
| HHO | 0.759689107 | 1.96 × 10−7 | 1.431980756 | 0.038740252 | 59.89341231 | 0.001721616 |
| GWO | 0.760495146 | 4.33 × 10−7 | 1.510919086 | 0.035735604 | 77.00217485 | 0.001428873 |
| ChOA | 0.778747386 | 6.84 × 10−7 | 1.561498887 | 0.031486912 | 13.00230926 | 0.013439016 |
| RUN | 0.760738786 | 3.73 × 10−7 | 1.495871948 | 0.03578791 | 57.51621103 | 0.001024176 |
| Method | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|
| INFO | 0.760784749 | 9.09 × 10−7 | 1.999999999 | 0.036848784 | 55.72870238 | 2.07 × 10−7 | 1.443467334 | 0.000982755 |
| MFO | 0.760573102 | 5.14 × 10−7 | 1.529488629 | 0.034473352 | 70.70524625 | 0 | 2 | 0.001330898 |
| SCA | 0.758573427 | 3.27 × 10−7 | 1.479787147 | 0.046141622 | 100 | 0 | 1.299741087 | 0.020743587 |
| TSA | 0.759753871 | 3.00 × 10−8 | 1.619380419 | 0.035766388 | 83.19040588 | 3.99 × 10−7 | 1.504899251 | 0.00182302 |
| HHO | 0.761355149 | 8.90 × 10−7 | 1.621226033 | 0.031536148 | 88.97195633 | 1.53 × 10−7 | 1.560107435 | 0.002601794 |
| GWO | 0.761522609 | 3.42 × 10−8 | 1.973842184 | 0.036949692 | 42.7698821 | 2.62 × 10−7 | 1.460667435 | 0.001163084 |
| ChOA | 0.777351746 | 4.64 × 10−7 | 1.519880609 | 0.029571053 | 24.13155704 | 0 | 1.520252231 | 0.015533816 |
| RUN | 0.760778654 | 1.90 × 10−7 | 1.488917271 | 0.036170888 | 54.72135704 | 1.50 × 10−7 | 1.483016386 | 0.000990819 |
| Method | INFO | MFO | SCA | TSA | HHO | GWO | ChOA | RUN |
|---|---|---|---|---|---|---|---|---|
| 0.760782737 | 7.61 × 10−1 | 7.82 × 10−1 | 0.760787945 | 0.762274159 | 0.761 | 0.75782536 | 0.76078498 | |
| 1.00 × 10−6 | 2.35 × 10−7 | 0 | 3.92 × 10−8 | 5.71 × 10−7 | 1.41 × 10−7 | 1.53 × 10−9 | 7.65 × 10−9 | |
| 2 | 1.46 | 1.29 | 1.515945641 | 1.562234058 | 1.42 | 1.091333206 | 1.84021139 | |
| 0.036874376 | 0.036408874 | 0.036890526 | 0.036128601 | 0.033272778 | 0.037122094 | 0.05449899 | 0.036773835 | |
| 56.17108115 | 58.79879946 | 53.82857553 | 70.07457274 | 49.82864639 | 66.37293159 | 47.7643334 | 54.00897362 | |
| 2.16 × 10−17 | 4.89 × 10−7 | 0 | 2.49 × 10−7 | 7.73 × 10−8 | 5.46 × 10−7 | 7.18 × 10−8 | 1.48 × 10−7 | |
| 2 | 1.980735265 | 1.717307943 | 1.465621068 | 1.515599863 | 1.953366972 | 1.549521311 | 1.42890028 | |
| 1.98 × 10−7 | 3.50 × 10−7 | 6.85 × 10−7 | 1.11 × 10−7 | 3.11 × 10−40 | 5.41 × 10−7 | 6.54 × 10−9 | 3.02 × 10−7 | |
| 1.440116403 | 2 | 1.558130572 | 1.85904076 | 1.49038742 | 1.842301795 | 1.618146711 | 1.647232901 | |
| RMSE | 0.00098297 | 0.000998934 | 0.015666298 | 0.002159304 | 0.002093376 | 0.001082604 | 0.011807743 | 0.000987658 |
| Method | Min | Mean | Max | STD |
|---|---|---|---|---|
| INFO | 0.000986022 | 0.000986022 | 0.000986022 | 4.50 × 10−12 |
| MFO | 0.001211865 | 0.004626596 | 0.038151316 | 0.009132335 |
| SCA | 0.01342705 | 0.045977858 | 0.222876722 | 0.035254772 |
| TSA | 0.002027996 | 0.009666823 | 0.041048048 | 0.012001515 |
| HHO | 0.001721616 | 0.013623637 | 0.053045786 | 0.015070571 |
| GWO | 0.001428873 | 0.01122106 | 0.044307694 | 0.014886843 |
| ChOA | 0.013439016 | 0.140441284 | 0.222883129 | 0.0847737 |
| RUN | 0.001024176 | 0.001859894 | 0.002444366 | 0.000471232 |
| Method | Min | Mean | Max | STD |
|---|---|---|---|---|
| INFO | 0.000982755 | 0.001020116 | 0.001375801 | 0.000102525 |
| MFO | 0.001330898 | 0.005416622 | 0.03343477 | 0.009512679 |
| SCA | 0.020743587 | 0.048102495 | 0.222874404 | 0.033606862 |
| TSA | 0.00182302 | 0.005201682 | 0.009756115 | 0.00243312 |
| HHO | 0.002601794 | 0.01939235 | 0.075410943 | 0.018505278 |
| GWO | 0.001163084 | 0.008847679 | 0.036965034 | 0.011666124 |
| ChOA | 0.015533816 | 0.131722062 | 0.222885353 | 0.088246876 |
| RUN | 0.000990819 | 0.002047384 | 0.003455065 | 0.000712643 |
| Method | Min | Mean | Max | STD |
|---|---|---|---|---|
| INFO | 0.00098297 | 0.001056164 | 0.001437688 | 0.000146373 |
| MFO | 0.000998934 | 0.004563716 | 0.038151316 | 0.00819224 |
| SCA | 0.015666298 | 0.042052252 | 0.069572049 | 0.009842541 |
| TSA | 0.002159304 | 0.007026558 | 0.037687456 | 0.008747154 |
| HHO | 0.002093376 | 0.040618119 | 0.298876672 | 0.073846334 |
| GWO | 0.001082604 | 0.009946247 | 0.039243665 | 0.012813202 |
| ChOA | 0.011807743 | 0.147804062 | 0.222894455 | 0.082865451 |
| RUN | 0.000987658 | 0.002021996 | 0.003785302 | 0.000846304 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, A.Y.; Ismaeel, A.A.K.; Said, M.; Ghoniem, R.M.; Deb, S.; Elsayed, A.G. Evaluation of Weighted Mean of Vectors Algorithm for Identification of Solar Cell Parameters. Processes 2022, 10, 1072. https://doi.org/10.3390/pr10061072
Hassan AY, Ismaeel AAK, Said M, Ghoniem RM, Deb S, Elsayed AG. Evaluation of Weighted Mean of Vectors Algorithm for Identification of Solar Cell Parameters. Processes. 2022; 10(6):1072. https://doi.org/10.3390/pr10061072
Chicago/Turabian StyleHassan, Amir Y., Alaa A. K. Ismaeel, Mokhtar Said, Rania M. Ghoniem, Sanchari Deb, and Abeer Galal Elsayed. 2022. "Evaluation of Weighted Mean of Vectors Algorithm for Identification of Solar Cell Parameters" Processes 10, no. 6: 1072. https://doi.org/10.3390/pr10061072
APA StyleHassan, A. Y., Ismaeel, A. A. K., Said, M., Ghoniem, R. M., Deb, S., & Elsayed, A. G. (2022). Evaluation of Weighted Mean of Vectors Algorithm for Identification of Solar Cell Parameters. Processes, 10(6), 1072. https://doi.org/10.3390/pr10061072







