Particle Residence Time Distribution in a Concurrent Multiphase Flow Reactor: Experiments and Euler-Lagrange Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Apparatus and Methods
2.2. Operating Conditions for the Analysis of the Particle Residence Time Distribution
2.3. Numerical Setup: The Euler-Lagrange Approach
2.4. Computational Mesh and Numerical and Boundary Conditions
3. Results and Discussion
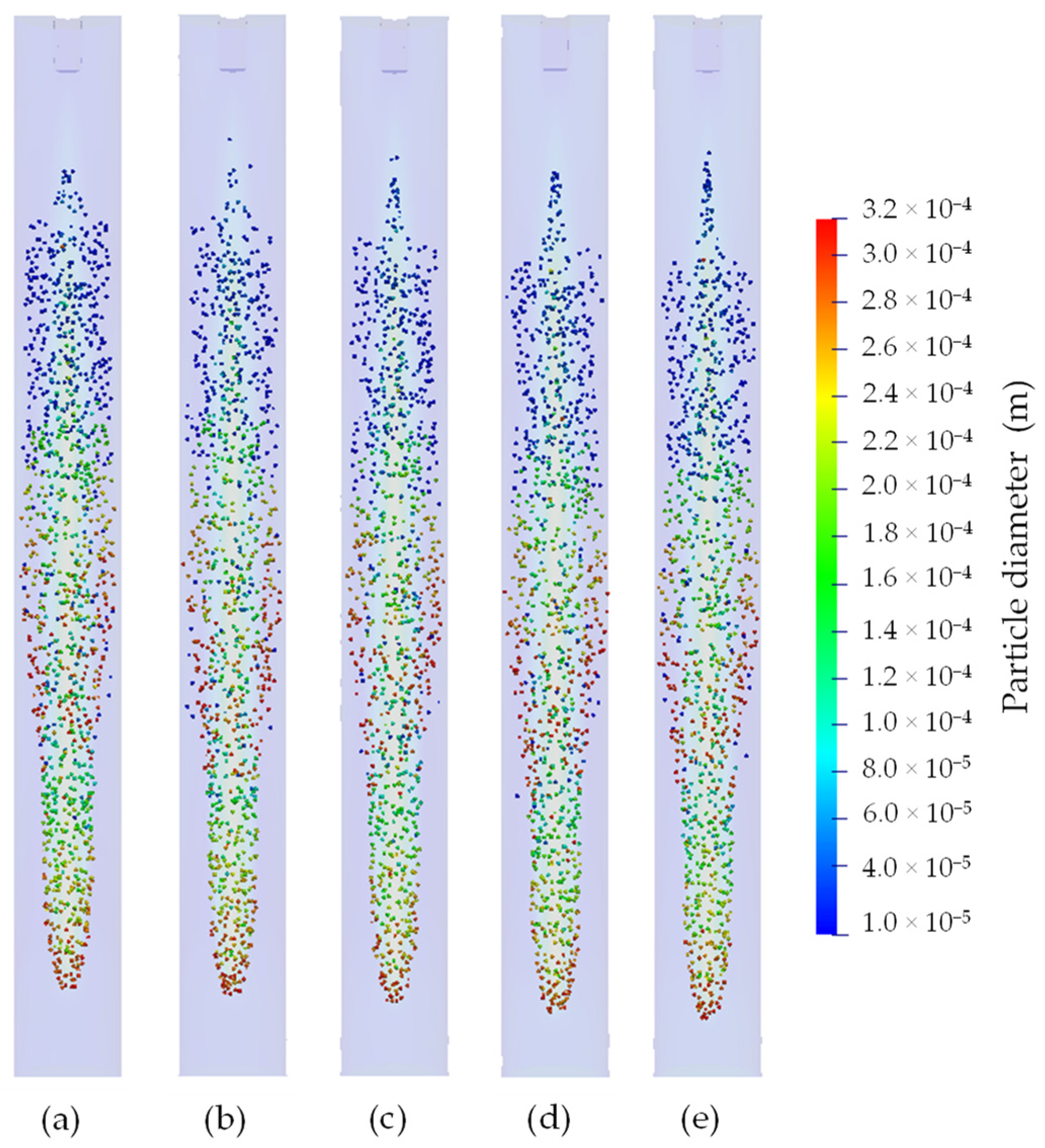
3.1. Particle Size Characterization
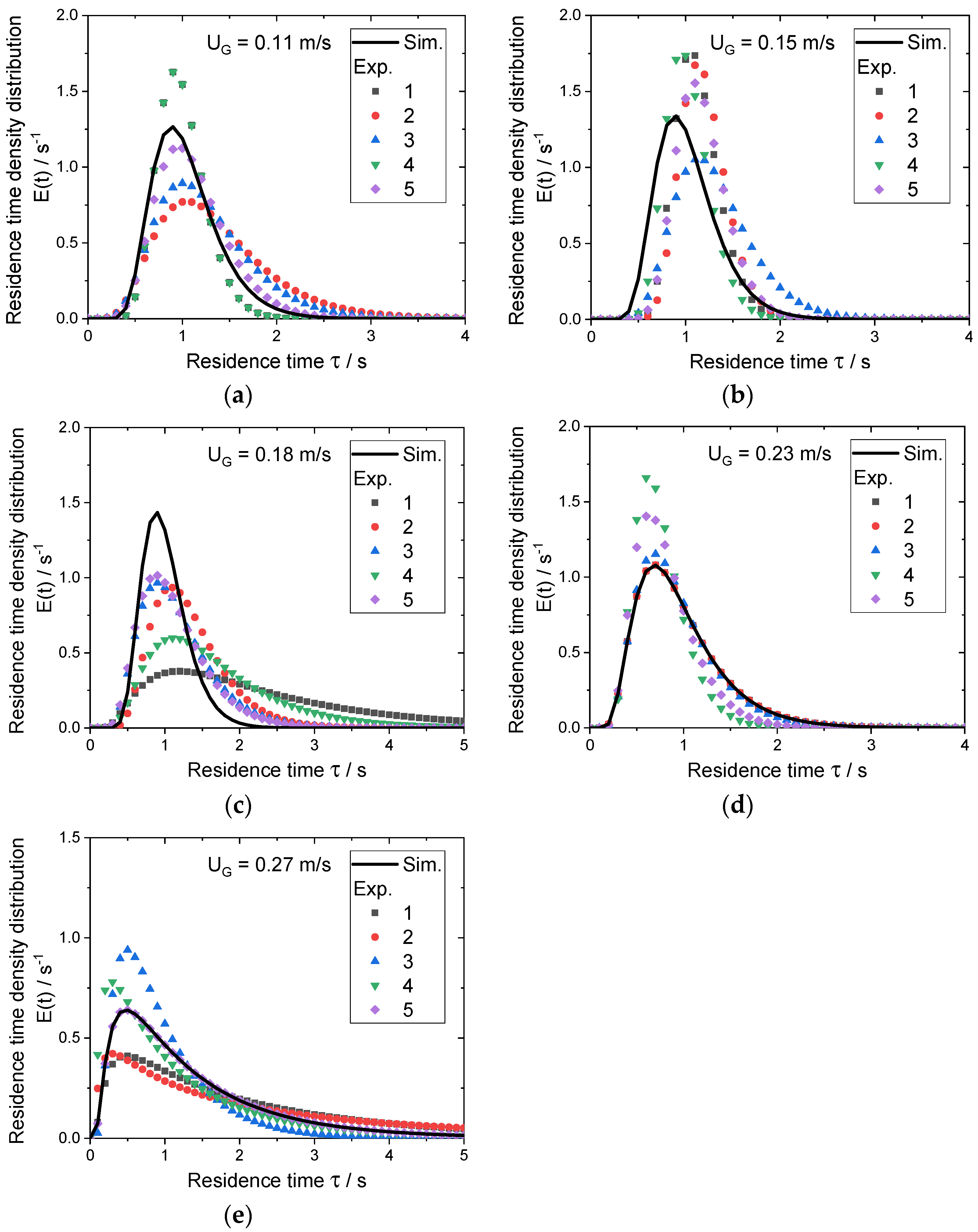
3.2. Physical Validation of the Proposed Euler-Lagrange Approach against Experimental Data for Different Operating Conditions
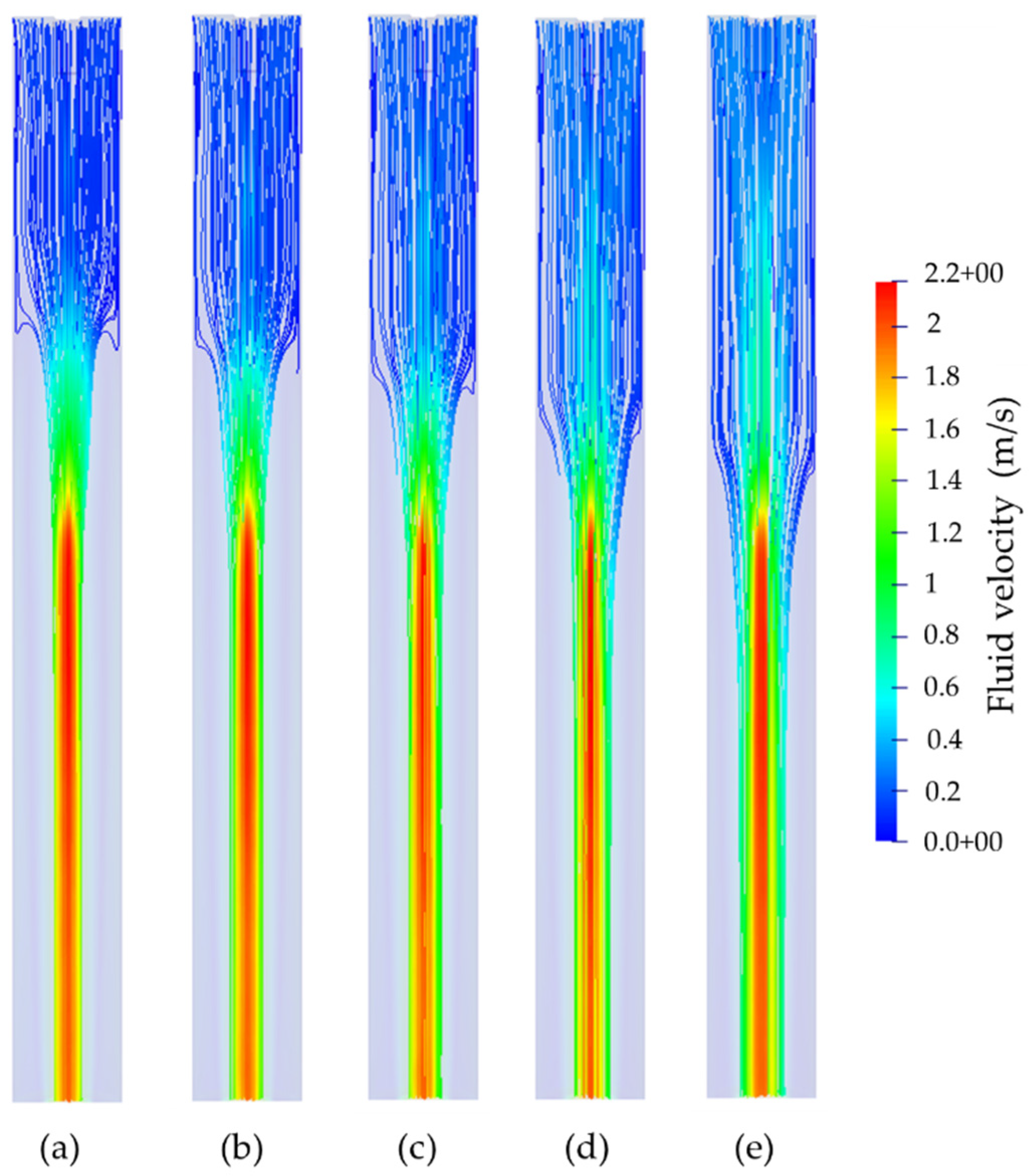
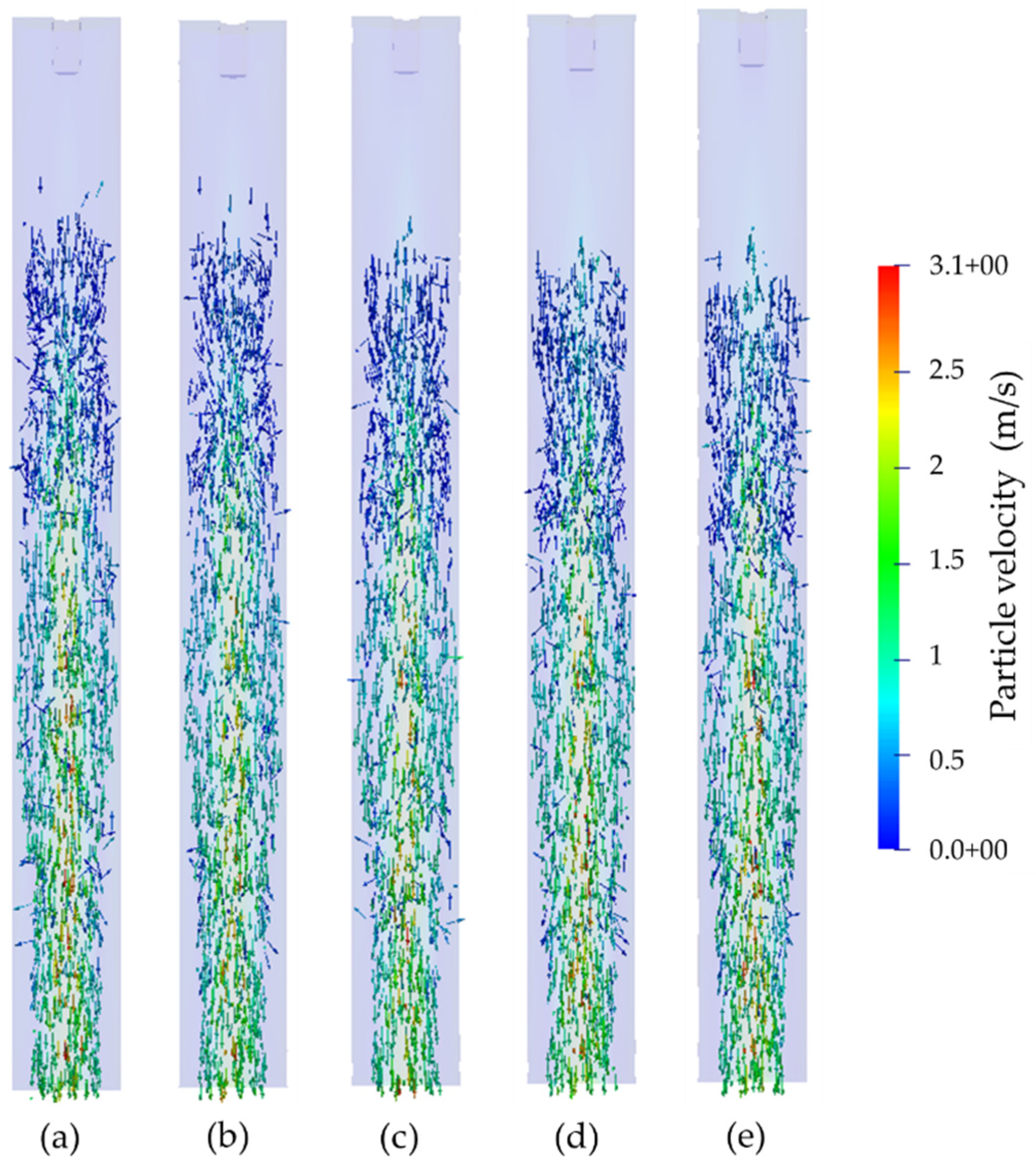
3.3. Numerical Analysis of the Fluid-Particle Dynamics in a Downer Reactor under Different Values of the Sheath Gas Velocity
3.4. Analysis of the Fluid-Particle Flow Structure in a Downer Reactor through the Experimental and Numerical Bodenstein Numbers (Bo), Variances , and Axial Dispersion Coefficients
4. Conclusions
- ▪ the numerical peak particle residence time varied in the range of 0.5–0.9 s, whereas the corresponding experimental data varied in the range of 0.42–1.08 s. The maximum particle residence times were between 2.4–5.0 s for the numerical simulations and 2.4–4.62 s for the experiments. The concurrent downer reactor presented a narrow residence time distribution, thus confirming the characteristic property of these reactors;
- ▪ the particle residence time density distribution was strongly dependent on the fluid flow rate. With increasing the sheath gas flow rate, the peak particle residence time decreased, whereas the maximum residence time of the particles significantly increased;
- ▪ it was possible to observe a drop-shaped particle flow pattern formation through the numerical simulations under different values of the sheath gas velocity. According to the numerical results, the distribution of the particles along the reactor length depends on their size. Thus, smaller particles tended to concentrate at the top of the reactor (i.e., at the beginning of the drop-shaped particle flow), resulting in higher residence times, whereas larger particles concentrated towards the end of the drop-shaped particle flow pattern (i.e., near the reactor outlet), which results in lower residence times.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CD | drag coefficient/- |
| Cμ | empirical constant for the turbulent model/- |
| dp | particle diameter/m |
| e | coefficient of restitution/- |
| gravitational-buoyance forces/N | |
| drag force/N | |
| normal contact force/N | |
| tangential contact force/N | |
| gravity acceleration vector/m/s2 | |
| G | equivalent shear modulus/Pa |
| turbulence intensity/- | |
| k | turbulent kinetic energy/m2/s2 |
| kn | stiffness/N/m |
| L | hydraulic diameter/m |
| LR | Length of the reactor/m |
| mp | particle mass/kg |
| n | unit vector between the involved particles/- |
| Np | total number of particles/- |
| p | mean pressure/Pa |
| rate of production of the turbulent kinetic energy/kg/ms3 | |
| relative Reynolds number of the particle/- | |
| Si,p | inter-phase momentum exchange/m/s2 |
| t | time/s |
| UG | gas velocity/m/s |
| reference velocity/m/s | |
| Vk | volume of the kth particle/m3 |
| mean fluid velocity vector/m/s | |
| particle velocity vector/m/s | |
| particle position vector/m | |
| x10,3 | tenth percentile of the volumetric distribution sum/µm |
| X50,3 | median of the volumetric distribution sum/µm |
| X90,3 | ninetieth percentile of the volumetric distribution sum/µm |
| x3,2 | Sauter diameter of the particle/µm |
| Greek Symbols | |
| β* | empirical constant for the SST k-ω turbulent model/- |
| β2 | empirical constant for the SST k-ω turbulent model/- |
| γ2 | empirical constant for the SST k-ω turbulent model/- |
| δij | Kronecker delta/- |
| δn | Overlap distance between the involved particles/m |
| ε | turbulent kinetic energy dissipation rate/m2/s3 |
| η | damping coefficient/Ns/m |
| µ | fluid dynamic viscosity/Pas |
| turbulent viscosity/Pas | |
| ρf | fluid density/kg/m3 |
| ρp | particle density/kg/m3 |
| σk | empirical constant for the SST k-ω turbulent model/- |
| σω,1 | empirical constant for the SST k-ω turbulent model/- |
| σω,2 | empirical constant for the SST k-ω turbulent model/- |
| turbulent Reynolds stresses/Pa | |
| mean particle residence time/s | |
| ω | turbulence frequency/1/s |
References
- Schmidt, J.; Sachs, M.; Fanselow, S.; Zhao, M.; Romeis, S.; Drummer, D.; Wirth, K.-E.; Peukert, W. Optimized polybutylene terephthalate powders for selective laser beam melting. Chem. Eng. Sci. 2016, 156, 1–10. [Google Scholar] [CrossRef]
- Wilczek, M.; Bertling, J.; Hintemann, D. Optimised technologies for cryogenic grinding. Int. J. Miner. Processing 2004, 74, 425–434. [Google Scholar] [CrossRef]
- Dechet, M.A.; Kloos, S.; Peukert, W.; Schmidt, J. Formation of spherical micron-sized polyamide particles for additive manufacturing via liquid-liquid phase separation. In Proceedings of the 33rd International Conference of the Polymer Processing Society, Cancun, Mexico, 10–14 December 2017. [Google Scholar]
- Gai, G.; Yang, Y.; Jin, L.; Zou, X.; Wu, Y. Particle shape modification and related property improvements. Powder Technol. 2008, 183, 115–121. [Google Scholar] [CrossRef]
- Gomez Bonilla, J.S.; Dechet, M.A.; Schmidt, J.; Peukert, W.; Bück, A. Thermal rounding of micron-sized polymer particles in a downer reactor: Direct vs. indirect heating. RPJ 2020, 26, 1637–1646. [Google Scholar] [CrossRef]
- Hague, R.; Campbell, I.; Dickens, P. Implications on design of rapid manufacturing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2003, 217, 25–30. [Google Scholar] [CrossRef]
- Ligon, S.C.; Liska, R.; Stampfl, J.; Gurr, M.; Mülhaupt, R. Polymers for 3D Printing and Customized Additive Manufacturing. Chem. Rev. 2017, 117, 10212–10290. [Google Scholar] [CrossRef]
- Bourell, D.L.; Marcus, H.L.; Barlow, J.W.; Beaman, J.J. Selective laser sintering of metals and ceramics. Int. J. Powder Met. 1992, 28, 369–381. [Google Scholar] [CrossRef]
- van der Schueren, B.; Kruth, J.P. Powder deposition in selective metal powder sintering. Rapid Prototyp. J. 1995, 1, 23–31. [Google Scholar] [CrossRef]
- Goodridge, R.D.; Tuck, C.J.; Hague, R.J.M. Laser sintering of polyamides and other polymers. Prog. Mater. Sci. 2012, 57, 229–267. [Google Scholar] [CrossRef]
- Chatham, C.A.; Long, T.E.; Williams, C.B. A review of the process physics and material screening methods for polymer powder bed fusion additive manufacturing. Prog. Polym. Sci. 2019, 93, 68–95. [Google Scholar] [CrossRef]
- Podczeck, F.; Mia, Y. The influence of particle size and shape on the angle of internal friction and the flow factor of unlubricated and lubricated powders. Int. J. Pharm. 1996, 144, 187–194. [Google Scholar] [CrossRef]
- Fu, X.; Huck, D.; Makein, L.; Armstrong, B.; Willen, U.; Freeman, T. Effect of particle shape and size on flow properties of lactose powders. Particuology 2012, 10, 203–208. [Google Scholar] [CrossRef]
- Ziegelmeier, S.; Christou, P.; Wöllecke, F.; Tuck, C.; Goodridge, R.; Hague, R.; Krampe, E.; Wintermantel, E. An experimental study into the effects of bulk and flow behaviour of laser sintering polymer powders on resulting part properties. J. Mater. Processing Technol. 2015, 215, 239–250. [Google Scholar] [CrossRef]
- Schmidt, J.; Sachs, M.; Blümel, C.; Winzer, B.; Toni, F.; Wirth, K.-E.; Peukert, W. A novel process route for the production of spherical LBM polymer powders with small size and good flowability. Powder Technol. 2014, 261, 78–86. [Google Scholar] [CrossRef]
- Mys, N.; van de Sande, R.; Verberckmoes, A.; Cardon, L. Processing of Polysulfone to Free Flowing Powder by Mechanical Milling and Spray Drying Techniques for Use in Selective Laser Sintering. Polymers 2016, 8, 150. [Google Scholar] [CrossRef]
- Mys, N.; Verberckmoes, A.; Cardon, L. Processing of Syndiotactic Polystyrene to Microspheres for Part Manufacturing through Selective Laser Sintering. Polymers 2016, 8, 383. [Google Scholar] [CrossRef]
- Dechet, M.A.; Gómez Bonilla, J.S.; Lanzl, L.; Drummer, D.; Bück, A.; Schmidt, J.; Peukert, W. Spherical Polybutylene Terephthalate (PBT)-Polycarbonate (PC) Blend Particles by Mechanical Alloying and Thermal Rounding. Polymers 2018, 10, 1373. [Google Scholar] [CrossRef]
- Bissett, H.; van der Walt, I.J.; Havenga, J.L.; Nel, J.T. Titanium and zirconium metal powder spheroidization by thermal plasma processes. J. S. Afr. Inst. Min. Metall. 2015, 115, 937–942. [Google Scholar] [CrossRef]
- Kotlyarov, V.I.; Beshkarev, V.T.; Kartsev, V.E.; Ivanov, V.V.; Gasanov, A.A.; Yuzhakova, E.A.; Samokhin, A.V.; Fadeev, A.A.; Alekseev, N.V.; Sinayskiy, M.A.; et al. Production of spherical powders on the basis of group IV metals for additive manufacturing. Inorg. Mater. Appl. Res. 2017, 8, 452–458. [Google Scholar] [CrossRef]
- Tang, J.; Nie, Y.; Lei, Q.; Li, Y. Characteristics and atomization behavior of Ti-6Al-4V powder produced by plasma rotating electrode process. Adv. Powder Technol. 2019, 30, 2330–2337. [Google Scholar] [CrossRef]
- Jin, H.; Xu, L.; Hou, S. Preparation of spherical silica powder by oxygen–acetylene flame spheroidization process. J. Mater. Process. Technol. 2010, 210, 81–84. [Google Scholar] [CrossRef]
- Murray, J.W.; Simonelli, M.; Speidel, A.; Grant, D.M.; Clare, A.T. Spheroidisation of metal powder by pulsed electron beam irradiation. Powder Technol. 2019, 350, 100–106. [Google Scholar] [CrossRef]
- Pawar, S.B. CFD analysis of flow regimes in airlift reactor using Eulerian-Lagrangian approach. Can. J. Chem. Eng. 2017, 95, 420–431. [Google Scholar] [CrossRef]
- Li, Y.; Cao, X.; Geng, Z.; Zhang, M. A novel quasi plug-flow reactor design for enzymatic hydrolysis of cellulose using rheology experiment and CFD simulation. Can. J. Chem. Eng. 2018, 96, 770–778. [Google Scholar] [CrossRef]
- Yu, X.; Makkawi, Y.; Ocone, R.; Huard, M.; Briens, C.; Berruti, F. A CFD study of biomass pyrolysis in a downer reactor equipped with a novel gas–solid separator—I: Hydrodynamic performance. Fuel Process. Technol. 2014, 126, 366–382. [Google Scholar] [CrossRef][Green Version]
- Marandi, R.; Kamyabi, M.; Mostoufi, N. Hydrodynamic design of multi-zone circulating reactors using CFD. Can. J. Chem. Eng. 2018, 96, 670–678. [Google Scholar] [CrossRef]
- Gómez Bonilla, J.S.; Unger, L.; Schmidt, J.; Peukert, W.; Bück, A. Particle Lagrangian CFD Simulation and Experimental Characterization of the Rounding of Polymer Particles in a Downer Reactor with Direct Heating. Processes 2021, 9, 916. [Google Scholar] [CrossRef]
- Zhang, Y.; Yi, W.; Fu, P.; Li, Z.; Wang, N.; Tian, C. Numerical simulation and experiment on catalytic upgrading of biomass pyrolysis vapors in V-shaped downer reactors. Bioresour. Technol. 2019, 274, 207–214. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, K.; Cui, Y.; Takei, M. Three-dimensional simulation of the particle distribution in a downer using CFD–DEM and comparison with the results of ECT experiments. Adv. Powder Technol. 2010, 21, 630–640. [Google Scholar] [CrossRef]
- Wang, C.; Li, C.; Zhu, J. Axial solids flow structure in a high density gas–solids circulating fluidized bed downer. Powder Technol. 2015, 272, 153–164. [Google Scholar] [CrossRef]
- Deng, R. Axial flow structure at the varying superficial gas velocity in a downer reactor. Chem. Eng. J. 2004, 99, 5–14. [Google Scholar] [CrossRef]
- Qi, C.-M.; Yu, Z.-Q.; Jin, Y.; Bai, D.-R.; Yao, W.-H. Study on the gas-solids cocurrently downflow fluidization (I). J. Chem. Ind. Eng. China (Chin. Ed.) 1990, 41, 273–280. [Google Scholar]
- Brust, H.; Wirth, K.-E. Residence Time Behavior of Gas in a Downer Reactor. Ind. Eng. Chem. Res. 2004, 43, 5796–5801. [Google Scholar] [CrossRef]
- Bachmann, P.; Bück, A.; Tsotsas, E. Investigation of the residence time behavior of particulate products and correlation for the Bodenstein number in horizontal fluidized beds. Powder Technol. 2016, 301, 1067–1076. [Google Scholar] [CrossRef]
- Brauer, H. Grundlagen der Einphasen- und Mehrphasenströmungen; Sauerländer: Aarau, Switzerland, 1971; pp. 364–368. [Google Scholar]
- Michelsen, M.L.; Østergaard, K. The use of residence time distribution data for estimation of parameters in the axial dispersion model. Chem. Eng. Sci. 1970, 25, 583–592. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST Turbulence model. In Turubulence, Heat and Mass Transfer; Begell House, Inc.: Danbury, CT, USA, 2003. [Google Scholar]
- Khare, P.; Wang, S.; Yang, V. Modeling of finite-size droplets and particles in multiphase flows. Chin. J. Aeronaut. 2015, 28, 974–982. [Google Scholar] [CrossRef]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Putnam, A. Integrable form of droplet drag coefficient. Ars J. 1961, 31, 1467–1468. [Google Scholar]
- Gosman, A.D.; Ioannides, E. Aspects of Computer Simulation of Liquid-Fueled Combustors. J. Energy 1983, 7, 482–490. [Google Scholar] [CrossRef]
- Mofakham, A.A.; Ahmadi, G. On random walk models for simulation of particle-laden turbulent flows. Int. J. Multiph. Flow 2020, 122, 103157. [Google Scholar] [CrossRef]
- OpenFOAM: User Guide (v2112). Available online: https://www.openfoam.com/documentation/guides/latest/doc/guide-meshing-snappyhexmesh-meshquality.html (accessed on 8 April 2022).
- Barton, I.E. Comparison of SIMPLE- and PISO-type algorithms for transient flows. Int. J. Numer. Meth. Fluids 1998, 26, 459–483. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Ltd.: Harlow, UK, 2007; p. 76. [Google Scholar]
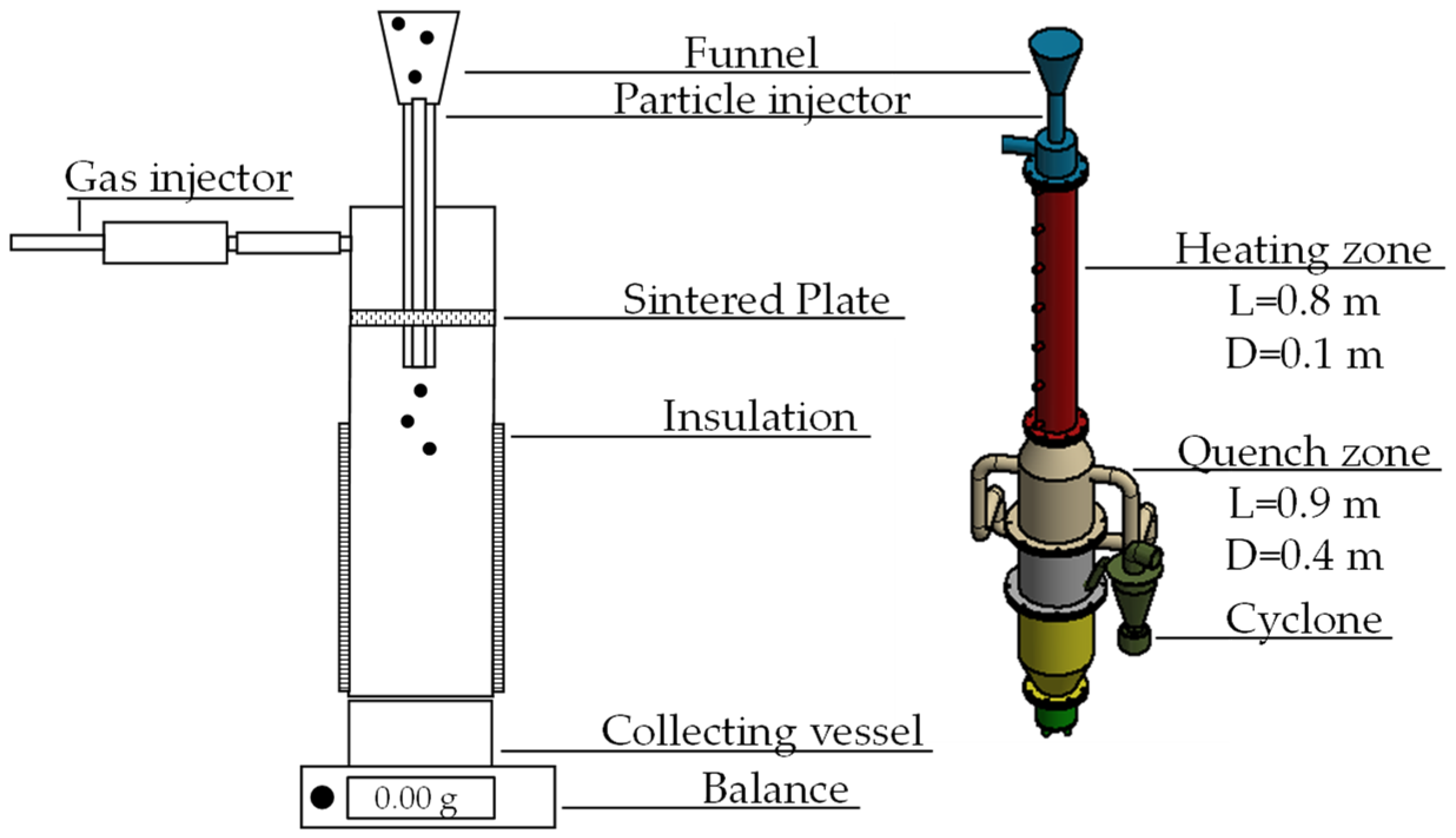
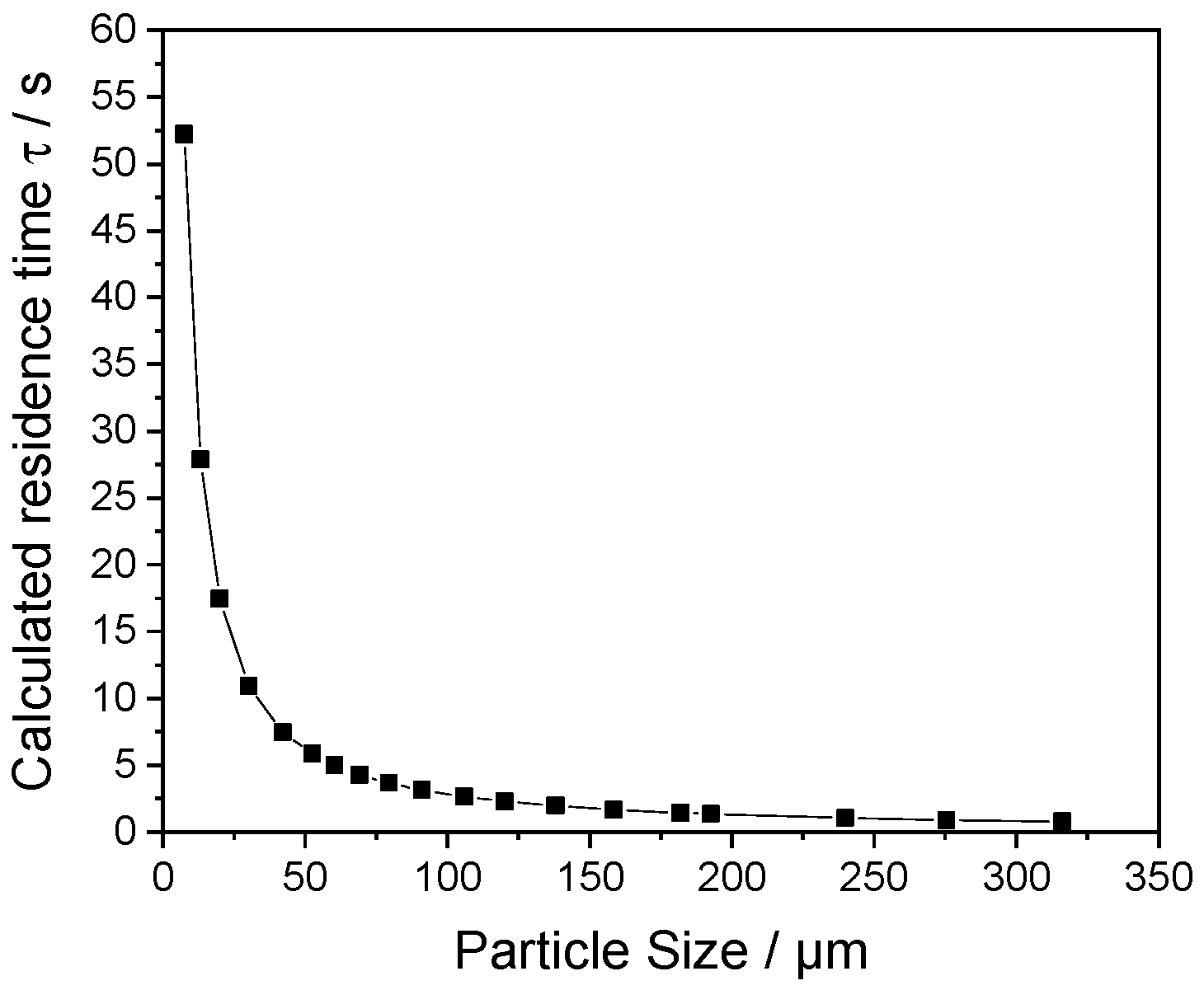
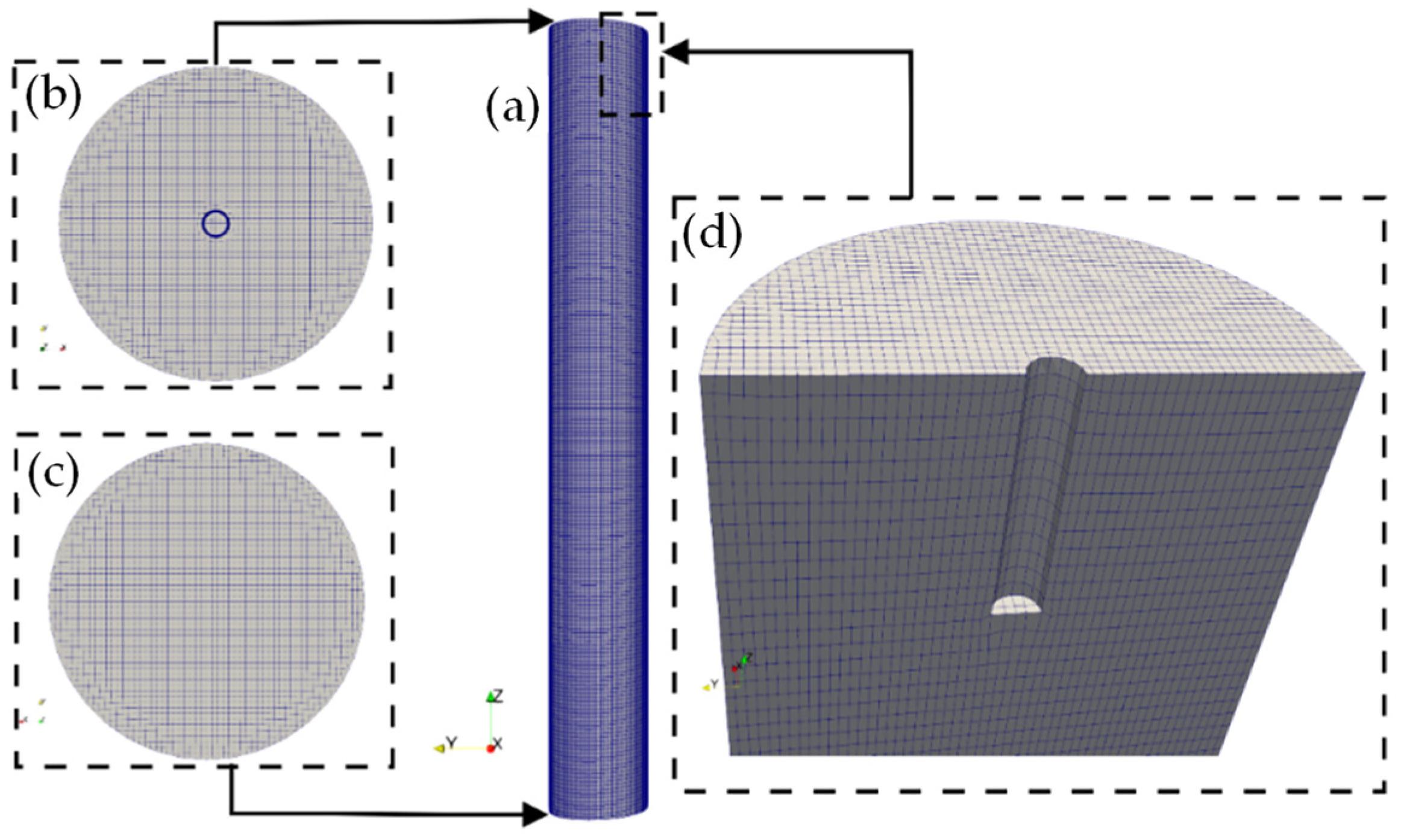
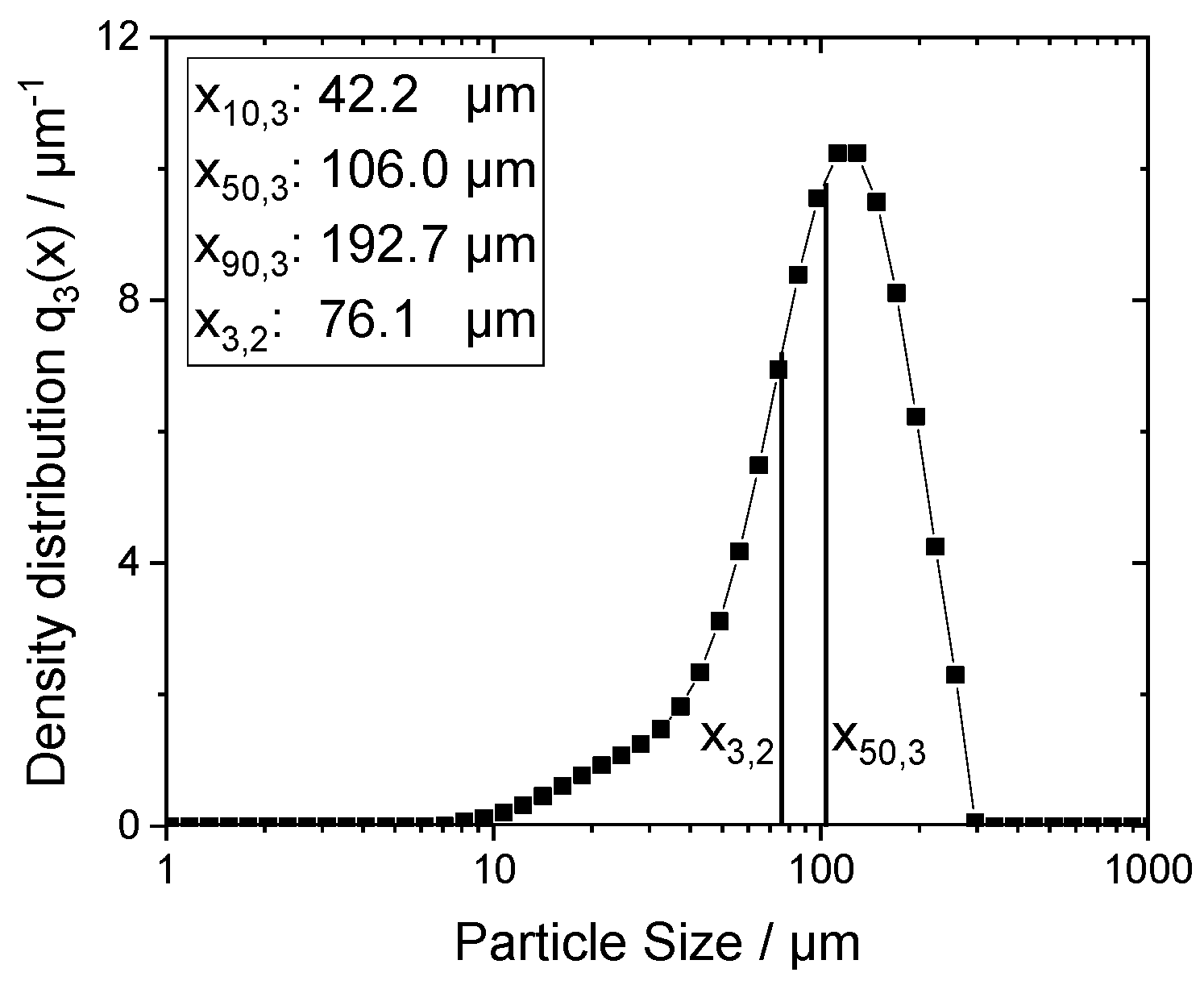

| Property | Value |
|---|---|
| Diameter of the particle injector/m | 26 × 10−3 |
| Length of the particle injector, i.e., below the sintered plate/m | 0.05 |
| Length of the downer reactor from the sintered plate/m | 0.8 |
| Diameter of the downer reactor/m | 0.1 |
| Sauter diameter of PP/m | 76.1 × 10−6 |
| Density of PP/kg/m3 | 907 |
| Property | Value |
|---|---|
| Sheath gas volume flow rate—Gas injector/Nm3/h | 3.0, 4.0, 5.0, 6.0 and 7.0 |
| Sheath gas velocity—Gas injector/m/s | 0.11, 0.15, 0.18, 0.23 and 0.27 |
| Reynolds number—fluid phase/- | 616, 1009, 840, 1289, 1513 |
| Reynolds number—solid phase/- | 1.6, 1.9, 2.2, 2.5, 2.8 |
| Cross sectional solid flux/kg/m2s | 0.32 |
| Property | Value |
|---|---|
| Discretization method (gas phase): | The finite volume method. |
| Pressure-velocity coupling (gas phase): | PIMPLE algorithm, i.e., blend of the SIMPLE and PISO algorithms [46] |
| Integration scheme (solid phase): | Euler scheme. |
| Wall boundary conditions: | gas phase: no-slip condition for the velocity; wall functions for the k and ω turbulent equations. solid phase: particle stick condition. |
| Inlet boundary conditions: | gas phase: velocity, k, and ω values are specified; null gradient for pressure. solid phase: injection of particles in the central inlet; particle rebound condition with e = 0.9 for the annular and central inlets (no particle backflow). |
| Outlet boundary conditions: | gas phase: pressure value is specified (atmospheric pressure); null gradients for velocity, k, and ω. solid phase: particle escape condition. |
| Convergence criteria: | 10−6 for all variables |
| Property | Value | ||||
|---|---|---|---|---|---|
| Sheath gas velocity/m/s | 0.11 | 0.15 | 0.18 | 0.23 | 0.27 |
| /s | 2.68 | 2.4 | 4.04 | 2.46 | 4.62 |
| /s | 2.5 | 2.5 | 2.4 | 3.0 | 5.0 |
| according to Equation (4)/s | 3.8 | ||||
| /s | 0.96 | 1.08 | 1.04 | 0.64 | 0.42 |
| /s | 0.9 | 0.9 | 0.9 | 0.7 | 0.5 |
| Property | Value | ||||
|---|---|---|---|---|---|
| Sheath gas velocity/m/s | 0.11 | 0.15 | 0.18 | 0.23 | 0.27 |
| /- | 3.494 | 7.048 | 2.669 | 4.469 | 0.775 |
| /- | 4.850 | 5.549 | 6.682 | 3.087 | 0.844 |
| /- | 0.572 | 0.284 | 0.749 | 0.447 | 2.580 |
| /- | 0.412 | 0.360 | 0.299 | 0.648 | 2.369 |
| /- | 0.048 | 0.024 | 0.063 | 0.037 | 0.218 |
| /- | 0.035 | 0.030 | 0.025 | 0.054 | 0.199 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unger, L.; Gómez Bonilla, J.S.; dos Santos, D.A.; Bück, A. Particle Residence Time Distribution in a Concurrent Multiphase Flow Reactor: Experiments and Euler-Lagrange Simulations. Processes 2022, 10, 996. https://doi.org/10.3390/pr10050996
Unger L, Gómez Bonilla JS, dos Santos DA, Bück A. Particle Residence Time Distribution in a Concurrent Multiphase Flow Reactor: Experiments and Euler-Lagrange Simulations. Processes. 2022; 10(5):996. https://doi.org/10.3390/pr10050996
Chicago/Turabian StyleUnger, Laura, Juan Sebastián Gómez Bonilla, Dyrney Araújo dos Santos, and Andreas Bück. 2022. "Particle Residence Time Distribution in a Concurrent Multiphase Flow Reactor: Experiments and Euler-Lagrange Simulations" Processes 10, no. 5: 996. https://doi.org/10.3390/pr10050996
APA StyleUnger, L., Gómez Bonilla, J. S., dos Santos, D. A., & Bück, A. (2022). Particle Residence Time Distribution in a Concurrent Multiphase Flow Reactor: Experiments and Euler-Lagrange Simulations. Processes, 10(5), 996. https://doi.org/10.3390/pr10050996









