Convective Heat and Mass Transfer in Third-Grade Fluid with Darcy–Forchheimer Relation in the Presence of Thermal-Diffusion and Diffusion-Thermo Effects over an Exponentially Inclined Stretching Sheet Surrounded by a Porous Medium: A CFD Study
Abstract
:1. Introduction
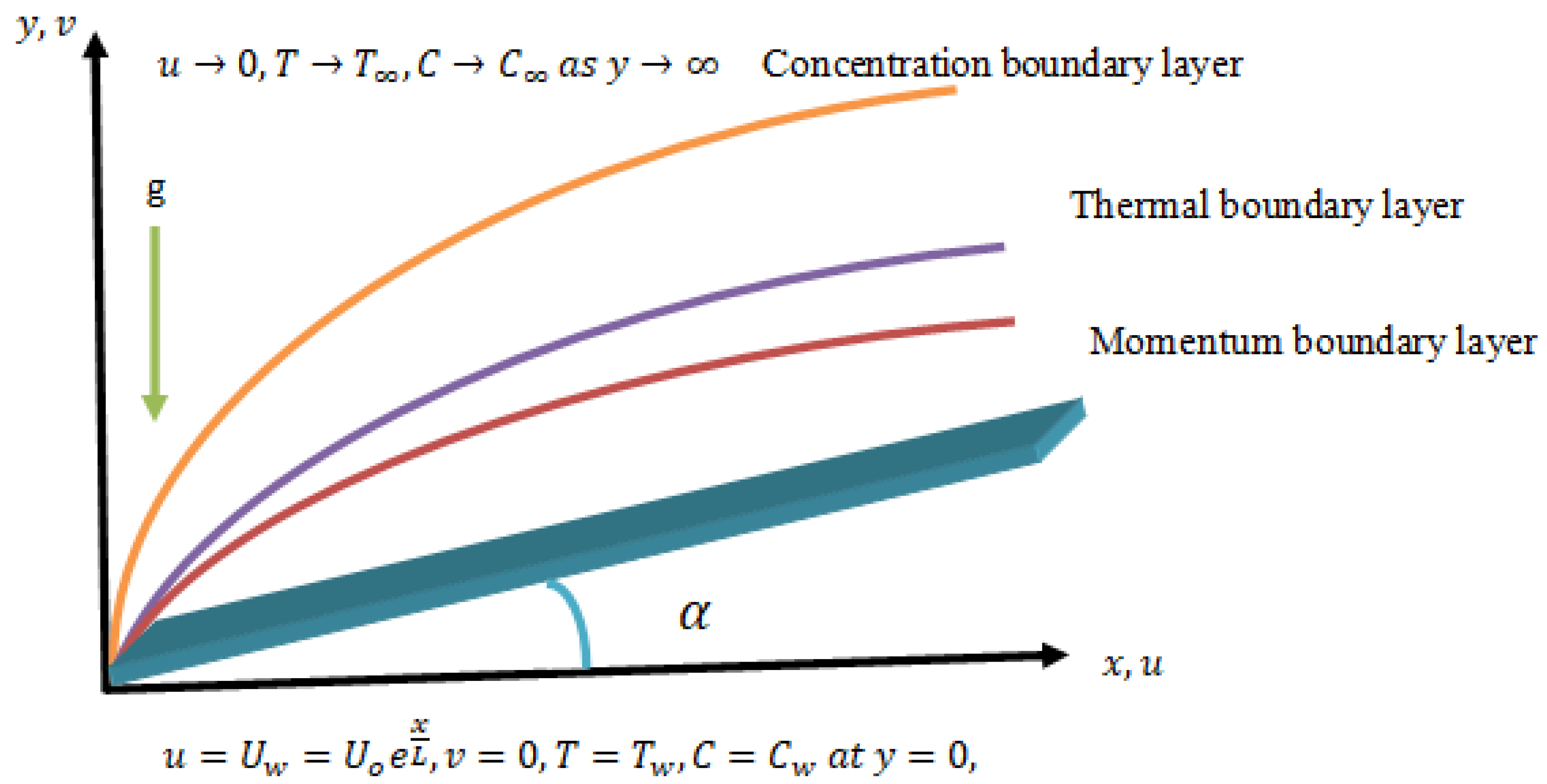
2. Mathematical Modeling
3. Solution Methodology
3.1. Similarity Formulation
3.2. Solution Technique
4. Results and Discussion
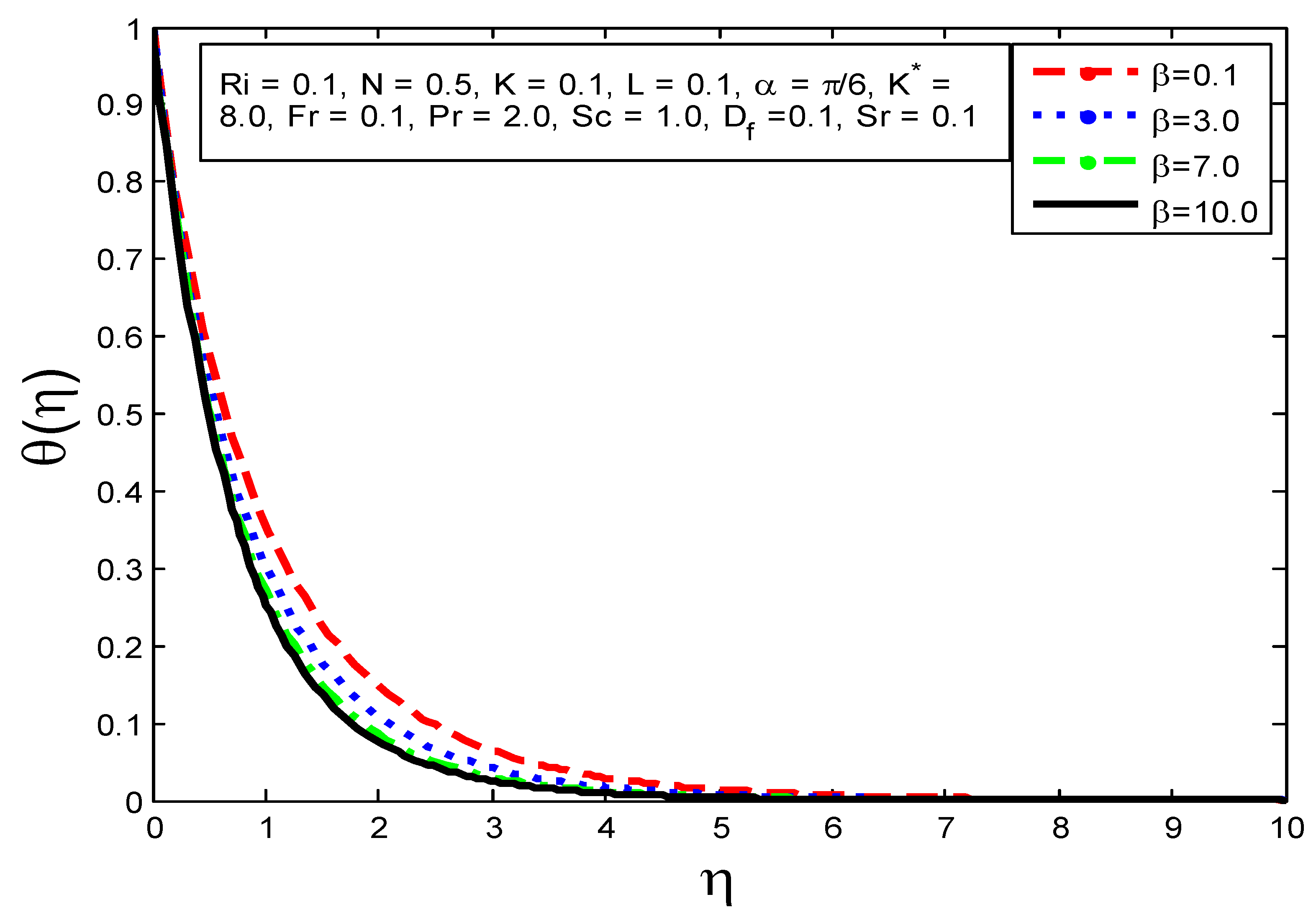
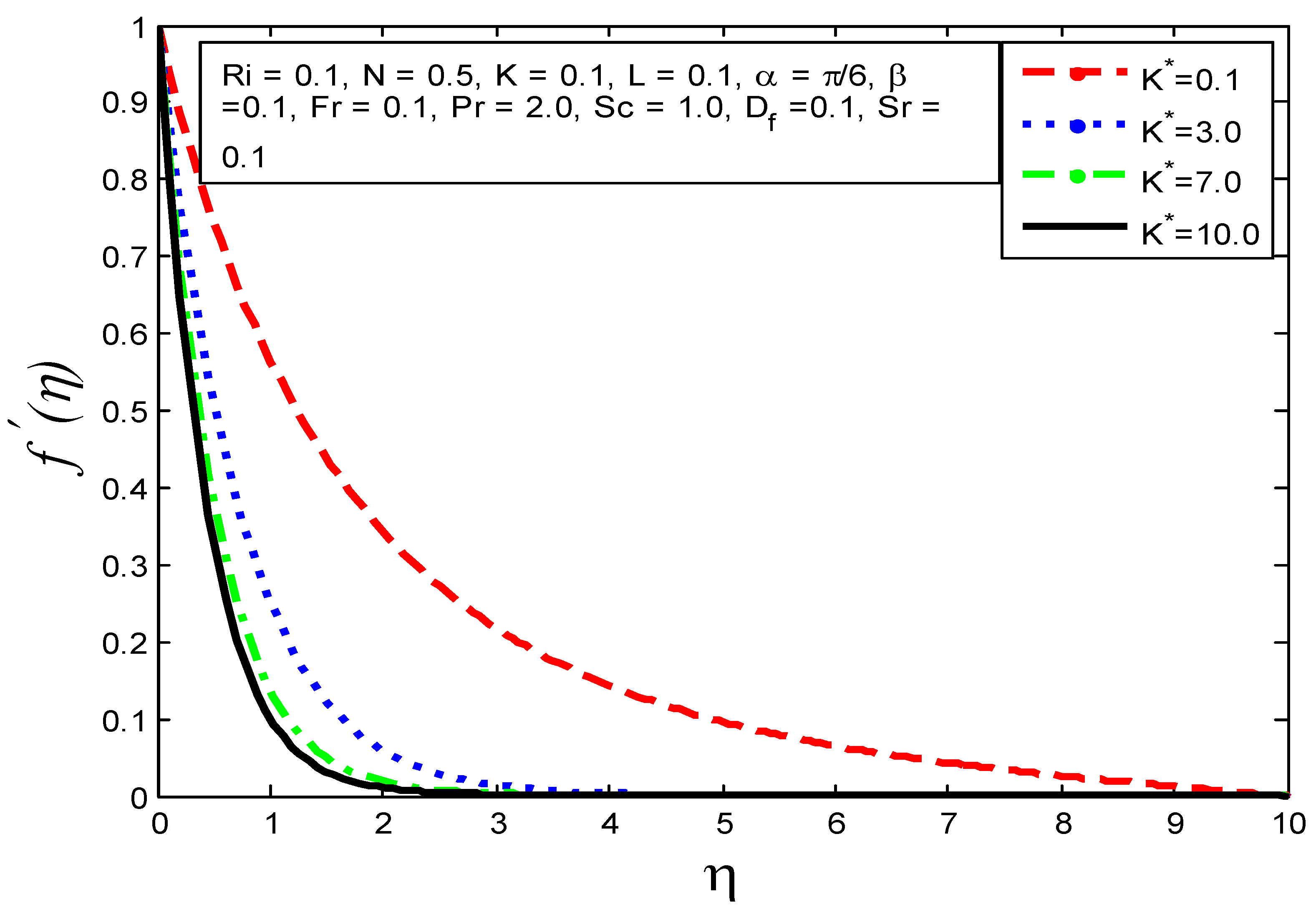
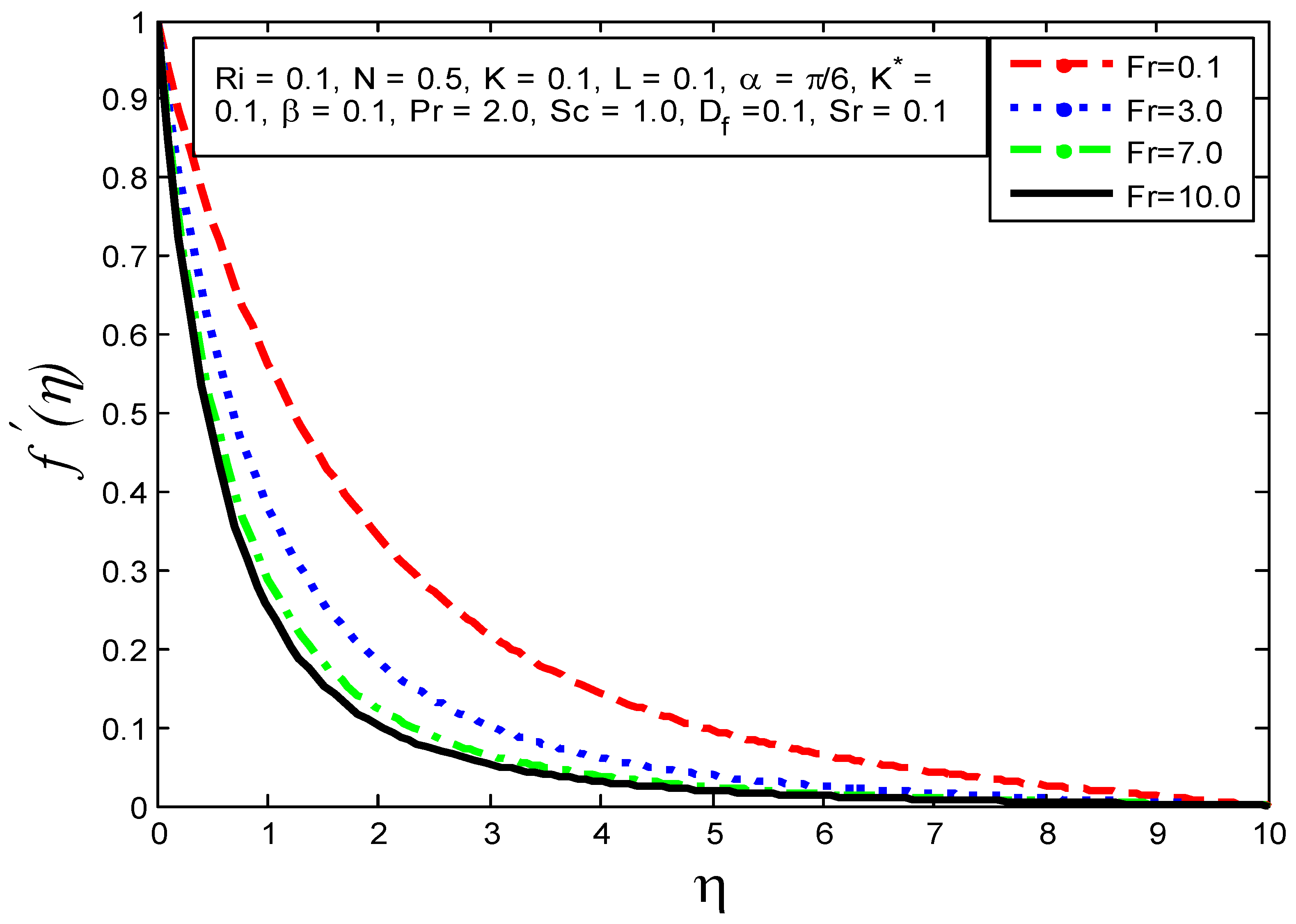
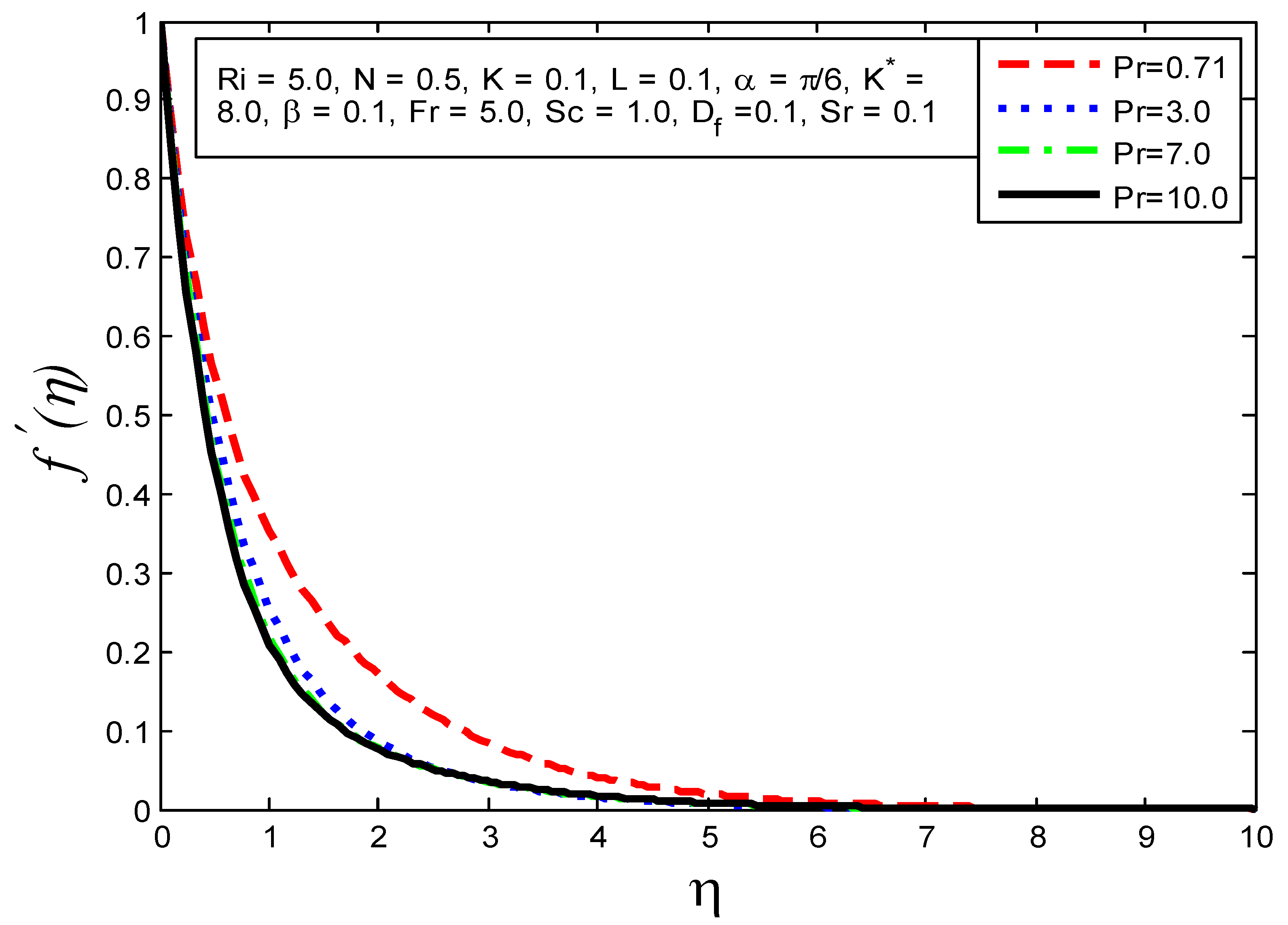
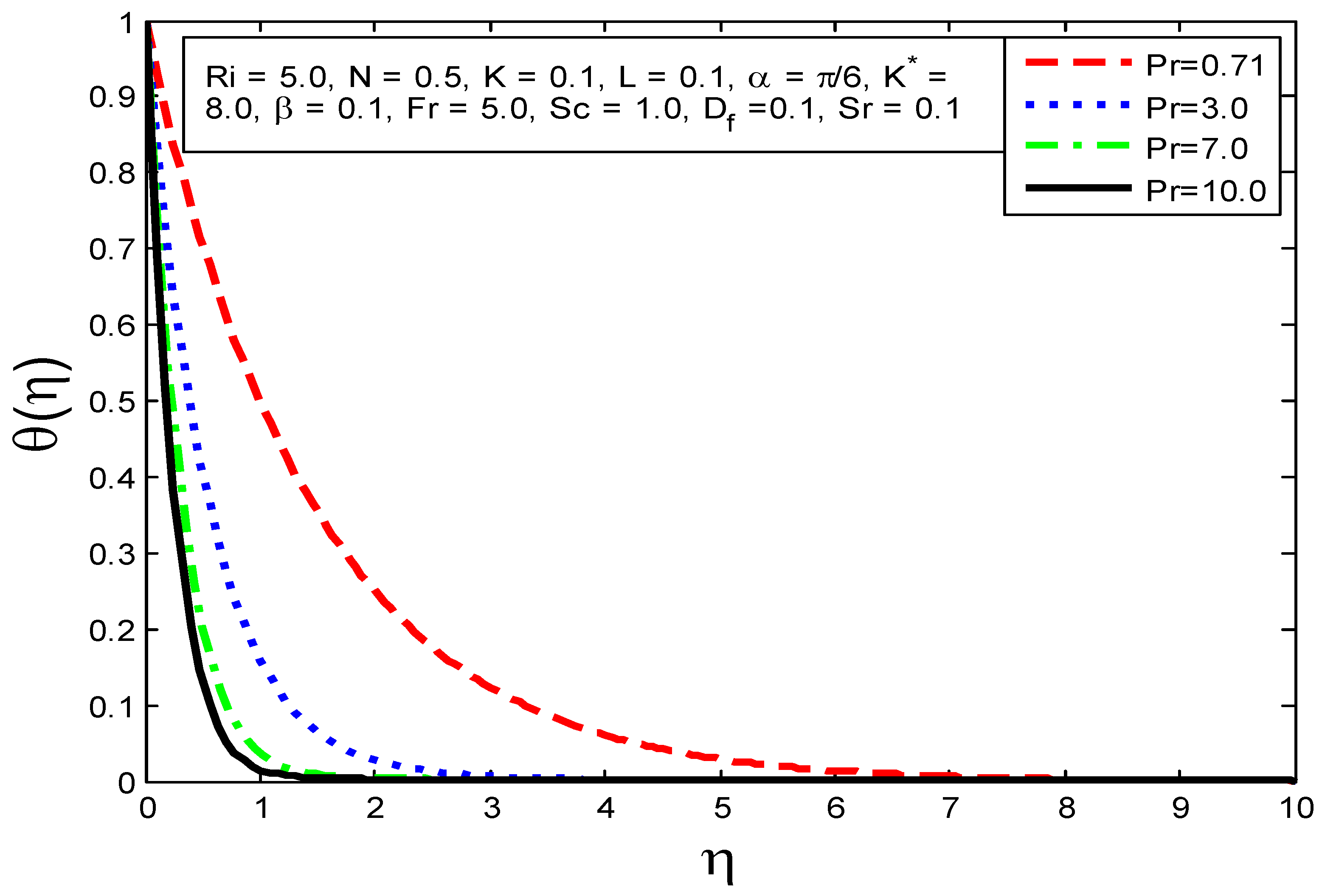
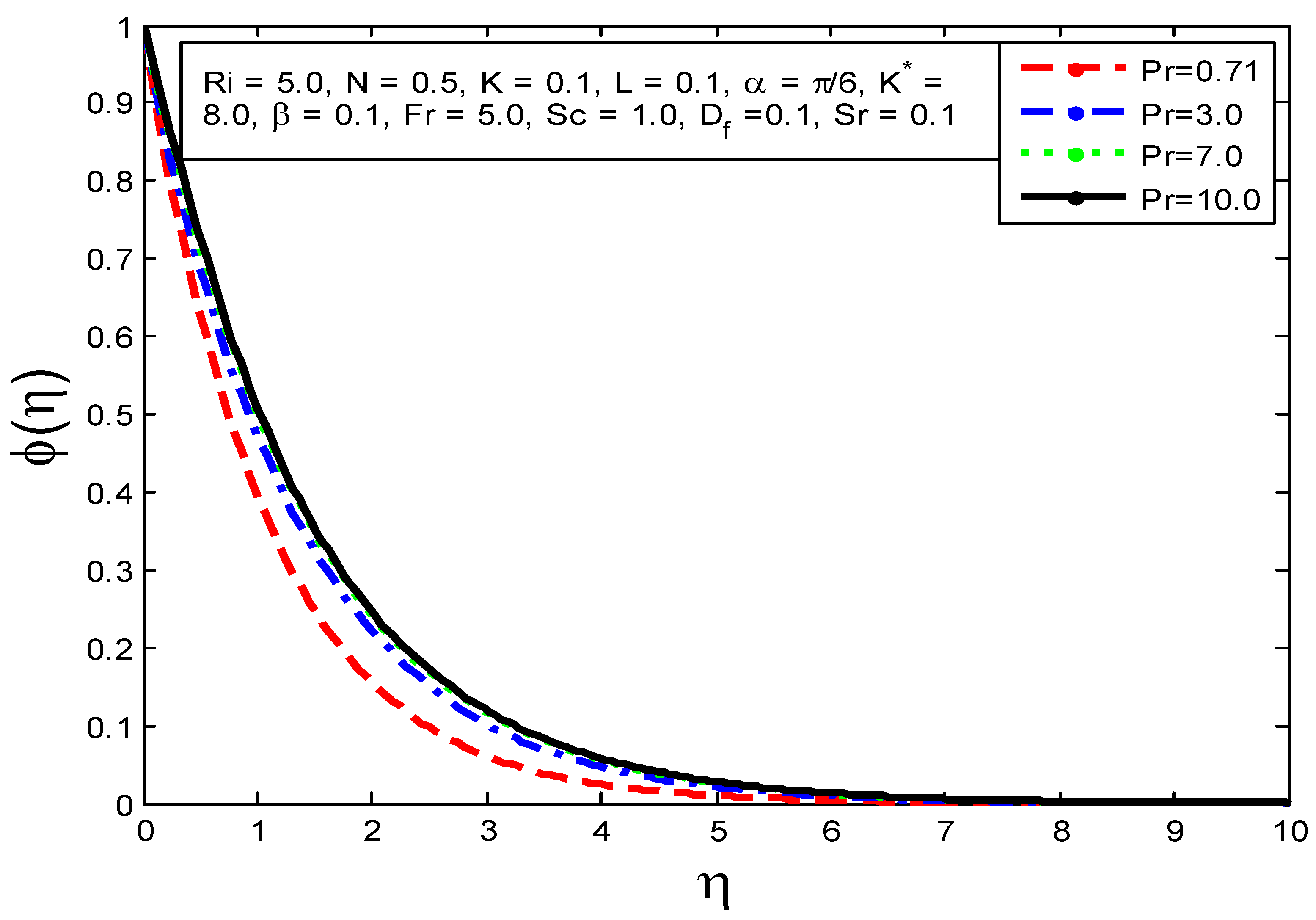
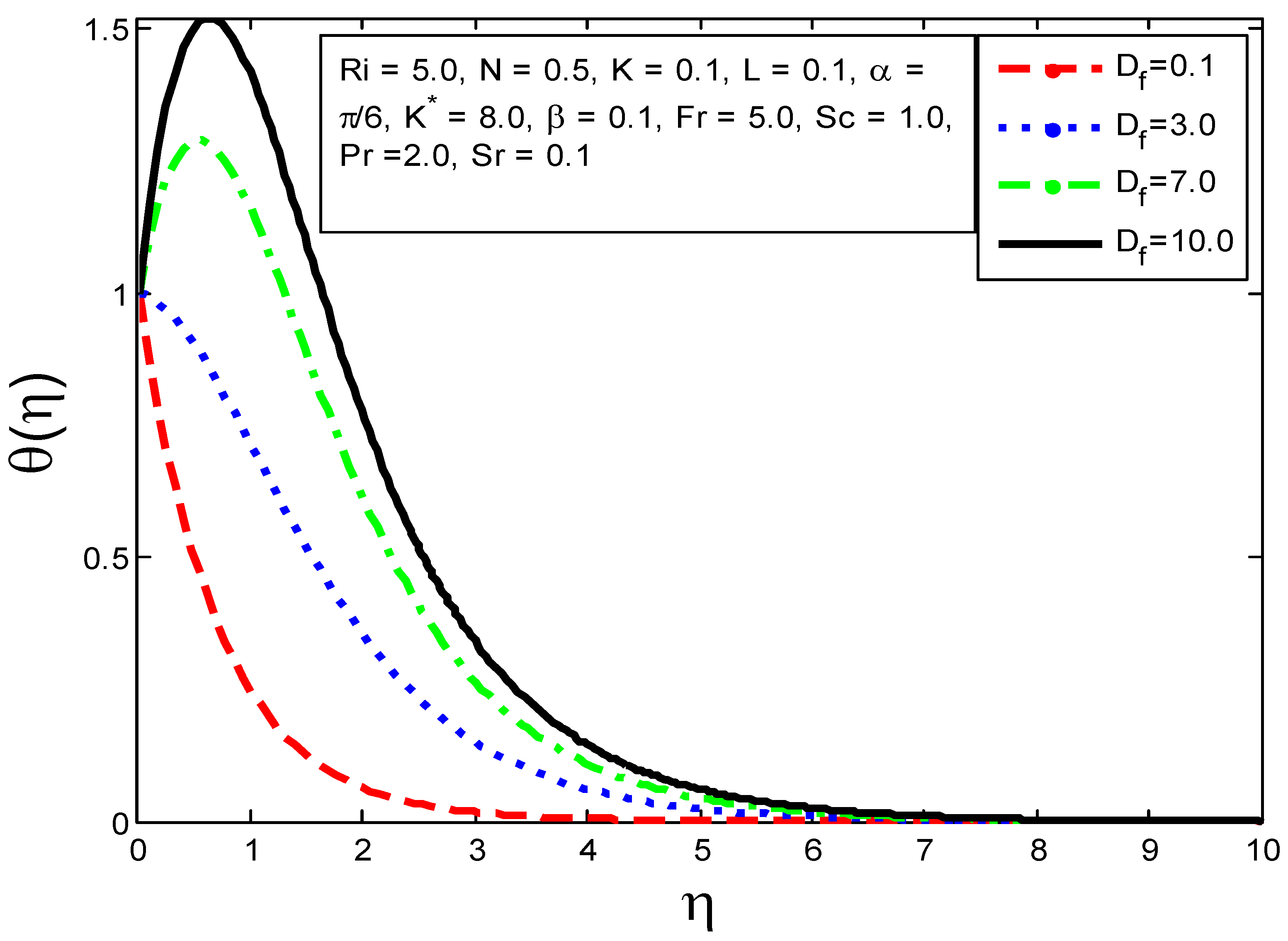
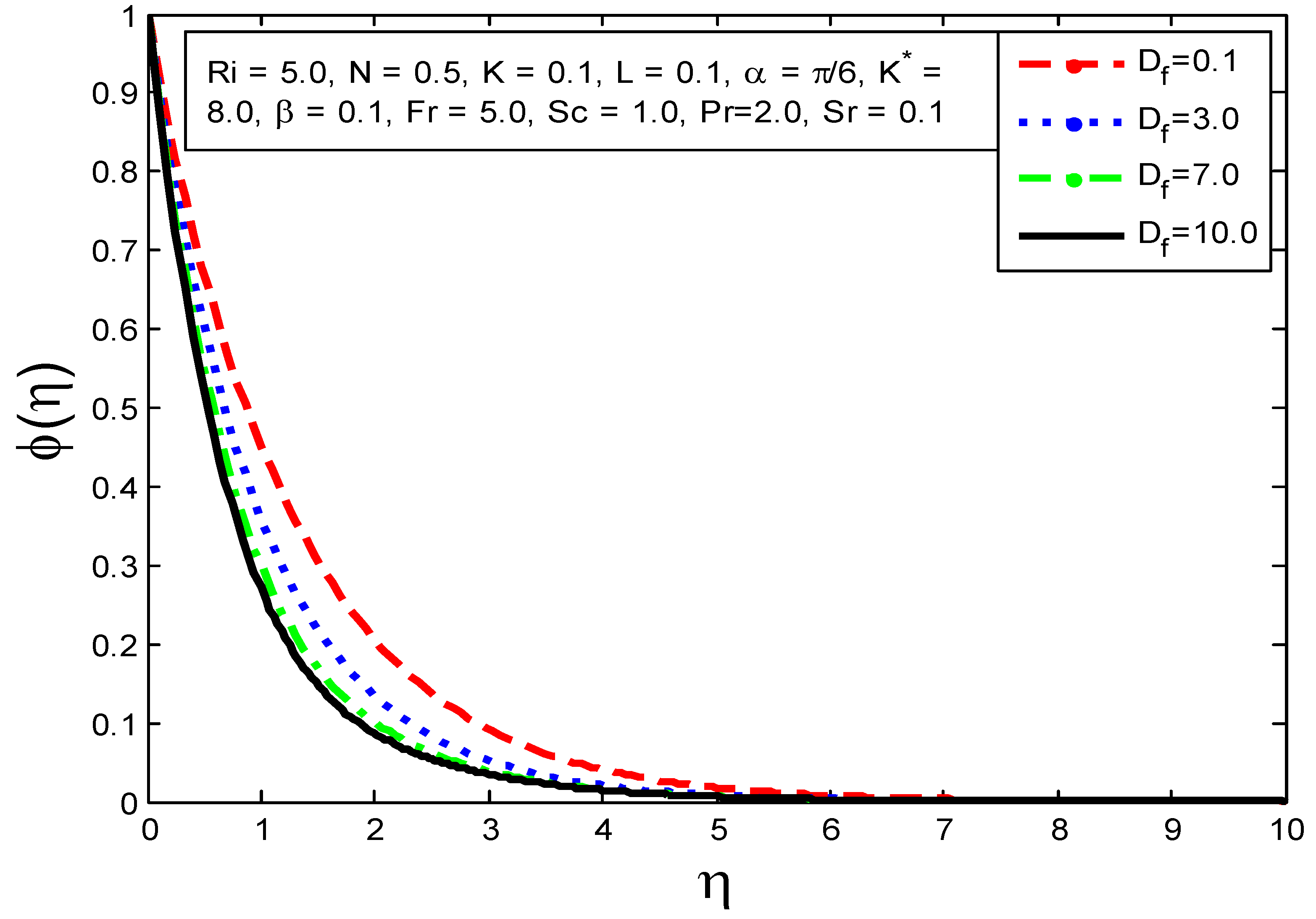
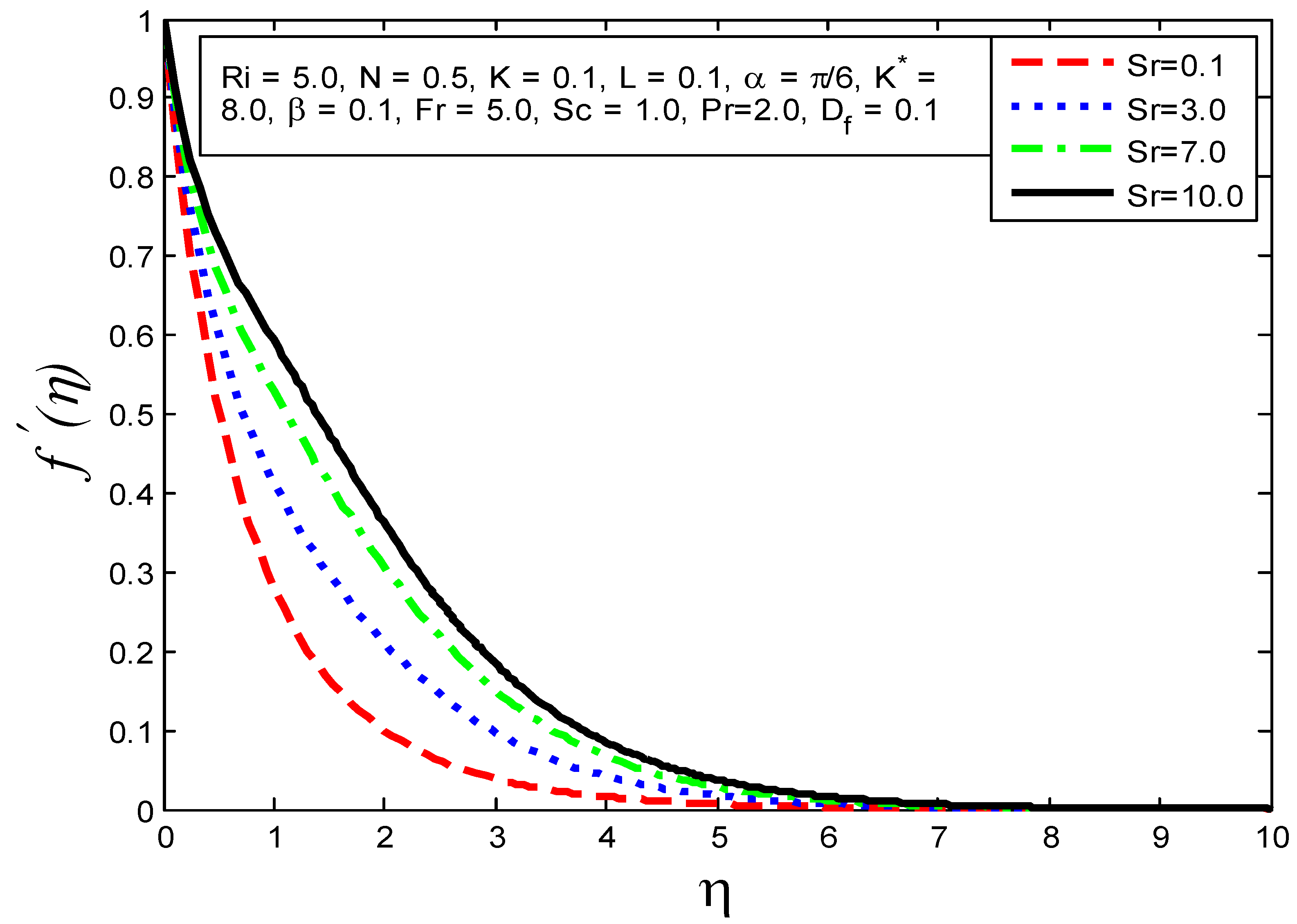
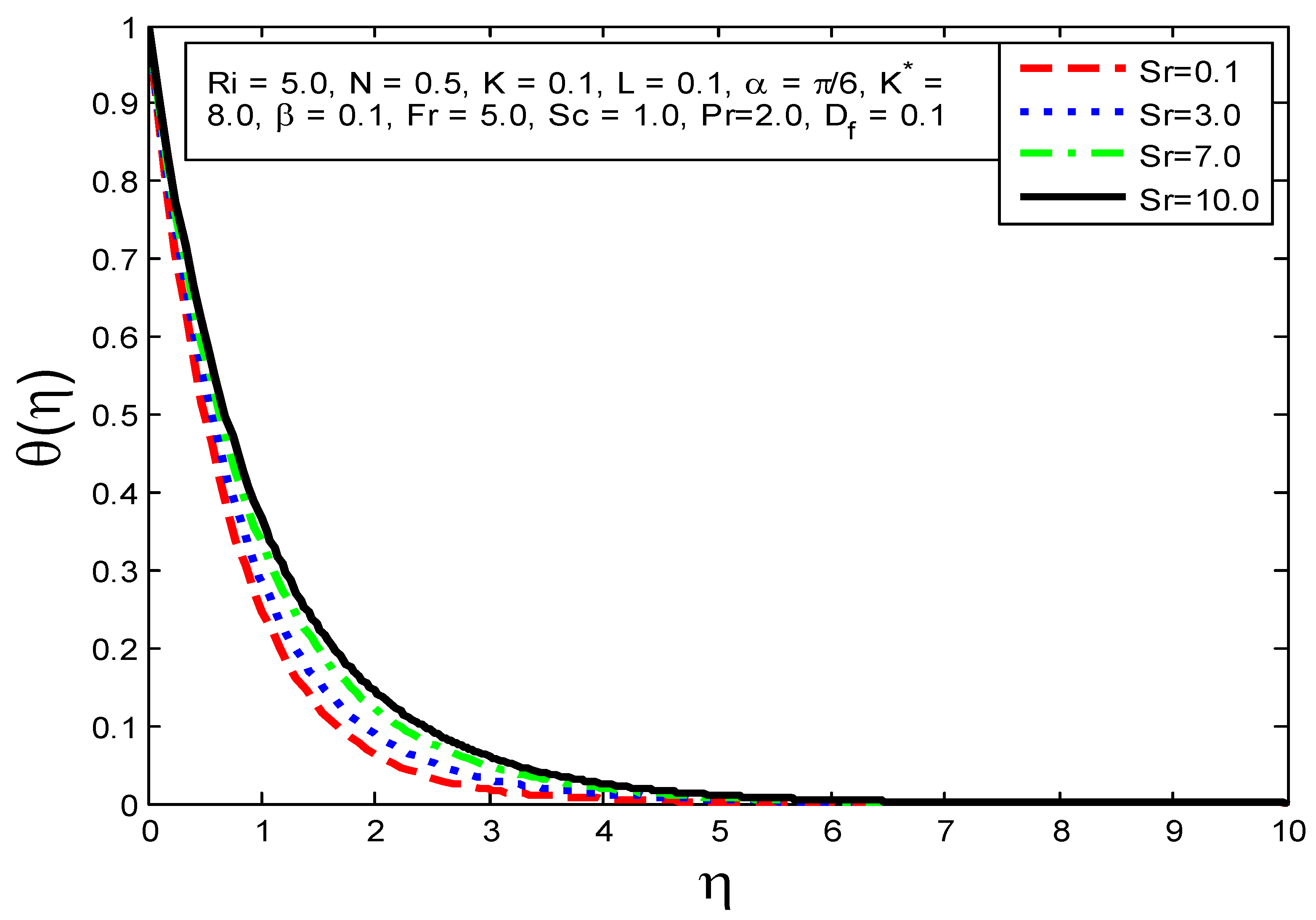
4.1. Influence of Flow Parameters on Velocity Profile Temperature Profile and Mass Concentration
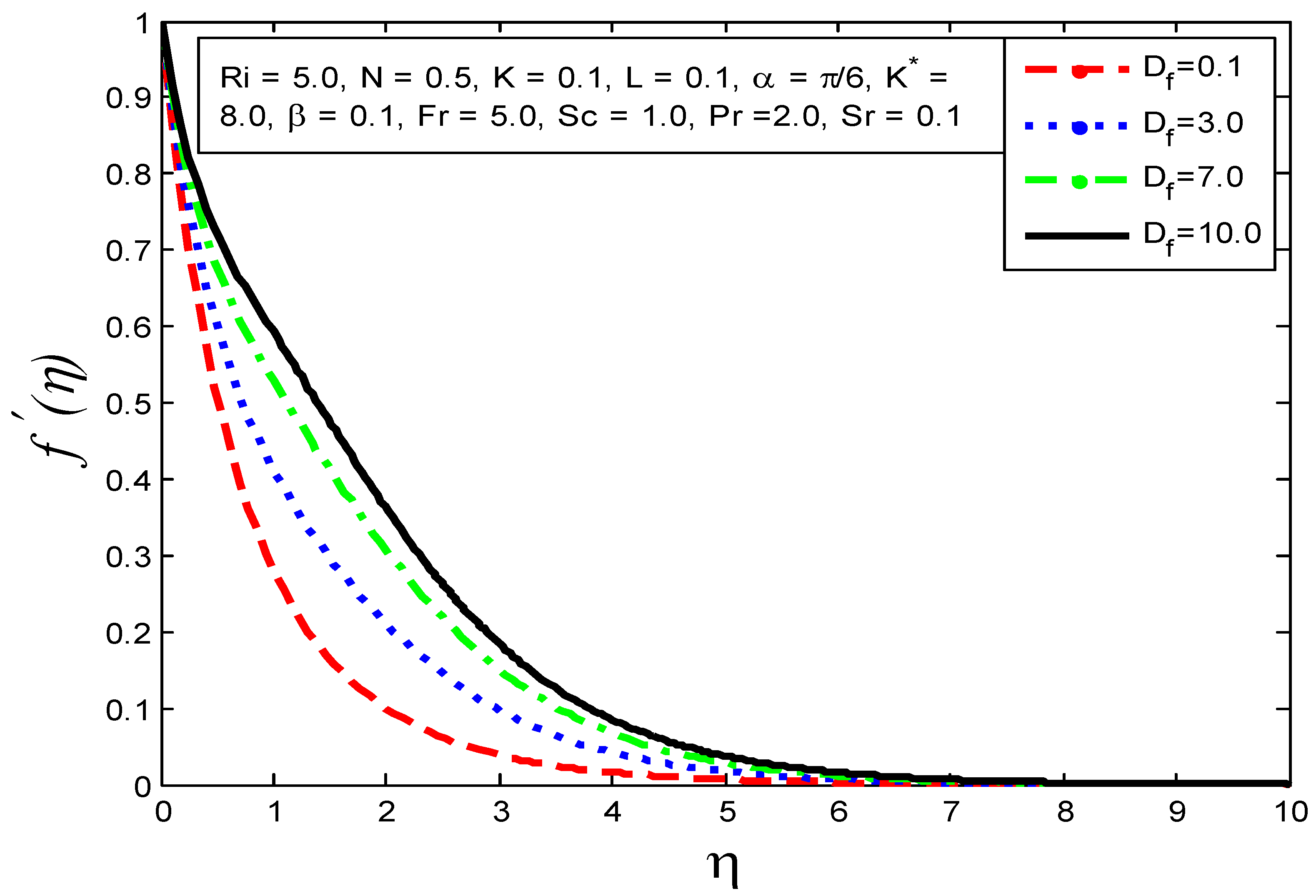
4.2. Influence of the Materials Parameters on and
5. Conclusions
- The velocity profile increases as , and increase and reductions in and Pr are enlarged.
- The temperature field is increased as , and are augmented but the reverse behavior is viewed when increasing the values of and .
- The concentration profile is increased as , and are augmented but attenuated as , Pr, and are elevated.
- The skin friction is increased owing to the rise in values of and the opposite trend is noted with the increasing values of .
- The rate of heat transfer is augmented as rises but reduces with increasing magnitudes of .
- The mass transfer rate increases as and are augmented.
- The tabular results for and are computed exactly at the surface.
- All the numerical results at the inclined exponentially stretching plate fixed at the angle of inclination of were computed.
- All the numerical results presented in graphs in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 satisfied the given boundary conditions asymptotically; therefore, the numerical results given in tabular form are accurate.
- The current results were compared with the available results in the existing literature for the special case, and there was good agreement between them showing the validation of the present study.
- In future, the study will be extended to third-grade nanofluid and hybrid nanofluid with the inclusion of different flow features and physical effects of the different fluid characteristics over the exponentially inclined stretching sheet embedded in a porous medium with different flow conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Nomenclature | Specific heat at constant pressure | ||
| Ambient temperature | Schmidt number | ||
| Ambient concentration | Thermal-diffusion parameter (Soret number) | ||
| Angle of inclination | Viscoelastic parameter | ||
| Buoyancy ratio parameter | Velocity components in and directions | ||
| Concentration in boundary layer | Wall temperature | ||
| Chemical reaction coefficient | Wall concentration | ||
| Chemical reaction parameter | Greeks | ||
| Coefficient of inertia | Dimensionless temperature | ||
| Coordinates | Dimensionless mass concentration | ||
| Cross-viscous parameter | Dynamic viscosity | ||
| Coordinates | Electrical conductivity | ||
| Concentration susceptibility | Fluid density | ||
| Drag Coefficient | Kinematic viscosity | ||
| Diffusion-thermo parameter (Dufour number) | Material moduli | ||
| Fluid temperature in boundary layer | Thermal diffusivity | ||
| Gravitational acceleration | Thermal-diffusion ratio | ||
| Grashof number | Third-grade fluid parameter | ||
| Local inertial coefficient | Thermal conductivity | ||
| Magnetic field strength | Volumetric coefficient thermal expansion | ||
| Magnetic field parameter | Volumetric coefficient concentration expansion | ||
| Mass diffusion coefficient | Subscripts | ||
| Mean temperature of fluid | Ambient conditions | ||
| Porous medium permeability | Wall conditions | ||
| Permeability parameter | |||
| Prandtl number | |||
| Reynolds number | |||
| Richardson number | |||
| Skin friction |
References
- Sahoo, B.; Do, Y. Effects of slip on sheet-driven flow and heat transfer of a third grade fluid past a stretching sheet. Int. Commun. Heat Mass Transf. 2010, 37, 1064–1071. [Google Scholar] [CrossRef]
- Javanmard, M.; Taheri, M.H.; Ebrahimi, S.M. Heat transfer of third-grade fluid flow in a pipe under an externally applied magnetic field with convection on wall. Appl. Rheol. 2018, 28, 56023. [Google Scholar]
- Pakdemirli, M. The boundary layer equations of third-grade fluids. Int. J. Non-Linear Mech. 1992, 27, 785–793. [Google Scholar] [CrossRef]
- Sahoo, B. Flow and heat transfer of a non-Newtonian fluid past a stretching sheet with partial slip. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 602–615. [Google Scholar] [CrossRef]
- Javanmard, M.; Taheri, M.H.; Askari, N.; Öztop, H.F.; Abu-Hamdeh, N. Third-grade non-Newtonian fluid flow and heat transfer in two coaxial pipes with a variable radius ratio with magnetic field. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 959–981. [Google Scholar] [CrossRef]
- Zhang, L.; Bhatti, M.M.; Michaelides, E.E. Electro-magnetohydrodynamic flow and heat transfer of a third-grade fluid using a Darcy-Brinkman-Forchheimer model. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 2623–2639. [Google Scholar] [CrossRef]
- Qayyum, S.; Hayat, T.; Alsaedi, A. Thermal radiation and heat generation/absorption aspects in third grade magneto-nanofluid over a slendering stretching sheet with Newtonian conditions. Phys. B Condens. Matter 2018, 537, 139–149. [Google Scholar] [CrossRef]
- Qayyum, S.; Hayat, T.; Alsaedi, A. Chemical reaction and heat generation/absorption aspects in MHD nonlinear convective flow of third grade nanofluid over a nonlinear stretching sheet with variable thickness. Results Phys. 2017, 7, 2752–2761. [Google Scholar] [CrossRef]
- Imtiaz, M.; Alsaedi, A.; Shafiq, A.; Hayat, T. Impact of chemical reaction on third grade fluid flow with Cattaneo-Christov heat flux. J. Mol. Liq. 2017, 229, 501–507. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, S.A.; Khan, M.I.; Alsaedi, A. Impact of activation energy in nonlinear mixed convective chemically reactive flow of third grade nanomaterial by a rotating disk. Int. J. Chem. React. Eng. 2019, 17, 20180170. [Google Scholar] [CrossRef]
- Forchheimer, P. Wasserbewegung durch boden. Z. Ver. Dtsch. Ing. 1901, 45, 1782–1788. [Google Scholar]
- Muskat, M.; Wyckoff, R.D. The flow of homogeneous fluids through porous media. Soil Sci. 1938, 46, 169. [Google Scholar] [CrossRef]
- Seddeek, M. Influence of viscous dissipation and thermophoresis on Darcy–Forchheimer mixed convection in a fluid saturated porous media. J. Colloid Interface Sci. 2006, 293, 137–142. [Google Scholar] [CrossRef] [PubMed]
- Shenoy, A.V. Darcy-Forchheimer natural, forced and mixed convection heat transfer in non-Newtonian power-law fluid-saturated porous media. Transp. Porous Media 1993, 11, 219–241. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Khan, Z.; Zuhra, S.; Chaudhary, N.I.; Khan, W.U.; He, Y.; Islam, S.; Shoaib, M. Cattaneo-christov heat flux model of 3D hall current involving biconvection nanofluidic flow with Darcy-Forchheimer law effect: Backpropagation neural networks approach. Case Stud. Therm. Eng. 2021, 26, 101168. [Google Scholar] [CrossRef]
- Pan, H.; Rui, H. Mixed Element Method for Two-Dimensional Darcy-Forchheimer Model. J. Sci. Comput. 2012, 52, 563–587. [Google Scholar] [CrossRef]
- Ramzan, M.; Gul, H.; Zahri, M. Darcy-Forchheimer 3D Williamson nanofluid flow with generalized Fourier and Fick’s laws in a stratified medium. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 327–335. [Google Scholar]
- Mahdi, R.A.; Mohammed, H.A.; Munisamy, K.; Saeid, N. Review of convection heat transfer and fluid flow in porous media with nanofluid. Renew. Sustain. Energy Rev. 2015, 41, 715–734. [Google Scholar] [CrossRef]
- Kafoussias, N.; Williams, E. Thermal-diffusion and diffusion-thermo effects on mixed free-forced convective and mass transfer boundary layer flow with temperature dependent viscosity. Int. J. Eng. Sci. 1995, 33, 1369–1384. [Google Scholar] [CrossRef]
- Abd El-Aziz, M. Thermal-diffusion and diffusion-thermo effects on combined heat and mass transfer by hydromagnetic three-dimensional free convection over a permeable stretching surface with radiation. Phys. Lett. A 2008, 372, 263–272. [Google Scholar] [CrossRef]
- Hayat, T.; Nawaz, M.; Asghar, S.; Mesloub, S. Thermal-diffusion and diffusion-thermo effects on axisymmetric flow of a second grade fluid. Int. J. Heat Mass Transf. 2011, 54, 3031–3041. [Google Scholar] [CrossRef]
- Srinivas, S.; Reddy, A.S.; Ramamohan, T. A study on thermal-diffusion and diffusion-thermo effects in a two-dimensional viscous flow between slowly expanding or contracting walls with weak permeability. Int. J. Heat Mass Transf. 2012, 55, 3008–3020. [Google Scholar] [CrossRef]
- Afify, A.A. Similarity solution in MHD: Effects of thermal diffusion and diffusion thermo on free convective heat and mass transfer over a stretching surface considering suction or injection. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2202–2214. [Google Scholar] [CrossRef]
- Seddeek, M.A. Thermal-diffusion and diffusion-thermo effects on mixed free-forced convective flow and mass transfer over an accelerating surface with a heat source in the presence of suction and blowing in the case of variable viscosity. Acta Mech. 2004, 172, 83–94. [Google Scholar] [CrossRef]
- Eldabe, N.T.; Rizkalla, R.R.; Abouzeid, M.; Ayad, V.M. Thermal diffusion and diffusion thermo effects of Eyring-Powell nanofluid flow with gyrotactic microorganisms through the boundary layer. Heat Transf.—Asian Res. 2020, 49, 383–405. [Google Scholar] [CrossRef]
- Ishak, A. MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malays. 2011, 40, 391–395. [Google Scholar]
- Sajid, M.; Hayat, T. Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet. Int. Commun. Heat Mass Transf. 2008, 35, 347–356. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Khan, Z.H. Heat transfer analysis of water-based nanofluid over an exponentially stretching sheet. Alex. Eng. J. 2014, 53, 219–224. [Google Scholar] [CrossRef] [Green Version]
- Bidin, B.; Nazar, R. Numerical solution of the boundary layer flow over an exponentially stretching sheet with thermal radiation. Eur. J. Sci. Res. 2009, 33, 710–717. [Google Scholar]
- Kumar, D.; Sinha, S.; Sharma, A.; Agrawal, P.; Dadheech, P.K. Numerical study of chemical reaction and heat transfer of MHD slip flow with Joule heating and Soret–Dufour effect over an exponentially stretching sheet. Heat Transf. 2022, 51, 1939–1963. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D Appl. Phys. 1999, 32, 577–585. [Google Scholar] [CrossRef]
- Pandit, S.; Sharma, S. Sensitivity analysis of emerging parameters in the presence of thermal radiation on magnetohydrodynamic nanofluids via wavelets. Eng. Comput. 2021, 1–10. [Google Scholar] [CrossRef]
- Pandit, S.; Sharma, S. Wavelet strategy for flow and heat transfer in CNT-water based fluid with asymmetric variable rectangular porous channel. Eng. Comput. 2020, 1–11. [Google Scholar] [CrossRef]
- Mittal, R.; Pandit, S. Numerical simulation of unsteady squeezing nanofluid and heat flow between two parallel plates using wavelets. Int. J. Therm. Sci. 2017, 118, 410–422. [Google Scholar] [CrossRef]
- Mittal, R.C.; Pandit, S. A Numerical Algorithm to Capture Spin Patterns of Fractional Bloch Nuclear Magnetic Resonance Flow Models. J. Comput. Nonlinear Dyn. 2019, 89, 799–808. [Google Scholar] [CrossRef]
- Jiwari, R.; Kumar, V.; Singh, S. Lie group analysis, exact solutions and conservation laws to compressible isentropic Navier–Stokes equation. Eng. Comput. 2020, 1–10. [Google Scholar] [CrossRef]
- Khan, M.N.; Ahmad, S.; Ahammad, N.A.; Alqahtani, T.; Algarni, S. Numerical investigation of hybrid nanofluid with gyrotactic microorganism and multiple slip conditions through a porous rotating disk. Waves Random Complex Media 2022, 1–16. [Google Scholar] [CrossRef]
- Li, Y.-M.; Ullah, I.; Ahammad, N.A.; Ullah, I.; Muhammad, T.; Asiri, S.A. Approximation of unsteady squeezing flow through porous space with slip effect: DJM approach. Waves Random Complex Media 2022, 1–15. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Moindal, I.C.; Hayat, T. MHD boundary layer flow of Casson fluid passing through an exponentially stretching permeable surface with thermal radiation. Chin. Phys. B 2014, 23, 104701. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A.; Yasmeen, T. Diffusion of chemically reactive species in third grade fluid flow over an exponentially stretching sheet considering magnetic field effects. Chin. J. Chem. Eng. 2017, 25, 257–263. [Google Scholar] [CrossRef]







| Pr | Magyari and Keller [31] | Present Study |
|---|---|---|
| 1.0 | 0.9547 | 0.9551 |
| 3 | 1.8691 | 1.8121 |
| 5 | 2.5001 | 2.5577 |
| 10 | 3.6604 | 3.6868 |
| Mukhopadhyay et al. [39] | Hayat et al. [40] | Present Study |
|---|---|---|
| −1.281812 | −1.2818 | −1.2819 |
| 0.1 | 2.08746 | 1.16064 | 0.62817 |
| 3.0 | 1.67881 | 1.31154 | 0.76902 |
| 7.0 | 1.17803 | 1.42548 | 0.86850 |
| 10.0 | 0.83114 | 1.48769 | 0.92125 |
| 1.0 | 1.42189 | 1.37481 | 0.82479 |
| 3.0 | 1.47903 | 1.27574 | 1.73512 |
| 7.0 | 1.53384 | 1.16031 | 2.88998 |
| 10.0 | 1.55589 | 1.09747 | 3.54354 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, A.; Shafqat, R.; Jeelani, M.B.; Alharthi, N.H. Convective Heat and Mass Transfer in Third-Grade Fluid with Darcy–Forchheimer Relation in the Presence of Thermal-Diffusion and Diffusion-Thermo Effects over an Exponentially Inclined Stretching Sheet Surrounded by a Porous Medium: A CFD Study. Processes 2022, 10, 776. https://doi.org/10.3390/pr10040776
Abbas A, Shafqat R, Jeelani MB, Alharthi NH. Convective Heat and Mass Transfer in Third-Grade Fluid with Darcy–Forchheimer Relation in the Presence of Thermal-Diffusion and Diffusion-Thermo Effects over an Exponentially Inclined Stretching Sheet Surrounded by a Porous Medium: A CFD Study. Processes. 2022; 10(4):776. https://doi.org/10.3390/pr10040776
Chicago/Turabian StyleAbbas, Amir, Ramsha Shafqat, Mdi Begum Jeelani, and Nadiyah Hussain Alharthi. 2022. "Convective Heat and Mass Transfer in Third-Grade Fluid with Darcy–Forchheimer Relation in the Presence of Thermal-Diffusion and Diffusion-Thermo Effects over an Exponentially Inclined Stretching Sheet Surrounded by a Porous Medium: A CFD Study" Processes 10, no. 4: 776. https://doi.org/10.3390/pr10040776
APA StyleAbbas, A., Shafqat, R., Jeelani, M. B., & Alharthi, N. H. (2022). Convective Heat and Mass Transfer in Third-Grade Fluid with Darcy–Forchheimer Relation in the Presence of Thermal-Diffusion and Diffusion-Thermo Effects over an Exponentially Inclined Stretching Sheet Surrounded by a Porous Medium: A CFD Study. Processes, 10(4), 776. https://doi.org/10.3390/pr10040776






