Fractional Order PID Design for a Proton Exchange Membrane Fuel Cell System Using an Extended Grey Wolf Optimizer
Abstract
:1. Introduction
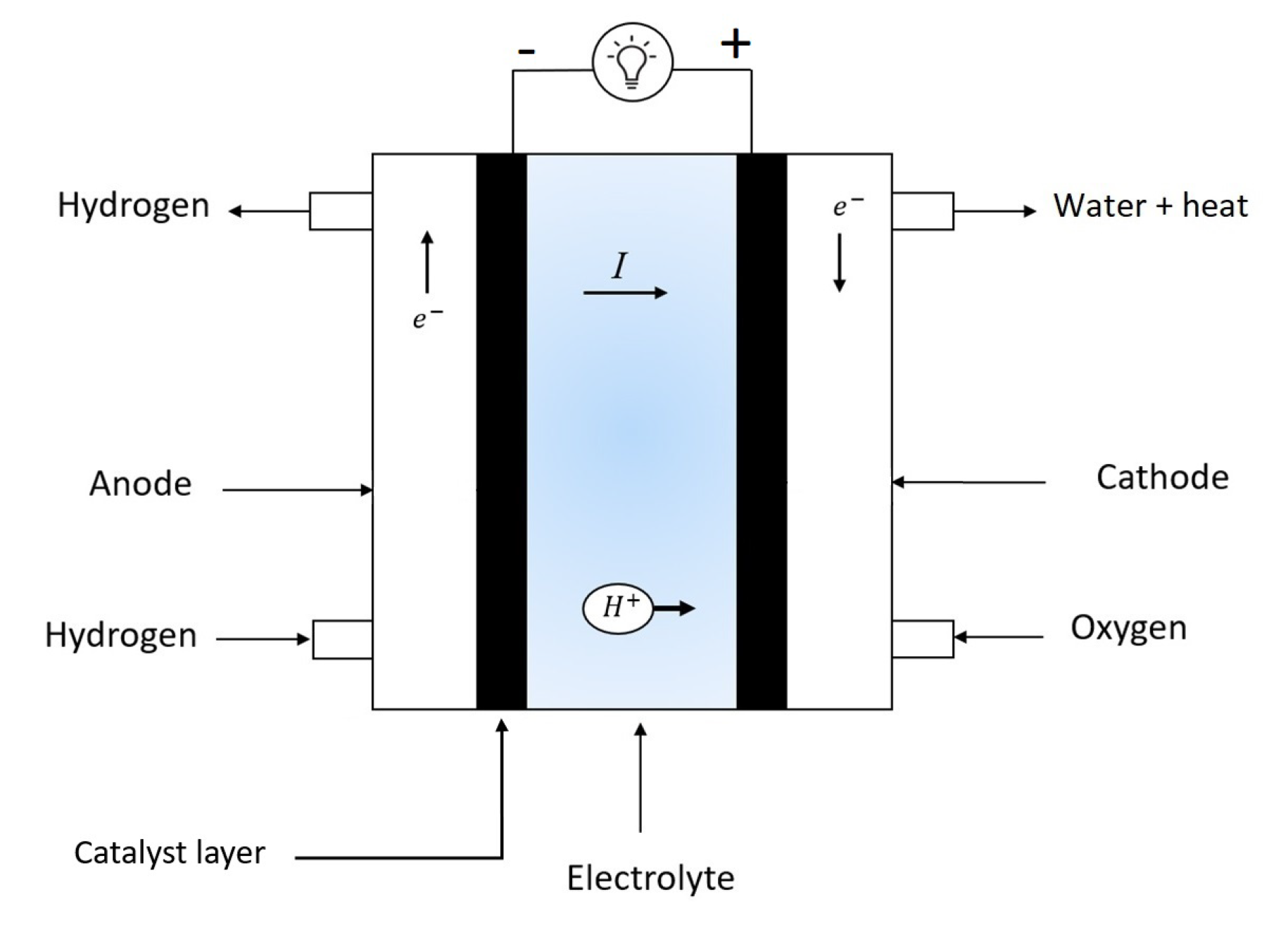
2. PEM Fuel Cell Modeling
2.1. Nernst Potential
2.2. The Activation Polarization
2.3. The Ohmic Losses
2.4. The Concentration Polarization
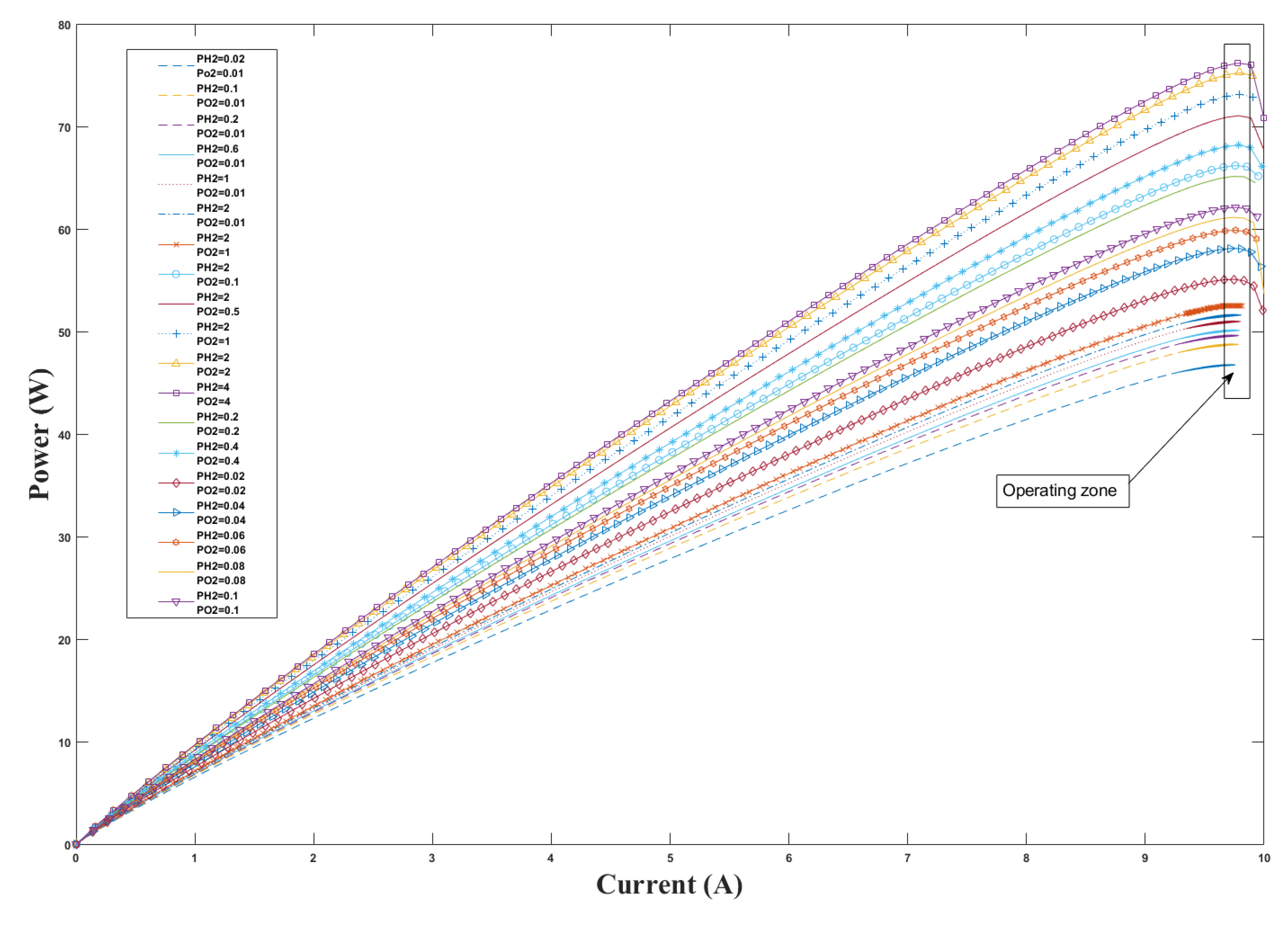
2.5. PEM Fuel Cell Stack Output Power
3. Control Design Methodology
3.1. Boost Converter State Space Modeling
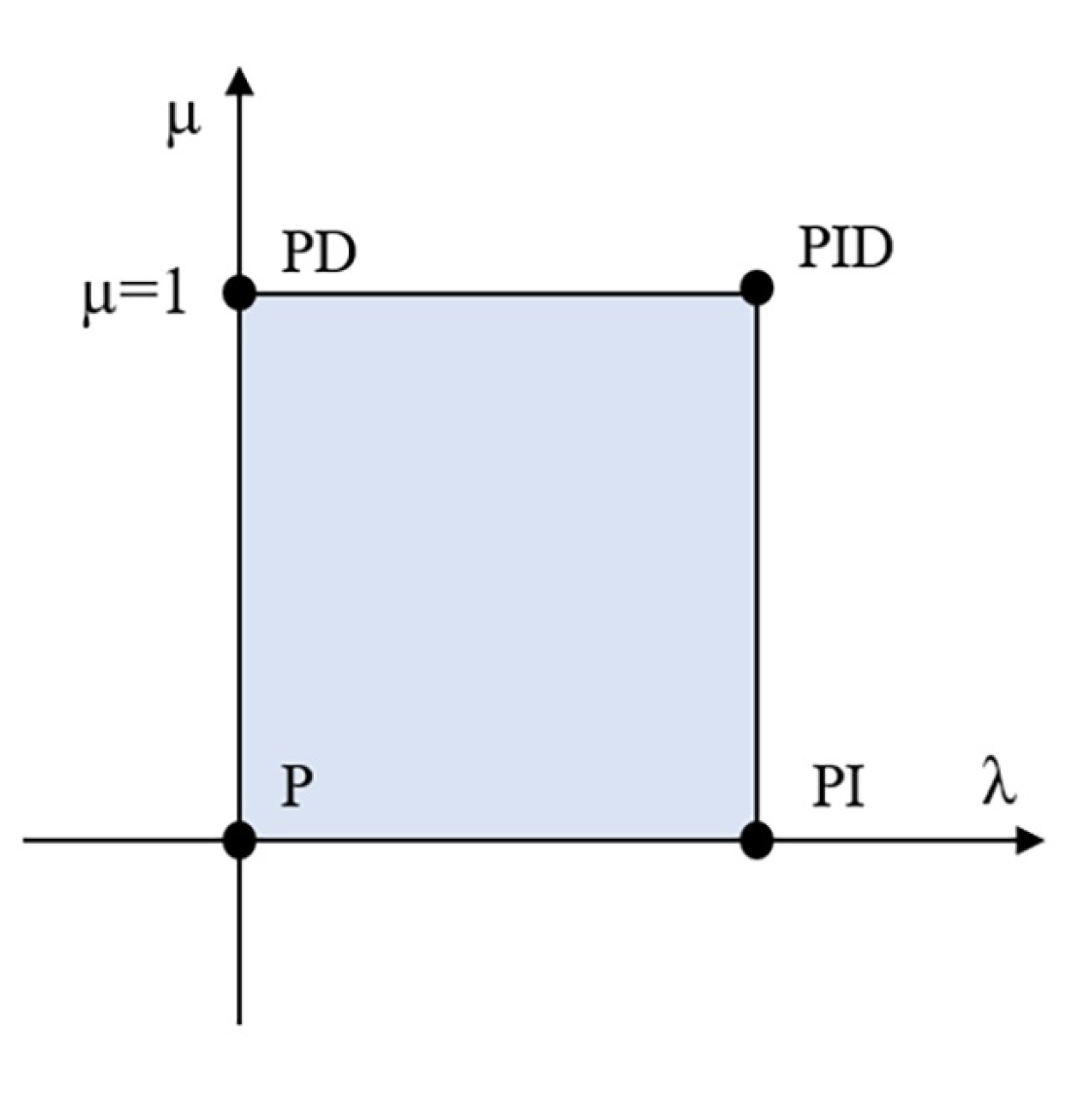
3.2. Fractional Order PID Controller
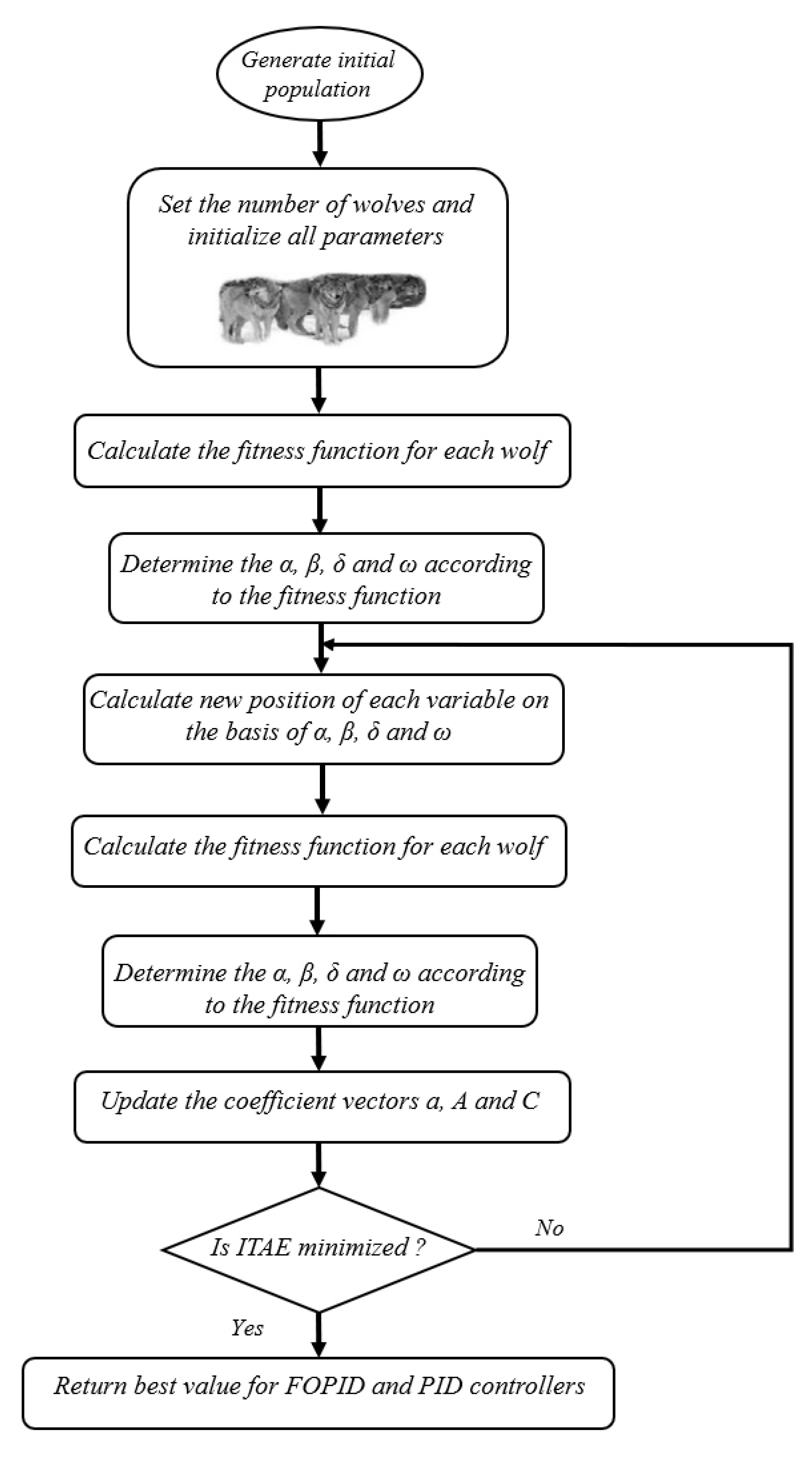
3.3. Optimization Using EGWO Method
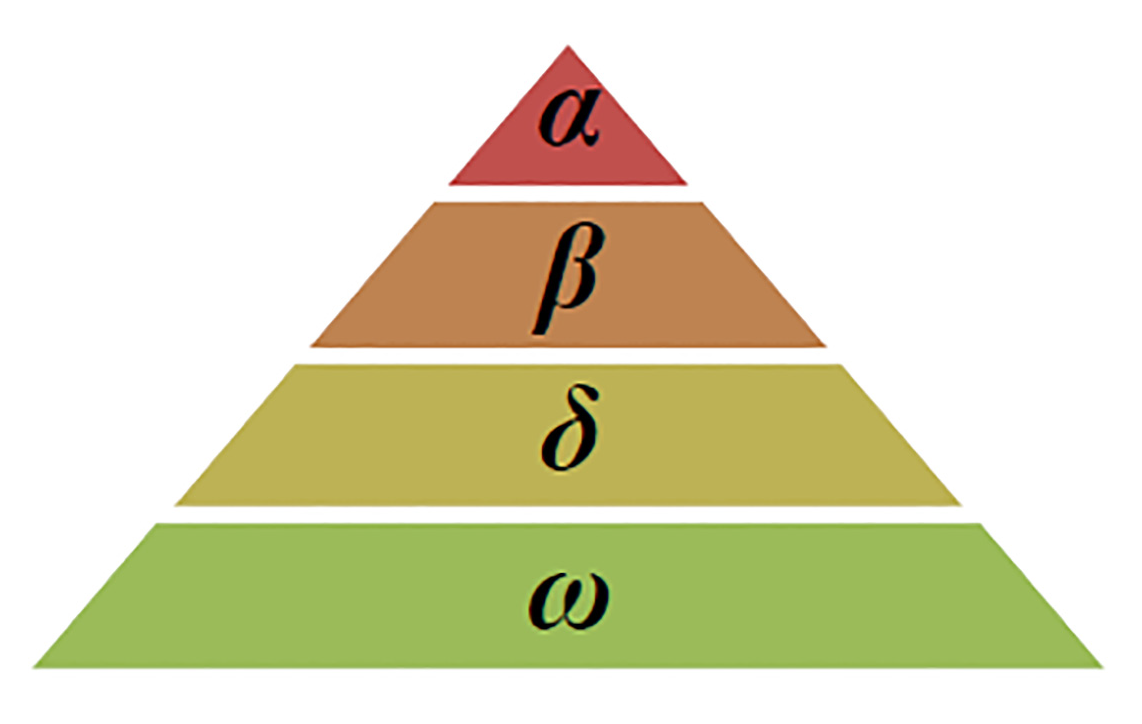
- Social hierarchy
- Prey search (exploration)
- Follow, hunt and approach the prey
- Pursue, circle and harass the prey until they stop moving
- Attack on the prey
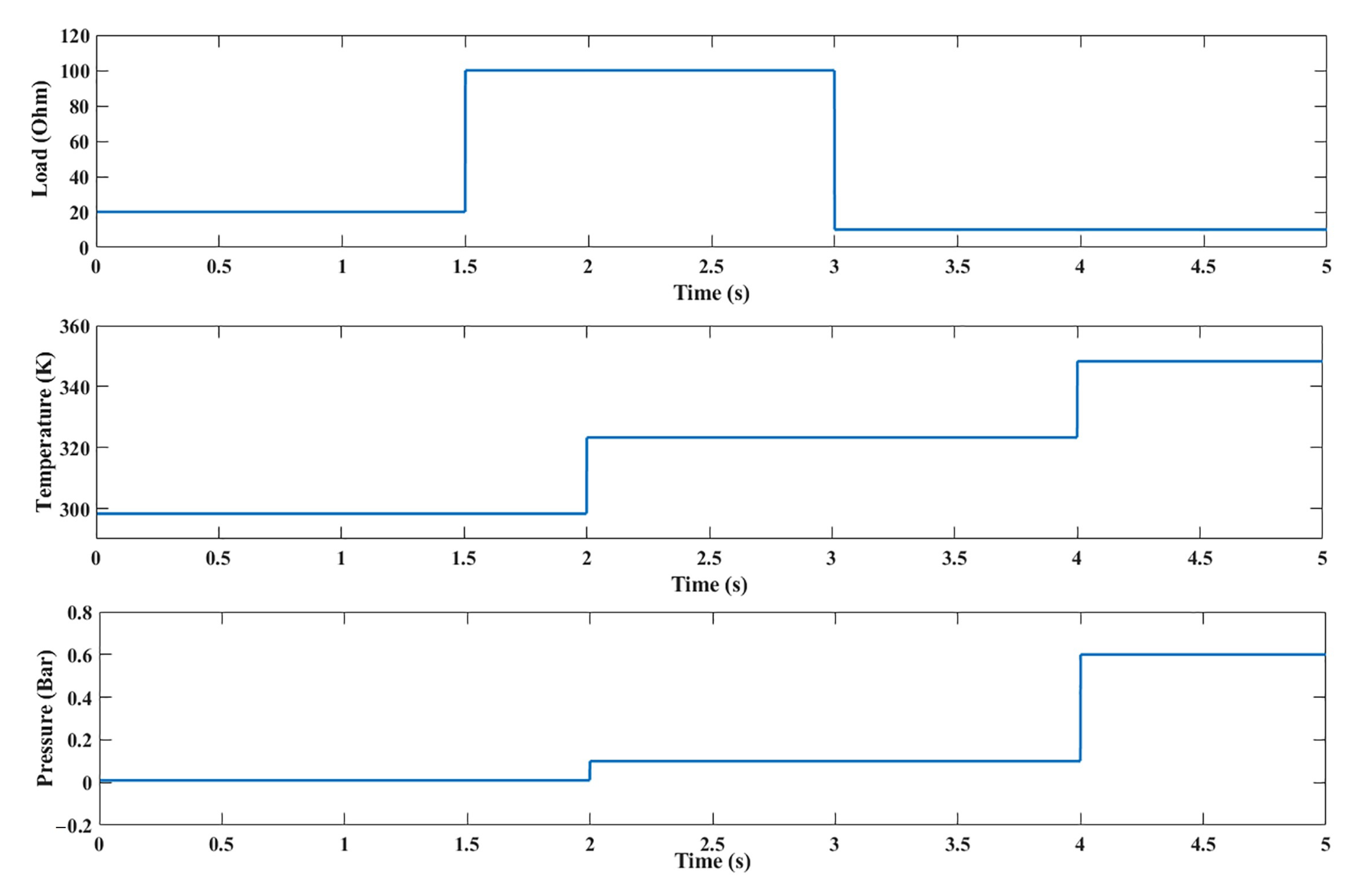
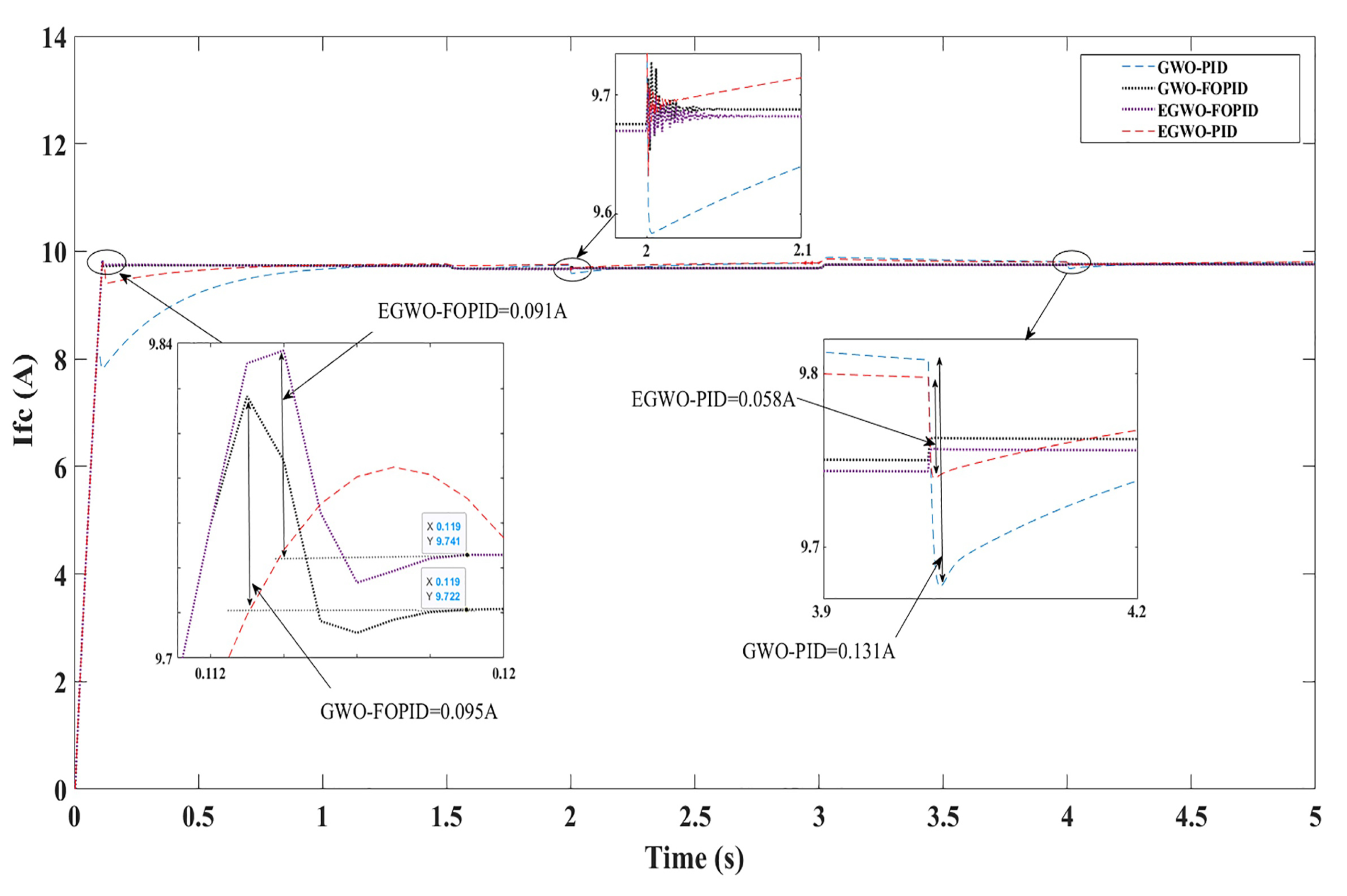
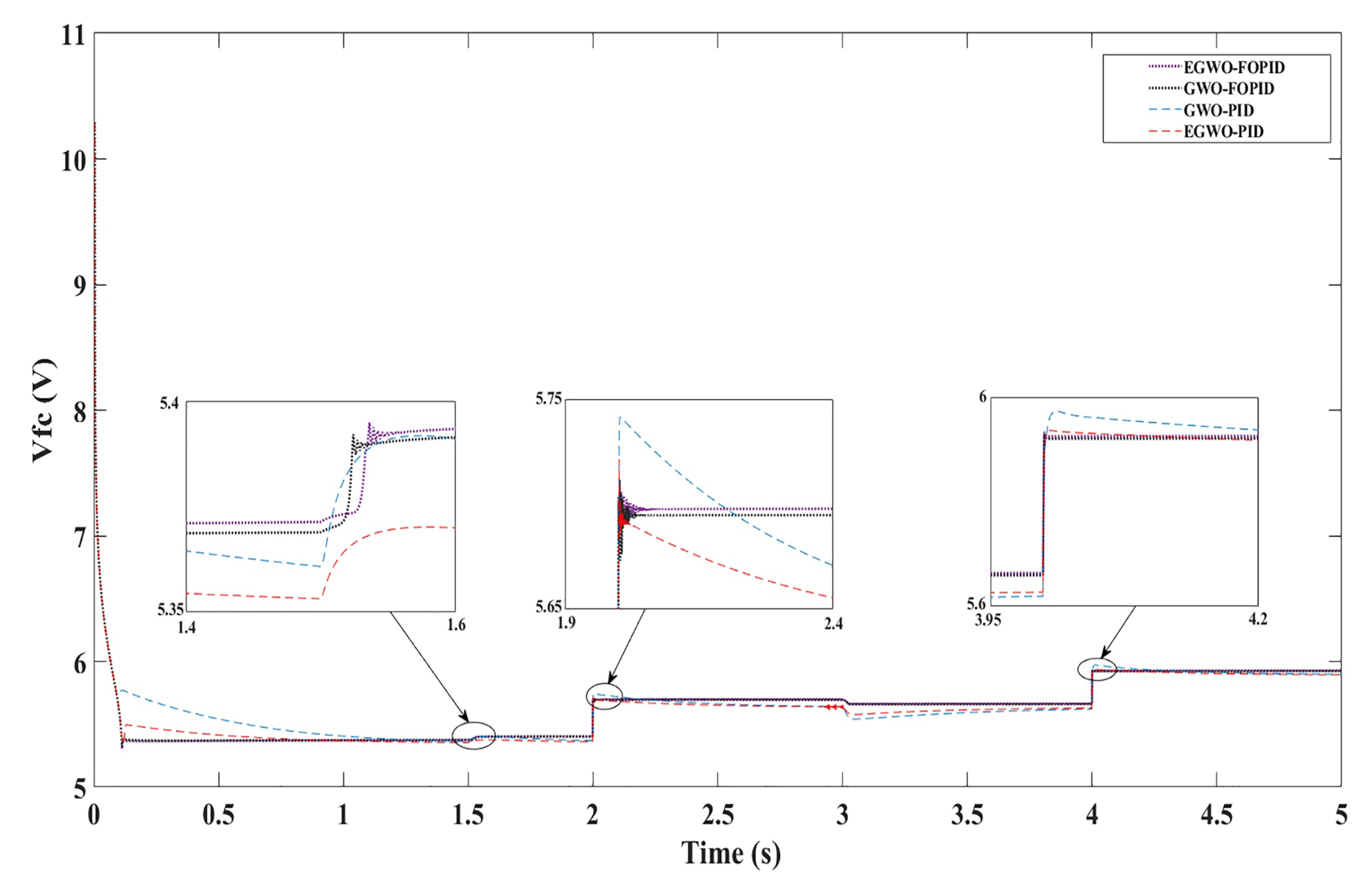
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GWO | grey wolf optimizer |
| EGWO | extended grey wolf optimizer |
| PI | proportional integral |
| PID | proportional integral derivative |
| GA | genetic algorithm |
| PSO | particle swarm optimization |
| QC-HOSM | quasi continuous high order sliding mode |
| FOPID | fractional-order proportional integral derivative |
| PEMFC | proton exchange membrane fuel cells |
| IGBT | insulated gate bipolar transistor |
| MOSFET | metal oxide semiconductor field effect transistor |
| ZN | ziegler-nichols |
| RMSE | root mean squared error |
| TSMC | total sliding-mode control |
| CCM | continuous conduction mode |
References
- Calvo, L.M.; Domingo, R. Influence of Maintenance Actions in the Drying Stage of a Paper Mill on CO2 Emissions. Processes 2021, 9, 1707. [Google Scholar] [CrossRef]
- Ou, T.; Peng, H.; Su, M.; Shi, Q.; Tang, J.; Chen, N.; Chen, D. Fast and Efficient Removal of Uranium onto a Magnetic Hydroxyapatite Composite: Mechanism and Process Evaluation. Processes 2021, 9, 1927. [Google Scholar] [CrossRef]
- Yoro, K.O.; Daramola, M.O. CO2 emission sources, greenhouse gases, and the global warming effect. Adv. Carbon Capture 2020, 9, 3–28. [Google Scholar]
- Ventura, M. Long term storability of hydrogen peroxide. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, AZ, USA, 10–13 July 2005; p. 4551. [Google Scholar]
- Zhang, Y.; Liu, C.; Wan, Z.; Yang, C.; Li, S.; Tu, Z.; Wu, M.; Chen, Y.; Zhou, W. Performance Enhancement of PEM Fuel Cells with an Additional Outlet in the Parallel Flow Field. Processes 2021, 9, 2061. [Google Scholar] [CrossRef]
- Encalada-Dávila, Á.; Espinoza-Andaluz, M.; Barzola-Monteses, J.; Li, S.; Andersson, M. Transport parameter correlations for digitally created PEFC gas diffusion layers by using openPNM. Processes 2021, 9, 1141. [Google Scholar] [CrossRef]
- Duan, Z.; Zhang, L.; Feng, L.; Yu, S.; Jiang, Z.; Xu, X.; Hong, J. Research on Economic and Operating Characteristics of Hydrogen Fuel Cell Cars Based on Real Vehicle Tests. Energies 2021, 14, 7856. [Google Scholar] [CrossRef]
- Rubio, G.A.; Agila, W.E. A Fuzzy Model to Manage Water in Polymer Electrolyte Membrane Fuel Cells. Processes 2021, 9, 904. [Google Scholar] [CrossRef]
- Costamagna, P.; Srinivasan, S. Quantum jumps in the PEMFC science and technology from the 1960s to the year 2000: Part II. J. Power Sources 2001, 102, 253–269. [Google Scholar] [CrossRef]
- Bacquart, T.; Moore, N.; Wilmot, R.; Bartlett, S.; Morris, A.S.O.; Olden, J.; Becker, H.; Aarhaug, T.A.; Germe, S.; Riot, P.; et al. Hydrogen for maritime application—Quality of hydrogen generated onboard ship by electrolysis of purified seawater. Processes 2021, 9, 1252. [Google Scholar] [CrossRef]
- Li, Q.; Liu, Z.; Sun, Y.; Yang, S.; Deng, C. A review on temperature control of proton exchange membrane fuel cells. Processes 2021, 9, 235. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Gallorini, F.; Ottaviano, A. Dynamic analysis of PEMFC-based CHP systems for domestic application. Appl. Energy 2012, 91, 13–28. [Google Scholar] [CrossRef]
- Yau, Y.T.; Hwu, K.I.; Shieh, J.J. Minimization of output voltage ripple of two-phase interleaved buck converter with active clamp. Energies 2021, 14, 5215. [Google Scholar] [CrossRef]
- Faifer, M.; Piegari, L.; Rossi, M.; Toscani, S. An Average Model of DC–DC Step-Up Converter Considering Switching Losses and Parasitic Elements. Energies 2021, 14, 7780. [Google Scholar] [CrossRef]
- Derbeli, M.; Farhat, M.; Barambones, O.; Sbita, L. Control of proton exchange membrane fuel cell (pemfc) power system using pi controller. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar]
- Namnabat, M.; Poodeh, M.B.; Eshtehardiha, S. Comparison the control methods in improvement the performance of the DC-DC converter. In Proceedings of the 2007 7th Internatonal Conference on Power Electronics, Daegu, Korea, 22–26 October 2007; Volume 13, pp. 246–251. [Google Scholar]
- Águila-León, J.; Chiñas-Palacios, C.D.; Vargas-Salgado, C.; Hurtado-Perez, E.; García, E.X. Optimal PID Parameters Tunning for a DC-DC Boost Converter: A Performance Comparative Using Grey Wolf Optimizer, Particle Swarm Optimization and Genetic Algorithms. In Proceedings of the 2020 IEEE Conference on Technologies for Sustainability (SusTech), Santa Ana, CA, USA, 23–25 April 2007; pp. 1–6. [Google Scholar]
- Li, H.; Ye, X. Sliding-mode PID control of DC-DC converter. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications, Taichung, Taiwan, 15–17 June 2010; pp. 730–734. [Google Scholar]
- Derbeli, M.; Barambones, O.; Sbita, L. A robust maximum power point tracking control method for a PEM fuel cell power system. Appl. Sci. 2018, 8, 2449. [Google Scholar] [CrossRef] [Green Version]
- Wai, R.J.; Shih, L.C. Design of voltage tracking control for DC–DC boost converter via total sliding-mode technique. IEEE Trans. Ind. Electron. 2010, 58, 2502–2511. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Derbeli, M.; Barambones, O.; Cheknane, A. Design and implementation of high order sliding mode control for PEMFC power system. Energies 2020, 13, 4317. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Derbeli, M.; Barambones, O.; Napole, C.; Cheknane, A.; Gonzalez De Durana, J.M. An efficient and robust current control for polymer electrolyte membrane fuel cell power system. Sustainability 2021, 13, 2360. [Google Scholar] [CrossRef]
- Yang, Q.; Lin, H.; Wang, X.; Zhang, L.Y.; Jing, M.; Yuan, W.; Li, C.M. Dynamically self-assembled adenine-mediated synthesis of pristine graphene-supported clean Pd nanoparticles with superior electrocatalytic performance toward formic acid oxidation. J. Colloid Interface Sci. 2022, 613, 515–523. [Google Scholar] [CrossRef]
- Fan, X.; Yuan, W.; Zhang, D.H.; Li, C.M. Heteropolyacid-mediated self-assembly of heteropolyacid-modified pristine graphene supported Pd nanoflowers for superior catalytic performance toward formic acid oxidation. ACS Appl. Energy Mater. 2018, 1, 411–420. [Google Scholar] [CrossRef]
- Truong, V.M.; Duong, N.B.; Yang, H. Effect of Gas Diffusion Layer Thickness on the Performance of Anion Exchange Membrane Fuel Cells. Processes 2021, 9, 718. [Google Scholar] [CrossRef]
- Morán-Durán, A.; Martínez-Sibaja, A.; Rodríguez-Jarquin, J.P.; Posada-Gómez, R.; González, O.S. PEM fuel cell voltage neural control based on hydrogen pressure regulation. Processes 2019, 7, 434. [Google Scholar] [CrossRef] [Green Version]
- Verastegui, J.E.E.; Zamora Antuñano, M.A.; Resendiz, J.R.; García García, R.; Kañetas, P.J.P.; Ordaz, D.L. Electrochemical Hydrogen Production Using Separated-Gas Cells for Soybean Oil Hydrogenation. Processes 2020, 8, 832. [Google Scholar] [CrossRef]
- Rezaei, M.; Dampage, U.; Das, B.K.; Nasif, O.; Borowski, P.F.; Mohamed, M.A. Investigating the Impact of Economic Uncertainty on Optimal Sizing of Grid-Independent Hybrid Renewable Energy Systems. Processes 2021, 9, 1468. [Google Scholar] [CrossRef]
- Sahli, Y.; Moussa, H.B.; Zitouni, B. Optimization study of the produced electric power by SOFCs. Int. J. Hydrog. Energy 2019, 44, 22445–22454. [Google Scholar] [CrossRef]
- Marques, J.G.; Costa, A.L.; Pereira, C. Gibbs free energy (ΔG) analysis for the NaOH (sodium-oxygen-hydrogen) thermochemical water splitting cycle. Int. J. Hydrog. Energy 2019, 44, 14536–14549. [Google Scholar] [CrossRef]
- Faddeev, N.; Anisimov, E.; Belichenko, M.; Kuriganova, A.; Smirnova, N. Investigation of the Ambient Temperature Influence on the PEMFC Characteristics: Modeling from a Single Cell to a Stack. Processes 2021, 9, 2117. [Google Scholar] [CrossRef]
- Djeziri, M.; Djedidi, O.; Benmoussa, S.; Bendahan, M.; Seguin, J.L. Failure Prognosis Based on Relevant Measurements Identification and Data-Driven Trend-Modeling: Application to a Fuel Cell System. Processes 2021, 9, 328. [Google Scholar] [CrossRef]
- Han, J.; Yu, S.; Yun, J. PEMFC Transient Response Characteristics Analysis in Case of Temperature Sensor Failure. Processes 2020, 8, 1353. [Google Scholar] [CrossRef]
- Al-Shamma’a, A.A.; Ali, F.A.A.; Alhoshan, M.S.; Alturki, F.A.; Farh, H.M.; Alam, J.; AlSharabi, K. Proton Exchange Membrane Fuel Cell Parameter Extraction Using a Supply–Demand-Based Optimization Algorithm. Processes 2021, 9, 1416. [Google Scholar] [CrossRef]
- Derbeli, M.; Farhat, M.; Barambones, O.; Sbita, L. Control of PEM fuel cell power system using sliding mode and super-twisting algorithms. Int. J. Hydrog. Energy 2017, 42, 8833–8844. [Google Scholar] [CrossRef]
- Bao, S.; Ebadi, A.; Toughani, M.; Dalle, J.; Maseleno, A.; Yıldızbası, A. A new method for optimal parameters identification of a PEMFC using an improved version of Monarch Butterfly Optimization Algorithm. Int. J. Hydrog. Energy 2020, 45, 17882–17892. [Google Scholar] [CrossRef]
- Yuan, W.; Zhang, J.; Shen, P.K.; Li, C.M. Self-assembled CeO2 on carbon nanotubes supported Au nanoclusters as superior electrocatalysts for glycerol oxidation reaction of fuel cells. Electrochim. Acta 2016, 190, 817–828. [Google Scholar] [CrossRef]
- PS, P.; Gudi, R.D.; Bhartiya, S. Dynamic modeling and control of an integrated reformer-membrane-fuel cell system. Processes 2018, 6, 169. [Google Scholar]
- Wu, Y.E.; Wang, J.W. Novel high-efficiency high step-up DC–DC converter with soft switching and low component voltage stress for photovoltaic system. Processes 2021, 9, 1112. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Babazadeh-Dizaji, R.; Hamzeh, M. High-Gain Buck-Boost Converter Suitable for Renewable Applications. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019; pp. 777–781. [Google Scholar]
- Tan, R.H.; Hoo, L.Y. DC-DC converter modeling and simulation using state space approach. In Proceedings of the IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 19–20 October 2015; pp. 42–47. [Google Scholar]
- Gohar Ali, H.; Vilanova Arbos, R.; Herrera, J.; Tobón, A.; Peláez-Restrepo, J. Non-linear sliding mode controller for photovoltaic panels with maximum power point tracking. Processes 2020, 8, 108. [Google Scholar] [CrossRef] [Green Version]
- Derbeli, M.; Barambones, O.; Silaa, M.Y.; Napole, C. Real-time implementation of a new MPPT control method for a DC-DC boost converter used in a PEM fuel cell power system. Actuators 2020, 9, 105. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ-controllers. IEEE Trans. Autom. Control 2021, 44, 208–214. [Google Scholar] [CrossRef]
- Ding, X.; Li, R.; Cheng, Y.; Liu, Q.; Liu, J. Design of and Research into a Multiple-Fuzzy PID Suspension Control System Based on Road Recognition. Processes 2021, 9, 2190. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Ding, J.; Chen, G.; Yuan, K. Short-term wind power prediction based on improved grey wolf optimization algorithm for extreme learning machine. Processes 2020, 8, 109. [Google Scholar] [CrossRef] [Green Version]
- Komijani, H.; Masoumnezhad, M.; Zanjireh, M.M.; Mir, M. Robust hybrid fractional order proportional derivative sliding mode controller for robot manipulator based on extended grey wolf optimizer. Robotica 2020, 38, 605–616. [Google Scholar] [CrossRef]
- Rahmani, M.; Komijani, H.; Rahman, M.H. New sliding mode control of 2-DOF robot manipulator based on extended grey wolf optimizer. Int. J. Control Autom. Syst. 2020, 18, 1572–1580. [Google Scholar] [CrossRef]
- Barisal, A.K. Comparative performance analysis of teaching learning based optimization for automatic load frequency control of multi-source power systems. Int. J. Electr. Power Energy Syst. 2015, 66, 67–77. [Google Scholar] [CrossRef]
- Zhu, W.; Guo, J.; Zhao, G. Optimal sizing of an island hybrid microgrid based on improved multi-objective grey wolf optimizer. Processes 2020, 8, 1581. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| A | 162 cm |
| 23 | |
| l | 175 × 10 cm |
| 0.1 V | |
| 0.0003 | |
| 0.062 A·cm | |
| 10 | |
| 0.9514 V | |
| −0.00312 V/K | |
| −7.4 × 10 V/K | |
| 1.87 × 10 V/K |
| Controller | Range | |||||
|---|---|---|---|---|---|---|
| FOPID | Min | 0.01 | 0 | 0.1 | 0.01 | 0.01 |
| Max | 12 | 12 | 15 | 0.95 | 0.95 | |
| PID | Min | 0.01 | 0 | 0.1 | - | - |
| Max | 12 | 12 | 15 | - | - |
| Controller | |||||
|---|---|---|---|---|---|
| GWO-PID | 2.5742 | 0.1000 | 8 | - | - |
| GWO-FOPID | 4.0066 | 2.4376 | 2.5327 | 0.8095 | 0.1000 |
| EGWO-PID | 5.3360 | 0.1000 | 15 | - | - |
| EGWO-FOPID | 3.0962 | 2.1614 | 7.0429 | 0.803 | 0.0109 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silaa, M.Y.; Barambones, O.; Derbeli, M.; Napole, C.; Bencherif, A. Fractional Order PID Design for a Proton Exchange Membrane Fuel Cell System Using an Extended Grey Wolf Optimizer. Processes 2022, 10, 450. https://doi.org/10.3390/pr10030450
Silaa MY, Barambones O, Derbeli M, Napole C, Bencherif A. Fractional Order PID Design for a Proton Exchange Membrane Fuel Cell System Using an Extended Grey Wolf Optimizer. Processes. 2022; 10(3):450. https://doi.org/10.3390/pr10030450
Chicago/Turabian StyleSilaa, Mohammed Yousri, Oscar Barambones, Mohamed Derbeli, Cristian Napole, and Aissa Bencherif. 2022. "Fractional Order PID Design for a Proton Exchange Membrane Fuel Cell System Using an Extended Grey Wolf Optimizer" Processes 10, no. 3: 450. https://doi.org/10.3390/pr10030450
APA StyleSilaa, M. Y., Barambones, O., Derbeli, M., Napole, C., & Bencherif, A. (2022). Fractional Order PID Design for a Proton Exchange Membrane Fuel Cell System Using an Extended Grey Wolf Optimizer. Processes, 10(3), 450. https://doi.org/10.3390/pr10030450







