Modeling in Brewing—A Review
Abstract
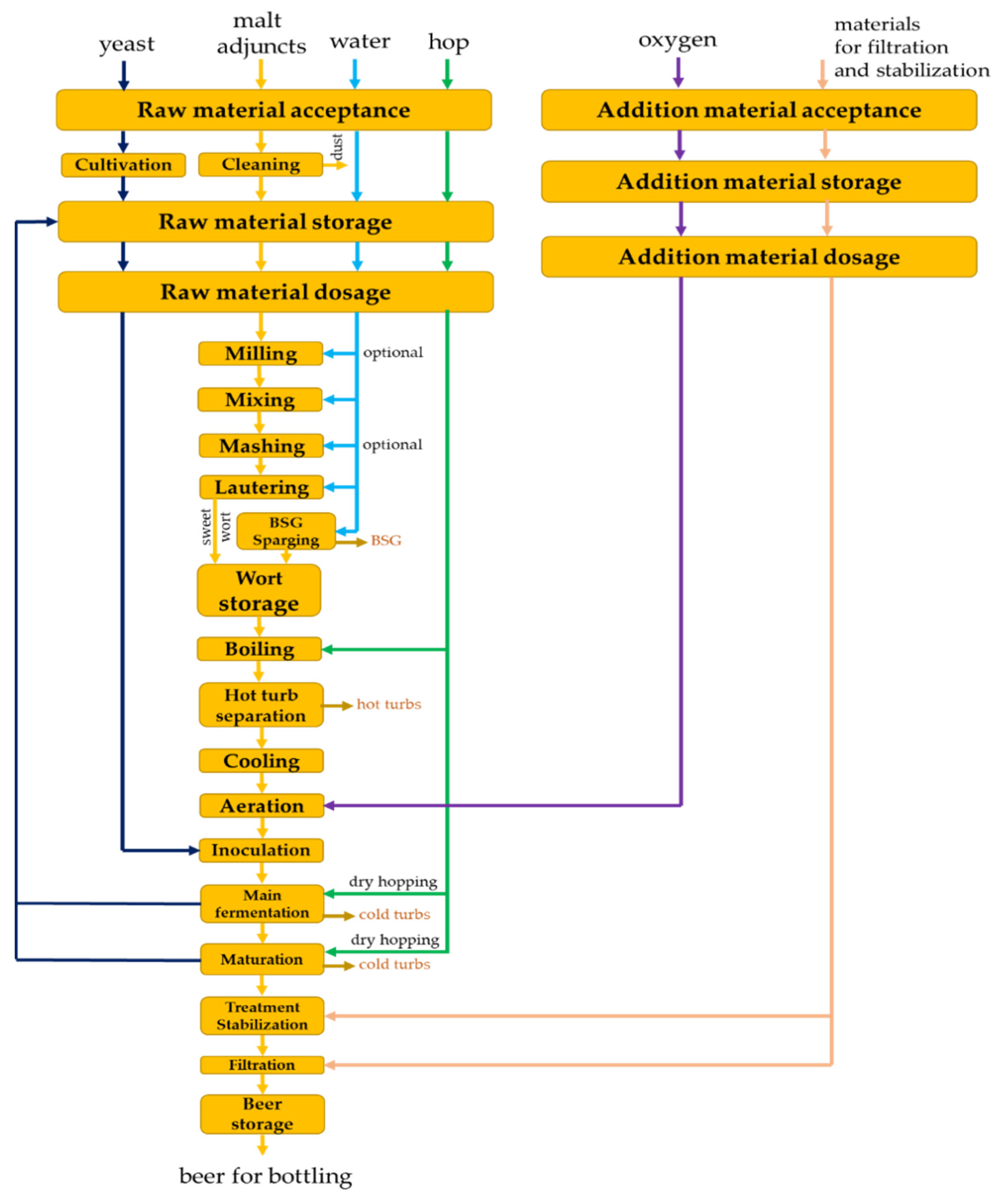
1. Introduction
2. Modeling, Optimization and Control of Processes in Obtaining Wort
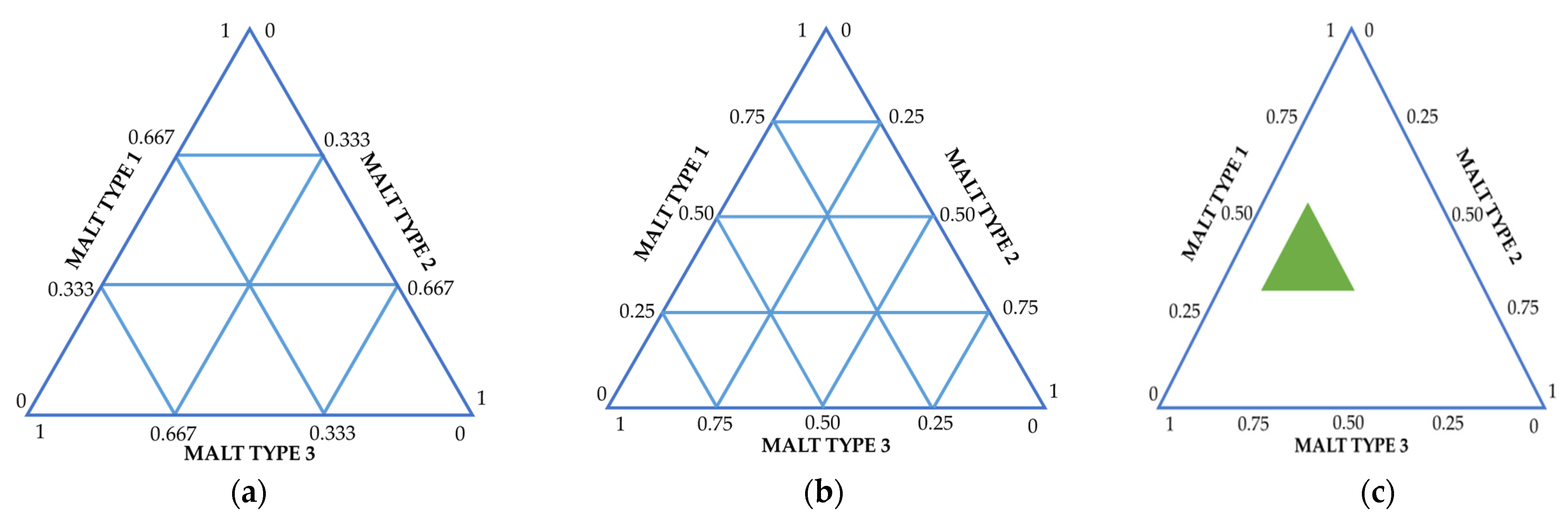
2.1. Modeling of the Malt Mixture
2.2. Modeling and Optimization of the Malt Milling Processes
2.3. Modeling and Optimization of the Mashing Process
2.4. Lautering Process Modeling and Optimization
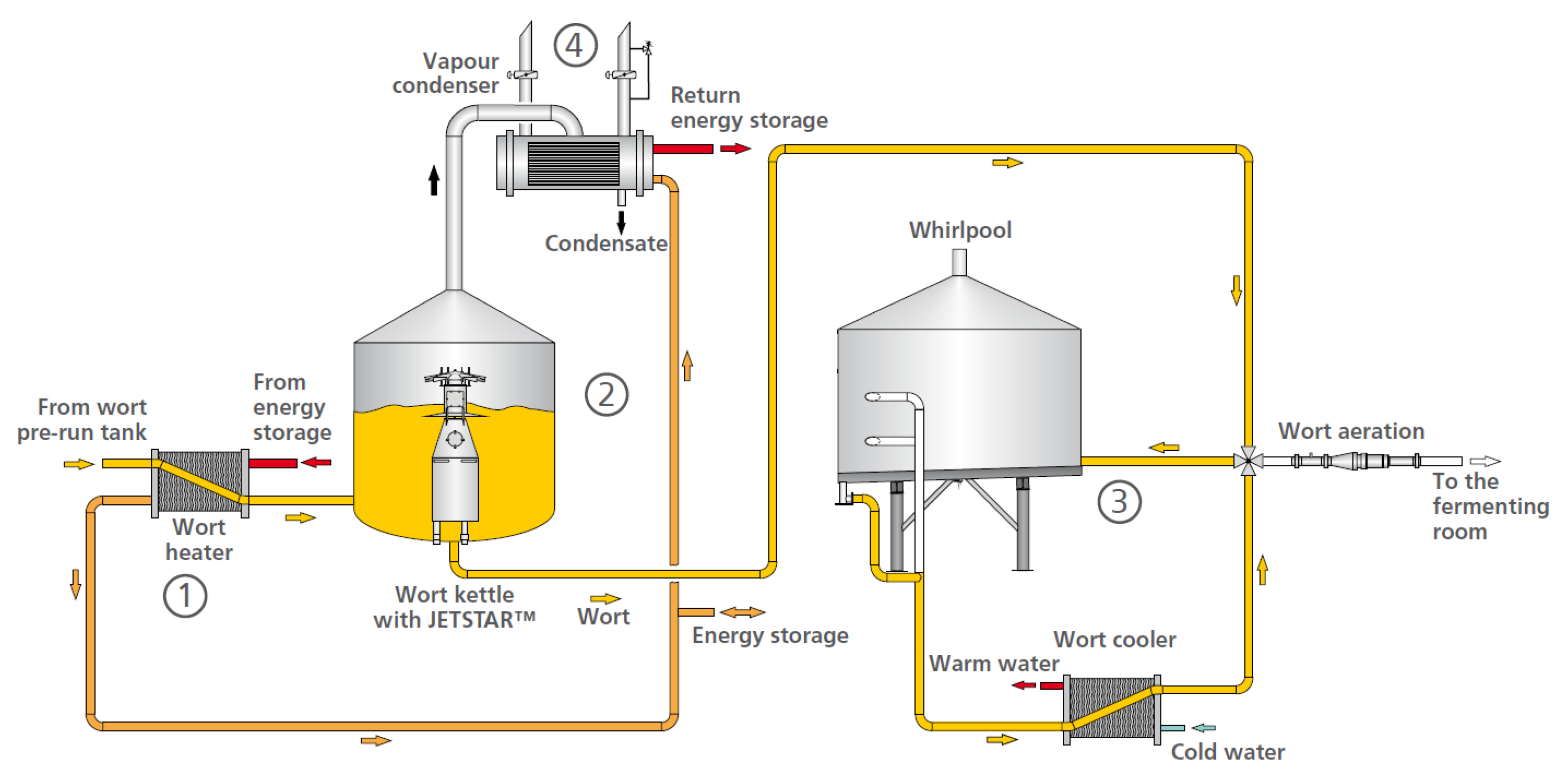
2.5. Modeling and Optimization of the Process of Boiling of Wort with Hops
2.5.1. Modeling and Optimization of the Boiling Process from a Technical Point of View
2.5.2. Modeling and Optimization of the Boiling Process from a Technological Point of View
- Phase 1 enhances the advantage of flash evaporation which is an improved DMS conversion due to higher temperatures. This is done by reducing the pump around velocity of wort through the boiler at a constant evaporation rate. The wort pumped through the boiler and treated at higher temperatures shows a strongly reduced content of DMS precursor (DMSP) when leaving the boiler and entering the kettle.
- Phase 2 is meant to even up the flash evaporation’s disadvantage which is the worse DMS evaporation. For this purpose the temperature difference of the flash evaporation (difference of wort temperature within boiler and within kettle) of the superheated wort has to be reduced. The reduction is realized by increasing the pump around velocity of wort through the boiler while the evaporation rate is kept constant.
2.5.3. Kinetics of the Wort Hopping Process
3. Modeling and Optimization of the Processes of Main Fermentation, Additional Fermentation and Maturation of Beer
- The absorption of amino acids by yeast cells occurs in a certain order, and for this purpose the amino acids are divided into 4 main groups—A, B, C and D—according to the order of their absorption (amino acids of group D are not absorbed by yeast cells). The order of absorption has a direct effect on the yeast metabolism [23,60,65,69]. This means that if a kinetic model of amino acid absorption is to be developed, the order of absorption must be reflected in it. A similar model was proposed in the work of Ramirez and Maciejowski, 2007 [70].
- More than 40 higher alcohol types are found in beer. They are produced in two main ways and have significant influence on the beer taste and aroma profile [60,71,72,73]. The first pathway of higher alcohol synthesis is anabolic and involves the synthesis of higher alcohols from carbohydrates, while the second one is catabolic and involves the synthesis of higher alcohols in the process of amino acid metabolism [60,62,71,72]. In both cases, the accumulation of higher alcohols is associated with cell growth and can be described by the YFA yield factor.
- Esters are the second group of metabolites that form beer taste and aroma profile. Their synthesis is directly related to cell growth, with the main amount of them accumulating in beer during the exponential phase of yeast cell growth [60,62,71,73]. The data from our research confirmed this statement [60,67,68]. The type of wort used, as well as the distribution of fermentable sugars in it, are essential for the amount of esters accumulated. The data showed that highly extractive wort accumulated larger amounts of esters, with the ratio of glucose and maltose in the wort having the greatest significance [60,62,63,72,73,74,75,76]. As already mentioned, ester synthesis is directly related to cell growth and is described by the YES coefficient. It is possible to make a model that involves the accumulation of esters from individual sugars, but this is quite a complex task and in most cases it is unnecessary from a practical point of view.
- Carbonyl compounds (aldehydes and vicinal diketones) are usually associated with a negative impact on beer aroma and taste profile. Their synthesis is almost entirely related to cell growth, as some of the aldehydes are synthesized during wort boiling. The latter cannot be reduced by yeast cells during beer maturation. The reduction of these compounds in the maturation process is extremely important for the final taste and aroma profile of the beer. The rate of the process of reduction of aldehydes and vicinal diketones depends on their current concentration in the green beer and the concentration of viable yeast cells in the fermentation medium [60,62,71,72,73,77].
4. Recent Trends in Modeling in Beer Production
4.1. Dry Hopping of Beer
4.2. Analytical Approaches for Modeling Cell Growth
4.3. Development of Functional Beverages Based on Wort
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Briggs, D.; Boulton, C.; Brookes, P.; Stevens, R. Brewing; Science and Practice, 1st ed.; Woodhead Pub: Cambridge, UK, 2004; p. 881. [Google Scholar]
- Kunze, W. Technology Brewing and Malting, 4th ed.; VLB: Berlin, Germany, 1996; p. 726. [Google Scholar]
- Kunze, W. Technology Brewing and Malting, 5th ed.; VLB: Berlin, Germany, 2004; p. 946. [Google Scholar]
- Puligundla, P.; Smogrovicova, D.; Mok, C.; Obulam, V.S.R. Recent developments in high gravity beer-brewing. Innov. Food Sci. Emerg. Technol. 2020, 64, 102399. [Google Scholar] [CrossRef]
- Karabín, M.; Jelínek, L.; Kotrba, P.; Cejnar, R.; Dostálek, P. Enhancing the performance of brewing yeasts. Biotech. Adv. 2018, 36, 691–706. [Google Scholar] [CrossRef] [PubMed]
- Sanz, V.; Torres, M.D.; Vilariño, J.M.V.; Domínguez, H. What is new on the hop extraction? Trends Food Sci. Technol. 2019, 93, 12–22. [Google Scholar] [CrossRef]
- Trummer, J.; Watson, H.; De Clippeleer, J.; Poreda, A. Brewing with 10% and 20% Malted Lentils—Trials on Laboratory and Pilot Scales. Appl. Sci. 2021, 11, 9817. [Google Scholar] [CrossRef]
- Lehnhardt, F.; Nobis, A.; Skornia, A.; Becker, T.; Gastl, M.A. Comprehensive evaluation of flavor instability of beer (Part 1): Influence of Release of Bound State Aldehydes. Foods 2021, 10, 2432. [Google Scholar] [CrossRef] [PubMed]
- Cadenas, R.; Caballero, I.; Nimubona, D.; Blanco, C.A. Brewing with starchy adjuncts: Its influence on the sensory and nutritional properties of beer. Foods 2021, 10, 1726. [Google Scholar] [CrossRef] [PubMed]
- Ledley, A.J.; Elias, R.J.; Hopfer, H.; Cockburn, D.W. A Modified brewing procedure informed by the enzymatic profiles of gluten-free malts significantly improves fermentable sugar generation in gluten-free brewing. Beverages 2021, 7, 53. [Google Scholar] [CrossRef]
- Shopska, V.; Denkova-Kostova, R.; Dzhivoderova-Zarcheva, M.; Teneva, D.; Denev, P.; Kostov, G. Comparative study on phenolic content and antioxidant activity of different malt types. Antioxidants 2021, 10, 1124. [Google Scholar] [CrossRef] [PubMed]
- Dabija, A.; Ciocan, M.E.; Chetrariu, A.; Codină, G.G. Maize and sorghum as raw materials for brewing, a Review. Appl. Sci. 2021, 11, 3139. [Google Scholar] [CrossRef]
- Cavallini, N.; Savorani, F.; Bro, R.; Cocchi, M.A. Metabolomic approach to beer characterization. Molecules 2021, 26, 1472. [Google Scholar] [CrossRef]
- Yorke, J.; Cook, D.; Ford, R. Brewing with unmalted cereal adjuncts: Sensory and analytical impacts on beer quality. Beverages 2021, 7, 4. [Google Scholar] [CrossRef]
- Cipollaro, M.; Fabbrizzi, S.; Sottini, V.A.; Fabbri, B.; Menghini, S. Linking sustainability, embeddedness and marketing strategies: A study on the craft beer sector in Italy. Sustainability 2021, 13, 10903. [Google Scholar] [CrossRef]
- Březinová, M. Beer industry in the Czech Republic: Reasons for founding a craft brewery. Sustainability 2021, 13, 9680. [Google Scholar] [CrossRef]
- Iorizzo, M.; Coppola, F.; Letizia, F.; Testa, B.; Sorrentino, E. Role of Yeasts in the Brewing Process: Tradition and Innovation. Processes 2021, 9, 839. [Google Scholar] [CrossRef]
- Salanță, L.C.; Coldea, T.E.; Ignat, M.V.; Pop, C.R.; Tofană, M.; Mudura, E.; Borșa, A.; Pasqualone, A.; Zhao, H. Non-Alcoholic and Craft Beer Production and Challenges. Processes 2020, 8, 1382. [Google Scholar] [CrossRef]
- Cela, N.; Condelli, N.; Caruso, M.C.; Perretti, G.; Di Cairano, M.; Tolve, R.; Galgano, F. Gluten-Free Brewing: Issues and Perspectives. Fermentation 2020, 6, 53. [Google Scholar] [CrossRef]
- Iattici, F.; Catallo, M.; Solieri, L. Designing New Yeasts for Craft Brewing: When Natural Biodiversity Meets Biotechnology. Beverages 2020, 6, 3. [Google Scholar] [CrossRef]
- Guido, L.F. Brewing and Craft Beer. Beverages 2019, 5, 51. [Google Scholar] [CrossRef]
- Mulero-Cerezo, J.; Briz-Redón, Á.; Serrano-Aroca, Á. Saccharomyces Cerevisiae Var. Boulardii: Valuable Probiotic Starter for Craft Beer Production. Appl. Sci. 2019, 9, 3250. [Google Scholar] [CrossRef]
- Kostov, G.; Shopska, V.; Iliev, V. Optimization of Technological and Energy Processes in the Production of Beverages. Part. 1. Brewing, 1st ed.; Academic Publishing House of the University of Food Technology: Plovdiv, Bulgaria, 2019; p. 294. [Google Scholar]
- Shopska, V.; Denkova-Kostova, R.; Ivanova, K.; Kostov, G. Tailor-Made Concept for New Beer Types with High Biological Value. In Beer: From Production to Distribution, 1st ed.; Legault, A., Ed.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2020; pp. 1–76. [Google Scholar]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process. and Product Optimization Using Designed Experiments, 4th ed.; John Wiley & Sons: New York, NY, USA, 216; p. 856. In Response Surface Methodology: Process. and Product Optimization Using Designed Experiments, 4th ed.; John Wiley & Sons: New York, NY, USA, 2016; p. 856. [Google Scholar]
- Cornell, J.A. Experiments with Mixtures: Designs, Models, and the Analysis of Mixture Data, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2020; p. 680. [Google Scholar]
- Ivanova, K.; Denkova, R.; Kostov, G.; Petrova, T.; Bakalov, I.; Ruscova, M.; Penov, N. Extrusion of brewers’ spent grains and application in the production of functional food. Characteristics of spent grains and optimization of extrusion. J. Inst. Brew. 2017, 123, 544–552. [Google Scholar] [CrossRef]
- Goode, D.L.; Arendt, E.K. Developments in the Supply of Adjunct Materials for Brewing. In Brewing: New Technologies; Bamforth, W., Ed.; Woodhead Publishing Limited: Sawston, UK; Cambridge, MA, USA, 2006; pp. 30–67. [Google Scholar]
- Fumi, M.D.; Galli, R.; Lambri, M.; Donadini, G.; De Faveri, D.M. Effect of full-scale brewing process on polyphenols in Italian all-malt and maize adjunct lager beers. J. Food Comp. Anal. 2011, 24, 568–573. [Google Scholar] [CrossRef]
- Stewart, G. Chapter 2—Adjuncts. In Brewing Materials and Processes; Bamforth, C.W., Ed.; Academic Press: San Diego, CA, USA, 2016; pp. 27–46. [Google Scholar] [CrossRef]
- Krottenthaler, M.; Back, W.; Zarnkow, M. Wort Production. In Handbook of Brewing: Processes, Technology, Markets, 1st ed.; Esslinger, H.M., Ed.; Wiley-VCH: Weinheim, Germany, 2009; pp. 165–205. [Google Scholar]
- Ivanov, K.; Petelkov, I.; Shopska, V.; Denkova, R.; Gochev, V.; Kostov, G. Investigation of mashing regimes for low-alcohol beer production. J. Inst. Brew. 2016, 122, 508–516. [Google Scholar] [CrossRef]
- Montanari, L.; Floridi, S.; Marconi, O.; Tironzelli, M.; Fantozzi, P. Effect of mashing procedures on brewing. Eur. Food Res. Technol. 2005, 221, 175–179. [Google Scholar] [CrossRef]
- Tschoeke, I.C.P.; Silva, J.M.C.L.R.; da Silva, J.P.; Marques, O.M.; Vinhas, G.M.; Santos, A.M.P.; Souza, T.P.C. Kinetic modelling of a brewery mashing: A multidimensional approach. Food Bioprod. Pract. 2019, 116, 130–139. [Google Scholar] [CrossRef]
- Brandam, C.; Meyer, X.M.; Proth, J.; Strehaiano, P.; Pingaud, H. An original kinetic model for the enzymatic hydrolysis of starch during mashing. Biochem. Eng. J. 2003, 13, 43–52. [Google Scholar] [CrossRef]
- Coulter, P.R.; Potter, O.E. A kinetic study of the susceptibility to enzymic hydrolysis of starch in malt. J. Inst. Brew. 1973, 79, 212–218. [Google Scholar] [CrossRef]
- Zanoni, B.; Schiraldi, A.; Simonetta, R. A naive model of starch gelatinization kinetics. J. Food Eng. 1995, 24, 25–33. [Google Scholar] [CrossRef]
- Byong, H.L. Fundamentals of Food Biotechnology, 2nd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2014; pp. 313–430. [Google Scholar]
- Daniels, R. Designing Great Beers: The Ultimate Guide to Brewing Classic Beer Styles, 1st ed.; Brewers Publications: Denver, CO, USA, 1996. [Google Scholar]
- Schultz, S.; Zien, P. Beer, Food, and Flavor: A Guide to Tasting, Pairing, and the Culture of Craft Beer, 1st ed.; Skyhorse: New York, NY, USA, 2012. [Google Scholar]
- Leva, A.; Donida, F.; Maggio, M. Object-oriented modelling of starch mashing for simulation-based control studies. Math. Comp. Mod. Dyn. Sys. 2010, 16, 225–240. [Google Scholar] [CrossRef]
- Viader, R.P.; Yde, M.S.H.; Hartvig, J.W.; Pagenstecher, M.; Carlsen, J.B.; Christensen, T.B.; Andersen, M.L. Optimization of Beer Brewing by Monitoring α-Amylase and β-Amylase Activities during Mashing. Beverages 2021, 7, 13. [Google Scholar] [CrossRef]
- Denk, V.; Felgentraeger, H.G.W.; Flad, W.; Leneol, M.; Michel, R.; Miedaner, H.; Stippler, K.; Hensel, H.; Narziss, L. ; O’Rourke. T. European Brewery Convention—Manual of Good Practice, Wort Boiling and Clarification; Fachverlag Hans Carl: Nurnberg, Germany, 2000; p. 176. [Google Scholar]
- Miedaner, H. Wort boiling today—Old and new aspects. J. Inst. Brew. 1986, 92, 330–335. [Google Scholar] [CrossRef]
- O’Rourke, T. Wort Boiling (part 2). Brew. Guard. 1999, 128, 38–43. [Google Scholar]
- O’Rourke, T. The function of wort boiling. Brew. Int. 2002, 2, 17–19. [Google Scholar]
- Kabzev, Y.; Ignatov, I. Technology of Beer; Academic Press of UFT: Plovdiv, Bulgaria, 2011; p. 338. [Google Scholar]
- Hancock, J.C.J.M.; Andrews, H. Wort boiling. Ferment 1996, 9, 344–351. [Google Scholar]
- Royston, M.G. Wort boiling and cooling. In Modern Brewing Technology; Findlay, W.P.K., Ed.; MacMillan Press: London, UK, 1971; pp. 77–79. [Google Scholar]
- Wilkinson, N.R. Wort Boiling and Clarification. Eur. Brew. Conv. Monograph 1991, 18, 100–105. [Google Scholar]
- Andrews, J.M.H. Proceedings of the 22nd Convention of the Institute Brewing, Australia, and New Zealand Section, Melbourne, Australia, 1–6 March 1992; p. 65.
- Scheuren, H.; Baldus, M.; Methner, F.-J.; Dillenburger, M. Evaporation behaviour of DMS in an aqueous solution at infinite dilution—A review. J. Inst. Brew. 2016, 122, 181–190. [Google Scholar] [CrossRef]
- New Food Magazine. Available online: https://www.newfoodmagazine.com/article/1660/trends-in-brewing-technology-wort-boiling/ (accessed on 10 December 2021).
- Doc Player. Available online: https://docplayer.net/37375319-Wort-boiling-with-the-jetstar-technology-and-energy-management-hand-in-hand-engineering-for-a-better-world.html (accessed on 10 December 2021).
- Huang, Y.; Tippmann, J.; Becker, T. Kinetic modeling of hop acids during wort boiling. Int. J. Biosci. Biochem. Bioinform. 2013, 3, 47–52. [Google Scholar] [CrossRef][Green Version]
- Intelmann, D.; Haseleu, G.; Dunkel, A.; Lagemann, A.; Stephan, A.; Hofmann, T. Comprehensive sensomics analysis of hop-derived bitter compounds during storage of beer. J. Agric. Food Chem. 2011, 59, 1939–1953. [Google Scholar] [CrossRef] [PubMed]
- Haseleu, G.; Lagemann, A.; Stephan, A.; Intelmann, D.; Dunkel, A.; Hofmann, T. Quantitative sensomics profiling of hop-derived bitter compounds throughout a full-scale beer manufacturing process. J. Agric. Food Chem. 2010, 58, 7930–7939. [Google Scholar] [CrossRef]
- Malowicki, M.G.; Shellhammer, T.H. Isomerization and degradation kinetics of hop (Humulus lupulus) acids in a model wort-boiling system. J. Agric. Food Chem. 2005, 53, 4434–4439. [Google Scholar] [CrossRef]
- Boulton, C. Fermentation of beer. In Brewing–New Technologies; Bamforth, C.W., Ed.; CRC Press: Boca Raton, FL, USA, 2006; pp. 228–253. [Google Scholar]
- Shopska, V.; Denkova, R.; Lyubenova, V.; Kostov, G. Kinetic Characteristics of Alcohol Fermentation in Brewing: State of art and control of the fermentation process. In Fermented Beverages; Grumezescu, A.M., Holban, A.M., Eds.; Woodhead Publishing: Cambridge, UK, 2019; pp. 529–575. [Google Scholar] [CrossRef]
- Tenge, C. Yeast. In Handbook of Brewing: Processes, Technology, Markets; Eslinger, H.M., Ed.; Wiley-Vch Verlag GmbH & Co. KGaA: Weinheim, Germany, 2009; pp. 119–147. [Google Scholar]
- Shopska, V.; Denkova, R.; Kostov, G. Beer production with encapsulated yeast cells. In Beer: Production, Consumption and Health Effects; Salazar, W.H., Ed.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2016; pp. 27–100. [Google Scholar]
- Verbelen, P.J.; Delvaux, F.R. Brewing yeast in action: Beer fermentation. In Applied Mycology; Rai, M., Bridge, P.D., Eds.; Cabi: Oxfordshire, UK, 2009; pp. 110–135. [Google Scholar] [CrossRef]
- Munroe, J. Fermentation. In Handbook of Brewing; Priest, D., Stewart, G., Eds.; Tylor and Francis Group: Oxfordshire, UK, 2006; pp. 487–524. [Google Scholar]
- Lodolo, E.J.; Kock, J.L.; Axcell, B.C.; Brooks, M. The yeast Saccharomyces cerevisiae—The main character in beer brewing. FEMS Yeast Res. 2008, 8, 1018–1036. [Google Scholar] [CrossRef]
- Petelkov, I.; Lyubenova, V.; Zlatkova, A.; Shopska, V.; Denkova, R.; Kaneva, M.; Kostov, G. Encapsulation of brewing yeast in alginate/chitosan matrix: Kinetic characteristics of the fermentation process at a constant fermentation temperature. Compt. Rend. Acad. Bulg. Sci. 2016, 69, 1355–1364. [Google Scholar]
- Petelkov, I.; Shopska, V.; Denkova-Kostova, R.; Kostov, G.; Lyubenova, V. Investigation of different regimes of beer fermentation with free and immobilized cells. Per. Pol. Chem. Eng. 2020, 64, 162–171. [Google Scholar] [CrossRef]
- Petelkov, I.; Shopska, V.; Denkova-Kostova, R.; Ivanova, K.; Kostov, G.; Lyubenova, V. Investigation of fermentation regimes for the production of low-alcohol and non-alcohol beers. Per. Pol. Chem. Eng. 2021, 65, 229–237. [Google Scholar] [CrossRef]
- He, Y.; Dong, J.; Yin, H.; Zhao, Y.; Chen, R.; Wan, X.; Chen, P.; Hou, X.; Liu, J.; Chen, L. Wort composition and its impact on the flavour-active higher alcohol and ester formation of beer—A review. J. Inst. Brew. 2014, 120, 157–163. [Google Scholar] [CrossRef]
- Ramirez, W.F.; Maciejowski, J. Optimal Beer Fermentation. J. Inst. Brew. 2007, 113, 325–333. [Google Scholar] [CrossRef]
- Pires, E.; Brányik, T. Biochemistry of Beer Fermentation; Springer International Publishing AG Switzerland: Berlin/Heidelberg, Germany, 2015; pp. 51–80. [Google Scholar]
- Nedović, V.; Gibson, B.; Mantzouridou, T.F.; Bugarski, B.; Djordjević, V.; Kalušević, A.; Paraskevopoulou, A.; Sandell, M.; Šmogrovičová, D.; Yilmaztekin, M. Aroma formation by immobilized yeast cells in fermentation processes. Yeast 2015, 32, 173–216. [Google Scholar] [CrossRef]
- Djordjević, V.; Willaert, R.; Gibson, B.; Nedović, V. Immobilized yeasts and secondary metabolites. In Fungal Metabolites, 1st ed.; Mérillon, J.-M., Ramawat, K.G., Eds.; Springer International Publishing Switzerland: Berlin/Heidelberg, Germany, 2006; pp. 599–639. [Google Scholar] [CrossRef]
- Saerens, S.M.; Delvaux, F.; Verstrepen, K.J.; Van Dijck, P.; Thevelein, J.M.; Delvaux, F.R. Parameters affecting ethyl ester production by Saccharomyces cerevisiae during fermentation. Appl. Environ. Microbiol. 2008, 74, 454–461. [Google Scholar] [CrossRef]
- Hiralal, L.; Olaniran, A.O.; Pillay, B. Aroma-active ester profile of ale beer produced under different fermentation and nutritional conditions. J. Biosci. Bioeng. 2014, 117, 57–64. [Google Scholar] [CrossRef]
- Lei, H.; Zhao, H.; Yu, Z.; Zhao, M. Effects of wort gravity and nitrogen level on fermentation performance of brewer’s yeast and the formation of flavor volatiles. Appl. Biochem. Biotechnol. 2012, 166, 1562–1574. [Google Scholar] [CrossRef]
- Krogerus, K.; Gibson, B.R. 125th anniversary review: Diacetyl and its control during brewery fermentation. J. Inst. Brew. 2013, 119, 86–97. [Google Scholar] [CrossRef]
- Lafontaine, S.R.; Shellhammer, T.H. Impact of static dry-hopping rate on the sensory and analytical profiles of beer. J. Inst. Brew. 2018, 124, 434–442. [Google Scholar] [CrossRef]
- Schönberger, C.; Kostelecky, T. 125th anniversary review: The role of hops in brewing. J. Inst. Brew. 2011, 117, 259–267. [Google Scholar] [CrossRef]
- Watson, B. Digging Deeper into Beer Styles, 2017, IRI Group and Brewers Association. Available online: https://www.brewersassociation.org/insights/digging-deeper-beer-styles/ (accessed on 28 December 2021).
- Wolfe, P.H. A Study of Factors Affecting the Extraction of Flavor When Dry-Hopping Beer. Master’s Thesis, Oregon State University, Corvallis, OR, USA, 2012. Available online: https://ir.library.oregonstate.edu/concern/graduate_thesis_or_dissertations/rx913t14h (accessed on 28 December 2021).
- Sharp, D.C.; Steensels, J.; Shellhammer, T.H. The effect of hopping regime, cultivar and β-glucosidase activity on monoterpene alcohol concentrations in wort and beer. J. Inst. Brew. 2017, 123, 185–191. [Google Scholar] [CrossRef]
- Takoi, K.; Koie, K.; Itoga, Y.; Katayama, Y.; Shimase, M.; Nakayama, Y.; Watari, J. Biotransformation of hop-derived monoterpene alcohols by lager yeast and their contribution to the flavor of hopped beer. J. Agric. Food Chem. 2010, 58, 5050–5058. [Google Scholar] [CrossRef] [PubMed]
- Oladokun, O.; James, S.; Cowley, T.; Smart, K.; Hort, J.; Cook, D. Dry-hopping: The effects of temperature and hop variety on the bittering profiles and properties of resultant beers. Brew. Sci. 2017, 70, 187–196. [Google Scholar]
- Kostov, G.; Denkova-Kostova, R.; Shopska, V.; Goranov, B. Analytical Approaches to Determine the Specific Biomass Growth Rate. In Brewing. ECMS 2019 Proceedings; Iacono, M., Palmieri, F., Gribaudo, M., Ficco, M., Eds.; European Council for Modeling and Simulation: Wildau, Germany, 2019; pp. 125–131. [Google Scholar] [CrossRef]
- Warpholomeew, S.D. ; Gurevich. K.G. Biokinetic–Practical Course; Fair-Press: Moscow, Russia, 1999; p. 720. (In Russian) [Google Scholar]
- Kostov, G.; Denkova-Kostova, R.; Shopska, V.; Goranov, B.; Ivanova, K. Analytical Approaches for Determining the Effects of Wort Extract on The Specific Growth Rate of The Yeast Population. In ECMS 2020 Proceedings; Steglich, M., Mueller, C., Neumann, G., Walther, M., Eds.; European Council for Modeling and Simulation: Wildau, Germany, 2020; pp. 146–152. [Google Scholar] [CrossRef]
- Carvalho, D.O.; Correia, E.; Lopes, L.; Guido, L.F. Further insights into the role of melanoidins on the antioxidant potential of barley malt. Food Chem. 2014, 160, 127–133. [Google Scholar] [CrossRef] [PubMed]
- Tomova, T.; Petelkov, I.; Shopska, V.; Denkova-Kostova, R.; Kostov, G.; Denkova, Z. Production of probiotic wort-based beverages with grapefruit (Citrus paradisi L.) or tangerine (Citrus reticulata L.) zest essential oil addition. Acta Sci. Pol. Technol. Aliment. 2021, 20, 237–245. [Google Scholar] [CrossRef] [PubMed]
- Pereira de Paula, B.; de Souza Lago, H.; Firmino, L.; Lemos Júnior, W.J.F.; Corrêa, M.F.D.; Guerra, A.F.; Pereira, K.S.; Coelho, M.A.Z. Technological features of Saccharomyces cerevisiae var. boulardii for potential probiotic wheat beer development. LWT 2021, 135, 110233. [Google Scholar] [CrossRef]
- Canonico, L.; Zannini, E.; Ciani, M.; Comitini, F. Assessment of non-conventional yeasts with potential probiotic for protein-fortified craft beer production. LWT 2021, 145, 111361. [Google Scholar] [CrossRef]
- Senkarcinova, B.; Dias, I.A.G.; Nespor, I.; Branyik, T. Probiotic alcohol-free beer made with Saccharomyces cerevisiae var. boulardii. LWT 2019, 100, 362–367. [Google Scholar] [CrossRef]
- Chan, M.; Chua, J.; Toh, M.; Liu, S.-Q. Survival of probiotic strain Lactobacillus paracasei L26 during co-fermentation with S. cerevisiae for the development of a novel beer beverage. Food Microb. 2019, 82, 541–550. [Google Scholar] [CrossRef] [PubMed]
- Dysvik, A.; Leanti, A.K.R.S.; Hovde, L.K.; Myhrer, K.S.; Ostlie, H.M.; De Rouck, G.; Rukke Elling-Olav, B.; Wicklund, T. Co-fermentation Involving Saccharomyces cerevisiae and Lactobacillus Species Tolerant to Brewing-Related Stress Factors for Controlled and Rapid Production of Sour Beer. Front. Microb. 2020, 11, 279. [Google Scholar] [CrossRef] [PubMed]
- Ricci, A.; Cirlini, M.; Guido, A.; Liberatore, C.M.; Ganino, T.; Lazzi, C.; Chiancone, B. From Byproduct to Resource: Fermented Apple Pomace as Beer Flavoring. Foods 2019, 8, 309. [Google Scholar] [CrossRef] [PubMed]
- Kammerer, D.R.; Kammerer, J.; Valet, R.; Carle, R. Recovery of polyphenols from the by-products of plant food processing and application as valuable food ingredients. Food Res. Int. 2014, 65, 2–12. [Google Scholar] [CrossRef]
- Paiva, R.A.M.; Mutz, Y.S.; Conte-Junior, C.A. A Review on the Obtaining of Functional Beers by Addition of Non-Cereal Adjuncts Rich in Antioxidant Compounds. Antioxidants 2021, 10, 1332. [Google Scholar] [CrossRef]
- Jahn, A.; Kim, J.; Bashir, K.M.I.; Cho, M.G. Antioxidant Content of Aronia Infused Beer. Fermentation 2020, 6, 71. [Google Scholar] [CrossRef]
- De Francesco, G.; Bravi, E.; Sanarica, E.; Marconi, O.; Cappelletti, F.; Perretti, G. Effect of Addition of Different Phenolic-Rich Extracts on Beer Flavour Stability. Foods 2020, 9, 1638. [Google Scholar] [CrossRef]
| No. | Process | Process Parameters | Method for Modeling | Target Functions |
|---|---|---|---|---|
| 1 | Modeling of the malt mixture | Proportions of malted/unmalted raw materials | Simplex methods for modeling and optimizing mixtures |
|
| 2 | Milling | Degree of milling | Empirical | Particle size of the grounded malt |
| 3 | Mashing | Mashing method Time—temperature mode of mashing | Empirical for the choice of a mashing method One-factor experiments Design of experiment Enzyme reaction kinetics |
|
| 4 | Lautering | Mash viscosity Lautering temperature Lautering time Lautering pressure Filtration cake height (for lautering tuns) | Single-factor experiments Design of experiment to optimize the mashing mode |
|
| 5 | Wort boiling | Volatility Heat exchange surface Stirring/boiling intensity Wort boiling time Hopping time Amount of extracted hop bitters | Single-factor experiments Simplex methods for modeling and optimization of mixtures in hopping |
|
| 6 | Beer fermentation and maturation | Temperature Time Alcohol Wort extract Metabolites—esters, higher alcohols, vicinal diketones, aldehydes | Single factror experiments for temperature determination Process kinetics |
|
| Enzymes | Optimum | Substrate | Product | ||
|---|---|---|---|---|---|
| Group | Representative | Т, °С | рН | - | - |
| Cytolytic | β-glucan solubilase | 62–65 | 6.8 | bound β-glucan | soluble high molecular weight β-glucan |
| endo-1,3-β-glucanase | below 60 | 4.6 | soluble high molecular weight β-glucan | low molecular weight β-glucan, cellobiosis, laminaribiosis | |
| endo-1,4-β-glucanase | 40–45 | 4.5–4.8 | soluble high molecular weight β-glucan | low molecular weight β-glucan, cellobiosis, laminaribiosis | |
| exo-β-glucanase | below 40 | 4.5 | cellobiosis, laminaribiosis | glucose | |
| Proteolytic | endopeptidases | 45–50 | 3.9–5.5 | proteins | peptides, free amino acids |
| carboxypeptidases | 50 | 4.6–4.8 | proteins, peptides | free amino acids | |
| aminopeptidases | 45 | 7.0–7.2 | proteins, peptides | free amino acids | |
| dipeptidase | 45 | 8.8 | dipeptides | free amino acids | |
| Amylolytic | α-amylase | 65–75 | 5.6–5.8 | starch | melagosaccharidesoligosaccharides |
| β-amylase | 60–65 | 5.4–5.6 | starch | maltose | |
| Others | maltase | 35–40 | 6.0 | maltose | glucose |
| pullulanase | 55–65 | 5.1 | limit dextrin | dextrin | |
| lipase | 55–65 | 6.8–7.0 | lipids, lipid hydroxyperoxide | glycerin and long-chain fatty acids, fatty acids | |
| lipoxygenase | 45–55 | 6.5–7.0 | long-chain fatty acids | fatty acids | |
| polyphenol oxidase | 60–65 | 6.5–7.0 | polyphenol | oxidized polyphenols | |
| phosphatase | 50–53 | 5.0 | organic phosphate | inorganic phosphate | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shopska, V.; Denkova-Kostova, R.; Kostov, G. Modeling in Brewing—A Review. Processes 2022, 10, 267. https://doi.org/10.3390/pr10020267
Shopska V, Denkova-Kostova R, Kostov G. Modeling in Brewing—A Review. Processes. 2022; 10(2):267. https://doi.org/10.3390/pr10020267
Chicago/Turabian StyleShopska, Vesela, Rositsa Denkova-Kostova, and Georgi Kostov. 2022. "Modeling in Brewing—A Review" Processes 10, no. 2: 267. https://doi.org/10.3390/pr10020267
APA StyleShopska, V., Denkova-Kostova, R., & Kostov, G. (2022). Modeling in Brewing—A Review. Processes, 10(2), 267. https://doi.org/10.3390/pr10020267






