Reliability Estimation in Multicomponent Stress-Strength Based on Inverse Weibull Distribution
Abstract
:1. Introduction
2. Maximum Likelihood Estimation of
Asymptotic Confidence Intervals
3. Simulation Study and Data Analysis
3.1. Simulation Study
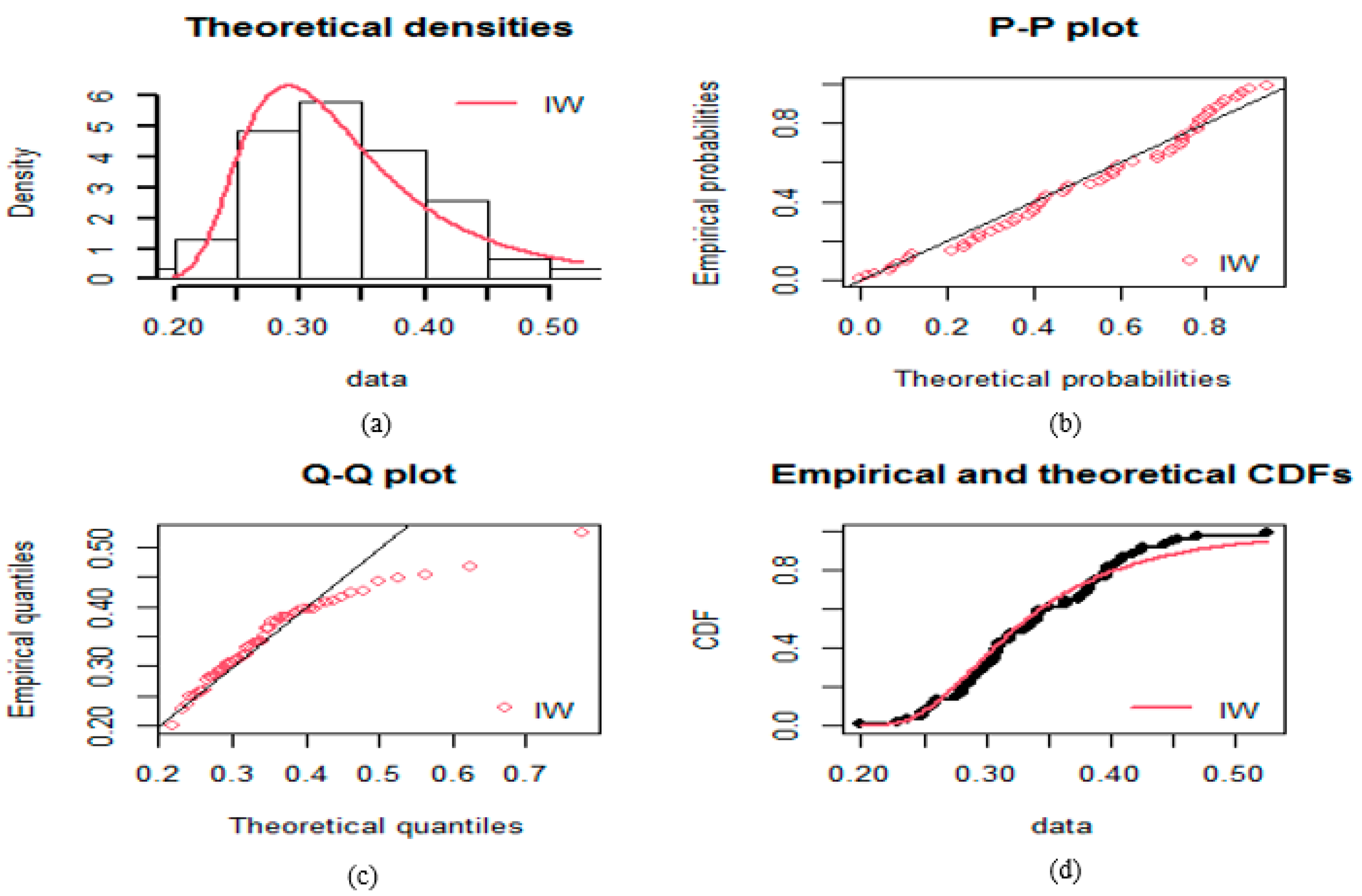
3.2. Real Data Application
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Church, J.D.; Harris, B. The estimation of reliability from stress-strength Relationships. Technometrics 1970, 12, 49–54. [Google Scholar] [CrossRef]
- Bhattacharyya, G.K.; Johnson, R.A. Estimation of reliability in the multi-component stress-strength model. J. Am. Stat. Assoc. 1974, 69, 966–970. [Google Scholar] [CrossRef]
- Hanagal, D.D. Estimation of system reliability in multicomponent series stress–strength models. J. Indian Stat. Assoc. 2003, 41, 1–7. [Google Scholar]
- Turkkan, N.; Pham-Gia, T. System stress-strength reliability: The multivariate Case. IEEE Trans. Reliab. 2007, 56, 115–124. [Google Scholar] [CrossRef]
- Serkan, E. Consecutive k-out-of n: G system in stress-strength setup. Commun. Stat. Simul. Comput. 2008, 37, 579–589. [Google Scholar]
- Serkan, E. Multivariate stress-strength reliability model and its evaluation for coherent structures. J. Multivar. Anal. 2008, 99, 1878–1887. [Google Scholar]
- Serkan, E.; Funda, I. Reliability evaluation for a multi-state system under stress-strength setup. Commun. Stat. Theory Methods 2011, 40, 547–558. [Google Scholar]
- Shawky, A.I.; Al-Gashgari, F.H. Bayesian and non-bayesian estimation of stress-strength model for Pareto type I Distribution. Iran. J. Sci. Technol. Trans. A Sci. 2013, 37, 335–342. [Google Scholar]
- Pak, A.; Gupta, A.K.; Khoolenjani, N.B. On Reliability in a Multicomponent Stress-Strength Model with Power Lindley Distribution. Rev. Colomb. Estadística 2018, 41, 251–267. [Google Scholar] [CrossRef]
- Pak, A.; Khoolenjani, N.B.; Rastogi, M.K. Bayesian inference on reliability in multicomponent stress-strength bathtub shaped model based on record values. Pak. J. Stat. Oper. Res. 2019, 15, 431–444. [Google Scholar] [CrossRef] [Green Version]
- Rao, G.S.; Bhatti, F.A.; Aslam, M.; Albassam, M. Estimation of reliability in a multicomponent stress–strength system for the exponentiated moment-based exponential distribution. Algorithms 2019, 12, 246. [Google Scholar] [CrossRef] [Green Version]
- Kotz, S.; Lumelskii, Y.; Pensky, M. The Stress-Strength Model and Its Generalizations; World Scientific: Singapore, 2003. [Google Scholar]
- Bhattacharya, D.; Roychowdhury, S. Reliability of a coherent system in a multicomponent stress strength Model. Am. J. Math. Manag. Sci. 2013, 32, 40–52. [Google Scholar]
- Ebrahimi, N. Estimation of reliability for a series stress-strength system. IEEE Trans. Reliab. 1982, 31, 202–205. [Google Scholar] [CrossRef]
- Pandey, M.; Uddin, M.B.; Ferdous, J. Reliability estimation of an s-out-of-k system with nonidentical component strengths: The Weibull case. Reliab. Eng. Syst. Saf. 1992, 36, 109–116. [Google Scholar] [CrossRef]
- Paul, R.K.; Uddin, M.B. Estimation of the reliability of the stress-strength model with nonidentical component strengths. Microelectron. Reliab. 1997, 37, 923–927. [Google Scholar] [CrossRef]
- Rao, G.S.; Kantam, R.R.L. Estimation of reliability in the multicomponent stress-strength model: Log-logistic Distribution. J. Appl. Stat. Sci. 2010, 3, 75–84. [Google Scholar]
- Rao, G.S. Estimation of reliability in multicomponent stress-strength model based on Rayleigh distribution. ProbStat Forum 2012, 5, 150–161. [Google Scholar]
- Rao, G.S. Estimation of reliability in multicomponent stress-strength model based on generalized inverted Exponential distribution. Int. J. Curr. Res. Rev. 2012, 4, 48–56. [Google Scholar]
- Rao, G.S. Estimation of reliability in multicomponent stress-strength model based on generalized exponential Distribution. Rev. Colomb. Estadística 2012, 35, 67–76. [Google Scholar]
- Hassan, A.S.; Basheikh, H.M. Estimation of reliability in multicomponent stress-strength model following exponential Pareto distribution. Egypt. Stat. J. 2012, 56, 82–95. [Google Scholar]
- Dey, S.; Mazucheli, J.; Anis, M.Z. Estimation of the reliability of multi-component stress–strength for a Kumaraswamy distribution. Commun. Stat. Theory Methods 2017, 46, 1560–1572. [Google Scholar] [CrossRef]
- Kizilaslan, F. Classical and Bayesian estimation of reliability in a multicomponent stress-strength model based on the proportional reversed hazard rate model. Math. Comput. Simul. 2017, 136, 36–62. [Google Scholar] [CrossRef]
- Badr, M.M.; Shawky, A.I.; Alharby, A.H. The Estimation of Reliability from Stress–Strength for Exponentiated Fréchet Distribution. Iran. J. Sci. Technol. Trans. A Sci. 2019, 43, 863–874. [Google Scholar] [CrossRef]
- Akgül, F.G. Reliability estimation in multicomponent stress–strength model for Topp- Leone distribution. J. Stat. Comput. Simul. 2019, 89, 2914–2929. [Google Scholar] [CrossRef]
- Keller, A.Z.; Kamath, A.R.R.; Perera, U.D. Reliability analysis of CNC Machine Tools. Reliab. Eng. 1982, 3, 449–473. [Google Scholar] [CrossRef]
- Calabria, R.R.; Pulcini, G. Confidence limits for reliability and tolerance limits in the inverse Weibull Distribution. Reliab. Eng. Syst. Saf. 1989, 24, 77–85. [Google Scholar] [CrossRef]
- Calabria, R.; Pulcini, G. On the maximum likelihood and least-squares estimation in the inverse Weibull Distributions. Ital. J. Appl. Stat. 1990, 2, 53–66. [Google Scholar]
- Calabria, R.; Pulcini, G. Bayes probability intervals in a load-strength model. Commun. Stat.-Theory Methods 1992, 21, 3393–3405. [Google Scholar] [CrossRef]
- Calabria, R.; Pulcini, G. Bayes 2-sample prediction for the inverse Weibull Distribution. Commun. Stat.-Theory Methods 1994, 23, 1811–1824. [Google Scholar] [CrossRef]
- Maswadah, M. Conditional confidence interval estimation for the inverse Weibull distribution based on Censored generalized order statistics. J. Stat. Comput. Simul. 2003, 73, 887–898. [Google Scholar] [CrossRef]
- Maswadah, M. Kernel Inference on the Inverse Weibull Distribution. Korean Commun. Stat. 2006, 13, 503–512. [Google Scholar] [CrossRef]
- Dumonceaux, R.; Antle, C. Discrimination between the Lognormal and Weibull Distribution. Technometrics 1973, 15, 923–926. [Google Scholar] [CrossRef]
- Prabhakar Murthy, D.N.; Xie, M.; Jiang, R. Weibull Models; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Bi, Q.; Gui, W. Bayesian and classical estimation of stress-strength reliability for inverse Weibull lifetime models. Algorithms 2017, 10, 71. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Distributions. In Continuous Univariate Distributions, 2nd ed.; Wiley: New York, NY, USA, 1995; Volume 2. [Google Scholar]
- Drapella, A. The complementary Weibull distribution: Unknown or just forgotten? Qual. Reliab. Eng. Int. 1993, 9, 383–385. [Google Scholar] [CrossRef]
- Khan, M.S.; Pasha, G.R.; Pasha, A.H. Theoretical analysis of inverse Weibull Distribution. WEAS Trans. Math. 2008, 7, 30–38. [Google Scholar]
- Li, C.; Hao, H. Reliability of a Stress–Strength Model with Inverse Weibull Distribution. IAENG Int. J. Appl. Math. 2017, 47, 302–306. [Google Scholar]
- Yadav, A.S.; Singh, S.K.; Singh, U. Estimation of stress–strength reliability for inverse Weibull Distribution under the progressive type-II censoring scheme. J. Ind. Prod. Eng. 2018, 35, 48–55. [Google Scholar] [CrossRef]
- Yang, L.; Wang, P.; Wang, Q.; Bi, S.; Peng, R.; Behrensdorf, J.; Beer, M. Reliability analysis of a complex system with hybrid structures and multi-level dependent life metrics. Reliab. Eng. Syst. Saf. 2021, 209, 107469. [Google Scholar] [CrossRef]
- Graves, L.; Hamada, M.S. A Note on Incorporating Simultaneous Multi-level Failure Time Data in System Reliability Assessments. Qual. Reliab. Eng. Int. 2016, 32, 1127–1135. [Google Scholar] [CrossRef]
- Rao, G.S.; Aslam, M.; Arif, O.H. Estimation of reliability in multicomponent stress–strength based on two parameter exponentiated Weibull Distribution. Commun. Stat.-Theory Methods 2017, 46, 7495–7502. [Google Scholar]
- Palumbo, B.; Pallotta, G. New approach to the identification of the inverse Weibull model. In Proceedings of the 46th Scientific Meeting of the Italian Statistical Society, Rome, Italy, 20–22 June 2012. [Google Scholar]
- Surles, J.G.; Padgett, W.J. Inference for reliability and stress-strength for a scaled Burr type X distribution. Lifetime Data Anal. 2001, 7, 187–200. [Google Scholar] [CrossRef] [PubMed]
- Kundu, D.; Gupta, R.D. Estimation of P[Y < X] for Weibull distributions. IEEE Trans. Reliab. 2016, 55, 270–280. [Google Scholar]

| (s, k) | (α, β) | ||||||
|---|---|---|---|---|---|---|---|
| (3, 1.5) | (2.5, 1.5) | (2, 1.5) | (1.5, 1.5) | (1.5, 2) | (1.5, 2.5) | (1.5, 3) | |
| (1, 3) | 0.857143 | 0.833333 | 0.800000 | 0.750000 | 0.692308 | 0.642857 | 0.600000 |
| (3, 5) | 0.692641 | 0.646998 | 0.585812 | 0.500000 | 0.409919 | 0.340330 | 0.285714 |
| n | m | (α, β) | ABias | AMSE | ASE | ALCI | ACP | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 10 | (3, 1.5) | −0.0564 | −0.1044 | 0.0045 | 0.0150 | 0.0708 | 0.1258 | 0.2774 | 0.4931 | 0.9989 | 0.9951 |
| 15 | 15 | −0.0561 | −0.1032 | 0.0040 | 0.0134 | 0.0579 | 0.1030 | 0.2268 | 0.4039 | 0.9966 | 0.9863 | |
| 20 | 20 | −0.0550 | −0.1021 | 0.0037 | 0.0125 | 0.0500 | 0.0893 | 0.1959 | 0.3501 | 0.9905 | 0.9720 | |
| 25 | 25 | −0.0548 | −0.1010 | 0.0045 | 0.0120 | 0.0447 | 0.0799 | 0.1752 | 0.3131 | 0.9753 | 0.9458 | |
| 30 | 30 | −0.0544 | −0.1011 | 0.0034 | 0.0116 | 0.0408 | 0.0730 | 0.1598 | 0.2861 | 0.9526 | 0.9102 | |
| 10 | 10 | (2.5, 1.5) | −0.0473 | −0.0832 | 0.0036 | 0.0111 | 0.0746 | 0.1293 | 0.2924 | 0.5068 | 0.9986 | 0.9956 |
| 15 | 15 | −0.0468 | −0.0826 | 0.0031 | 0.0097 | 0.0610 | 0.1060 | 0.2390 | 0.4154 | 0.9984 | 0.9957 | |
| 20 | 20 | −0.0452 | −0.0815 | 0.0027 | 0.0088 | 0.0526 | 0.0919 | 0.2062 | 0.3602 | 0.9977 | 0.9900 | |
| 25 | 25 | −0.0450 | −0.0810 | 0.0026 | 0.0083 | 0.0470 | 0.0823 | 0.1844 | 0.3225 | 0.9960 | 0.9851 | |
| 30 | 30 | −0.0447 | −0.0808 | 0.0025 | 0.0079 | 0.0429 | 0.0752 | 0.1682 | 0.2946 | 0.9899 | 0.9763 | |
| 10 | 10 | (2, 1.5) | −0.0303 | −0.0509 | 0.0024 | 0.0068 | 0.0786 | 0.1327 | 0.3082 | 0.5203 | 0.9992 | 0.9983 |
| 15 | 15 | −0.0293 | −0.0501 | 0.0018 | 0.0053 | 0.0642 | 0.1088 | 0.2516 | 0.4266 | 0.9994 | 0.9984 | |
| 20 | 20 | −0.0291 | −0.0498 | 0.0016 | 0.0047 | 0.0556 | 0.0944 | 0.2180 | 0.3701 | 0.9992 | 0.9981 | |
| 25 | 25 | −0.0288 | −0.0497 | 0.0014 | 0.0041 | 0.0497 | 0.0846 | 0.1950 | 0.3316 | 0.9994 | 0.9981 | |
| 30 | 30 | −0.0289 | −0.0490 | 0.0013 | 0.0038 | 0.0454 | 0.0772 | 0.1781 | 0.3028 | 0.9989 | 0.9974 | |
| 10 | 10 | (1.5, 1.5) | −0.0023 | −0.0004 | 0.0016 | 0.0041 | 0.0837 | 0.1360 | 0.3280 | 0.5331 | 0.9989 | 0.9989 |
| 15 | 15 | −0.0095 | −0.0019 | 0.0010 | 0.0028 | 0.0682 | 0.1116 | 0.2673 | 0.4375 | 0.9993 | 0.9993 | |
| 20 | 20 | −0.0014 | −0.0002 | 0.0008 | 0.0022 | 0.0593 | 0.0968 | 0.2324 | 0.3794 | 0.9995 | 0.9997 | |
| 25 | 25 | −0.0010 | −0.0003 | 0.0006 | 0.0017 | 0.0530 | 0.0867 | 0.2077 | 0.3399 | 0.9995 | 0.9997 | |
| 30 | 30 | −0.0004 | −0.0007 | 0.0005 | 0.0014 | 0.0483 | 0.0793 | 0.1895 | 0.3107 | 0.9995 | 0.9998 | |
| 10 | 10 | (1.5, 2) | 0.0321 | 0.0525 | 0.0030 | 0.0073 | 0.0884 | 0.1378 | 0.3465 | 0.5402 | 0.9928 | 0.9959 |
| 15 | 15 | 0.0332 | 0.0517 | 0.0024 | 0.0058 | 0.0723 | 0.1132 | 0.2833 | 0.4436 | 0.9913 | 0.9958 | |
| 20 | 20 | 0.0328 | 0.0522 | 0.0020 | 0.0050 | 0.0627 | 0.0983 | 0.2459 | 0.3852 | 0.9932 | 0.9963 | |
| 25 | 25 | 0.0336 | 0.0521 | 0.0019 | 0.0045 | 0.0561 | 0.0880 | 0.2198 | 0.3451 | 0.9888 | 0.9954 | |
| 30 | 30 | 0.0332 | 0.0524 | 0.0017 | 0.0043 | 0.0513 | 0.0805 | 0.2009 | 0.3154 | 0.9887 | 0.9928 | |
| 10 | 10 | (1.5, 2.5) | 0.0623 | 0.0907 | 0.0061 | 0.0131 | 0.0920 | 0.1383 | 0.3607 | 0.5422 | 0.9769 | 0.9877 |
| 15 | 15 | 0.0622 | 0.0906 | 0.0053 | 0.0115 | 0.0754 | 0.1136 | 0.2956 | 0.4454 | 0.9645 | 0.9855 | |
| 20 | 20 | 0.0615 | 0.0902 | 0.0049 | 0.0106 | 0.0655 | 0.0987 | 0.2568 | 0.3870 | 0.9536 | 0.9777 | |
| 25 | 25 | 0.0622 | 0.0902 | 0.0048 | 0.0101 | 0.0586 | 0.0885 | 0.2296 | 0.3468 | 0.9324 | 0.9677 | |
| 30 | 30 | 0.0621 | 0.0901 | 0.0046 | 0.0098 | 0.0535 | 0.0808 | 0.2098 | 0.3169 | 0.9121 | 0.9491 | |
| 10 | 10 | (1.5, 3) | 0.0872 | 0.1194 | 0.0101 | 0.0194 | 0.0950 | 0.1380 | 0.3725 | 0.5409 | 0.9443 | 0.9787 |
| 15 | 15 | 0.0867 | 0.1186 | 0.0091 | 0.0175 | 0.0780 | 0.1134 | 0.3056 | 0.4444 | 0.9136 | 0.9605 | |
| 20 | 20 | 0.0868 | 0.1179 | 0.0088 | 0.0165 | 0.0676 | 0.0985 | 0.2651 | 0.3860 | 0.8618 | 0.9325 | |
| 25 | 25 | 0.0871 | 0.1176 | 0.0086 | 0.0159 | 0.0605 | 0.0883 | 0.2373 | 0.3461 | 0.8008 | 0.8984 | |
| 30 | 30 | 0.0867 | 0.1174 | 0.0083 | 0.0155 | 0.0553 | 0.0807 | 0.2169 | 0.3163 | 0.7391 | 0.8356 | |
| Strength (X) | Stress (Y) | |
|---|---|---|
| Mean | ||
| Median | ||
| Standard Deviation | ||
| Standard Error | 0.01196 | 0.00844 |
| Skewness | ||
| Kurtoses | 5.38230 | 2.67273 |
| 0.00469 | 0.00235 | |
| 5.50125 | 5.04997 | |
| Log-Likelihood | 71.12399 | 76.47376 |
| KS Test Statistic | 0.05329 | 0.08753 |
| KS Test p-value | 0.98371 | 0.68698 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shawky, A.I.; Khan, K. Reliability Estimation in Multicomponent Stress-Strength Based on Inverse Weibull Distribution. Processes 2022, 10, 226. https://doi.org/10.3390/pr10020226
Shawky AI, Khan K. Reliability Estimation in Multicomponent Stress-Strength Based on Inverse Weibull Distribution. Processes. 2022; 10(2):226. https://doi.org/10.3390/pr10020226
Chicago/Turabian StyleShawky, Ahmed Ibrahim, and Khushnoor Khan. 2022. "Reliability Estimation in Multicomponent Stress-Strength Based on Inverse Weibull Distribution" Processes 10, no. 2: 226. https://doi.org/10.3390/pr10020226
APA StyleShawky, A. I., & Khan, K. (2022). Reliability Estimation in Multicomponent Stress-Strength Based on Inverse Weibull Distribution. Processes, 10(2), 226. https://doi.org/10.3390/pr10020226






