A Dynamic Principal Component Analysis and Fréchet-Distance-Based Algorithm for Fault Detection and Isolation in Industrial Processes
Abstract
:1. Introduction
- A novel application of the Fréchet distance metric combined with DPCA to isolate process abnormalities and identify their root causes.
- Reduction of computational cost for the Fréchet distance calculations between reference and measured fault trajectories.
- A sensitive and robust FDI method with simple implementation and high accuracy that greatly fits into the Industry 4.0 framework.
2. Methods
2.1. Theory of PCA and DPCA
- Unknown fault inputs within a system result in specific system responses.
- The dynamics and gain of specific fault responses are dependent on the type and magnitude of the fault signal.
- The characteristic response to a system fault within the PC subspace will be unique if faults are observable and independent on the fault input magnitude.
2.2. The Fréchet Distance Metric
2.3. The Proposed Algorithm
| Algorithm 1 Steps of the proposed FDI algorithm. |
Phase 1—Establishing the DPCA model and fault library
|
3. Case Study
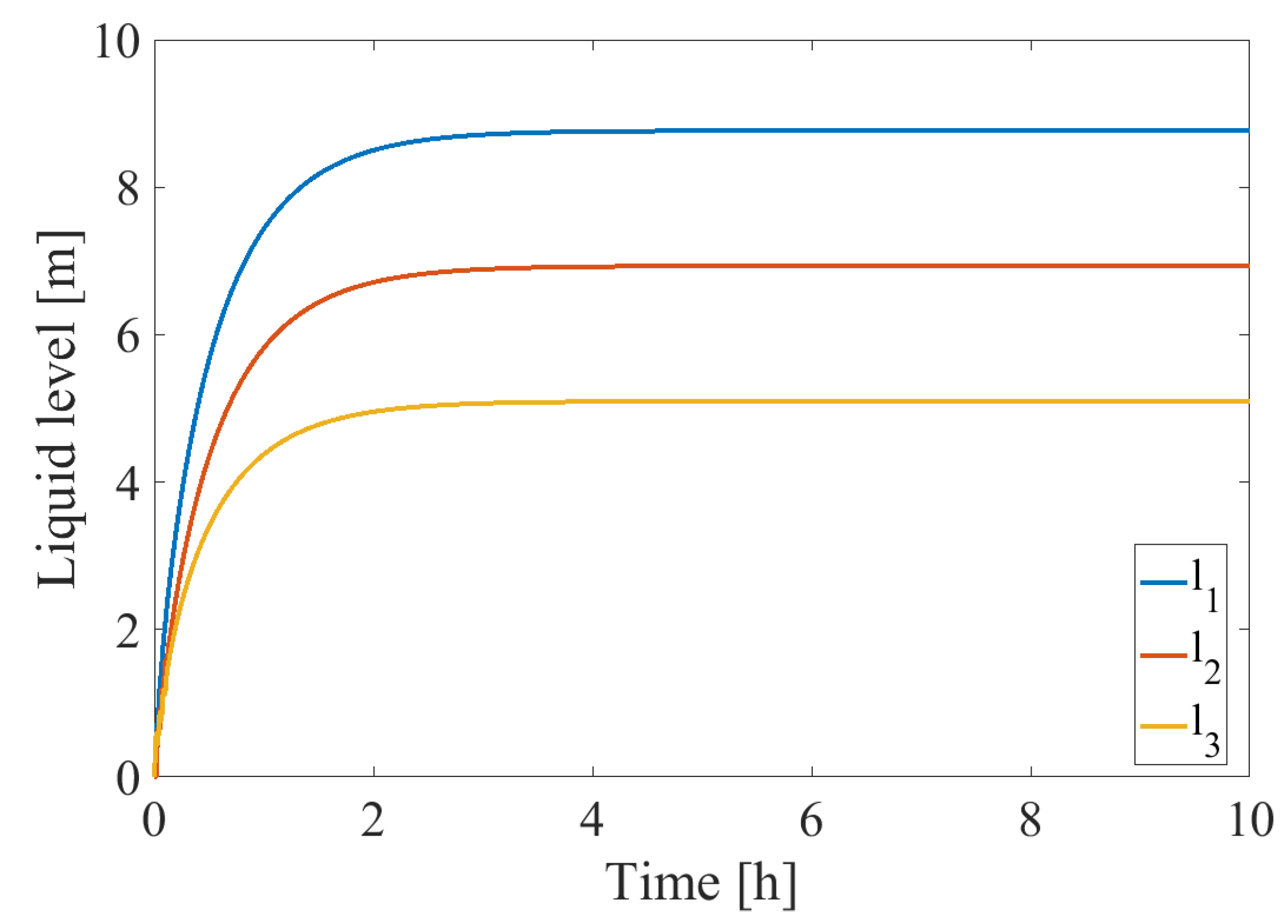
3.1. The Investigated System
3.2. Performance Metrics
- Samples incorrectly classified as faults under normal operating conditions (FN-False Negative).
- Samples correctly classified under normal operating conditions (TP-True Positive).
- Samples incorrectly classified as normal under abnormal operating conditions (FP-False Positive).
- Samples correctly classified under abnormal operating conditions (TN-True Negative).
4. Results
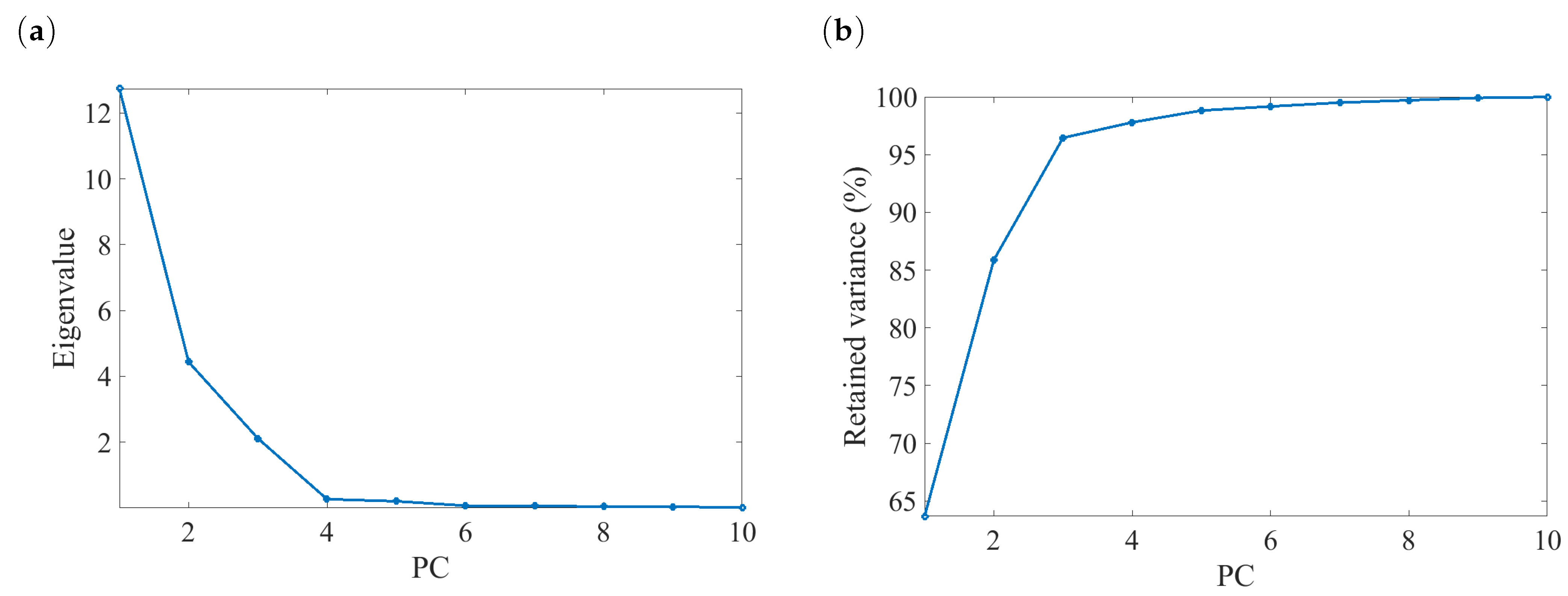
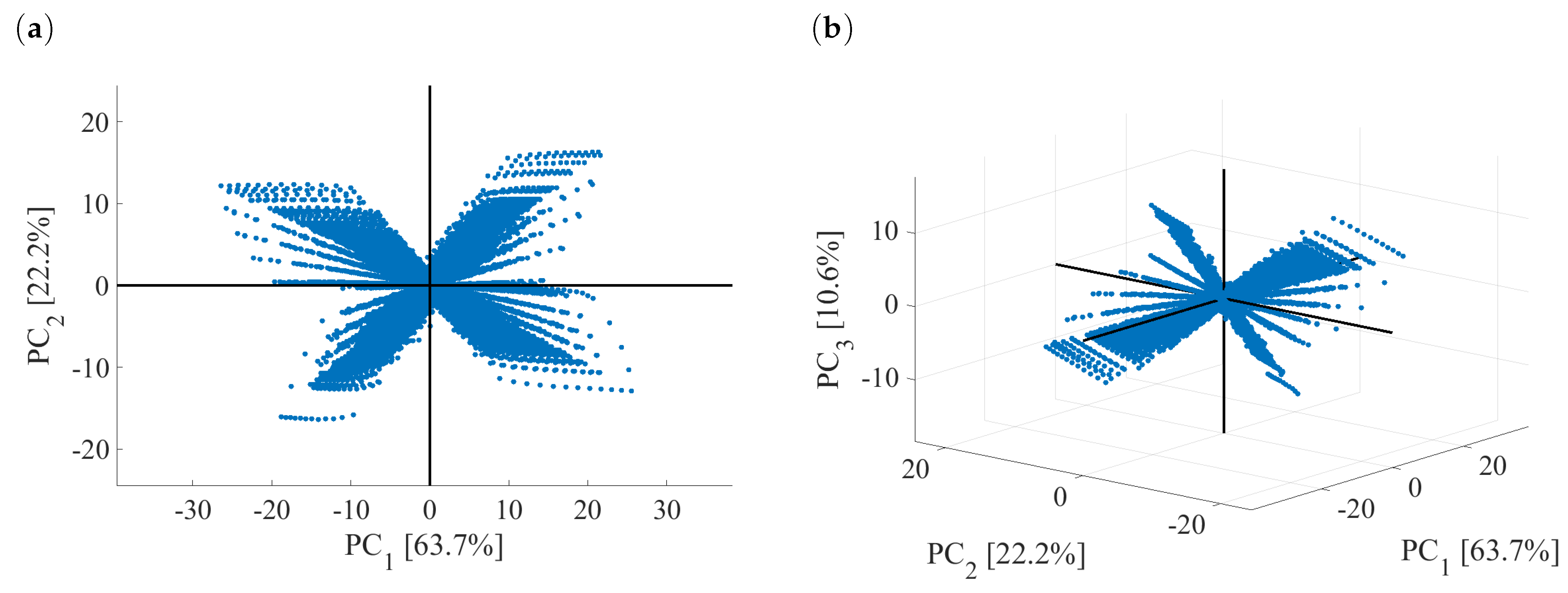
4.1. Development of DPCA Model
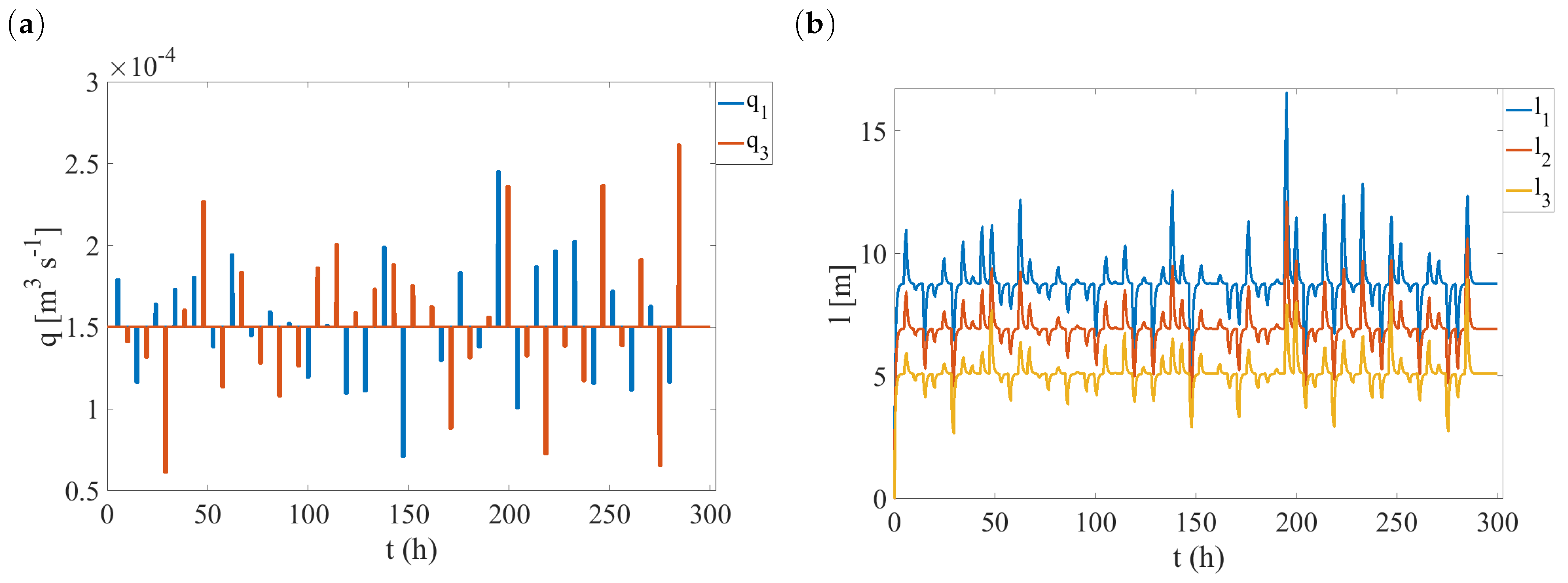
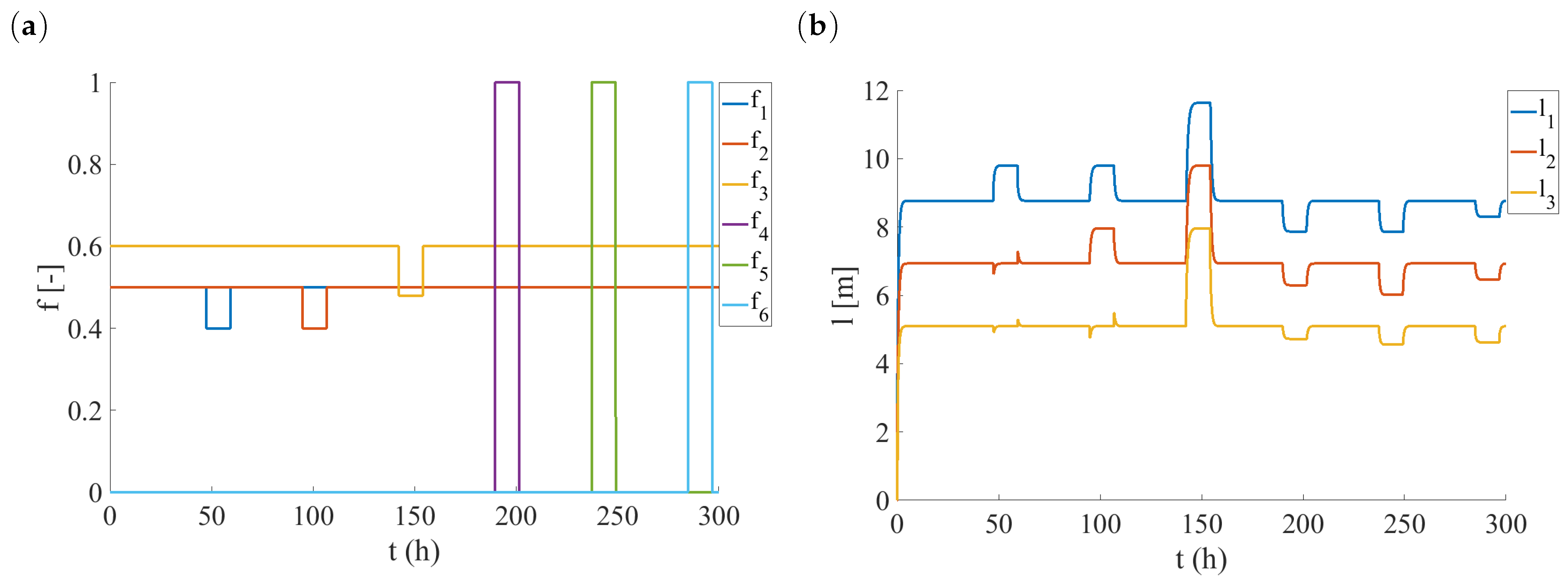
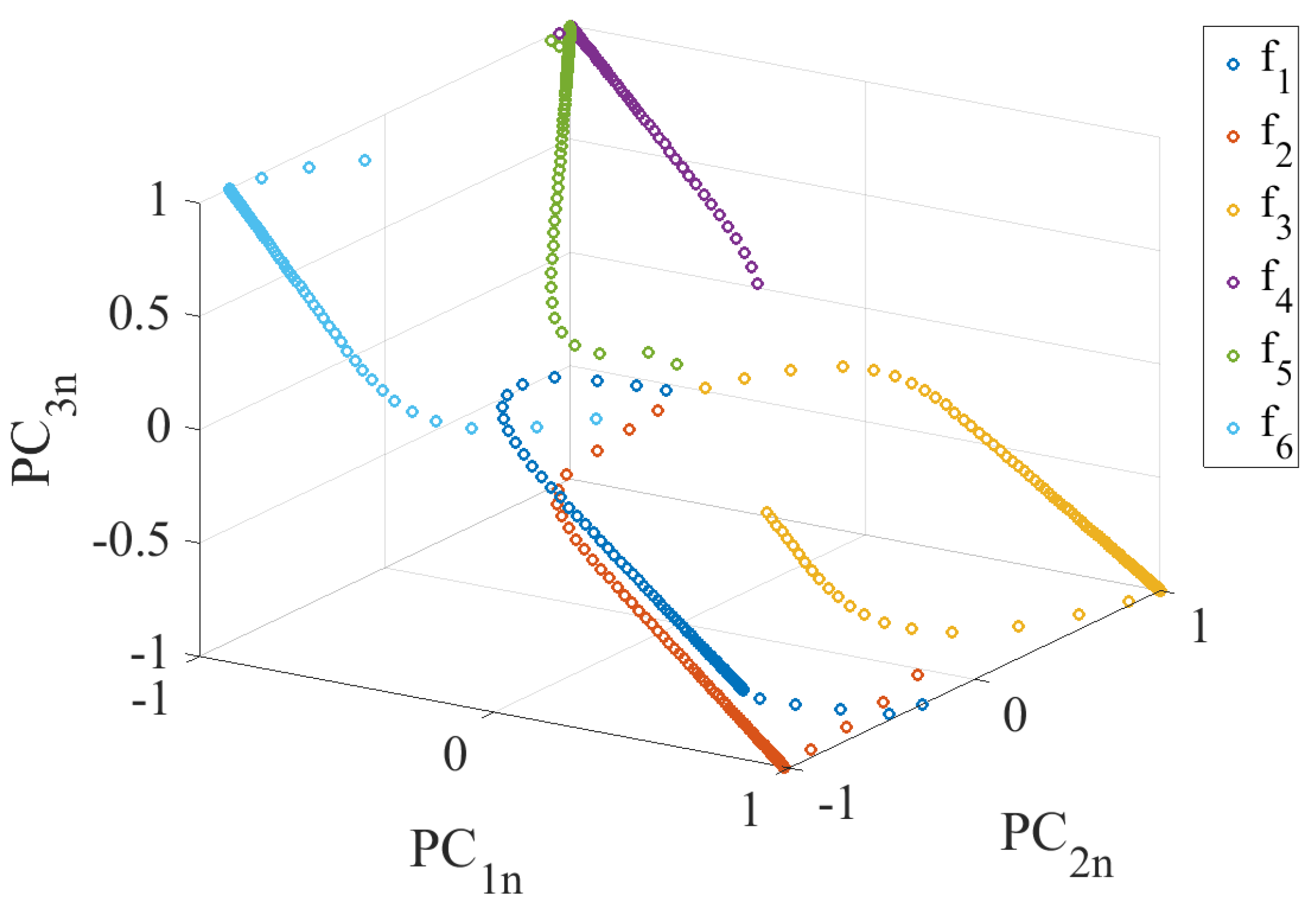
4.2. Fault Library Generation
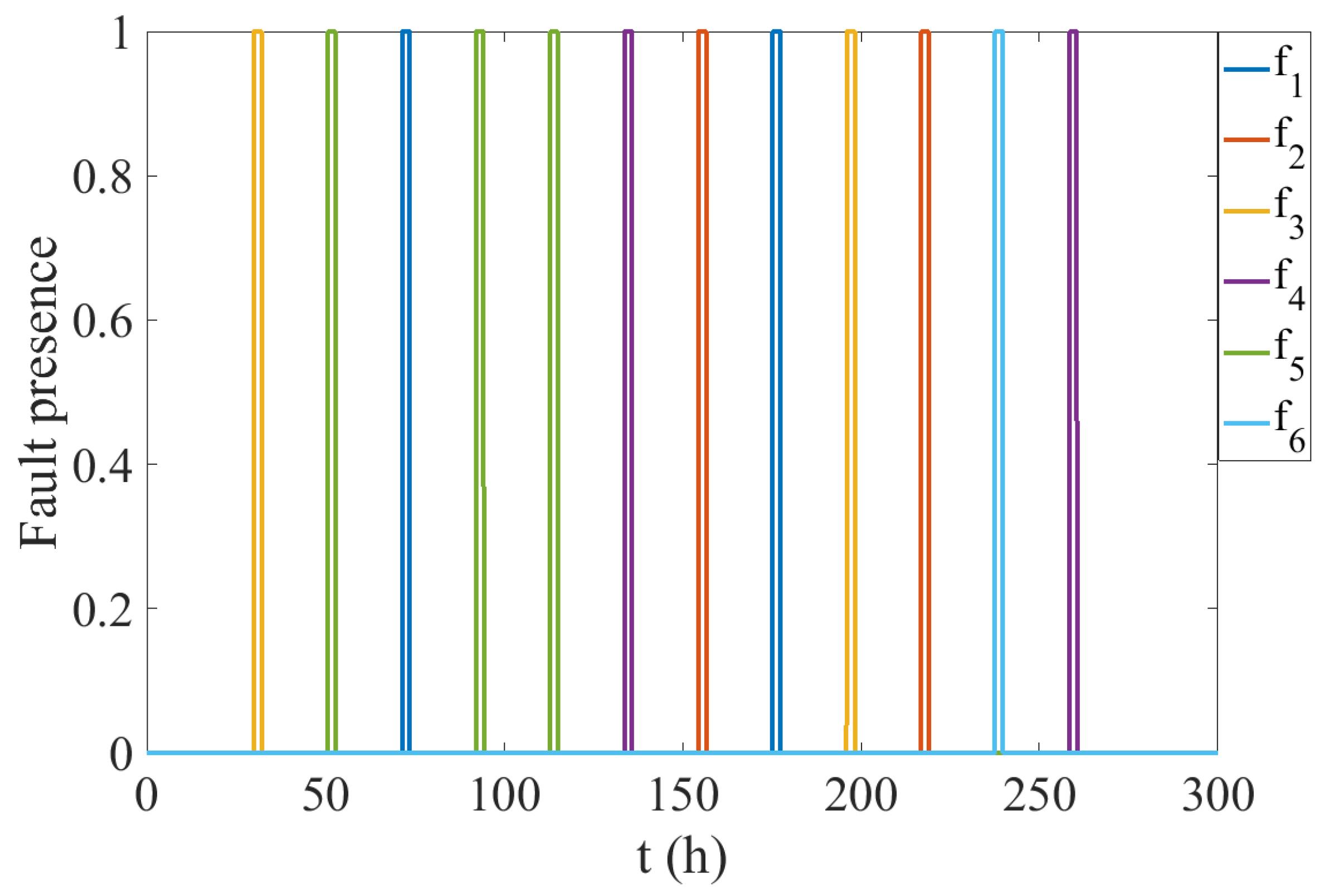
4.3. Fault Detection and Isolation
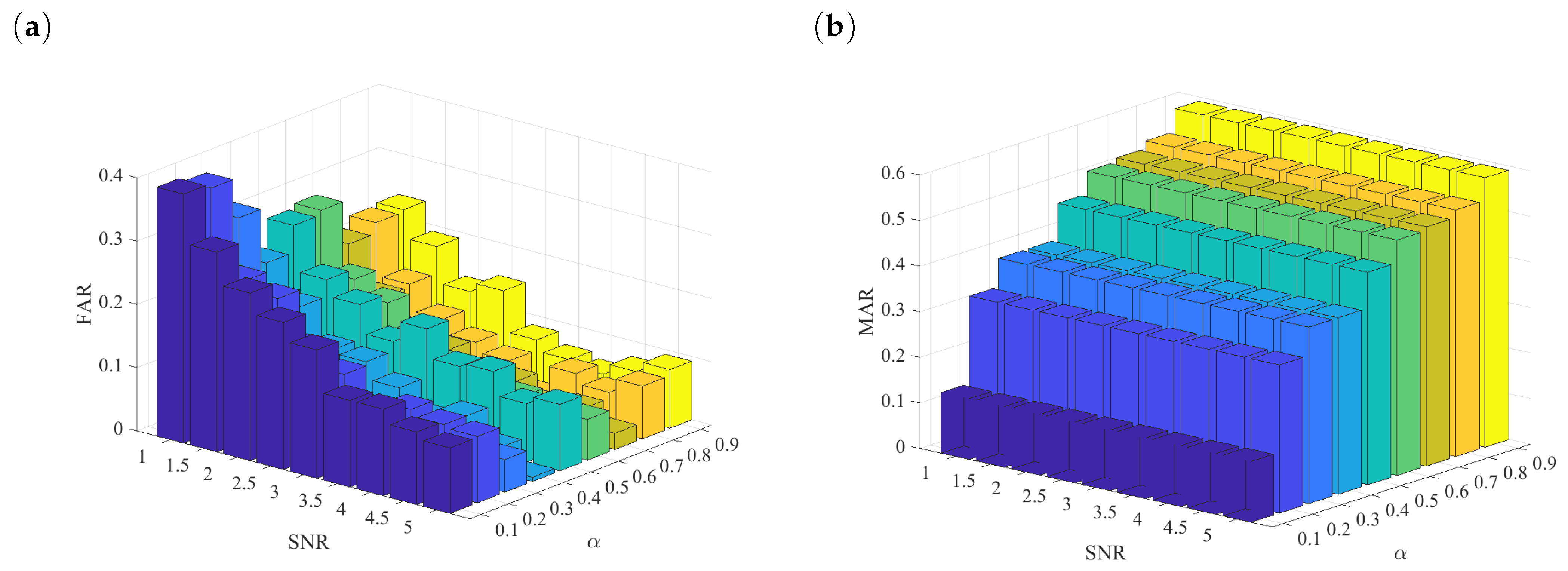
4.4. Performance Metrics of the Method
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Venkatasubramanian, V.; Rengaswamy, R.; Yin, K.; Kavuri, S.N. A review of process fault detection and diagnosis: Part I: Quantitative model-based methods. Comput. Chem. Eng. 2003, 27, 293–311. [Google Scholar]
- De, S.; Shanmugasundaram, D.; Singh, S.; Banerjee, N.; Soni, K.; Galgalekar, R. Chronic respiratory morbidity in the Bhopal gas disaster cohorts: A time-trend analysis of cross-sectional data (1986–2016). Public Health 2020, 186, 20–27. [Google Scholar]
- Kalantarnia, M.; Khan, F.; Hawboldt, K. Modelling of BP Texas City refinery accident using dynamic risk assessment approach. Process Saf. Environ. Prot. 2010, 88, 191–199. [Google Scholar]
- Laboureur, D.M.; Han, Z.; Harding, B.Z.; Pineda, A.; Pittman, W.C.; Rosas, C.; Jiang, J.; Mannan, M.S. Case study and lessons learned from the ammonium nitrate explosion at the West Fertilizer facility. J. Hazard. Mater. 2016, 308, 164–172. [Google Scholar]
- Chien, S.S.; Chang, Y.T. Explosion, subterranean infrastructure and the elemental of earth in the contemporary city: The case of Kaohsiung, Taiwan. Geoforum 2021, 127, 424–434. [Google Scholar]
- Sivaraman, S.; Tauseef, S.; Siddiqui, N. Investigative and probabilistic perspective of the accidental release of styrene: A case study in Vizag, India. Process Saf. Environ. Prot. 2022, 158, 55–69. [Google Scholar]
- Park, Y.J.; Fan, S.K.S.; Hsu, C.Y. A review on fault detection and process diagnostics in industrial processes. Processes 2020, 8, 1123. [Google Scholar]
- Zhong, M.; Xue, T.; Ding, S.X. A survey on model-based fault diagnosis for linear discrete time-varying systems. Neurocomputing 2018, 306, 51–60. [Google Scholar]
- Li, Y.; Karimi, H.R.; Ahn, C.K.; Xu, Y.; Zhao, D. Optimal residual generation for fault detection in linear discrete time-varying systems with uncertain observations. J. Frankl. Inst. 2018, 355, 3330–3353. [Google Scholar]
- Nemati, F.; Hamami, S.M.S.; Zemouche, A. A nonlinear observer-based approach to fault detection, isolation and estimation for satellite formation flight application. Automatica 2019, 107, 474–482. [Google Scholar]
- Wang, P.; Zou, P.; Yu, C.; Sun, J. Distributed fault detection and isolation for uncertain linear discrete time-varying heterogeneous multi-agent systems. Inf. Sci. 2021, 579, 483–507. [Google Scholar]
- Wu, Y.; Zhao, D.; Liu, S.; Li, Y. Fault detection for linear discrete time-varying systems with multiplicative noise based on parity space method. ISA Trans. 2022, 121, 156–170. [Google Scholar]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar]
- Toma, R.N.; Prosvirin, A.E.; Kim, J.M. Bearing fault diagnosis of induction motors using a genetic algorithm and machine learning classifiers. Sensors 2020, 20, 1884. [Google Scholar]
- Lee, C.Y.; Cheng, Y.H. Motor fault detection using wavelet transform and improved PSO-BP neural network. Processes 2020, 8, 1322. [Google Scholar]
- Ait-Izem, T.; Harkat, M.F.; Djeghaba, M.; Kratz, F. On the application of interval PCA to process monitoring: A robust strategy for sensor FDI with new efficient control statistics. J. Process Control. 2018, 63, 29–46. [Google Scholar]
- Vanhatalo, E.; Kulahci, M.; Bergquist, B. On the structure of dynamic principal component analysis used in statistical process monitoring. Chemom. Intell. Lab. Syst. 2017, 167, 1–11. [Google Scholar]
- Venkatasubramanian, V.; Rengaswamy, R.; Kavuri, S.N.; Yin, K. A review of process fault detection and diagnosis: Part III: Process history based methods. Comput. Chem. Eng. 2003, 27, 327–346. [Google Scholar]
- Bakdi, A.; Kouadri, A. A new adaptive PCA based thresholding scheme for fault detection in complex systems. Chemom. Intell. Lab. Syst. 2017, 162, 83–93. [Google Scholar]
- Kramer, M.A. Nonlinear principal component analysis using autoassociative neural networks. AIChE J. 1991, 37, 233–243. [Google Scholar]
- Mansouri, M.; Nounou, M.; Nounou, H.; Karim, N. Kernel PCA-based GLRT for nonlinear fault detection of chemical processes. J. Loss Prev. Process Ind. 2016, 40, 334–347. [Google Scholar]
- Li, W.; Yue, H.H.; Valle-Cervantes, S.; Qin, S.J. Recursive PCA for adaptive process monitoring. J. Process Control. 2000, 10, 471–486. [Google Scholar]
- Ammiche, M.; Kouadri, A.; Bensmail, A. A modified moving window dynamic PCA with fuzzy logic filter and application to fault detection. Chemom. Intell. Lab. Syst. 2018, 177, 100–113. [Google Scholar]
- Ku, W.; Storer, R.H.; Georgakis, C. Disturbance detection and isolation by dynamic principal component analysis. Chemom. Intell. Lab. Syst. 1995, 30, 179–196. [Google Scholar]
- Rato, T.J.; Reis, M.S. Fault detection in the Tennessee Eastman benchmark process using dynamic principal components analysis based on decorrelated residuals (DPCA-DR). Chemom. Intell. Lab. Syst. 2013, 125, 101–108. [Google Scholar]
- Huang, S.; Yang, X.; Wang, L.; Chen, W.; Zhang, F.; Dong, D. Two-stage turnout fault diagnosis based on similarity function and fuzzy c-means. Adv. Mech. Eng. 2018, 10, 1687814018811402. [Google Scholar]
- Bounoua, W.; Bakdi, A. Fault detection and diagnosis of nonlinear dynamical processes through correlation dimension and fractal analysis based dynamic kernel PCA. Chem. Eng. Sci. 2021, 229, 116099. [Google Scholar]
- Stanimirova, I.; Daszykowski, M.; Walczak, B. Dealing with missing values and outliers in principal component analysis. Talanta 2007, 72, 172–178. [Google Scholar]
- Dray, S.; Josse, J. Principal component analysis with missing values: A comparative survey of methods. Plant Ecol. 2015, 216, 657–667. [Google Scholar]
- Kwon, J.; Oh, H.S.; Lim, Y. Dynamic principal component analysis with missing values. J. Appl. Stat. 2020, 47, 1957–1969. [Google Scholar]
- Bakshi, B.R. Multiscale PCA with application to multivariate statistical process monitoring. AIChE J. 1998, 44, 1596–1610. [Google Scholar]
- Misra, M.; Yue, H.H.; Qin, S.J.; Ling, C. Multivariate process monitoring and fault diagnosis by multi-scale PCA. Comput. Chem. Eng. 2002, 26, 1281–1293. [Google Scholar]
- Sophian, A.; Tian, G.Y.; Taylor, D.; Rudlin, J. A feature extraction technique based on principal component analysis for pulsed Eddy current NDT. NDT Int. 2003, 36, 37–41. [Google Scholar]
- Lau, C.; Ghosh, K.; Hussain, M.A.; Hassan, C.C. Fault diagnosis of Tennessee Eastman process with multi-scale PCA and ANFIS. Chemom. Intell. Lab. Syst. 2013, 120, 1–14. [Google Scholar]
- Weng, H.; Wang, S.; Wan, Y.; Lin, X.; Li, Z.; Huang, J. Discrete Fréchet distance algorithm based criterion of transformer differential protection with the immunity to saturation of current transformer. Int. J. Electr. Power Energy Syst. 2020, 115, 105449. [Google Scholar]
- Jackson, J.E.; Mudholkar, G.S. Control procedures for residuals associated with principal component analysis. Technometrics 1979, 21, 341–349. [Google Scholar]
- Eiter, T.; Mannila, H. Computing Discrete Fréchet Distance; Technical Report CD-TR 94/64; Christian Doppler Laboratory for Expert Systems: Vienna, Austria, 1994. [Google Scholar]
- Theilliol, D.; Noura, H.; Ponsart, J.C. Fault diagnosis and accommodation of a three-tank system based on analytical redundancy. ISA Trans. 2002, 41, 365–382. [Google Scholar]
- Li, Y.; Cao, W.; Hu, W.; Xiong, Y.; Wu, M. Incipient fault detection for geological drilling processes using multivariate generalized Gaussian distributions and Kullback–Leibler divergence. Control. Eng. Pract. 2021, 117, 104937. [Google Scholar]
- Cuadros-Rodríguez, L.; Pérez-Castaño, E.; Ruiz-Samblás, C. Quality performance metrics in multivariate classification methods for qualitative analysis. TrAC Trends Anal. Chem. 2016, 80, 612–624. [Google Scholar]
- Khoukhi, A.; Khalid, M.H. Hybrid computing techniques for fault detection and isolation, a review. Comput. Electr. Eng. 2015, 43, 17–32. [Google Scholar]
- Janeliukstis, R.; Rucevskis, S.; Chate, A. Condition monitoring with defect localisation in a two-dimensional structure based on linear discriminant and nearest neighbour classification of strain features. Nondestruct. Test. Eval. 2020, 35, 48–72. [Google Scholar]
- Oliveira, B.; Seibert, A.; Borges, V.; Albertazzi, A.; Schmitt, R. Employing a U-net convolutional neural network for segmenting impact damages in optical lock-in thermography images of CFRP plates. Nondestruct. Test. Eval. 2021, 36, 440–458. [Google Scholar]





| 0.5 | 0.5 | 0.6 | ||
| 0.6 | 0 |
| Consideration | Model-Based Techniques | Neural Networks | Proposed Method |
|---|---|---|---|
| Complexity | Requires deep mathematical and system knowledge to implement (−) | Easy implementation (+) | Easy implementation (+) |
| Requirements | Exact process model (−) | Abundance of reliable process data (−) | Abundance of reliable process data (−) |
| Adaptability to new faults | Easy adaptability (+) | Requires additional training to identify new fault classes (−) | Easy addition of new faults to the data base after fault occurrence (+) |
| Computational load | Low computational cost (+) | Depending on the network structure computational cost may be high (−) | Low computational cost (+) |
| Design procedure | Straightforward & simple (+) | Great consideration has to be given to determine the optimal network structure (−) | Straightforward and simple (+) |
| Robustness against noise and disturbances | Robustness may be an issue for nonlinear systems (−) | Great robustness depending on the network structure (+) | Robustness is easy to adjust through the use of nonlinear PCA (+) |
| Sensitivity to faults | Great sensitivity (+) | Great sensitivity (+) | Sensitivity may be an issue based on the utilized statistic (−) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarcsay, B.L.; Bárkányi, Á.; Chován, T.; Németh, S. A Dynamic Principal Component Analysis and Fréchet-Distance-Based Algorithm for Fault Detection and Isolation in Industrial Processes. Processes 2022, 10, 2409. https://doi.org/10.3390/pr10112409
Tarcsay BL, Bárkányi Á, Chován T, Németh S. A Dynamic Principal Component Analysis and Fréchet-Distance-Based Algorithm for Fault Detection and Isolation in Industrial Processes. Processes. 2022; 10(11):2409. https://doi.org/10.3390/pr10112409
Chicago/Turabian StyleTarcsay, Bálint Levente, Ágnes Bárkányi, Tibor Chován, and Sándor Németh. 2022. "A Dynamic Principal Component Analysis and Fréchet-Distance-Based Algorithm for Fault Detection and Isolation in Industrial Processes" Processes 10, no. 11: 2409. https://doi.org/10.3390/pr10112409
APA StyleTarcsay, B. L., Bárkányi, Á., Chován, T., & Németh, S. (2022). A Dynamic Principal Component Analysis and Fréchet-Distance-Based Algorithm for Fault Detection and Isolation in Industrial Processes. Processes, 10(11), 2409. https://doi.org/10.3390/pr10112409








