An Enhanced Evaporation Rate Water-Cycle Algorithm for Global Optimization

Abstract

Water-cycle algorithm based on evaporation rate (ErWCA) is a powerful enhanced version of the water-cycle algorithm (WCA) metaheuristics algorithm. ErWCA, like other algorithms, may still fall in the sub-optimal region and have a slow convergence, especially in high-dimensional tasks problems. This paper suggests an enhanced ErWCA (EErWCA) version, which embeds local escaping operator (LEO) as an internal operator in the updating process. ErWCA also uses a control-randomization operator. To verify this version, a comparison between EErWCA and other algorithms, namely, classical ErWCA, water cycle algorithm (WCA), butterfly optimization algorithm (BOA), bird swarm algorithm (BSA), crow search algorithm (CSA), grasshopper optimization algorithm (GOA), Harris Hawks Optimization (HHO), whale optimization algorithm (WOA), dandelion optimizer (DO) and fire hawks optimization (FHO) using IEEE CEC 2017, was performed. The experimental and analytical results show the adequate performance of the proposed algorithm.

1. Introduction

Optimization is the rule of selecting the best design variables to find maximum/minimum values for a specific problem [1,2,3,4]. Optimization approaches examine the search space to find the best optimal/near-optimal results for the given task [5,6,7,8].

Metaheurstic algorithms have attracted great attention, and significant interest due to their simplicity and powerfulness in solving optimization tasks, especially complex ones. Metaheuristic algorithms can be divided into two big classes: single-based algorithms and population-based algorithms. The former class contains algorithms such as simulated annealing (SA) [9], tabu search (TS) [10], and $\beta$-hill climbing [11] whereas the latter class contains algorithms such as grey wolf optimization (GWO) [12], particle swarm optimization (PSO) [13], salp swarm algorithm (SSA) [14,15], gravitational search algorithm [16], moth-flame optimization (MFO) [17], virus colony search (VCS) [18], crow search algorithm (CSA) [19], snake optimizer (SO) [20], lightning search algorithm (LSA) [21], Ant Lion Optimization (ALO) [22], Arithmetic optimization algorithm [23], Remora Optimization Algorithm [24], Wild Horse Optimizer [25], COOT bird [26], Aquila Optimizer (AO) [27], harris hawks optimization (HHO) [28,29], and whale optimizer algorithm (WOA) [30,31].

Metaheuristic algorithms have been successfully applied to many domains (fields) [32,33]. Examples of such fields include feature selection [34,35], cloud computing [36], ransomware detection [37], text mining [38], deep learning [39], signal processing [40], photovoltaic models [41], medical applications [42], and engineering problems [43,44].

Water-cycle algorithm (WCA) is a swarm intelligence algorithm developed by Eskandar et al. [45] which simulates the running of streams and river towards the sea. ErWCA is a variant of WCA which adds the concept of river/stream evaporation rate [46]. The original ErWCA has good exploration abilities. However, it has low capabilities of exploitation. In this study, a modified version of ErWCA is proposed, called enhanced ErWCA (EErWCA), in which the local escape operator (LEO) is added to increase the exploitation of ErWCA in addition to two operators which are borrowed from slime mould optimization [47] to increase its exploration abilities.

The major contributions of this paper are highlighted as the following points:

• ErWCA is enhanced by embedding local escape operator and two other control-randomization operators in the updating phase and using the control-randomization operator.
• EErWCA is tested using 29 CEC 2017 and compared with the classical and eight other algorithms.
• Three different engineering problems are used to prove the effectiveness of the proposed algorithm in solving constrained problems.

This study is organized as follows: Section 2 represents the related works. Section 3 shows the mathematical formulation of evaporation rate water-cycle algorithm, whereas the proposed algorithm is shown in Section 4. Section 5 shows the experimental and analytical results of the proposed algorithm, whereas Section 6 concludes the paper and gives some future work ideas.

2. Related Works

Metaheuristic algorithms have been playing a major role in solving many optimization problems. A set of functions named CEC has been benchmarked as optimization problems that many researchers have been solving in their studies using several metaheuristic algorithms. A study of [48] proposed advancement of the LSHADE algorithm with rank-based selective pressure strategy for solving CEC 2017 benchmark problems. An enhanced version of cuckoo search was proposed by [49] to solve the CEC 2017 and CEC 2020 benchmark problems by adding a new global and local search technique, applying a dual search strategy, using a linearly decreasing switch probability, and linearly decreasing the population size. The study of [50] proposed a population-based artificial electric field algorithm for the CEC2017 benchmark set. Empirical investigations into the composite differential evolution on CEC 2017 constrained optimization problems was presented by [51].

On the other hand, many engineering problems have been solved by optimization algorithms, such as the design of an industrial refrigerator system problem, speed reducer problem, and multi-product batch plant problem. Several papers have studied the industrial refrigerator system problem. The authors of [52] proposed a simultaneous optimization of the refrigeration system and heat exchanger network using the particle swarm optimization (PSO) algorithm to optimize the pressure/temperature levels. The work of [53] used classic and non-classic computational intelligence (CI) techniques, including genetic algorithm (GA), simulated annealing (SA), differential evolution (DE), heat transfer search (HTS), chemical reaction optimization (CRO), multi-objective GA (MOGA), nondominated sorting genetic algorithm II (NSGA II), and artificial neural network (ANN) to optimize several refrigeration systems. In addition, a method for selecting the best refrigerants and the optimal configurations of the refrigeration system was proposed by [54] by finding the most critical temperature levels, the most suitable refrigerants, and extracting a set of refrigeration system configurations using mixed-integer linear programming.

In addition, the design of the speed reducer problem is found in the studies of [55,56]. The authors of [55] used optimization to express the time-varying meshing stiffness in the dynamic equations by using the Ishikawa algorithm and to optimize the load sharing performance and volume. A modified probabilistic procedure for deriving an ultimate strength and strain design model for a speed reducer was proposed by [56].

The multi-product batch plant problem is also considered in many studies. The study of [57] considered ant colony optimization (ACO) and simulated annealing (SA) to tune the parameter of ACO using real-world examples. The authors of [58] proposed a hybrid evolutionary approach for large-scale multi-stage multi-product batch plant scheduling problems based on the coevolutionary algorithm framework, where new evolutionary operations are adopted for the unit assignment and order sequence.

This paper uses the enhanced ErWCA population-based algorithm to solve both the CEC benchmark problems and the engineering problems presented above. This study uses the exploitation of slime mould optimization as a replacement for the exploitation used by the original algorithm.

3. Evaporation Rate Water-Cycle Algorithm

ErWCA is a metaheuristic population-based algorithm which is inspired by the hydrologic cycle. Evaporated water returns to the earth and is carried into the atmosphere in the form of rain.

Mathematical Formulation

The first generation of individuals (raindrops) is produced randomly between upper and lower boundaries. Then, all individuals are evaluated using the objective function. The best one is selected as the sea, and other good individuals are selected as rivers. The following equations are used in initialization.

$$\mathrm{Raindrop}=[R_1,R_2,R_3,\dots ,R_m]$$

(1)

$$\mathrm{population}\mathrm{of}\mathrm{raindrop}=\left[\begin{array}{c}Sea\\ Rive{r}_1\\ Rive{r}_2\\ .\\ .\\ Stream{M}_{sr+1}\\ Stream{M}_{sr+2}\\ .\\ .\\ Stream{M}_{pop}\end{array}\right]=\left[\begin{array}{ccccc}{R}_1^1& R_2^1& \dots & \dots & R_M^1\\ R_1^2& R_2^2& \dots & \dots & R_M^2\\ \dots & \dots & \dots & \dots & \dots \\ R_1^{M_{pop}}& R_2^{M_{pop}}& \dots & \dots & R_1^{M_{pop}}\end{array}\right]$$

(2)

where M refers to the raindrops number and $M_{pop}$ refers to the size of the population.

The flow intensity for each stream can be obtained based on the objective function value from the following equation

$$Cos{t}_i=f(R_1^i,R_2^i,R_3^i,...,R_m^i)i=1,2,3,\dots ,M_{pop}$$

(3)

The other individuals can be evaluated from the below equation.

$$M_{sr}=\mathrm{Number}\mathrm{of}\mathrm{Rivers}+1$$

(4)

$$M_{Raindrops}=M_{pop}-M_{sr}$$

(5)

The intensity of flow streams that directly flow to either rivers or sea can be calculated from the following equations

$$C_m=Cos{t}_m-Cos{t}_{M_{sr+1}}$$

(6)

$$M{S}_m=round\left\{\right|\frac{C_m}{{\sum }_{m=1}^{M_{sr}}{C}_m}|\times M_{Raindrops}\}$$

(7)

where $M_{sr}$ refers to stream numbers.

The location of the new streams and rivers can be given bellow.

$$R_{Stream}^{i+1}=R_{Stream}^i+rand\times K\times (R_{River}^i-R_{Stream}^i)$$

(8)

$$R_{Stream}^{i+1}=R_{Stream}^i+rand\times K\times (R_{Sea}^i-R_{Stream}^i)$$

(9)

$$R_{River}^{i+1}=R_{Stream}^i+rand\times K\times (R_{Sea}^i-R_{River}^i)$$

(10)

where $rand$ refers to a number between 0 and 1, K is a value between (1,2), and their sum equals 2.

If the distance between sea and river $<d_{max}$, then the evaporation and raining phases have started. The following equation can give the new stream position.

$$R_{Stream}^{new}=LoB+rand\times (UpB-LoB)$$

(11)

where $UpB$ and $LoB$ are upper and lower boundaries. The evaporation condition is also applied to the stream that flows to the sea. The following equation can give the new stream position

$$R_{Stream}^{new}=R_{sea}+\sqrt{q}\times randn(1,M_{var})$$

(12)

where q refers to a constant that equals $0.1$ and the $d_{max}$ value decreases according to the following equation

$$d_{max}^{i+1}=d_{max}^i-\frac{d_{max}^i}{Max\_Iter}$$

(13)

Many rivers are not able to reduce the distance to the sea. Therefore, an evaporation rate concept is added as follows:

$$ER=\frac{Sum\left(M{S}_m\right)}{M_{sr}-1}\times rand,m=2,\dots ,M_{sr}$$

(14)

4. Proposed Algorithm EErWCA

ErWCA has many drawbacks as it is stuck in local regions or has low convergence in high-dimensional problems. In addition, the no free lunch (NFL) theorm, which states that there is no algorithm that is good in solving all optimization problems, encourages us to develop an enhanced version of ErWCA. In this paper, the exploitation phase is replaced by slime mould algorithm (SMA) exploitation phase.

Here, we used two operators, a and W, as follows

$$a=arctanh(-(\frac{t}{Max\_Iter})+1)$$

(15)

where t and $Max\_Iter$ refer to the current and maximum number of iterations, respectively.

$$W\left(S\right)=\left\{\begin{array}{cc}1+r.log(\frac{bF-S\left(i\right)}{bF-wf}+1)\hfill & rand\ge 0.5\hfill \\ 1-r.log(\frac{bF-S\left(i\right)}{bF-wf}+1)\hfill & otherwise\hfill \end{array}\right.$$

(16)

where $bF$ and $wf$ refer to optimal fitness value and the best fitness value, respectively, and $S\left(i\right)$ refers to the rank of the first population half.

In order to update the river position, the following equation is used to update the river.

$$R_{River}^{i+1}=R_{Stream}^i+a\times (W\times R_{Sea}^i-R_{River}^i)$$

(17)

Local Escaping Operator (LEO)

LEO is based on two parts: the first on ($X{1}_n^m \& X{2}_n^m$) and the second is based on ($X_{r1}^m \& X_{r2}^m$). The 1st part update position is based on four random solutions, which make ($X_{LEO}^m$) based on a random position. In this paper, we try to enhance $X{1}_n^m$ and $X{2}_n^m$.

$$\delta =2\times rand\times (|\frac{x_{best1}+x_{best2}+x_{best3}+x_{best4}}{4}-x_n^m|)$$

(18)

The flow chart is given in Figure 1, and the pseudo-code is given in Algorithm 1. The local escaping operator is used at the beginning of each iteration, and the SA solution is generated and compared with each current solution.

Algorithm 1 Enhanced ErWCA

1:   Determine the initial ErWCA parameters $d_{max}$, $N_{sr}$, $N_{pop}$, and $Max\_Iter$ 2:   Initialize population randomly. 3:   Form initial streams, rivers, and sea. 4:   while ($t\le Max\_Iter$) do do 5:       Evaluate each stream fitness, Equation (3). 6:       Apply LEO operator 7:       Determine intensity of flow for river and sea using Equations (7) and (8). 8:       Generate a random solution using SA and update the current agent if the generated solution is better. 9:       Streams flow to the river and sea using Equations (10) and (11). 10:     Exchange positions of river and sea. 11:     Rivers flow to the sea Equation (11). 12:     if ($X_{river}<X_{Sea}$) then 13:         Exchange river with the sea. 14:     end if 15:     if Check evaporation rate between river and sea then 16:         Update streams and rivers. 17:     end if 18:     if Check evaporation rate between sea and river then 19:         Update streams and rivers. 20:     end if 21:     Reduce $d_{max}$. 22: end while 23: Return best solution.

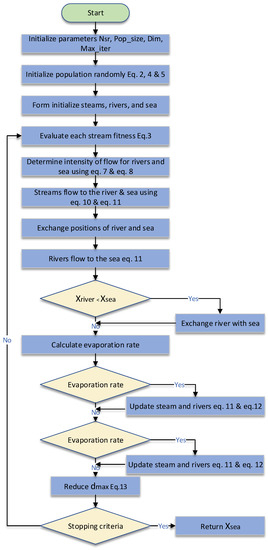
Figure 1. EErWCA flow Chart.

5. Experimental Results and Discussion

In this section, we test our proposed algorithm versus the classical ErWCA, and nine other metaheuristic algorithms, namely: evaporation rate water-cycle algorithm (ErWCA) [46], water-cycle algorithm [45], butterfly optimization algorithm (BOA) [59], bird swarm algorithm (BSA) [60], crow search algorithm (CSA) [61], grasshopper optimization algorithm (GOA) [62], harris hawks optimization (HHO) [63], whale optimization algorithm (WOA) [64], dandelion optimizer (DO) [65] and fire hawks optimization (FHO) [66] using 29 CEC2017 benchmark functions [67]. All experiments were calculated with an average of 30 runs using Matlab version 2021b on a 64bit system with Core i7 and 8 GB RAM. Table 1 shows the parameter settings of the experiment, whereas Table 2 shows the parameter settings of the compared algorithms.

Table 1. Experiment parameter settings.

No.	Parameter Name	Value
1	Population Size	30
2	Dim	30
3	Max number of iteration	500

Table 2. Meta-heuristic algorithms parameter settings.

Alg.	Parameter	Value
ErWCA	$N_{sr}$	$0.01$
	$d_{max}$	4
WCA	$N_{sr}$	$0.01$
	$d_{max}$	4
BOA	c	0.01
	a	[0.1, 0.3]
	p	0.8
BSA	mix-rate	1.0
	F	$3\times rand$
CSA	$Ap$	0.1
	$fl$	0.2
GOA	$c_{max}$	1
	$c_{min}$	0.00004
HHO	$E_0$	$[-1,1]$
WOA	a	$[2,0]$
	$a_2$	[−1, −2]
DO	$\alpha$	$[0,1]$
	k	[0, 1]

Table 3 gives the results of the algorithms in terms of average and standard deviation.

Table 3. The comparison results of all algorithms over 29 functions using Dim = 30 CEC 2017.

Fun		EErWCA	ErWCA	WCA	BOA	BSA	CSA	GOA	HHO	WOA	DO	FHO
F1	min	$2.17\times {10}^6$	$1.02\times {10}^6$	$1.61\times {10}^6$	$2.09\times {10}^{10}$	$2.23\times {10}^{10}$	$3.77\times {10}^6$	$4.49\times {10}^{10}$	$1.19\times {10}^7$	$3.2\times {10}^8$	$8.05\times {10}^6$	$7.11\times {10}^9$
	max	$5.49\times {10}^6$	$2.09\times {10}^4$	$2.09\times {10}^4$	$5.43\times {10}^{10}$	$5.64\times {10}^{10}$	$4.35\times {10}^7$	$1.13\times {10}^{11}$	$2.74\times {10}^7$	$4.71\times {10}^9$	$3.07\times {10}^5$	$3.39\times {10}^6$
	mean	$2.12\times {10}^5$	$5.01\times {10}^6$	$7.55\times {10}^6$	$3.86\times {10}^{10}$	$4.19\times {10}^{10}$	$1.39\times {10}^7$	$6.75\times {10}^{10}$	$1.72\times {10}^7$	$1.64\times {10}^6$	$8.39\times {10}^4$	$1.39\times {10}^{10}$
	std	$1.01\times {10}^6$	$5.95\times {10}^6$	$7.43\times {10}^3$	$9.19\times {10}^6$	$9.01\times {10}^6$	$8.31\times {10}^6$	$1.52\times {10}^{10}$	$3.88\times {10}^6$	$1.05\times {10}^9$	$8.25\times {10}^4$	$6.31\times {10}^9$
	rank	4	1	2	9	10	5	11	6	7	3	8
F3	min	$3.69\times {10}^4$	$3.28\times {10}^2$	$5.61\times {10}^2$	$3.87\times {10}^4$	$6.17\times {10}^4$	$1.45\times {10}^4$	$8.02\times {10}^4$	$1.54\times {10}^4$	$1.51\times {10}^5$	$3.21\times {10}^2$	$3.02\times {10}^4$
	max	$7.37\times {10}^4$	$2.11\times {10}^4$	$8.26\times {10}^4$	$9.62\times {10}^4$	$3.82\times {10}^4$	$7.24\times {10}^5$	$4.14\times {10}^4$	$4.55\times {10}^5$	$5.99\times {10}^3$	$6.99\times {10}^4$	$6.99\times {10}^4$
	mean	$5.89\times {10}^4$	$4.85\times {10}^6$	$6.16\times {10}^6$	$6.86\times {10}^4$	$8.70\times {10}^4$	$2.28\times {10}^4$	$2.70\times {10}^5$	$2.69\times {10}^4$	$2.56\times {10}^5$	$1.68\times {10}^6$	$5.04\times {10}^4$
	std	$8.70\times {10}^6$	$5.34\times {10}^6$	$5.15\times {10}^6$	$1.03\times {10}^4$	$7.81\times {10}^6$	$5.38\times {10}^6$	$1.31\times {10}^5$	$6.65\times {10}^6$	$7.49\times {10}^4$	$1.54\times {10}^6$	$8.13\times {10}^3$
	rank	7	2	3	8	9	4	11	5	10	1	6
F4	min	$4.23\times {10}^6$	$4.00\times {10}^6$	$4.68\times {10}^6$	$1.02\times {10}^4$	$3.58\times {10}^6$	$4.92\times {10}^6$	$4.41\times {10}^6$	$4.88\times {10}^6$	$6.30\times {10}^6$	$4.06\times {10}^6$	$1.13\times {10}^6$
	max	$5.51\times {10}^6$	$5.38\times {10}^6$	$5.33\times {10}^6$	$2.32\times {10}^4$	$1.74\times {10}^4$	$6.48\times {10}^6$	$2.23\times {10}^4$	$6.34\times {10}^6$	$1.20\times {10}^6$	$5.55\times {10}^6$	$1.85\times {10}^6$
	mean	$5.00\times {10}^6$	$4.86\times {10}^6$	$4.92\times {10}^6$	$1.58\times {10}^4$	$1.13\times {10}^4$	$5.72\times {10}^6$	$1.15\times {10}^4$	$5.49\times {10}^6$	$8.58\times {10}^6$	$5.03\times {10}^6$	$1.41\times {10}^6$
	std	$2.51\times {10}^6$	$3.22\times {10}^6$	$1.87\times {10}^6$	$3.31\times {10}^6$	$3.44\times {10}^3$	$3.66\times {10}^5$	$4.37\times {10}^6$	$3.43\times {10}^6$	$1.58\times {10}^6$	$3.01\times {10}^6$	$1.70\times {10}^6$
	rank	3	1	2	11	9	6	10	5	7	4	8
F5	min	$5.53\times {10}^6$	$6.10\times {10}^2$	$6.29\times {10}^6$	$8.42\times {10}^6$	$7.78\times {10}^6$	$6.18\times {10}^6$	$8.50\times {10}^6$	666.12	$7.17\times {10}^6$	$6.14\times {10}^6$	$6.94\times {10}^6$
	max	$6.28\times {10}^6$	$7.77\times {10}^6$	$8.59\times {10}^6$	$9.40\times {10}^6$	$9.93\times {10}^6$	$7.44\times {10}^6$	$1.12\times {10}^6$	$8.34\times {10}^6$	$9.60\times {10}^6$	$7.54\times {10}^6$	$7.54\times {10}^6$
	mean	$5.84\times {10}^6$	$6.96\times {10}^6$	$7.44\times {10}^6$	$8.89\times {10}^6$	$8.83\times {10}^5$	$6.68\times {10}^6$	$9.66\times {10}^6$	$7.36\times {10}^6$	$8.40\times {10}^6$	$6.68\times {10}^6$	$7.28\times {10}^6$
	std	$2.10\times {10}^6$	$4.58\times {10}^6$	$5.31\times {10}^6$	$2.34\times {10}^4$	$5.37\times {10}^6$	$2.91\times {10}^5$	$6.44\times {10}^6$	$4.14\times {10}^6$	$6.26\times {10}^6$	$3.44\times {10}^6$	$1.35\times {10}^6$
	rank	1	4	7	10	9	2	11	6	8	3	5
F6	min	$6.00\times {10}^6$	$6.26\times {10}^6$	$6.37\times {10}^6$	$6.63\times {10}^6$	$6.71\times {10}^6$	$6.34\times {10}^6$	$6.77\times {10}^6$	$6.51\times {10}^6$	$6.62\times {10}^5$	$6.24\times {10}^6$	$6.30\times {10}^6$
	max	$6.00\times {10}^6$	$6.73\times {10}^6$	$6.79\times {10}^6$	$6.88\times {10}^6$	$7.01\times {10}^6$	$6.66\times {10}^6$	$7.33\times {10}^6$	$6.75\times {10}^6$	$7.02\times {10}^6$	$6.64\times {10}^6$	$6.41\times {10}^6$
	mean	$6.00\times {10}^6$	$6.49\times {10}^6$	$6.59\times {10}^6$	$6.75\times {10}^6$	$6.84\times {10}^6$	$6.50\times {10}^6$	$7.08\times {10}^6$	$6.63\times {10}^6$	$6.79\times {10}^6$	$6.40\times {10}^6$	$6.36\times {10}^6$
	std	$7.08\times {10}^4$	$1.13\times {10}^6$	$1.17\times {10}^6$	$6.80\times {10}^5$	$7.40\times {10}^6$	$7.96\times {10}^6$	$1.57\times {10}^6$	$5.40\times {10}^5$	$1.10\times {10}^6$	$9.38\times {10}^6$	$2.68\times {10}^6$
	rank	1	4	6	8	10	5	11	7	9	3	2
F7	min	$7.67\times {10}^6$	$9.30\times {10}^6$	$9.42\times {10}^6$	$1.26\times {10}^6$	$1.32\times {10}^6$	$8.49\times {10}^6$	$1.40\times {10}^6$	$1.06\times {10}^6$	$1.09\times {10}^6$	$8.75\times {10}^6$	$1.06\times {10}^6$
	max	$8.71\times {10}^5$	$1.37\times {10}^6$	$1.55\times {10}^6$	$1.42\times {10}^6$	$1.57\times {10}^6$	$1.06\times {10}^6$	$3.15\times {10}^6$	$1.40\times {10}^6$	$1.40\times {10}^6$	$1.15\times {10}^3$	$1.35\times {10}^6$
	mean	$8.24\times {10}^6$	$1.10\times {10}^6$	$1.20\times {10}^3$	$1.35\times {10}^3$	$1.44\times {10}^6$	$9.38\times {10}^6$	$1.85\times {10}^6$	$1.27\times {10}^6$	$1.27\times {10}^6$	$1.02\times {10}^6$	$1.22\times {10}^6$
	std	$2.50\times {10}^6$	$1.08\times {10}^6$	$1.46\times {10}^6$	$3.29\times {10}^6$	$6.68\times {10}^6$	$6.13\times {10}^5$	$3.38\times {10}^6$	$7.18\times {10}^6$	$8.43\times {10}^6$	$7.30\times {10}^6$	$7.71\times {10}^6$
	rank	1	4	5	9	10	2	11	8	7	3	6
F8	min	$8.47\times {10}^6$	$9.03\times {10}^6$	$9.37\times {10}^6$	$1.08\times {10}^6$	$1.05\times {10}^6$	$8.92\times {10}^6$	1139.73	$9.22\times {10}^6$	$9.51\times {10}^5$	$8.57\times {10}^6$	$1.00\times {10}^7$
	max	$9.23\times {10}^6$	$1.07\times {10}^3$	$1.08\times {10}^6$	$1.17\times {10}^6$	$1.19\times {10}^6$	$9.71\times {10}^6$	$1.32\times {10}^6$	$1.03\times {10}^6$	$1.19\times {10}^6$	$1.01\times {10}^6$	$1.05\times {10}^6$
	mean	$8.82\times {10}^6$	$9.80\times {10}^6$	$9.91\times {10}^6$	$1.12\times {10}^6$	$1.12\times {10}^6$	$9.25\times {10}^6$	$1.22\times {10}^6$	$9.75\times {10}^6$	$1.04\times {10}^6$	$9.42\times {10}^6$	$1.02\times {10}^6$
	std	$1.77\times {10}^6$	$4.10\times {10}^6$	$3.85\times {10}^6$	$1.96\times {10}^6$	$3.74\times {10}^6$	$1.53\times {10}^6$	$4.62\times {10}^6$	$2.08\times {10}^6$	$5.29\times {10}^6$	$4.09\times {10}^6$	$1.06\times {10}^6$
	rank	1	5	6	9	1	2	1	4	8	3	7
F9	min	$9.50\times {10}^6$	$3.24\times {10}^6$	$3.43\times {10}^6$	$6.84\times {10}^6$	$6.57\times {10}^6$	$1.41\times {10}^6$	$9.95\times {10}^6$	$5.76\times {10}^6$	$6.11\times {10}^6$	$2.78\times {10}^6$	$2.24\times {10}^6$
	max	$3.69\times {10}^6$	$1.18\times {10}^4$	$9.13\times {10}^3$	$1.19\times {10}^4$	$1.26\times {10}^4$	$5.04\times {10}^3$	$3.60\times {10}^4$	$9.71\times {10}^3$	$1.82\times {10}^4$	$1.41\times {10}^4$	$7.32\times {10}^3$
	mean	$1.40\times {10}^6$	$5.47\times {10}^6$	$6.21\times {10}^6$	$9.69\times {10}^6$	$9.29\times {10}^6$	$2.84\times {10}^6$	$2.16\times {10}^4$	$7.81\times {10}^6$	$1.02\times {10}^4$	$4.63\times {10}^6$	$4.22\times {10}^6$
	std	$5.31\times {10}^6$	$1.73\times {10}^6$	$1.37\times {10}^6$	$1.22\times {10}^6$	$1.80\times {10}^6$	$9.21\times {10}^6$	$6.00\times {10}^6$	$7.34\times {10}^6$	$2.67\times {10}^6$	$2.09\times {10}^6$	$1.09\times {10}^6$
	rank	1	5	6	9	8	2	11	7	10	4	3
F10	min	$3.36\times {10}^6$	$3.42\times {10}^6$	$4.17\times {10}^6$	$8.31\times {10}^3$	$6.31\times {10}^6$	$3.31\times {10}^6$	$7.87\times {10}^6$	$4.65\times {10}^6$	$5.71\times {10}^6$	$3.70\times {10}^6$	$7.46\times {10}^6$
	max	$6.68\times {10}^6$	$6.63\times {10}^6$	$7.82\times {10}^6$	$9.25\times {10}^6$	$9.27\times {10}^6$	$5.86\times {10}^3$	$1.00\times {10}^4$	$7.10\times {10}^6$	$8.85\times {10}^6$	$6.46\times {10}^6$	$9.48\times {10}^6$
	mean	$4.42\times {10}^6$	$5.58\times {10}^6$	$5.97\times {10}^6$	$8.76\times {10}^6$	$8.05\times {10}^6$	$4.84\times {10}^6$	$8.73\times {10}^6$	$5.71\times {10}^6$	$7.23\times {10}^6$	$4.90\times {10}^6$	$8.46\times {10}^6$
	std	$7.17\times {10}^6$	$7.12\times {10}^2$	$8.18\times {10}^6$	$2.29\times {10}^6$	$7.44\times {10}^6$	$5.66\times {10}^6$	$5.05\times {10}^6$	$6.69\times {10}^6$	$7.77\times {10}^6$	$7.08\times {10}^6$	$4.82\times {10}^6$
	rank	1	4	6	11	8	2	10	5	7	3	9
F11	min	$1.14\times {10}^6$	$1.19\times {10}^6$	$1.21\times {10}^6$	$3.44\times {10}^3$	$3.43\times {10}^3$	$1.19\times {10}^6$	$7.99\times {10}^6$	$1.17\times {10}^6$	$1.86\times {10}^3$	$1.15\times {10}^6$	$2.02\times {10}^6$
	max	$1.36\times {10}^6$	$1.60\times {10}^6$	$1.59\times {10}^6$	$8.67\times {10}^6$	$1.41\times {10}^3$	$1.41\times {10}^6$	$4.92\times {10}^4$	$1.36\times {10}^6$	$1.20\times {10}^4$	$1.34\times {10}^6$	$3.46\times {10}^6$
	mean	$1.21\times {10}^6$	$1.34\times {10}^6$	$1.35\times {10}^6$	$5.59\times {10}^6$	$8.40\times {10}^6$	$1.31\times {10}^3$	$2.31\times {10}^4$	$1.28\times {10}^6$	$6.07\times {10}^6$	$1.23\times {10}^3$	$2.77\times {10}^6$
	std	$4.30\times {10}^6$	$9.54\times {10}^6$	$8.04\times {10}^6$	$1.19\times {10}^3$	$2.70\times {10}^6$	$5.03\times {10}^6$	$1.11\times {10}^4$	$4.74\times {10}^6$	$2.58\times {10}^6$	$5.29\times {10}^6$	$3.98\times {10}^6$
	rank	1	5	6	8	10	4	11	3	9	2	7
F12	min	$8.29\times {10}^4$	$1.40\times {10}^5$	$1.28\times {10}^5$	$2.69\times {10}^9$	$2.44\times {10}^9$	$5.09\times {10}^5$	$2.44\times {10}^9$	$3.29\times {10}^6$	$5.56\times {10}^7$	$1.40\times {10}^5$	$6.36\times {10}^8$
	max	$3.80\times {10}^6$	$2.60\times {10}^6$	$4.05\times {10}^6$	$1.35\times {10}^{10}$	$1.73\times {10}^{10}$	$2.00\times {10}^8$	$1.68\times {10}^{10}$	$5.62\times {10}^7$	$9.38\times {10}^8$	$1.16\times {10}^7$	$1.41\times {10}^9$
	mean	$1.32\times {10}^6$	$6.36\times {10}^5$	$1.03\times {10}^6$	$7.83\times {10}^9$	$6.98\times {10}^9$	$5.16\times {10}^7$	$7.91\times {10}^9$	$1.98\times {10}^7$	$3.03\times {10}^8$	$4.47\times {10}^6$	$9.32\times {10}^8$
	std	$9.22\times {10}^5$	$6.40\times {10}^5$	$9.85\times {10}^5$	$2.22\times {10}^9$	$4.07\times {10}^9$	$5.01\times {10}^7$	$3.39\times {10}^9$	$1.27\times {10}^7$	$2.03\times {10}^8$	$2.85\times {10}^6$	$1.77\times {10}^8$
	rank	3	1	2	10	9	6	11	5	7	4	8
F13	min	$1.40\times {10}^6$	$4.11\times {10}^6$	$5.87\times {10}^6$	$3.5\times {10}^8$	$2.27\times {10}^8$	$2.46\times {10}^4$	$6.25\times {10}^8$	$8.71\times {10}^4$	$2.44\times {10}^5$	$2.32\times {10}^4$	$8.07\times {10}^7$
	max	$5.64\times {10}^4$	$1.68\times {10}^5$	$1.37\times {10}^5$	$1.25\times {10}^{10}$	$1.00\times {10}^{10}$	$2.38\times {10}^5$	$2.16\times {10}^{10}$	$7.41\times {10}^5$	$6.82\times {10}^6$	$3.30\times {10}^5$	$4.59\times {10}^8$
	mean	$1.10\times {10}^4$	$3.30\times {10}^4$	$3.25\times {10}^4$	$4.59\times {10}^9$	$3.18\times {10}^9$	$6.77\times {10}^4$	$7.24\times {10}^9$	$4.01\times {10}^5$	$1.80\times {10}^6$	$1.08\times {10}^5$	$3.03\times {10}^8$
	std	$1.23\times {10}^4$	$3.16\times {10}^4$	$2.97\times {10}^4$	$3.54\times {10}^9$	$3.1\times {10}^9$	$4.94\times {10}^4$	$6.31\times {10}^9$	$1.41\times {10}^5$	$1.83\times {10}^6$	$7.01\times {10}^4$	$6.96\times {10}^7$
	rank	1	3	2	10	9	4	11	6	7	5	8
F14	min	$3.56\times {10}^6$	$1.69\times {10}^6$	$2.02\times {10}^6$	$6.32\times {10}^4$	$4.85\times {10}^4$	$1.62\times {10}^6$	$2.50\times {10}^5$	$3.64\times {10}^4$	$6.45\times {10}^4$	$1.75\times {10}^6$	$1.24\times {10}^5$
	max	$8.31\times {10}^4$	$1.97\times {10}^5$	$1.70\times {10}^5$	$2.03\times {10}^6$	$6.09\times {10}^6$	$6.41\times {10}^4$	$4.47\times {10}^7$	$1.55\times {10}^6$	$8.64\times {10}^6$	$9.09\times {10}^4$	$2.03\times {10}^6$
	mean	$3.15\times {10}^4$	$2.47\times {10}^4$	$2.43\times {10}^4$	$6.89\times {10}^5$	$1.04\times {10}^6$	$9.88\times {10}^6$	$8.67\times {10}^6$	$3.63\times {10}^5$	$2.28\times {10}^6$	$3.64\times {10}^4$	$6.54\times {10}^5$
	std	$2.39\times {10}^4$	$4.47\times {10}^4$	$4.05\times {10}^4$	$5.11\times {10}^5$	$1.25\times {10}^6$	$1.36\times {10}^4$	$1.04\times {10}^7$	$3.97\times {10}^5$	$2.22\times {10}^6$	$2.58\times {10}^4$	$4.74\times {10}^5$
	rank	4	3	2	8	9	1	11	6	10	5	7
F15	min	$1.52\times {10}^6$	$1.70\times {10}^6$	$2.07\times {10}^6$	$4.87\times {10}^6$	$5.90\times {10}^5$	$6.34\times {10}^6$	$1.27\times {10}^8$	$1.24\times {10}^4$	$7.82\times {10}^4$	$8.01\times {10}^6$	$3.01\times {10}^6$
	max	$3.10\times {10}^4$	$4.35\times {10}^4$	$7.34\times {10}^4$	$2.73\times {10}^8$	$6.79\times {10}^8$	$6.95\times {10}^4$	$3.41\times {10}^9$	$1.40\times {10}^5$	$1.59\times {10}^7$	$8.03\times {10}^4$	$3.30\times {10}^7$
	mean	$7.60\times {10}^6$	$8.15\times {10}^6$	$1.44\times {10}^4$	$5.50\times {10}^7$	$1.34\times {10}^8$	$2.04\times {10}^4$	$9.46\times {10}^8$	$6.37\times {10}^4$	$1.42\times {10}^6$	$3.45\times {10}^4$	$1.72\times {10}^7$
	std	$7.42\times {10}^6$	$9.97\times {10}^6$	$1.72\times {10}^4$	$6.60\times {10}^7$	$1.83\times {10}^8$	$1.54\times {10}^4$	$8.71\times {10}^8$	$2.97\times {10}^4$	$2.99\times {10}^6$	$2.20\times {10}^4$	$7.58\times {10}^6$
	rank	1	2	3	9	10	4	11	6	7	5	8
F16	min	$2.08\times {10}^6$	$2.32\times {10}^6$	$2.20\times {10}^6$	$4.31\times {10}^3$	$4.03\times {10}^6$	$2.40\times {10}^6$	$3.63\times {10}^6$	$2.50\times {10}^6$	$2.93\times {10}^6$	$2.15\times {10}^6$	$2.87\times {10}^6$
	max	$3.02\times {10}^6$	$3.66\times {10}^6$	$3.68\times {10}^6$	$7.30\times {10}^6$	$8.59\times {10}^6$	$3.73\times {10}^6$	$6.99\times {10}^6$	$3.84\times {10}^6$	$5.74\times {10}^6$	$3.40\times {10}^6$	$4.06\times {10}^3$
	mean	$2.43\times {10}^3$	$2.93\times {10}^6$	$2.92\times {10}^6$	$5.90\times {10}^6$	$5.37\times {10}^6$	$3.14\times {10}^6$	$5.00\times {10}^6$	$3.26\times {10}^6$	$4.23\times {10}^6$	$2.73\times {10}^6$	$3.53\times {10}^6$
	std	$2.42\times {10}^6$	$3.32\times {10}^6$	$3.30\times {10}^6$	$6.88\times {10}^6$	$1.13\times {10}^6$	$3.64\times {10}^6$	$7.66\times {10}^6$	$3.80\times {10}^6$	$6.28\times {10}^6$	$2.76\times {10}^6$	$3.38\times {10}^6$
	rank	1	4	3	11	10	5	9	6	8	2	7
F17	min	$1.74\times {10}^6$	$1.95\times {10}^3$	$2.04\times {10}^6$	$2.63\times {10}^6$	$2.43\times {10}^6$	$1.91\times {10}^6$	$3.00\times {10}^6$	$1.82\times {10}^6$	$2.17\times {10}^6$	$1.90\times {10}^6$	$2.17\times {10}^6$
	max	$2.14\times {10}^6$	$2.74\times {10}^6$	$2.98\times {10}^6$	$1.05\times {10}^4$	$5.09\times {10}^6$	$2.93\times {10}^6$	$4.92\times {10}^6$	$3.34\times {10}^6$	$3.73\times {10}^6$	$2.64\times {10}^6$	$2.58\times {10}^6$
	mean	$1.88\times {10}^6$	$2.39\times {10}^6$	$2.47\times {10}^6$	$4.62\times {10}^6$	$3.25\times {10}^6$	$2.34\times {10}^6$	$3.78\times {10}^6$	$2.61\times {10}^6$	$2.75\times {10}^6$	$2.27\times {10}^3$	$2.39\times {10}^6$
	std	$1.22\times {10}^6$	$2.17\times {10}^6$	$2.00\times {10}^5$	$1.88\times {10}^6$	$5.83\times {10}^6$	$2.52\times {10}^6$	$4.09\times {10}^6$	$3.57\times {10}^6$	$3.16\times {10}^6$	$2.03\times {10}^6$	$1.09\times {10}^6$
	rank	1	4	6	11	9	3	10	7	8	2	5
F18	min	$1.39\times {10}^4$	$1.48\times {10}^4$	$1.74\times {10}^4$	$8.30\times {10}^5$	$2.34\times {10}^5$	$2.69\times {10}^4$	$1.01\times {10}^7$	$1.71\times {10}^5$	$1.99\times {10}^5$	$9.22\times {10}^4$	$1.28\times {10}^6$
	max	$1.78\times {10}^6$	$1.70\times {10}^6$	$2.11\times {10}^6$	$5.06\times {10}^7$	$1.13\times {10}^8$	$3.49\times {10}^5$	$4.24\times {10}^8$	$1.33\times {10}^7$	$4.41\times {10}^7$	$2.03\times {10}^6$	$4.01\times {10}^7$
	mean	$4.04\times {10}^5$	$1.98\times {10}^5$	$3.45\times {10}^5$	$8.70\times {10}^6$	$1.87\times {10}^7$	$1.10\times {10}^5$	$1.01\times {10}^8$	$2.59\times {10}^6$	$1.03\times {10}^7$	$5.76\times {10}^5$	$7.49\times {10}^6$
	std	$4.04\times {10}^5$	$3.07\times {10}^5$	$4.43\times {10}^5$	$9.97\times {10}^6$	$2.96\times {10}^7$	$7.93\times {10}^4$	$1.08\times {10}^8$	$3.19\times {10}^6$	$1.07\times {10}^7$	$4.41\times {10}^5$	$8.88\times {10}^6$
	rank	4	2	3	8	10	1	11	6	9	5	7
F19	min	$1.93\times {10}^6$	$2.25\times {10}^6$	$2.32\times {10}^6$	$2.12\times {10}^6$	$5.77\times {10}^6$	$6.07\times {10}^6$	$2.31\times {10}^8$	$3.17\times {10}^4$	$1.38\times {10}^5$	$7.76\times {10}^6$	$4.56\times {10}^6$
	max	$1.43\times {10}^4$	$2.86\times {10}^4$	$1.30\times {10}^5$	$3.49\times {10}^8$	$1.06\times {10}^9$	$1.38\times {10}^6$	$2.51\times {10}^9$	$2.47\times {10}^6$	$5.71\times {10}^7$	$1.89\times {10}^5$	$4.85\times {10}^7$
	mean	$4.81\times {10}^6$	$8.64\times {10}^6$	$1.31\times {10}^4$	$8.07\times {10}^7$	$1.96\times {10}^8$	$2.34\times {10}^5$	$1.13\times {10}^9$	$5.87\times {10}^5$	$1.75\times {10}^7$	$6.03\times {10}^4$	$2.50\times {10}^7$
	std	$3.26\times {10}^6$	$6.61\times {10}^6$	$2.49\times {10}^4$	$9.10\times {10}^7$	$2.39\times {10}^8$	$3.25\times {10}^5$	$6.82\times {10}^8$	$4.90\times {10}^5$	$1.53\times {10}^7$	$5.10\times {10}^4$	$1.15\times {10}^7$
	rank	1	2	3	9	10	5	11	6	7	4	8
F20	min	$2.04\times {10}^6$	$2.35\times {10}^6$	$2.27\times {10}^6$	$2.68\times {10}^6$	$2.64\times {10}^6$	$2.32\times {10}^6$	$2.84\times {10}^6$	$2.38\times {10}^6$	$2.36\times {10}^6$	$2.27\times {10}^6$	$2.52\times {10}^6$
	max	$2.54\times {10}^6$	$3.45\times {10}^6$	$3.18\times {10}^6$	$3.20\times {10}^6$	$3.54\times {10}^6$	$2.95\times {10}^6$	$3.57\times {10}^6$	$3.15\times {10}^3$	$3.14\times {10}^6$	$3.05\times {10}^6$	$3.12\times {10}^6$
	mean	$2.26\times {10}^6$	$2.79\times {10}^6$	$2.78\times {10}^6$	$2.96\times {10}^6$	$3.01\times {10}^6$	$2.55\times {10}^6$	$3.23\times {10}^6$	$2.72\times {10}^6$	$2.83\times {10}^3$	$2.57\times {10}^6$	$2.81\times {10}^3$
	std	$1.35\times {10}^6$	$2.59\times {10}^6$	$2.47\times {10}^6$	$1.19\times {10}^6$	$2.39\times {10}^6$	$2.03\times {10}^6$	$1.96\times {10}^6$	$2.25\times {10}^5$	$2.09\times {10}^6$	$2.01\times {10}^5$	$1.90\times {10}^6$
	rank	1	6	5	9	10	2	11	4	8	3	7
F21	min	$2.34\times {10}^6$	$2.38\times {10}^3$	$2.43\times {10}^6$	$2.27\times {10}^6$	$2.54\times {10}^6$	$2.42\times {10}^6$	$2.64\times {10}^6$	$2.48\times {10}^6$	$2.49\times {10}^6$	$2.40\times {10}^6$	$2.50\times {10}^6$
	max	$2.41\times {10}^6$	$2590.13$	$2.73\times {10}^6$	$2.73\times {10}^6$	$2.86\times {10}^6$	$2.55\times {10}^6$	$2.90\times {10}^6$	$2.64\times {10}^6$	$2.71\times {10}^6$	$2.58\times {10}^6$	$2.55\times {10}^6$
	mean	$2.38\times {10}^6$	$2.49\times {10}^6$	$2.50\times {10}^6$	$2.50\times {10}^6$	$2.71\times {10}^6$	$2.48\times {10}^3$	$2.75\times {10}^6$	$2.56\times {10}^6$	$2.61\times {10}^6$	$2.46\times {10}^6$	$2.53\times {10}^6$
	std	$1.52\times {10}^6$	$5.16\times {10}^6$	$5.78\times {10}^6$	$1.40\times {10}^6$	$8.02\times {10}^6$	$3.98\times {10}^6$	$6.51\times {10}^6$	$4.80\times {10}^6$	$4.52\times {10}^5$	$4.44\times {10}^6$	$1.28\times {10}^6$
	rank	1	4	6	5	10	3	11	8	9	2	7
F22	min	$2.30\times {10}^6$	$2.30\times {10}^3$	$2.30\times {10}^3$	$3.19\times {10}^6$	$6.48\times {10}^6$	$2.32\times {10}^6$	$7.26\times {10}^3$	$2.33\times {10}^6$	$2.69\times {10}^6$	$2.30\times {10}^6$	$3.32\times {10}^6$
	max	$2.30\times {10}^6$	$9.31\times {10}^6$	$9.30\times {10}^6$	$6.52\times {10}^6$	$1.04\times {10}^4$	$6.54\times {10}^6$	$1.15\times {10}^4$	$8.49\times {10}^3$	$1.02\times {10}^4$	$8.91\times {10}^6$	$9.95\times {10}^6$
	mean	$2.30\times {10}^6$	$5.53\times {10}^6$	$6.15\times {10}^6$	$4.34\times {10}^6$	$8.98\times {10}^6$	$2.51\times {10}^6$	$1.01\times {10}^4$	$7.13\times {10}^6$	$7.56\times {10}^6$	$5.85\times {10}^6$	$4.43\times {10}^6$
	std	$1.38\times {10}^6$	$2.12\times {10}^6$	$1.90\times {10}^6$	$8.04\times {10}^5$	$9.29\times {10}^6$	$7.63\times {10}^6$	$9.31\times {10}^6$	$1.40\times {10}^6$	$2.36\times {10}^6$	$1.96\times {10}^6$	$1.95\times {10}^6$
	rank	1	5	7	3	10	2	11	8	9	6	4
F23	min	$2.69\times {10}^6$	$2.76\times {10}^6$	$2.82\times {10}^6$	$2.81\times {10}^6$	$3.12\times {10}^6$	$2.89\times {10}^6$	$3.00\times {10}^3$	$2.91\times {10}^3$	$2.93\times {10}^6$	$2.74\times {10}^6$	$2.74\times {10}^3$
	max	$2.80\times {10}^6$	$3.02\times {10}^3$	$3.22\times {10}^3$	$3.45\times {10}^6$	$3.80\times {10}^6$	$3.26\times {10}^6$	$3.60\times {10}^6$	$3.49\times {10}^6$	$3.34\times {10}^3$	$3.03\times {10}^6$	$3.33\times {10}^3$
	mean	$2.74\times {10}^6$	$2.87\times {10}^3$	$2.98\times {10}^6$	$3.20\times {10}^6$	$3.51\times {10}^6$	$3.08\times {10}^6$	$3.22\times {10}^6$	$3.21\times {10}^6$	$3.13\times {10}^6$	$2.89\times {10}^6$	$2.94\times {10}^6$
	std	$2.93\times {10}^6$	$5.65\times {10}^6$	$9.54\times {10}^6$	$1.44\times {10}^6$	$1.76\times {10}^6$	$9.68\times {10}^6$	$1.58\times {10}^6$	$1.43\times {10}^6$	$1.06\times {10}^6$	$5.93\times {10}^6$	$9.20\times {10}^6$
	rank	1	2	5	8	11	6	10	9	7	3	4
F24	min	$2.88\times {10}^6$	$2.91\times {10}^6$	$2.94\times {10}^6$	$3.39\times {10}^6$	$3.28\times {10}^6$	$3.00\times {10}^6$	$3.14\times {10}^6$	$3.09\times {10}^6$	$3.08\times {10}^6$	$2.94\times {10}^6$	$2.94\times {10}^3$
	max	$3.05\times {10}^6$	$3.33\times {10}^6$	$3.51\times {10}^6$	$4.27\times {10}^6$	$4.00\times {10}^6$	$3.46\times {10}^6$	$3.64\times {10}^6$	$3.68\times {10}^6$	$3.43\times {10}^6$	$3.18\times {10}^6$	$3.33\times {10}^3$
	mean	$2.93\times {10}^6$	$3.04\times {10}^6$	$3.16\times {10}^6$	$3.80\times {10}^6$	$3.65\times {10}^6$	$3.23\times {10}^6$	$3.30\times {10}^6$	$3.40\times {10}^6$	$3.23\times {10}^6$	$3.06\times {10}^6$	$2.94\times {10}^6$
	std	$3.44\times {10}^6$	$8.93\times {10}^6$	$1.48\times {10}^6$	$2.16\times {10}^6$	$1.63\times {10}^6$	$1.08\times {10}^6$	$1.49\times {10}^6$	$1.36\times {10}^6$	$9.87\times {10}^6$	$7.35\times {10}^6$	$9.20\times {10}^6$
	rank	1	3	5	11	10	7	8	9	6	4	2
F25	min	$2.88\times {10}^6$	$2.88\times {10}^6$	$2.94\times {10}^6$	$3.39\times {10}^6$	$3.28\times {10}^6$	$3.00\times {10}^6$	$3.14\times {10}^6$	$3.09\times {10}^6$	$3.08\times {10}^6$	$2.94\times {10}^6$	$2.87\times {10}^3$
	max	$2.94\times {10}^6$	$2.94\times {10}^6$	$3.51\times {10}^6$	$4.27\times {10}^6$	$4.00\times {10}^6$	$3.46\times {10}^6$	$3.64\times {10}^6$	$3.68\times {10}^6$	$3.43\times {10}^6$	$3.18\times {10}^6$	$3.33\times {10}^3$
	mean	$2.90\times {10}^6$	$2.90\times {10}^6$	$3.16\times {10}^6$	$3.80\times {10}^6$	$3.65\times {10}^6$	$3.23\times {10}^6$	$3.30\times {10}^6$	$3.40\times {10}^6$	$3.23\times {10}^6$	$3.06\times {10}^6$	$2.94\times {10}^6$
	std	$1.76\times {10}^6$	$1.62\times {10}^6$	$1.48\times {10}^6$	$2.16\times {10}^6$	$1.63\times {10}^6$	$1.08\times {10}^6$	$1.49\times {10}^6$	$1.36\times {10}^6$	$9.87\times {10}^6$	$7.35\times {10}^6$	$9.20\times {10}^6$
	rank	2	1	5	11	10	7	8	9	6	4	3
F26	min	$2.97\times {10}^3$	$2.80\times {10}^3$	$2.94\times {10}^6$	$3.39\times {10}^6$	$3.28\times {10}^6$	$3.00\times {10}^6$	$3.14\times {10}^6$	$3.09\times {10}^6$	$3.08\times {10}^6$	$2.94\times {10}^6$	$2.87\times {10}^3$
	max	$5.25\times {10}^6$	$7.90\times {10}^6$	$3.51\times {10}^6$	$4.27\times {10}^6$	$4.00\times {10}^6$	$3.46\times {10}^6$	$3.64\times {10}^6$	$3.68\times {10}^6$	$3.43\times {10}^6$	$3.18\times {10}^6$	$3.33\times {10}^3$
	mean	$4.73\times {10}^6$	$6.20\times {10}^6$	$3.16\times {10}^6$	$3.80\times {10}^6$	$3.65\times {10}^6$	$3.23\times {10}^6$	$3.30\times {10}^6$	$3.40\times {10}^6$	$3.23\times {10}^6$	$3.06\times {10}^6$	$2.94\times {10}^6$
	std	$4.04\times {10}^6$	$1.16\times {10}^6$	$1.48\times {10}^6$	$2.16\times {10}^6$	$1.63\times {10}^6$	$1.08\times {10}^6$	$1.49\times {10}^6$	$1.36\times {10}^6$	$9.87\times {10}^6$	$7.35\times {10}^6$	$9.20\times {10}^6$
	rank	10	11	3	9	8	5	6	7	4	2	1
F27	min	$3.20\times {10}^6$	$3.22\times {10}^3$	$3.23\times {10}^6$	$3.56\times {10}^6$	$3.48\times {10}^6$	$3.39\times {10}^6$	$3.31\times {10}^6$	$3.24\times {10}^6$	$3.32\times {10}^6$	$3.22\times {10}^6$	$3.36\times {10}^6$
	max	$3.25\times {10}^6$	$3.36\times {10}^6$	$3.53\times {10}^6$	$4.03\times {10}^6$	$5.73\times {10}^6$	$4.06\times {10}^6$	$4.50\times {10}^6$	$3.79\times {10}^6$	$3.83\times {10}^6$	$3.41\times {10}^6$	$3.76\times {10}^6$
	mean	$3.22\times {10}^3$	$3.27\times {10}^6$	$3.31\times {10}^6$	$3.79\times {10}^6$	$4.15\times {10}^6$	$3.67\times {10}^6$	$3.66\times {10}^6$	$3.42\times {10}^6$	$3.46\times {10}^6$	$3.28\times {10}^3$	$3.51\times {10}^6$
	std	$1.10\times {10}^6$	$3.42\times {10}^6$	$8.21\times {10}^6$	$1.40\times {10}^6$	$5.53\times {10}^6$	$1.75\times {10}^6$	$3.33\times {10}^6$	$1.09\times {10}^6$	$1.25\times {10}^5$	$4.61\times {10}^6$	$1.17\times {10}^6$
	rank	1	2	4	10	11	9	8	5	6	3	7
F28	min	$3.21\times {10}^6$	$3.13\times {10}^6$	$3.20\times {10}^6$	$6.06\times {10}^6$	$5.18\times {10}^6$	$3.27\times {10}^6$	$4.91\times {10}^6$	$3.25\times {10}^6$	$3.37\times {10}^6$	$3.20\times {10}^6$	$3.52\times {10}^6$
	max	$3.32\times {10}^6$	$3.27\times {10}^6$	$3.28\times {10}^6$	$8.47\times {10}^6$	$9.97\times {10}^6$	$3.42\times {10}^6$	$1.12\times {10}^4$	$3.38\times {10}^6$	$4.11\times {10}^6$	$3.27\times {10}^6$	$3.93\times {10}^6$
	mean	$3.27\times {10}^6$	$3.23\times {10}^6$	$3.23\times {10}^6$	$7.27\times {10}^6$	$6.55\times {10}^6$	$3.35\times {10}^6$	$7.56\times {10}^6$	$3.31\times {10}^6$	$3.56\times {10}^6$	$3.23\times {10}^6$	$3.78\times {10}^6$
	std	$2.93\times {10}^6$	$2.98\times {10}^6$	$2.51\times {10}^6$	$5.82\times {10}^6$	$1.07\times {10}^3$	$3.83\times {10}^6$	$1.55\times {10}^6$	$2.51\times {10}^6$	$1.40\times {10}^6$	$2.68\times {10}^6$	$1.00\times {10}^6$
	rank	4	2	1	10	9	6	11	5	7	3	8
F29	min	$3.29\times {10}^6$	$3.63\times {10}^6$	$3.67\times {10}^6$	5328.56	$4.94\times {10}^6$	$3.94\times {10}^3$	$4.85\times {10}^3$	$3.99\times {10}^6$	$4.00\times {10}^6$	$3.56\times {10}^6$	$4.06\times {10}^3$
	max	$3.85\times {10}^6$	$4.54\times {10}^3$	$4.83\times {10}^6$	$1.18\times {10}^4$	$9.66\times {10}^6$	$5.14\times {10}^6$	$2.51\times {10}^4$	$5.27\times {10}^6$	$6.68\times {10}^6$	$4.54\times {10}^6$	$5.73\times {10}^6$
	mean	$3.53\times {10}^6$	$4.15\times {10}^6$	$4.37\times {10}^6$	$7.75\times {10}^3$	$6.91\times {10}^6$	$4.50\times {10}^6$	$6.55\times {10}^6$	$4.65\times {10}^6$	$5.34\times {10}^6$	$4.02\times {10}^6$	$4.58\times {10}^6$
	std	$1.59\times {10}^6$	$2.32\times {10}^6$	$2.59\times {10}^6$	$1.65\times {10}^6$	$1.16\times {10}^6$	$2.86\times {10}^6$	$3.59\times {10}^6$	$4.07\times {10}^6$	$5.39\times {10}^5$	$2.25\times {10}^6$	$4.21\times {10}^6$
	rank	1	3	4	11	10	5	9	7	8	2	6
F30	min	$5.58\times {10}^6$	$7.08\times {10}^6$	$7.19\times {10}^6$	$6.49\times {10}^7$	$1.12\times {10}^7$	$4.32\times {10}^5$	$1.44\times {10}^8$	$3.58\times {10}^5$	$2.35\times {10}^6$	$1.40\times {10}^5$	$3.05\times {10}^7$
	max	$2.07\times {10}^4$	$8.83\times {10}^5$	$2.73\times {10}^6$	$2.06\times {10}^9$	$6.98\times {10}^8$	$8.20\times {10}^6$	$2.32\times {10}^9$	$8.87\times {10}^6$	$1.91\times {10}^8$	$1.74\times {10}^6$	$1.13\times {10}^8$
	mean	$1.06\times {10}^4$	$8.16\times {10}^4$	$1.34\times {10}^5$	$3.49\times {10}^8$	$1.93\times {10}^8$	$3.26\times {10}^6$	$1.01\times {10}^9$	$3.78\times {10}^6$	$4.47\times {10}^7$	$6.27\times {10}^5$	$6.12\times {10}^7$
	std	$3.64\times {10}^6$	$1.79\times {10}^5$	$4.96\times {10}^5$	$3.62\times {10}^8$	$1.65\times {10}^8$	$2.32\times {10}^6$	$6.12\times {10}^8$	$2.26\times {10}^6$	$4.38\times {10}^7$	$4.28\times {10}^5$	$1.98\times {10}^7$
	rank	1	2	3	10	9	5	11	6	7	4	8

From the previous table, and it can be seen that EErWCA is ranked first in 16 functions out of 29. This proves the superiority of the LEO operator when it is implemented as a local operator in avoiding sub-optimal regions. In addition, a non-parametric test called the Wilcoxon signed-rank test was used to prove the performance of our algorithm. Table 4 shows the results of the Wilcoxon test. Moreover, Figure 2 and Figure 3 show the convergence of EErWCA with other competitors. It is obvious that EErWCA has a more rapid convergence than the classical algorithm and other algorithms. Furthermore, Figure 4 and Figure 5 show the box plot of the suggested algorithm compared with other algorithms.

Table 4. The Wilcoxon signed-rank test for the comparative algorithms against the proposed EErWCA using CEC2017 benchmark functions, where a = 0.05 and dim = 30.

Function	Measures	EErWCA vs. ErWCA	EErWCA vs. WCA	EErWCA vs. BOA	EErWCA vs. BSA	EErWCA vs. CSA	EErWCA vs. GOA	EErWCA vs. HHO	EErWCA vs. WOA	EErWCA vs. DO	EErWCA vs. FHO
F1	AVG	$2.77\times {10}^{-1}$	$8.42\times {10}^{-1}$	$1.21\times {10}^{-12}$	$3.02\times {10}^{-11}$	$4.69\times {10}^{-8}$	$1.07\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.83\times {10}^{-6}$	$3.02\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F3	AVG	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$1.81\times {10}^{-2}$	$1.55\times {10}^{-9}$	$1.01\times {10}^{-8}$	$3.02\times {10}^{-11}$	$3.34\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$2.68\times {10}^{-4}$
F4	AVG	$1.62\times {10}^{-1}$	$5.55\times {10}^{-2}$	$1.21\times {10}^{-12}$	$3.02\times {10}^{-11}$	$1.41\times {10}^{-9}$	$5.09\times {10}^{-8}$	$3.02\times {10}^{-11}$	$5.60\times {10}^{-7}$	$3.02\times {10}^{-11}$	$3.019\times {10}^{-11}$
F5	AVG	$4.50432\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$1.20233\times {10}^{-8}$	$3.68973\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.019\times {10}^{-11}$
F6	AVG	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.019\times {10}^{-11}$
F7	AVG	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$7.38908\times {10}^{-11}$	$3.68973\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.019\times {10}^{-11}$
F8	AVG	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$6.12104\times {10}^{-10}$	$5.49405\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.019\times {10}^{-11}$
F9	AVG	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$8.10136\times {10}^{-10}$	$3.68973\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$8.99341\times {10}^{-11}$
F10	AVG	$9.51\times {10}^{-6}$	$3.20\times {10}^{-9}$	$1.21\times {10}^{-12}$	$3.02\times {10}^{-11}$	$1.53\times {10}^{-5}$	$1.32\times {10}^{-4}$	$3.02\times {10}^{-11}$	$3.20\times {10}^{-9}$	$3.69\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F11	AVG	$9.83289\times {10}^{-8}$	$5.46175\times {10}^{-9}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$5.07231\times {10}^{-10}$	$5.07231\times {10}^{-10}$	$3.01986\times {10}^{-11}$	$1.72903\times {10}^{-6}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F12	AVG	$4.98\times {10}^{-4}$	$1.33\times {10}^{-2}$	$1.21\times {10}^{-12}$	$3.02\times {10}^{-11}$	$1.16\times {10}^{-7}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$4.08\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F13	AVG	$5.94\times {10}^{-2}$	$2.24\times {10}^{-2}$	$1.21\times {10}^{-12}$	$3.02\times {10}^{-11}$	$6.72\times {10}^{-10}$	$2.83\times {10}^{-8}$	$3.02\times {10}^{-11}$	$5.57\times {10}^{-10}$	$3.82\times {10}^{-10}$	$3.01986\times {10}^{-11}$
F14	AVG	$2.75\times {10}^{-3}$	$4.92\times {10}^{-1}$	$1.21\times {10}^{-12}$	$1.61\times {10}^{-10}$	$4.92\times {10}^{-1}$	$1.77\times {10}^{-3}$	$3.02\times {10}^{-11}$	$2.03\times {10}^{-9}$	$5.49\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F15	AVG	$9.93\times {10}^{-2}$	$1.09\times {10}^{-1}$	$1.21\times {10}^{-12}$	$3.02\times {10}^{-11}$	$3.77\times {10}^{-4}$	$8.29\times {10}^{-6}$	$3.02\times {10}^{-11}$	$1.96\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F16	AVG	$3.35195\times {10}^{-8}$	$1.55808\times {10}^{-8}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$2.87897\times {10}^{-6}$	$2.37147\times {10}^{-10}$	$3.01986\times {10}^{-11}$	$3.15889\times {10}^{-10}$	$3.01986\times {10}^{-11}$	$4.50432\times {10}^{-11}$
F17	AVG	$2.01522\times {10}^{-8}$	$9.91863\times {10}^{-11}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$2.19589\times {10}^{-7}$	$1.85673\times {10}^{-9}$	$3.01986\times {10}^{-11}$	$3.4742\times {10}^{-10}$	$3.68973\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F18	AVG	$3.01\times {10}^{-4}$	$2.92\times {10}^{-2}$	$1.21\times {10}^{-12}$	$5.97\times {10}^{-9}$	$7.48\times {10}^{-2}$	$2.49\times {10}^{-6}$	$3.02\times {10}^{-11}$	$1.89\times {10}^{-4}$	$8.48\times {10}^{-9}$	$4.07716\times {10}^{-11}$
F19	AVG	$8.24\times {10}^{-2}$	$8.19\times {10}^{-1}$	$1.21\times {10}^{-12}$	$3.02\times {10}^{-11}$	$2.27\times {10}^{-3}$	$4.20\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F20	AVG	$4.62\times {10}^{-10}$	$6.72\times {10}^{-10}$	$1.21\times {10}^{-12}$	$3.02\times {10}^{-11}$	$1.17\times {10}^{-4}$	$1.25\times {10}^{-7}$	$3.02\times {10}^{-11}$	$5.57\times {10}^{-10}$	$7.39\times {10}^{-11}$	$4.50432\times {10}^{-11}$
F21	AVG	$6.69552\times {10}^{-11}$	$3.33839\times {10}^{-11}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$1.3111\times {10}^{-8}$	$1.46431\times {10}^{-10}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F22	AVG	$9.51394\times {10}^{-6}$	$1.38525\times {10}^{-6}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F23	AVG	$9.91863\times {10}^{-11}$	$5.49405\times {10}^{-11}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$9.7555\times {10}^{-10}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F24	AVG	$3.19674\times {10}^{-9}$	$1.46431\times {10}^{-10}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$1.25408\times {10}^{-7}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$6.79\times {10}^{-2}$
F25	AVG	$2.77\times {10}^{-1}$	$8.42\times {10}^{-1}$	$1.21\times {10}^{-12}$	$3.02\times {10}^{-11}$	$4.69\times {10}^{-8}$	$1.07\times {10}^{-9}$	$3.02\times {10}^{-11}$	$3.83\times {10}^{-6}$	$3.02\times {10}^{-11}$	$4.55\times {10}^{-1}$
F26	AVG	$2.27\times {10}^{-3}$	$3.02\times {10}^{-11}$	$1.21\times {10}^{-12}$	$3.02\times {10}^{-11}$	$1.06\times {10}^{-3}$	$5.37\times {10}^{-2}$	$3.02\times {10}^{-11}$	$5.46\times {10}^{-9}$	$1.21\times {10}^{-10}$	$6.06576\times {10}^{-11}$
F27	AVG	$1.17374\times {10}^{-9}$	$6.06576\times {10}^{-11}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$1.60621\times {10}^{-6}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F28	AVG	$2.15403\times {10}^{-6}$	$3.36814\times {10}^{-5}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.96477\times {10}^{-8}$	$3.01986\times {10}^{-11}$	$3.82489\times {10}^{-9}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F29	AVG	$4.61591\times {10}^{-10}$	$7.38908\times {10}^{-11}$	$1.21178\times {10}^{-12}$	$3.01986\times {10}^{-11}$	$2.00229\times {10}^{-6}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$3.01986\times {10}^{-11}$
F30	AVG	$1.11\times {10}^{-4}$	$1.52\times {10}^{-3}$	$1.21\times {10}^{-12}$	$3.02\times {10}^{-11}$	$3.47\times {10}^{-10}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.02\times {10}^{-11}$	$3.01986\times {10}^{-11}$

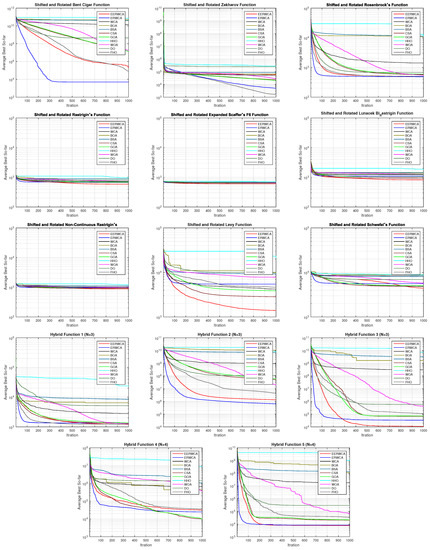
Figure 2. Convergence curve of some functions from F1–F15 for all algorithms using CEC2017 and dim = 30.

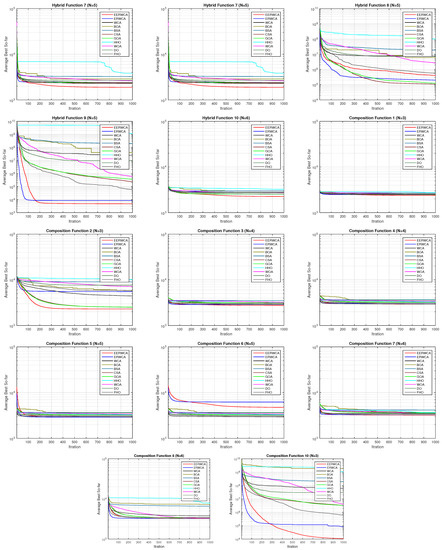
Figure 3. Convergence curve of some functions from F16–F30 for all algorithms using CEC2017 and dim = 30.

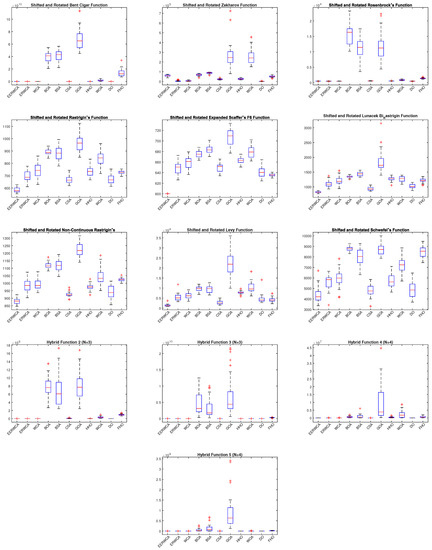
Figure 4. Box plots of some functions from F1–F15 for all algorithms using CEC2017 and dim = 30.

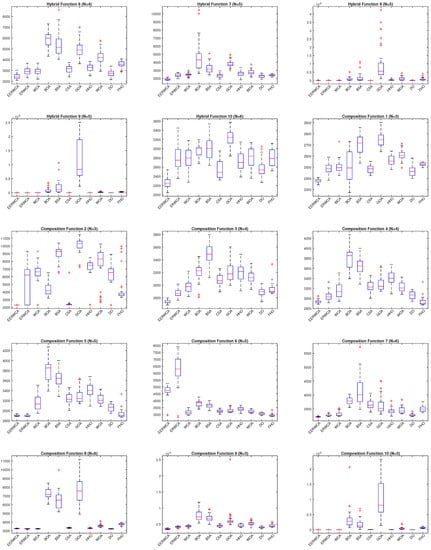
Figure 5. Box plots of some functions from F16–F30 for all algorithms using CEC2017 and dim = 30.

5.1. Experimental Series 2: Engineering Problems

This section discusses the results obtained from conducting the experiments for several engineering problems, including the industrial refrigeration system problem, the speed reducer problem, and the multi-product batch plant problem. The statistical results, convergence curves, and box plots are displayed for each problem.

5.1.1. Design of Industrial Refrigeration System Problem

The problem of the industrial refrigeration system aims to find the best refrigerants, the ideal temperature levels, the proper cycle configuration, and the best compression technology to minimize cost and produce the optimal refrigeration system for the clients [54].

The statistical results for the proposed algorithm for the industrial refrigeration system problem are shown in Table 5. The results for the proposed algorithm are compared with other algorithms, including ErWCA, WCA, BOA, BSA, COA, CSA, GOA, HHO, and WOA. The minimum, maximum, average, and standard deviation values are presented in the table. It is observed from the table that the proposed EErWCA is ranked first among the other algorithms for the average results. In addition, Table 6 shows the best algorithm results and the value achieved for each dimension. It is observed from the table that the EErWCA has a low best value, and the ErWCA and WCA algorithms are competitive with the proposed algorithm for the best results. Figure 6 shows the algorithms’ convergence plots and box plots. The convergence curves show the values of the average best for the algorithms for each iteration. It is observed that the proposed EErWCA achieved the best value progressing to the last iteration. ErWCA, on the other hand, had good values in earlier iterations but failed to achieve better values at the last iteration compared to the proposed EErWCA. The box plot shows that the proposed algorithm has a very low standard deviation. It also has low values for the maximum and minimum values, which shows the superiority of the proposed algorithm. Other algorithms such as ErWCA, WCA, CSA, HHO, and WOA have a low standard deviation, and minimum and maximum values. In contrast, BSA has the largest standard deviation, and maximum and minimum values.

Table 5. Statistical results of EErWCA versus other metaheuristics on optimal design of industrial refrigeration system.

Mea.	EErWCA	ErWCA	WCA	BOA	BSA	COA	CSA	GOA	HHO	WOA
min	0.046781	0.032213	0.032213	24.34002	16.64046	3654.843	0.202915	8716.021	0.364219	0.405337
max	1,881,267	936,195.3	936,195.3	1.09 × 108	1.11 × 108	62,206,678	1,636,799	65,297,497	984,165.9	1.46 × 108
mean	108,038.4	124,825.7	343,270.8	15,693,452	18,784,693	9,378,549	649,780.4	9,506,237	349,833.5	5,008,193
STD	377,490.9	323,684.1	458,857.1	23,600,650	26,950,500	14,020,748	484,065.8	14,314,970	466,964.4	26,683,805
rank	1	2	3	9	10	7	5	8	4	6

Table 6. Results of EErWCA versus other metaheuristics on optimal design of industrial refrigeration system.

	Best	×1	×2	×3	×4	×5	×6	×7	×8	×9	×10	×11	×12	×13	×14
EErWCA	0.046781	0.001	0.001	0.001	0.001001	0.00773	0.001	1.52404	1.523999	4.99997	2.087664	0.007892	0.00789	0.01958	0.235028
ErWCA	0.032213	0.001	0.001	0.001	0.001	0.001	0.001	1.524	1.524	5	2	0.001	0.001	0.007293	0.087556
WCA	0.032213	0.001	0.001	0.001	0.001	0.001	0.001	1.524	1.524	5	2	0.001	0.001	0.007293	0.087556
BOA	24.34002	0.001	0.014124	0.008668	0.001	0.006265	0.001	2.424603	2.785133	2.520375	2.638812	0.13586	0.001	0.001	0.001
BSA	16.64046	0.001	0.008118	0.007184	1.975456	2.722751	0.001	2.695728	2.75106	1.999971	2.484036	1.971782	0.001	0.001	0.004513
COA	3654.843	0.001	0.002534	3.531012	5	2.47318	3.041167	4.596045	5	5	4.845687	0.001	0.001	0.001	0.001
CSA	0.202915	0.001	0.00107	0.001136	0.001156	0.001092	0.001	3.70834	1.526876	4.999623	5	0.001	0.001	0.009608	0.115344
GOA	8716.021	0.001	0.116401	3.365744	0.01427	2.575789	1.660094	2.992306	3.971143	4.629864	4.642211	0.001	0.001	0.001	0.001
HHO	0.364219	0.001	0.001	0.005309	0.242903	0.010031	0.004435	2.86165	2.513477	2.024121	2.000021	0.001	0.001	0.006787	0.079804
WOA	0.405337	0.001	0.001	0.001	0.582783	0.001	0.001	1.667485	2.171946	4.99986	1.999999	0.001	0.001	0.001	0.010963

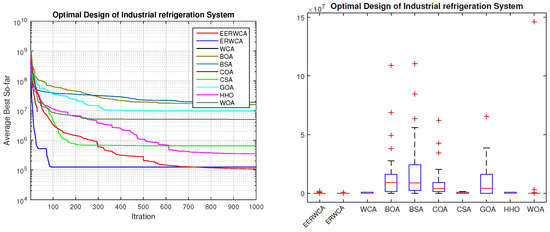
Figure 6. Design of Industrial refrigeration System.

5.1.2. Design of Speed Reducer Problem

The design of the speed reducer problem aims to find the minimum speed reducer weight based on the gear teeth stress, stress of the surface, shafts transverse deflections, and shafts stresses. The problem has seven design variables (z1–z7). The following equations represent the problem:

$$\begin{array}{cc}\hfill \mathrm{Min}f(\overrightarrow{z})& =0.7854z_1{z}_2^2(3.3333z_3^2+14.9334z_3-43.0934)\hfill \\ & -1.508z_1(z_6^2+z_7^2)+7.4777(z_6^3+z_7^3)\hfill \\ & +0.7854(z_4{z}_6^2+z_5{z}_7^2)\hfill \end{array}$$

Subject to:

$$\begin{array}{c}{g}_1(\overrightarrow{z})=\frac{27}{z_1{z}_2^2{z}_3}-1\le 0\hfill \\ g_2(\overrightarrow{z})=\frac{397.5}{z_1{z}_2^2{z}_3}-1\le 0\hfill \\ g_3(\overrightarrow{z})=\frac{1.93z_4^3}{z_2{z}_3{z}_6^4}-1\hfill \\ g_4(\overrightarrow{z})=\frac{1.93z_5^3}{z_2{z}_3{z}_7^4}-1\le 0\hfill \\ g_5(\overrightarrow{z})=\frac{1}{110z_6^3}\sqrt{{\left(\frac{745z_4}{z_2{z}_3}\right)}^2+16.9\times {10}^6}-1\le 0\hfill \\ g_6(\overrightarrow{z})=\frac{1}{85z_7^3}\sqrt{{\left(\frac{745z_5}{z_2{z}_3}\right)}^2+157.5\times {10}^6}-1\le 0\hfill \\ g_7\left(\overrightarrow{z}\right)=\frac{z_2{z}_3}{40}-1\le 0\hfill \\ g_8(\overrightarrow{z})=\frac{5z_2}{z_1}-1\le 0\hfill \\ g_9(\overrightarrow{z})=\frac{z_1}{12z_2}-1\le 0\hfill \\ g_{10}(\overrightarrow{z})=\frac{1.5z_6+1.9}{z_4}-1\le 0\hfill \\ g_{11}(\overrightarrow{z})=\frac{1.1z_7+1.9}{z_5}-1\le 0\hfill \end{array}$$

with $2.6\le z_1\le 3.6,0.7\le z_2\le 0.8,17\le z_3\le 28,7.3\le z_4\le 8.3,7.8\le z_5\le 8.3,2.9\le z_6\le 3.9,\mathrm{and}5\le z_7\le 5.5.$

For this type of problem, Table 7 and Table 8, and Figure 7 show the results of applying the proposed algorithm and comparing the results with other algorithms. Table 7 shows that the proposed EErWCA has the rank of 1 for the average results compared to the other algorithms. CSA, WCA, and ErWCA have similar results to the proposed algorithm. Table 8 shows the best results and the value for each dimension for all the algorithms. The best value is achieved equally for the proposed EErWCA, ErWCA, WCA, and CSA. The convergence plot for the average best, which is presented as the first figure in Figure 7, shows competitive results toward a better solution for all algorithms. On the other hand, the box plot in Figure 7 shows a low standard deviation for most of the algorithms except for BOA, GOA, and WOA.

Table 7. Statistical results of EErWCA versus other metaheuristics on speed reducer design.

Measures	EErWCA	ErWCA	WCA	BOA	BSA	COA	CSA	GOA	HHO	WOA
min	2993.634	2993.634	2993.634	3096.64	2993.7	3008.4	2993.634	3034.447	2994.197	2993.701
max	2994.306	3002.967	3006.627	12,808.17	3536.411	3147.676	3000.09	8843.277	4307.676	5905.984
mean	2993.657	2994.568	2994.5	4605.827	3025.235	3056.898	2993.947	4425.907	3146.587	3487.556
STD	0.122528	2.847755	3.296278	1934.142	99.6893	33.93009	1.224181	1503.485	259.7566	687.8122
rank	1	4	3	10	5	6	2	9	7	8

Table 8. Results of EErWCA versus other metaheuristics on speed reducer design.

	Best	×1	×2	×3	×4	×5	×6	×7
EErWCA	2993.634	3.497599	0.7	17	7.3	7.713535	3.350056	5.285631
ErWCA	2993.634	3.497599	0.7	17	7.3	7.713535	3.350056	5.285631
WCA	2993.634	3.497599	0.7	17	7.3	7.713535	3.350056	5.285631
BOA	3096.64	3.543767	0.7	17.10648	7.3	7.964609	3.571151	5.287996
BSA	2993.7	3.497654	0.7	17	7.3	7.716848	3.350044	5.285662
COA	3008.4	3.490789	0.7	17	8.280791	7.722827	3.35311	5.288259
CSA	2993.634	3.497599	0.7	17	7.3	7.713535	3.350056	5.285631
GOA	3034.447	3.571421	0.701486	17	7.649347	7.714521	3.353149	5.288426
HHO	2994.197	3.49797	0.7	17	7.3	7.732423	3.350521	5.285312
WOA	2993.701	3.49765	0.7	17	7.3	7.712778	3.350306	5.28539

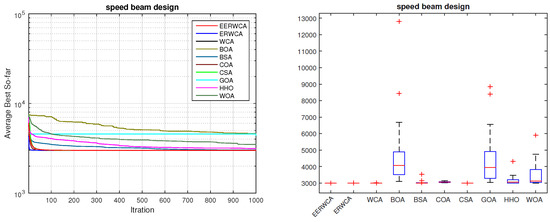
Figure 7. Design of Speed Reducer.

5.1.3. Design of Multi-Product Batch Plant Problem

The multi-product batch plant problem is represented when several products show a high degree of similarity and, thus, need the same process for production, and the same equipment configuration [68,69].

Table 9 shows that the proposed EErWCA achieved the first rank against the other algorithms. CSA and WCA achieve the best results while EErWCA and ErWCA have similar best results to the CSA and WCA (Table 10). The convergence curve in Figure 8 shows that the best value of the average best is achieved in early iterations for many algorithms with the exception of GOA and BOA, where the best value is not achieved compared to the other algorithms. HHO also shows late progress in achieving the best value compared to the other algorithms. On the other hand, the box plot in Figure 8 shows very competitive results for all the algorithms by having a very low standard deviation.

Table 9. Statistical results of EErWCA versus other metaheuristics on multi-product batch plant.

Measures	EErWCA	ErWCA	WCA	BOA	BSA	COA	CSA	GOA	HHO	WOA
min	53,730.23	53,742.04	53,655.26	85,428.4	65,476.74	71,645.61	53,639.63	125,170.2	64,778.06	76,198.96
max	69,515.04	87,986.7	74,078.6	3.48 × 108	366,060.1	152,015.5	90,826.57	4.71 × 1010	90,866.09	165,947.4
mean	59,552.25	63,954.91	61,881.41	15,523,439	106,832.5	101,835.2	60,671.93	3.39 × 109	74,008.67	112,619.2
STD	3435.181	7243.705	5361.169	63,161,457	52,821.84	19,813.64	7773.95	1.03 × 1010	6004.125	25,070.13
rank	1	4	3	9	7	6	2	10	5	8

Table 10. Results of EErWCA versus other metaheuristics on multi-product batch plant.

	Best	×1	×2	×3	×4	×5	×6	×7	×8	×9	×10
EErWCA	53,730.23	1.4738	0.902599	1.057608	973.952	1460.816	1292.906	19.9999	15.9999	224.9307	131.0022
ErWCA	53,742.04	0.879451	0.537306	0.970167	957.5071	1436.261	1336.526	20	15.99997	247.3582	115.6977
WCA	53,655.26	0.51	0.51	0.51	967.1175	1450.676	1301.476	20	16	230.4552	126.5518
BOA	85,428.4	1.518289	1.633461	1.291396	1149.43	1196.297	1024.16	13.10134	9.576884	161.7096	100.4147
BSA	65,476.74	0.70488	1.551702	0.847311	1012.547	1160.721	928.2855	10.54547	15.99954	161.102	94.62521
COA	71,645.61	0.51	0.51	0.51	1300.827	2500	2276.628	20	16	485.6925	78.80057
CSA	53,639.63	0.510173	0.510954	0.510004	964.0163	1446.027	1307.54	19.99954	15.99949	233.8113	124.0984
GOA	125,170.2	1.638572	3.111043	2.266871	1145.717	1248.944	1296.439	7.316115	15.46341	140.0631	125.618
HHO	64,778.06	1.713052	1.587087	1.188423	524.3093	743.4804	1127.821	9.999611	8.001561	150.0532	48.29276
WOA	76,198.96	1.576433	1.501728	1.39028	746.8241	1203.952	864.5001	9.999428	8.189601	131.1378	55.74986

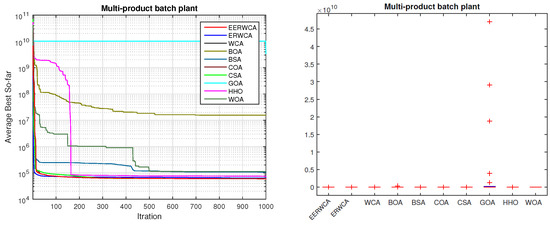
Figure 8. Design of multi-product batch plant.

The results are summarized in Table 11. It shows the Wilcoxon test results for each algorithm against the proposed EErWCA for each engineering problem.

Table 11. Statistical results of EErWCA versus other metaheuristics on engineering problems.

EErWCA vs.	ErWCA	WCA	BOA	BSA	COA	CSA	GOA	HHO	WOA
Industrial refrigeration system	$1.33668\times {10}^{-5}$	0.347800991	$8.10136\times {10}^{-10}$	$1.17374\times {10}^{-9}$	$2.87158\times {10}^{-10}$	0.000729511	$2.66947\times {10}^{-9}$	0.01563812	0.01031467
Speed reducer	$6.55864\times {10}^{-8}$	$6.61784\times {10}^{-9}$	$3.01986\times {10}^{-11}$	$3.33839\times {10}^{-11}$	$3.01986\times {10}^{-11}$	$8.30095\times {10}^{-7}$	$3.01986\times {10}^{-11}$	$3.3384\times {10}^{-11}$	$3.3384\times {10}^{-11}$
Multi-product batch plant	0.093340797	0.652043622	$3.01986\times {10}^{-11}$	$3.33839\times {10}^{-11}$	$3.01986\times {10}^{-11}$	0.673495053	$3.01986\times {10}^{-11}$	$6.0658\times {10}^{-11}$	$3.0199\times {10}^{-11}$

6. Conclusions and Future Work

Evaporation rate water-cycle algorithm (ErWCA) is a new version of the water-cycle algorithm (WCA) inspired by the hydrologic cycle. However, ErWCA has many drawbacks and limitations. In this paper, we try to use the slime mould algorithm (SMA) exploitation phase instead of the original ErWCA exploitation. Moreover, we introduce a new local escape operator to help the hybrid proposed algorithm escape from local optima. The novel algorithm was tested using 29 functions from the CEC 2017 benchmark and compared with the classical algorithm and three other state-of-the-art well-known algorithms. The statistical analysis and experimental results prove the superiority of the developed algorithm. The statistical analysis and experimental results prove the superiority of the developed algorithm. The limitation of this work is that EErWCA, like all other metaheurstics algorithms, cannot guarantee the optimal solution to all problems. In the future, it will be possible to combine this algorithm with many other operators such as chaotic local search, distribution operator, local escaping operator, and more. In future work, we will also try to produce many versions of this algorithm, including multi-objective, discrete, chaotic, etc. We will also investigate the possibility of applying this version to fields such as feature selection, scheduling, power, agriculture, etc. In addition, the currently proposed method can be used to solve similar hard problems such as data mining, advanced industrial engineering, feature selection, prediction, scheduling in IoT cloud environments, and others.