A Multiple Solution Approach to Real-Time Optimization

Abstract

Modifier Adaptation (MA) is a method of real-time optimization (RTO) which modifies a single model to match the first order properties of the plant. Known uncertainties in the parameters of this model are discarded in favor of real-time measurements, but they can be used to quantify the mismatch between the plant and model. Using multi-model methods increases the computation time, but can improve rate of convergence of the RTO scheme. This article proposes a framework, known as multiple solution modifier adaptation (MSMA), which produces several models which are all modified in the same way as standard MA, each producing a potential solution to be applied to the plant. From this framework, three recommended schemes are proposed on how to select the operating point to be applied to the plant: (1) Selecting the solution based off the modifiers; (2) Selecting the mean solution from convex models; (3) Selecting the closest solution to the current operating point. Each of these methods have different advantages, including limiting the increase in computational complexity and improving the model adequacy conditions of the scheme. These recommended schemes are shown on three different case studies of varying complexity with all three schemes showing improvements over standard MA.

1. Introduction

Through advances in computing power and mathematical techniques, advanced optimization techniques have grown to be a vital part of process systems engineering. Optimization of a process allows for an appreciable increase in the efficiency, reduction in waste, guarantee of safety, improved product quality, and maximized profits. A well optimized process provides a competitive edge over the field, benefits the whole supply chain down to the consumer, and allows for a sustainable operation in a world of increasing resource scarcity.

The standard approach to finding the optimum of a process is to create a mathematical model, and apply optimization techniques to this model to determine the operating conditions which minimize (or maximize) an objective function. This operating point must also satisfy a set of conditions known as constraints, and an infeasible operating point violates the process constraints. A model cannot fully accurately predict the outcome of a real process, as no model is perfect. The presence of simplifications, noise and uncertainty of the process results in an unavoidable mismatch between the eventual realization of the process (known as the plant) and model.

If the degree of uncertainty of the model can be determined, it can be accounted for in the optimization, however the resulting operating point can never be guaranteed to be at the true optimum of the plant, and may still result in infeasible operation. In order for improvements to be made, additional information about the plant is required to allow for an improvement to the operation of the process, and potentially the ability to find the true optimum of the plant. This information comes in the form of measurements from sensors in the plant, which allow for the states to be estimated. Utilizing these measurements in process optimization is the basis of the field known as real-time optimization (RTO). This information alone is sufficient to apply standard optimization techniques directly to the plant (e.g., gradient-based algorithms, Hooke-Jeeves algorithm, etc.) without the need of a model, by estimating the true value of the objective function and the constraint functions and directly modifying the operating conditions towards optimality. Using this unstructured approach often results in poor performance as the experiment cost (i.e., the cost to get an accurate measurement) and violating the constraints of the process during an experiment are not of great enough importance in standard computational optimization techniques.

The need for an approach which can find the optimum of a process with minimal risk in the experiments, and reduced total number of experiments is desired. One such approach is to use the measurements directly and avoid the need for an optimization scheme in a feedback style control scheme [1,2,3]. Another approach for which this can be achieved is by marrying the measurements taken directly from the plant with the uncertain model, and is a step in the right direction to formulating an approach which can rapidly converge towards the true plant optimum without violating the constraints of the plant. The most popular approach to RTO using a model structure is the two-step approach [4,5,6], which uses the measurements to estimate the value of the uncertain parameters of the model. Using these new parameters, a new operating point can be found which has an increased chance of approaching the true plant optimum and remaining feasible than using standard optimization techniques. This approach however has a detrimental flaw in that convergence is achieved when the measurements from the plant predict a model which has the current operating point as the optimum [7]. This convergence criteria does not always coincide with the optimal conditions of the plant.

One method of ensuring that an RTO scheme will only converge at an operating condition which satisfies the Karush–Kuhn–Tucker (KKT) conditions of the plant is to ensure that at the current operating point, the first order conditions of optimality of the model are equal to the measured values of the plant [8,9,10]. This is the basis behind a group of RTO schemes known as modifier adaptation (MA) [11]. If the model is modified such that the first order properties of the model equal the measured values of the plant, upon convergence the operating point must be the optimum of the modified model, which by definition is also the optimum of the plant. The simplest approach to ensuring first-order matching is through the addition of affine modifiers directly to the objective and constraint functions of the nominal model.

The guarantee of KKT matching upon convergence is a strong result, but comes with equally strong drawbacks. The primary drawback is that in order calculate the modifiers which allow the model to match the first-order properties of the plant, the value and the gradient of the plant objective and constraints are required at each iteration of the RTO scheme. Estimating the gradient of the plant numerically requires both additional experiments at operating conditions local to the current operating point, and very accurate estimates of the states as errors in the measurements are amplified in the gradient calculation. Therefore, many advances to the MA framework have come with the intention to reduce the impact of these issues, and offer methods which reduce the number of experiments required for the gradient estimation [12]. Such methods include using previous measurements for the gradient estimation [13,14], nested MA [15], directional MA [16,17,18], and using quadratic approximations [19,20].

Another direction of advancing MA comes in the form of using additional information from the measurements to allow for a more informed decision to be made in determining where improvements to the operating point can be made. Some examples of using additional information comes in the form of transient measurements between experiments [21,22,23], which can provide better state estimates and reduce the time required for each experiment to be performed, or using information of uncontrollable disturbances [24,25], but are measured and therefore can be accounted for. Another set of data which is not fully utilized is the set of previous measurement from the plant, which are typically discarded in favor of the most recent measurements. For this, the use of Gaussian processes can interpolate between the data points and with or without a model, this newly created fit can be used to predict the outcomes of the plant [26,27].

A typical approach to process modeling is during the conceptualization and design stages of a plant, a model is produced using measurements from a pilot plant of the process. The parameters of a mathematical model are adjusted to fit these measurements, but will not be able to fully accurately fit this data (without over fitting) due to the presence of noise and errors in the foundations of the model (from simplifications). The uncertainty in these parameters provide valuable insight into the mismatch between the plant and model (assuming the pilot plant is an accurate representation of the true plant). An operating point which is robust to this uncertainty can be found using multi-model-based optimization techniques such as worst-case analysis. Both the uncertainty in the parameters and the real-time measurements are both used to estimate the plant-model mismatch, therefore either one or the other is typically used, rather than both. Another disadvantage behind using a multi-model approach in an RTO setting is that solving the RTO solution is required to be fast and solving multi-model is typically more computationally intensive (therefore slower) compared to single-model approaches. Despite this, recently the authors to this article, and others have shown that using mutliple models to generate a single non-linear program (NLP) to be solved for the RTO approach can improve the rate and stability of convergence, and reduce the likelihood of breaking the constraints of the plant before convergence [28,29,30]. These methods are set-up to use the uncertainty in the model parameters to produce a single NLP to be solved, whereas the methods proposed in this article solve each model NLP independently to produce a set of candidate solution, which are then combined into a single operating point to be applied to the plant.

This article is structured as follows; firstly, the problem to be solved is mathematically defined, along with the standard MA framework. Next, in Section 3, the proposed multiple solution modifier adaptation framework is defined and the two primary research questions are posed. The following two sections offer answers to these research equations, firstly looking at how the multiple solutions can be generated in Section 4, then how they can be processed into a single RTO solution in Section 5. Finally, some of the most promising approaches in the framework are compared against one another on the benchmark case study of the Williams-Otto CSTR, a distillation column, and a semi-batch reactor.

2. Problem Definition

2.1. Model-Based Optimization

The objective of process optimization is to find a set of inputs, given by $\mathit{u}\in {\mathbb{R}}^{n_u}$, which minimize an objective function, given by $\Phi \in \mathbb{R}$, subject to some constraints, given by $\mathit{G}\in {\mathbb{R}}^{n_g}$. For the plant, this can be cast as the solution to the following non-linear program (NLP):

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathit{u}}_p^{*}\in & \arg \underset{\mathit{u}}{min}\phantom{\mathrm{s}.\mathrm{t}.}{\Phi }_p\left(\mathit{u}\right),\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\phantom{\arg \min }{\mathit{G}}_p\left(\mathit{u}\right)\le \mathbf{0},\hfill \end{array}\end{array}$$

(1)

where a subscript p refers to a property of the plant. Typically, a process with have a set of outputs, given by $\mathit{y}\in {\mathbb{R}}^{n_y}$, which are functions of the inputs. The objective and constraint functions are typically a function of both the inputs and outputs, such that,

$$\begin{array}{cc}\hfill \Phi \left(\mathit{u}\right)& =\varphi (\mathit{u},\mathit{y}(\mathit{u}\left)\right),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \mathit{G}\left(\mathit{u}\right)& =\mathit{g}(\mathit{u},\mathit{y}(\mathit{u}\left)\right).\hfill \end{array}$$

(3)

It is assumed that the objective and constraint functions are known functions w.r.t. the input and outputs. However, the exact mapping between the outputs and the inputs for the plant is considered to be unknown, therefore the plant NLP cannot be directly solved. The standard approach to overcoming this unknown is to produce a model of the process which predicts the outputs of the plant. One such type of model is known as a parameterized state-space model which is formed of two sets of equations,

$$\begin{array}{cc}\hfill \frac{\partial \mathit{x}}{\partial t}& =\mathit{F}(\mathit{x},\mathit{u},\mathbf{\theta }),\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \mathit{y}& =\mathit{H}\left(\mathit{x},\mathit{u},\mathbf{\theta }\right),\hfill \end{array}$$

(5)

where $\mathit{x}$ represents the states, t represents time, and $\mathbf{\theta }$ represents the model parameters. For RTO, the primary interest is in the steady-state outputs, therefore the time derivative can be set to $\mathbf{0}$ and rearranged for the states (i.e., $\mathit{x}=\mathit{f}(\mathit{u},\mathbf{\theta })$; if this cannot be mathematically rearranged, it can be solved numerically in the optimization of the NLP). Using this function for the states, a functional representation of the outputs can be achieved,

$$\begin{array}{c}\hfill \mathit{y}(\mathit{u},\mathbf{\theta })=\mathit{H}\left(\mathit{f}(\mathit{u},\mathbf{\theta }),\mathit{u},\mathbf{\theta }\right).\end{array}$$

(6)

The model-based NLP can be formulated using this functional representation of the outputs,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathit{u}}^{*}\in & \arg \underset{\mathit{u}}{min}\phantom{\mathrm{s}.\mathrm{t}.}\varphi \left(\mathit{u},\mathit{y}(\mathit{u},\mathbf{\theta })\right),\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\phantom{\arg \min }\mathit{g}\left(\mathit{u},\mathit{y}(\mathit{u},\mathbf{\theta })\right)\le \mathbf{0},\hfill \\ \hfill & \phantom{\mathrm{s}.\mathrm{t}.\arg \min }\mathit{u}\in \mathcal{U}.\hfill \end{array}\end{array}$$

(7)

This NLP is solved using the nominal parameters, $\mathbf{\theta }={\mathbf{\theta }}_{nom}$. The solution to the model-based NLP is only guaranteed to be at true plant optimum if there is no plant-model mismatch, i.e., $\mathit{y}(\mathit{u},{\mathbf{\theta }}_{nom})={\mathit{y}}_p\left(\mathit{u}\right)$. However, in practice there is always some degree of plant-model mismatch present, therefore the model-based NLP will always produce a suboptimal solution (barring chance) and potentially even operate at an infeasible operating condition for the plant.

Using higher fidelity models can assist in ensuring the model-based optimum is closer to the true optimum, but this is a costly endeavor and cannot fully account for the discrepancy, especially if the plant is being operated in a different set-up to what was originally defined during the modeling stage. Another approach is to use the known uncertainty in the model to account for the mismatch, however this typically leads to a feasible, but highly suboptimal operating point [31,32,33].

2.2. Modifier Adaptation

The approach to rectifying this discrepancy between the plant and model of interest to this article is real-time optimization (RTO), specifically modifier adaptation (MA). Using measurements of the plant, a true insight into the state of the plant at the current operating point can be observed. MA uses this window into the plant to determine the first-order properties of the plant, and using these properties, a linear term is added to the model characteristic functions to force the modified models to match the first order conditions of optimality observed of the plant. The modified NLP used by the standard MA scheme is as follows,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathit{u}}_k^{*}\in & \mathsf{arg}\underset{\mathit{u}}{min}\phantom{\mathrm{s}.\mathrm{t}.}{\Phi }_k\left(\mathit{u}\right),\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\phantom{\arg \min }{\mathit{G}}_k\left(\mathit{u}\right)\le \mathbf{0},\hfill \\ \hfill & \phantom{\mathrm{s}.\mathrm{t}.\arg \min }\mathit{u}\in \mathcal{U},\hfill \end{array}\end{array}$$

(8)

where k refers to the iteration number, and ${\Phi }_k$ and ${\mathit{G}}_k$ are the modified cost and constraints, respectively, which are defined as,

$$\begin{array}{c}\hfill {\Phi }_k\left(\mathit{u}\right)=\varphi \left(\mathit{u},\mathit{y}(\mathit{u},{\mathbf{\theta }}_{nom})\right)+{\epsilon }_k^{\varphi }+{(\mathit{u}-{\mathit{u}}_k)}^{\mathsf{T}}{\mathbf{\lambda }}_k^{\varphi },\end{array}$$

(9)

$$\begin{array}{c}\hfill {\mathit{G}}_k\left(\mathit{u}\right)=\mathit{g}\left(\mathit{u},\mathit{y}(\mathit{u},{\mathbf{\theta }}_{nom})\right)+{\mathbf{\epsilon }}_k^g+{(\mathit{u}-{\mathit{u}}_k)}^{\mathsf{T}}{\mathbf{\lambda }}_k^g,\end{array}$$

(10)

where $\epsilon$ and $\mathbf{\lambda }$ represent the zeroth and first order modifiers, respectively. ${\epsilon }_k^{\varphi }$ can be neglected from the formulation of the modified objective function as it does not directly influence the NLP solution. The other modifiers are defined as the difference between the observed values of the plant, and the estimated values of the model at the current operating point,

$$\begin{array}{cc}\hfill {\mathbf{\lambda }}_k^{\varphi }=& {\left.{\nabla }_u{\Phi }_p\left(\mathit{u}\right)\right|}_{{\mathit{u}}_k}-{\left.{\nabla }_u\Phi (\mathit{u},{\mathbf{\theta }}_{nom})\right|}_{{\mathit{u}}_k},\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\mathbf{\lambda }}_k^g=& {\left.{\nabla }_u{\mathit{G}}_p\left(\mathit{u}\right)\right|}_{{\mathit{u}}_k}-{\left.{\nabla }_u\mathit{G}(\mathit{u},{\mathbf{\theta }}_{nom})\right|}_{{\mathit{u}}_k},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\mathbf{\epsilon }}_k^g=& {\mathit{G}}_p\left({\mathit{u}}_k\right)-\mathit{G}({\mathit{u}}_k,{\mathbf{\theta }}_{nom}).\hfill \end{array}$$

(13)

where ${\nabla }_u$ is the gradient operator. The main advantage of MA lies in its mathematically proven ability to guarantee KKT matching upon convergence [11]. Said differently, the linear correction terms of the model expressions of the cost and constraints functions of Equations (9) and (10) are sufficient to reconcile the 1st order conditions of optimality of the model and of the plant upon convergence. It follows that Problem (1) for the plant and Problem (8) for the modified model share the same solutions upon convergence, despite the fact that the model and plant are different. An adequate model for MA is one which satisfies the second order conditions of optimality at the plant optimum, as if this is not met then the plant optimum cannot be the solution to Problem (8) when the current operating point is at the plant optimum, and convergence cannot occur. As the modifiers do not affect the second order properties, the model must meet these, which are that the model has a positive definite Hessian of the Lagrangian at the plant optimum (i.e., a minimum can be observed).

2.3. Model Uncertainty in MA

During the modeling stage of a process, the parameters of the model are defined from observations of experiments. These parameter calculations are condensed into a nominal value—the set of parameters which have the highest confidence to accurately predict the plant outcome—and an uncertainty in the set of nominal parameters. Standard MA techniques neglect the uncertainty in these nominal parameters in favor of using the measurements of the plant to account for the uncertainty. However, there is merit to be taken from this known uncertainty in the parameters before experiments are taken from the plant.

One such approach which takes advantage of the known uncertainty in the model parameters in MA is an approach which utilizes the Lipschitz constants of the process [34]. Lipschitz constants are defined as the maximum gradient of the characteristic functions, which can be used to define a region of guaranteed feasibility around the current operating point. These constants for the plant cannot be directly measured, however an upper bound can be used from the model to estimate this region. By using the uncertainty in the model parameters a more conservative estimate can be obtained for these constants [30].

Another approach is to ensure that each iteration satisfies the modified constraints for not only the nominal parameters, but for each set of parameters in the uncertainty set [29]. Alternatively, a single model can be generated which upper-bounds the second derivative of all the models in the uncertainty set [28]. All these approaches to using the known model uncertainty aim to use this uncertainty to create a single NLP to be solved by the RTO scheme.

This article is interested in maintaining the individual NLPs for each set of parameters which could accurately predict the plant, and using the set of solutions to create a fully informed decision on the next set of operating conditions.

3. Multiple Solution MA

The general principle behind multiple solution modifier adaptation (MSMA) is to generate a set of potential operating points, and use this set operating points to find the ‘best’ operating point for the next iteration of the RTO scheme. Naturally from this, two research questions arise:

1.

Solution Production: How can the set of potential solutions be generated?

2.

Solution Processing: How can the set of potential solutions be combined into a single operating point to be applied to the plant?

The use of multiple models to produce multiple solutions can be summarized by the following NLP,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathit{u}}_{k,\pi }^{*}\in & \mathsf{arg}\underset{\mathit{u}}{min}\phantom{\mathrm{s}.\mathrm{t}.}{\Phi }_{k,\pi }\left(\mathit{u}\right),\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\phantom{\arg \min }{\mathit{G}}_{k,\pi }\left(\mathit{u}\right)\le \mathbf{0},\hfill \\ \hfill & \phantom{\mathrm{s}.\mathrm{t}.\arg \min }\mathit{u}\in \mathcal{U},\hfill \end{array}\end{array}$$

(14)

$$\begin{array}{cc}\hfill {\mathit{u}}_{k+1}=& f_{MS}({\mathit{u}}_k,{\mathit{u}}_{k,1}^{*},{\mathit{u}}_{k,2}^{*},\dots ,{\mathit{u}}_{k,\pi }^{*}),\hfill \end{array}$$

(15)

where $\pi$ refers to the model number. Problem (14) is the NLP used to calculate the individual solutions which make up the set of potential solutions, and Equation (15) refers to the solution processing, which uses the current operating point and the set of potential operating points to find the next RTO iterate. The functions used in the NLP used to calculate the potential operating points follow the same principle as standard MA, by introducing modifiers which rectify the current value and gradient such that they match the estimated values of the plant at the current operating point. This is achieved in the same manner, through modifiers which are added to the model optimization functions.

$$\begin{array}{cc}\hfill {\Phi }_{k,\pi }\left(\mathit{u}\right)=& {\Phi }_{\pi }\left(\mathit{u}\right)+{(\mathit{u}-{\mathit{u}}_k)}^{\mathsf{T}}{\mathbf{\lambda }}_{k,\pi }^{\varphi }+{\mathbf{\epsilon }}_{k,\pi }^{\varphi },\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\mathit{G}}_{k,\pi }\left(\mathit{u}\right)=& {\mathit{G}}_{\pi }\left(\mathit{u}\right)+{(\mathit{u}-{\mathit{u}}_k)}^{\mathsf{T}}{\mathbf{\lambda }}_{k,\pi }^g+{\mathbf{\epsilon }}_{k,\pi }^g,\hfill \end{array}$$

(17)

where ${\Phi }_{\pi }$ and ${\mathit{G}}_{\pi }$ are the choice of model used to calculate the solutions. The modifiers are dependent on the model used,

$$\begin{array}{cc}\hfill {\mathbf{\epsilon }}_{k,\pi }^{\varphi }=& {\Phi }_p\left({\mathit{u}}_k\right)-{\Phi }_{\pi }\left({\mathit{u}}_k\right),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\mathbf{\epsilon }}_{k,\pi }^g=& {\mathit{G}}_p\left({\mathit{u}}_k\right)-{\mathit{G}}_{\pi }\left({\mathit{u}}_k\right),\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\mathbf{\lambda }}_{k,\pi }^{\varphi }=& {\left.{\nabla }_u{\Phi }_p\left(\mathit{u}\right)\right|}_{{\mathit{u}}_k}-{\left.{\nabla }_u{\Phi }_{\pi }\left(\mathit{u}\right)\right|}_{{\mathit{u}}_k},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\mathbf{\lambda }}_{k,\pi }^g=& {\left.{\nabla }_u{\mathit{G}}_p\left(\mathit{u}\right)\right|}_{{\mathit{u}}_k}-{\left.{\nabla }_u{\mathit{G}}_{\pi }\left(\mathit{u}\right)\right|}_{{\mathit{u}}_k}.\hfill \end{array}$$

(21)

Importantly, the information used to calculate these modifiers requires the same estimates used by standard MA from the plant, therefore additional experiments are not required. The main advantage of modifier adaptation is the guarantee of KKT matching upon convergence, therefore it is desirable that the solution processing method maintains this property. As is seen in Section 5, depending on the method used, the resulting RTO solution may not be equal to any of the individual proposed solutions generated by the models. This can result in premature convergence which does not satisfy the KKT conditions of the plant. An example of this may be that two models suggest operating points in opposite directions, and the resulting processed solution may suggest the current operating point, even though the estimated first order properties of the plant suggest that the current operating point does not satisfy the KKT conditions of the plant. A sufficient condition to avoid this is as follows,

Condition 1.

Convergence, defined as,

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}{\mathit{u}}_{k+1}={\mathit{u}}_k,\end{array}$$

(22)

only occurs if the current operating point is equal to one or more of the potential solutions generated by the models.

With the above condition defined, the following can be proposed on the KKT matching of the plant.

Theorem 1

(Plant KKT matching). If using an MSMA scheme which has converged to a point, ${\mathit{u}}_{\infty }={lim}_{k\to \infty }{\mathit{u}}_k$, Condition 1 is met, and perfect estimates of the gradient and value of the plant are known at the current operating point. Then this converged point is a KKT point of the plant.

Proof of Theorem 1. 

As stated in Theorem 1 and Condition 1, the converged operating point is also a converged point of one of the corresponding models. Thus, as each model matches the gradient of the plant at the current operating point, this must also be a KKT point of the plant, as with standard MA. □

With the overarching mechanisms of the proposed MSMA approach clearly outlined, with a sufficient condition for plant KKT matching upon convergence. In the following sections, the two research questions posed earlier are fleshed out and several methods are investigated.

4. Producing the Proposed Solutions

As shown in the previous section, the MSMA approach requires the functions ${\Phi }_{\pi }\left(\mathit{u}\right)$ and $G_{\pi }\left(\mathit{u}\right)$ to be defined. This section will investigate three different approaches to generating these functions.

4.1. Using Known Model Uncertainties

The first approach considers generates the NLPs using the known uncertainty in the model. This uncertainty can either be structural, where several potential structures for the model are known and each can be used to formulate a separate NLP; or through parametric uncertainty, where the model parameters are known to have uncertainties in their precise values due to simplifications, noise or other sources; or a combination of structural and parametric uncertainties. The NLP functions can be formulated as follows,

$$\begin{array}{cc}\hfill {\Phi }_{\pi }\left(\mathit{u}\right)=& \Phi (\mathit{u},{\mathbf{\theta }}_{\pi }),\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\mathit{G}}_{\pi }\left(\mathit{u}\right)=& \mathit{G}(\mathit{u},{\mathbf{\theta }}_{\pi }),{\mathbf{\theta }}_{\pi }\in \vartheta ,\hfill \end{array}$$

(24)

where $\vartheta$ is a set of parameters which contains the structural and parametric uncertainties in the model. As each of these models are corrected such that the value and gradient matches the estimated value of the plant (and therefore match each other) at the current operating point, this approach assumes that by changing the parameters of the model that second or higher order changes to the model are seen. If changes in the chosen parameters only result in linear changes to the model, the resulting modified models will be identical, and the advantages of a multi-solution approach would be lost.

Additionally, using this approach results in many NLPs of similar complexity to the nominal model being solved for each RTO iteration. Depending on the fidelity of these models, this can be a resource heavy task which cannot always be appropriate in practice, especially if there are many sets of parameters. Therefore, there is a natural trade-off between the number of models and the benefit gained, with each additional model providing diminishing returns. As the modifier adaptation method uses global modifiers to rectify the local properties, the usefulness of using a high-fidelity model is up for debate, and lower fidelity models which have parameters which can shed light on the plant-model mismatch may be more appropriate for this method.

4.2. Using Convexified Models

The second approach to generating the set of solutions considered looks into using convexified models. Convex models offer benefits not only within RTO but also general optimization, where they are generally easier to solve, reducing the computational intensity for each iteration. There are several approaches which have been applied to RTO regarding the use of convex models. Here, a set of convex NLPs is formulated using the models generated from the previous approach.

This approach to convexification is to use each of the models formulated from the known uncertainties, and fit a quadratic function w.r.t. the inputs to the objective and constraint functions [35]. This results in a set of quadratic models used in the NLP,

$$\begin{array}{cc}\hfill {\Phi }_{\pi }\left(\mathit{u}\right)=& {\mathit{u}}^{\mathsf{T}}{\mathit{Q}}_{\pi }^{\Phi }\mathit{u}+{\mathit{L}}_{\pi }^{\Phi }\mathit{u}+C_{\pi }^{\Phi },\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill G_{\pi ,j}\left(\mathit{u}\right)=& {\mathit{u}}^{\mathsf{T}}{\mathit{Q}}_{\pi }^{G_j}\mathit{u}+{\mathit{L}}_{\pi }^{G_j}\mathit{u}+C_{\pi }^{G_j},\forall j\in [1,\dots ,n_g],\hfill \end{array}$$

(26)

where $\mathit{Q}$, $\mathit{L}$, and C, are the quadratic, linear and constant terms for each function, respectively. These terms can be found through a least squares regression across a set of inputs points for each set of parameters in the parameter set, i.e.

$$\begin{array}{cc}\hfill \left[{\mathit{Q}}_{\pi }^{\Phi },{\mathit{L}}_{\pi }^{\Phi },C_{\pi }^{\Phi }\right]=& \underset{\mathit{Q},\mathit{L},C}{min}\sum _{\mathit{u}\in \mathcal{U}}\left|\right|P_2\left(\mathit{u}\right)-\Phi (\mathit{u},{\mathbf{\theta }}_{\pi })|{|}^2,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill \left[{\mathit{Q}}_{\pi }^{G_j},{\mathit{L}}_{\pi }^{G_j},C_{\pi }^{G_j}\right]=& \underset{\mathit{Q},\mathit{L},C}{min}\sum _{\mathit{u}\in \mathcal{U}}\left|\right|P_2\left(\mathit{u}\right)-G_j(\mathit{u},{\mathbf{\theta }}_{\pi })|{|}^2,\hfill \end{array}$$

(28)

where $P_2\left(\mathit{u}\right)$ is a second order polynomial w.r.t. the inputs,

$$\begin{array}{cc}\hfill P_2\left(\mathit{u}\right)=& {\mathit{u}}^{\mathsf{T}}\mathit{Q}\mathit{u}+\mathit{L}\mathit{u}+C.\hfill \end{array}$$

(29)

As convexity is desired, a condition is placed on the eigenvalues of $\mathit{Q}$ such that they are positive. Using quadratic approximations vastly simplifies the multiple NLPs to be solved at each iteration, significantly reducing the computational cost of generating the set of potential operating points. This comes are the cost of losing artifacts from the original model which might explain important phenomena of the process. As the modifiers which are added by the MA scheme already correct the local properties and ruin the global predictive power of the modified model, replacing the detailed model with a quadratic approximation will not have catastrophic implications.

4.3. Using Location Based Models

The previous methods have relied on a set of known uncertainties being readily available, and that this set provides valuable insight into the plant-model mismatch. This is not always the case. This last method offers an alternative approach to generating a set of NLPs to solve, formulated using a single model of the plant.

Using a quadratic fit on the model was utilized in the previous approach, however this fit was carried out over the whole input space, producing a function which provides a general overview of the global properties of the model, but may remove useful information on the local properties of the plant. An alternative is to split the input space into several regions and fit a separate quadratic function to each region. These regions can either be from a uniform grid, or generated through an analysis of the model to formulate regions which follow a pseudo-quadratic nature, thus the resulting fit will be more likely to maintain the local properties of the plant. Each MSMA model has as associated input region,

$$\begin{array}{c}\hfill {\mathcal{U}}_{\pi }\in \mathcal{U}\end{array}$$

(30)

Then using the same quadratic equations as before (Equations (25) and (26)), but with quadratic constants solved using the sub-regions and minimized against the single available model (as shown here using the nominal parameters),

$$\begin{array}{cc}\hfill \left[{\mathit{Q}}_{\pi }^{\Phi },{\mathit{L}}_{\pi }^{\Phi },C_{\pi }^{\Phi }\right]=& \underset{\mathit{Q},\mathit{L},C}{min}\sum _{\mathit{u}\in {\mathcal{U}}_{\pi }}\left|\right|P_2\left(\mathit{u}\right)-\Phi (\mathit{u},{\mathbf{\theta }}_{nom})|{|}^2,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill \left[{\mathit{Q}}_{\pi }^{G_j},{\mathit{L}}_{\pi }^{G_j},C_{\pi }^{G_j}\right]=& \underset{\mathit{Q},\mathit{L},C}{min}\sum _{\mathit{u}\in {\mathcal{U}}_{\pi }}\left|\right|P_2\left(\mathit{u}\right)-G_j(\mathit{u},{\mathbf{\theta }}_{nom})|{|}^2.\hfill \end{array}$$

(32)

Using either method of using uniform or non-uniform grids, allowing these regions to overlap allows for several fitted models to represent each point in the input space. The proximity of these models can be used to formulate weights used in the processing of solutions, and fittings of regions which are far from the current operating point can be neglected entirely, resulting in fewer NLPs to solve at each iteration. Using uniform grids, the number of regions grows to the power of the number of inputs, therefore quickly becomes too many models to reasonably handle. Therefore, using a non-uniform approach to generating these regions may be necessary.

4.4. Solution Production Illustrative Example

This example illustrates the three methods of generating multiple models used by MSMA. The methods produce the multiple solutions using models derived from a model of the plant. The model function used to illustrate these methods is a single variable constraint, taken from [29].

$$\begin{array}{c}\hfill G(u,\mathbf{\theta })={(u-2)}^2-3-{\theta }_{1}sin\left({\theta }_{2}u\right),u\in [0,4].\end{array}$$

(33)

Where necessary, the value and uncertainty of the parameters are known and given as a closed set,

$$\begin{array}{c}\hfill \vartheta :=\left\{\mathbf{\theta }\in {\mathbb{R}}^2|\left[\begin{array}{c}1.7\\ 2.4\end{array}\right]\le \mathbf{\theta }\le \left[\begin{array}{c}2.3\\ 2.6\end{array}\right]\right\}\end{array}$$

(34)

where the nominal parameters are defined as,

$$\begin{array}{c}\hfill {\mathbf{\theta }}_{nom}=\left[\begin{array}{c}2\\ 2.5\end{array}\right].\end{array}$$

(35)

For the purposes of illustrating the solution producing approaches, 5 sets of model parameters are chosen which include the 4 extrema of the parameter set, and the nominal model. Figure 1 shows the three methods of generating the models used to generate the potential solutions. Figure 1a shows the set of models produced by using 5 sets of parameters from the known uncertainty. Figure 1b shows a set of 5 quadratic models, produced by fitting a quadratic function to each of the models from the set of known uncertainties in the parameters.

Finally, Figure 1c shows a set of quadratic models produced from a single set of parameters (here the nominal parameters), but each using a limited set of inputs. Where the original model curvature is convex (i.e., a postive definite Hessian), the fitted quadratic provides a good approximation of the model; and where the original model curvature is concave (i.e., a negative definite Hessian), the fitted quadratic is forced to be convex.

5. Processing the Proposed Solutions

The selection of the processing method strongly relates to the success of the method, with different objectives being achieved (or attempted to be achieved) by each. Some methods focus on improving the feasibility of iterates, improving rate and chance of convergence, or appropriate model selection.

5.1. Selection Based on Modifiers

One such method which has been proposed previously on dealing with multiple models is to use the relative magnitude of the modifiers for each model to select the most appropriate model. This approach has been suggested for handling different structures which provide more accurate approximations of the plant based on the location in the operating space [36,37]. Alternatively, it has also been suggested as a method of handling degradation in the plant which changes the underlying mechanisms of the plant, and thus changes the most appropriate model for use in the RTO scheme [38,39]. The standard approach to model selection is to define an overall modifier based on a weighted sum of the individual modifiers,

$$\begin{array}{c}\hfill {\Psi }_{k,\pi }={\mathit{w}}_{\epsilon }^{\varphi }{\mathbf{\epsilon }}_{k,\pi }^{\varphi }+{\mathit{w}}_{\lambda }^{\varphi }{\mathbf{\lambda }}_{k,\pi }^{\varphi }+{\mathit{w}}_{\epsilon }^g{\mathbf{\epsilon }}_{k,\pi }^g+{\mathit{w}}_{\lambda }^g{\mathbf{\lambda }}_{k,\pi }^g\end{array}$$

(36)

where $\mathit{w}$ refers to the weights. Then the model is selected based on the minimum overall modifier as follows,

$$\begin{array}{cc}\hfill f_{MS}({\mathit{u}}_k,{\mathit{u}}_{k,\pi }^{*})=& (\mathit{I}-\mathit{K}){\mathit{u}}_k+\mathit{K}{\mathit{u}}_{k,{\pi }_k}^{*},\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill {\pi }_k\in & \arg \underset{\pi }{min}{\Psi }_{k,\pi }.\hfill \end{array}$$

(38)

By choosing the model based on the modifiers, the model can be selected before all solutions are solved, thus removing one of the primary concerns of MSMA, of solving many NLPs per iterate. As the final RTO solution is inherently a solution to one of the models which matches the estimates of the plant, then Condition 1 is met and KKT matching is guaranteed upon convergence if perfect estimates of the plant are available.

As a result of choosing the most appropriate NLP before solving for multiple solution, the information from the other models and solutions is discarded. The choice of the weights is highly influential to the success of the approach. The weights serve to bring all the modifiers to a similar order of magnitude, such that a single constraint or the objective does not dominate the overall modifier term. Additionally, they offer the ability to have certain constraints or the objective more influence over the choice of model. In the end, the choice of the weights are highly process specific and depend on the decisions of the operator. Alternatively, the magnitudes of each modifier can be ranked, and the sum of the ranks can be used to choose the model.

5.2. Selection Based on Central Tendencies

One of the simplest methods of combining the multiple solutions is to combine the proposed solutions from all the approaches based on the central tendencies. Three central tendencies are considered in this work, arithmetic mean, geometric median, and most likely. All of these allow for the whole set of data to be considered in the choice of the next operating point.

5.2.1. Arithmetic Mean

Similarly to the median, using the arithmetic mean, either all of the points can be considered equally, or through the use of weightings, certain operating points can be favored, potentially improving the convergence rate and feasibility of the iterates. The selection function using the arithmetic mean is as follows,

$$\begin{array}{c}\hfill f_{MS}({\mathit{u}}_k,{\mathit{u}}_{k,\pi }^{*})=(\mathit{I}-\mathit{K}){\mathit{u}}_k+\mathit{K}\sum _{i=1}^{n_{\pi }}{w}_i{\mathit{u}}_{k,i}^{*}\end{array}$$

(39)

where $w_i$ are weights which sum to 1. As with the median, using the mean can produce points which are not from the original set of potential operating points, thus Condition 1 may not be satisfied upon convergence. This can be overcome using a property of convex models,

Proposition 1

(KKT matching using the convex models). Using any solution processing method which selects a point within the convex hull of the potential solutions along with a solution production method using convex NLPs in the MSMA scheme given by (14) and (15). If perfect estimates of the value of the plant constraints, and gradient of the plant objective and constraints are available, upon convergence the converged point is a KKT point of the plant.

Proof of Proposition 1. 

Consider the current operating point ${\mathit{u}}_k$. If this operating point is infeasible for the plant, i.e., $\exists j_v\in \{1,\dots ,n_g\}$ such that $G_{j_v,p}\left({\mathit{u}}_k\right)>0$. The modified convex NLP can be written as the sum of an affine term (which their equal to the estimates of the plant), and a curvature term,

$$\begin{array}{c}\hfill G_{j_v,k}\left(\mathit{u}\right)=G_{j_v,p}\left({\mathit{u}}_k\right)+{\left.{\nabla }_{\mathit{u}}{G}_{j_v,p}\right|}_{{\mathit{u}}_k}{(\mathit{u}-{\mathit{u}}_k)}^{\mathsf{T}}+[\mathrm{Curvature}\mathrm{term}].\end{array}$$

(40)

The solution to the NLP using this modified constraint must have a constraint less than or equal to 0 (to be feasible), and the curvature term is positive as the base NLP is convex. Therefore, each solution in the set of potential operating points generated from the convex NLPs must be within the semi-infinite open region defined by the gradient of the violated constraint,

$$\begin{array}{c}\hfill {\left.{\nabla }_{\mathit{u}}{G}_{j_v,p}\right|}_{{\mathit{u}}_k}{(\mathit{u}-{\mathit{u}}_k)}^{\mathsf{T}}<0.\end{array}$$

(41)

Therefore, the current operating point is outside of the convex hull of the potential solutions and cannot be the next operating point, and convergence cannot occur at an infeasible point of the plant.

Next, if this operating point is feasible for the plant, using the same logic as for the constraints, the set of potential operating points generated from the convex NLPs must either be within the semi-infinite open region defined by the gradient of the objective function,

$$\begin{array}{c}\hfill {\left.{\nabla }_{\mathit{u}}{\varphi }_p\right|}_{{\mathit{u}}_k}{(\mathit{u}-{\mathit{u}}_k)}^{\mathsf{T}}<0.\end{array}$$

(42)

or at the current operating point. If one convex NLP suggests the current operating point as the solution to the MA problem given by Equations (14) and (15), then as all models, by definition, have the same first order properties as one another at the current operating points, all potential operating points must be at the current operating point. Therefore, either the set of operating points must either be within the semi-infinite open region defined above, and convergence to ${\mathit{u}}_k$ will not occur at the current operating point, or all potential points are at the current operating point, and Condition 1 is met, thus from Theorem 1 the converged operating point is a KKT point of the plant. □

As the mean of a set is within the convex hull of the set, Proposition 1 is valid using the solution processing method given by Equation (39) if the solutions are produced using a set of convex models.

5.2.2. Geometric Median

Using the geometric median finds an operating point which balances the directions to each of the potential operating points in the set generated by the models, thus naturally handling outliers. The geometric median can be found by solving the following,

$$\begin{array}{cc}\hfill f_{MS}({\mathit{u}}_k,{\mathit{u}}_{k,\pi }^{*})=& (\mathit{I}-\mathit{K}){\mathit{u}}_k+\mathit{K}{\mathit{u}}_k^{*}\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill {\mathit{u}}_k^{*}\in & arg\underset{\mathit{u}}{min}\sum _{i=1}^{n_{\pi }}{w}_i\left|\right|\mathit{u}-{\mathit{u}}_{k,i}\left|\right|.\hfill \end{array}$$

(44)

where $w_i$ are weights which can optionally be used to favor certain models/solutions. Using the median can produce points which are not from the original set of potential operating points, thus upon convergence Condition 1 may not be satisfied. If convex models are used, Proposition 1 is satisfied, but this can also be rectified by limiting the minimization to the domain of the potential operating points, thus finding the potential solution which the best approximates the median, i.e.,

$$\begin{array}{cc}\hfill {\mathit{u}}_k^{*}\in & arg\underset{\mathit{u}\in {\mathit{u}}_{k,\pi }^{*}}{min}\sum _{i=1}^{n_{\pi }}{w}_i\left|\right|\mathit{u}-{\mathit{u}}_{k,i}\left|\right|.\hfill \end{array}$$

(45)

Using the limited median satisfies Condition 1, and KKT matching is guaranteed upon convergence if perfect estimates of the plant are available.

5.2.3. Most Likely

Another approach to selecting the most appropriate solution is through the use of the most likely operating point via a distribution or a mixture distribution. By fitting a distribution to the set of model solutions, typically one for each structure forming a mixture distribution, and using this to select the next operating point. When using a single model which follows a close to normal distribution of points, the resulting solution will be identical to using averages. However, if multiple structures (and multiple distributions) are used, then the most likely point will not be between the two distributions but within one of them.

For a mixture distribution, for example one for each structure of model available, if each structure suggests a distinct set of potential operating points, then the most likely point from the overall distribution will depend on the variance, with the individual distribution with the least variance being favored. This is not necessarily the best choice from the set of points, as the most appropriate structure, and thus the better operating point, may have more variance in the suggested points.

The choice of distribution depends on the set of operating points obtained, but as convergence is approached, the set of points will approach a singular point, therefore the chosen distribution should be able to accurately handle this case, such as Gaussian (normal) or skew-Gaussian (skew-normal) distributions. The simplest case is using a multivariate Gaussian mixture model and the probability for a given set of operating conditions from this distribution is given by the following,

$$\begin{array}{c}\hfill \mathit{U}\sim \mathcal{N}(\mathbf{\mu },\mathbf{\Sigma })=\sum _{i=1}^D{w}_i\mathcal{N}({\mathbf{\mu }}_{\mathbf{i}},{\mathbf{\Sigma }}_{\mathit{i}}),\end{array}$$

(46)

where D is the number of distributions, w is a weighting factor, $\mathbf{\mu }$ is the distribution mean, and $\mathbf{\Sigma }$ is the distribution covariance matrix for distribution i.

The sum of the weights must equal 1 for the probabilities to remain meaningful, i.e., between 0 and 1, but as is seen in the next equation, the relative magnitudes are more important. $f_{\mathit{U}}$ refers to the overall PDF of the mixture distribution, and can be used to find the mode of the distribution. The final operating point is filtered from the point of maximum likelihood,

$$\begin{array}{cc}\hfill f_{MS}({\mathit{u}}_k,{\mathit{u}}_{k,\pi }^{*})=& (\mathit{I}-\mathit{K}){\mathit{u}}_k+\mathit{K}{\mathit{u}}_k^{*},\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill {\mathit{u}}_k^{*}\in & arg\underset{\mathit{u}}{max}{f}_{\mathit{U}}\left(\mathit{u}\right).\hfill \end{array}$$

(48)

Alternatively, Condition 1 can be enforced if the maximum is limited to the set of suggested operating points, i.e.,

$$\begin{array}{cc}\hfill {\mathit{u}}_k^{*}\in & arg\underset{\mathit{u}\in {\mathit{u}}_{k,\pi }^{*}}{max}{f}_{\mathit{U}}\left(\mathit{u}\right).\hfill \end{array}$$

(49)

5.3. Selection Based on Closeness

The final method to combining the solutions is considering the distance between the current operating point and the potential operating points. Taking larger steps in the input space is risky, as the only known of the plant is the current operating point. Therefore, a potential choice from the set of solutions is the closest to the current operating point. This is defined by using a normalized distance,

$$\begin{array}{cc}\hfill f_{MS}({\mathit{u}}_k,{\mathit{u}}_{k,\pi }^{*})=& (\mathit{I}-\mathit{K}){\mathit{u}}_k+\mathit{K}{\mathit{u}}_k^{*},\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill {\mathit{u}}_k^{*}\in & arg\underset{\mathit{u}\in {\mathit{u}}_{k,\pi }^{*}}{min}\left|\right|\mathit{u}-{\mathit{u}}_k\left|\right|.\hfill \end{array}$$

(51)

As the closest operating point is inherently one of the potential operating points suggested by the models, Condition 1 is satisfied, and KKT matching is guaranteed upon convergence if perfect estimates of the plant are available. Alternatively to selecting the closest solution, if convex NLPs are used, the closest operating point within the convex hull of the set of potential solutions can be used.

5.4. Solution Processing Illustrative Example

A two variable, $\mathit{u}=[u_1,u_2]$, example has been developed to illustates the approaches above of combining a set of potential operating points into a single point for use by the RTO scheme. To allow full comparison of the solution processing, all methods are illustrated using the solutions produced using the parametric uncertainty, and all weights for the modifiers, solutions and distributions are discarded, i.e., equal weightings. In this example, structural plant-model mismatch is introduced via the non-linear function $\zeta \left(u_1\right)$, which is applied to the first input. The system cost and constraints are given via parametric functions,

$$\begin{array}{cc}\hfill \Phi (\mathit{u},\mathbf{\theta })=& 4-{\theta }_1\zeta \left(u_1\right)-u_2,\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill G(\mathit{u},\mathbf{\theta })=& {\theta }_2{(\zeta \left(u_1\right)-0.9u_2)}^2+u_2-1.8.\hfill \end{array}$$

(53)

where

$$\begin{array}{c}\hfill \mathbf{\theta }=\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\end{array}\right]\end{array}$$

(54)

are the parameters. The model has two different potential structures of $\zeta \left(u_1\right)$ as given:

$$\begin{array}{cc}\hfill \left(\mathrm{Plant}\right)& \zeta \left(u_1\right)=e^{u_1}+e^{-u_1}-1,\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill (\mathrm{Model}1)& \zeta \left(u_1\right)=u_1^2+1,\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill (\mathrm{Model}2)& \zeta \left(u_1\right)=\sqrt{3u_1^2+1}.\hfill \end{array}$$

(57)

The plant is accurately described using the following parameters,

$$\begin{array}{c}\hfill {\mathbf{\theta }}_p=\left[\begin{array}{c}1\\ 1.5\end{array}\right].\end{array}$$

(58)

The current operating point, ${\mathit{u}}_k$, is defined to be at the point $[0.5,1.5]$. Figure 2 illustrates the current plant objective and constraint functions with the true plant optimum and current operating point.

The set of parameters used to formulate the models is formed of the choice of either structure 1 or 2 for $\zeta$, and a value of $\mathbf{\theta }$ taken from a normal distribution. The choice of these parameters is based off a comparison to the true plant constraint and objective to account for some of the structural mismatch in $\zeta \left(u_1\right)$,

$$\begin{array}{cc}\hfill {\vartheta }_1\sim & \mathcal{N}\left(\left[\begin{array}{c}1\\ 1.8\end{array}\right],\left[\begin{array}{cc}0.2& 0\\ 0& 0.2\end{array}\right]\right),\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill {\vartheta }_2\sim & \mathcal{N}\left(\left[\begin{array}{c}0.9\\ 1.8\end{array}\right],\left[\begin{array}{cc}0.5& 0\\ 0& 0.3\end{array}\right]\right)\hfill \end{array}$$

(60)

where ${\vartheta }_1$ and ${\vartheta }_2$ represent the set of parameters for model structures 1 and 2, respectively. The set of points used by the solution processing function is generated by taking 30 sets of parameters for each of the two model structures from the above distribution, generating 60 potential operating points.

Figure 3 shows the solution from using each of the three different approaches discussed in the previous section. Firstly, selection based on the modifiers suggests a point which is relatively close to the most likely point. Next, selection based on using either the mean or the median suggests a point which is also relatively close to the plant optimum, but is not guaranteed to be a point suggested by any of the models in the set of potential operating points. Selection based on closest is the only method which produces a point which is feasible for the plant (before filtering), and also suggests a potential operating point from the set of models, thus guaranteed to satisfy Condition 1.

Finally, selection based on most likely utilizes a fitted distribution. This fitted distribution is formed of a mixture Gaussian distribution, formed of two Gaussian distributions, one fitted to each of the model structures. The resulting most-likely solution is at the point where both distributions overlap. As this problem is non-linear, despite the error in the parameters being characterized as being normally distributed, the resulting set of solutions are not. Clearly there is a skewness to the data, with a bunching of points, with a long tail of other solutions. As a standard Gaussian distribution has no skewness, this tail will draw the distribution from the true density of the solutions, therefore the most-likely point obtained from the mixture Gaussian fit is a poor representation of the true most-likely point, and is one of the key issues with dealing with distributions and non-linear functions.

5.5. Recommended Schemes

A wide range of options have been suggested for the production and processing of the solutions in the MSMA framework. In this penultimate section, some combinations which work well together are highlighted with some comments on their effectiveness.

1. Selection based on modifiers using known model uncertainties. The first suggested approach uses the modifiers to determine the NLP to use for the RTO scheme before the solutions are solved. By using the known uncertainties in the model parameters, the choice of NLP (and effectively the choice of model parameters) becomes a rudimentary parameter estimator. The prime advantage of this approach is the reduced computation required per RTO iteration, with only the additional calculation of the modifiers of the set of models over standard MA. This comes at the expense of removing the information contained in the set of potential operating points (as they are discarded before being solved).

2. Selection based on central tendencies using quadratic approximations. The next suggested approach uses the central tendencies of the set of solutions generated by either region-based or uncertainty based models. The use of convex quadratic models allows for the solutions to be found fast, and the guarantee of KKT matching upon convergence is maintained by the approach.

3. Selection based on closeness using known model uncertainties. The final suggested approach is to take advantage of the closest operating point. Using the closest point is considered the safest option suggested and can be combined with using the model uncertainties to find the true optimum of the plant. This approach is the most computationally demanding of the suggested approaches, but can be supplemented with quadratic approximations or lower fidelity models to reduce the computation times, or by refining the set of models to reduce the number of potential solutions.

5.6. Analysis of Schemes

The primary limitation to using MSMA approaches (other than using the modifiers to find the most appropriate model) is that in order to find the set of potential operating points, many model NLPs must be solved at each iteration of the RTO scheme. Therefore, if the model is of high-fidelity, this is a costly and time-consuming task which may increase the total RTO convergence time if it takes significantly longer than the convergence time of the plant.

The MA approach adds affine modifiers to the model which results in an NLP which accurately predicts the local aspects of the plant, but can result in poor predictions of global picture of the plant. Therefore, using high-fidelity models in the MA scheme may produce artifacts in the optimization functions, such as local minima, which are not of significance when looking for the true plant optimum, and may slow down the convergence of the RTO scheme. The use of lower-fidelity models is favored when this is the case as the global properties of the plant are maintained without these artifacts. Another advantage to using lower-fidelity models which is relevant to MSMA is the solve time for each NLP is significantly reduced, resulting in RTO solve times which do not slow down the convergence of the RTO scheme.

Using the multi-model schemes which are recommended have the potential to improve the convergence properties of MA. This will be analyzed by looking firstly at the model adequacy conditions of the proposed schemes. For this article, a model is considered adequate if convergence to the plant optimum is possible (i.e., if the current operating point is the plant optimum, then the solution to the RTO scheme is also at this operating point). For standard MA, a necessary condition for this is that the model has a positive definite Hessian of the Lagrangian at the plant optimum, but this is only sufficient to guarantee that the current operating point is a local minimum of the NLP, and not a global minimum.

For using the modifiers as the selection method, the model is adequate if, when operating at the plant optimum, the model which has the minimum overall modifier is adequate under standard MA. That is that the chosen model by the solution processing equation has a positive definite Hessian of the Lagrangian at the plant optimum. The basis of this selection method is that the model with the minimum overall modifier will more closely match the plant. Therefore, this can also apply to the Hessian of the Lagrangian of the chosen model, where it may be more similar to the plant, which will be positive definite at the plant optimum. This could provide a better level of guarantee of model adequacy than standard MA, but is case dependent and not guaranteed.

For using central tendencies, it depends on the method used. For the geometric median, if at least half of the NLPs are adequate, then model adequacy is also satisfied for the median (as half the set of potential operating points will all suggest the current operating point, which will then equal the median). This is not required as under certain conditions, solutions from non-adequate NLPs will cancel one another out in the median calculation. For the mean and most likely, as every potential solution contributes to the next operating point, model adequacy is only obtained if all individual models have a positive definite Lagrangian at the plant optimum. In reality, if measurement noise is considered, as long as the majority of the model NLPs are adequate, good convergence stability can be observed. If quadratic approximations are used then every individual model will have a positive definite Lagrangian, therefore when used in conjunction with the central tendency methods, model adequacy is guaranteed.

Finally, considering the closest operating point. If any model in the set of NLPs satisfies the model adequacy of standard MA, then this will be produce a solution at the current operating point, and therefore be the closest solution, and the model adequacy is guaranteed.

The other convergence properties which may improve when using multi-model approaches is an increased rate of convergence and a increased likelihood that the next iteration is feasible for the plant. These two properties are highly linked, as typically an increase to the rate of convergence is determined by the magnitude of the filter used by the scheme, which can be made more aggressive if the probability of safety is increased. Proof of improvement to these properties cannot be done mathematically without making further assumptions about the mismatch between the plant and model, which is typically not possible to check in reality. This is because under the current assumption of structural mismatch, there can always be an edge case where improvement is not observed (e.g., in cases where standard MA lucks out and finds the true plant optimum in a single iteration, which cannot be improved upon).

These schemes also depend on the accuracy of the set of models used to define the potential solutions. Poor performance may be observed if an inaccurate model used to produce one of the potential solutions, for example if a model constraint with a significantly larger second derivative is used, then this will likely be the closest solution, and result in a slow convergence. Despite this lack of mathematical proof of improvement, what can be looked into is several case studies of differing complexity and compare the performance of the proposed schemes to standard MA. This is not rigorous, but does highlight where improvement may be observed, and potentially why it is observed. For this reason, three different case studies will be analyzed in the following section, with a CSTR, a distillation column, and a semi-batch reactor.

6. Case Studies

Each of the three recommended schemes are illustrated on three different case studies of varying difficulty. The first is a benchmark case study in RTO schemes known as the Williams-Otto CSTR [8,40]. This CSTR has 6 state equations, and 3 inputs, where the nominal model is inadequate for use with standard MA. The second case is a distillation column for the separation of methanol from n-propanol. This system has over 200 state equations for the plant, therefore is more computationally challenging. The final case study looks at a semi-batch bioreactor with two inputs which are controlled over the whole batch time. After discretization, a higher-dimensional problem is produced, with a total number of inputs of 12. At the end of this section, some comments are made about what improvement may be observed using the MSMA approaches.

For each case study, a simulation of the plant is run, and steady-state measurements are taken at the current operating point which are used to replicate taking measurements in practice. Therefore, knowledge of the set of equations used to simulate the plant is not known/used by the RTO schemes. In these case studies, measurement noise, disturbances, or other errors have not been considered. This produces an idealized scenario which cannot be realistically met in industrial applications. This idealized simulation does still provide valuable insight into the proposed approaches, where the rate of convergence, stability of convergence (from a mathematical standpoint), and robustness against infeasible operation caused by plant-model mismatch can all be assessed.

6.1. Williams-Otto CSTR

Each of the three recommended schemes are illustrated on the Williams-Otto case study [40], which is a benchmark case study for RTO schemes.

6.1.1. System Overview

This problem is concerned with the optimization of a CSTR which converts two reactants, A and B, into desired products, P and E. There is also an intermediate component, C, and an undesired product, G. The system of equations which determine the states of the plant can be written as the following three reactions,

$$\begin{array}{cc}\hfill A+B& \to C,\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill B+C& \to P+E,\hfill \end{array}$$

(62)

$$\begin{array}{cc}\hfill C+P& \to G,\hfill \end{array}$$

(63)

The operating conditions are controlled via three independent inputs. These inputs are the flow rates of the reactants in kg h⁻¹, and the temperature of the reactor in ${}^{\circ }\mathrm{C}$, given as $\mathit{u}=[F_A,F_B,T]$. The states of this system are the mass fractions of the components, and the measured outputs are the states. The CSTR is assumed to be ideal, and the reactions are assumed to be elementary.

The model of this system is given as a simplified reaction mechanism with only two reactions [8],

$$\begin{array}{cc}\hfill A+2B& \to P+E,\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill A+B+P& \to G,\hfill \end{array}$$

(65)

The NLP to be solved is as follows,

$$\begin{array}{cc}\hfill {\mathit{u}}^{*}=\arg \underset{\mathit{u}}{max}& J(\mathit{u},{\mathit{y}}_p\left(\mathit{u}\right)),\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& g(\mathit{u},{\mathit{y}}_p\left(\mathit{u}\right))=X_G-0.08\le 0,\hfill \end{array}$$

(67)

where J is the objective function, and g is the constraint. The aim of this NLP is the maximize the objective function which is defined with respect to the profit of the system, given as,

$$J=1143.38X_{P}F+25.92X_{E}F-76.23F_A-114.34F_B.$$

(68)

where $F=F_A+F_B$ is the overall flow rate of the system. The inputs are limited to the following input space,

$$\begin{array}{c}\hfill \left[\begin{array}{c}3\\ 6\\ 80\end{array}\right]\le \left[\begin{array}{c}{F}_A\\ F_B\\ T\end{array}\right]\le \left[\begin{array}{c}4.5\\ 11\\ 105\end{array}\right].\end{array}$$

(69)

The parameters used for the plant and model, along with the state equations are given in Appendix A. The known uncertainty in the parameters is confined to the activation energies of the two reactions, which is characterized via a joint normal distribution. The set of models is formed of 8 sets of parameters which are one standard deviation from the mean, 12 sets of parameters which are two standard deviations from the mean, and the nominal model, forming a uniform set of 21 models.

6.1.2. Standard MA

The standard MA approach using the nominal parameters for the model is illustrated in Figure 4. The resulting RTO trajectory does not convergence to the plant optimum when using either a high input gain ($\mathit{K}=0.7\mathit{I}$), or a low gain ($\mathit{K}=0.3\mathit{I}$). It has been shown that using the nominal parameters, the Hessian of the Lagrangian is positive definite at the plant optimum, however when operating at the plant optimum, the modified NLP has a global minimum away from the plant optimum, thus convergence cannot occur [28].

6.1.3. MSMA: Selection Based on Modifiers

The first approach investigated uses the modifiers to determine which model is the most appropriate for use in the MA scheme. The difference between the plant and model value and gradients of the objective function and constraint functions are considered. In order to make these values comparable, the relative difference for each quantity is defined, and then ranked from lowest to highest. The sum of these ranks is used to define the model used for the next iteration of the MA scheme (with the lowest overall rank being chosen).

Using this approach with an input filter of $\mathit{K}=0.7\mathit{I}$ the true optimum can be found, as shown in Figure 5. Initially this scheme does not perform well, and is likely because the chosen model does not direct the RTO scheme in the correct direction. However, an appropriate model is found, and convergence occurs after around 10 iterations, which is not observed by standard MA. Using the modifiers to select the model used has a fundamental flaw in that no matter which model is selected, they are all corrected such that the value and gradient match the plant. Therefore, ideally choosing a model which has similar second order properties to the plant is desired. However, this is not known for the plant without further experiments, and even if it was known, it could be corrected for [41], rather than used as a basis for model selection.

This comes at the profit of being able to apply this approach to virtually any scenario for which standard MA is applicable, as the number of experiments required is similar, and the computing power required for each RTO calculation is comparable.

6.1.4. MSMA: Selection Based on Central Tendencies

The second approach investigated relates to the use of central tendencies. For this case, the model uncertainties are assumed to be unknown, and only the set of nominal parameters are known, therefore using region-based quadratic approximations is applicable. These regions are formulated firstly by gridding the input space, here an $11\times 11\times 11$ grid is used. This grid can be used for form overlapping regions, here each region is formed of a $4\times 4\times 4$ set of points, resulting in $8^3$ regions. At each region, a convex second order polynomial w.r.t. the inputs is fit to the region, and the quadratic term is saved. As the system is relatively simple, solving the state equation for the model can be done rapidly (in this case a few milliseconds), therefore calculating the constants used in the parameters to formulate the set convex regions takes under a minute wall clock time.

At each operating point, the set of regions which have used points local to this operating point are used to find the set of potential operating points. Most points have 27 overlapping regions, but towards the edge of the input space, fewer regions exist. The mean of the potential operating points is taken as the next operating point, using an input filter gain of $\mathit{K}=0.7\mathit{I}$. As the models used are convex, the model adequacy conditions are guaranteed, and this approach rapidly converges to the true optimum of the plant without violating the constraints, as shown in Figure 6. As at each iteration, only up to 27 convex quadratic NLPs are solved, this can be solved rapidly.

6.1.5. MSMA: Selection Based on Closeness

The final approach investigated looks at using the closest potential operating point to the current operating point as the next RTO iteration. This approach requires solving the optimum of all the models for each iteration, and selecting the closest to the current operating point, which is more computationally intensive than the previous approaches. As each NLP is approximately the same fidelity as the nominal model, this takes in the order 20 times longer than for standard MA. This approach does however successfully convergence to the true optimum faster than the other approaches using an input filter gain of $\mathit{K}=0.7\mathit{I}$, as shown in Figure 7.

6.2. Distillation Column

As a more elaborate example with more complex dynamics to illustrate the proposed methods on, a simulation of a distillation column has been simulated [23,42]. This example is of a high purity binary distillation column, used in the separation of methanol and n-propanol. The column has 40 trays ($N=40$), with the feed on tray 21 ($N_f=21$), a partial reboiler, and total condenser. The open-loop system inputs are the reboiler heat duty, Q, and the reflux volumetric flow rate, $L_{vol}$. A PI control scheme is in place based around controlling the temperatures on the key stages of trays 14 and 28.

6.2.1. System Overview

A detailed description of the plant simulation is given in [23]. To summarize, this 204 state DAE is formed of 82 differential states and 122 algebraic states. The differential states are formed of 42 composition states, and 40 molar holdup states. Whilst the algebraic states are formed of 41 volumetric fluxes, 40 liquid fluxes, and 41 temperatures.

Significant structural changes have been given to the model to provide structural mismatch to the plant. The model is based off a distillation column with $100\%$ efficient trays, but with a fewer number of trays, such that the overall separation is comparable. Therefore, the nominal model has a rectifying section with 9 trays and a stripping section with 14 trays. Other simplifications include,

1.

The molar-hold up of the trays are assumed to be constant

2.

The reboiler and condenser molar holdup are assumed to be constant (with variable volumetric holdup)

3.

The condenser is assumed to operate at the saturated liquid temperature

4.

Incorrect feed concentration and flow rate

The resulting model has 71 states. Additionally, the feed is assumed to be fixed with a flow rate of 14 $\mathrm{L} {\mathrm{h}}^{-1}$ and a concentration of 0.32 at 71 ${}^{\circ }\mathrm{C}$, however the true flow rate into the plant is with a concentration of 0.30, and a flow rate of 14.93 Lh⁻¹. The uncertainty in the model is confined to the number of trays in the rectifying section, with the range being from 7 to 11. This forms a pool of five models to be used by the proposed multiple model schemes.

The NLP for the system is based on the flow rates of the bottoms and distillate, and the cost of the heat flux to the reboiler. Typically the objective of a separation process like this one will solely depend on the heat flux, however in this case it would result in an optimum solely defined by the constraints. The constraints on the system relate to the concentration of the bottoms and distillate. The NLP for the system is as follows,

$$\begin{array}{cc}\hfill \underset{\mathit{r}}{min}& \varphi \left(\mathit{u}\right(\mathit{r}),\mathit{y}(\mathit{r}\left)\right):=0.12Q-23040D-86400B+3.7\hfill \end{array}$$

(70a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \mathit{g}(\mathit{u}\left(\mathit{r}\right),\mathit{y}\left(\mathit{r}\right)):=\left[x_B-0.005,0.986-x_D\right]\le \mathbf{0},\hfill \end{array}$$

(70b)

$$\begin{array}{cc}\hfill & T_{28,s}\in \left[70,74\right],T_{14,s}\in \left[82,86\right].\hfill \end{array}$$

(70c)

where x is the mass fraction of methanol, B and D are the bottoms and distillate flow rates, respectively, $\mathit{r}=[T_{28,s},T_{14,s}]$, and $T_{28,s}$ and $T_{14,s}$ are the set points to the temperatures in the key trays of the rectifying section and the stripping section, respectively.

6.2.2. Standard MA

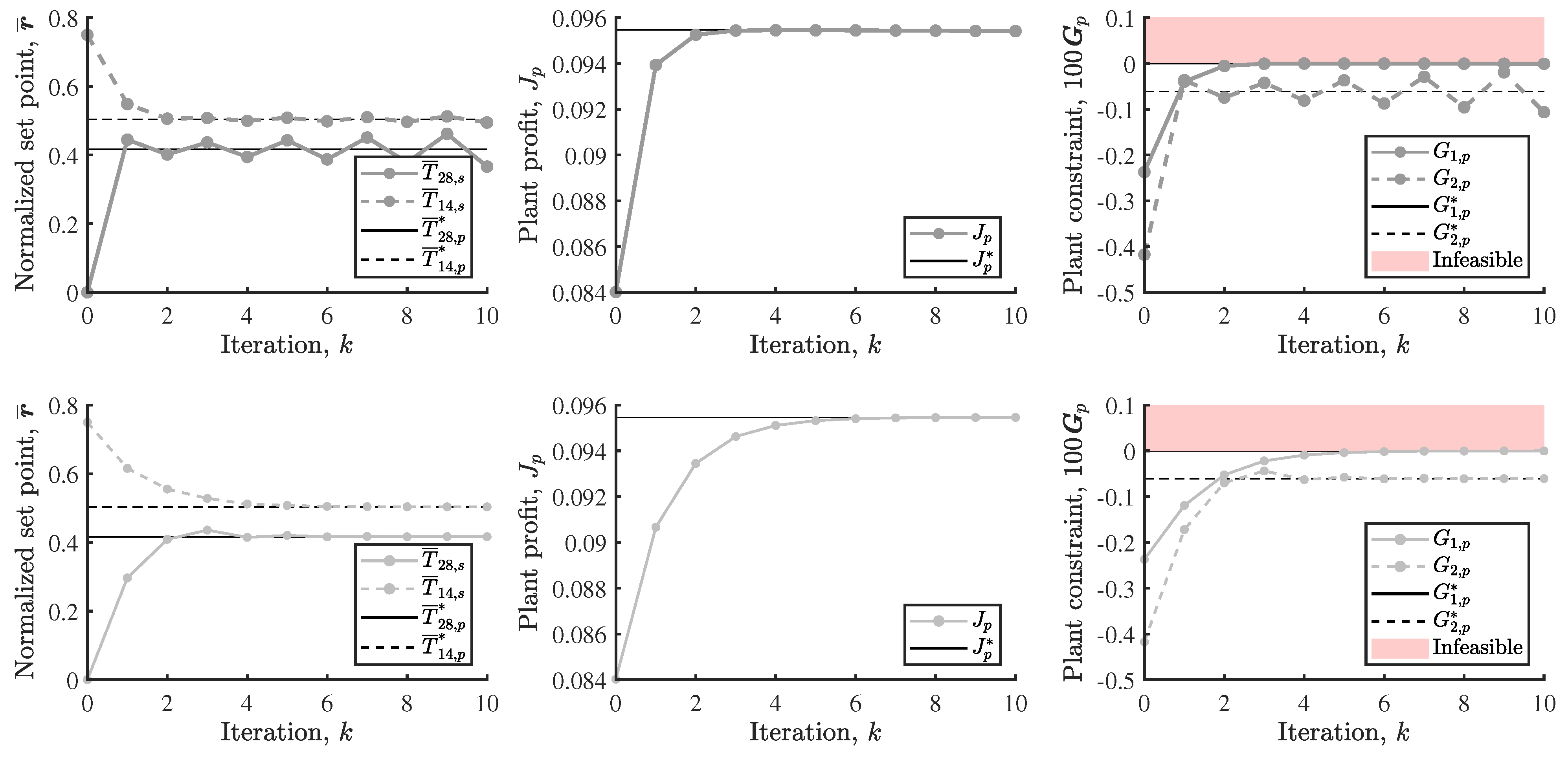
The first approach is using standard MA which will give a baseline for the performance of MA schemes on the distillation column defined above. The three characteristics which are used to gauge the performance of the scheme are the controller set points, the constraint function values, and the objective function value. The controller set points are displayed as their normalized forms, which are defined as follows,

$$\begin{array}{c}\hfill {\overline{T}}_{28}=\frac{T_{28}-70}{4},\end{array}$$

(71)

$$\begin{array}{c}\hfill {\overline{T}}_{14}=\frac{T_{14}-82}{4}.\end{array}$$

(72)

The performance of the standard MA scheme is illustrated in Figure 8 using both an input filter of $\mathit{K}=0.9\mathit{I}$, and $\mathit{K}=0.6\mathit{I}$. With the high gain, the system does not converge, but does approach a cycle with similar plant profit to the true plant optimum, without breaking the constraints. The RTO trajectory with the reduced filter approaches the optimum more slowly, but does successfully converge to the plant to optimum.

6.2.3. MSMA: Selection Based on Modifiers

The first of the MSMA scheme investigated is the minimum modifier approach, where the solution is selected based on the relative magnitudes of the modifiers. The performance of the minimum modifier MSMA scheme is illustrated in Figure 9, where the scheme successfully converges to the optimum with a decaying oscillation in the set points around the true plant optimum. The choice of model NLP by the minimum modifier selection is where the number of rectifying trays is 8, other than the second iteration, where 9 trays is preferred.

This result is an improvement over standard MA, where a lower input gain was required in order to achieve stability in the convergence, which slowed the convergence rate. This only comes at the additional cost of calculating the modifiers of each of the 5 models.

6.2.4. MSMA: Selection Based on Central Tendencies

The next MSMA approach uses regional quadratic approximations of the nominal model to generate the solutions, and uses the mean of these quadratics to generate the next RTO solution. The regions are formed from a uniform $11\times 11$ gridded set point space, and each region is formed of a $4\times 4$ region within this uniform gird.

The performance of the regional quadratic MSMA scheme is illustrated in Figure 10, where the scheme successfully converges to the optimum. As the regional quadratics used to find the set of potential operating points are bounded to a small subspace of the true set point space, the magnitude of step-size for some of the solutions is short, thus the resulting trajectory is more cautious than other MSMA approaches, and similar to that of the reduced gain standard MA.

6.2.5. MSMA: Selection Based on Closeness

The final MSMA approach uses the closest solution from the set of solutions to define the next operating point. The performance of the closest MSMA scheme is illustrated in Figure 11, where the scheme successfully converges to the optimum faster than any of the previous approaches, without any instability or oscillation in the set points. The choice of model NLP is where the number of rectifying trays is 7 for the whole trajectory, other than the fifth iteration, where 11 trays is preferred.

6.2.6. Analysis of Computational Complexity

For this case study, one method to solve the steady state of the column for a given set of inputs is to use an ODE solver over a long time horizon until steady-state is reached. This is initialized by running the model of the column at the current operating point and using these saved states as a basis for each model run for the current iteration. This also has the benefit of being more likely to achieve the same steady-state as the plant if multiple steady-states exist for a given set of inputs. This analysis is carried out by firstly looking at the computation time of the model and standard MA. As each RTO scheme is run on the same machinery, the relative complexity of each proposed method can be compared to one another.

A single solving of the nominal model depends on the current states and relative change to the input, but is of the order of 0.5 s to 1 s wall time. Each of the models in the set takes roughly a similar amount of time as one another, with the shorter columns being marginally faster than larger columns as they have fewer states. As the system only has two inputs, the number of function evaluations is relatively low, with only 30–100 model simulations required to find the optimum of the model, taking approximately 30 s. For standard MA, this is very similar, with the linear modifier term taking negligible time to solve.

The computation required to solve the modifiers for most MA schemes can be carried out as soon as the previous operating point is found. This is because the majority of the computation required is in solving several steady-state simulations of the model (if done numerically), which do not depend on the measured/estimated values of the plant. Therefore, the additional modifier calculations associated with the method of using the modifiers to determine the solution (and the closest solution method) will not cause additional time operating suboptimally. As the chosen model has fewer states than the nominal model, the overall computation time is marginally faster than standard MA.

As for use of the regional quadratics, pre-processing of the pool of models is required to create the set of convex models used by this scheme. This requires running the nominal model at each point in the gridded input space (121 simulations, approximately 110 s), then fitting the quadratic for each region (512 regions, approximately 25 s), taking 135 s in total and requires 45 kB of data to be saved. Solving the quadratic NLPs is very fast in comparison to the model column. Even solving the minimization of all maximum number of 27 nearby quadratics only takes between 1 s to 2 s per iteration, or over 10 times less computation time as standard MA.

Finally, for the closest solution, solving the individual NLPs takes a similar solving time as for the nominal one, therefore the total computation time per iteration is approximately 5 times longer that of standard MA.

Overall, this lines up well with the discussion in the previous sections, where using the modifiers results in similar complexity to standard MA, using regional quadratics on low dimensional problems is faster than standard MA, and using the closest solution is slower than MA.

6.3. Semi-Batch Bioreactor

The final case study looks at a semi-batch reactor. An example of a semi-batch reactor is the photobioreactor for the production of phycocyanin [43], which has been investigated by other RTO [44] and MPC schemes [45]. Two of the three recommended multiple solution MA approaches (of using the modifiers, and closeness for selection) are applied, along with a third scheme of using the central tendencies without convex NLPs to investigate why this is not a recommended scheme.

6.3.1. System Overview

This reactor uses the blue-green cyanobacterium known as Arthrospira platensis as the biomass (X), which is grown on nitrates (N) to produce the phycocyanin (P). The primary objective of this reactor is to maximize the concentration of P at the end of the batch cycle ($t=240\mathrm{h}$), whilst meeting the path and terminal constraints. The initial conditions are fixed, and the decision variables are the light intensity throughout the batch cycle $I\left(t\right)$$\left[\mathsf{\mu }\mathrm{mol}{\mathrm{m}}^{-2}{\mathrm{s}}^{-1}\right]$, and the nitrate inflow rate $F_N\left(t\right)$$\left[\mathrm{m}\mathrm{g}{\mathrm{L}}^{-1}{\mathrm{h}}^{-1}\right]$. These continuous variables can be discretized such that the optimization can be carried out. The easiest method of discretizing the inputs is to break the batch cycle into 6 uniform time segments of $40\mathrm{h}$ each, and during each time segment, the inputs are held constant. Therefore the system has 12 decision variables.

The constraints on the system consist of two path constraints, and a terminal constraint. The first path constraint is on the phycocyanin-to-biomass ratio, which must be kept below $11\mathrm{mg} {\mathrm{g}}^{-1}$, while the second path constraint is that the nitrate concentration is kept below $800\mathrm{mg} {\mathrm{L}}^{-1}$. The terminal constraint is that the nitrate concentration is below $150\mathrm{mg} {\mathrm{L}}^{-1}$. The initial conditions of the reactor are such that the concentration of the biomass is at $1\mathrm{g} {\mathrm{L}}^{-1}$, the nitrate is at $150\mathrm{mg} {\mathrm{L}}^{-1}$, and the phycocyanin is at $0\mathrm{mg} {\mathrm{L}}^{-1}$. Measurements of the concentrations of the components are taken at regular intervals of $10\mathrm{h}$, therefore the NLP for the system can be defined as follows,

$$\begin{array}{cc}\hfill min& \varphi (\mathit{u}\left(t\right),\mathit{y}\left(t\right)):=C_P\left(240\right)\hfill \end{array}$$

(73a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& C_P\left(0\right)=0,C_X\left(0\right)=1,C_N\left(0\right)=150,\hfill \end{array}$$

(73b)

$$\begin{array}{ccc}\hfill & g_1(\mathit{u}\left(t\right),\mathit{y}\left(t\right)):=C_P\left(t\right)-11C_X\left(t\right)\le 0\hfill & \hfill t\in \left\{0,10,\dots ,240\right\},\end{array}$$

(73c)

$$\begin{array}{ccc}\hfill & g_2(\mathit{u}\left(t\right),\mathit{y}\left(t\right)):=C_N\left(t\right)-800\le 0\hfill & \hfill t\in \left\{0,10,\dots ,240\right\},\end{array}$$

(73d)

$$\begin{array}{cc}\hfill & g_3(\mathit{u}\left(t\right),\mathit{y}\left(t\right)):=C_N\left(240\right)150\le 0,\hfill \end{array}$$

(73e)

$$\begin{array}{cc}\hfill & 120\le I\left(t\right)\le 400,0\le F_N\left(t\right)\le 40.\hfill \end{array}$$

(73f)

where $C_X\left(t\right)$ is the concentration of the biomass in $[\mathrm{g} {\mathrm{L}}^{-1}]$, $C_N$ is the concentration of nitrate in $[\mathrm{mg} {\mathrm{L}}^{-1}]$, and $C_P$ is the concentration of phycocyanin in $[\mathrm{mg} {\mathrm{L}}^{-1}]$, and are the measured states of the system. $\mathit{u}\left(t\right)$ represents the inputs of $[I\left(t\right),F_N\left(t\right)]$, and $\mathit{y}\left(t\right)$ are the measured outputs of the concentration of each component at each time interval. Therefore, there is a total of 51 discrete constraints on the system.

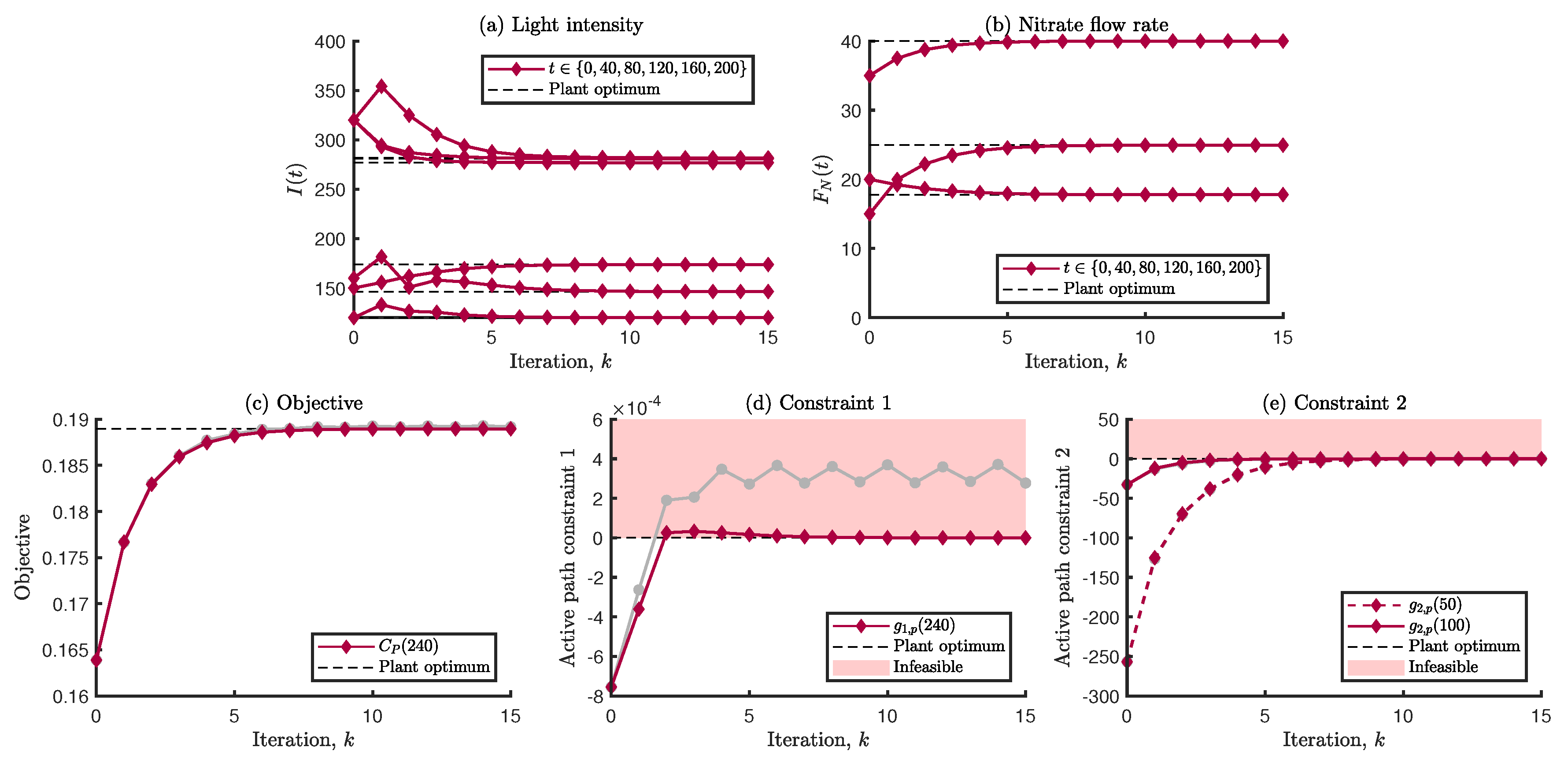
A detailed review of the simulation used for this case study is given in Appendix B. The objective of the plant at the optimal conditions is illustrated in Figure 12a, where the black line shows the concentration of P. The objective of the system is to maximize the terminal concentration, which for the optimal conditions is $C_P\left(240\right)=0.1890 \mathrm{mg} {\mathrm{L}}^{-1}$. The first path constraint is also illustrated in Figure 12a, where the value of $C_P$ is limited to be below the value of $11C_X$, which is only active at $t=240 \mathrm{h}$. The second path constraint and the terminal constraint are illustrated in Figure 12b, where the value of $C_N$ is limited to be below $800 \mathrm{mg} {\mathrm{L}}^{-1}$, which is only active at $t=50 \mathrm{h}$ and $t=100 \mathrm{h}$. Therefore, there are three active constraints, where the following are true:

$$\begin{array}{cc}\hfill C_P\left(240\right)-11C_X\left(240\right)& =0,\hfill \end{array}$$

(74)

$$\begin{array}{cc}\hfill C_N\left(50\right)-800& =0,\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill C_N\left(100\right)-800& =0.\hfill \end{array}$$

(76)

The model is assumed to follow a simplified set of state equations, where part of the light intensity term is neglected, leading to structural mismatch between the plant and model. In addition to the structural mismatch, there is an error in one of the parameters, $Y_{N/X}$, which is $20\%$ higher than the true value used to simulate the plant. The pool of models is developed through the uncertainty in three of the parameters, including $Y_{N/X}$. The other parameters match those used to simulate the plant. This is given in more detail in Appendix B.

From this uncertainty, the pool of models is formed from 9 discrete set of parameters. These are produced from all of the combinations from the extreme values of the uncertain parameters (i.e., mean plus the uncertainty), producing 8 different sets, plus the set of parameters using the mean values.

6.3.2. Standard MA

Firstly, as a benchmark to compare the proposed approaches to, the standard MA approach is applied to this case study. As with the other case studies, noise and errors in the gradient estimation methods are not considered, therefore it is assumed that measurements of the plant gradient can be taken at the current operating point, and all measurements are perfect without error. This is unrealistic, but allows for the convergence and robustness of the approach to be compared at ideal conditions.

The results of the standard MA approach with an input gain of $\mathit{K}=0.5\mathit{I}$ are shown in Figure 13. For the inputs, the 10 of the 12 inputs converge to near optimal points, however, the value of the light intensity for the fourth and sixth time ranges do not converge and are unstable. The value of the inputs for the flowrate of nitrate after $t=80$ follow the same RTO iterates, as the solution to the modified model always predicts $F_N=40$ as the optimum, therefore they all exponentially approaches this solution, and all four lines fully overlap.

As the instability in the inputs comes from times after $t=120$, the active path constraints earlier than this are stable and converge near to the plant optimum. However, the active constraint after this time are unstable and infeasible, as shown in Figure 13d.

Running at lower input gains does not solve the instability in the inputs, which suggests the model is inadequate. Analyzing the Lagrange of the modified model at the plant optimum, there exists vectors which are orthogonal to the active constraints (and to the active input limits) which do not satisfy the second order conditions of optimality, therefore this model is not adequate.

6.3.3. MSMA: Selection Based on Modifiers

The first approach is the minimum modifier selection method, as illustrated in Figure 14, using an input filter gain of $\mathit{K}=0.5\mathit{I}$. This method successfully overcomes the model adequacy issues of standard MA and rapidly converges to the plant optimum in less than 10 iterations. The RTO trajectory slightly breaks the active path constraint, $g_1\left(240\right)$, as shown in Figure 14d, and has some erratic behavior with the light intensity in the first few iterations, but overall is a big improvement over standard MA.

6.3.4. MSMA: Selection Based on Central Tendencies

Next, the MSMA approach using the mean solution is applied using the full models (i.e., non-convex NLPs). As is discussed in the previous sections, the nominal model is inadequate for this system, and it is included in the set of models. The analysis of the model adequacy conditions for the mean selection method has shown that this method should also fail to converge.

As illustrated in Figure 15, the RTO approach does fail to converge using an input filter gain of $\mathit{K}=0.5\mathit{I}$, hence why this is not a recommend approach. As only three of the nine models in the set are adequate, the instability is even greater than that of standard MA. This highlights both that using central tendencies without convex models comes with additional risks, and that the selection of the set of models used to produce the potential solutions is important to the method. For the value of $Y_{N/X}$, the uncertainty is approximately $\pm 20\%$ of the true value, but the nominal value is already $20\%$ over the true value, therefore some models use the value of $Y_{N/X}$ that is $40\%$ over the true value used to simulate the plant. Making sure every model in the set does somewhat accurately model the plant is important, especially for using the mean and most likely, which take all the models into consideration.

6.3.5. MSMA: Selection Based on Closeness

The final MSMA approach using the closest solution is applied. Using an input filter gain of $\mathit{K}=0.5\mathit{I}$, the solution is shown in Figure 16, where the RTO system successfully converges to the plant optimum. Compared to the minimum modifier method, this approach is far smoother, but breaks the constraints more, and takes longer to converge to the optimum. The basis for using the closest solution is to reduce the risk by taking shorter steps. This works against the method when the current operating point is infeasible as remaining close to the current operating point will also likely give infeasible conditions.

6.4. Conclusions of MSMA Performance

Three case studies have been simulated giving an idea of the expected performance that MSMA scheme can provide. For the WO CSTR and the semi-batch reactor, the improvement to the model adequacy conditions are shown, where for the minimum modifier selection, central tendencies using convex NLPs, and closest solution methods are all able to converge to the plant optimum.

Using any of the recommended approaches on these case studies improves the performance of the RTO trajectory by either providing stability, reducing infeasibility in the iterates before convergence, or by increasing the rate of improvement to the objective function. Using the minimum modifier overall performed well for the second and third case studies, where it is the (joint-) best scheme, however for the first case study it performs less well. Using the regional quadratics with the mean solution also performs well and does not require a set of uncertainty to be used. However, it is difficult to use on higher dimensional problems, and using the mean without convex NLPs performs poorly. The final recommended approach is using the closest solution, which is the most consistent when applied to the cases above. This comes at the cost of having to solve all the models in the set, which can be time consuming for more complex problems.

7. Conclusions

Modifier adaptation is an RTO approach which uses estimates of the first order properties of the plant to modify a nominal model such that it matches these estimates at the current operating point. During the design stage of an industrial process, this nominal model is generated, and due to simplifications, noise and disturbances, there is always some degree of plant-model mismatch. Typically, the parameters used in the model come with a degree of uncertainty to account for this discrepancy. The use of this known uncertainty to account for this mismatch is limited in RTO, where it is discarded in favor of real-time measurements.

A new framework is introduced known as multiple solution modifier adaptation (MSMA) which uses this known uncertainty, along with the real-time measurements to improve the choice of the next RTO iteration. The framework is broken down into two choices, firstly how to generate the set of potential solutions, and secondly how to combine these potential operating points into a single set of inputs to apply to the plant. Several different methods have been introduced for each of these options, which are applicable in a wide range of scenarios, even when the uncertainties in the model parameters are unknown.

Each of the methods proposed have been shown to maintain KKT matching upon convergence if either the selected operating point is one of the potential operating points, or within the convex hull of a set of points generated from convex NLPs. Three approaches are recommended from this framework. The improvement to the performance is analyzed through three different case studies, where the recommended schemes outperform standard MA in terms of rate of convergence and stability at the plant optimum.

These case studies have been simulated under an idealized scenario of no measurement noise, no disturbances, and no other errors (other than plant-model mismatch). Therefore, the conclusions of the performance of these approach need to be considered with this in mind, and further work is required to understand how the proposed schemes operate under more realistic assumptions.