Modeling the Transient Flow Behavior of Multi-Stage Fractured Horizontal Wells in the Inter-Salt Shale Oil Reservoir, Considering Stress Sensitivity
Abstract
:1. Introduction
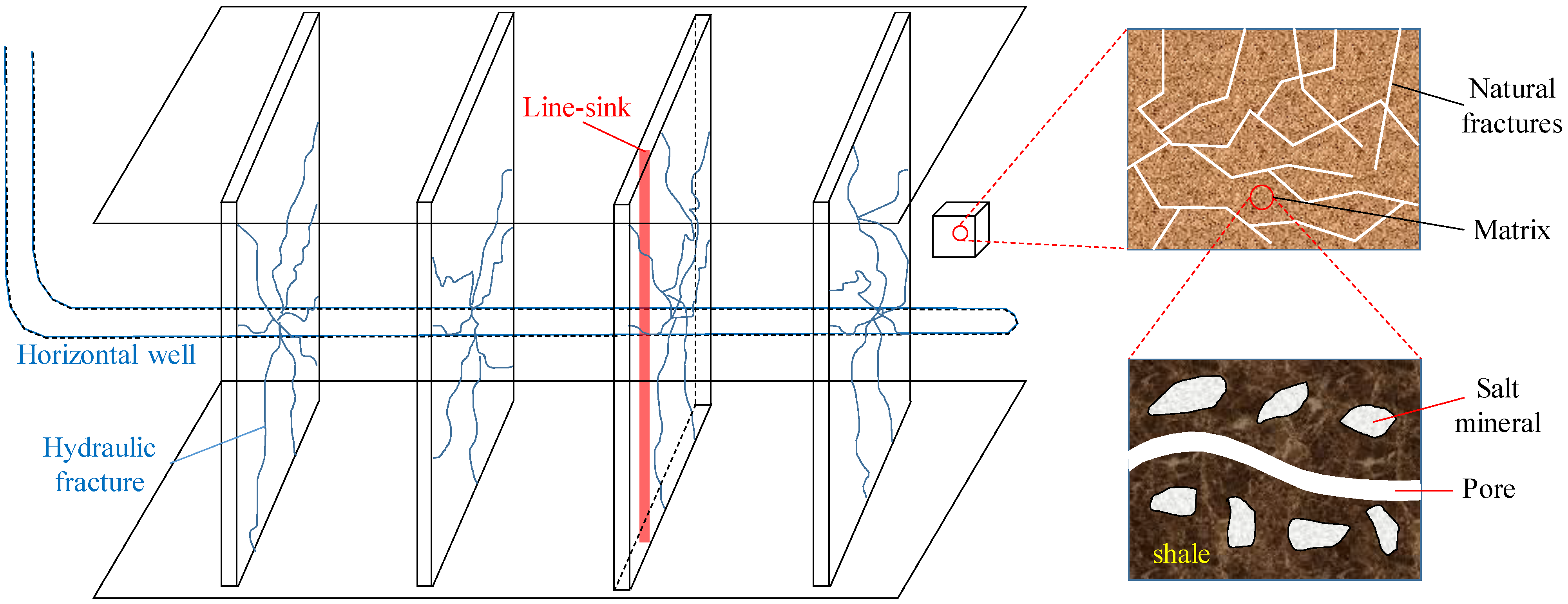
2. Physical Modeling
- (1)
- The reservoir is bounded by two parallel impermeable boundaries at the top and bottom, with an infinite lateral boundary. The reservoir’s thickness is h, and the initial formation pressure is pi and is equal everywhere.
- (2)
- The inter-salt shale oil reservoir is assumed to be a dual-porosity medium, which is based on the Warren–Root model. The matrix porosity and fracture porosity are ϕm and ϕf, respectively, and the permeabilities are Km and Kf. As Kf is much larger than Km, pseudo-steady cross-flow occurs between these two systems.
- (3)
- A fractured horizontal well can be located anywhere (represented by zw) in the formation, with the horizontal section of the well parallel to the top and bottom boundaries. A total of M transverse fractures are formed after multi-stage fracturing.
- (4)
- The matrix permeability can be affected by the dissolution of salt. The fracture permeability is affected by the stress-sensitive effect, and oil flow in fracture system obeys Darcy’s law.
- (5)
- The single-phase oil is compressible with a constant viscosity and compression coefficient, but the wellbore storage effect and the skin effect are considered.
- (6)
- The oil flow in the inter-salt shale oil reservoir is at a constant reservoir temperature.
3. Mathematical Modeling
3.1. Mathematical Model of a Line-Sink in an Inter-Salt Shale Oil Reservoir
- Governing equations
- Boundary conditions
- Initial conditions
3.2. The Dimensionless Form of the Line-Sink Model
3.3. Solution of the Mathematical Line-Sink Model
3.3.1. Pedrosa’s Linearization
3.3.2. Perturbation Technique
3.3.3. Laplace Transformation
3.4. Pressure Responses of the MFHW in an Inter-Salt Shale Oil Reservoir
4. Results and Discussion
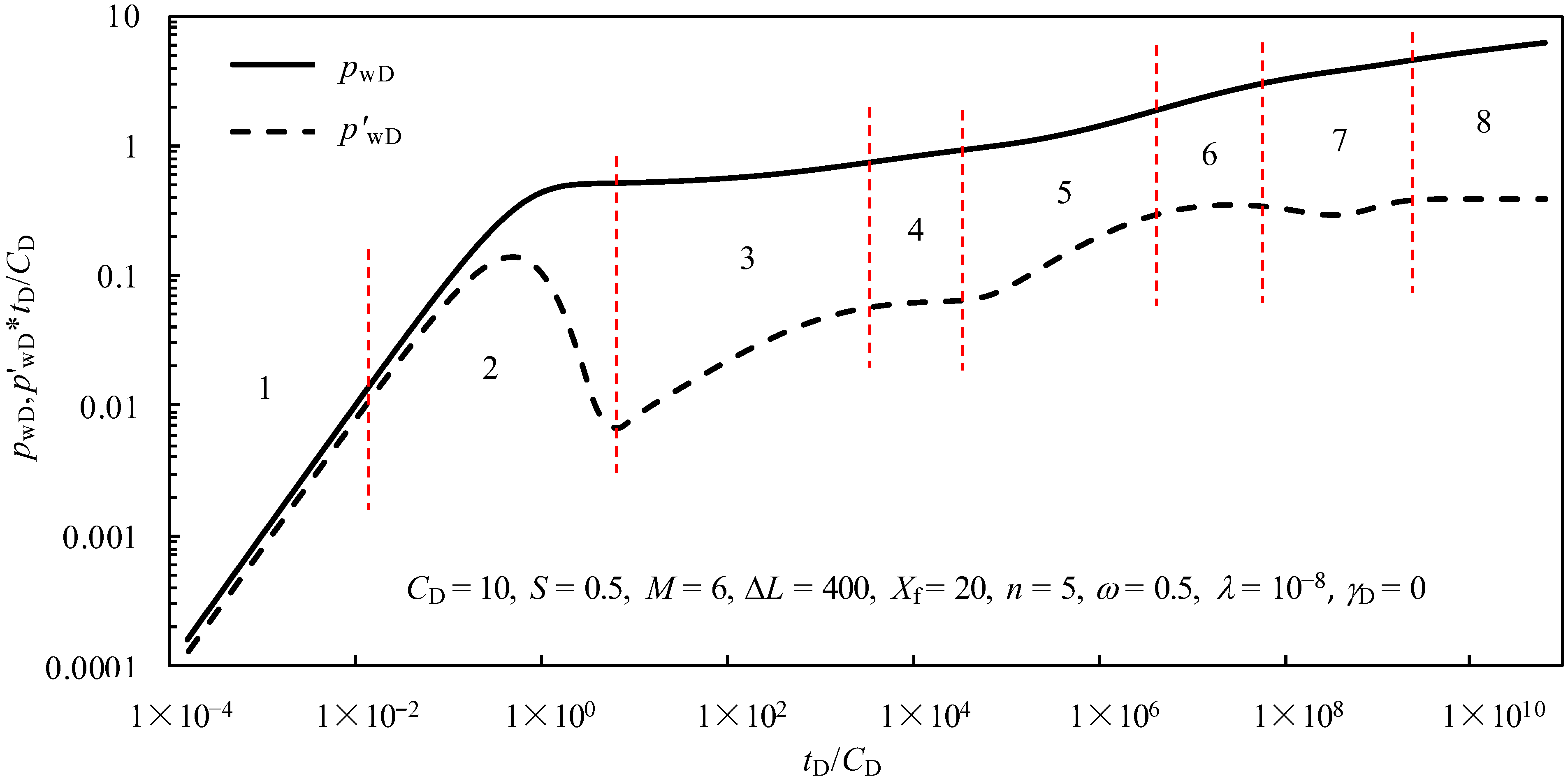
4.1. Behaviorial Analysis of Transient Pressure
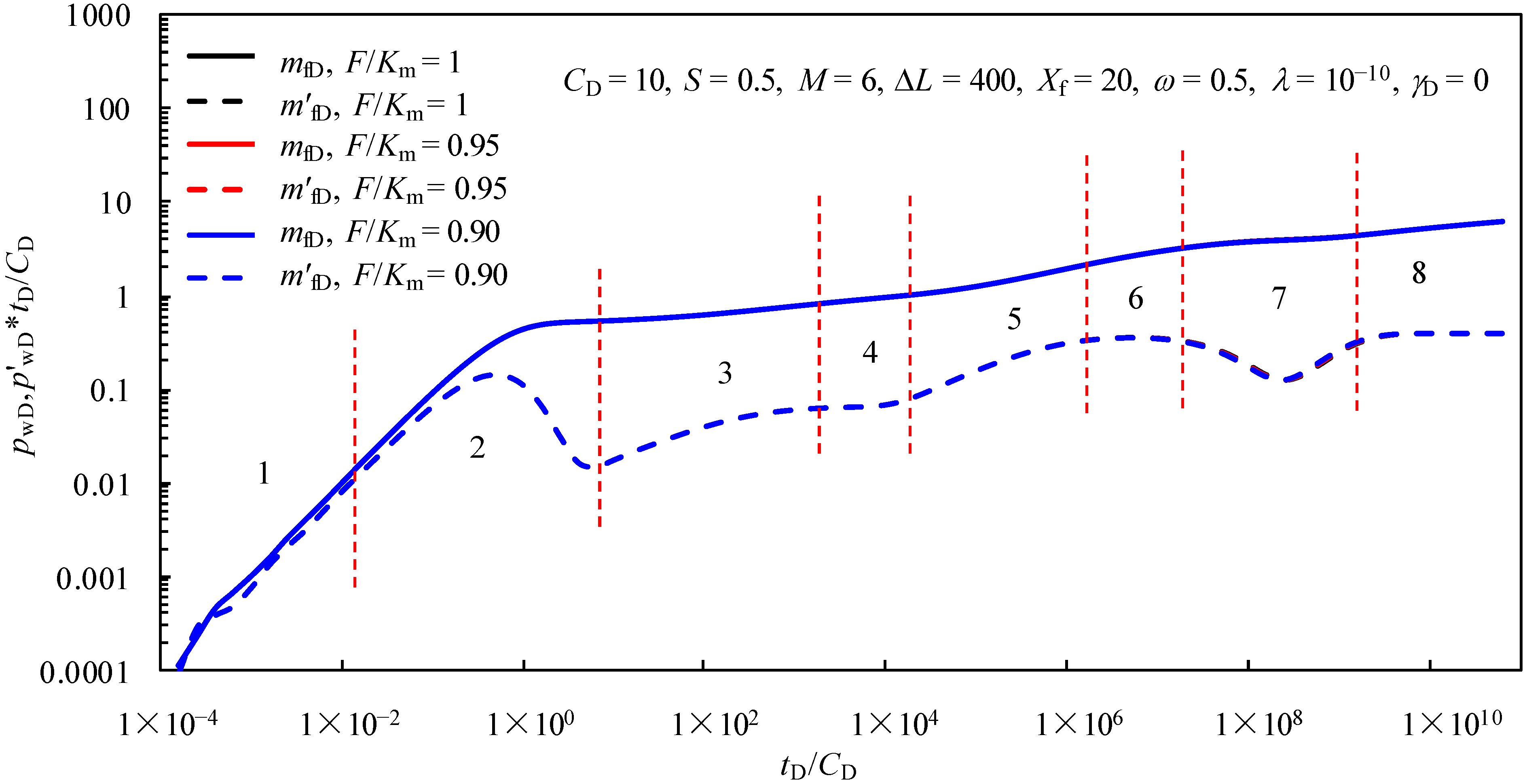
4.2. Effect of Salt Dissolution
4.3. Effect of Stress Sensitivity
4.4. Effect of the Storativity Ratio
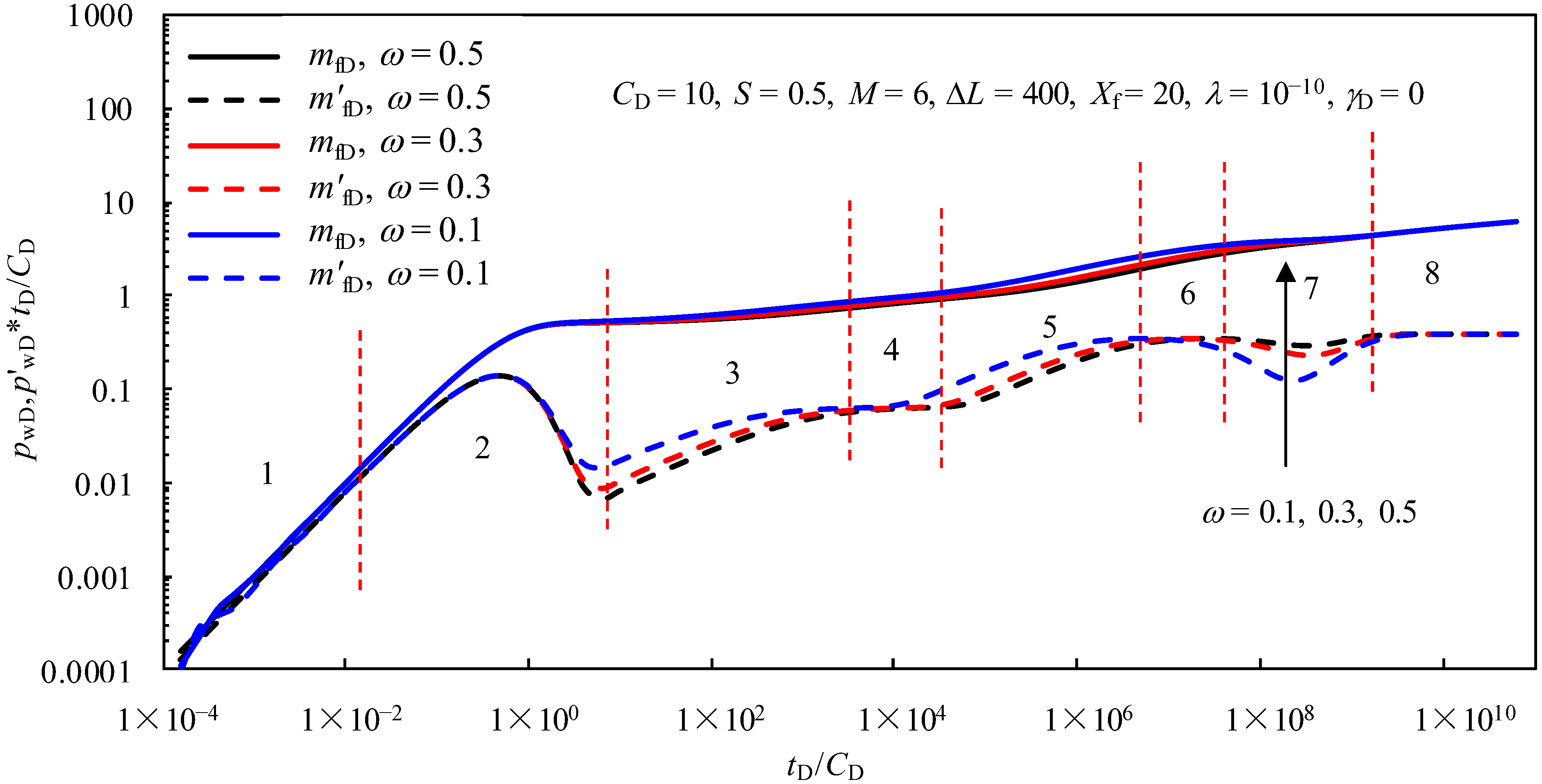
4.5. Effect of the Interporosity Flow Coefficient
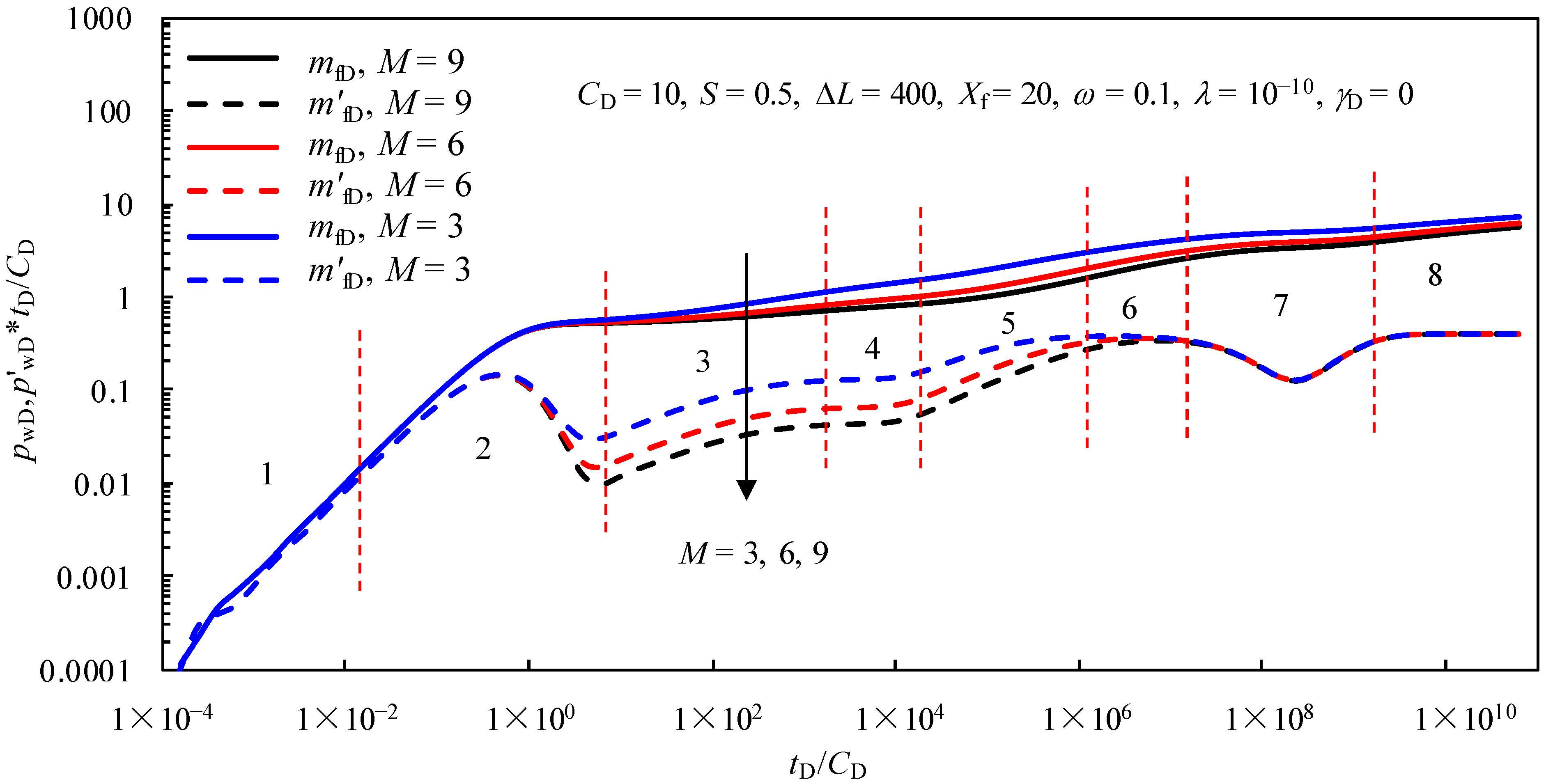
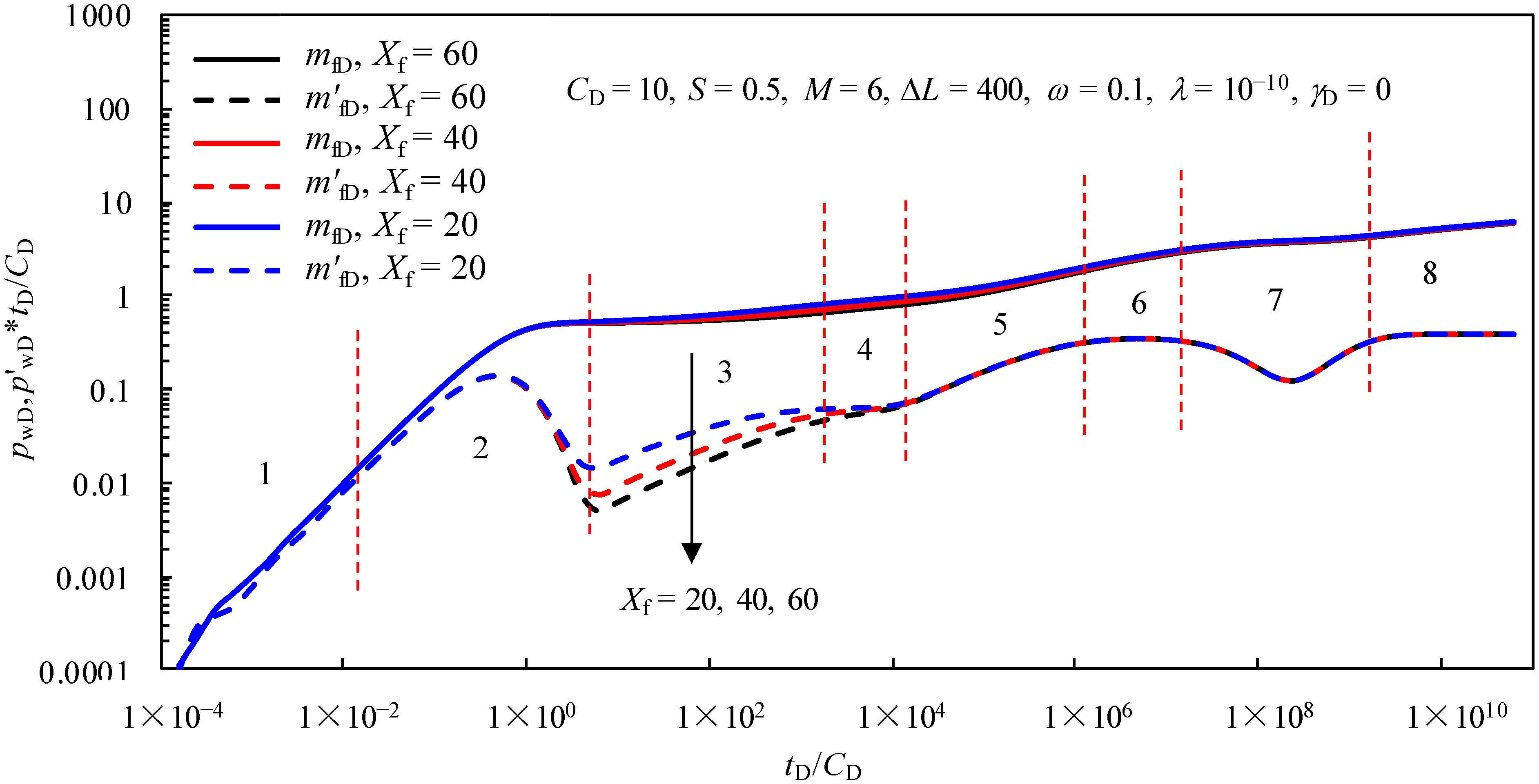
4.6. Effects of the Parameters of the Hydraulic Fractures
5. Conclusions
- (1)
- The pressure response and corresponding pressure derivative curves of a MFHW in the inter-salt shale oil reservoir with consideration of the stress sensitivity of natural fractures were analyzed, and eight main flow periods could be observed in the type curves of transient pressure.
- (2)
- The influence of salt dissolution on the transient pressure curves of the fractured horizontal well in an inter-salt shale oil reservoir was negligible because the permeability decreased by only 5.06% when the average pressure dropped from 22.5 MPa to 7.5 MPa according to the experimental results of the effect of salt dissolution on the shale’s permeability.
- (3)
- The effect of the stress sensitivity of the fracture system on the pressure derivative curves became apparent in the radial flow period of natural fractures (Period 6). The pressure derivative curves gradually turned upward with an increase in the dimensionless permeability modulus. The stronger the stress sensitivity, the more serious the damage to the reservoir. It was therefore more difficult for the shale oil to flow, and greater drawdown pressure was required.
- (4)
- The effects of the storativity ratio, the interporosity flow coefficient and the parameters of the hydraulic fractures on the transient pressure curves were analyzed to better understand the transient flow behavior of the MFHW in an inter-salt shale oil reservoir.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Letters | |
| B | fluid volume factor, m3/sm3 |
| C | wellbore storage coefficient, m3/Pa |
| Cft | total compressibility coefficient of the fracture system, Pa−1 |
| Cmt | total compressibility coefficient of the matrix system, Pa−1 |
| CL | fluid compressibility coefficient, Pa−1 |
| Cp | rock compressibility coefficient, Pa−1 |
| c1, c2 | empirical coefficients, which can be determined by experiments |
| Kf | permeability of the fracture, m2 |
| Kfi | initial permeability of the fracture, m2 |
| Km | permeability of the matrix, m2 |
| Kmi | initial permeability of the matrix, m2 |
| L | Characteristic length, m |
| LfLi, LfRi | Lengths of the left and right wings of the ith fracture, m |
| M | Number of hydraulic fractures |
| N | Number of segments on the wing of each fracture |
| p | pressure, Pa |
| p | reference pressure, Pa |
| pi | initial pressure, Pa |
| pf | fracture pressure, Pa |
| pm | matrix pressure, Pa |
| qex | cross flow from the matrix to the fracture, kg/(m3·s) |
| qi,j | flux per unit of length of a discrete segment (i, j), m2/s |
| qsc | surface oil production rate, m3/s |
| r | radial distance, m |
| S | skin factor, dimensionless |
| t | time, s |
| vfr | radial velocity component of oil flow in fracture, m/s |
| Greek letters | |
| α | matrix block shape factor, 1/m2 |
| β | empirical coefficient, which can be determined by experiments |
| γ | permeability modulus, Pa−1 |
| ρ0 | reference oil density under the reference pressure, kg/m3 |
| ρf | Oil density in the fracture system, kg/m3 |
| ρm | oil density in the matrix system, kg/m3 |
| ϕ0 | initial porosity, dimensionless |
| ϕf | fracture porosity, dimensionless |
| ϕm | matrix porosity, dimensionless |
| μ | oil viscosity, Pa·s |
| ξD | perturbation deformation function |
| ξD0 | zero-order perturbation deformation function |
| Superscripts | |
| Laplace transform domain | |
| Subscripts | |
| D | dimensionless |
| i | initial condition |
| sc | standard state |
| f | fracture system |
| m | matrix system |
Appendix A. Experimental Evaluation of the Salt Dissolution
| Inlet Pressure | Outlet Pressure | Pressure Difference | Permeability |
|---|---|---|---|
| 25 | 20 | 5 | 0.514 |
| 20 | 15 | 5 | 0.5 |
| 15 | 10 | 5 | 0.493 |
| 10 | 5 | 5 | 0.488 |

References
- Fan, X.; Su, J.Z.; Chang, X.; Huang, Z.W.; Zhou, T.; Guo, Y.T.; Wu, S.Q. Brittleness evaluation of the inter-salt shale oil reservoir in Jianghan Basin in China. Mar. Pet. Geol. 2019, 102, 109–115. [Google Scholar] [CrossRef]
- Yang, L.; Lu, H.; Fan, X.; Huang, Z.; Zhou, T. Salt occurrence in matrix pores of intersalt shale oil reservoirs. Sci. Technol. Eng. 2020, 20, 1839–1845. [Google Scholar]
- Li, Z.; Zhao, Y.; Wang, H.; Zhao, Q.; Lu, T.; Xu, Z. Effects of Injection Water Salinity on Physical Properties of Inter-Salt Shale Oil Reservoir. Spec. Oil Gas Reserv. 2020, 27, 131–137. [Google Scholar]
- Zhang, Y.; Zhang, M.; Mei, H.; Zeng, F. Study on salt precipitation induced by formation brine flow and its effect on a high-salinity tight gas reservoir. J. Pet. Sci. Eng. 2019, 183, 106384. [Google Scholar] [CrossRef]
- Kilmer, N.H.; Morrow, N.R.; Pitman, J.K. Pressure sensitivity of low permeability sandstones. J. Pet. Sci. Eng. 1987, 1, 65–81. [Google Scholar] [CrossRef]
- Schutjens PM, T.M.; Hanssen, T.H.; Hettema MH, H.; Merour, J.; De Bree, P.; Coremans JW, A.; Helliesen, G. Compaction-Induced Porosity/Permeability Reduction in Sandstone Reservoirs: Data and Model for Elasticity-Dominated Deformation. SPE Reserv. Eval. Eng. 2004, 7, 202–216. [Google Scholar] [CrossRef]
- Fatt, I.; Davis, T.H. The reduction in permeability with overburden pressure. Trans. AIME 1952, 4, 16. [Google Scholar] [CrossRef]
- Mclatchie, A.; Hemstock, R.A.; Young, J.W. The effective compressiblity of reservoir rock and its effects on permeability. J. PetroI. Technol. 1952, 10, 49–51. [Google Scholar] [CrossRef]
- Gray, D.H.; Fatt, I.; Bergarnini, G. The effect of stress on permeability of sandstone cores. Sot. Pet. Eng. J. 1963, 3, 95–100. [Google Scholar] [CrossRef]
- Vairogs, J.; Hearn, C.L.; Dareing, D.W.; Rhoades, V.W. Effect of rock stress on gas production from low perrneability resevoirs. J. Pet. Technol. 1971, 23, 1161. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Ambastha, A.K. New insights in pressure-transient analysis for stress-sensitive reservoirs. Presented at the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 25–28 September 1994. [Google Scholar] [CrossRef]
- Chin, L.Y.; Raghavan, R.; Thomas, L.K. Fully coupled geomechanics and fluid-flow analysis of wells with stress-dependent permeability. Soc. Petroleum Eng. 2000, 5, 32–45. [Google Scholar] [CrossRef]
- Franquet, M.; Ibrahim, M.; Wattenbarger, R.A.; Maggard, J.B. Effect of pressure dependent permeability in tight gas reservoirs, transient radial flow. Presented at the Canadian International Petroleum Conference, Calgary, AB, Canada, 8–10 June 2004. [Google Scholar] [CrossRef]
- Ali, T.A.; Sheng, J.J. Evaluation of the effect of stress-dependent permeability on production performance in shale gas reservoirs. Presented at the SPE Eastern Regional Meeting, Morgantown, WV, USA, 13–15 October 2015. [Google Scholar] [CrossRef]
- Barenblatt, G.I.; Zheltov, Y.P. Fundamental equations of filtration of homogeneous liquids in fissured rocks. Sov. Phys. Dokl. 1960, 5, 522. [Google Scholar]
- Warren, J.E.; Root, P.J. The behavior of naturally fractured reservoirs. Sot Pet. Eng. 1963, 228, 245–255. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.K.; Rahman, M.M.; Joarder, A.H. Analytical Production Modeling for Hydraulically Fractured Gas Reservoirs. Pet. Sci. Technol. 2007, 25, 683–704. [Google Scholar] [CrossRef]
- Rahman, M.M. Productivity Prediction for Fractured Wells in Tight Sand Gas Reservoirs Accounting for Non-Darcy Effects. Presented at the Russian Oil & Gas Technical Conference and Exhibition, Moscow, Russia, 28–30 October 2008. [Google Scholar] [CrossRef]
- Xie, W.; Li, X.; Zhang, L.; Wang, J.; Cao, L.; Yuan, L. Two-phase pressure transient analysis for multi-stage fractured horizontal well in shale gas reservoirs. J. Nat. Gas Sci. Eng. 2014, 21, 691–699. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Liu, Q.; Tan, X. Pressure performance of multi-stage fractured horizontal well considering stress sensitivity and dual permeability in fractured gas reservoirs. J. Pet. Sci. Eng. 2020, 201, 108154. [Google Scholar] [CrossRef]
- Guo, J.; Wang, H.; Zhang, L. Transient pressure and production dynamics of multi-stage fractured horizontal wells in shale gas reservoirs with stimulated reservoir volume. J. Nat. Gas Sci. Eng. 2016, 35, 425–443. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Liu, Q. Pressure performance of multi-stage fractured horizontal well with stimulated reservoir volume and irregular fractures distribution in shale gas reservoirs. J. Nat. Gas Sci. Eng. 2020, 77, 103209. [Google Scholar] [CrossRef]
- Zongxiao, R.; Zhan, Q.; Huayi, J.; Erbiao, L.; Jiaming, Z.; Ze, Y.; Hongbin, Y. Transient pressure behaviour of multi-stage fractured horizontal well in stress-sensitive coal seam. Int. J. Oil Gas Coal Technol. 2019, 22, 163. [Google Scholar] [CrossRef]
- Ren, J.; Guo, P.; Peng, S.; Ma, Z. Performance of multi-stage fractured horizontal wells with stimulated reservoir volume in tight gas reservoirs considering anomalous diffusion. Environ. Earth Sci. 2018, 77, 768. [Google Scholar] [CrossRef]
- Zongxiao, R.; Xiaodong, W.; Guoqing, H.; Lingyan, L.; Xiaojun, W.; Guanghui, Z.; Hun, L.; Jiaming, Z.; Xianwei, Z. Transient pressure behavior of multi-stage fractured horizontal wells in stress-sensitive tight oil reservoirs. J. Pet. Sci. Eng. 2017, 157, 1197–1208. [Google Scholar] [CrossRef]
- Li, X.P.; Cao, L.N.; Luo, C.; Zhang, B.; Zhang, J.Q.; Tan, X.H. Characteristics of transient production rate performance of horizontal well in fractured tight gas reservoirs with stress-sensitivity effect. J. Pet. Sci. Eng. 2017, 158, 92–106. [Google Scholar] [CrossRef]
- Pedrosa, O.A. Pressure transient response in stress-sensitive formations. In Proceedings of the SPE California Regional Meeting, Oakland, CA, USA, 2–4 April 1986; pp. 203–210. [Google Scholar]
- Kikani, J.; Pedrosa, O.A. Perturbation analysis of stress-sensitive reservoirs. SPE Form. Eval. 1991, 6, 379–396. [Google Scholar] [CrossRef]
- Yeung, K.; Chakrabarty, C.; Zhang, X. An approximate analytical study of aquifers with pressure-sensitive formation permeability. Water Resour. Res. 1993, 29, 3495–3501. [Google Scholar] [CrossRef]
- Van Everdingen, A.F.; Hurst, W. The application of the Laplace transformation to flow problems in reservoirs. Trans. AIME 1949, 186, 97–104. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Bumb, A.C.; McKee, C.R. Gas-well testing in the presence of desorption for coalbed methane and devonian shale. SPE Form. Eval. 1988, 3, 179–185. [Google Scholar] [CrossRef]
- Zhan, H.; Zlotnik, V.A. Groundwater flow to horizontal and slanted wells in unconfined aquifers. Wat. Resour. Res. 2002, 38, 1108. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Zhang, L.; Zhao, J.; Luo, J.; Zhang, B. “Triple porosity” modeling of transient well test and rate decline analysis for multi-fractured horizontal well in shale gas reservoirs. J. Pet. Sci. Eng. 2013, 110, 253–261. [Google Scholar] [CrossRef]
- Gao, Y.; Rahman, M.M.; Lu, J. Novel mathematical model for transient pressure analysis of multi-fractured horizontal well in naturally-fractured oil reservoir. ACS Omega 2021, 6, 15205–15221. [Google Scholar] [CrossRef]
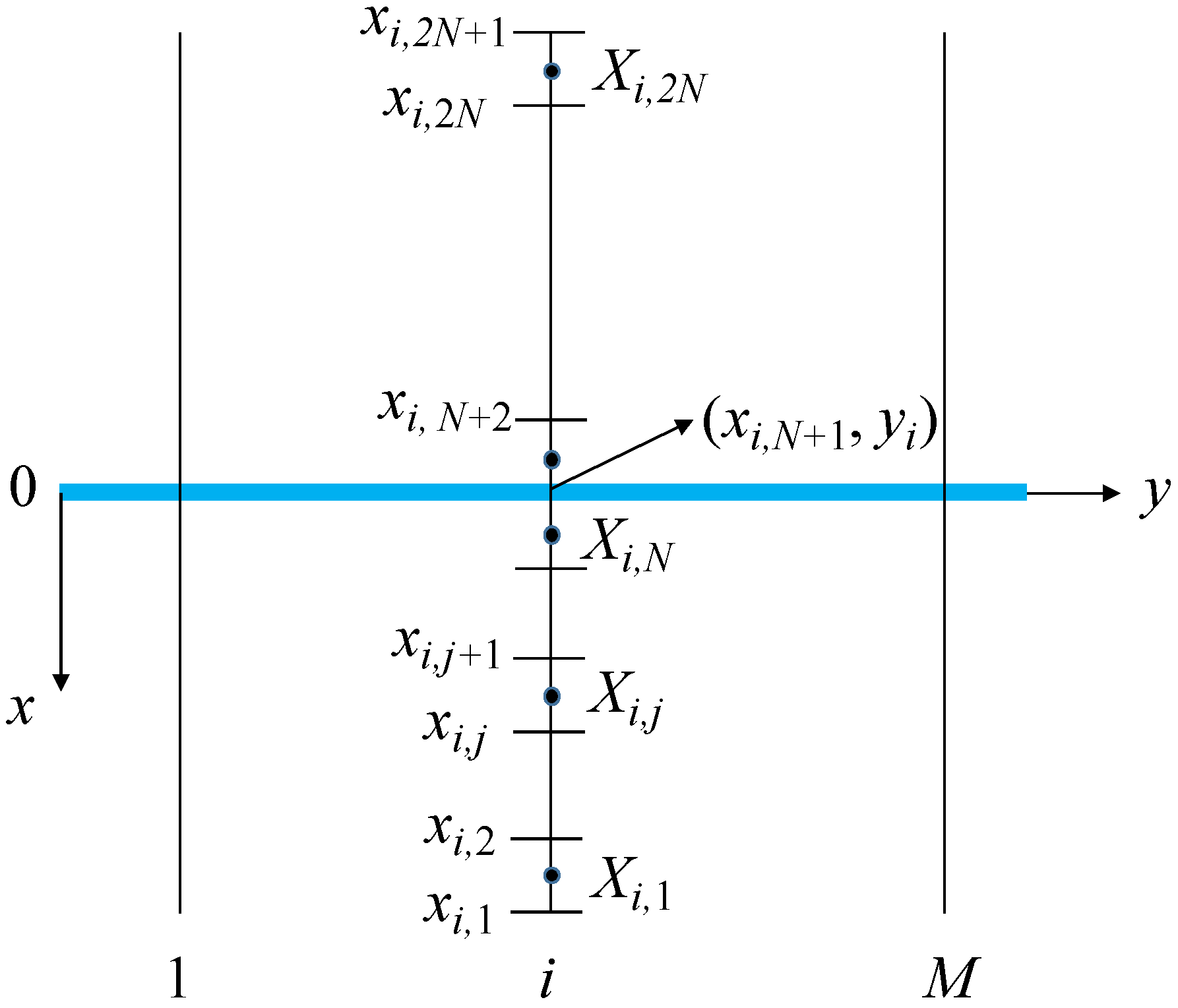



| Dimensionless pressure | (l = f, m) |
| Dimensionless time | |
| Dimensionless radius | |
| Storage coefficient | |
| Transfer coefficient | |
| Dimensionless permeability modulus | |
| Dimensionless wellbore storage coefficient | |
| Dimensionless production rate |
| Parameters | Symbols | Values | Units |
|---|---|---|---|
| Formation thickness | h | 50 | m |
| Formation pressure | pi | 2.34 × 107 | Pa |
| Permeability modulus | γ | 0.12 | MPa−1 |
| Matrix porosity | ϕm | 0.10 | dimensionless |
| Matrix permeability | Km | 2.4 × 10−19 | m2 |
| Fracture porosity | ϕf | 0.039 | dimensionless |
| Fracture permeability | Kf | 2.0 × 10−13 | m2 |
| Oil viscosity | μ | 2.95 × 10−3 | Pa·s |
| Matrix compressibility | cmt | 6.2 × 10−11 | 1/Pa |
| Fracture compressibility | cft | 4.3 × 10−9 | 1/Pa |
| Half-length of the hydraulic fracture | Xf | 230 | m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, T.; Guo, X.; Peng, K.; Song, W.; Hu, C. Modeling the Transient Flow Behavior of Multi-Stage Fractured Horizontal Wells in the Inter-Salt Shale Oil Reservoir, Considering Stress Sensitivity. Processes 2022, 10, 2085. https://doi.org/10.3390/pr10102085
Huang T, Guo X, Peng K, Song W, Hu C. Modeling the Transient Flow Behavior of Multi-Stage Fractured Horizontal Wells in the Inter-Salt Shale Oil Reservoir, Considering Stress Sensitivity. Processes. 2022; 10(10):2085. https://doi.org/10.3390/pr10102085
Chicago/Turabian StyleHuang, Ting, Xiao Guo, Kai Peng, Wenzhi Song, and Changpeng Hu. 2022. "Modeling the Transient Flow Behavior of Multi-Stage Fractured Horizontal Wells in the Inter-Salt Shale Oil Reservoir, Considering Stress Sensitivity" Processes 10, no. 10: 2085. https://doi.org/10.3390/pr10102085
APA StyleHuang, T., Guo, X., Peng, K., Song, W., & Hu, C. (2022). Modeling the Transient Flow Behavior of Multi-Stage Fractured Horizontal Wells in the Inter-Salt Shale Oil Reservoir, Considering Stress Sensitivity. Processes, 10(10), 2085. https://doi.org/10.3390/pr10102085







