Particle Flow Simulation of Failure Process of Defective Sandstone under Different Intermediate Principal Stress under True Triaxial Action
Abstract
:1. Introduction
2. Determination of Mechanical Parameters of Specimens
3. Model Building
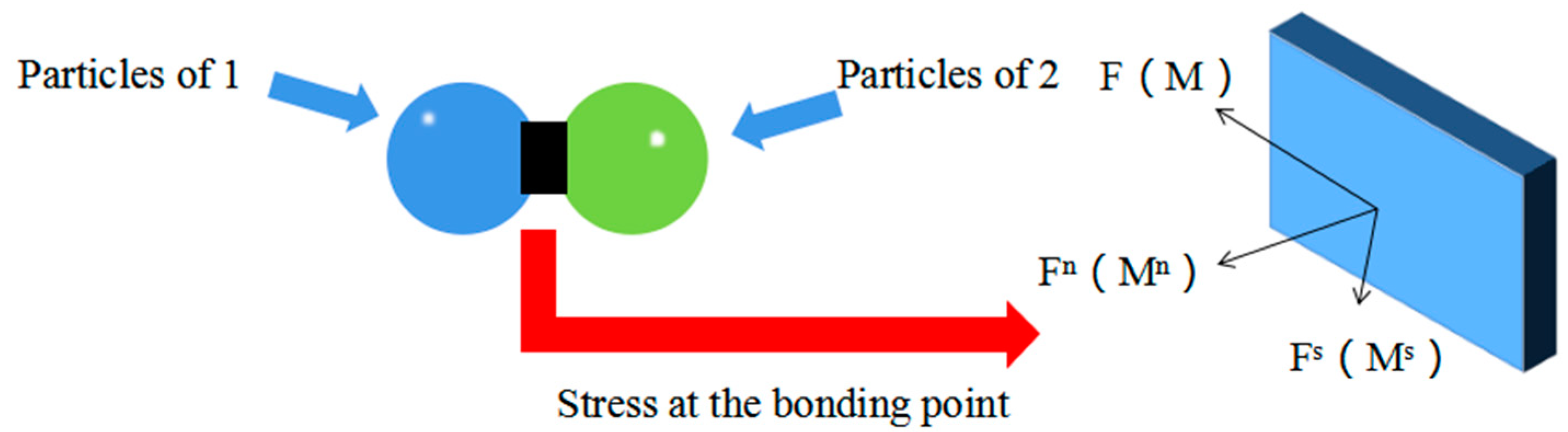
3.1. Matdem and Bonding Theory
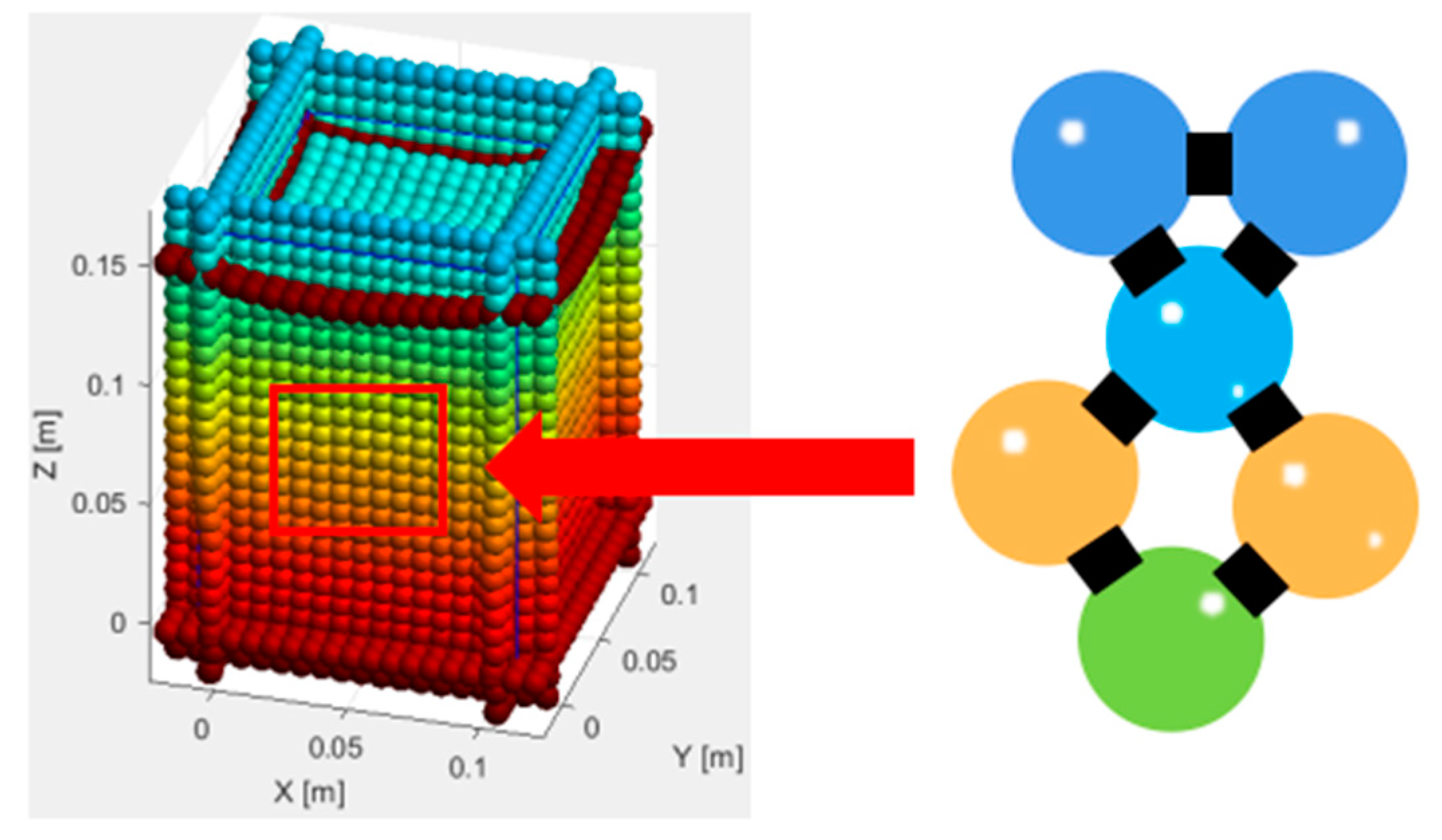
3.2. Establishment of Particle Flow Model
4. Result Analysis
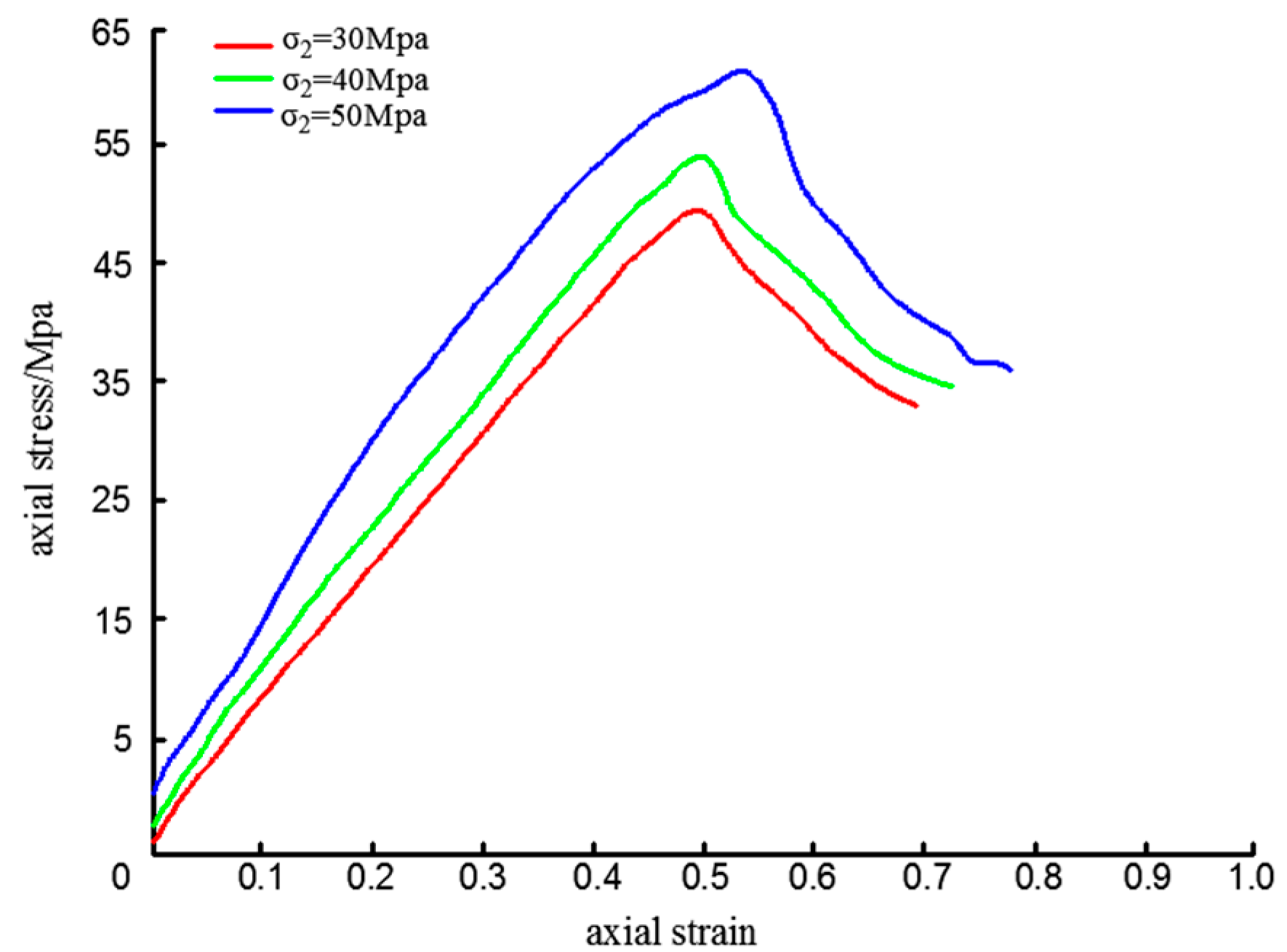
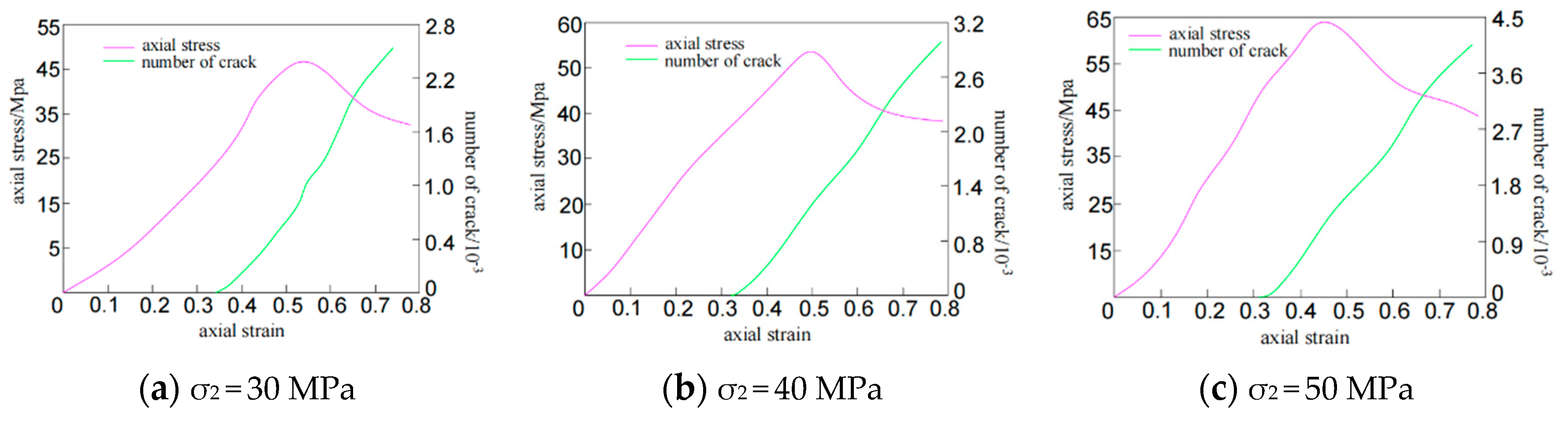
4.1. Mechanical Response Characteristics of Sandstone
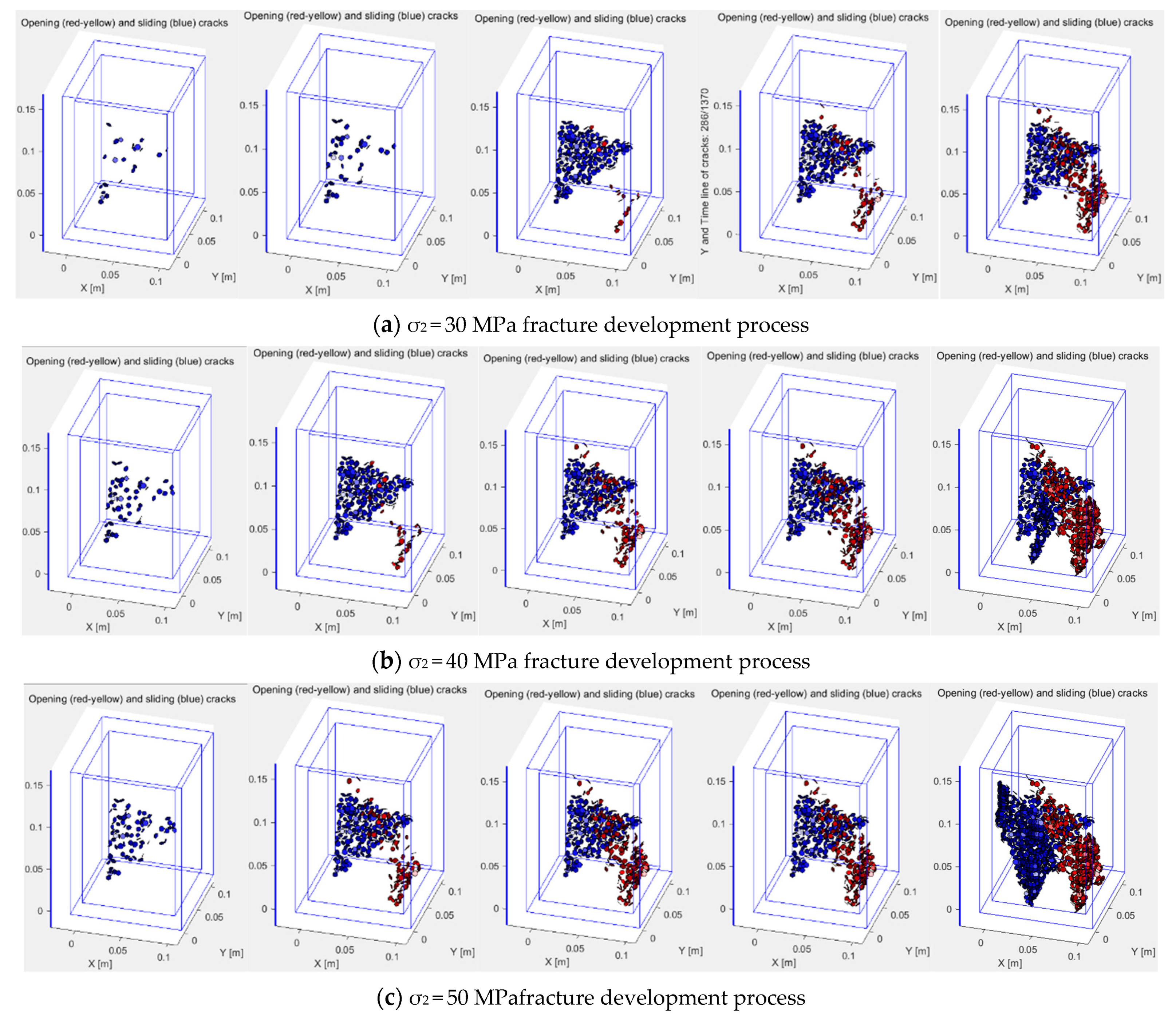
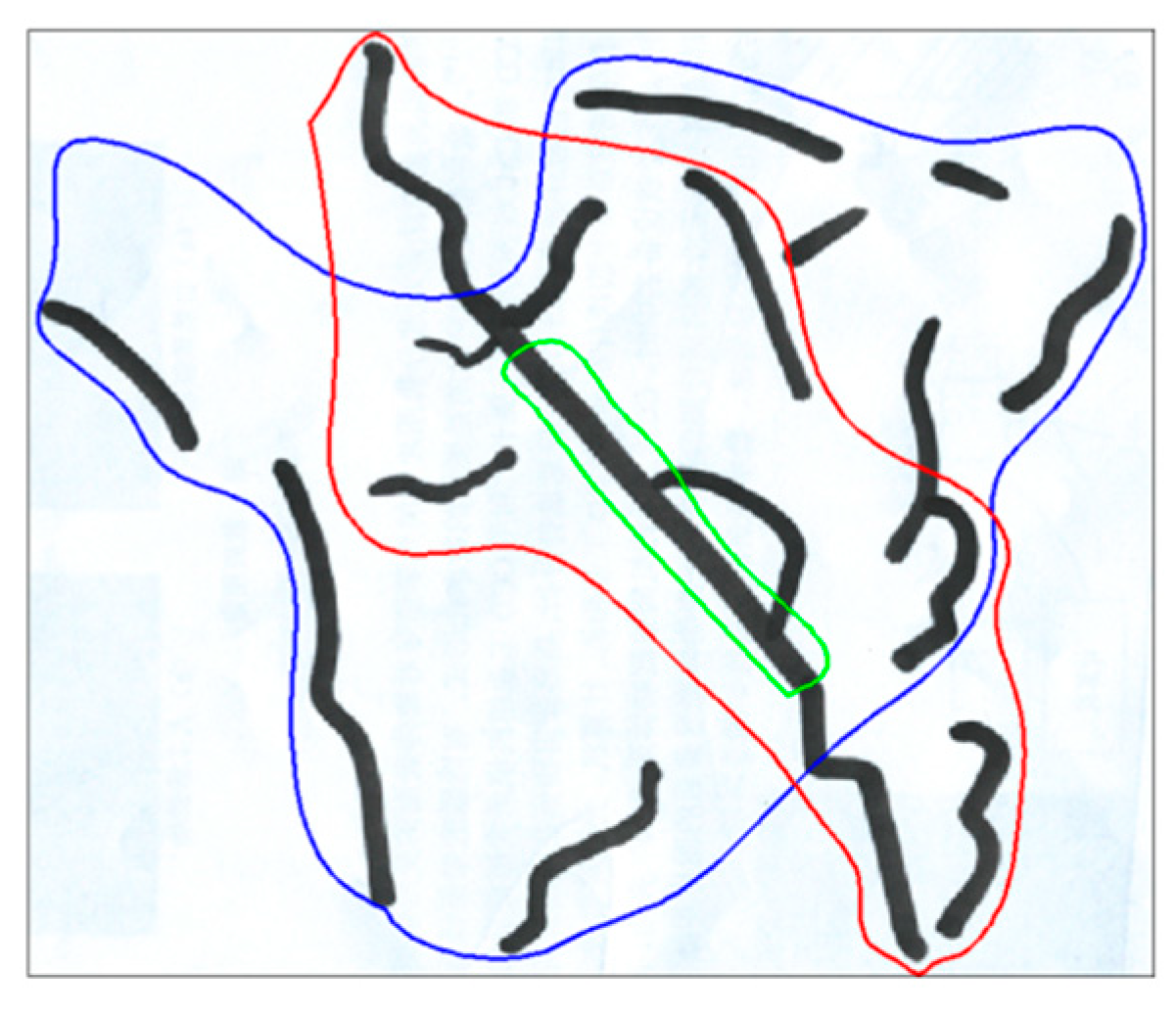
4.2. Sandstone Fracture Mode and Damage Characteristics
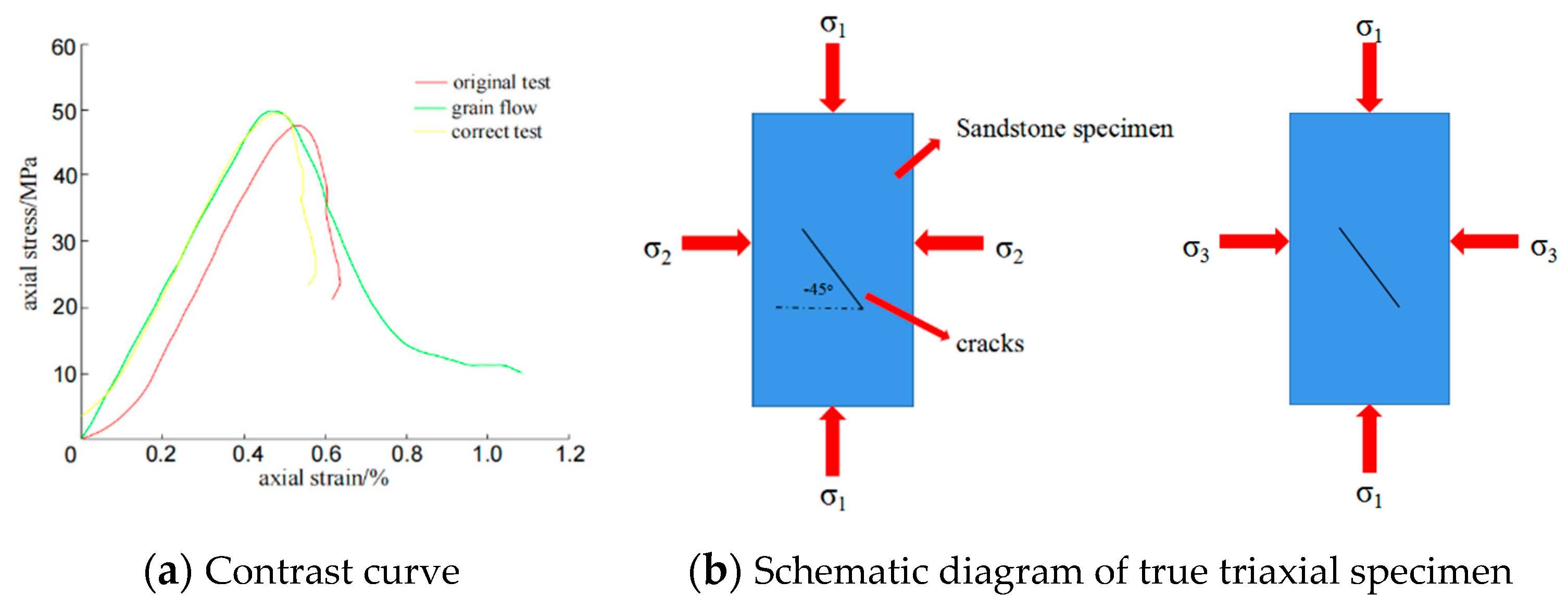
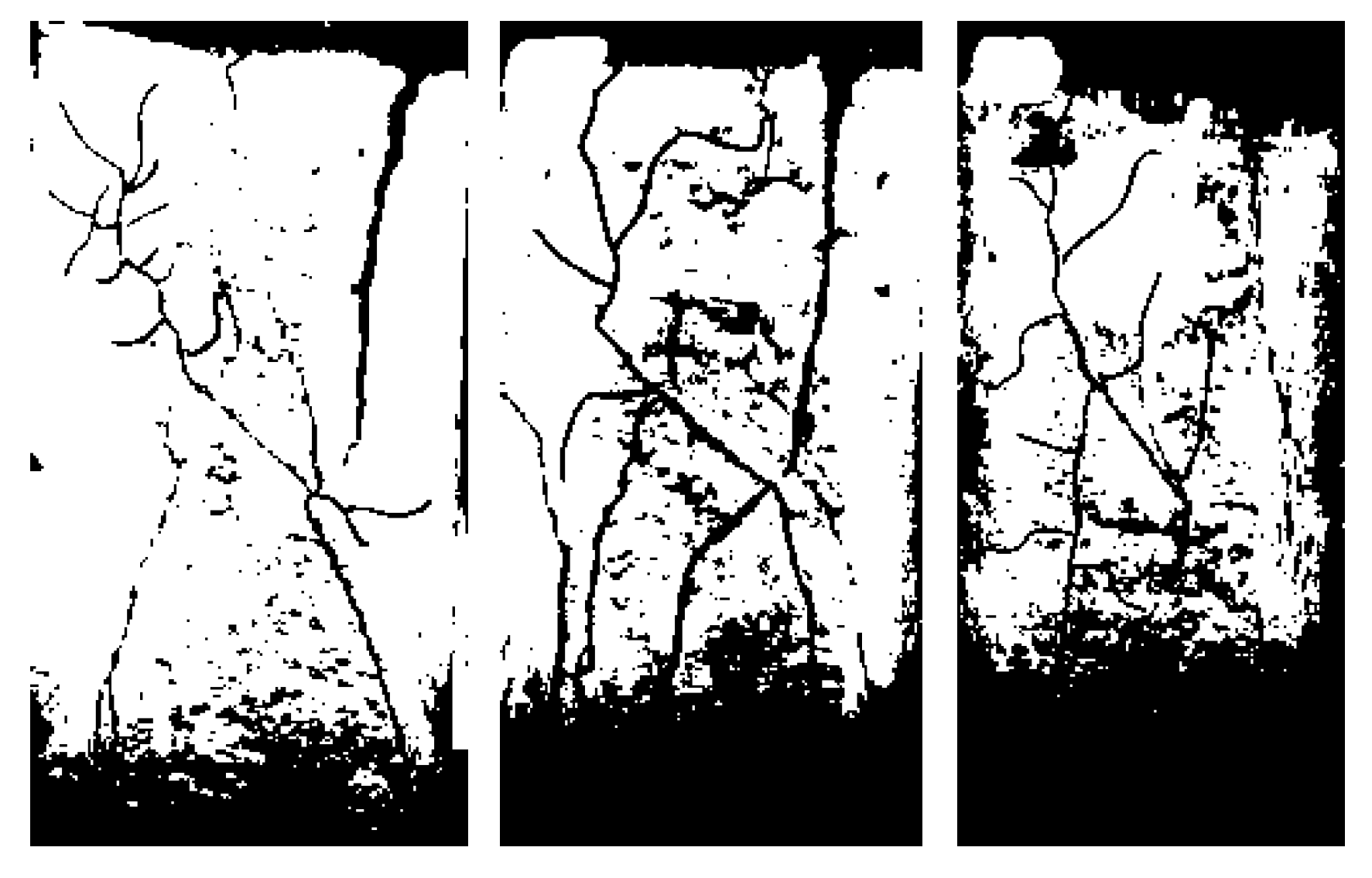
5. True Triaxial Verification Test
6. Conclusions
- (1)
- Under the condition of true triaxial stress, the intermediate principal stress helps to increase the strength of fractured sandstone. In the process of increasing the intermediate principal stress σ2 from 40 MPa to 50 MPa, when the intermediate principal stress exceeds 30% of the maximum principal stress, the peak stress intensity increases by 16.67%, and the excessive intermediate principal stress will cause the strength of fractured rock to decrease.
- (2)
- Under the influence of true triaxial action, the macro fracture mode of sandstone is -45O macro fracture surface along the fracture development direction, and when the principal stress and fracture development direction are -90O, it is easy to produce macro fracture surface perpendicular to the fracture trend. With the increase of intermediate principal stress, the fracture degree of specimen increases, and finally the specimen forms a form of interlacing cracks.
- (3)
- Under the action of true triaxial stress, the crack initiation stress increases with the increase of the medium principal stress, indicating that the increase of the medium principal stress is beneficial to the stability of the fractured sandstone specimen. When the specimen stress exceeds 85% to 90% of the peak stress, the specimen instability failure occurs. When the intermediate principal stress increases from 40 MPa to 50 MPa, the crack initiation stress decreases slightly, indicating that the excessive intermediate principal stress accelerates the propagation of cracks inside the sandstone specimen, and the sandstone specimen is completely unstable and shear cracks play a dominant role.
- (4)
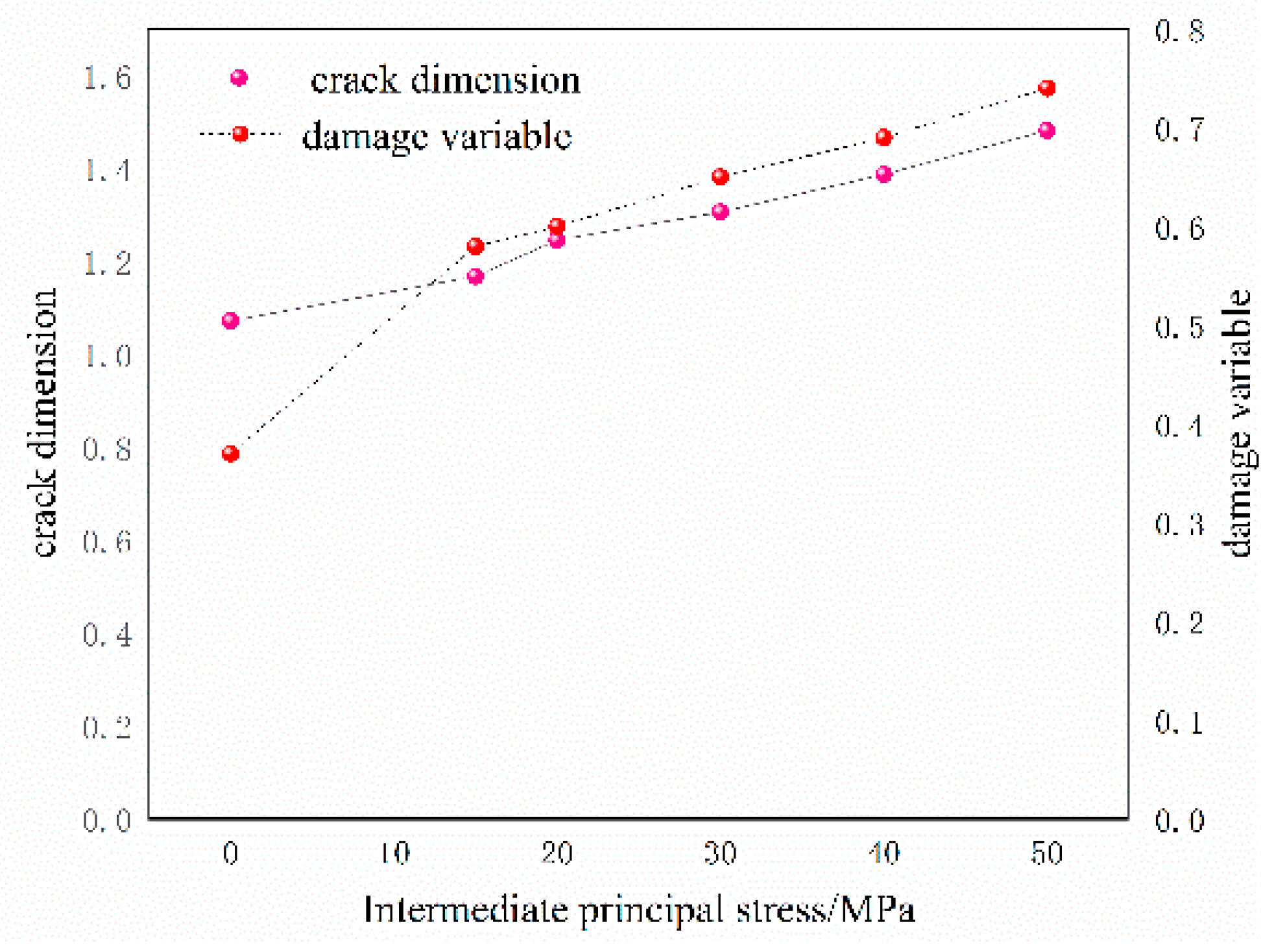
- With the increase of the intermediate principal stress, the fractal dimension of the fracture presents an obvious phenomenon of increasing dimension, and the damage degree of the fracture deepens, the fracture grid is gradually complex, and the compression shear stress fracture and tensile stress fracture gradually expand and form macro fracture, and the fracture degree of the sandstone specimen continues to increase, resulting in sandstone deformation and failure.
- (5)
- The comparison between the true triaxial test and the particle flow simulation test shows that the results are basically similar, which can truly reflect the failure mechanism and failure mode of the specimen, and proves that the particle flow simulation test has certain reliability and rationality.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Entacher, M.; Schuller, E.; Galler, R. Rock Failure and Crack Propagation Beneath Disc Cutters. Rock Mech. Rock Eng. 2015, 48, 1559–1572. [Google Scholar] [CrossRef]
- Pandey, A.C.; Kumar, A. Analysing topographical changes in open cast coal-mining region of Patratu, Jharkhand using CARTOSAT-I Stereopair satellite images. Geocarto Int. 2014, 29, 731–744. [Google Scholar] [CrossRef]
- Undul, O.; Amann, F.; Plotze, M.L. Micro-textural effects on crack initiation and crack propagation of andesitic rocks. Eng. Geol. 2015, 193, 267–275. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, N.; Wang, X.; Jia, X.; Yao, D. Numerical Study of the Strength and Characteristics of Sandstone Samples with Combined Double Hole and Double Fissure Defects. Sustainability 2021, 13, 7090. [Google Scholar] [CrossRef]
- Liu, J.; Cong, Y.; Zhang, L.; Wang, Z. Microscopic damage mechanism of granite under true triaxial loading and unloading. J. Cent. South Univ. 2021, 52, 2677–2688. [Google Scholar]
- Wang, J.; Fu, J.X.; Song, W.D.; Zhang, Y.F.; Wang, Y. Particle flow simulation of mechanical properties and microcrack evolution characteristics of rock-fill combination model. J. China Univ. Min. Technol. 2020, 49, 453–462. [Google Scholar]
- Shan, R.L.; Bai, Y.; Ju, Y.; Han, T.Y.; Dou, H.Y.; Li, Z.L. Study on the Triaxial Unloading Creep Mechanical Properties and Damage Constitutive Model of Red Sandstone Containing a Single Ice-Filled Flaw. Rock Mech. Rock Eng. 2020, 54, 833–855. [Google Scholar] [CrossRef]
- Yao, N.; Ye, Y.C.; Hu, B.; Wang, W.Q.; Wang, Q.H. Particle flow code modeling of the mechanical behavior of layered rock under uniaxial compression. Arch. Min. Sci. 2019, 64, 181–196. [Google Scholar]
- Liu, X.; Deng, Z.; Liu, Y.; Lu, Y.; Liu, S.; Han, Y. Macro-micro analysis of particle flow in pre-peak cyclic direct shear test of rock joints. J. Coal 2019, 44, 2103–2115. [Google Scholar]
- Faizi, S.A.; Kwok, C.Y.; Duan, K. The effects of intermediate principle stress on the mechanical behavior of transversely isotropic rocks: Insights from DEM simulations. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1262–1280. [Google Scholar] [CrossRef]
- Lu, W.; Zhu, Z.; He, Y.; Que, X. Strength Characteristics and Failure Mechanism of a Columnar Jointed Rock Mass Under Uniaxial, Triaxial, and True Triaxial Confinemen. Rock Mech. Rock Eng. 2021, 54, 2425–2439. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Liao, H.J.; Dang, F.N. Effect of intermediate principal stress on strength of soft rock under complex stress states. J. Cent. South Univ. 2014, 21, 1583–1593. [Google Scholar] [CrossRef]
- Li, X.; Du, K.; Li, D. True Triaxial Strength and Failure Modes of Cubic Rock Specimens with Unloading the Minor Principal Stress. Rock Mech. Rock Eng. 2015, 48, 2185–2196. [Google Scholar] [CrossRef]
- Vergara, M.R.; Kudella, P.; Triantafyllidis, T. Large Scale Tests on Jointed and Bedded Rocks Under Multi-Stage Triaxial Compression and Direct Shear. Rock Mech. Rock Eng. 2015, 48, 75–92. [Google Scholar] [CrossRef]
- Xie, H.; Zhu, J.; Zhou, T.; Zhao, J. Fracture of Sedimentary Rocks under a Complex Triaxial Stress State. Mech. Solids 2016, 51, 522–526. [Google Scholar]
- Xie, H.; Zhu, J.; Zhou, T.; Zhao, J. Novel Three-dimensional Rock Dynamic Tests Using the True Triaxial Electromagnetic Hopkinson Bar System. Rock Mech. Rock Eng. 2021, 54, 2079–2086. [Google Scholar] [CrossRef]
- Raziperchikolaee, S.; Alvarado, V.; Yin, S. Assessment of permeability changes during rock deformation and failure of a sandstone sample using a stress-dependent pore network model. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 53. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, C.Y.; Li, B.T.; Lu, Y.Q.; Yang, X. A dissolution-diffusion sliding model for soft rock grains with hydro-mechanical effect. J. Rock Mech. Geotech. Eng. 2018, 10, 457–467. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, X.T.; Wang, Z.; Zhang, X. Strength and failure characteristics of jointed marble under true triaxial compression. Bull. Eng. Geol. Environ. 2019, 79, 891–905. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Peng, J.; Teh, C.I. Numerical investigation of mineralogical composition effect on strength and micro-cracking behavior of crystalline rocks. J. Nat. Gas Sci. Eng. 2018, 53, 191–203. [Google Scholar] [CrossRef]
- Zhang, H.; Wan, Z.; Feng, Z.; Wu, J. Shear-induced Permeability Evolution of Sandstone Fractures. Geofluids 2018, 2018, 2416481. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Lu, W.; He, Y.; Que, X. Experimental Study on the Strength Failure Characteristics of Columnar Jointed Rock Masses under Three-Dimensional Stress. KSCE J. Civ. Eng. 2021, 25, 2411–2425. [Google Scholar] [CrossRef]
- Zhou, Y.; Sheng, Q.; Li, N.; Fu, X. The Dynamic Mechanical Properties of a Hard Rock Under True Triaxial Damage-Controlled Dynamic Cyclic Loading with Different Loading Rates: A Case Study. Rock Mech. Rock Eng. 2022, 55, 2471–2492. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, X. Characterisation of confinement effect on jointed rock pillars using a Synthetic Rock Mass approach. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 1690–1711. [Google Scholar] [CrossRef]
- Sun, Y.; Sumelka, W. State-dependent fractional plasticity model for the true triaxial behaviour of granular soil. Arch. Mech. 2019, 71, 23–47. [Google Scholar]


| Mechanical Parameters | Test Value |
| Poisson’s ratio | 0.3 |
| Compressive strength/MPa | 48.24 |
| Modulus of elasticity/Gpa | 13.1 |
| Mesoscopic Parameters | Taking Values |
| porosity | 0.6 |
| Elastic modulus of particles/GPa | 18 |
| Normal and tangential stiffness ratio of particles | 4.8 |
| solid friction factor | 0.3 |
| Parallel bond elastic modulus/GPa | 16 |
| parallel-bond stiffness ratio | 4.5 |
| Parallel bond normal strength/MPa | 55 |
| Parallel bond tangential strength/MPa | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Su, H.; Luo, C.; Ma, S.; Ding, H. Particle Flow Simulation of Failure Process of Defective Sandstone under Different Intermediate Principal Stress under True Triaxial Action. Processes 2022, 10, 2028. https://doi.org/10.3390/pr10102028
Wang Z, Su H, Luo C, Ma S, Ding H. Particle Flow Simulation of Failure Process of Defective Sandstone under Different Intermediate Principal Stress under True Triaxial Action. Processes. 2022; 10(10):2028. https://doi.org/10.3390/pr10102028
Chicago/Turabian StyleWang, Ziyi, Hengyu Su, Chang Luo, Shu Ma, and Heng Ding. 2022. "Particle Flow Simulation of Failure Process of Defective Sandstone under Different Intermediate Principal Stress under True Triaxial Action" Processes 10, no. 10: 2028. https://doi.org/10.3390/pr10102028
APA StyleWang, Z., Su, H., Luo, C., Ma, S., & Ding, H. (2022). Particle Flow Simulation of Failure Process of Defective Sandstone under Different Intermediate Principal Stress under True Triaxial Action. Processes, 10(10), 2028. https://doi.org/10.3390/pr10102028





