What Features of Ligands Are Relevant to the Opening of Cryptic Pockets in Drug Targets?
Abstract
:1. Introduction
2. Materials and Methods
2.1. Datasets
2.1.1. Dataset I: PDBbind-CN
2.1.2. Dataset II: NR-DBIND
Structure Preparation and Visualization
Identification and Characterization of Binding Pockets
2.2. Methods
2.2.1. Development of Models to Separate Inducers and Non-Inducers
Model Building
Model Validation
Performance Measurement
Interpretation of Models
2.2.2. Analysis of Similarity of Ligands
2.2.3. Molecular Dynamics (MD) Simulations on Mdmx Inhibitors
3. Results
3.1. Model Performance
3.2. Interpretation of Models
3.3. Analysis of Functional Groups
3.4. Fragment Analysis on PDBbind Set
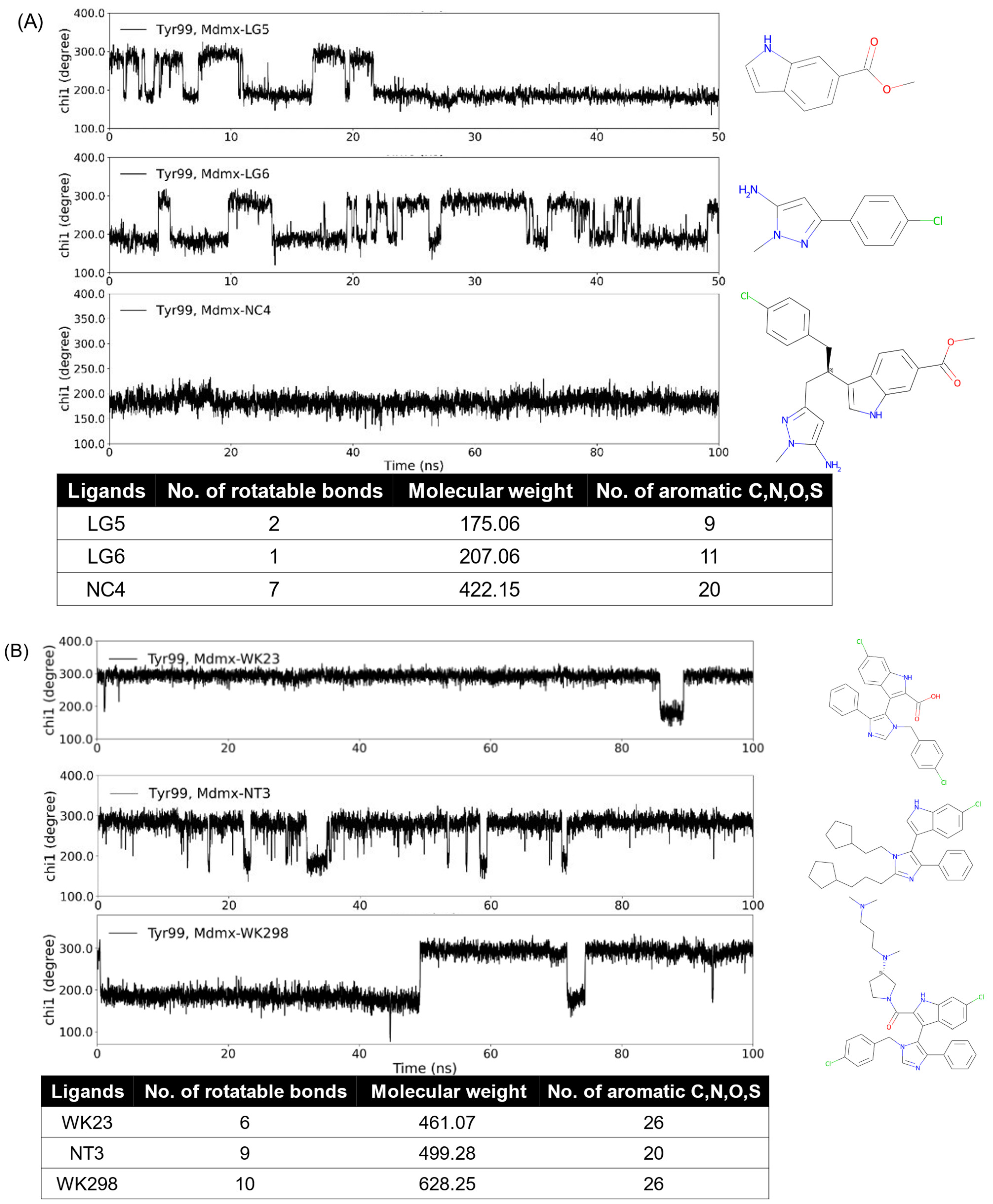
3.5. Analysis of Mdmx Inhibitors
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Owens, J. Determining Druggability. Nat. Rev. Drug Discov. 2007, 6, 187. [Google Scholar] [CrossRef]
- Hopkins, A.L.; Groom, C.R. The Druggable Genome. Nat. Rev. Drug Discov. 2002, 1, 727–730. [Google Scholar] [CrossRef] [PubMed]
- Santos, R.; Ursu, O.; Gaulton, A.; Bento, A.P.; Donadi, R.S.; Bologa, C.G.; Karlsson, A.; Al-Lazikani, B.; Hersey, A.; Oprea, T.I.; et al. A Comprehensive Map of Molecular Drug Targets. Nat. Rev. Drug Discov. 2017, 16, 19–34. [Google Scholar] [CrossRef] [PubMed]
- Oprea, T.I.; Bologa, C.G.; Brunak, S.; Campbell, A.; Gan, G.N.; Gaulton, A.; Gomez, S.M.; Guha, R.; Hersey, A.; Holmes, J.; et al. Unexplored Therapeutic Opportunities in the Human Genome. Nat. Rev. Drug Discov. 2018, 17, 317–332. [Google Scholar] [CrossRef] [PubMed]
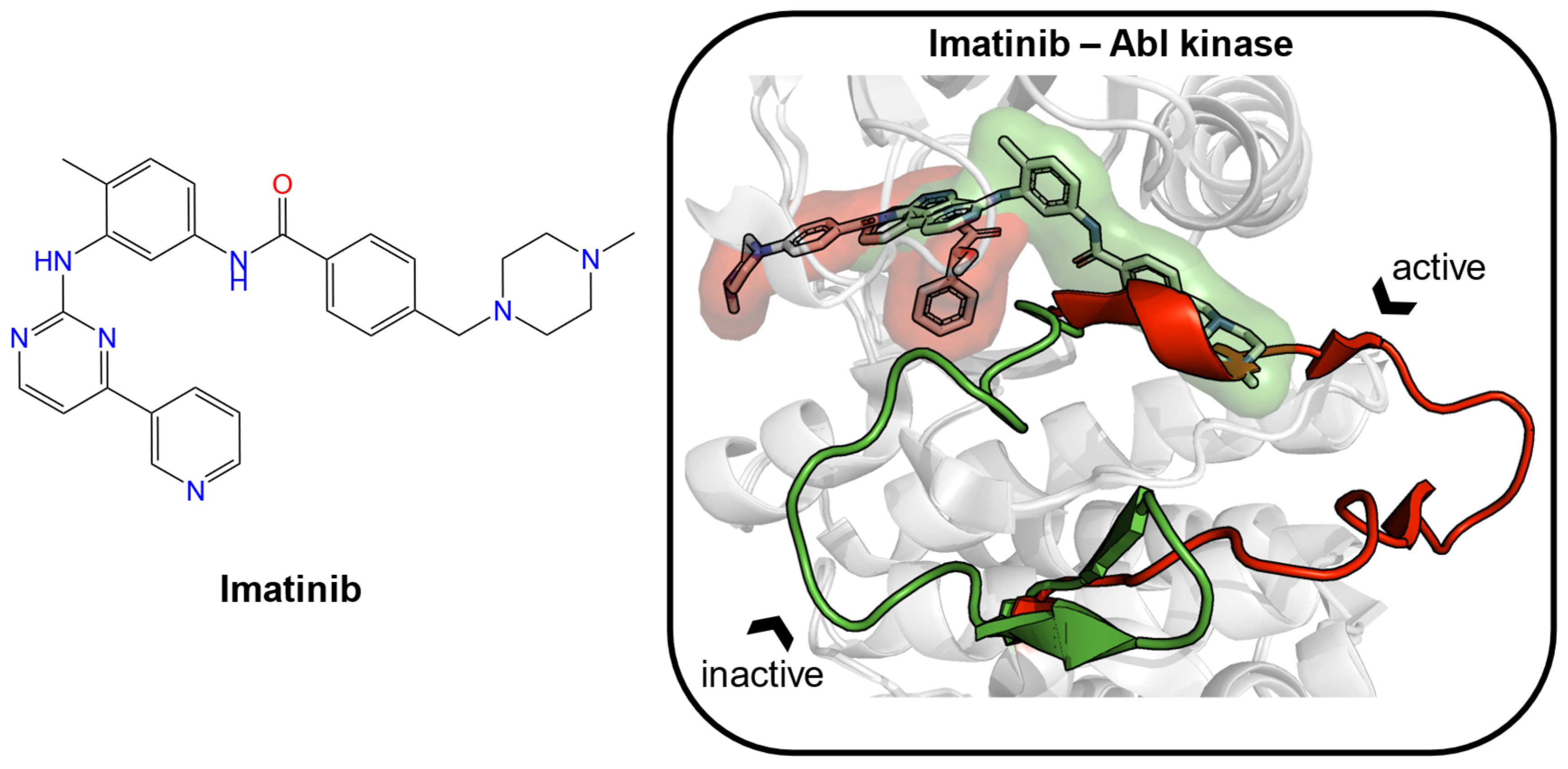
- Nagar, B.; Bornmann, W.G.; Pellicena, P.; Schindler, T.; Veach, D.R.; Miller, W.T.; Clarkson, B.; Kuriyan, J. Crystal Structures of the Kinase Domain of C-Abl in Complex with the Small Molecule Inhibitors PD173955 and Imatinib (STI-571). Cancer Res. 2002, 62, 4236–4243. [Google Scholar]
- Schindler, T.; Bornmann, W.; Pellicena, P.; Miller, W.T.; Clarkson, B.; Kuriyan, J. Structural Mechanism for STI-571 Inhibition of Abelson Tyrosine Kinase. Science 2000, 289, 1938–1942. [Google Scholar] [CrossRef] [Green Version]
- Wodicka, L.M.; Ciceri, P.; Davis, M.I.; Hunt, J.P.; Floyd, M.; Salerno, S.; Hua, X.H.; Ford, J.M.; Armstrong, R.C.; Zarrinkar, P.P.; et al. Activation State-Dependent Binding of Small Molecule Kinase Inhibitors: Structural Insights from Biochemistry. Chem. Biol. 2010, 17, 1241–1249. [Google Scholar] [CrossRef] [Green Version]
- Umezawa, K.; Kii, I. Druggable Transient Pockets in Protein Kinases. Molecules 2021, 26, 651. [Google Scholar] [CrossRef]
- Vajda, S.; Beglov, D.; Wakefield, A.E.; Egbert, M.; Whitty, A. Cryptic Binding Sites on Proteins: Definition, Detection, and Druggability. Curr. Opin. Chem. Biol. 2018, 44, 1–8. [Google Scholar] [CrossRef]
- Mizukoshi, Y.; Takeuchi, K.; Tokunaga, Y.; Matsuo, H.; Imai, M.; Fujisaki, M.; Kamoshida, H.; Takizawa, T.; Hanzawa, H.; Shimada, I. Targeting the Cryptic Sites: NMR-Based Strategy to Improve Protein Druggability by Controlling the Conformational Equilibrium. Sci. Adv. 2020, 6, eabd0480. [Google Scholar] [CrossRef]
- Kii, I.; Sumida, Y.; Goto, T.; Sonamoto, R.; Okuno, Y.; Yoshida, S.; Kato-Sumida, T.; Koike, Y.; Abe, M.; Nonaka, Y.; et al. Selective Inhibition of the Kinase DYRK1A by Targeting Its Folding Process. Nat. Commun. 2016, 7, 11391. [Google Scholar] [CrossRef] [PubMed]
- Cimermancic, P.; Weinkam, P.; Rettenmaier, T.J.; Bichmann, L.; Keedy, D.A.; Woldeyes, R.A.; Schneidman-Duhovny, D.; Demerdash, O.N.; Mitchell, J.C.; Wells, J.A.; et al. CryptoSite: Expanding the Druggable Proteome by Characterization and Prediction of Cryptic Binding Sites. J. Mol. Biol. 2016, 428, 709–719. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kozakov, D.; Grove, L.E.; Hall, D.R.; Bohnuud, T.; Mottarella, S.E.; Luo, L.; Xia, B.; Beglov, D.; Vajda, S. The FTMap Family of Web Servers for Determining and Characterizing Ligand-Binding Hot Spots of Proteins. Nat. Protoc. 2015, 10, 733–755. [Google Scholar] [CrossRef] [Green Version]
- Beglov, D.; Hall, D.R.; Wakefield, A.E.; Luo, L.; Allen, K.N.; Kozakov, D.; Whitty, A.; Vajda, S. Exploring the Structural Origins of Cryptic Sites on Proteins. Proc. Natl. Acad. Sci. USA 2018, 115, E3416–E3425. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clark, J.J.; Benson, M.L.; Smith, R.D.; Carlson, H.A. Inherent versus Induced Protein Flexibility: Comparisons within and between Apo and Holo Structures. PLoS Comput. Biol. 2019, 15, e1006705. [Google Scholar] [CrossRef] [Green Version]
- Evans, D.J.; Yovanno, R.A.; Rahman, S.; Cao, D.W.; Beckett, M.Q.; Patel, M.H.; Bandak, A.F.; Lau, A.Y. Finding Druggable Sites in Proteins Using TACTICS. J. Chem. Inf. Model. 2021, 61, 2897–2910. [Google Scholar] [CrossRef] [PubMed]
- Kuzmanic, A.; Bowman, G.R.; Juarez-Jimenez, J.; Michel, J.; Gervasio, F.L. Investigating Cryptic Binding Sites by Molecular Dynamics Simulations. Acc. Chem. Res. 2020, 53, 654–661. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Fang, X.; Lu, Y.; Wang, S. The PDBbind Database: Collection of Binding Affinities for Protein−Ligand Complexes with Known Three-Dimensional Structures. J. Med. Chem. 2004, 47, 2977–2980. [Google Scholar] [CrossRef]
- Wang, R.; Fang, X.; Lu, Y.; Yang, C.-Y.; Wang, S. The PDBbind Database: Methodologies and Updates. J. Med. Chem. 2005, 48, 4111–4119. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Westbrook, J.D.; Shao, C.; Feng, Z.; Zhuravleva, M.; Velankar, S.; Young, J. The Chemical Component Dictionary: Complete Descriptions of Constituent Molecules in Experimentally Determined 3D Macromolecules in the Protein Data Bank. Bioinformatics 2015, 31, 1274–1278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A New Generation of Protein Database Search Programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- The PyMOL Molecular Graphics System; Version 2.4.0; Schrödinger, LLC: New York, NY, USA, 2021.
- Schrödinger Release 2020-3; Schrödinger, LLC: New York, NY, USA, 2020.
- Halgren, T. New Method for Fast and Accurate Binding-Site Identification and Analysis. Chem. Biol. Drug Des. 2007, 69, 146–148. [Google Scholar] [CrossRef]
- Halgren, T.A. Identifying and Characterizing Binding Sites and Assessing Druggability. J. Chem. Inf. Model. 2009, 49, 377–389. [Google Scholar] [CrossRef] [PubMed]
- Réau, M.; Lagarde, N.; Zagury, J.F.; Montes, M. Nuclear Receptors Database Including Negative Data (NR-DBIND): A Database Dedicated to Nuclear Receptors Binding Data Including Negative Data and Pharmacological Profile. J. Med. Chem. 2019, 62, 2894–2904. [Google Scholar] [CrossRef] [PubMed]
- Madhavi Sastry, G.; Adzhigirey, M.; Day, T.; Annabhimoju, R.; Sherman, W. Protein and Ligand Preparation: Parameters, Protocols, and Influence on Virtual Screening Enrichments. J. Comput.-Aided Mol. Des. 2013, 27, 221–234. [Google Scholar] [CrossRef] [PubMed]
- Shelley, J.C.; Cholleti, A.; Frye, L.L.; Greenwood, J.R.; Timlin, M.R.; Uchimaya, M. Epik: A Software Program for PKaprediction and Protonation State Generation for Drug-like Molecules. J. Comput.-Aided Mol. Des. 2007, 21, 681–691. [Google Scholar] [CrossRef]
- Sushko, I.; Novotarskyi, S.; Körner, R.; Pandey, A.K.; Rupp, M.; Teetz, W.; Brandmaier, S.; Abdelaziz, A.; Prokopenko, V.V.; Tanchuk, V.Y.; et al. Online Chemical Modeling Environment (OCHEM): Web Platform for Data Storage, Model Development and Publishing of Chemical Information. J. Comput.-Aided Mol. Des. 2011, 25, 533–554. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learning 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Svetnik, V.; Liaw, A.; Tong, C.; Christopher Culberson, J.; Sheridan, R.P.; Feuston, B.P. Random Forest: A Classification and Regression Tool for Compound Classification and QSAR Modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How Many Trees in a Random Forest? In Proceedings of the Machine Learning and Data Mining in Pattern Recognition; Perner, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 154–168. [Google Scholar]
- Tetko, I.V.; Tanchuk, V.Y.; Villa, A.E.P. Prediction of N-Octanol/Water Partition Coefficients from PHYSPROP Database Using Artificial Neural Networks and E-State Indices. J. Chem. Inf. Comput. Sci. 2001, 41, 1407–1421. [Google Scholar] [CrossRef] [PubMed]
- Tetko, I.V.; Tanchuk, V.Y.; Kasheva, T.N.; Villa, A.E.P. Estimation of Aqueous Solubility of Chemical Compounds Using E-State Indices. J. Chem. Inf. Comput. Sci. 2001, 41, 1488–1493. [Google Scholar] [CrossRef] [PubMed]
- Tetko, I.V.; Tanchuk, V.Y. Application of Associative Neural Networks for Prediction of Lipophilicity in ALOGPS 2.1 Program. J. Chem. Inf. Comput. Sci. 2002, 42, 1136–1145. [Google Scholar] [CrossRef]
- Kier, L.B.; Hall, L.H. An Electrotopological-State Index for Atoms in Molecules. Pharm. Res. 1990, 7, 801–807. [Google Scholar] [CrossRef] [PubMed]
- Kier, L.B.; Hall, L.H. Molecular Structure Description: The Electrotopological State; Elsevier Science: Amsterdam, The Netherlands, 1999; ISBN 9780124065550. [Google Scholar]
- Methods and Principles in Medicinal Chemistry Previous Volumes of This Series: Pharmacokinetics and Metabolism in Drug Design, Pharmacophores and Pharmacophore Searches Chirality in Drug Research Fragment-Based Approaches in Drug Discovery High-Throughput Screening in Drug Discovery Mass Spectrometry in Medicinal Chemistry Molecular Drug Properties Nuclear Receptors as Drug Targets. Available online: https://www.wiley.com/en-us/content-search?cq=Wiley%27s+Methods+and+Principles+in+Medicinal+Chemistry+Series&pq=Wiley%27s+Methods+and+Principles+in+Medicinal+Chemistry+Series (accessed on 20 November 2021).
- Hall, L.H.; Kier, L.B. Electrotopological State Indices for Atom Types: A Novel Combination of Electronic, Topological, and Valence State Information. J. Chem. Inf. Comput. Sci. 1995, 35, 1039–1045. [Google Scholar] [CrossRef]
- Shapley, L.S. A Value Fo N-Person Games; Princeton University Press: Princeton, NJ, USA, 2016; pp. 307–318. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS 2017); Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1135–1144. [Google Scholar]
- Shrikumar, A.; Greenside, P.; Kundaje, A. Learning Important Features Through Propagating Activation Differences. arXiv 2019, arXiv:1704.02685. [Google Scholar]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.-R.; Samek, W. On Pixel-Wise Explanations for Non-Linear Classifier Decisions by Layer-Wise Relevance Propagation. PLoS ONE 2015, 10, e0130140. [Google Scholar] [CrossRef] [Green Version]
- Lipovetsky, S.; Conklin, M. Analysis of Regression in Game Theory Approach. Appl. Stoch. Models Bus. Ind. 2001, 17, 319–330. [Google Scholar] [CrossRef]
- Štrumbelj, E.; Kononenko, I. Explaining Prediction Models and Individual Predictions with Feature Contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Datta, A.; Sen, S.; Zick, Y. Algorithmic Transparency via Quantitative Input Influence: Theory and Experiments with Learning Systems. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2016; pp. 598–617. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Rogers, D.; Hahn, M. Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef] [PubMed]
- Shvarts, A.; Steegenga, W.T.; Riteco, N.; van Laar, T.; Dekker, P.; Bazuine, M.; van Ham, R.C.; van der Houven van Oordt, W.; Hateboer, G.; van der Eb, A.J.; et al. MDMX: A Novel P53-Binding Protein with Some Functional Properties of MDM2. EMBO J. 1996, 15, 5349–5357. [Google Scholar] [CrossRef] [PubMed]
- Popowicz, G.M.; Czarna, A.; Wolf, S.; Wang, K.; Wang, W.; Dömling, A.; Holak, T.A. Structures of Low Molecular Weight Inhibitors Bound to MDMX and MDM2 Reveal New Approaches for P53-MDMX/MDM2 Antagonist Drug Discovery. Cell Cycle 2010, 9, 1104–1111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- AMBER 2020; University of California: San Francisco, CA, USA, 2020; Available online: https://ambermd.org/doc12/Amber20.pdf (accessed on 20 November 2021).
- Popowicz, G.M.; Czarna, A.; Holak, T.A. Structure of the Human Mdmx Protein Bound to the P53 Tumor Suppressor Transactivation Domain. Cell Cycle 2008, 7, 2441–2443. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, W.L.; Madura, J.D. Quantum and Statistical Mechanical Studies of Liquids. 25. Solvation and Conformation of Methanol in Water. J. Am. Chem. Soc. 2002, 105, 1407–1413. [Google Scholar] [CrossRef]
- Jakalian, A.; Bush, B.L.; Jack, D.B.; Bayly, C.I. Fast, Efficient Generation of High-Quality Atomic Charges. AM1-BCC Model: I. Method. J. Comput. Chem. 2000, 21, 132–146. [Google Scholar] [CrossRef]
- Jakalian, A.; Jack, D.B.; Bayly, C.I. Fast, Efficient Generation of High-Quality Atomic Charges. AM1-BCC Model: II. Parameterization and Validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J.P. Development and Use of Quantum Mechanical Molecular Models. 76. AM1: A New General Purpose Quantum Mechanical Molecular Model. J. Am. Chem. Soc. 2002, 107, 3902–3909. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. Ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from Ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Popowicz, G.M.; Czarna, A.; Rothweiler, U.; Szwagierczak, A.; Krajewski, M.; Weber, L.; Holak, T.A. Molecular Basis for the Inhibition of P53 by Mdmx. Cell Cycle 2007, 6, 2386–2392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vorberg, S.; Tetko, I.V. Modeling the Biodegradability of Chemical Compounds Using the Online CHEmical Modeling Environment (OCHEM). Mol. Inform. 2014, 33, 73–85. [Google Scholar] [CrossRef] [Green Version]
- Tetko, I.V.; Lowe, D.M.; Williams, A.J. The Development of Models to Predict Melting and Pyrolysis Point Data Associated with Several Hundred Thousand Compounds Mined from PATENTS. J. Cheminform. 2016, 8, 2. [Google Scholar] [CrossRef] [Green Version]
- Tetko, I.V.; Novotarskyi, S.; Sushko, I.; Ivanov, V.; Petrenko, A.E.; Dieden, R.; Lebon, F.; Mathieu, B. Development of Dimethyl Sulfoxide Solubility Models Using 163 000 Molecules: Using a Domain Applicability Metric to Select More Reliable Predictions. J. Chem. Inf. Model. 2013, 53, 1990–2000. [Google Scholar] [CrossRef]
- Salmina, E.S.; Haider, N.; Tetko, I.V. Extended Functional Groups (EFG): An Efficient Set for Chemical Characterization and Structure-Activity Relationship Studies of Chemical Compounds. Molecules 2016, 21, 1. [Google Scholar] [CrossRef] [Green Version]
- Wilcken, R.; Liu, X.; Zimmermann, M.O.; Rutherford, T.J.; Fersht, A.R.; Joerger, A.C.; Boeckler, F.M. Halogen-Enriched Fragment Libraries as Leads for Drug Rescue of Mutant P53. J. Am. Chem. Soc. 2012, 134, 6810–6818. [Google Scholar] [CrossRef]
- Davies, T.G.; Wixted, W.E.; Coyle, J.E.; Griffiths-Jones, C.; Hearn, K.; McMenamin, R.; Norton, D.; Rich, S.J.; Richardson, C.; Saxty, G.; et al. Monoacidic Inhibitors of the Kelch-like ECH-Associated Protein 1: Nuclear Factor Erythroid 2-Related Factor 2 (KEAP1:NRF2) Protein–Protein Interaction with High Cell Potency Identified by Fragment-Based Discovery. J. Med. Chem. 2016, 59, 3991–4006. [Google Scholar] [CrossRef]
- Xia, Z. In Silico Structure-Based Approaches to Design Mdmx Inhibitors, Munich. Ph.D. Thesis, Technische Universität München, München, Germany, January 2022. [Google Scholar]
- Lee, K.; Yang, A.; Lin, Y.C.; Reker, D.; Bernardes, G.J.L.; Rodrigues, T. Combating Small-Molecule Aggregation with Machine Learning. Cell Rep. Phys. Sci. 2021, 2, 100573. [Google Scholar] [CrossRef]


| Threshold (ΔV, Å3) | No. of Inducers | No. of Non- Inducers | Training Set | External Validation Set | ||||
|---|---|---|---|---|---|---|---|---|
| AUC | Balanced Accuracy | Accuracy | AUC | Balanced Accuracy | Accuracy | |||
| 0 | 759 (117) * | 317 (18) * | 0.61 | 68 | 72 | 0.56 | 56 | 81 |
| 20 | 498 (112) | 578 (23) | 0.67 | 69 | 69 | 0.51 | 51 | 76 |
| 30 | 405 (110) | 671 (25) | 0.69 | 73 | 75 | 0.59 | 59 | 78 |
| 40 | 356 (105) | 720 (30) | 0.68 | 73 | 76 | 0.54 | 54 | 67 |
| 50 | 319 (103) | 757 (32) | 0.7 | 74 | 78 | 0.58 | 58 | 75 |
| 60 | 293 (100) | 783 (35) | 0.71 | 76 | 80 | 0.65 | 65 | 80 |
| 70 | 251 (97) | 825 (38) | 0.73 | 77 | 81 | 0.60 | 60 | 73 |
| 80 | 216 (93) | 860 (42) | 0.68 | 75 | 81 | 0.67 | 67 | 79 |
| 90 | 185 (90) | 891 (45) | 0.64 | 73 | 83 | 0.57 | 57 | 64 |
| 100 | 170 (86) | 906 (49) | 0.68 | 77 | 86 | 0.60 | 60 | 64 |
| Increases Probability of Being Inducers | Decreases Probability of Being Inducers | ||
|---|---|---|---|
| Descriptor | Description | Descriptor | Description |
| SddssS | 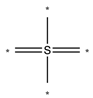 | SdO (sulfo) | 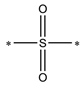 |
| ALogPS_logP | Octanol/water partition coefficient | AlogPS_logS | Solubility in water |
| HALOG | Number of halogen atoms | SaaNH |  |
| aCNOS | The sum of aromatic C, N, O, and S atoms | SsNH2 | 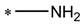 |
| SaaCH |  | SeaC3NHaa | 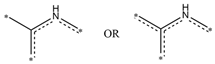 |
| Se1C3S4ad |  | S | Number of sulfur atoms |
| SaasC | 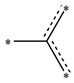 | SdssC | 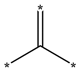 |
| SeaC2C2aa | 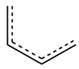 | ||
| RBONDS | Number of rotatable bonds | ||
| P | Number of phosphorus atoms | ||
| SeaC2C3aa |  | ||
| MW | Molecular weight | ||
| SdO (acid) |  | ||
| Functional Group | The Ratio in Inducers (%) | The Ratio in Non-Inducers (%) | p-Value |
|---|---|---|---|
| Sulfonamides | 6.3 | 23.4 | −4.8 × 10−12 |
| Sulfonic acid derivatives | 7.3 | 24.1 | −4.03 × 10−11 |
| Halogens | 44.1 | 28.7 | 1.93 × 10−6 |
| Halogenated benzene | 28.1 | 15.1 | 1.83 × 10−6 |
| Aryl halides | 36.5 | 24.3 | 7.79 × 10−5 |
| Tertiary mixed amines | 11.5 | 4.5 | 6.66 × 10−5 |
| Five-membered heterocycles with two heteroatoms | 17.4 | 9.9 | 9.45 × 10−4 |
| Pyridine | 11.8 | 5.6 | 7.52 × 10−4 |
| Phosphorus | 13.5 | 6.8 | 6.28 × 10−4 |
| Phosphoric acids | 10.1 | 4.3 | 5.95 × 10−4 |
| Carboxylic acids | 31.6 | 21.2 | 3.62 × 10−4 |
| Aromatic halogen | 33.3 | 22.1 | 1.61 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Z.; Karpov, P.; Popowicz, G.; Sattler, M.; Tetko, I.V. What Features of Ligands Are Relevant to the Opening of Cryptic Pockets in Drug Targets? Informatics 2022, 9, 8. https://doi.org/10.3390/informatics9010008
Xia Z, Karpov P, Popowicz G, Sattler M, Tetko IV. What Features of Ligands Are Relevant to the Opening of Cryptic Pockets in Drug Targets? Informatics. 2022; 9(1):8. https://doi.org/10.3390/informatics9010008
Chicago/Turabian StyleXia, Zhonghua, Pavel Karpov, Grzegorz Popowicz, Michael Sattler, and Igor V. Tetko. 2022. "What Features of Ligands Are Relevant to the Opening of Cryptic Pockets in Drug Targets?" Informatics 9, no. 1: 8. https://doi.org/10.3390/informatics9010008
APA StyleXia, Z., Karpov, P., Popowicz, G., Sattler, M., & Tetko, I. V. (2022). What Features of Ligands Are Relevant to the Opening of Cryptic Pockets in Drug Targets? Informatics, 9(1), 8. https://doi.org/10.3390/informatics9010008






