Abstract
This paper proposes a new method to generate edited topics or clusters to analyze images for prioritizing quality issues. The approach is associated with a new way for subject matter experts to edit the cluster definitions by “zapping” or “boosting” pixels. We refer to the information entered by users or experts as “high-level” data and we are apparently the first to allow in our model for the possibility of errors coming from the experts. The collapsed Gibbs sampler is proposed that permits efficient processing for datasets involving tens of thousands of records. Numerical examples illustrate the benefits of the high-level data related to improving accuracy measured by Kullback–Leibler (KL) distance. The numerical examples include a Tungsten inert gas example from the literature. In addition, a novel laser aluminum alloy image application illustrates the assignment of welds to groups that correspond to part conformance standards.
1. Introduction
Clustering is an informatics technique that allows practitioners to focus attention on a few important factors in a process. In clustering, the analyst takes unsupervised or untagged data and divides it into what are intended to be intuitive groupings. Then, knowledge is gained about the whole dataset or “corpus” and any new items can be automatically assigned to groups. As a result, clustering can provide a data-driven prioritization for quality issues relevant to allocating limited attention and resources. Informatics professionals are asked now more than ever to be versant in using the information technology revolution [1,2,3]. This revolution exposed practitioners to large databases of images (and texts) that provided insights into quality issues. Practitioner might easily create clustering or logistic regression models using the rating field. Yet, the practitioner generally has no systematic technique for analyzing the freestyle text or image. This is true even while the text or image clearly contains much relevant information for causal analysis [4,5].
This article proposes methods with sufficient generality to provide the ability to apply the analysis either for images or texts. Each image (or record) could correspond to more than a single quality issue. For example, one part of a weld image might include nonconformity at the same time reveals another type of nonconformity. In addition, it might be too expensive to go through all the images (or documents), to identify the quality issues manually. The purpose of this article is to propose a new way to identify quality issues combined with different images (or texts) by generating clustering charts to prioritize quality issues. For example, if the engineers knew that type 1 defects were much more common than the other types, they could focus on the techniques relevant to type 1 for quality improvement and address the most important issues of that type. This new method will require relatively little effort from practitioners compared with manually tagging all or a large fraction of the data.
Even while the information technology revolution is exposing practitioners to new types of challenges it is also making some relevant estimation methods like Bayesian analysis easier [6,7,8,9]. One aspect that many Bayesian applications have in common is that they do not apply informative prior distributions. This is presumably because, in all these cases, the relevant practitioners did not have sufficient knowledge before analysis that they could confidently apply to make the derived models more accurate. The phrase “supervised” data analysis refers to the case in which all the data used for analysis has been analyzed by subject matter experts (SMEs) and categorized into classes by cause or type. Past analyses of text or image data in quality contexts have focused on supervised data analyses [10,11]. Yet, more generally perhaps, datasets are sufficiently large that having personnel read or observe all or even a significant fraction of the articles or images and categorize them into types is prohibitively expensive. Apley and Lee [12] developed a framework for integrating on-line and off-line data which is also presented in this article. This framework did not include new types and convenient types of data. Here, we are seeking to have the data presented in different forms.
The approach proposed in this paper is apparently the first to model replication and other errors in both high-level expert and “low-level” data for unstructured multi-field text or image modeling for image analysis. Allen, Xiong and Afful-Dadzie [4] did this for text data. The practical benefit that we seek is to permit the user to edit the cluster or topic definitions easily. In general, Bayesian mixture models provide clusters with interpretable meaning and are generalizations of latent semantic indexing approaches [13]. The Latent Dirichlet Allocation (LDA) method [13] has received a lot of attention because the cluster definitions derived often seem interpretable. Yet, these definitions may seem inaccurate and disagree with expert judgement. Most recently, many researchers have further refined Bayesian mixture models to make the results even more interpretable and predictive [14,15,16,17,18]. This research has generally caused the complexity of the models to grow together with the number of estimated parameters. The approach taken here is to use a relatively simple formulation and attempt to mitigate the misspecification issues by permitting user interaction through the high-level data.
To generate clustering models to analyze image data, we must identify clusters definitions which is the most challenging step, tally the total proportions of all the images associated with each cluster, sort the tallies and bar chart the results. Another objective we have for this article is to compare the proposed clustering methods with alternatives methods that have been used before. This follows because those methods require that the cluster definitions are pre-defined, all pixels in each image relate to a single cluster, and a “training set” of images have been pre-tagged or supervised [19,20,21]. For two simulated numerical examples, we compare the proposed clustering methods with three relevant alternatives: Latent Dirichlet Allocation [13,22,23], “fuzzy c means” clustering methods [24,25] and pre-processing using principle components analysis followed by fuzzy c means clustering [26]. Apparently, comparisons of a similar scope do not appear in the image analysis literature which generally focuses on the goal of retrieving relevant documents. Our research here applies the existing results for text analysis [4]. To generate helpful prioritizations, we need the estimated topic definitions and proportions to be accurate. Therefore, we also propose new measures of model accuracy relevant to our goals for image analysis.
Next section, we describe the laser welding image problem that motivates the Expert Refined Topic (ERT) modeling methods for image analysis. The motivation relates to the issue that none of the topics or clusters identified directly corresponds to the issues defined in the American National Standard Institute (ANSI) conformance standards.
Motivating Problem: Laser Welding
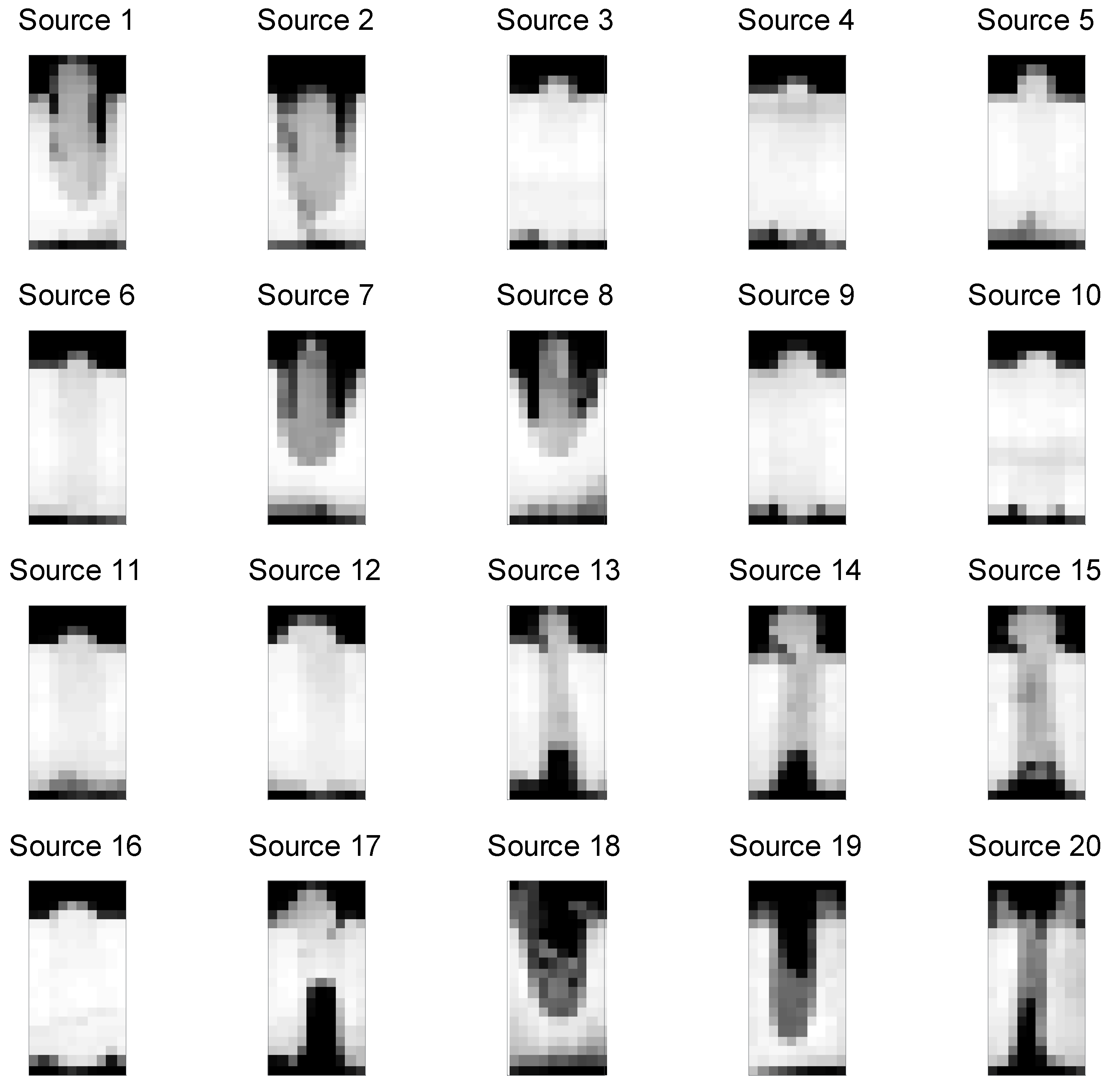
Many manufacturing processes involve images used to evaluate the conformance of parts to standards [6,27,28]. Figure 1 shows digital images from 20 laser aluminum alloy parts, which were sectioned and photographed. The first image (Source 1) can be represented as a vector of pixel numbers with added counts for the darker pictures. This is given in Table 1(a). This “bag of words” representation is common to topic models but has drawbacks including the document lengths being related to the number of distinct levels of grayscale [13]. Table 1(b) includes the inputs from our methods which are described in Section 4. In this example, the number of images is small enough such that supervision of all images manually is not expensive. In addition, generating the image data of cut sections of the welds is expensive because the process is destructive, i.e., the sectioned parts cannot be sold. Generally, manufacturing situations that involve nondestructive evaluation can easily generate thousands of images or more. In these situations, human supervision of even a substantial fraction of these images is prohibitively expensive. Our problem statement is to create topic definitions and an automatic system that can cluster items (weld images) into groups that conform to pre-known categories while spanning the set of actual items. We seek to do this with a reasonable request of information from the welding engineers involved.
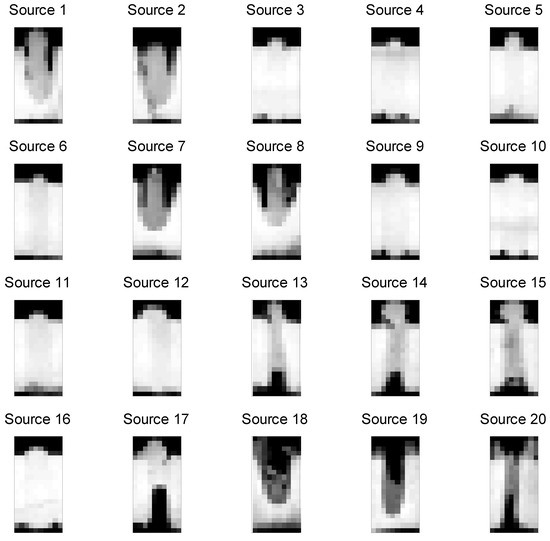
Figure 1.
A corpus of 20 weld images which have been destructively sampled.

Table 1.
(a) Data for the first low-level image; (b) 25 high-level data points with zaps with one million (M) effective trials and boosts.
In addition, in Figure 1, the images may seem blurry. This follows because they are 20 × 10 = 200 pixels because it was judged that such simple images are sufficient for establishing conformance and are easier to store and process than higher resolution images. We will discuss the related issues of resolution and gray scale bit selection after the methods have been introduced. In the next section, we review the methods associated with Latent Dirichlet Allocation (LDA) [13].
LDA is perhaps the most widely cited method relevant to unsupervised image processing. The cluster or “topic” definitions identified by LDA can themselves be represented as images. They are defined formally by the posterior means for the pixel or “word” probabilities associated with each topic. Figure 2 shows the posterior mean topic definitions from applying 3000 iterations of collapsed Gibbs sampling using our own C++ implementation. The topic definitions are probabilities that each pixel would be selected in a random draw or word. The fact that they can be interpreted themselves as images is a positive properties of topic models such as LDA.

Figure 2.
Latent Dirichlet Allocation (LDA) results for a 5-topic model. These are images which define the clusters or topics. Each topic definition is a list of probabilities or densities for each pixel.
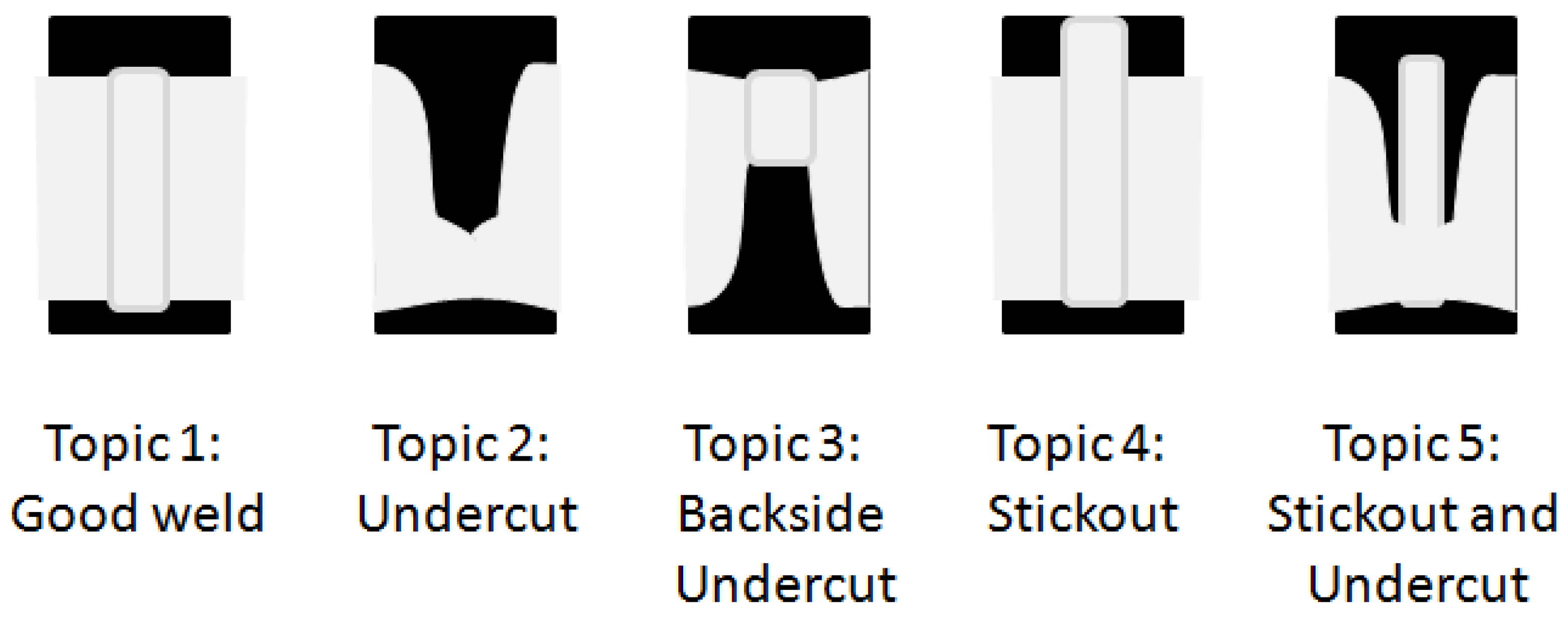
At present, there are many methods to determine the number of topics in the fitted model [29,30,31,32,33]. Appendix B describes the selection of five topics for this problem. Figure 3 illustrates the most relevant international American National Standard Institute/American Welding Society (ANSI/AWS) conformance issues for the relevant type of aluminum alloy pipe welds [30]. These were hand drawn but they are quite standard and illustrate the issues an arc welding quality inspector might look for in examining images from a sectioned part.
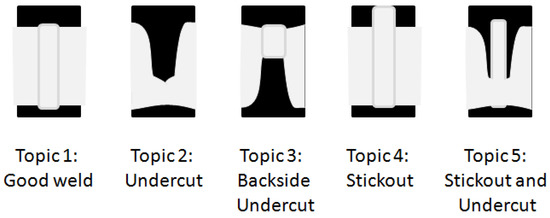
Figure 3.
Laser pipe welding conformance issues relevant to American National Standard Institute/American Welding Society (ANSI/AWS) standards. These are cluster definitions one might want so that topics align with human used words and concepts. These images could appear in a welding training manual describing defect types.
If it were possible to have the topic definitions correspond closely with these known conformance issues, then the resulting model could not only assign the probability that welds are conforming but also provide the probabilities of specific issues applying. In addition, the working vocabulary of welding engineers including “undercut”, “penetration” and “stickout” could be engaged to enhance interpretability [34]. The primary purpose of this article is to propose methods that provide recourse for users to shape the topics directly without tagging individual images.
Section 2 describes the related works. In Section 3, we describe the notation and review the Latent Dirichlet Allocation methods whose generalization forms the basis of ERT models, which are then proposed for image analysis. The ERT model application involves a step in which “handles” are applied using thought experiments to generate high-level data in Section 4.
Then we describe the “collapsed” Gibbs sampling formulation, which permits the exploration of databases involving thousands of images or documents. The proposed formulation is exact in certain cases that we describe and approximate in others, with details provided in Appendix A. In Section 5, two numerical examples illustrate the benefits for cases in which the ground truth is known. In Section 6, we illustrate the potential value of the method in the context of a real-world, laser welding image application and conclude with a brief discussion of the balance between high-level and ordinary data in modeling in Section 7.
2. Related Works
Latent Dirichlet Allocation (LDA) was proposed by [13]. It is the most cited method for clustering unsupervised images or text documents perhaps because of its relative simplicity and because the resulting cluster or topic definitions are often interpretable [29]. The LDA method is simply to fit a complicated seeming distribution to data using a distribution fitting method. This clustering method has a wide variety of applications including grouping the activities of daily life [31].
In the original LDA article, Blei et al. focused on an approximate maximum likelihood estimation method. They also introduced a method to determine the number of clusters or topics based on the so-called “perplexity” metric. This metric gives an approximate indication of how well the distribution predicts a held-out test sample. Other methods for determining the number of topics have been subsequently introduced. A general discussion suggest that perplexity is still relevant [32] for cases without any tagged data. One automatic alternative to perplexity-based plotting is argued to be faster in analyst time but approximately equivalently accurate [33]. Further alternative entropy-based measures to perplexity are proposed for cases in which perplexity does not achieve a minimum or the elbow curves are not clear [34]. Note that in our primary example, we do not have tagged data and our perplexity does achieve a minimum value. Therefore, we apply perplexity plot-based model determination.
3. Notation
In our notation, the ordinary or low-level data are the pixels indices in each image or document. Specifically, represents a so-called word in an image or document for d = 1, …, D and for n = 1, …, Nd. Therefore, “D” is the number of images or documents and “Nd” is the number of words in the dth document. We use the term “documents” to describe the low-level data instead of images because the images are converted to un-ordered listings of pixel indices before there are analyzed. This means that we convert 2D images into 1D vectors of pixel indices. We use 8-bit gray scale which runs from 0 to 255. The higher the gray scale the more repeated pixel indices which are the words in the documents. Table 1(a) provides an example of how the images are related to words in the documents. This example applies to the relatively simple face image example in Section 5, which only has 25 pixels in each image. The laser welding source images in Figure 1 all have over 15,000 words, i.e., Nd > 15,000 for d = 1, …, 20.
A random variable is the multinomial or cluster or topic assignment, , for . The T-dimensional random vector represents the probabilities a randomly selected pixel in document d is assigned to each of the T topics or clusters. The parameter “WC” represents the number or pixels or words in the dictionary. For example, in our laser welding study there are D = 20 images each with 200 pixels. Therefore, WC = 200. The WC-dimensional random vector represents the probability that randomly selected words are assigned to each pixel in the topic indexed by t = 1, …, T. The posterior mean of for each pixel is generally used to define the topics as has been shown in Figure 2. The prior parameters and are usually scalars in that all documents and all pixels are initially treated equally. Generally, low values or “diffuse priors” are applied such that only a small amount of shrinkage is applied, and adjustments are made on a case-by-case basis [35].
The key purpose of this article is to study the effects of our proposed high-level data on image analysis applications. The high-level data derives from imagined counts from binomial thought experiments with possible values as high as . The elicitation question is, “Out of random draws relating to topic t, how many times would pixel c occur?” If and , the user or expert is zapping the pixel in that image. This is equivalent to erasing that pixel in the topic. If and , then the user or expert is boosting or affirming that pixel in that topic.
Latent Dirichlet Allocation
With these parameter definitions, LDA is defined by the following joint posterior distribution function proportional condition:
where
and
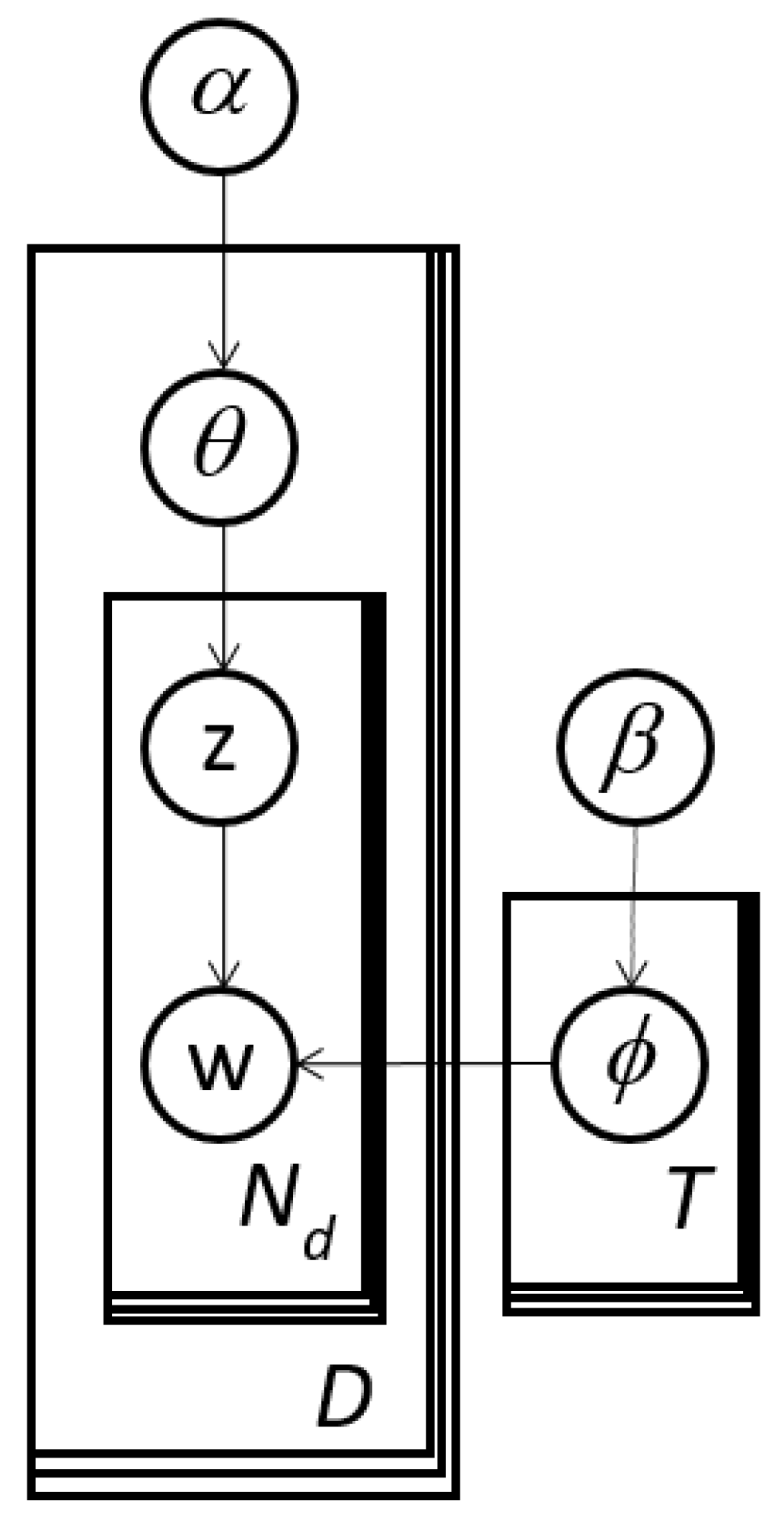
The graphical model in Figure 4 summarizes the conditional relationships between the variables in the LDA model. The rectangles indicate the number of elements in each random vector or matrix. For example, the random matrices z and w have Nd elements for each of the D images as mentioned previously.
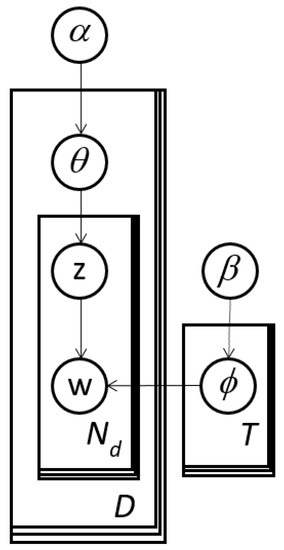
Figure 4.
LDA expressed as a graphical model. It is equivalent to the distribution definition in Equation (1).
Griffiths and Steyvers [35] invented the so-called collapsed Gibbs updating function which permits Gibbs sampling for estimation of the proportionality constant in Equation (1) via only sampling the random variables. The other random variables ( and ) are effectively “integrated out” and their posterior means are estimated after thousands of iterations as functions of the sampled values. This approach is many times faster than ordinary Gibbs sampling and can avoid the need for abandoning the Bayesian model formulation.
To apply collapsed Gibbs sampling for LDA, we define the indexing matrix Ct,d,c, which is the number of times word c is assigned to topic t in document d, where t is topic index, d is the document index and c is the word index, as the following:
where I() is an indicator function: 1 if the condition is true and 0 if false. Then, the topic-document count matrix is:
and the topic-word count matrix is:
We further define qt,c and . The collapsed Gibbs multinomial probabilities for sampling the topic for word b in document a are:
The posterior mean for the topic definition probabilities,, are:
The collapsed Gibbs estimation process begins with a uniform random sampling of the for every document, a, and word, b, and then continues with repeated applications of multinomial sampling based on Equation (7), again for all a and b pairs. After a sufficient number of complete replications, the assignments approximately stabilize and the posterior mean probabilities are estimated using Equation (8). Replication sufficiency can be established by monitoring the approximate stability of the estimated parameters, e.g., in Equation (8). The iterations before the establishment of stability may be called the “burn-in” period. After convergence, the probabilities can then be converted into images by linear scaling based on the high and low values for all pixels so that all resulting values range between 0 and 255 and then rounding down to obtain the grayscale images, e.g., see Figure 2.
Topic modeling methods including those based on Gibbs sampling have been criticized for being unstable [36], i.e., they produce different groupings on subsequent runs even for the same data. Some measure stability and directly try to minimize cross-run differences based on established stability measures [37]. Others propose innovative stability or similarity measurements [38]. Still others propose both innovate stability measures and methods to maximize stability [39]. An objective of the methods described in the next section is to make the final results more repeatable and accurate by focusing directly on accuracy, i.e., increased stability is a by-product. The numerical study in Section 5 seeks to demonstrate that the proposed methods are both more stable and more accurate than previous methods.
4. Methods
Widely acknowledged principles for modeling and automation include that the models should be both “observable” so that the users can see how they operate and “directable” so that users can make adjustments on a case-by-case basis [40]. We argue that topic models are popular partly because they are simpler and, therefore, more observable than alternative models, which might include expert systems having thousands of ad hoc, case-specific rules. Yet, the only “directability” in topics models comes through the prior parameters α and β. Specifically, adjustments to α and β only control the degree of posterior uniformity in the document-topic probabilities and the degree of uniformity of the topic-word probabilities, respectively. Therefore, α and β are merely Bayesian shrinkage parameters.
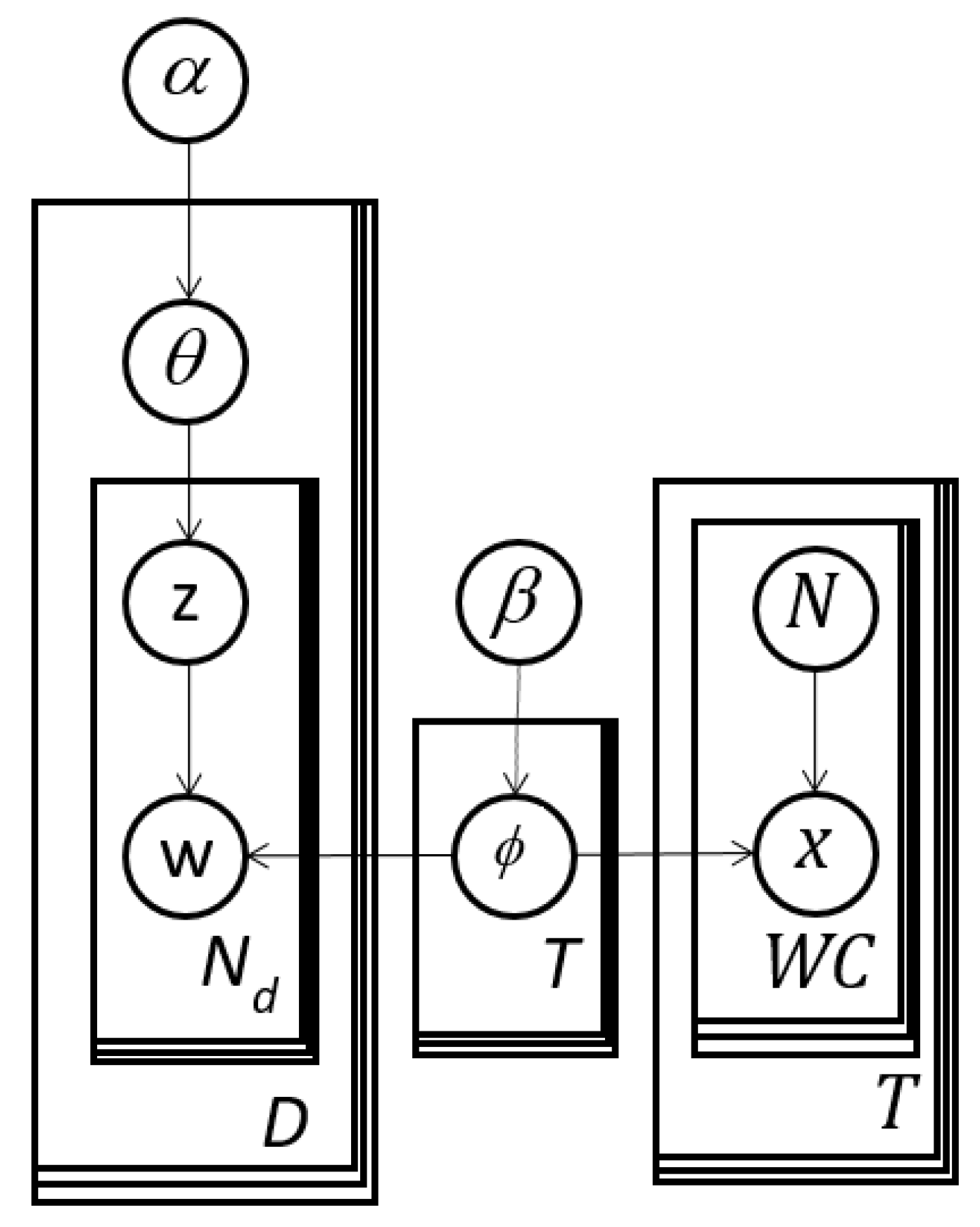
We propose for image analysis the subject matter expert refined topic (ERT) model in Figure 5 to make the LDA topic model more directable. The left-hand-side is identical to LDA in Figure 4, which has multinomial response data, w. The right-hand-side is new and begins with the arrow from ϕ to x. This portion introduces binomially distributed response data, for t = 1, …, T and c = 1, …, WC. The represent the number of times for a given topic, t, word c is selected in trials. Therefore, is a sample size for thought experts.
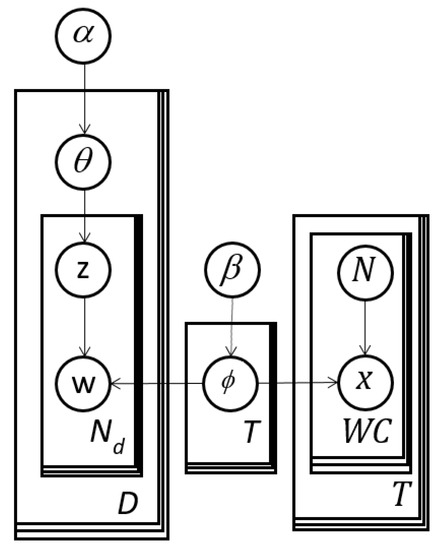
Figure 5.
Expert Refined Topic (ERT) model with a handle permitting expert or user editing of the cluster or topic definitions. This figure is equivalent to the distribution in Equation (9).
Like LDA, ERT models are merely distributions to be fit to data. The usual data points are assumed to be random (multinomial) responses (ws) which are part of the LDA “wing” (left-hand-side of Figure 5). The inputs from the experts (or just users) are random counts (xs) from imaged “thought” experiments on the right-hand-side (right wing) of Figure 5.
In our examples, we use = 1M for cases when the expert or user is confident that they want to remove a word (“zap”). Smaller sizes, e.g., = 1000, might subjectively indicate less confidence or weight in the expert data. In our preliminary robustness studies, sample sizes below 1M often had surprisingly little effect for zapping. Note also that the choice of in the model is arbitrary and many combinations of topics t and words c can have .
We refer to the right-hand-side portions in Figure 4 (the rectangles including N and x) as handles because they permit users to interact with the model in a novel way in analogy to using a carrying appendage on a pot. These experiments are “designed” because the analyst can plan and direct the data collection. These binomial thought experiments have relatively high leverage on specific latent variables, i.e., ϕ. We propose that users can apply this model in two or more stages. After initially applying ordinary LDA, the user can study the results and then gather data from experiments involving potentially subject matter experts (SMEs) leading to Expert Refined Topic (ERT) models or Subject Matter Expert Refined Topic (SMERT) models. Note that a similar handle could be added to any other topic model with a similarly defined topic definition matrix, ϕ.
The so-called “latency experiments” [4] could be literal as having the expert create prototype images for each topic and then extracting the binomial counts from these images. Alternatively, the experiments could be simple thought experiments, i.e., out of several trials, how many draws would you expect to result in a certain pixel image being derived? One difference than makes ERT models different for images as compared with text [4] is that zapping is essentially an “eraser” for the topic definitions. This could even be accomplished using eraser icons on touch screens.
As an example, consider that an expert might be evaluating topic 1 in Figure 2. The expert might conclude that topic t = 1 should be transformed to resemble topic 2 (undercut) in Figure 3. The expert might focus on pixel c = 22, which is in the middle top. The expert concludes that in N1,22 = 1 million samples from the topic (trials), the topic index should be found x1,22 = 0 times, i.e., the pixel should be black because it is in the middle of the cavity. We have found in our numerical work that the boosting and zapping tables need to address a large fraction of the words in each topic to be effective, i.e., little missing data. Otherwise, the estimation process can shift the topic numbers to avoid the effects of supervision.
The Collapsed Gibbs Sampler
The joint posterior distribution that defines the ERT model has proportionality given by:
where and N are vectors defining assignments for all words in all documents. The binomial distribution function is:
Here, we generalize our definitions such that qt,c and we also define . Further, we define the set S to include combinations of t and c such that > 0 in the high-level data (i.e., the zaps). Appendix A builds on previous research [4,41,42]. Appendix A describes the derivation of the following collapsed Gibbs updating function for the combinations with and :
For, and the updating function is:
The posterior mean for the combinations with t and is:
For t and we have:
Note that if = 0 for all t = 1, …, T and c = 1, …, WC, then Equation (12) reduces to Equation (7) and Equation (14) reduces to Equation (8). As is clear from Figure 4 and Figure 5, the ERT model is a generalization of the LDA model. In addition, as clarified in Appendix A, Equations (11)–(14) are approximate for cases in which the set S contains more than a single pixel in each topic. Yet, the numerical investigations that follow and the computational experiment in Appendix C indicate that the quality of the approximation is often acceptable.
Note that the pseudocode for ERT sampling is identical to LDA sampling pseudocode with Equation (12) replacing Equation (7). Therefore, the scaling of computational costs with the number of pixel gray scale values follows because the document lengths grow proportionally (see Table 1(a)). Boosting minimally affects the computation since it does not relate to the set S. Zaps, however, require the calculation of two additional sums, which directly inflate the core costs linearly in the number of zapped words.
In our computational studies, we have found that each iteration is slower because of the associated sums in Equation (7). Yet, the burn-in period required is less, e.g., 300 iterations instead of 500. Intuitively, burn-in is faster because the high-level data anchors the topic definitions.
5. Results: Examples
In this section, three examples are described for which the first two have the true model or “ground truth” known. The first is a “simple face” example and the second is the well-studied vertical and horizontal bars example [35]. The third and fourth are the widely studied Fashion Modified National Institute of Standards and Technology (MNIST) and Tungsten inert gas welding examples. Note that we did no hyperparameter tuning our examples and simply used and for simplicity. An additional hand-written numbers example is provided in Appendix D.
5.1. Simple Face Example
The first five out of 100 total source images each with 100 words for the simple face example are shown in Figure 6. Each word in each document was generated through a random selection among the 3 topics based on the overall topic probabilities: 0.60 for topic 1, 0.35 for topic 2 and 0.05 for topic 3, represented in Figure 7a. This makes the images as 5 × 5 pixels resembling parts of the human face (eyes, nose and mouth).

Figure 6.
The first 5 out of 200 total images for the simple face example. Each image has 25 pixel values of various gray scale amounts.

Figure 7.
Information generated by the analyses including the: (a) ground truth used to generate low-level data; (b) LDA model; (c) ERT model.
In the generation process, the pixel index was selected randomly based on the topic probabilities. The document corresponding to the first image is given in Table 1(a). The ordering of the pixel indices within the document is unimportant because of the well-known bag of words assumption common to topic models. Therefore, without loss of generality, we sorted the indices. We then applied 3000 iterations of LDA updating function in Equation (7) with each iteration assigning topics for all the 100 × 100 = 10,000 words. Then, we used the posterior mean formula in Equation (8) to create the initial topic definitions in Figure 7b. Figure 7c is a more accurate representation of the Figure 7a than Figure 7b. This demonstrates the usefulness of the ERT approach intuitively.
In a second stage of the analysis, we prepare the so-called high-level data in Table 1(b) and apply the ERT analysis method to produce the topic definitions in Figure 7c. The high-level data was developed in response to the lack of interpretability of the topics in Figure 7b. As mentioned previously, the high-level data could derive from literal experiments on experts. Here, the subject matter expert (SME) identifies three topics for words in the documents: eyes, nose and mouth. Once the first topic is identified as eyes, the SME uses binomial thought experiments to effectively “erase” all the pixels in topic 1 not relating to eyes. Similarly, for topic 2, all pixels are erased not pertaining to nose. The mouth topic is rare so the SME uses expertise to “draw” the mouth using thought experiments each with two trials and two successes.
Clearly, the ERT model posterior means ϕ values in Figure 7c resemble much more closely the ground truth in Figure 7a than the LDA posterior mean in Figure 7b. One way to quantify topic model accuracy is to use the symmetrized Kullback–Leibler (KL) divergences or “KL distances” from all combinations of estimated topic posterior means to the true topic probabilities [37]. These distances are, formally, , where and are the two distributions (i.e., the case topic models). Being close to the ground truth summarizes both the stability and accuracy of the fit model.
Table 2(a) shows the KL distances for the LDA posterior mean ϕ and Table 2(b) shows the distances for the ERT model posterior mean ϕ. The closeness is measured by identifying the combination of true and estimated topic pairing that minimize the sum of distances and then comparing the resulting distances. The gain from adding the 25 high-level data points in Table 1(b) is apparent. For example, the maximum distance for the LDA model is 16.5 units while the maximum distance for the ERT model is 1.5 units.

Table 2.
Kullback–Leibler (KL) distances from: (a) sampling (S) to LDA topics; (b) sampling to ERT topics.
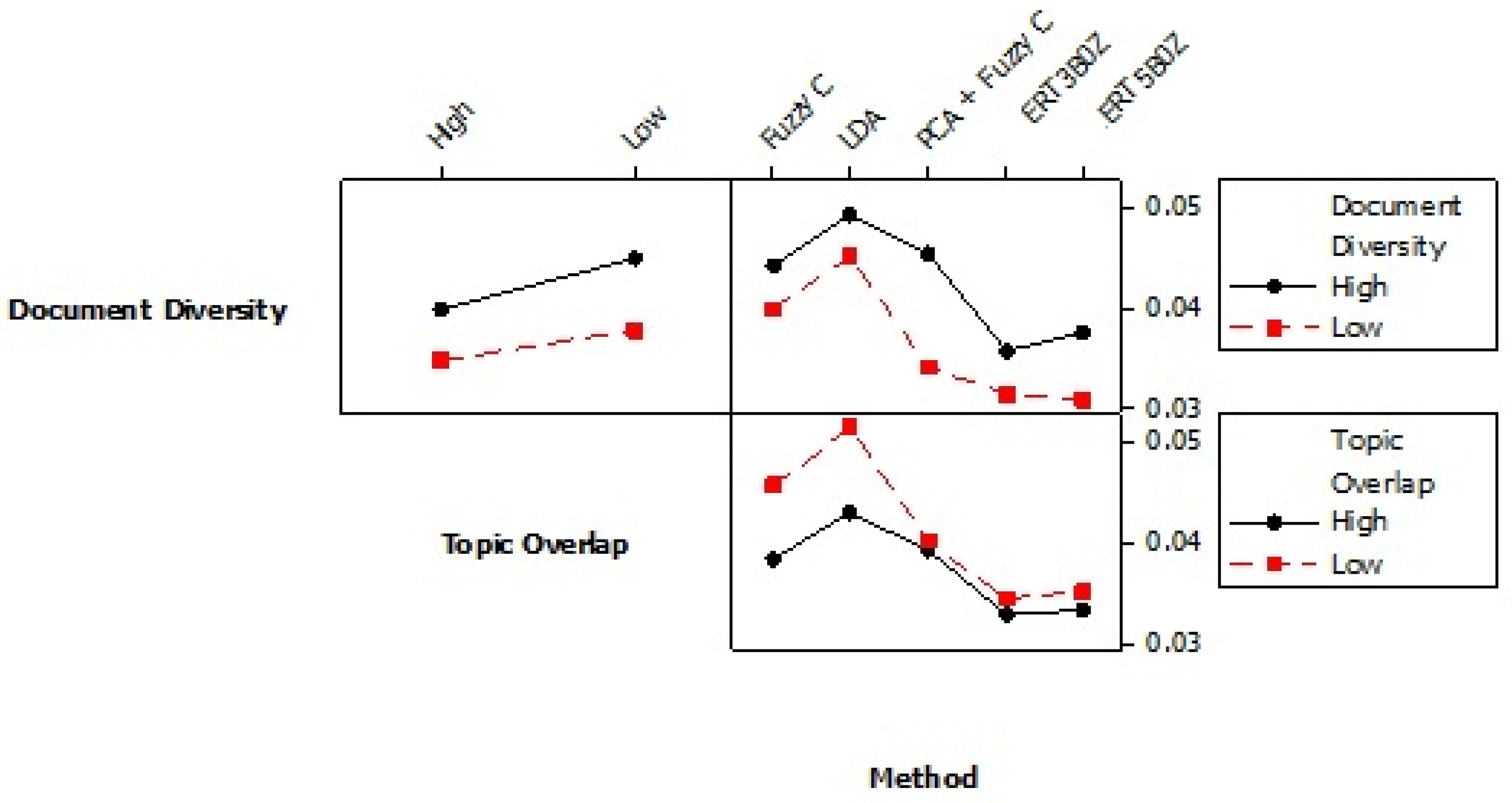
In our previous research relating to text analysis [4], we describe the fuzzy c means clustering methods and pre-processing using principle components analysis (PCA) followed by fuzzy c means clustering. We also defined the minimum average root mean squared (MARMS) error. This is the difference between the estimated topic definitions probabilities and the ground truth values from the simulation root mean squared. Here, we include part of the results of the computational experiment omitted from 4 for space reasons. Figure 8 shows the accuracies of the various alternatives including two ERT variations. The first ERT variation has three high level data points per topic. The second has five per topic.
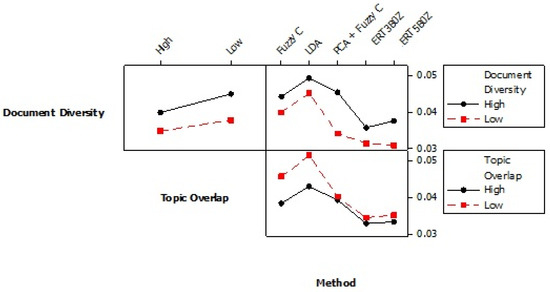
Figure 8.
Interaction plot for topic definition minimum average root mean squares (MARMS).
Note that there is replication error from the simulation such that only a portion of the factor effects was found to be significant. For example, the different between the ERT variations is not significant but the improvement over the alternatives is significant. The comparison shows that ERT offers reduced errors regardless of document how diverse or different the simulated documents are (document diversity) and how much overlap the topics have in using the same words or pixels (topic overlap).
5.2. Bar Example
Figure 9a shows the ground truth model for a 10-topic example involving vertical and horizontal bars from [35]. In the original example, the authors sampled 1000 documents each of length 100 words and the derived LDA model based on Equations (7) and (8) very closely resembled the true model. Our purpose is to evaluate a more challenging case with only D = 200 document with Nd = 100-pixel indices (words). Each of the 20,000 low-level words is derived from first sampling the topic with the topic probabilities given in Figure 9a and then sampling the words based on the probabilities indicated in the images. The derived LDA posterior mean values from 3000 collapsed Gibbs sampling iterations are pictured in Figure 9b. Without loss of generality, we order the estimated topics by their posterior mean topic proportions, shown in parentheses in Figure 9b.

Figure 9.
(a) Ground truth used to generate low-level data; (b) LDA model; (c) ERT model.
In general, the estimated posterior means in Figure 9b are identifiable as either vertical or horizontal bars. Therefore, the function of the second stage editing using the high-level data in Table 3 is to clean up or erase the blemishes to the topic definitions. By saying that in one out of 1M binomial thought experiments, zero would have a specific word on a topic, that word is erased or zapped from the definition. Similarly, other words could be boosted but Table 3 only contains zaps. Figure 9c shows the posterior means derived from 3000 iterations of collapsed Gibbs ERT model sampling using the approximate updating and mean estimation formulas in Equations (11)–(14).

Table 3.
The 200 high-level data points for the bar numerical example. This shows many zaps in the topic definitions.
With 10 topics, there is greater ambiguity about how the estimated topics map onto the ground truth topics. Table 4(a) shows the KL distances from the true topics to the estimated topics derived using LDA. Table 4(b) shows the KL distances from the true topics to the estimated topics using ERT posterior mean probabilities. The largest distance is reduced from 6.0 units to 0.013 units through the addition of the 25 high-level data points and the application of the ERT model.

Table 4.
KL distances from: (a) sampling (S) to LDA topics; (b) sampling to ERT (SM) topics.
5.3. Fashion Example
Next, we consider the “Fashion-MNIST” dataset with 10,000 28 × 28-pixel grayscale images [43]. The dataset is tagged with 10 categories: t-shirt/top, trouser, pullover, dress, coat, sandal, shirt, sneaker, bag and ankle boot. In a preprocessing step, we reduce the number of grayscale levels by a factor of 200 to keep our document lengths sufficiently small for our VBA implementation storage sizes. The granularity seems visually acceptable for differentiating between categories (Figure 10a–c). Next, we created the documents by repeating the pixel numbers proportionally to the reduced gray scale values. For example, a value of 2 for pixel 37 results in “37, 37” being included in the document.
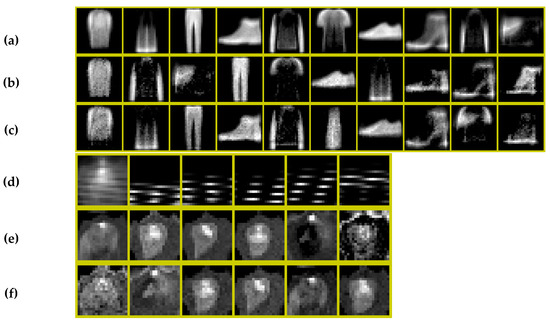
Figure 10.
Fashion data (a) LDA topics with 10,000 images, (b) LDA topics with 1000 images, (c) ERT model with 1000 images and Tungsten Inert Gas (TIG) data (d) LDA topics with 10,000 images, (e) LDA topics with 1000 images, (f) ERT model with 1000 images.
With all 10,000 images and 10 topics, LDA can approximately recover the categories as shown in Figure 10a. This figure is based on 500 iterations. Note that the skinny dress is apparently missing and there are two tea shirts. When analyzed using LDA and only the first 1000 images and again 500 iterations, the results are blurrier, and the dress is still missing as shown in Figure 10b. If the top 20 pixels for the LDA run are used to supervise the ERT model based on 1000 datapoints, the result from 300 iterations is shown in Figure 10c. This required approximately 11 h using an i7 1.8 GHz processor with 16 GB of RAM. The result is arguably more accurate than LDA based on all 10,000 images because the dress appears as topic 6 and there is only a single tea shirt.
5.4. Tungsten Inert Gas Welding Example
Next, we consider the “Tungsten Inert Gas (TIG) Welding” dataset with 10,000 20 × 20 truncated pixel grayscale images [44]. The dataset is tagged with 6 categories: good weld, burn through, contamination, lack of fusion, misalignment and lack of penetration. In a preprocessing step, we reduce the number of grayscale levels by a factor of 50 to keep our document lengths sufficiently small for our VBA implementation storage sizes. The granularity seems visually acceptable for differentiating between categories (Figure 10d–f). Next, we created the documents by repeating the pixel numbers proportionally to the reduced gray scale values.
With all 10,000 images and 10 topics, LDA can approximately recover the categories as shown in Figure 10d. This figure is based on 500 iterations. Note that all the topics are difficult for us to interpret with the naked eye (as is true for the images with a few exceptions). When analyzed using LDA and only the first 1000 images and again 500 iterations, the results are blurrier (Figure 10e). If the top 20 pixels for the LDA run are used to supervise the ERT model based on 1000 datapoints, the result from 50 iterations is shown in Figure 10f. This required approximately 1 h using an i7 1.8 GHz processor with 16 GB of RAM. The result is arguably more like the ideal pictures in [45] accurate than either LDA application.
6. Results: Laser Welding Study
In the previous section, we applied ERT modeling to two numerical examples in which the ground truth was known. Next, we focus on analyzing the 20 source images for the laser welding aluminum alloy study shown in Figure 1. None of the LDA derived posterior mean topics in Figure 2 directly corresponded to any of the nonconformity issues in Figure 3 from standard textbooks [30]. As a result, even if we could perfectly classify the existing or new welds perfectly into the LDA derived topics, we would have difficulty documenting the failures and analyzing their causes.
Looking at the source welds, we can clearly identify which welds have which nonconformities as pictured in Figure 3. Therefore, we have “expert” judgment that the classical nonconformity codes are relevant. We began our development of the 198 high-level data in Table 5, by identifying an approximate correspondence between the topics in Figure 2 and the ideals in Figure 3. We identified topic 1 as undercut, topic 2 as stickout, topic 3 as good welds, topic 4 as backside undercut and topic 5 as stickout and undercut. Intuitively, we boosted parts of the images that look like the architypes in Figure 3 and zapped the other parts.

Table 5.
The 198 high-level data points for the laser welding example.
With these identifications, we then determined which pixels needed erasing and which pixels needed boosting or addition. We did this manually but with software there is the possibility of selecting the pixels en-mass in a fully interactive fashion. Most of the topics had large sections of pixels that needed filling-in but a few pixels required erasure. For example, all the pixels in the lower middle section of topic 1 needed boosting so that the resulting topic definition in Figure 11 resembled undercut in Figure 3.

Figure 11.
Alternative methods applied to the laser welding problem: (a) fuzzy c clustering, (b) LDA, (c) Principal Component Analysis (PCA) + fuzzy c methods and (d) ERT model topic definitions.
Once we identified the high-level data set, our custom C++ software was able to perform 3000 iterations of collapsed Gibbs sampling and derive the posterior mean probabilities shown in Figure 11 in 12 min on our 2.5 GHz Core 2 Quad processor.
Results from four alternative cluster definition methods are described in Figure 11. The fuzzy c method only identifies topics 1 and 2 accurately in terms of standard conventions in Figure 3. LDA is only marginally better in Figure 11b. Principal Component Analysis (PCA) followed by fuzzy identifies approximately three topics correctly.
For ERT, examination of the posterior mean probabilities for the document-topic probabilities, , provides both an indication of the value of the derived ERT model and a level of validation. Table 6 shows the document-topic probabilities based on the topic definitions in Figure 11d. If we interpret these probabilities as indications of the probability each topic is relevant, we find that the most probable topics match in 20 out of 20 cases how a subject matter expert (SME) would classify the source welds. For example, the first image (source 1) clearly corresponds to a weld with both undercut and stickout. Clearly, engineers would find these probabilities significantly more relevant than probabilities for LDA model topic in Figure 2.

Table 6.
Topic assignment probabilities from the ERT for the 20 laser welding images.
7. Discussion
The authors have significant experience applying topic models to real-world data sets. In our applications, we have often found that the initially derived topic model definitions usually were more interpretable than the LDA topics for the welding and simple face problems (Figure 2 and Figure 7b) but less comprehensible than the LDA topics for the bar example in Figure 8b. So far, we have never encountered an example in which we did not wish that we could edit some or all of the topics to enhance the model accuracy and/or subjective interpretability.
The intent of the proposed subject matter expert refined topic (ERT) models with their handles is to facilitate user interaction with the models, i.e., the directability. We suggest that model handles function in relation to topic models in an analogous manner erasers function in relation to pencils. Admittedly, there is a need to balance between the degree of subjectivity possibly entering through the handle and the relative objectivity of the ordinary low-level data. In our primary application, we included supervision of only 198 out of 200 × 5 = 1000 possible pixels or 19.8%. With this limited addition, we have derived highly interpretable topic definitions in the form of posterior mean ϕ. In addition, we have achieved perfect assignment of the source welds to the interpretable topic definitions or clusters (20/20).
There are important limitations of current codes. First, the number of grayscale levels must be reduced (generally) to achieve manageable file sizes. This issue is not special to ERT and relates to the bag of words image representation in which each grayscale level makes the documents proportionally longer. Reducing granularity can make the images blurry, e.g., see Figure 9. In addition, in ERT the user must boost almost every topic, or the estimation will adjust such that the zapping will apply harmlessly to images with darkness already at the associated pixel locations. Yet, the effort to boost each topic can be minimal. For example, we supplied only 20 pixels (out of 784 pixels) per topic to supervise the Fashion MNIST images in Section 5.
8. Conclusions
In conclusion, in this article we propose a method to edit the cluster definitions in topic modeling with applications in image analysis. The proposed method creates high-level data which is a potentially important concept with a broad range of possible applications. We demonstrate in our numerical example that the proposed ERT modeling method can derive more accurate and more stable topic model fits than LDA. In addition, for our main laser welding application we show that a small amount of high-level data is able to perturb the model so that the clusters align with intuitive and popular definitions of defects or nonconformities. We suggest that the concepts of ERT and handles can be explored in a wide range of supervised and unsupervised modeling situations. The resulting high-level data may become a major output from knowledge workers in the future.
There are a number of opportunities for future work. First, more computationally efficient and stable methods for fitting ERT models to images can be developed. The collapsed Gibbs sampling method is only approximate for cases with more than a single zap and it can be time consuming. Second, other types of high-level data besides boosts and zaps can be developed. Perhaps these might relate to archetypal images. Third, the concept of handles can be extended to other types of distribution fits such as regression and time series modeling. Fourth, more efficient methods for image processing besides the bag of words methods can be explored and related to ERT-type modeling. The document lengths can be prohibitively long if too many gray scale gradations are applied in the current representations. New representations can be studied that are more concise. Fifth, documented editing using ERT can be enhanced with tablet applications that permit quick boosting (using pen-type features) and zapping (using eraser-type features). Fifth, exploration of the E-M algorithm for ERT procedures could speed up estimation. Using standard notation [13], we have as the document-specific estimated topic definition probabilities, , and the document-specific indicator function for the words is . We conjecture that the conditional multinomial may approximately satisfy:
Further, accuracy issues associated with ERT models can be studied further including through investigating alternatives quality measures (to KL distance) such as topic model semantic [46] and topic [47] coherence measures.
Author Contributions
Conceptualization, T.T.A.; methodology, T.T.A. and H.X.; software, T.T.A. and H.X.; validation, T.T.A. and S.-H.T.; formal analysis, T.T.A.; investigation, T.T.A.; resources, T.T.A. and H.X.; data curation, T.T.A. and H.X.; writing—original draft preparation, T.T.A. and H.X.; writing—review and editing, T.T.A. and S.-H.T.; visualization, T.T.A. and S.-H.T.; supervision, T.T.A.; project administration, T.T.A.; funding acquisition, T.T.A., H.X. and S.-H.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by NSF Grant #1912166.
Acknowledgments
Dave Farson was very helpful in providing the images and expert knowledge. David Woods provided significant inspiration. Ning Zheng provided insights and encouragement.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Derivations
This appendix describes exact and approximate formulas for the posterior mean relating to the ERT model formulation. We focus on the posterior mean because the collapsed Gibbs sampler probability in equation is simply related to the posterior mean. It is the posterior mean probability with the current sampling point (word in a document) removed. This holds both for the LDA and ERT model as shown by generalizing the steps provided in detail in [38] to reproduce the results in [35].
We also focus on the case in which there is a single zapped word or pixel for which closed form solutions can be developed. Again, we define qt,c and . Equations (7)–(10) give the joint posterior density function. Here, we focus only on dependence on the topic probabilities, for t = 1, …, T and c = 1, …, WC. We need to compute the normalizing constant, V, for the joint probability distribution, having marginalized out all dependence except on the for c = 1, …, WC. The constant is obtained by integrating over the unit simplex, S:
The posterior mean for is, therefore, exactly given by:
Unfortunately, there does not appear to be any closed form solution to this equation for the general case. In addition, numerical integration of the above equation is too computationally expensive to be relevant for Gibbs sampling. Yet, for the case in which there is only a single nonzero , analytical formulas can be computed. Without loss of generality, we have = 0 for c ≠ and > 0. The marginal for c = is:
Multiplying by and integrating over the support [0, 1], the posterior mean for is, after rearranging and applying xΓ(x) = Γ(x + 1):
Equation (A4) reproduces Equation (13) and both clearly generalize the LDA posterior mean in Equation (6). The marginal for with c ≠ for topics is more complicated and is most easily expressed using so-called “regularized hypergeometric” functions. The marginal is:
where = and where the is the regularized hypergeometric function. Next, we multiply by , and represent the posterior mean as integral function of :
Next, we change variables using y = . Note that as a generalized binomial expansion series. The expansion uses the “Pochhammer” symbol, which is a subscript, to denote the generalized binomial coefficient. This follows because qt,c is generally non-integer. For simplicity, we quote the results assuming integral but the results easily generalize. The result is:
Next, we use the general identity (from functions.wolfram.com):
Substituting in the zero limit gives a zero value, so the definite integral becomes:
where is a generalized hypergeometric function. It can be checked numerically that this complicated sum is equivalent to Equation (14).
Appendix B. Perplexity and the Number of Topics
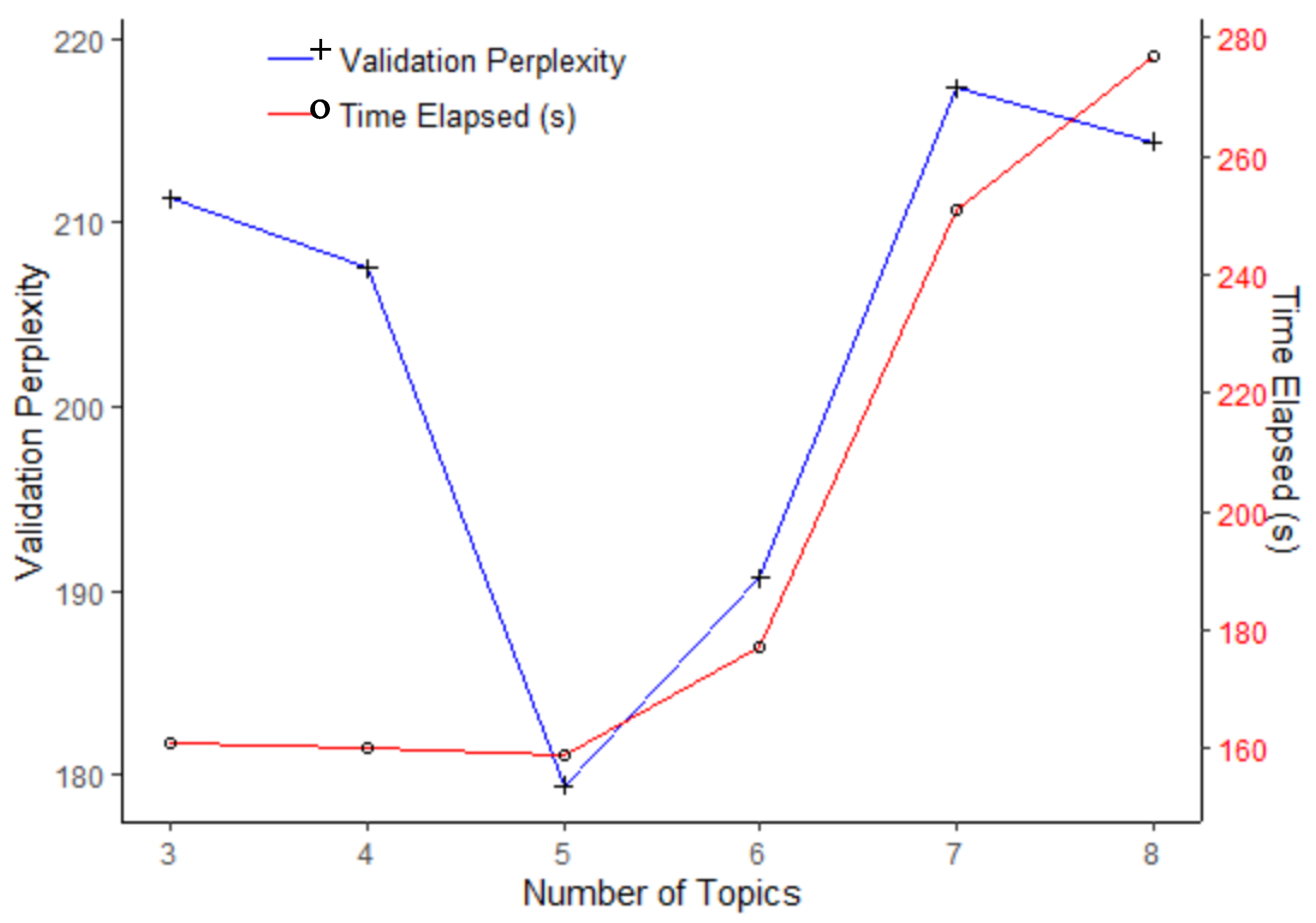
This appendix describes a study to determine the appropriate number of topics in laser welding study. There are many methods to evaluate options [35,36,37]. Here, we use the original perplexity method [13]. For computational convenience and to standardize the images, we selected 5000 randomly chosen pixels for each. Then, we select 20% of the images for the evaluation set (the last four). Figure A1 shows the resulting perplexities for different numbers of topics on the left-hand-side. The result is that five topics minimize the perplexity and conform to the standard mentioned previously. The right-hand-side of Figure A1 shows the increasing computational times associated with LDA estimation for increasing numbers of topics.
An explanation of the right-hand-side of Figure A1 relates to Gibbs sampling in Equation (7). For low values of the number of topics, the computational overhead dominates, e.g., initializing the memory and loading the data. Then, the time in dependent of the number of topics T. Then, starting at T = 5 topics, the elapsed time grows roughly linear in T as the dimension of the multinomial increases in the core topic sampling process.
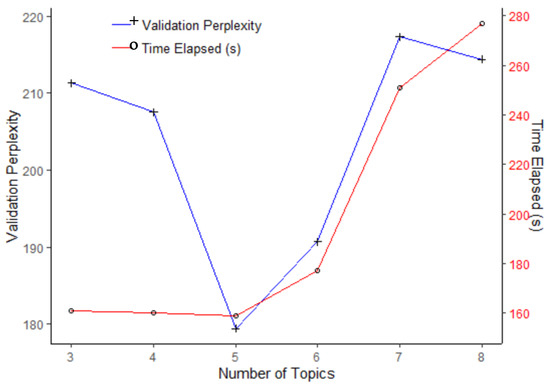
Figure A1.
Perplexity vs. number of topics for the laser welding study.
Figure A1.
Perplexity vs. number of topics for the laser welding study.
Appendix C. Approximation Evaluation Study
This appendix describes a numerical experiment evaluating the quality of the approximation in Equations (13) and (14) in relation to the exact posterior mean in Equation (17). We focus on a single topic and a four-word dictionary. We consider the six parameters q1, q2, q3, q4, Δ1 and Δ2 and the eight-run resolution III fractional factorial experiment shown in Table A1. The response is root mean squared error (RMSE) for the 4-posterior means. The main effects plot is in Figure A2. The exact and approximate posterior values were computed with perfect repeatability using Mathematica. The findings include the following. All the errors are in the third or fourth decimal point and represent less than 2% of the estimated probabilities. If the count for a dimension that is zapped is high (q1), the approximation deteriorates somewhat. If = 0, then the approximation is exact.

Table A1.
Eight cases with the exact posterior probability and the approximate values.
Table A1.
Eight cases with the exact posterior probability and the approximate values.
| # | q1 | q2 | q3 | q4 | Δ1 | Δ2 | Exact | Approximate | RMSE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ1 | μ2 | μ3 | μ4 | μ1 | μ2 | μ3 | μ4 | ||||||||
| 1 | 1 | 1 | 10 | 100 | 200 | 100 | 0.003 | 0.005 | 0.090 | 0.902 | 0.003 | 0.005 | 0.090 | 0.902 | 0.000024 |
| 2 | 10 | 1 | 10 | 10 | 100 | 100 | 0.077 | 0.008 | 0.458 | 0.458 | 0.076 | 0.008 | 0.458 | 0.458 | 0.001007 |
| 3 | 1 | 10 | 10 | 10 | 200 | 0 | 0.004 | 0.332 | 0.332 | 0.332 | 0.004 | 0.332 | 0.332 | 0.332 | 0.000000 |
| 4 | 10 | 10 | 10 | 100 | 100 | 0 | 0.071 | 0.310 | 0.310 | 0.310 | 0.071 | 0.310 | 0.310 | 0.310 | 0.000000 |
| 5 | 1 | 1 | 100 | 100 | 100 | 0 | 0.003 | 0.005 | 0.496 | 0.496 | 0.003 | 0.005 | 0.496 | 0.496 | 0.000000 |
| 6 | 10 | 1 | 100 | 10 | 200 | 0 | 0.031 | 0.009 | 0.873 | 0.087 | 0.031 | 0.009 | 0.873 | 0.087 | 0.000000 |
| 7 | 1 | 10 | 100 | 10 | 100 | 100 | 0.005 | 0.045 | 0.864 | 0.086 | 0.005 | 0.045 | 0.864 | 0.086 | 0.000225 |
| 8 | 10 | 10 | 100 | 100 | 200 | 100 | 0.024 | 0.032 | 0.472 | 0.472 | 0.024 | 0.031 | 0.472 | 0.472 | 0.000708 |
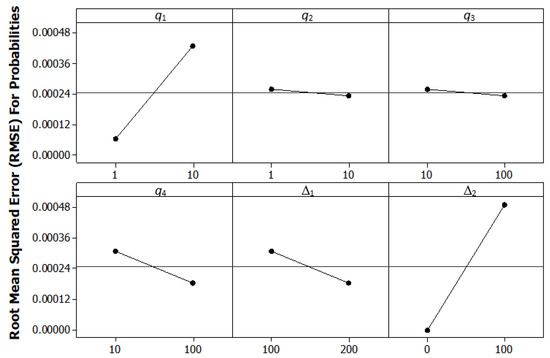
Figure A2.
Main effects plot of the RMSE.
Figure A2.
Main effects plot of the RMSE.
Appendix D. Handwritten Digits Example
Next, we consider the “Handwritten Digits” dataset with 10,000 30 × 30 pixel grayscale images [44]. The dataset is tagged with 10 categories which are the numbers 0 through 9. In a preprocessing step, we again reduce the number of grayscale levels by a factor of 200 to keep our document lengths sufficiently small for our VBA implementation storage sizes. In addition, we created the documents by repeating the pixel numbers proportionally to the reduced gray scale counts.
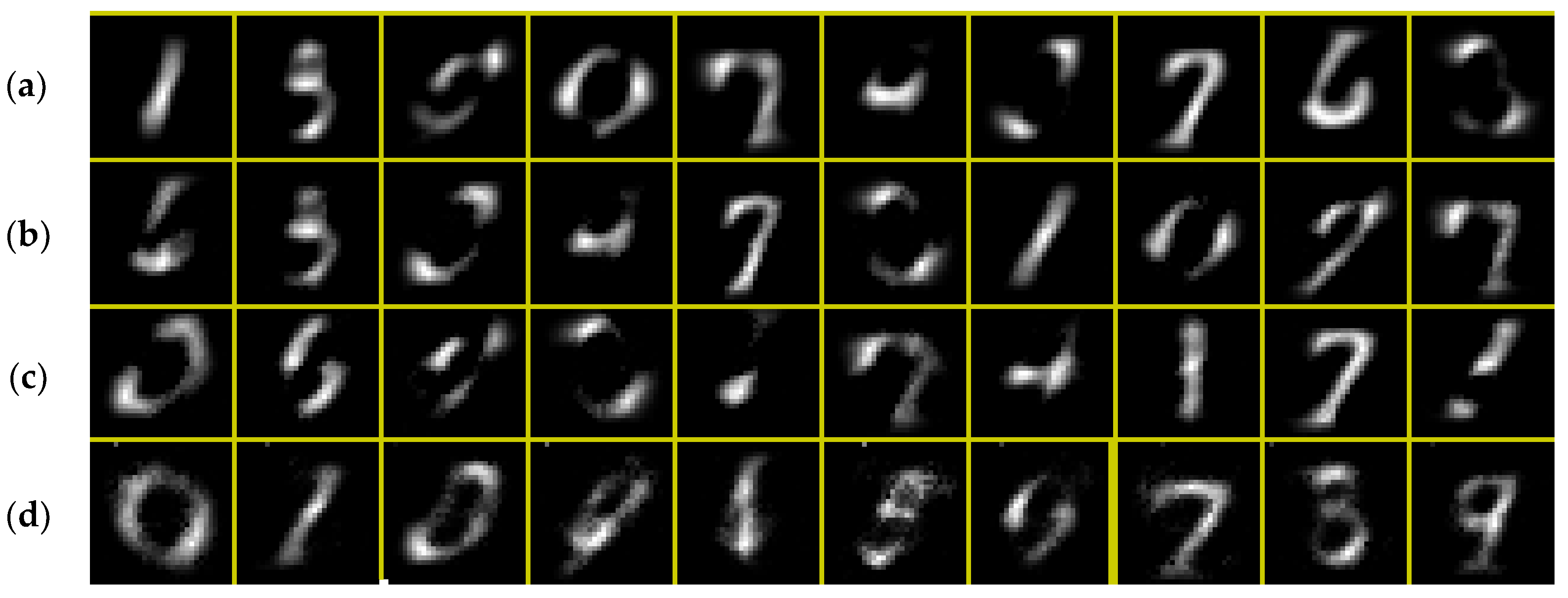
With all 10,000 images and 10 topics, LDA is not able to approximately recover the categories as shown in Figure A3a. This figure is based on 500 iterations. Note that the several numbers are not clearly apparent including 2, 4, 5, 8 and 9. This occurs presumably because the handwriting is variable such that the pixels for each number are quite different across images.
When analyzed using LDA and only the first 1000 images and again 500 iterations, the results are blurrier, and the same numbers are still missing as shown in Figure A3b. If the top 20 pixels for the LDA run are used to supervise the ERT model based on 1000 datapoints, the result from 300 iterations is shown in Figure A3c. Again, this required approximately 11 h using an i7 1.8 GHz processor with 16 GB of RAM. This result is equally accurate or desirable compared with LDA with all 10,000 images.
As a result of the poor quality for all the previous methods, we consider an additional approach for identifying high-level data. The top 50 pixels from manually selected “anchoring” images are applied. The selected are (in order 0–9): 95, 8, 82, 74, 64, 480, 430, 52, 386 and 364. The results are greatly improved as shown in Figure A3d. Admittedly, topics 2 and the 3 are still not clear. Further improvements might be achievable through pre-processing the images with suitable shifting and scaling so that the same numbers could consistently use the same pixels.
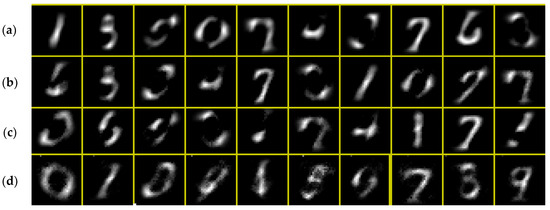
Figure A3.
Numbers data (a) LDA topics with 10,000 images, (b) LDA topics with 1000 images, (c) ERT model with 1000 images using LDA boosts, (d) ERT with 1000 images improved high-level data.
Figure A3.
Numbers data (a) LDA topics with 10,000 images, (b) LDA topics with 1000 images, (c) ERT model with 1000 images using LDA boosts, (d) ERT with 1000 images improved high-level data.
References
- Reese, C.S.; Wilson, A.G.; Guo, J.; Hamada, M.S.; Johnson, V.E. A Bayesian model for integrating multiple sources of lifetime information in system-reliability assessments. J. Qual. Technol. 2011, 43, 127–141. [Google Scholar] [CrossRef]
- Nair, V. Special Issue on Statistics in Information Technology. Technometrics 2007, 49, 236. [Google Scholar] [CrossRef]
- Nembhard, H.B.; Ferrier, N.J.; Osswald, T.A.; Sanz-Uribe, J.R. An integrated model for statistical and vision monitoring in manufacturing transitions. Qual. Reliab. Eng. Int. 2003, 19, 461–476. [Google Scholar] [CrossRef]
- Allen, T.T.; Xiong, H.; Afful-Dadzie, A. A directed topic model applied to call center improvement. Appl. Stoch. Models Bus. Ind. 2016, 32, 57–73. [Google Scholar] [CrossRef]
- Allen, T.T.; Sui, Z.; Parker, N.L. Timely decision analysis enabled by efficient social media modeling. Decis. Anal. 2017, 14, 250–260. [Google Scholar] [CrossRef]
- Megahed, F.M.; Woodall, W.H.; Camelio, J.A. A review and perspective on control charting with image data. J. Qual. Technol. 2011, 43, 83–98. [Google Scholar] [CrossRef]
- Colosimo, B.M.; Pacella, M. Analyzing the effect of process parameters on the shape of 3D profiles. J. Qual. Technol. 2011, 43, 169–195. [Google Scholar] [CrossRef]
- Hansen, M.H.; Nair, V.N.; Friedman, D.J. Monitoring wafer map data from integrated circuit fabrication processes for spatially clustered defects. Technometrics 1997, 39, 241–253. [Google Scholar] [CrossRef]
- Huang, D.; Allen, T.T. Design and analysis of variable fidelity experimentation applied to engine valve heat treatment process design. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2005, 54, 443–463. [Google Scholar] [CrossRef]
- Ferreiro, S.; Sierra, B.; Irigoien, I.; Gorritxategi, E. Data mining for quality control: Burr detection in the drilling process. Comput. Ind. Eng. 2011, 60, 801–810. [Google Scholar] [CrossRef]
- Alfaro-Almagro, F.; Jenkinson, M.; Bangerter, N.K.; Andersson, J.L.; Griffanti, L.; Douaud, G.; Sotiropoulos, S.N.; Jbabdi, S.; Hernandez-Fernandez, M.; Vallee, E. Image processing and Quality Control for the first 10,000 brain imaging datasets from UK Biobank. Neuroimage 2018, 166, 400–424. [Google Scholar] [CrossRef] [PubMed]
- Apley, D.W.; Lee, H.Y. Simultaneous identification of premodeled and unmodeled variation patterns. J. Qual. Technol. 2010, 42, 36–51. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet Allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Murray, J.S.; Reiter, J.P. Multiple imputation of missing categorical and continuous values via Bayesian mixture models with local dependence. J. Am. Stat. Assoc. 2016, 111, 1466–1479. [Google Scholar] [CrossRef]
- Miller, J.W.; Harrison, M.T. Mixture models with a prior on the number of components. J. Am. Stat. Assoc. 2018, 113, 340–356. [Google Scholar] [CrossRef]
- Van Havre, Z.; White, N.; Rousseau, J.; Mengersen, K. Overfitting Bayesian mixture models with an unknown number of components. PLoS ONE 2015, 10, e0131739. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Lai, Y.; Kleijn, W.B.; Song, Y.-Z.; Wang, L.; Guo, J. Variational Bayesian learning for Dirichlet process mixture of inverted Dirichlet distributions in non-Gaussian image feature modeling. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 449–463. [Google Scholar] [CrossRef]
- Tseng, S.H.; Allen, T. A Simple Approach for Multi-fidelity Experimentation Applied to Financial Engineering. Appl. Stoch. Models Bus. Ind. 2015, 31, 690–705. [Google Scholar] [CrossRef]
- Jeske, D.R.; Liu, R.Y. Mining and tracking massive text data: Classification, construction of tracking statistics, and inference under misclassification. Technometrics 2007, 49, 116–128. [Google Scholar] [CrossRef]
- Genkin, A.; Lewis, D.D.; Madigan, D. Large-scale Bayesian logistic regression for text categorization. Technometrics 2007, 49, 291–304. [Google Scholar] [CrossRef]
- Topalidou, E.; Psarakis, S. Review of multinomial and multiattribute quality control charts. Qual. Reliab. Eng. Int. 2009, 25, 773–804. [Google Scholar] [CrossRef]
- Blei, D.M.; Lafferty, J.D. A correlated topic model of science. Ann. Appl. Stat. 2007, 1, 17–35. [Google Scholar] [CrossRef]
- Blei, D.M.; Mcauliffe, J.D. Supervised topic models. In Proceedings of the 20th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007; pp. 121–128. [Google Scholar]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated Clust. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Liao, T.; Li, D.-M.; Li, Y.-M. Detection of welding flaws from radiographic images with fuzzy clustering methods. Fuzzy Sets Syst. 1999, 108, 145–158. [Google Scholar] [CrossRef]
- Sebzalli, Y.; Wang, X. Knowledge discovery from process operational data using PCA and fuzzy clustering. Eng. Appl. Artif. Intell. 2001, 14, 607–616. [Google Scholar] [CrossRef]
- Yan, H.; Paynabar, K.; Shi, J. Image-based process monitoring using low-rank tensor decomposition. IEEE Trans. Autom. Sci. Eng. 2014, 12, 216–227. [Google Scholar] [CrossRef]
- Qiu, P. Jump regression, image processing, and quality control. Qual. Eng. 2018, 30, 137–153. [Google Scholar] [CrossRef]
- Rosen-Zvi, M.; Chemudugunta, C.; Griffiths, T.; Smyth, P.; Steyvers, M. Learning author-topic models from text corpora. ACM Trans. Inf. Syst. (TOIS) 2010, 28, 1–38. [Google Scholar] [CrossRef]
- Ihianle, I.K.; Naeem, U.; Islam, S.; Tawil, A.-R. A Hybrid Approach to Recognising Activities of Daily Living from Object Use in the Home Environment. Informatics 2018, 5, 6. [Google Scholar] [CrossRef]
- Arun, R.; Suresh, V.; Madhavan, V.C.E.; Murty, N.M. On Finding the Natural Number of Topics with Latent Dirichlet Allocation: Some Observations. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2010; pp. 391–402. [Google Scholar]
- Jeffus, L.; Bower, L. Welding Skills, Processes and Practices for Entry-Level Welders; Cengage Learning: Boston, MA, USA, 2009. [Google Scholar]
- Cao, J.; Xia, T.; Li, J.; Zhang, Y.; Tang, S. A Density-Based Method for Adaptive LDA Model Selection. Neurocomputing 2009, 72, 1775–1781. [Google Scholar] [CrossRef]
- Koltsov, S. Application of Rényi and Tsallis entropies to topic modeling optimization. Phys. A Stat. Mech. Its Appl. 2018, 512, 1192–1204. [Google Scholar] [CrossRef]
- Griffiths, T.L.; Steyvers, M. Finding scientific topics. Proc. Natl. Acad. Sci. USA 2004, 101, 5228–5235. [Google Scholar] [CrossRef] [PubMed]
- Waal, A.D.; Barnard, E. Evaluating topic models with stability. In Human Language Technologies; Meraka Institute: Pretoria, South Africa, 2008. [Google Scholar]
- Amritanshu, A.; Fu, W.; Menzies, T. What is Wrong with Topic Modeling? And how to fix it using search-based software engineering. Inf. Softw. Technol. 2008, 98, 74–88. [Google Scholar]
- Chuang, J.; Roberts, M.E.; Stewart, B.M.; Weiss, R.; Tingley, D.; Grimmer, J.; Heer, J. TopicCheck: Interactive alignment for assessing topic model stability. In Proceedings of the 2015 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Denver, CO, USA, 31 May–5 June 2015; pp. 175–184. [Google Scholar]
- Koltcov, S.; Nikolenko, S.I.; Koltsova, O.; Filippov, V.; Bodrunova, S. Stable Topic Modeling with Local Density Regularization. In Proceedings of the Third International Conference on Internet Science, Florence, Italy, 12–14 September 2016. [Google Scholar]
- Woods, D.D.; Patterson, E.S.; Roth, E.M. Can we ever escape from data overload? A cognitive systems diagnosis. Cogn. Technol. Work 2002, 4, 22–36. [Google Scholar] [CrossRef]
- Steyvers, M.; Griffiths, T. Probabilistic topic models. Handb. Latent Semant. Anal. 2007, 427, 424–440. [Google Scholar]
- Carpenter, B. Integrating out multinomial parameters in Latent Dirichlet Allocation and naive Bayes for collapsed Gibbs sampling. Rapp. Tech. 2010, 4, 464. [Google Scholar]
- Fashion MNIST. Available online: https://www.kaggle.com/zalando-research/fashionmnist#fashion-mnisttest.csv (accessed on 18 May 2020).
- Digit Recognizer. Available online: https://www.kaggle.com/c/digit-recognizer/data (accessed on 16 June 2020).
- Bacioiu, D.; Melton, G.; Papaelias, M.; Shaw, R. Automated defect classification of Aluminium 5083 TIG welding using HDR camera and neural networks. J. Manuf. Process. 2019, 45, 603–613. [Google Scholar] [CrossRef]
- Mimno, D.; Wallach, H.M.; Talley, E.; Leenders, M.; McCallum, A. Optimizing Semantic Coherence in Topic Models. In Proceedings of the Conference on Empirical Methods in Natural Language Processing; Association for Computational Linguistics: Stroudsburg, PA, USA, 2011; pp. 262–272. [Google Scholar]
- Newman, D.; Lau, J.H.; Grieser, K.; Baldwin, T. Automatic Evaluation of Topic Coherence. In Human Language Technologies: The 2010 Annual Conference of the North American Chapter of the Association for Computational Linguistics; Association for Computational Linguistics: Los Angeles, CA, USA, 2010. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).