Artificial Neural Networks and Particle Swarm Optimization Algorithms for Preference Prediction in Multi-Criteria Recommender Systems
Abstract
:1. Introduction
2. Related Work
3. Recommender Systems
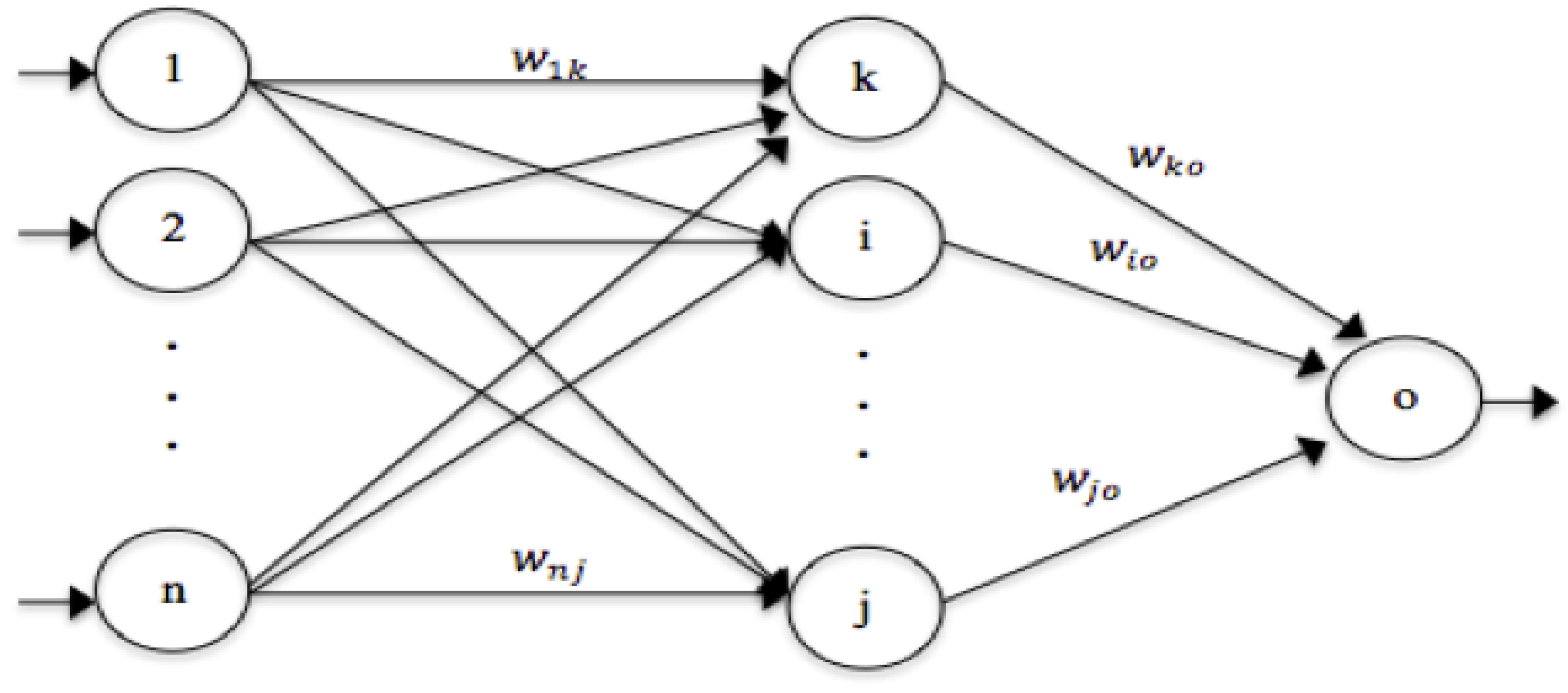
4. Particle Swarm Optimization (PSO)
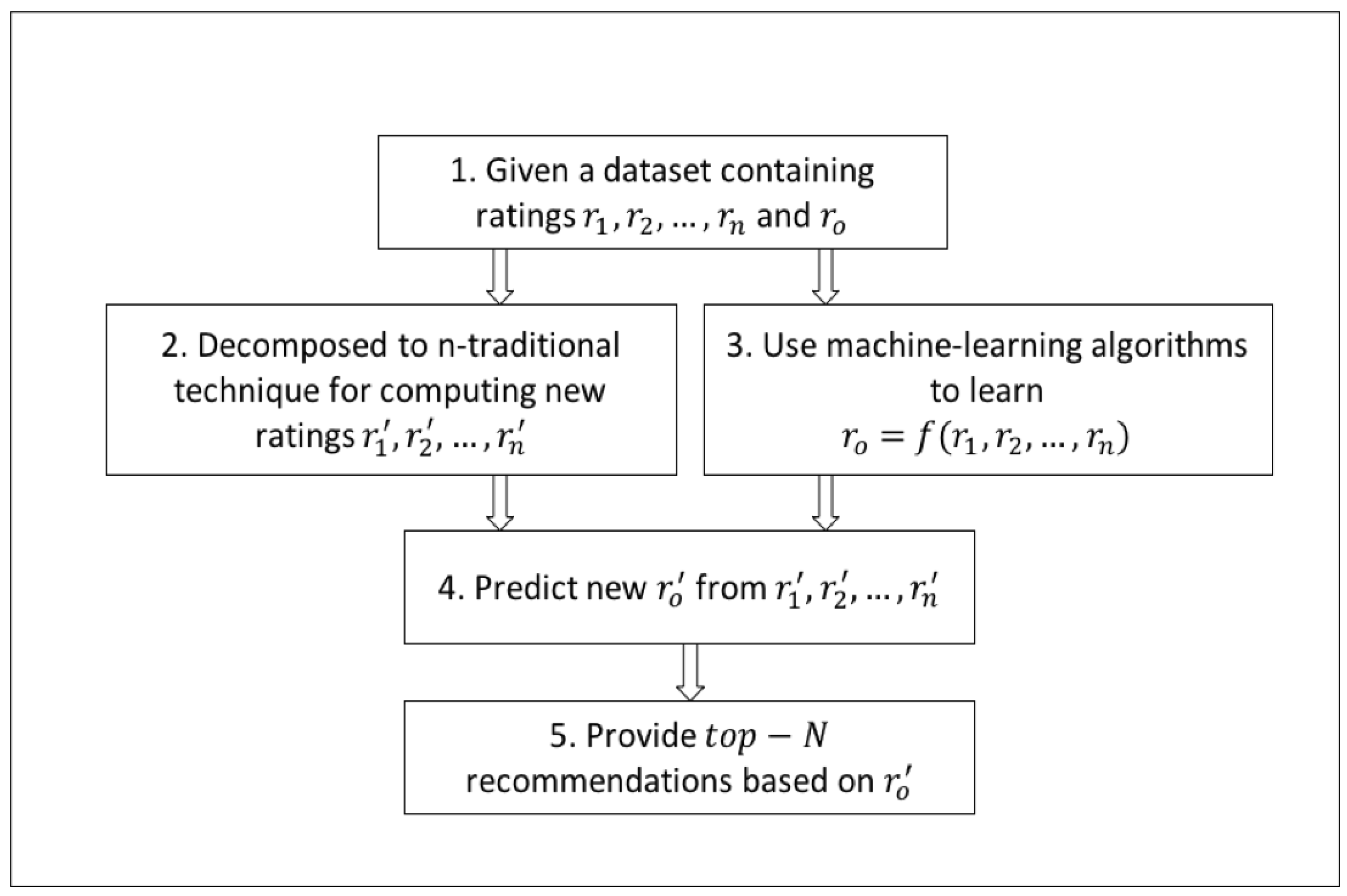
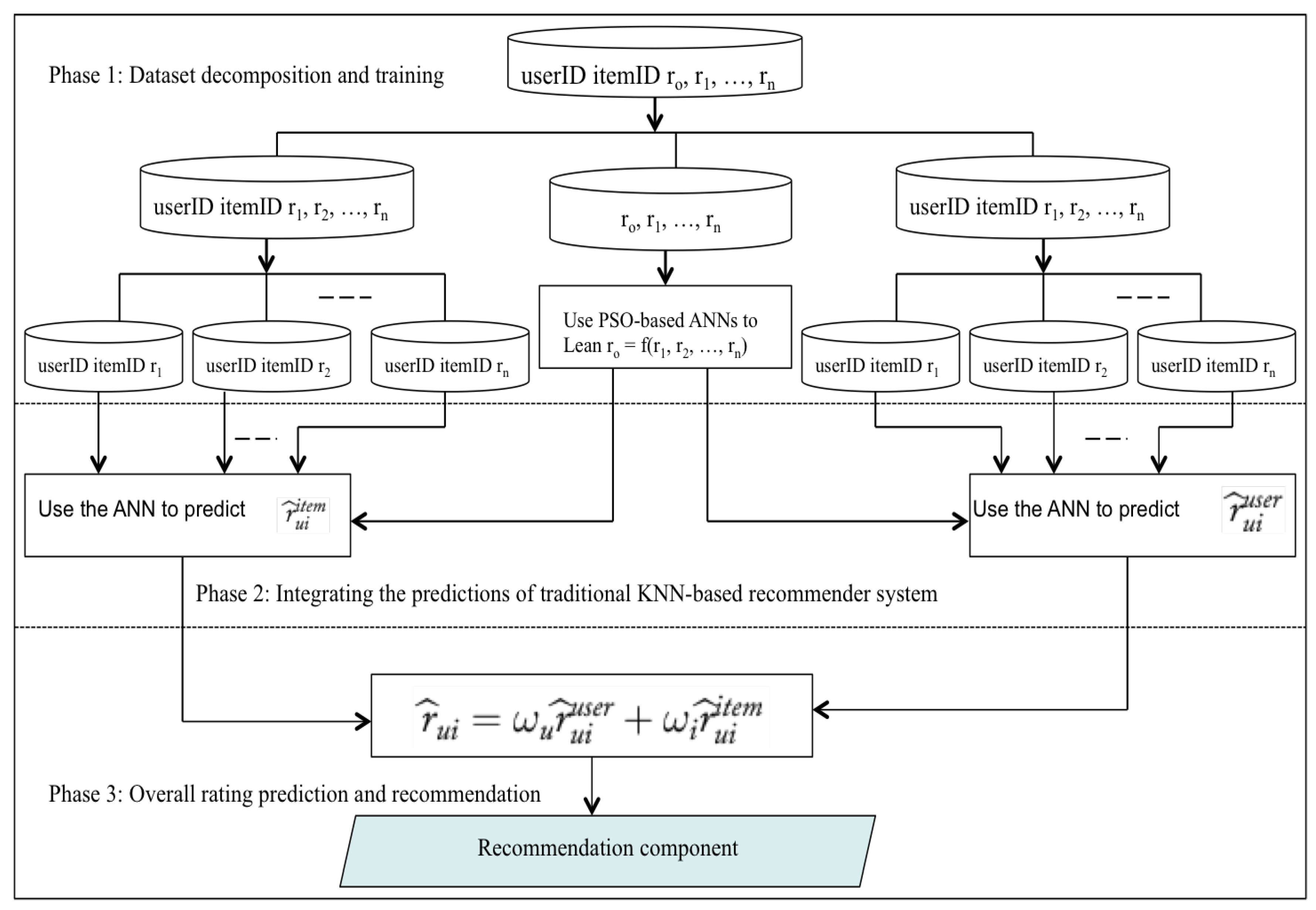
5. The Proposed Model and Approach
- Decompose the n-dimensional multi-criteria rating problem into n distinct single rating problems.
- Choose a prediction function or algorithm that can learn the relationships between the criteria ratings and the overall rating.
- Integrate the prediction algorithm with the distinct single rating techniques of step 1 for predicting the criteria ratings and the overall rating.
- Provide a list of recommendations.
6. Experimental Methodology
- Single_U: A user-based kNN recommender system that computes similarities between users using Equation (3)
- Single_I: An item-based kNN recommender system that computes similarities between items using a modified version of Equation (3) to find similarities between item i and item j.
- ANNs_U: A model-based MCRSs that integrates PSO-based ANNs with Single_U in item 1 to estimate the overall rating. We named the rating provided by this model as .
- ANNs_I: A model-based MCRSs that integrates PSO-based ANNs with Single_I in item 2 to estimate the overall rating. We named the rating provided by this model as .
- Mean average error (MAE)
- Root mean square error (RMSE)
- Precision, recall, and F-measure
- Fraction of concordant pairs (FCP)
- Normalized discounted cumulative gain (NDCG)
- Mean reciprocal ranking (MRR)
- Gini coefficient.
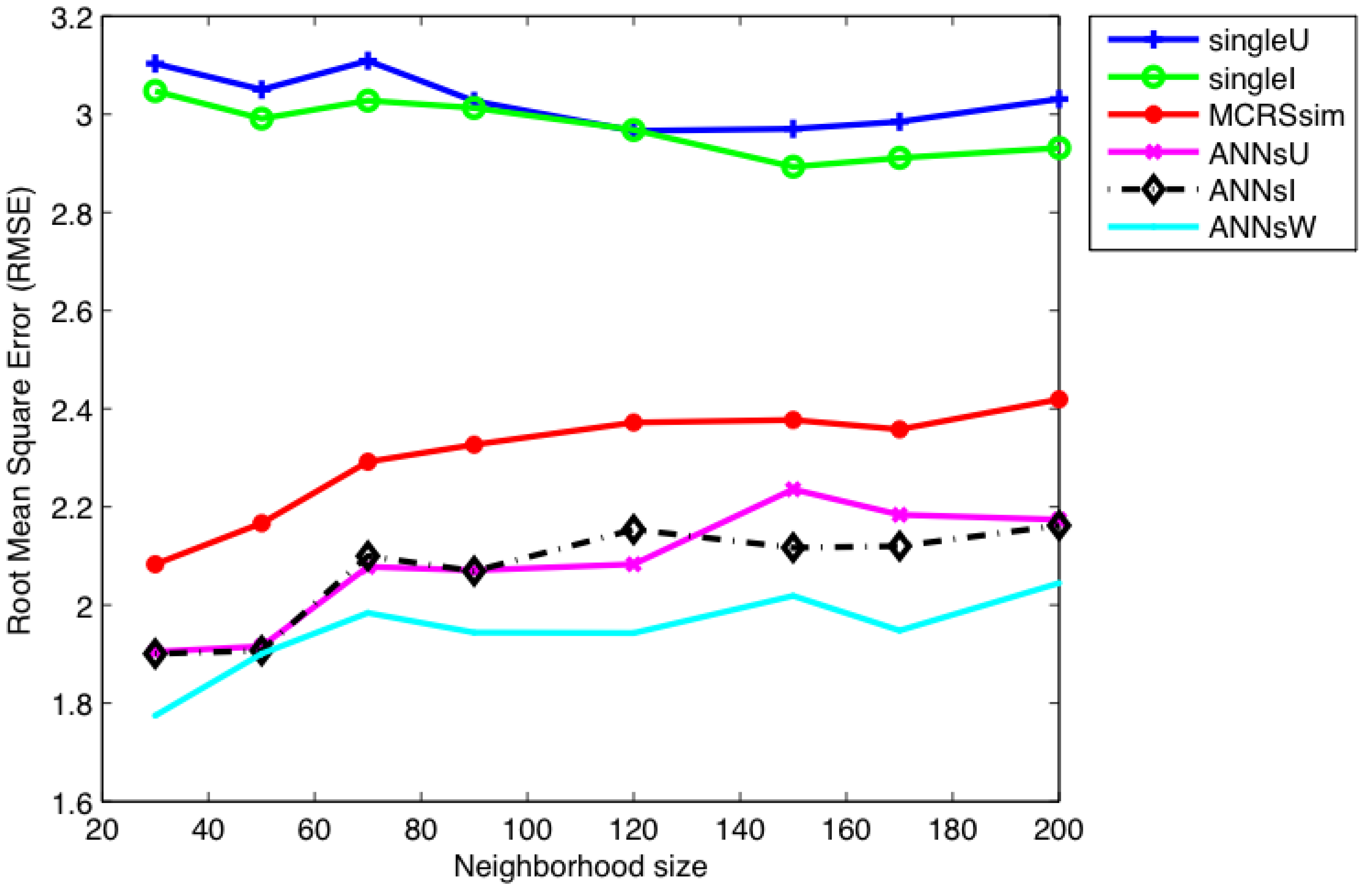
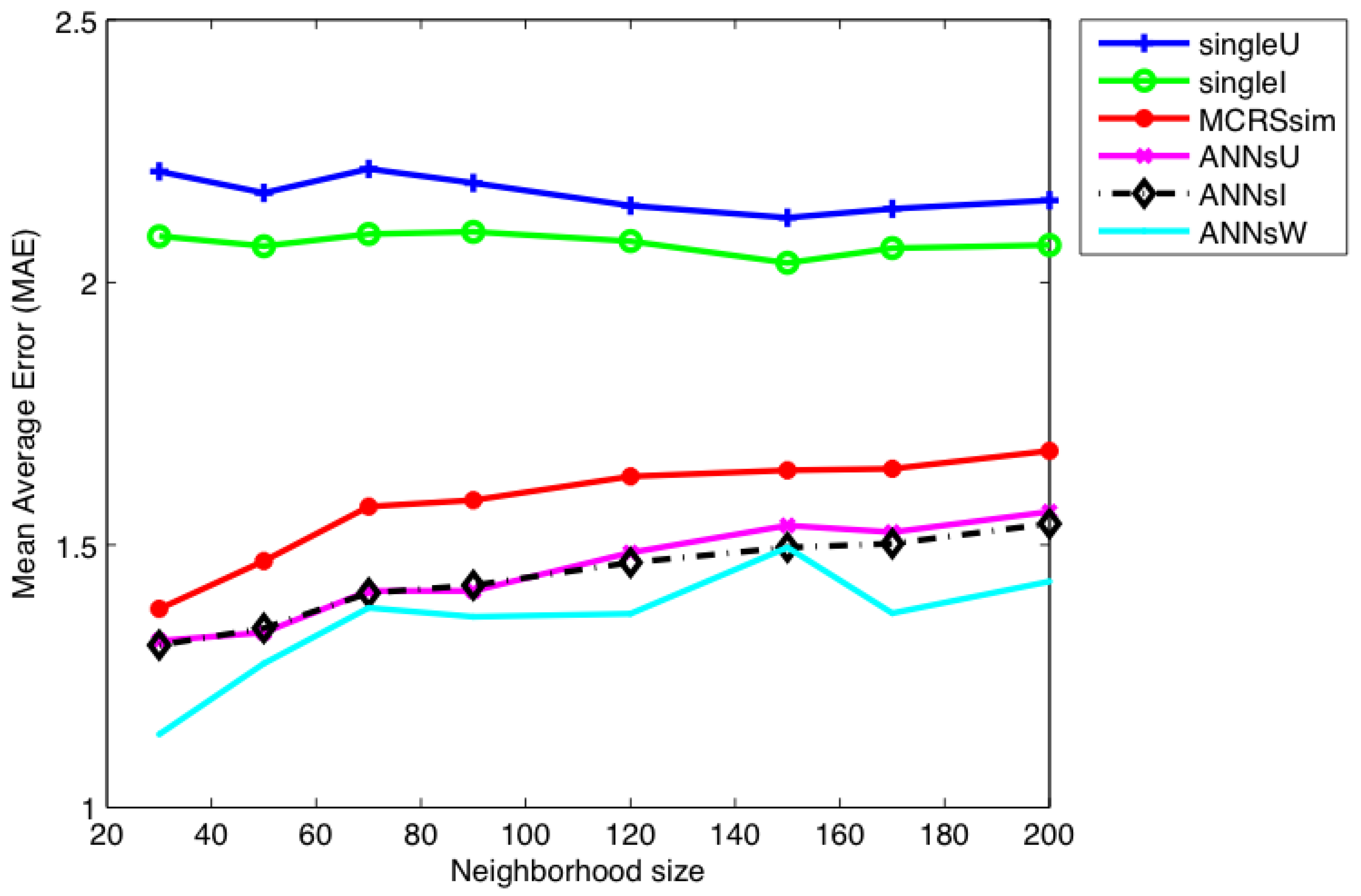
7. Results and Discussion
8. Conclusions and Future Work
Author Contributions
Conflicts of Interest
References
- Bobadilla, J.; Ortega, F.; Hernando, A.; Bernal, J. A collaborative filtering approach to mitigate the new user cold start problem. Knowl.-Based Syst. 2012, 26, 225–238. [Google Scholar] [CrossRef]
- Hassan, M.; Hamada, M. Recommending Learning Peers for Collaborative Learning through Social Network Sites. In Proceedings of the 2016 7th IEEE International Conference on Intelligent Systems, Modelling and Simulation (ISMS), Bangkok, Thailand, 25–27 January 2016; pp. 60–63. [Google Scholar]
- Lu, J.; Wu, D.; Mao, M.; Wang, W.; Zhang, G. Recommender system application developments: A survey. Decis. Support Syst. 2015, 74, 12–32. [Google Scholar] [CrossRef]
- Hassan, M.; Hamada, M. Performance Comparison of Featured Neural Network Trained with Backpropagation and Delta Rule Techniques for Movie Rating Prediction in Multi-criteria Recommender Systems. Informatica 2016, 40, 409. [Google Scholar]
- Adomavicius, G.; Kwon, Y. Multi-criteria recommender systems. In Recommender Systems Handbook; Springer: Boston, MA, USA, 2011; pp. 769–803. [Google Scholar]
- Mirjalili, S.; Hashim, S.Z.M.; Sardroudi, H.M. Training feedforward neural networks using hybrid particle swarm optimization and gravitational search algorithm. Appl. Math. Comput. 2012, 218, 11125–11137. [Google Scholar] [CrossRef]
- Hassan, M.; Hamada, M. Performance Comparison of Feed-Forward Neural Networks Trained with Different Learning Algorithms for Recommender Systems. Computation 2017, 5, 40. [Google Scholar] [CrossRef]
- Üçoluk, G. Genetic algorithm solution of the TSP avoiding special crossover and mutation. Intell. Autom. Soft Comput. 2002, 8, 265–272. [Google Scholar] [CrossRef]
- Pradeepkumar, D.; Ravi, V. Forecasting financial time series volatility using Particle Swarm Optimization trained Quantile Regression Neural Network. Appl. Soft Comput. 2017, 58, 35–52. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, M.; Ruan, K.; Gong, C.; Zhang, Y.; Yang, S.X. A Ranging Model Based on BP Neural Network. Intell. Autom. Soft Comput. 2016, 22, 325–329. [Google Scholar] [CrossRef]
- Xue, Y.; Zhong, S.; Ma, T.; Cao, J. A hybrid evolutionary algorithm for numerical optimization problem. Intell. Autom. Soft Comput. 2015, 21, 473–490. [Google Scholar] [CrossRef]
- Zhang, J.R.; Zhang, J.; Lok, T.M.; Lyu, M.R. A hybrid particle swarm optimization–back-propagation algorithm for feedforward neural network training. Appl. Math. Comput. 2007, 185, 1026–1037. [Google Scholar] [CrossRef]
- Du, K.L.; Swamy, M. Particle swarm optimization. In Search and Optimization by Metaheuristics; Springer: Basel, Switzerland, 2016; pp. 153–173. [Google Scholar]
- Settles, M.; Rodebaugh, B.; Soule, T. Comparison of genetic algorithm and particle swarm optimizer when evolving a recurrent neural network. In Genetic and Evolutionary Computation—GECCO 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 148–149. [Google Scholar]
- Adomavicius, G.; Manouselis, N.; Kwon, Y. Multi-criteria recommender systems. In Recommender Systems Handbook; Springer: Boston, MA, USA, 2015; pp. 847–880. [Google Scholar]
- Hill, W.; Stead, L.; Rosenstein, M.; Furnas, G. Recommending and evaluating choices in a virtual community of use. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Denver, CO, USA, 7–11 May 1995; ACM Press/Addison-Wesley Publishing Co.: New York, NY, USA, 1995; pp. 194–201. [Google Scholar]
- Resnick, P.; Iacovou, N.; Suchak, M.; Bergstrom, P.; Riedl, J. GroupLens: An open architecture for collaborative filtering of netnews. In Proceedings of the 1994 ACM conference on Computer supported cooperative work, Chapel Hill, NC, USA, 22–26 October 1994; ACM: New York, NY, USA, 1994; pp. 175–186. [Google Scholar]
- Shardanand, U.; Maes, P. Social information filtering: Algorithms for automating “word of mouth”. In Proceedings of the SIGCHI conference on Human factors in computing systems, Denver, CO, USA, 7–11 May 1995; ACM Press/Addison-Wesley Publishing Co.: New York, NY, USA, 1995; pp. 210–217. [Google Scholar]
- Adomavicius, G.; Tuzhilin, A. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions. IEEE Trans. Knowl. Data Eng. 2005, 17, 734–749. [Google Scholar] [CrossRef]
- Plantié, M.; Montmain, J.; Dray, G. Movies recommenders systems: Automation of the information and evaluation phases in a multi-criteria decision-making process. In Database and Expert Systems Applications; Springer: Berlin/Heidelberg, Germany, 2005; pp. 633–644. [Google Scholar]
- Bilge, A.; Kaleli, C. A multi-criteria item-based collaborative filtering framework. In Proceedings of the 2014 11th IEEE International Joint Conference on Computer Science and Software Engineering (JCSSE), Chon Buri, Thailand, 14–16 May 2014; pp. 18–22. [Google Scholar]
- Adomavicius, G.; Kwon, Y. New recommendation techniques for multicriteria rating systems. IEEE Intell. Syst. 2007, 22. [Google Scholar] [CrossRef]
- Sanchez-Vilas, F.; Ismoilov, J.; Lousame, F.P.; Sanchez, E.; Lama, M. Applying multicriteria algorithms to restaurant recommendation. In Proceedings of the 2011 IEEE/WIC/ACM International Conferences on Web Intelligence and Intelligent Agent Technology, IEEE Computer Society, Lyon, France, 22–27 August 2011; Volume 1, pp. 87–91. [Google Scholar]
- Lousame, F.P.; Sánchez, E. View-based recommender systems. In Proceedings of the Third ACM Conference on Recommender Systems, New York, NY, USA, 23–25 October 2009; ACM: New York, NY, USA, 2009; pp. 389–392. [Google Scholar]
- Fu, Y.; Liu, B.; Ge, Y.; Yao, Z.; Xiong, H. User preference learning with multiple information fusion for restaurant recommendation. In Proceedings of the 2014 SIAM International Conference on Data Mining, Philadelphia, PA, USA, 24–26 April 2014; SIAM: Philadelphia, PA, USA, 2014; pp. 470–478. [Google Scholar]
- Fang, Y.; Si, L. Matrix co-factorization for recommendation with rich side information and implicit feedback. In Proceedings of the 2nd International Workshop on Information Heterogeneity and Fusion in Recommender Systems, Chicago, IL, USA, 23–27 October 2011; ACM: New York, NY, USA, 2011; pp. 65–69. [Google Scholar]
- Cheng, C.; Yang, H.; King, I.; Lyu, M.R. Fused Matrix Factorization with Geographical and Social Influence in Location-Based Social Networks. In Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence (AAAI’12), Toronto, ON, Canada, 22–26 July 2012; Volume 12, pp. 17–23. [Google Scholar]
- Nilashi, M.; bin Ibrahim, O.; Ithnin, N.; Sarmin, N.H. A multi-criteria collaborative filtering recommender system for the tourism domain using Expectation Maximization (EM) and PCA–ANFIS. Electr. Commer. Res. Appl. 2015, 14, 542–562. [Google Scholar] [CrossRef]
- Reynolds, D. Gaussian mixture models. In Encyclopedia of Biometrics; Springer: New York, NY, USA, 2015; pp. 827–832. [Google Scholar]
- Farokhi, N.; Vahid, M.; Nilashi, M.; Ibrahim, O. A multi-criteria recommender system for tourism using fuzzy approach. J. Soft Comput. Decis. Support Syst. 2016, 3, 19–29. [Google Scholar]
- Fomba, S.; Zaraté, P.; Kilgour, M.; Camilleri, G.; Konate, J.; Tangara, F. A Recommender System Based on Multi-Criteria Aggregation. Int. J. Decis. Support Syst. Technol. (IJDSST) 2017, 9, 1–15. [Google Scholar] [CrossRef]
- Xu, Z. Choquet integrals of weighted intuitionistic fuzzy information. Inf. Sci. 2010, 180, 726–736. [Google Scholar] [CrossRef]
- Lakiotaki, K.; Matsatsinis, N.F.; Tsoukias, A. Multicriteria user modeling in recommender systems. IEEE Intell. Syst. 2011, 26, 64–76. [Google Scholar] [CrossRef]
- Choudhary, P.; Kant, V.; Dwivedi, P. A Particle Swarm Optimization Approach to Multi Criteria Recommender System Utilizing Effective Similarity Measures. In Proceedings of the 9th International Conference on Machine Learning and Computing, Singapore, 24–26 February 2017; ACM: New York, NY, USA, 2017; pp. 81–85. [Google Scholar]
- Jannach, D.; Karakaya, Z.; Gedikli, F. Accuracy improvements for multi-criteria recommender systems. In Proceedings of the 13th ACM Conference on Electronic Commerce, Valencia, Spain, 4–8 June 2012; ACM: New York, NY, USA, 2012; pp. 674–689. [Google Scholar]
- Cawley, G.C.; Talbot, N.L. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Hassan, M.; Hamada, M. Enhancing learning objects recommendation using multi-criteria recommender systems. In Proceedings of the 2016 IEEE International Conference on Teaching, Assessment, and Learning for Engineering (TALE), Bangkok, Thailand, 7–9 December 2016; pp. 62–64. [Google Scholar]
- Hassan, M.; Hamada, M. Smart media-based context-aware recommender systems for learning: A conceptual framework. In Proceedings of the 2017 16th International Conference on Information Technology Based Higher Education and Training (ITHET), Ohrid, Macedonia, 10–12 July 2017; pp. 1–4. [Google Scholar]
- Yera, R.; Martinez, L. Fuzzy tools in recommender systems: A survey. Int. J. Comput. Intell. Syst. 2017, 10, 776–803. [Google Scholar] [CrossRef]
- Bobadilla, J.; Ortega, F.; Hernando, A.; Gutiérrez, A. Recommender systems survey. Knowl.-Based Syst. 2013, 46, 109–132. [Google Scholar] [CrossRef]
- Bobadilla, J.; Hernando, A.; Ortega, F.; Bernal, J. A framework for collaborative filtering recommender systems. Expert Syst. Appl. 2011, 38, 14609–14623. [Google Scholar] [CrossRef]
- Hassan, M.; Hamada, M. A Neural Networks Approach for Improving the Accuracy of Multi-Criteria Recommender Systems. Appl. Sci. 2017, 7, 868. [Google Scholar] [CrossRef]
- Kennedy, J. Particle swarm optimization. In Encyclopedia of Machine Learning; Springer: New York, NY, USA, 2011; pp. 760–766. [Google Scholar]
- Jona, J.; Nagaveni, N. A hybrid swarm optimization approach for feature set reduction in digital mammograms. WSEAS Trans. Inf. Sci. Appl. 2012, 9, 340–349. [Google Scholar]
- Hu, X.; Eberhart, R.C.; Shi, Y. Particle swarm with extended memory for multiobjective optimization. In Proceedings of the 2003 IEEE, Swarm Intelligence Symposium, 2003 (SIS’03), Indianapolis, IN, USA, 26 April 2003; pp. 193–197. [Google Scholar]
- Triba, M.N.; Le Moyec, L.; Amathieu, R.; Goossens, C.; Bouchemal, N.; Nahon, P.; Rutledge, D.N.; Savarin, P. PLS/OPLS models in metabolomics: The impact of permutation of dataset rows on the K-fold cross-validation quality parameters. Mol. BioSyst. 2015, 11, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Rohani, A.; Taki, M.; Abdollahpour, M. A novel soft computing model (Gaussian process regression with K-fold cross validation) for daily and monthly solar radiation forecasting (Part: I). Renew. Energy 2018, 115, 411–422. [Google Scholar] [CrossRef]
- Tvedskov, T.; Meretoja, T.; Jensen, M.; Leidenius, M.; Kroman, N. Cross-validation of three predictive tools for non-sentinel node metastases in breast cancer patients with micrometastases or isolated tumor cells in the sentinel node. Eur. J. Surg. Oncol. 2014, 40, 435–441. [Google Scholar] [CrossRef] [PubMed]
- Shao, C.; Paynabar, K.; Kim, T.; Jin, J.; Hu, S.; Spicer, J.; Wang, H.; Abell, J. Feature selection for manufacturing process monitoring using cross-validation. J. Manuf. Syst. 2013, 32, 550–555. [Google Scholar] [CrossRef]
- Jiang, P.; Chen, J. Displacement prediction of landslide based on generalized regression neural networks with K-fold cross-validation. Neurocomputing 2016, 198, 40–47. [Google Scholar] [CrossRef]
- Jannach, D.; Lerche, L.; Gedikli, F.; Bonnin, G. What recommenders recommend–an analysis of accuracy, popularity, and sales diversity effects. In International Conference on User Modeling, Adaptation, and Personalization; Springer: Berlin/Heidelberg, Germany, 2013; pp. 25–37. [Google Scholar]
- Owen, S.; Anil, R.; Dunning, T.; Friedman, E. Mahout in Action; Manning Publications Co.: Shelter Island, NY, USA, 2011. [Google Scholar]
| … | ||||||
|---|---|---|---|---|---|---|
| 54,5,3,5 | 55,5,4,5 | 34,2,3,3 | 34,3,3,3 | … | 12,1,3,1 | |
| 24,1,3,1 | 55,5,5,5 | 55,4,4,4 | 34,2,3,5 | … | 44,3,3,5 | |
| 21,5,2,4 | 55,5,5,5 | 54,5,4,4 | 32,5,4,3 | … | 43,5,4,3 | |
| 24,1,5,1 | 22,2,2,2 | 55,4,3,4 | 35,3,3,5 | … | 45,2,3,5 | |
| . | ||||||
| . | ||||||
| . | ||||||
| 33,3,3,2 | 21,1,1,5 | 55,4,5,4 | 44,4,3,5 | … | 12,1,1,1 |
| User | Movie | Direction | Action | Story | Visual | Overall |
|---|---|---|---|---|---|---|
| ID | ID | |||||
| 101 | 1 | C | ||||
| 3 | B | |||||
| 5 | ||||||
| 102 | 3 | |||||
| 5 | C | |||||
| 6 | C | B |
| User | Movie | Direction | Action | Story | Visual | Overall |
|---|---|---|---|---|---|---|
| ID | ID | |||||
| 101 | 1 | 13 | 6 | 5 | 8 | 5 |
| 3 | 9 | 10 | 10 | 11 | 8 | |
| 5 | 8 | 11 | 10 | 11 | 11 | |
| 102 | 3 | 13 | 13 | 13 | 13 | 13 |
| 5 | 5 | 6 | 13 | 13 | 13 | |
| 6 | 6 | 9 | 7 | 8 | 8 |
| Size of K | Single_I | Single_U | MCRSs_Sim | ANNs_I | ANNs_U | ANNs_W |
|---|---|---|---|---|---|---|
| RMSE | 3.030 | 2.973 | 2.300 | 2.081 | 2.066 | 1.945 |
| MAE | 2.169 | 2.075 | 1.575 | 1.448 | 1.436 | 1.353 |
| Precision | 0.795 | 0.802 | 0.817 | 0.828 | 0.835 | 0.838 |
| Recall | 0.800 | 0.805 | 0.810 | 0.821 | 0.824 | 0.833 |
| F1 | 0.797 | 0.803 | 0.813 | 0.824 | 0.829 | 0.835 |
| MRR × 10−2 | 0.109 | 0.122 | 0.166 | 0.280 | 0.170 | 0.570 |
| NDCG | 0.887 | 0.902 | 0.925 | 0.961 | 0.921 | 0.975 |
| Gini | 0.739 | 0.768 | 0.832 | 0.836 | 0.839 | 0.858 |
| FCP | 0.620 | 0.641 | 0.738 | 0.816 | 0.822 | 0.839 |
| Actual | Single_I | Single_U | MCRSs_Sim | ANNs_I | ANNs_U | ANNs_W | |
|---|---|---|---|---|---|---|---|
| Actual | 1.000 | 0.834 | 0.739 | 0.894 | 0.916 | 0.896 | 0.935 |
| Single_I | 0.834 | 1.000 | 0.664 | 0.921 | 0.956 | 0.759 | 0.891 |
| Single_U | 0.739 | 0.664 | 1.000 | 0.666 | 0.737 | 0.872 | 0.793 |
| MCRSs_Sim | 0.894 | 0.921 | 0.666 | 1.000 | 0.968 | 0.794 | 0.903 |
| ANNs_I | 0.916 | 0.956 | 0.737 | 0.968 | 1.000 | 0.814 | 0.943 |
| ANNs_U | 0.896 | 0.759 | 0.872 | 0.794 | 0.814 | 1.000 | 0.922 |
| ANNs_W | 0.935 | 0.891 | 0.793 | 0.903 | 0.943 | 0.922 | 1.000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamada, M.; Hassan, M. Artificial Neural Networks and Particle Swarm Optimization Algorithms for Preference Prediction in Multi-Criteria Recommender Systems. Informatics 2018, 5, 25. https://doi.org/10.3390/informatics5020025
Hamada M, Hassan M. Artificial Neural Networks and Particle Swarm Optimization Algorithms for Preference Prediction in Multi-Criteria Recommender Systems. Informatics. 2018; 5(2):25. https://doi.org/10.3390/informatics5020025
Chicago/Turabian StyleHamada, Mohamed, and Mohammed Hassan. 2018. "Artificial Neural Networks and Particle Swarm Optimization Algorithms for Preference Prediction in Multi-Criteria Recommender Systems" Informatics 5, no. 2: 25. https://doi.org/10.3390/informatics5020025
APA StyleHamada, M., & Hassan, M. (2018). Artificial Neural Networks and Particle Swarm Optimization Algorithms for Preference Prediction in Multi-Criteria Recommender Systems. Informatics, 5(2), 25. https://doi.org/10.3390/informatics5020025





