Abstract
Programming online judges (POJs) are an emerging application scenario in e-learning recommendation areas. Specifically, they are e-learning tools usually used in programming practices for the automatic evaluation of source code developed by students when they are solving programming problems. Usually, they contain a large collection of such problems, to be solved by students at their own personalized pace. The more problems in the POJ the harder the selection of the right problem to solve according to previous users performance, causing information overload and a widespread discouragement. This paper presents a recommendation framework to mitigate this issue by suggesting problems to solve in programming online judges, through the use of fuzzy tools which manage the uncertainty related to this scenario. The evaluation of the proposal uses real data obtained from a programming online judge, and shows that the new approach improves previous recommendation strategies which do not consider uncertainty management in the programming online judge scenarios. Specifically, the best results were obtained for short recommendation lists.
1. Introduction
Programming online judges (POJs) are e-learning platforms which have been widely accepted in the last few years for programming practices in computer science education and for training in competitive programming scenarios [1,2]. Basically, they are composed of a collection of programming exercises to be completed by the users. As an important feature, these platforms automate the evaluation of the proposed solution by doing an instantaneous verdict regarding its correctness. Key examples of POJs are the University of Valladolid Online Judge with more than 210,000 users and 1700 problems, and the Peking University Online Judge with more than 600,000 users and 3000 problems.
The typical interaction sequence between the user and the POJ is as follows:
- The user selects a problem to solve from the online judge (Figure 1).
 Figure 1. Typical interface with the set of problems to solve in an online judge.
Figure 1. Typical interface with the set of problems to solve in an online judge. - The code for solving such a problem is written.
- This source code is uploaded to the online judge (Figure 2).
 Figure 2. Typical interface to upload a problem solution in an online judge.
Figure 2. Typical interface to upload a problem solution in an online judge. - The judge automatically indicates whether the solution is correct or not. If not, classifies the failure mainly in Wrong Answer, Time limited exceeded or Runtime Error, allowing new solution attempts to the same problem.
One of the most important advantages of POJs is that they allow users to select and try to solve the problems they consider suitable for improving their knowledge acquisition at their personalized pace. According to the amount of problems finally solved by each user, the POJ also publishes a ranking (Figure 3). The reaching of a top position in this ranking is an extra motivation for the users, being then this gamification environment a very good scenario for boosting the users’ programming abilities and knowledge [3].
Figure 3.
Typical interface showing the users’ ranking in an online judge.
The wide acceptance of POJs and the increasing number of users that are currently solving a very high percentage of all the available problems, have implied an increment of such available problems. Therefore, it is currently difficult for several users to find out the appropriate problem for trying to solve, according to their current experience and learning needs. This is a typical information overloading scenario, in which users can experiment a high discouragement and frustration when the actual difficult level of the problems they are trying to solve does not match with their current knowledge profile and therefore it is difficult to develop a successful solution.
Nowadays, the classical solution to face these information overload problems is the development of a recommender system focused on the corresponding scenario. Recommender Systems goal is to provide users the items that best fit their preferences and needs in an overload search space [4,5,6]. They have been successfully used in scenarios such as tourism [7], e-commerce, e-learning, or social networks [8]. In the specific case of e-learning, there are also specific application scenarios such as the recommendation in learning objects repositories [9], in learning management systems [10], or in the students’ course recommendation [11]. However, in contrast to its wide use in other e-learning context, there have been few research efforts focused on the development of recommendation tools for POJs [12,13].
Regarding the e-learning systems research area, it is important to remark that the problem we are facing in the current research is different from the task related to users’ guiding through the learning context, which is usually handled with very traditional approaches such as Intelligent Tutoring Systems or ontologies-supported approaches [14,15]. Generally, such approaches require as input an important amount of structured information characterizing e-learning content and user activity associated to the corresponding e-learning scenario, for guaranteeing an appropriate user characterization. At this moment such information is not available for typical POJs scenarios, making very difficult the use of traditional approaches such as the previous ones. Therefore, recommender systems will be used in this context as an appropriate solution for reducing information overload in these scenarios. Specifically, we will focus on collaborative filtering recommendation [16], which is a popular paradigm that does not depend on the availability of structured information.
This paper is then focused on the development of an uncertainty-aware framework for recommending problems to be solved in POJs, supporting and guiding the users in the search of problems they should be able to solve during their knowledge acquisition, and avoiding in this way failures and frustration. The management of the uncertainty associated to the user’s behavior in the current scenario, would improve the recommendation generation process in relation to previous proposals that perform a crisp management of the user profile.
The main contributions of the paper are:
- A fuzzy based uncertainty-aware approach for recommending problems to solve in POJs.
- A data preprocessing strategy to be used on the user profile to remove anomalous behaviors that could affect the later recommendation generation.
This paper is structured as follows. Section 2 shows the needed background for the proposal presentation, including programming online judges, fuzzy tools in recommender systems, and recommender systems approaches for POJs. Section 3 presents the new uncertainty-aware proposal for problems recommendation in POJs, which also includes a novel data preprocessing approach to be used in this scenario. Section 4 presents the evaluation of the proposal, including comparison against previous related works. Section 5 concludes the current research, pointing out future works.
2. Background
This section reviews in short different concepts about programming online judges, fuzzy tools in recommender systems, and the application of recommender systems in POJ scenarios. These research topics are of particular interest regarding the current contribution.
2.1. Programming Online Judges
POJs are typically web applications that contain a large list of programming problems to be solved. Several authors have reported their experiences with online judges for supporting programming subjects. As far as we know, the first references to POJs in literature were performed by Kurnia et al. [1], presenting POJs as useful tools for evaluating source codes that solve the proposed problems. Furthermore, Leal and Silva [17] developed more portable online judges applications that can be also used on-the-fly in programming contests. More recently, Llana et al. [18] introduced new administration facilities through new POJs interfaces; and Wang et al. [2] exposed their experiences on the integration of a POJ in a practice-oriented programming course. The literature has also reported the integration of POJs with learning management systems such as Moodle [19]. Beyond these representative works, Ala-Mutka [20] and Caiza and Del Amo [21] have developed more exhaustive surveys on tools for automatic evaluation of solutions to programming problems.
The current contribution presents a fuzzy-based approach for suggesting problems to be solved by the users in this scenario, assuming that the objective of the users in this kind of applications is to solve as many problems as they can, to improve the knowledge acquisition process. These users’ goal in POJ has been previously documented by several authors [13,22,23], pointing out that this success implies a stronger degree of achievement and satisfaction [23], increasing then the learners’ efforts and performance in knowledge acquisition according to a basic pedagogical rule (“learners’ effort will increase if they are more satisfied”) [22].
2.2. Fuzzy Tools in Recommender Systems
Recommender systems are software tools focused on providing users the information that best fits their preferences and needs, in a search space overloaded with possible options. They can be classified in two big families: the content-based recommendation approaches, and the collaborative filtering-based recommendation approaches [8]. Content-based approaches are mainly focused on using item attributes for building items’ and users’ profiles, and at last generating the recommendations depending on the matching degree between the current user and all the available items. In contrast, collaborative filtering generates the recommendations by matching the current user profiles with the profile of other users, for generating the most appropriate item recommendations. This matching could be through direct similarity calculation (in the case of memory-based collaborative filtering), or through the learning of more complex predictive models (in model-based collaborative filtering) [16]. Specifically, memory-based collaborative filtering has been a popular approach regarding it reaches an appropriate balance between its simplicity, justifiability, efficiency, and stability [24]. Therefore, this approach will be used as base for the current proposal.
Furthermore, the previous two families of recommender systems approaches have been explored by using several tools taken from the soft computing fields in recommendation scenarios. Specifically, a recent survey has showed that fuzzy logic tools have been successfully used in the last few years [25], both in content-based and collaborative filtering. Specifically, such survey refers to several research works that have effectively incorporated fuzzy modelling in memory-based collaborative filtering.
Regarding the relatively large amount of recommendation approaches using fuzzy tools [25], here we will focus on such works that also incorporate memory-based collaborative filtering, being this group directly related to the current proposal. Particularly, Al-Shamri and Al-Ashwal [26] present a fuzzy-weighted Pearson correlation coefficient for collaborative recommender systems, Zhang et al. [27] introduce a recommendation approach which combines fuzzy extensions of user-based and item-based collaborative filtering, and Cheng and Wang [28] present a fuzzy recommender system based on the integration of subjective preferences and objective information, where the preferences are presented through a fuzzy linguistic model. Following similar ideas, Menhaj and Jamalzehi [29] propose a proximity-based similarity measure containing a fuzzy inference system that depends on homophily correlation and influence correlation, and Son [30] proposes a novel hybrid user-based method that integrates fuzzy similarity degrees between users based on the demographic data.
On the other hand, the recent literature has reported some efforts toward the application of fuzzy tools in e-learning recommender systems [25]. Former works propose frameworks for a personalized learning recommender system, which aims to help students to find learning materials they would need to read [31]. More recently, other works have presented a fuzzy tree-structured learning activity model and a learner profile model to comprehensively describe the complex learning activities and learner profiles [32,33]. Eventually, Myszkorowski and Zakrzewska [34] use fuzzy logic for creating groups of students with similar needs enabling to differentiate appropriately their environment features.
The works referred in this section suggest that the incorporation of fuzzy modeling could lead to positive results in collaborative filtering-based, e-learning recommendation. The proposal developed in the current paper, aims at using fuzzy tools to improve recommendations in POJs scenario.
2.3. Recommender Systems in POJs Scenarios
The POJs recommendation scenario is different from the typical e-commerce collaborative filtering scenario, because the relation user-item is much more complex in the case of POJs. Basically, while in e-commerce scenarios this relationship tends to be only modeled through a simple rating, in POJs the user usually needs several solution attempts to successfully solved the associated item (in this case the problems). Therefore, it is necessary to propose new approaches focused in this specific scenario.
However, even though the use of recommender systems have been currently expanded to several domains, there have been too few research efforts focused on the development of problems recommendation tools for POJs.
An early reported research of a recommendation approach in POJs uses a basic user-based collaborative filtering that considers the problems solved/not solved by the users which are similar to the active one [12]. The effectiveness of this method was evaluated with data collected from a POJ, proving that the collaborative filtering principle can perform well in this specific scenario.
Caro and Jimenez [35] have also explored several similarity-based approaches for recommender systems in POJs, specifically considering user-based and item-based similarity schemes. This work uses a graph representation for modelling the relationship between users and problems, and incorporates concepts from social network analysis theory to develop new recommendation strategies. The evaluation of the proposal is performed through a dataset gathered by an online judge developed by the authors.
Recently, Yera and Martínez [13] have completed a further detailed representation of the user profiles, by taking into account in addition to solved/not solved problems, the amount of previous failed attempts which occur before the final effective or ineffective problem solution. The experimental study developed in this work, proves that the development of advanced user similarity functions that consider this additional information leads to an improvement in the recommendation performance. In addition, this proposal also includes a classification scheme for users and problems according to the efforts required by users when they solve problems, for using this information later in the development of a data preprocessing step to eliminate anomalous users’ interactions that would affect the recommendation accuracy.
This recent research exposes an emerging but effective framework for suggesting problems to solve in POJs. However, as a major challenge it has to improve the reliability and flexibility of the user profiling, considering it is supported on crisp models. Therefore, the current proposal introduces a new method centered on a more flexible and reliable user profile management, through the use of fuzzy tools to support recommendation generation. Moreover, it is presented a new data preprocessing approach that couples well with the new fuzzy logic-supported proposal.
3. Problems Recommendation in Programming Online Judges Using Fuzzy Tools
In this section it is introduced the fuzzy-based recommendation framework for POJs. This framework is composed by four phases (Figure 4):
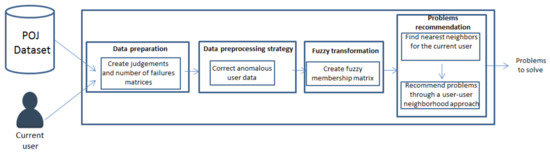
Figure 4.
Framework for problems recommendation in POJ using fuzzy tools.
- Data preparation, to put data into a suitable format for recommendation generation (Section 3.1),
- The data preprocessing strategy to remove anomalous behaviors over the initial data (Section 3.2),
- The fuzzy transformation of the POJ data, to provide flexibility to the representation of the interaction between any user and problem (Section 3.3), and
- The users similarity calculation and final problems recommendation (Section 3.4).
Table 1 summarizes the most relevant notation used in this section for our proposal.

Table 1.
Main notation used across the proposal presentation.
3.1. Data Preparation
The current proposal receives as input the past performances of all the POJ users, i.e., a set of triplets , each one representing an attempt of the user u for solving the problem p, receiving as verdict the judgement j, which could be accepted if the problem was successfully solved, or not accepted, if not. The current work will not differentiate between the several kinds of failures mentioned in Introduction section (e.g., Wrong Answer, Time limited exceeded or Runtime Error).
In order to transform these data into a suitable format for recommendation generation in the POJ context, they are converted in two different matrices, M and F, with dimensions . Being and the number of users and problems. Such matrices respectively represent the judgements and the number of failures of each user, trying to solve each problem. Specifically, if the user u has successfully solved the problem p, and otherwise. In the case of F, is the number of attempted solutions the user u has tried over the problem p, disregarding if it was finally solved or not.
3.2. Data Preprocessing Strategy
This section presents a simple but effective method for data preprocessing, to be applied on the F users’ profiles data. Initially, it is introduced a global approach that considers the amount of solution attempts provided by a user u over a problem p. This approach is then extended into an evaluation-based approach that also takes into account whether the user u is successful in the resolution of the problem p or not.
A previous work referred in Section 2.3 has also focused on preprocessing POJs users’ data [13]. However, such previously presented approach cannot be applied to the current proposal because it is based on crisp classifications of users trying to solve a specific problem (e.g., solved needing few attempts, not solved having too many attempts, and so on). In contrast, the aim of our current proposal is to avoid the use of crisp classifications, and then to perform an effective management of the uncertainty in the original POJ data through fuzzy tools. It is then necessary the use of further data preprocessing methods that could be coupled to the uncertainty-aware approach we are proposing here.
Therefore, our current work considers the outliers detection on the amount of users attempts trying to solve a specific problem, as the basic data preprocessing scheme to follow. Specifically, for each user, it is considered the problems where the number of attempts is out of the range , being the average number of attempts for user u and the average deviation of such attempts. In addition, it is considered the coefficient for adding some flexibility to the definition of the range.
For the problems which are out of this range, we propose to replace the associated amount of attempts, with the value (Equation (2)). This transformation is fully-represented in Equation (4), on the left side of the arrow appears the two conditions (problem p attempted by u, and not in the mentioned range), and on the right side appears the transformation to do. We name this strategy as the global data preprocessing approach:
Alternatively, we also propose an evaluation-based data preprocessing strategy, in which the outliers detection is done independently first for the set of accepted (solved) problems, and then for the problems attempted but at last not solved. Here, two pairs are defined for each user:
- A pair characterizing accepted problems, and
- A pair characterizing problems attempted but failed.
Here is also used with the same purpose in relation to the previous strategy:
In both cases, if the amount of attempts associated to an accepted problem p falls out of the range , for recommendation purposes its amount of previous failures is replaced by (Equation 11). On the other hand, if the problem was attempted but failed, and its amount of failures is out of the range , then it is replaced by , for recommendation purposes (Equation (12)), being both conditions checked for all the users in the POJ dataset. Here and will be always available for any user that has submitted solutions to the system, considering that they are calculated through values (e.g., the current amount of solution attempts of user u over problem p), which is always an integer value.
Finally, we will consider a third strategy that performs the data preprocessing only over the problems failed by the user. Therefore, it only applies the Equation (12), disregarding the cases in which Equation (11) is verified. This strategy is named in the rest of the paper as the failed-evaluation-based strategy.
3.3. Fuzzy Transformation
In this section is introduced a fuzzy transformation whose input is the matrix F preprocessed in the previous step, such a transformation manages in a proper and flexible way the inherent vagueness and uncertainty associated to the users’ attempts behaviour and information. This fuzzy modelling allows, as a concrete benefit to the current framework, a more robust representation of the users’ behavior. Such robustness and flexibility cannot be easily handled through other comparable soft computing approaches [25], such as Bayesian networks, Markov models, or neural networks.
To provide flexibility to the modelling of the relationship between any user u and problem p, it is then considered the fuzzy set difficult that represents the difficulty level of a problem, which is represented through the membership function presented in Figure 5. As it is typically considered in this kind of fuzzy representation, it is very difficult the predefined initialization for the parameter t in the mentioned figure. This parameter is focused on characterizing the uncertainty level associated to each possible number of failures associated to some user in relation to a specific problem. Its optimal values will be analyzed as part of the experimental section.
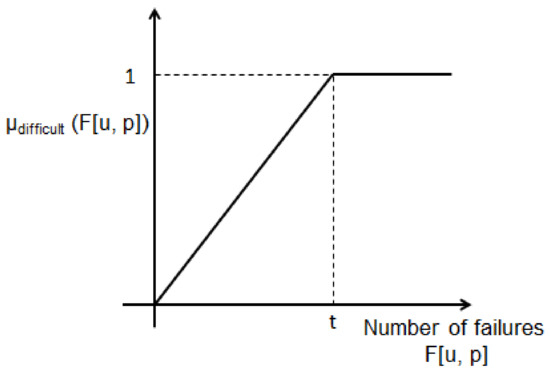
Figure 5.
Membership function for the fuzzy set difficult.
Regarding this fuzzy set, the matrix F containing the number of failures for each user is then transformed into a matrix which has the membership values associated to such kind of failures according to the fuzzy set difficult (Equation (13)).
This new matrix is actively used at the users similarity calculation in the next phase of our contribution.
This fuzzy representation through matrix assumes that all problems with more than t attempts are considered of similar difficulty for the current user (i.e., the maximal difficulty). We want to remark that this assumption could not be considered through the former matrix F, that only represents a numeric scale which lacks of flexibility. We have performed additional experiments, not included in this paper, verifying that the execution of the procedure considering outperforms the same procedure but considering F.
3.4. Users Similarity Calculation and Problems Recommendation
As a collaborative filtering recommendation approach, the current proposal needs to define a user similarity calculation scheme for considering the information available in the current scenario, in this case the M and matrices. In order to obtain such scheme, first it is necessary to consider the set of problems which solutions have been attempted (successfully or unsuccessfully), by each pair of users u and v (Equation (14)).
Afterwards, it is defined the similarity between the users u and v according to a specific problem p, taking as basis the absolute difference between the membership values in the matrix, for both users at the problem p. Specifically, it will be considered for those problems located in the set , and which have the same final verdict for both users (). In other cases, the value of will be zero. Equation (15) formalizes this similarity function.
Finally, the global similarity between two users u and v is calculated as the average value for all the values, considering all the problems p in the set (Equation (16)).
This similarity function is used by the current proposal, for finding the top k nearest neighbors for a current user u, to suggest him/her problems to solve.
These top k users are employed to calculate a score for each problem p not solved by the active user u, as the sum of the similarities between u and the neighbors that solved p (Equation (17)). At last, the top n problems p with the highest scores are recommended to u as the final recommendation list. This list can be composed by both problems previously attempted or not attempted by the user u, it will depend on problems attempted by the top k nearest neighbors.
4. Experimental Study
The evaluation of the current proposal is done through a dataset obtained from the Caribbean Online Judge, composed of 1910 users, 584 problems, and around 148,000 user attempts. This dataset has been already used in previous research works presented in the background section [13].
Considering this dataset, the training and test sets were created according to a typical splitting procedure for this kind of recommender systems scenarios [36]. Specifically, it is based on a popular hold out scheme where all the solved problems for each user are randomly splitted in two sets which are respectively appended to the training set and the test set. As a feature of the hold out protocol, this splitting procedure was developed 10 times, composing 10 pairs of training-test sets. The recommendation accuracy of each set is calculated independently, and the average of the accuracy values are then showed in the results presented in the current section.
The F1 measure will be used for evaluating the generated recommendations, being a popular evaluation criteria for the top-n recommendation generation task [36]. F1 (Equation (18)) is defined in terms of Precision and Recall measures (Equations (19) and (20)), that in addition, as it is presented in Table 2, depend on the amount of recommended problems that were solved (precision) and the amount of solved problems that were recommended (recall).

Table 2.
Possible recommendation results, regarding solved and recommended problems.
Specifically, the evaluation protocol is performed by obtaining a list of recommended problems for each user, considering training set data. Such list, as well as the solved problems at the test set, are used for calculating F1 for each user. Finally, the global F1 value is calculated by averaging the F1 values obtained for each user.
The current proposal depends on three main parameters:
- The amount of k nearest neighbors: It will be used , considering it is a value previously used in related works presented in the background section. As future works, it will be explored the behavior of the proposal for other values of k.
- The value of t, in the fuzzy membership function presented in Figure 5. This value is connected to the number of attempts where the difficulty of the problems can be considered as maximum (see Section 3.3). Therefore, it could be linked with the global average of , being the average number of attempts for user u (see Table 1). Regarding that the average of for the current data was 1.18 with a mean deviation of 1.17, here it will be considered . Specifically, it will be reported the results for , , and . Further experiments were developed considering other values (e.g., ), but their performances were under the associated to the mentioned ones.
- The value of in the data preprocessing strategy. To verify whether the flexibility in the definition of the interval for the outliers characterization leads to positive results, it will be considered (no flexibility), and (a small flexibility, considering correct values to some small amounts of attempts treated as outliers by ).
The current experiments have two main objectives. In both cases it will be considered two scenarios regarding the size of the recommendation list:
- At first it will be considered recommendation lists with large sizes, varying such size n in the range [5, 25] with step 10, and
- At second it will be considered smaller recommendation lists, varying n in the range [1, 5] with step 1.
Objective 1: Determine whether the fuzzy recommendation approach outperforms previous approaches that do not consider the management of the uncertainty associated to POJ data.
In order to accomplish this objective, we compare the accuracy (F1) of the current proposal (without the data preprocessing step), in relation to the proposals presented by Yera and Caballero [12] (UCF-OJ in the results tables), and Yera and Martínez [13], in the last case also without considering the data preprocessing step (UCF-OJ++ in the tables). It is also included a comparison against a successful approach presented at [35], specifically the problem-based approach using as similarity the weight of the relation between two problems, regarding the social network analysis-related strategies presented in the mentioned [35] (PCF-OJ in the tables). Other approaches in [35] perform worse in this scenario and then were not included here. As it was explained before, the current proposal considers , , and as possible values of the parameter t, being identified as Fuzzy-UCF-OJ in the mentioned tables.
Table 3 and Table 4 show the results of this comparison for larger and smaller recommendation lists, respectively. As it was expected the performance associated to the new proposal is similar or better than the related to the previous approaches. Specifically, the more notable improvements were obtained for in larger recommendation lists, and for all cases in smaller recommendation lists. However, for larger values of n the improvement becomes modest in relation to Yera and Martínez [13]. Furthermore, the best results of the proposal were obtained for and , leaving for a lower accuracy value.

Table 3.
Comparison between the current proposal and previous approaches, without considering data preprocessing step at Section 3.2. Large recommendation lists.

Table 4.
Comparison between the current proposal and previous approaches, without considering data preprocessing step at Section 3.2. Smaller recommendation lists.
It is also remarkable the poor performance associated to the work [35]. In this case, this approach was originally evaluated in a different dataset in relation to the used in the current proposal. Therefore, we think that its positive performance previously reported by [35], could be closely related to the nature of data where it is used. Furthermore, this mentioned work disregards the number of previous attempts as a valuable information for recommendation generation, being proved later in [13] that this information could be important in such task. We think that this fact could justify this unexpected behavior, although a future analysis should be developed to support these assumptions and to fully exploit the results exposed by [35].
Table 5 presents the statistical comparison using Wilcoxon test [36], between the previous work that performs best in the state-of-art [13], and the three evaluated proposals (with , , and ). For all cases, our proposals statistically outperform the previous work (p < 0.05).

Table 5.
Statistical analysis of the results, without considering data preprocessing at Section 3.2. Wilcoxon test (p < 0.05).
Objective 2: Determine the effect of the proposed data preprocessing strategy, in contrast to previous approaches that also consider data preprocessing in POJ scenarios.
To accomplish this objective it will be considered the use of the data preprocessing strategy previously presented in this work, to clean the original data and therefore improve the recommendation accuracy. With this aim in mind, it will be considered the values of t and previously mentioned in this section, together with the three data preprocessing schemes explained in the previous section (global, evaluation-based, and failed-evaluation-based). In the failed-evaluation-based strategy, it was only considered because other values obtained poor results and therefore they were not reported. We also consider a comparison against a previous related work that also considers data preprocessing [13], which is identified as UCF-OJ++ + preproc in the tables. Our current proposal in this case is identified as Fuzzy-UCF-OJ + preproc.
The analysis of the presented results for large recommendation lists (Table 6), at first concludes that for smaller sizes of such list the proposal introduces an improvement in the recommendation accuracy (e.g., for , the best F1 value for the proposal was 0.3674, while for the previous work was 0.3615). However, for larger sizes the improvements become more modest.

Table 6.
Comparison between the current proposal and previous approaches, considering data preprocessing. Large recommendation lists.
Additionally, it is worthy to note that although for higher values of n the best performance was obtained for the global strategy for and ; for smaller values in such Table 6 (where the improvement is more relevant), it is not a specific execution scenario that leads to the achievement of the best F1 values. Here, the best performance was obtained for the failed-evaluation-based strategy with and (in ), and for the evaluation-based strategy also with and (in ).
Globally, as an unexpected finding in large recommendation lists, it was detected that the most sophisticated data preprocessing strategy (the evaluation-based), does not necessarily lead to the reaching of a better recommendation accuracy.
In contrast to the results obtained for large recommendation lists, in the case of smaller recommendation lists with sizes lying in the range [1, 5] (Table 7), for all cases it was obtained that the more sophisticated data preprocessing strategies lead to the reaching of the best results (i.e., evaluation-based and failed-evaluation-based).

Table 7.
Comparison between the current proposal and previous approaches, without considering data preprocessing. Smaller recommendation lists.
Table 8 presents the statistical comparison using Wilcoxon test [36], between the previous work that performs best in the state-of-art [13], and four evaluated proposals which have positive performance across all the parameter settings. For all cases, our proposals statistically outperforms the previous work (p < 0.05).

Table 8.
Statistical analysis of the results, considering data preprocessing at Section 3.2. Wilcoxon test (p < 0.05).
Overall, these last results suggest that the use of techniques for preprocessing the data in the current POJ scenario can improve the recommendation accuracy, in a similar way to other preprocessing approaches for recommendation scenarios [37,38].
Beyond the two main objectives of the current evaluation, mentioned at the beginning of this section and focused on the accuracy of the proposal, we also focus briefly on analyzing the amount of data modified by the data preprocessing strategies. Table 9 presents the percentage of data modified in the data preprocessing step. In the case of the global and the failed-eval-based strategies the values were always under 17%, which guarantee a low intrusiveness level and match with values previously obtained in similar works according to this criteria [39]. For the eval-based strategy, the intrusion degree was higher.

Table 9.
Percentage of data modified during the preprocessing step.
Summarizing, the globally-obtained results suggest that the current proposal can be associated to a POJ for generating effective problems’ recommendations. Furthermore, it is important to point out that such proposal could be coupled with other very popular e-learning frameworks, being Massive Open Online Courses (MOOCs) a key example of such platforms. MOOCs and POJs have as common features, the fact that both contain e-learning content where users have to access at their personalized pace. However, while current POJs are mainly focused on programming practices, the users at MOOCs are usually learning and practising simultaneously inside the platform. Therefore, it is expected larger levels of participation in MOOCs, in relation to POJs. This increasing number of users leads to a sparser user preference dataset, which could make necessary the transformation of the current proposal, to be used in this new scenario. In fact, recent works have faced the recommendation in MOOCs through different innovative approaches such as the reciprocal recommendation [40], or the use of information from external sources [41]. Our future work will then explore these approaches to extend the current proposal to guarantee a successful tentative integration with MOOC-like frameworks. Furthermore, with the same aim in mind, it will be developed user studies for a better understanding of their motivations and needs.
In other direction, future works will also consider an adaptive modification of the size n of the top n recommendation list, varying it according to past user behavior. This approach has been successfully used in previous works such as [42].
5. Conclusions
The current contribution has been focused on the incorporation of fuzzy logic tools for proposing an approach to recommend problems to solve in POJs scenarios. This approach also incorporates a data preprocessing strategy to correct anomalous users’ behavior which could affect the recommendation generation. A relevant feature of the current work is the management of the uncertainty associated to the POJ scenario, not performed previously as far as we know. The development of the experimental evaluation of the proposal leads to the following conclusions:
- Both the fuzzy approach and the data preprocessing strategy outperform previous related works in relation to the accuracy of the problem recommendation task, according to the F1 metric.
- The best performances were globally associated to smaller sizes of recommendation list ().
- The use of more sophisticated data preprocessing strategy (the evaluation-based strategy), leads to the best results in small sizes of recommendation list ().
- The global and the failed-eval-based data preprocessing strategies modify always under 17% of the data, guaranteeing a low intrusiveness level of the proposal.
Next future work will explore: (1) the adaptive modification of the size n of the top n recommendation list, (2) the integration of the current framework in MOOCs scenarios, as well as (3) considering the behavior of the users across the time. Furthermore, we will explore the use of alternative recommendation techniques in the current scenario, that would allow a balance between recommendation accuracy, efficiency, diversity, and transparency.
Acknowledgments
This research work was partially supported by the Research Project TIN2015-66524-P, and a Scholarship for Young Doctors (2017) provided by CEATIC, UJaen, Spain.
Author Contributions
The three authors contributed to the design of the proposal and the experiments; R.Y.T. implemented the proposal and run the experiments. Eventually, the three authors contributed to the analysis of the results and to the conclusions from them.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kurnia, A.; Lim, A.; Cheang, B. Online judge. Comput. Educ. 2001, 36, 299–315. [Google Scholar] [CrossRef]
- Wang, G.P.; Chen, S.Y.; Yang, X.; Feng, R. OJPOT: Online judge & practice oriented teaching idea in programming courses. Eur. J. Eng. Educ. 2016, 41, 304–319. [Google Scholar]
- Seaborn, K.; Fels, D.I. Gamification in theory and action: A survey. Int. J. Hum.-Comput. Stud. 2015, 74, 14–31. [Google Scholar] [CrossRef]
- Bobadilla, J.; Ortega, F.; Hernando, A.; Gutiérrez, A. Recommender systems survey. Knowl.-Based Syst. 2013, 46, 109–132. [Google Scholar] [CrossRef]
- Ortega, F.; Hernando, A.; Bobadilla, J.; Kang, J.H. Recommending items to group of users using Matrix Factorization based Collaborative Filtering. Inf. Sci. 2016, 345, 313–324. [Google Scholar] [CrossRef]
- Venkatraman, S. A Proposed Business Intelligent Framework for Recommender Systems. Informatics 2017, 4, 40. [Google Scholar] [CrossRef]
- Noguera, J.; Barranco, M.; Segura, R.; Martínez, L. A Mobile 3D-GIS Hybrid Recommender System for Tourism. Inf. Sci. 2012, 215, 37–52. [Google Scholar] [CrossRef]
- Lu, J.; Wu, D.; Mao, M.; Wang, W.; Zhang, G. Recommender system application developments: A survey. Decis. Support Syst. 2015, 74, 12–32. [Google Scholar] [CrossRef]
- Sergis, S.; Sampson, D. Learning Object Recommendations for Teachers Based On Elicited ICT Competence Profiles. IEEE Trans. Learn. Technol. 2016, 9, 67–80. [Google Scholar] [CrossRef]
- Salehi, M.; Kamalabadi, I. Hybrid recommendation approach for learning material based on sequential pattern of the accessed material and the learner’s preference tree. Knowl.-Based Syst. 2013, 48, 57–69. [Google Scholar] [CrossRef]
- Sobecki, J. Comparison of Selected Swarm Intelligence Algorithms in Student Courses Recommendation Application. Int. J. Softw. Eng. Knowl. Eng. 2014, 24, 91–109. [Google Scholar] [CrossRef]
- Yera, R.; Caballero Mota, Y. An e-Learning Collaborative Filtering Approach to Suggest Problems to Solve in Programming Online Judges. Int. J. Distance Educ. Technol. 2014, 12, 51–65. [Google Scholar]
- Yera, R.; Martínez, L. A recommendation approach for programming online judges supported by data preprocessing techniques. Appl. Intell. 2017, 47, 277–290. [Google Scholar] [CrossRef]
- Badaracco, M.; Martínez, L. A fuzzy linguistic algorithm for adaptive test in Intelligent Tutoring System based on competences. Expert Syst. Appl. 2013, 40, 3073–3086. [Google Scholar] [CrossRef]
- Miranda, S.; Orciuoli, F.; Sampson, D.G. A SKOS-based framework for Subject Ontologies to improve learning experiences. Comput. Hum. Behav. 2016, 61, 609–621. [Google Scholar] [CrossRef]
- Adomavicius, G.; Tuzhilin, A.T. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions. IEEE Trans. Knowl. Data Eng. 2005, 17, 734–749. [Google Scholar] [CrossRef]
- Leal, J.P.; Silva, F. Mooshak: A Web-based multi-site programming contest system. Softw. Pract. Exp. 2003, 33, 567–581. [Google Scholar] [CrossRef]
- Llana, L.; Martin-Martin, E.; Pareja-Flores, C.; Velázquez-Iturbide, J.Á. FLOP: A User-Friendly System for Automated Program Assessment. J. Univers. Comput. Sci. 2014, 20, 1304–1326. [Google Scholar]
- Verdú, E.; Regueras, L.M.; Verdú, M.J.; Leal, J.P.; de Castro, J.P.; Queirós, R. A distributed system for learning programming on-line. Comput. Educ. 2012, 58, 1–10. [Google Scholar] [CrossRef]
- Ala-Mutka, K.M. A survey of automated assessment approaches for programming assignments. Comput. Sci. Educ. 2005, 15, 83–102. [Google Scholar] [CrossRef]
- Caiza, J.; Del Amo, J. Programming Assignments Automatic Grading: Review of Tools and Implementations. In Proceedings of the INTED 2013, Valencia, Spain, 4–6 March 2013; pp. 5691–5700. [Google Scholar]
- Nadolski, R.J.; Van den Berg, B.; Berlanga, A.J.; Drachsler, H.; Hummel, H.G.; Koper, R.; Sloep, P.B. Simulating light-weight personalised recommender systems in learning networks: A case for pedagogy-oriented and rating-based hybrid recommendation strategies. J. Artif. Soc. Soc. Simul. 2009, 12, 4. [Google Scholar]
- Regueras, L.M.; Verdú, E.; Muňoz, M.F.; Pérez, M.A.; De Castro, J.P.; Verdú, M.J. Effects of competitive e-learning tools on higher education students: A case study. IEEE Trans. Educ. 2009, 52, 279–285. [Google Scholar] [CrossRef]
- Ning, X.; Desrosiers, C.; Karypis, G. A Comprehensive Survey of Neighborhood-Based Recommendation Methods. In Recommender Systems Handbook; Springer: Berlin, Germany, 2015; pp. 37–76. [Google Scholar]
- Yera, R.; Martínez, L. Fuzzy Tools in Recommender Systems: A Survey. Int. J. Comput. Intell. Syst. 2017, 10, 776–803. [Google Scholar] [CrossRef]
- Al-Shamri, M.Y.H.; Al-Ashwal, N.H. Fuzzy-weighted Pearson Correlation Coefficient for Collaborative Recommender Systems. In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS), Angers, France, 4–7 July 2013; pp. 409–414. [Google Scholar]
- Zhang, Z.; Lin, H.; Liu, K.; Wu, D.; Zhang, G.; Lu, J. A hybrid fuzzy-based personalized recommender system for telecom products/services. Inf. Sci. 2013, 235, 117–129. [Google Scholar] [CrossRef]
- Cheng, L.C.; Wang, H.A. A fuzzy recommender system based on the integration of subjective preferences and objective information. Appl. Soft Comput. 2014, 18, 290–301. [Google Scholar] [CrossRef]
- Menhaj, M.B.; Jamalzehi, S. Scalable user similarity estimation based on fuzzy proximity for enhancing accuracy of collaborative filtering recommendation. In Proceedings of the 2016 4th International Conference on Control, Instrumentation, and Automation (ICCIA), Qazvin, Iran, 27–28 January 2016; pp. 220–225. [Google Scholar]
- Son, L.H. HU-FCF: A hybrid user-based fuzzy collaborative filtering method in Recommender Systems. Expert Syst. Appl. 2014, 41, 6861–6870. [Google Scholar] [CrossRef]
- Lu, J. A Personalized e-Learning Material Recommender System. In Proceedings of the 2nd International Conference on Information Technology for Applications, Harbin, China, 9–11 January 2004; pp. 1–6. [Google Scholar]
- Wu, D.; Lu, J.; Zhang, G. A Fuzzy Tree Matching-Based Personalized E-Learning Recommender System. IEEE Trans. Fuzzy Syst. 2015, 23, 2412–2426. [Google Scholar] [CrossRef]
- Poorni, G.; Balaji, K.; DeepthiNivetha, C. A Personalized E-Learning Recommender System Using the Concept of Fuzzy Tree Matching. Int. J. Adv. Res. Comput. Eng. Technol. 2015, 4, 4039–4043. [Google Scholar]
- Myszkorowski, K.; Zakrzewska, D. Using Fuzzy Logic for Recommending Groups in E-Learning Systems. In Computational Collective Intelligence. Technologies and Applications; Springer: Berlin, Germany, 2013; pp. 671–680. [Google Scholar]
- Caro, M.; Jimenez, G. Similar Users or Similar Items? Comparing Similarity-Based Approaches for Recommender Systems in Online Judges. In Proceedings of the ICCBR 2017, Rondheim, Norway, 26–28 June 2017; Springer: Berlin, Germany, 2017; pp. 92–107. [Google Scholar]
- Gunawardana, A.; Shani, G. A Survey of Accuracy Evaluation Metrics of Recommendation Tasks. J. Mach. Learn. Res. 2009, 10, 2935–2962. [Google Scholar]
- Castro, J.; Yera, R.; Martínez, L. An empirical study of natural noise management in group recommendation systems. Decis. Support Syst. 2017, 94, 1–11. [Google Scholar] [CrossRef]
- Castro, J.; Yera, R.; Martínez, L. A fuzzy approach for natural noise management in group recommender systems. Expert Syst. Appl. 2018, 94, 237–249. [Google Scholar] [CrossRef]
- Yera, R.; Caballero Mota, Y.; Martínez, L. Correcting noisy ratings in collaborative recommender systems. Knowl.-Based Syst. 2015, 76, 96–108. [Google Scholar]
- Prabhakar, S.; Spanakis, G.; Zaïane, O. Reciprocal Recommender System for Learners in Massive Open Online Courses (MOOCs). In Proceedings of the International Conference on Web Learning (ICWL), Cape Town, South Africa, 20–22 September 2017; Springer: Berlin, Germany, 2017; pp. 157–167. [Google Scholar]
- Symeonidis, P.; Malakoudis, D. MoocRec.com: Massive Open Online Courses Recommender System. In RecSys Posters, Proceedings of the 10th ACM Conference on Recommender Systems, Boston, MA, USA, 15–19 September 2016; ACM: New York, NY, USA, 2016. [Google Scholar]
- De Meo, P.; Quattrone, G.; Terracina, G.; Ursino, D. An XML-Based Multiagent System for Supporting Online Recruitment Services. IEEE Trans. Syst. Man Cybern. Part A 2007, 37, 464–480. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).