Visual Exploration of Large Multidimensional Data Using Parallel Coordinates on Big Data Infrastructure
Abstract
:1. Introduction
2. Related Work
2.1. Overcoming Clutter in Parallel Coordinates
2.2. Scalable Visualization Systems
3. System Overview
3.1. Distributed Processing Work-Flow
3.2. Bounding Data Transfer
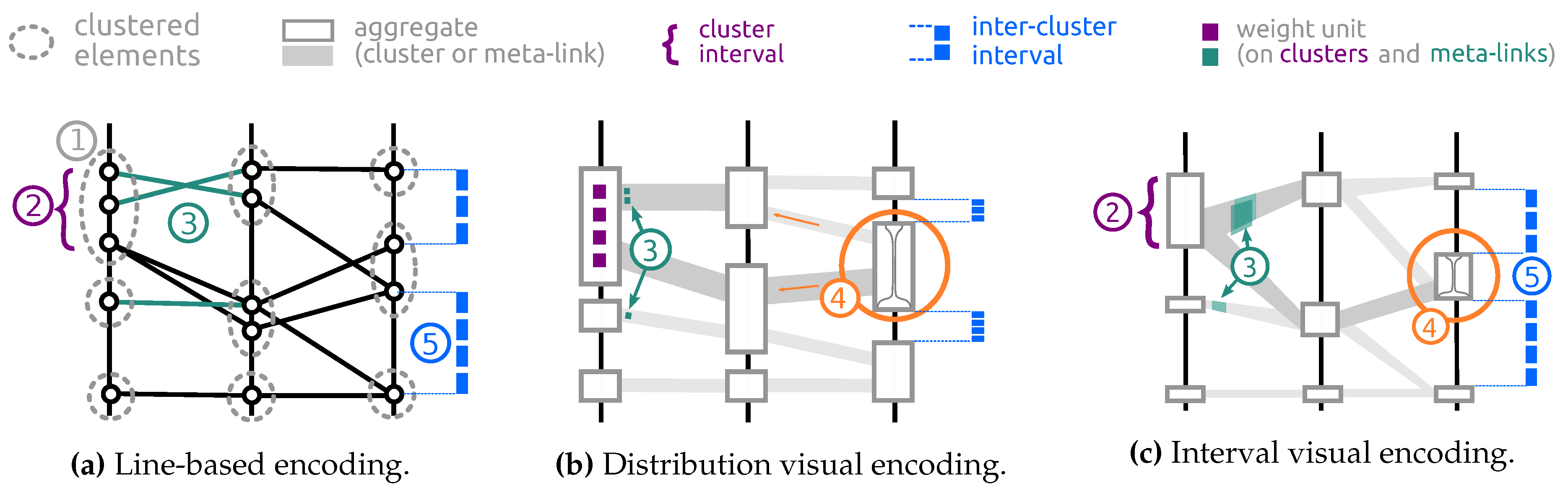
4. Abstract Parallel Coordinates Design
5. Enabling Interactivity
5.1. Tasks & Interactions
5.2. Client-Only Interaction & Parameters
- Zoom and pan: the most classical interaction tool to explore and navigate within a representation.
- Axis height: used to tune the aspect ratio of the representation by increasing or reducing the height of the axes.
- Cluster width: can help the user by emphasizing or reducing the focus on the clusters (and the histogram within).
- Meta-link thickness: changing the thickness makes possible to emphasize the meta-links between clusters rather than the clusters themselves.
- Meta-link curvature: curving and bundling the meta-link is often used to reduce the clutter, tuning the degree of curvature makes possible to optimize the clutter reduction and Meta-link visibility.
- Inter-axis spacing: increasing (or reducing) the space between axes makes possible to increase the focus either on clusters or on meta-links and changes the aspect ratio of the representation.
- Axis inversion: inverting an axis may help reducing unnecessary clutter by decreasing the number of crossings.
5.3. Server-Supported Interaction
- Axis reordering: the use of this interaction tool is to compensate the main drawback of parallel coordinates: as axes are aligned, comparisons can only be made between pairs of attributes. Furthermore, datasets with a lot of attributes are difficult to read because of the horizontal resolution limit of screens. Moving an axis within the representation implies to update the meta-links between the moved axis and its neighbors (before and after the displacement).
- Removing or adding axis: Removing an axis is used to reduce the width of the representation by hiding unnecessary axis. As the need for an attribute can change over time and with user needs, each hidden axis can be shown again.
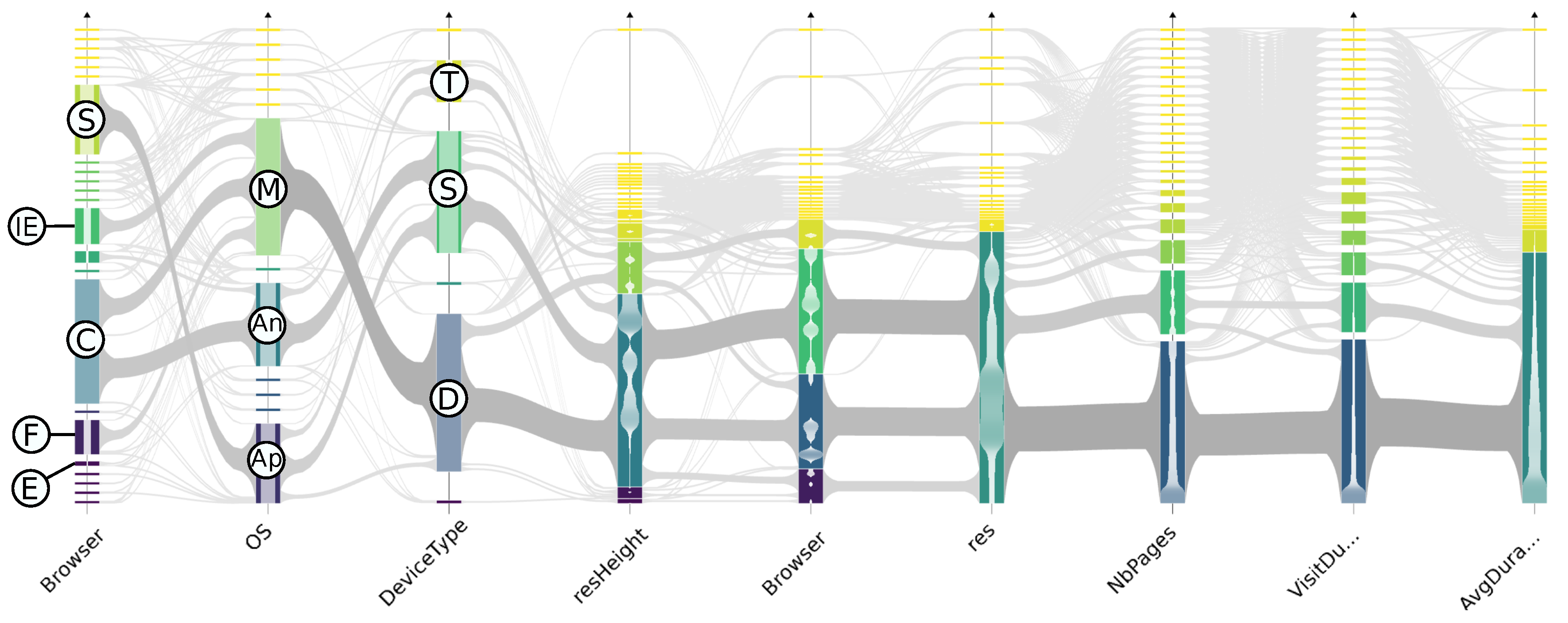
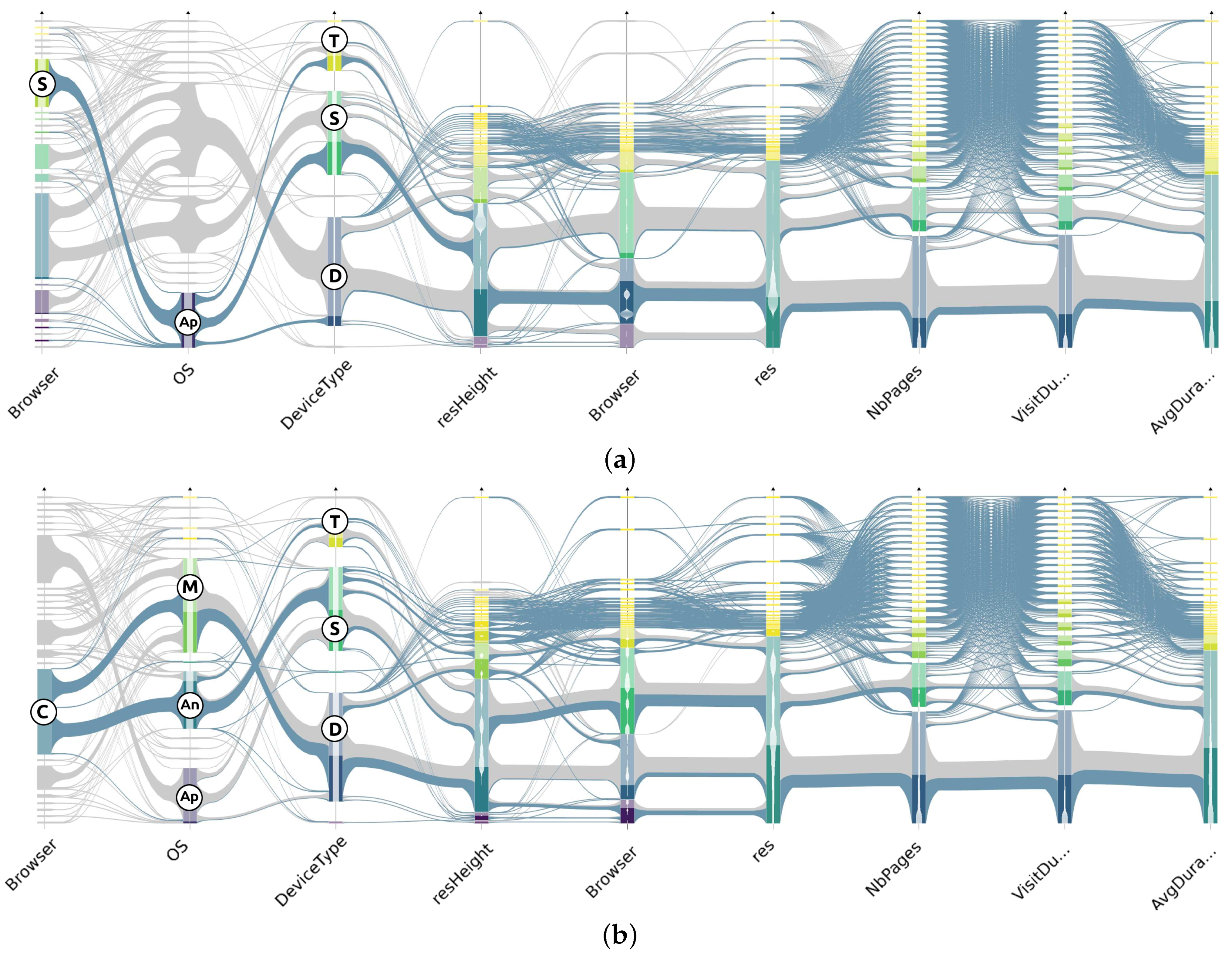
- Aggregate selection: This interaction allows to bring the focus on aggregates and emphasizes the distribution of the selected subset on the displayed attributes. The total number of meta-links for a given abstracted dataset is always less than . Hence, the maximum number of different single-aggregate selections is , considering that subset selection can be applied to any cluster or meta-link in any axis ordering. The total number of aggregates to compute for the operation is bounded by . This boundary remains reasonable for moderate k (resolution parameter) and d (number of dimensions) values.
- Compound selection: This interaction has similar effect as the Aggregate selection (see Figure 5b) but is triggered by axis sliders that define an interval of interest on each dimension and allows the selection of several groups of consecutive clusters on different dimensions at once, corresponding to set operations between aggregates’ subsets. Unlike aggregate selection, these selections cannot be reasonably pre-computed: multiple dimension criteria create a combinatorial explosion of different sub-selections. This is why we handle their computation in real-time.
6. Perceptual Scalability
6.1. Comparison to Traditional Parallel Coordinates
6.1.1. Gain Overview
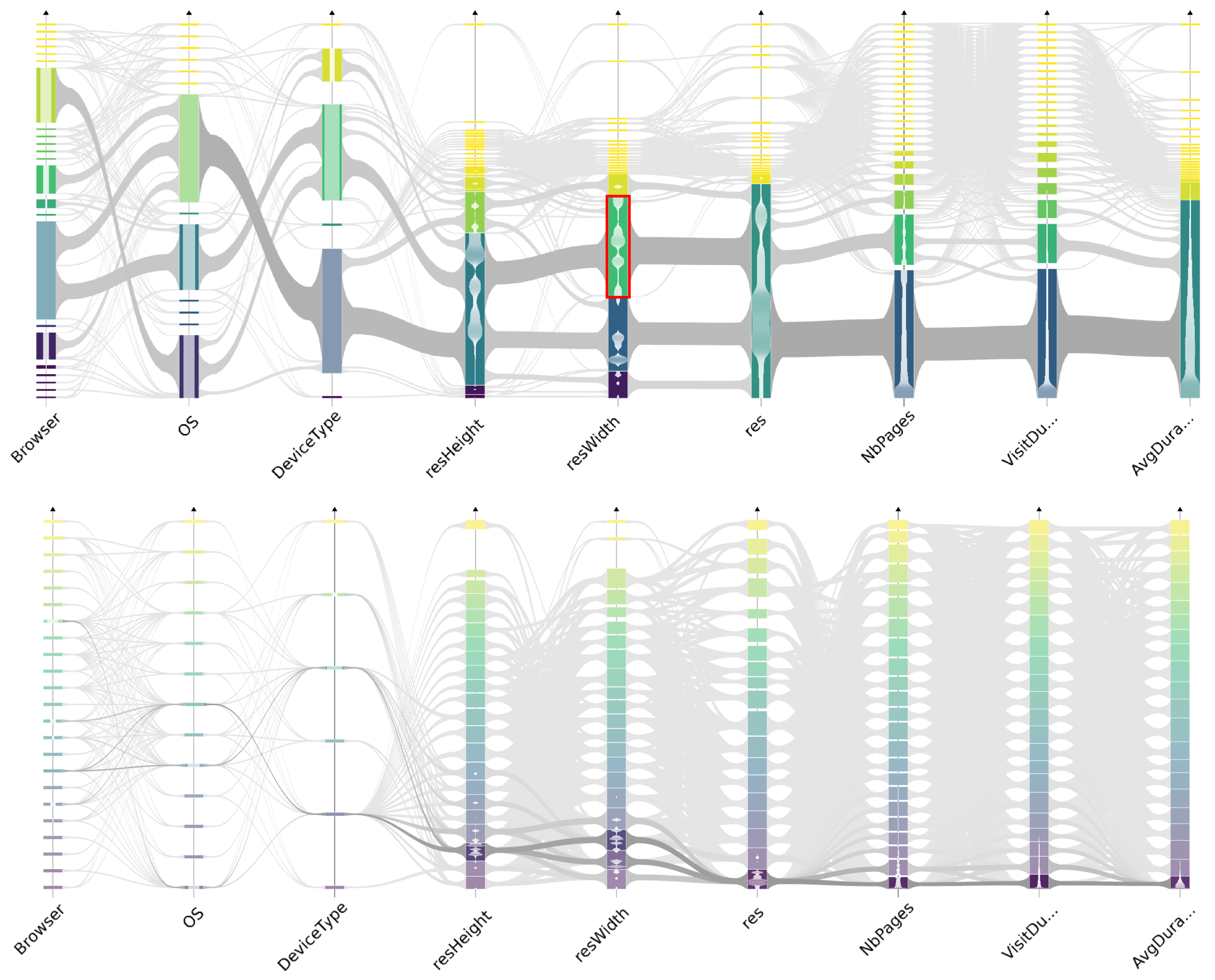
6.1.2. Subset Highlighting
6.2. Large Dataset Visual Analysis
7. System Scalability
7.1. Implementation Details
7.2. Performance Evaluation Scope
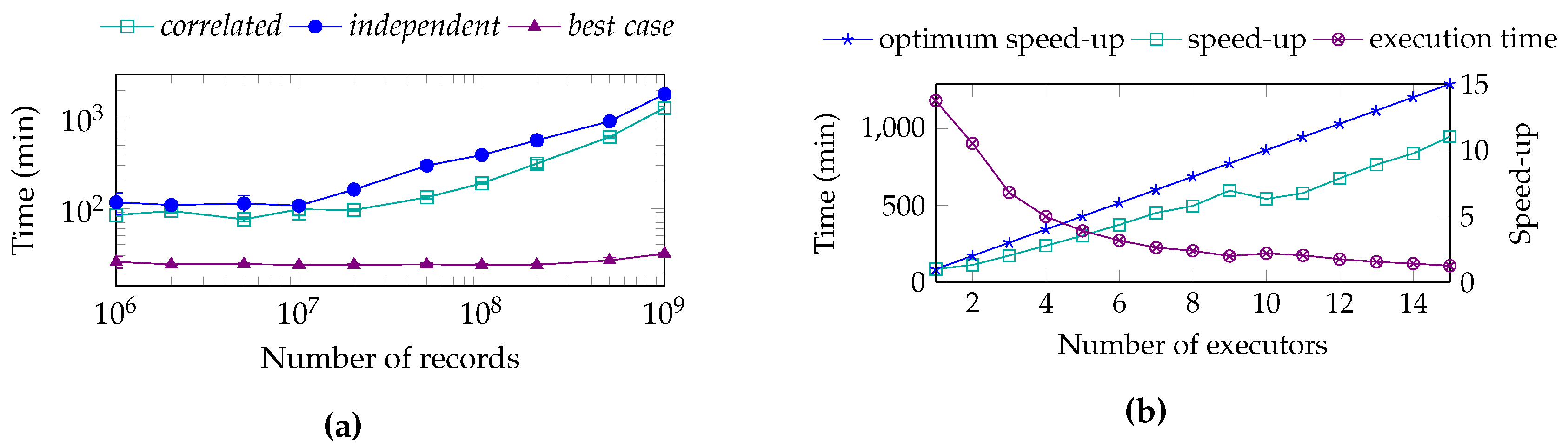
7.3. Pre-Computing Performance
7.4. Prepared Selections Query Performance
7.5. On-Demand Query Performance
7.6. Discussion
8. Conclusions & Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References and Note
- Elmqvist, N.; Dragicevic, P.; Fekete, J. Rolling the Dice: Multidimensional Visual Exploration using Scatterplot Matrix Navigation. IEEE Trans. Vis. Comput. Gr. 2008, 14, 1148–1539. [Google Scholar] [CrossRef] [PubMed]
- Alpern, B.; Carter, L. The Hyperbox. In Proceedings of the 2nd IEEE Computer Society Press: Los Alamitos Conference on Visualization ’91, San Diego, CA, USA, 22–25 October 1991; pp. 133–139. [Google Scholar]
- Kandogan, E. Star coordinates: A multi-dimensional visualization technique with uniform treatment of dimensions. In Proceedings of the IEEE Information Visualization Symposium, Salt Lake City, UT, USA, 8–13 October 2000; Volume 650, p. 22. [Google Scholar]
- Andrews, D.F. Plots of high-dimensional data. Biometrics 1972, 28, 125–136. [Google Scholar] [CrossRef]
- Inselberg, A. The plane with parallel coordinates. Vis. Comput. 1985, 1, 69–91. [Google Scholar] [CrossRef]
- Wegman, E.J. Hyperdimensional Data Analysis Using Parallel Coordinates. J. Am. Stat. Assoc. 1990, 85, 664–675. [Google Scholar] [CrossRef]
- Heinrich, J.; Weiskopf, D. State of the art of parallel coordinates. STAR Proc. Eurogrph. 2013, 2013, 95–116. [Google Scholar]
- Raidou, R.G.; Eisemann, M.; Breeuwer, M.; Eisemann, E.; Vilanova, A. Orientation-Enhanced Parallel Coordinate Plots. IEEE Trans. Vis. Comput. Graph. 2016, 22, 589–598. [Google Scholar] [CrossRef] [PubMed]
- Ellis, G.; Dix, A. Enabling Automatic Clutter Reduction in Parallel Coordinate Plots. IEEE Trans. Vis. Comput. Graph. 2006, 12, 717–724. [Google Scholar] [CrossRef] [PubMed]
- McDonnell, K.T.; Mueller, K. Illustrative Parallel Coordinates. Comput. Graph. Forum 2008, 27, 1031–1038. [Google Scholar] [CrossRef]
- Baldi, P.; Sadowski, P.; Whiteson, D. Searching for exotic particles in high-energy physics with deep learning. Nat. Commun. 2014, 5, 4308. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Cui, W.; Qu, H.; Wu, Y.; Yuan, X.; Zhuo, W. Splatting the Lines in Parallel Coordinates; Blackwell Publishing Ltd.: Oxford, UK, 2009; Volume 28, pp. 759–766. [Google Scholar]
- Nhon, D.T.; Wilkinson, L.; Anand, A. Stacking Graphic Elements to Avoid Over-Plotting. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1044–1052. [Google Scholar]
- Zhou, H.; Yuan, X.; Qu, H.; Cui, W.; Chen, B. Visual Clustering in Parallel Coordinates; Blackwell Publishing Ltd.: Oxford, UK, 2008; Volume 27, pp. 1047–1054. [Google Scholar]
- Theisel, H. Higher Order Parallel Coordinates. In Proceedings of the 5th International Fall Workshop Vision, Modeling and Visualization, Saarbrücken, Germany, 22–24 November 2000; pp. 415–420. [Google Scholar]
- Graham, M.; Kennedy, J. Using curves to enhance parallel coordinate visualisations. In Proceedings of the 7th International Conference on Information Visualization, London, UK, 18 July 2003; pp. 10–16. [Google Scholar]
- Ellis, G.P.; Dix, A.J. A Taxonomy of Clutter Reduction for Information Visualisation. IEEE Trans. Vis. Comput. Graph. 2007, 13, 1216–1223. [Google Scholar] [CrossRef] [PubMed]
- Fua, Y.; Ward, M.O.; Rundensteiner, E.A. Hierarchical Parallel Coordinates for Exploration of Large Datasets. In Proceedings of the IEEE Visualization ’99, San Francisco, CA, USA, 24–29 October 1999; pp. 43–50. [Google Scholar]
- Andrienko, G.; Andrienko, N. Parallel Coordinates for Exploring Properties of Subsets. In Proceedings of the Second IEEE Computer Society International Conference on Coordinated & Multiple Views in Exploratory Visualization, Washington, DC, USA, 13 July 2004; pp. 93–104. [Google Scholar]
- Artero, A.O.; de Oliveira, M.C.F.; Levkowitz, H. Uncovering Clusters in Crowded Parallel Coordinates Visualizations. In Proceedings of the 10th IEEE Symposium on Information Visualization (InfoVis 2004), Austin, TX, USA, 10–12 October 2004; pp. 81–88. [Google Scholar]
- Johansson, J.; Cooper, M.D. A Screen Space Quality Method for Data Abstraction. Comput. Graph. Forum 2008, 27, 1039–1046. [Google Scholar] [CrossRef]
- Johansson, J.; Ljung, P.; Jern, M.; Cooper, M.D. Revealing Structure within Clustered Parallel Coordinates Displays. In Proceedings of the IEEE Symposium on Information Visualization (InfoVis 2005), Minneapolis, MN, USA, 23–25 October 2005; Stasko, J.T., Ward, M.O., Eds.; IEEE Computer Society: Washington, DC, USA, 2005; p. 17. [Google Scholar]
- Luo, Y.; Weiskopf, D.; Zhang, H.; Kirkpatrick, A.E. Cluster Visualization in Parallel Coordinates Using Curve Bundles. IEEE Trans. Vis. Comput. Graph. 2008, 18, 1–12. [Google Scholar]
- Siirtola, H. Direct manipulation of parallel coordinates. In Proceedings of the IEEE International Conference on Visualization, London, UK, 19–21 July 2000; pp. 373–378. [Google Scholar]
- Beham, M.; Herzner, W.; Gröller, M.E.; Kehrer, J. Cupid: Cluster-Based Exploration of Geometry Generators with Parallel Coordinates and Radial Trees. IEEE Trans. Vis. Comput. Graph. 2014, 20, 1693–1702. [Google Scholar] [CrossRef] [PubMed]
- Van Long, T.; Linsen, L. MultiClusterTree: Interactive Visual Exploration of Hierarchical Clusters in Multidimensional Multivariate Data; Blackwell Publishing Ltd.: Oxford, UK, 2009; Volume 28, pp. 823–830. [Google Scholar]
- Palmas, G.; Bachynskyi, M.; Oulasvirta, A.; Seidel, H.P.; Weinkauf, T. An edge-bundling layout for interactive parallel coordinates. In Proceedings of the IEEE Pacific Visualization Symposium, Yokohama, Japan, 4–7 March 2014; pp. 57–64. [Google Scholar]
- Novotny, M.; Hauser, H. Outlier-Preserving Focus + Context Visualization in Parallel Coordinates. IEEE Trans. Vis. Comput. Graph. 2006, 12, 893–900. [Google Scholar] [CrossRef] [PubMed]
- Kosara, R.; Bendix, F.; Hauser, H. Parallel sets: Interactive exploration and visual analysis of categorical data. IEEE Trans. Vis. Comput. Graph. 2006, 12, 558–568. [Google Scholar] [CrossRef] [PubMed]
- Lex, A.; Streit, M.; Partl, C.; Kashofer, K.; Schmalstieg, D. Comparative analysis of multidimensional, quantitative data. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1027–1035. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Jiang, B.; Heer, J. imMens: Real-time Visual Querying of Big Data. Comput. Graph. Forum 2013, 32, 421–430. [Google Scholar] [CrossRef]
- Rübel, O.; Prabhat; Wu, K.; Childs, H.; Meredith, J.S.; Geddes, C.G.R.; Cormier-Michel, E.; Ahern, S.; Weber, G.H.; Messmer, P.; et al. High performance multivariate visual data exploration for extremely large data. In Proceedings of the ACM/IEEE Conference on High Performance Computing, Austin, TX, USA, 15–21 November 2008; p. 51. [Google Scholar]
- Perrot, A.; Bourqui, R.; Hanusse, N.; Lalanne, F.; Auber, D. Large interactive visualization of density functions on big data infrastructure. In Proceedings of the 5th IEEE Symposium on Large Data Analysis and Visualization (LDAV), Chicago, IL, USA, 25–26 October 2015; pp. 99–106. [Google Scholar]
- Chan, S.M.; Xiao, L.; Gerth, J.; Hanrahan, P. Maintaining interactivity while exploring massive time series. In Proceedings of the IEEE Symposium on Visual Analytics Science and Technology, Columbus, OH, USA, 19–24 October 2008; pp. 59–66. [Google Scholar]
- Piringer, H.; Tominski, C.; Muigg, P.; Berger, W. A Multi-Threading Architecture to Support Interactive Visual Exploration. IEEE Trans. Vis. Comput. Graph. 2009, 15, 1113–1120. [Google Scholar] [CrossRef] [PubMed]
- Elmqvist, N.; Fekete, J.D. Hierarchical Aggregation for Information Visualization: Overview, Techniques, and Design Guidelines. IEEE Trans. Vis. Comput. Graph. 2010, 16, 439–454. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Ahern, S.; Bethel, E.W.; Chen, J.; Childs, H.; Cormier-Michel, E.; Geddes, C.; Gu, J.; Hagen, H.; Hamann, B.; et al. FastBit: Interactively searching massive data. J. Phys. 2009, 180, 012053. [Google Scholar] [CrossRef]
- Card, S.K.; Robertson, G.G.; Mackinlay, J.D. The information visualizer, an information workspace. Proceeding of the CHI Conference on Human Factors in Computing Systems, New Orleans, LA, USA, 27 April–2 May 1991; Robertson, S.P., Olson, G.M., Olson, J.S., Eds.; ACM: New York, NY, USA, 1991; pp. 181–186. [Google Scholar]
- Godfrey, P.; Gryz, J.; Lasek, P. Interactive Visualization of Large Data Sets. IEEE Trans. Knowl. Data Eng. 2016, 28, 2142–2157. [Google Scholar] [CrossRef]
- Steinley, D. K-means clustering: A half-century synthesis. Br. J. Math. Stat. Psychol. 2006, 59, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 1996; pp. 226–231. [Google Scholar]
- Riehmann, P.; Hanfler, M.; Froehlich, B. Interactive Sankey Diagrams. In Proceedings of the IEEE Symposium on Information Visualization (InfoVis 2005), Minneapolis, MN, USA, 23–25 October 2005; Stasko, J.T., Ward, M.O., Eds.; IEEE Computer Society: Washington, DC, USA, 2005; p. 31. [Google Scholar]
- Wegman, E.J.; Luo, Q. High Dimensional Clustering Using Parallel Coordinates and the Grand Tour. In Classification and Knowledge Organization: Proceedings of the 20th Annual Conference of the Gesellschaft für Klassifikation e.V., University of Freiburg, Baden-Württemberg, Germany, 6–8 March 1996; Klar, R., Opitz, O., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 93–101. [Google Scholar]
- Ward, M.O.; Grinstein, G.G.; Keim, D.A. Interactive Data Visualization—Foundations, Techniques, and Applications; A K Peters: Natick, MA, USA, 2010. [Google Scholar]
- Auber, D.; Chiricota, Y.; Delest, M.; Domenger, J.; Mary, P.; Melançon, G. Visualisation de graphes avec Tulip: Exploration interactive de grandes masses de données en appui à la fouille de données et à l’extraction de connaissances. In Proceedings of the Extraction et Gestion des Connaissances (EGC’2007), Actes des Cinquièmes Journées Extraction et Gestion des Connaissances, Namur, Belgique, 23–26 January 2007; pp. 147–156. [Google Scholar]
- Elasticsearch, 1999.
- Börzsönyi, S.; Kossmann, D.; Stocker, K. The Skyline Operator. In Proceedings of the 17th International Conference on Data Engineering; IEEE Computer Society: Washington, DC, USA, 2001; pp. 421–430. [Google Scholar]
- Doshi, P.R.; Rundensteiner, E.A.; Ward, M.O. Prefetching for Visual Data Exploratio. In Proceedings of the Eighth International Conference on Database Systems for Advanced Applications (DASFAA ’03), Kyoto, Japan, 26–28 March 2003; pp. 195–202. [Google Scholar]







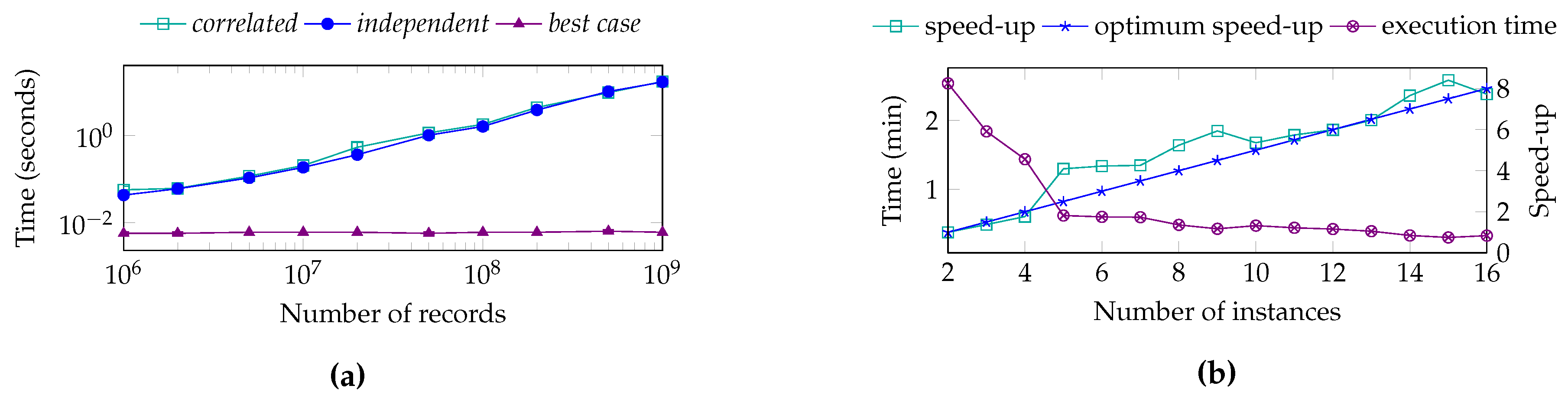
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sansen, J.; Richer, G.; Jourde, T.; Lalanne, F.; Auber, D.; Bourqui, R. Visual Exploration of Large Multidimensional Data Using Parallel Coordinates on Big Data Infrastructure. Informatics 2017, 4, 21. https://doi.org/10.3390/informatics4030021
Sansen J, Richer G, Jourde T, Lalanne F, Auber D, Bourqui R. Visual Exploration of Large Multidimensional Data Using Parallel Coordinates on Big Data Infrastructure. Informatics. 2017; 4(3):21. https://doi.org/10.3390/informatics4030021
Chicago/Turabian StyleSansen, Joris, Gaëlle Richer, Timothée Jourde, Frédéric Lalanne, David Auber, and Romain Bourqui. 2017. "Visual Exploration of Large Multidimensional Data Using Parallel Coordinates on Big Data Infrastructure" Informatics 4, no. 3: 21. https://doi.org/10.3390/informatics4030021
APA StyleSansen, J., Richer, G., Jourde, T., Lalanne, F., Auber, D., & Bourqui, R. (2017). Visual Exploration of Large Multidimensional Data Using Parallel Coordinates on Big Data Infrastructure. Informatics, 4(3), 21. https://doi.org/10.3390/informatics4030021





