Abstract
The world is undergoing rapid changes in its climate, environment, and ecosystems due to increasing population growth, urbanization, and industrialization. Numerical simulation is becoming an important vehicle to enhance the understanding of these changes and their impacts, with regional and global simulation models producing vast amounts of data. Comprehending these multidimensional data and fostering collaborative scientific discovery requires the development of new visualization techniques. In this paper, we present a cyberinfrastructure solution—PolarGlobe—that enables comprehensive analysis and collaboration. PolarGlobe is implemented upon an emerging web graphics library, WebGL, and an open source virtual globe system Cesium, which has the ability to map spatial data onto a virtual Earth. We have also integrated volume rendering techniques, value and spatial filters, and vertical profile visualization to improve rendered images and support a comprehensive exploration of multi-dimensional spatial data. In this study, the climate simulation dataset produced by the extended polar version of the well-known Weather Research and Forecasting Model (WRF) is used to test the proposed techniques. PolarGlobe is also easily extendable to enable data visualization for other Earth Science domains, such as oceanography, weather, or geology.
1. Introduction
The world is undergoing significant environmental and global climate change due to increasing population growth, urbanization, and industrialization [1,2,3,4]. These changes [5,6,7] are exemplified in the Earth’s polar regions, as evidenced by melting sea ice [8] and glacier retreat [9], which significantly affect the living environment of wildlife and biodiversity in these areas. To better understand these climate phenomena and their driving mechanics, there exists an urgent need for new data, techniques, and tools to support scientific studies and the development of effective strategies to mitigate their negative influences [10].
Climate simulation has been considered a critically important means to address the aforementioned research challenges [11]. Global or regional climate models, such as WRF (Weather Research and Forecasting), are often used by the climate modeling community to unveil the historical climate trajectory and make projections for future changes. Through long-duration computations, these simulation models often generate very large climate data [12]. It is estimated that worldwide climate simulation data will reach hundreds of exabytes by 2020 [13]. Besides falling into the category of “big data” due to its size, climate data is multidimensional in nature. In other words, the time-series data not only spread across a geographic area on the Earth’s surface (horizontal dimension), but they also occupy different altitudes with varying pressure levels (vertical dimensions).
Scientific visualization is considered an effective vehicle for studying such complex, big volume, and multiple dimension data [14]. By providing visual representations and analytics, visualization has the capability to validate hypothesis, uncover hidden patterns, and identify driving factors of various climate and atmospheric phenomena [15]. Nonetheless, the scientific visualization community still faces challenges in efficient handling of big data, the complex projection between the viewport coordinate system and the raw geospatial dataset, and finding innovative ways to present the voluminous data in order to reveal hidden knowledge. With the widespread adoption of Web technology, there is also an urgent demand for a Web-based visualization platform to allow web-scale access, visualization, and analysis of spatial dataset.
This paper introduces our PolarGlobe solution, a Web-based virtual globe platform that supports multi-faceted visualization and analysis of multi-dimensional scientific data. Built upon the popular Cesium 3D globe system, the PolarGlobe tool has the advantage of being seamlessly integrative with Web browsers, eliminating the need to install or configure any plug-ins before data viewing. In addition, an emerging graphics language (WebGL) is utilized to operate the GPU (Graphics Processing Unit) and develop functions for data rendering. The remainder of this paper is organized as follows: Section 2 reviews relevant works in the literature; Section 3 introduces the visual analytical techniques being applied to the PolarGlobe system; Section 4 demonstrates the PolarGlobe GUI (graphic user interface); Section 5 describes a number of experiments to test system performance; and Section 6 concludes this work and discusses future research directions.
2. Literature Review
In this section, we organize the review of previous works from two perspectives: (1) previously established visualization platforms and (2) key techniques employed to support such visualization.
2.1. Popular Visualization Platforms for Climate Research
Visualization has a long tradition in supporting climate research [16]. Standard 2D presentation techniques such as time/bar charts, 2D maps, and scatterplots are most frequently used in analyzing climate data [17]. Popular visualization tools, such as UV-CDAT (Ultrascale Visualization Climate Data Analysis Tool) [18], provide great support for data regridding, exploratory data analysis, and parallel processing of memory-greedy operations [19]. However, these tools suffer great limitations in the context of cyberinfrastructure and big data science [20]. For instance, users need to download and setup the software in order to get access to the tools. To visualize a scene, users also need to write corresponding (python) code, which often requires a long learning curve. As climate simulation data is becoming multi-dimensional, the lack of support in multi-dimensional data analysis poses many challenges for visualizing these data, especially those with time-series stamps. Moreover, in most tools, data is visualized as an individual piece without being integrated with terrain and morphology data to enhance understanding.
Overcoming these limitations has become a significant research thread of virtual globe visualization. Inspired by the vision of “Digital Earth” (by former US vice president Al Gore) [21], a number of virtual globe tools have been developed to digitally depict our living planet. Popular ones include Google Earth [22], NASA WorldWind (National Aeronautics and Space Administration; [23], and Microsoft Virtual Earth [24]. Using these tools, climate data visualization can be integrated into the actual terrain and Earth scene. Sun et al. (2012) developed a geovisual analytical system to support the visualization of climate model output using Google Earth [25]. Varun et al. [26] developed iGlobe, an interactive visualization system that integrates remote sensing data, climate data, and other environmental data to understand weather and climate change impacts. Helbig et al. [27] presents a workflow for 3D visualization of atmospheric data in a virtual reality environment. HurricaneVis [28] is a desktop visualization platform that focuses on scalar data from numerical weather model simulations of tropical cyclones. Leveraging the power of graphics cards, multivariate real-time 4D visualization can also be achieved [29]. These works demonstrate a great advantage in data visualization over traditional approaches that rely solely on 2D maps and scatter plots. However, most of these applications are desktop-based or require pre-installation and configuration, limiting their widespread use and adoption by Internet users.
As cyberinfrastructure evolves, research that develops web-based visual analytical tools has gradually increased. For instance, Fetchclimate [30] and the USGS (United States Geological Survey) National Climate Change Viewer (UCCV) [31] provide solutions for environment information retrieval and mapping. Similar online visualization applications have also been applied to other geoscience disciplines such as hydrology [32,33,34], oceanography [35], and polar [20,29], etc. Open source packages, such as Cesium [36] or NASA’s new WebWorldWind [37], are also exploited to construct web-based environmental applications [38,39]. Though these existing studies provide a satisfying solution to 2D spatiotemporal data visualization, they have very limited capability at visualizing high-dimensional spatiotemporal climate data.
2.2. Key Techniques in Multidimensional Visualization of Spatial Data
Spatiotemporal multidimensional data visualization is a hotspot in the field of scientific visualization. The existing work varies from organizing and visualizing time-varying big data to applying multiple visual analytic techniques for planning, predicting, and decision-making. There are two key issues in developing an efficient web-based visual analytic tool.
The first is efficient management and transmission of big data from the server to client end. With the popularity of ‘big data’ in both academia and industry, increasing research focuses on managing big data for scientific visualization [40,41]. Others address big data usage on visualization in emerging environments [42,43]. In climate study, Li and Wang [39] proposed a video encoding and compression technique to efficiently organize and transmit time-varying big data over successive timestamps.
The second is exploiting visualization techniques to provide real-time realistic visualization. Wong et al. [44] assembled multiple information visualization and scientific visualization techniques to explore large-scale climate data captured after a natural phenomenon. Li et al. [45] implemented a volume rendering technique for visualizing large-scale geosciences phenomena, i.e., dust storms. An octree data structure, in combination with a view-dependent LOD (Level of Detail) strategy, is used to index 3D spatial data to improve rendering efficiency. Liang et al. [46] further improved this method to introduce a volumetric ray-casting algorithm to avoid loss of accuracy. The algorithm avoids over- or under-sampling when converting geospatial data from a spherical coordinate system to a Cartesian coordinate system for visualization. To boost rendering performance, GPU is always employed for parallel rendering [47,48]. In order to present volumetric data from multiple facets, these techniques need to be extended to include more novel visual effects for a comprehensive visual exploration.
In the next section we describe, in detail, our proposed techniques, including an enhanced octree model to support efficient visualization and analysis of climate data in a cyberinfrastructure environment.
3. Methodology
3.1. Three-Dimensional Data Volume Rendering
The goal of this section is to explain the creation of a panoramic view of climate variables on and above the Earth’s surface. To accommodate the multivariate characteristics of climate data (horizontal and vertical), we developed a volume rendering technique to present the variances in the north polar region and its upper air [49]. To take full advantage of highly detailed datasets such as reanalysis data, point clouds visualization is adopted. To support this visualization strategy, a value filter and a region filter were also developed to provide more perspectives and enable a better understanding of various climate phenomena. Challenges in efficiently transferring large datasets between client and server, and rendering big data in the client browser, were also addressed. For instance, there are almost 4 million points at a single timestamp in the climate simulation data we adopted [50]. To overcome these obstacles, an enhanced octree-based Level of Detail (LOD) method is utilized in the point cloud visualization.
The LOD strategy is adopted, because it is a widely-used technique in multi-dimensional visualization that decreases total data volume while boosting rendering and data transfer speed at the same time [51]. Based on the principle that the further the data is observed, the fewer details will need to be shown, the loading and rendering of 3D volume data can be greatly improved. When the octree-based LOD is applied to 3D volume visualization, the data size is reduced by a power of eight (23). Because our goal is to realize Web-scale visualization for multi-dimensional data such that people from any place of the world can access the system, the octree is implemented on both the backend (Web server side) and frontend (client browser side). The server side is responsible for preparing the LOD data to respond to clients’ requests. The frontend deals with acquiring the proper LOD data and rendering them in the browser using WebGL (Web Graphics Language). We describe the implementation of these two parts in detail below.
3.1.1. Data Preparation at the Server Side
Though the octree can be built from original data and kept in the memory of the server for responding to requests from clients from time to time, this is not only time consuming, which will keep the user waiting longer to acquire the LOD data, but it is also a great burden on the server’s memory, especially when the data volume is big or multiple data sources are in use. To overcome these limitations, we adopted a strategy that pre-processes the original data and produces different LOD data as files. In order to prepare the LOD data, the first task is to decompose the original data volume (which consists of numerous points distributed in a 3D grid) into multiple special cubes. These cubes are considered special because their length, measured by the number of points along one side, should be a power of 2. This length will be evenly cut along each side of the cube by 2. Such decomposition ensures an evenly increasing ratio of data size along with the increasing LOD. The iterative decomposition process continues until every cube contains only one point—the highest LOD. The following equation can be used to determine the length of the initial cube:
where M is the minimum size amongst the length, width, and height of the original data volume, and floor() is a function to receive the integer part of a floating number, given any positive input.
In Equation (1), L is the minimum power of a power of 2 number that is no smaller than M. After identifying the size of the initial cube, the decomposition process starts by dividing the cube into eight equally sized sub-cubes. The sub-cubes generated after the first decomposition are called the roots of the octrees. For convenience, let us state that the roots are at level 0. Because each cube is represented by one data value, a generalization process should be invoked to derive this value. A typical approach is to average the values on all the grid points falling in the cube. This process requires extra storage in order to store the generalized value for the cubes that share the same root.
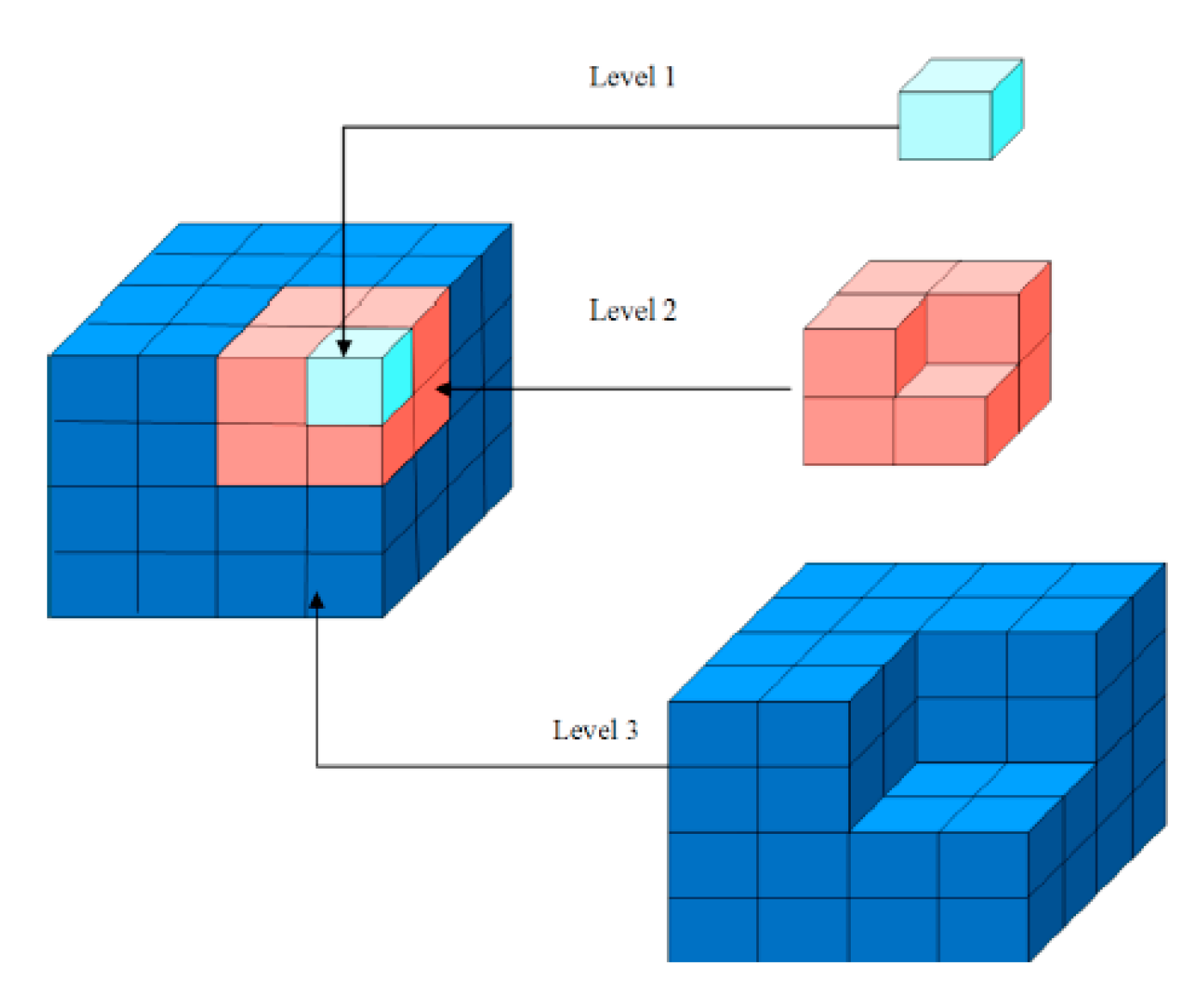
To address this data challenge, we propose a new octree multi-level storage strategy, or differential storage, to reduce data redundancy across octree layers. The idea comes from differential backup that saves only the changes made in a computer system since the last backup. For our purposes, each higher layer of the octree only stores the differential or incremental dataset(s) from its precedent layers. These values are a sample from the original data points rather than averaged from them. Figure 1 demonstrates a design of the proposed octree with differential storage support. This data structure saves substantial storage space. For example, we estimate saving approximately 14% of the storage space for a three-layer octree using this data structure.
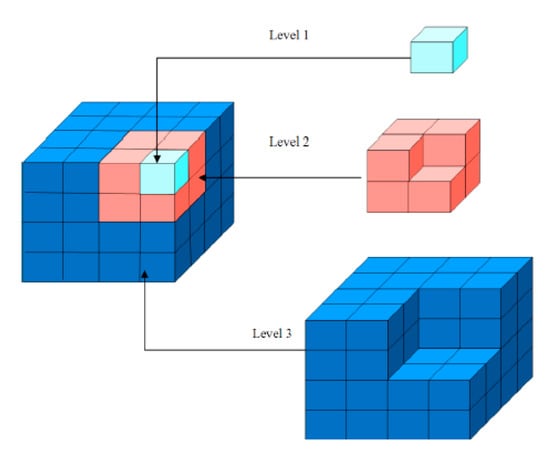
Figure 1.
Differential-storage-enhanced octree model.
Once the octree model is established, all cubes and sub-cubes are indexed. The root contains eight initial cubes with index from 0 to 7. As the decomposition continues, every cube is split into eight sub-cubes of the same size until the LOD reaches the highest level n. The naming of each sub-cube follows the patterns of (1) the name of its parent cube+; and (2) its index (from 0 to 7). Hence, the sub-cubes with the same root have the same prefix in its name. The strategy used to record data is what distinguishes levels 1 and higher from level 0. At level n, all the generalized data derived from the same roots are written in a single file whose filename contains the level number and the index of the root recorded at level n−1. Those sub-cubes with no grid points are ignored. Using this strategy, the web server can rapidly locate the LOD data with a specified region and level. It repeats the process applied to level 1 until level n is reached. It then splits every cube produced in level n−1 to get 8 n sub-cubes where no more than one point in a cube exists. The generalized data values, as well as some necessary metadata (such as the range of value variation and the maximum LOD), are recorded in a single file for data initialization at the client side.
3.1.2. Data Rendering on the Client Side
Thus far, LOD data is prepared at all levels. The server will return the data by specifying the root index and the LOD as parameters in the request. The client side is now able to access any data it needs. The workflow at the client side starts with retrieving the data at level 0 from the server for initialization. Using the indices recorded in level 0 data, the whole data volume is split up into multiple cubes (differed by their indices) for rendering, management, and further operation. If the cubes have been initialized or a user changes the view perspective, the rendered data will be refreshed by updating the LOD information in each cube. Since the location of each cube is known, the distances from the viewport to all cubes are a fixed number at all levels. For a given cube, the data at which LOD should be rendered is decided by the below equation:
where dist denotes the view distance, and C is a constant value which needs to be adjusted by user experience.
Applying this equation, the data with higher details are loaded as the view distance decreases. Giving the calculated level and its own index, the cube sends a request to the server and retrieves the desired LOD data. Once a request is sent, the level in the unit is marked and temporarily cached in memory for future rendering purposes. This way, repeated requests for the same data are avoided.
Data loading and rendering performance are greatly enhanced with the proposed LOD strategy, especially when the data is observed from a long distance. If the view distance becomes very short or the observer dives inside the data cubes, however, a large portion or even all of the data is loaded at the highest LOD. This may keep the user waiting a long time and can greatly impede the efficiency of visualization. To resolve this issue, we developed a perspective-based data clipper to eliminate the invisible parts of the data.
The data clipping strategy adopts popular interactive clipping techniques in volume visualization [52] and the WebGL implementation of clipping pixels, in order to remove the data not visible in the current viewport. Benefitting from the decomposition of the whole data volume, the clipping process can be achieved by checking whether the centers of the decomposed cube are within the viewport by applying the following equation:
where ep denotes the vector consisting of the visual coordinates of the position at the center of a decomposed cube with a number 1 appended (e.g., [x, y, z, 1]). VP is the view-projection matrix with a 4 × 4 dimension, produced by how a user views the scene and the view projection setting. cp is the desired vector, from which whether a point is within the viewport or not can be determined.
For convenience, the elements of the vector are sequentially marked as xclip, yclip, zclip, and wclip, and the following calculation is performed:
If xviewport, yviewport, and zviewport both range from −1 to 1 (boundaries excluded), the decomposed units are determined to be visible. In this case, the data point is reserved and rendered. The data points that do not fall in the above range are disregarded.
3.2. Data Filtering
This point cloud visualization provides an overview of the entire multi-dimensional data volume. By adjusting the size or transparency of the points, the internal variation of the data may also be observed. However, when millions of points are being simultaneously rendered in the viewport, the information that a user needs may still be hidden. In order to uncover important details of the data, we suggest three strategies to filter the data points and reveal only the data variables of interests to end-users in both space and time.
First, a value-based filter is introduced in the system. This approach has a great advantage for 3D visualization. Specifically, filtering the value range requires that only part of the data points need to be rendered. For example, high temperature values can be filtered out to allow scientists to focus on analyzing cold spots. These cold spots or regions will form a particular shape and temperature variance will be differed by colors. This function allows users to investigate data variation by colors as well as by shape.
Second, a filter of data by regions is developed to regional studies as well as global studies. For instance, geographical coordinates of the boundary information can filter data within a country or state. To accomplish this task, point-in-polygon operations are performed for each data point in the original dataset after orthogonal projection. However, this may present a problem when the boundary polygons are complex, as computing time for determining the relationship of a polygon and a point substantially increases as the number of the vertices in the polygon increases. In order to reduce the computing burden, a generalization process is applied to the polygon before the point-in-polygon calculation.
In our work, the Douglas-Peucker line simplification algorithm is adopted [53]. The algorithm performs as follows: (1) for every two vertices in the polygon that share the same edge, if the distance between them is under a threshold, they will be merged into a new one—the midpoint of the shared edge; (2) Step 1 is repeated until there are no pairs of points whose interval is less than the threshold. It should be noted that while this simplification process helps accelerate the filtering speed, it could also affect result accuracy. Our preliminary experiments show that with the proper threshold, the time cost of filtering regional points is greatly reduced with little impact on filtering precision.
The last filter targets the vertical variation. Drawing lines on the surface of Earth, the values on the vertical slices of the data volume along those lines are extracted and rendered in a special way. This process is explained in the following section.
3.3. Vertical Profile Visualization
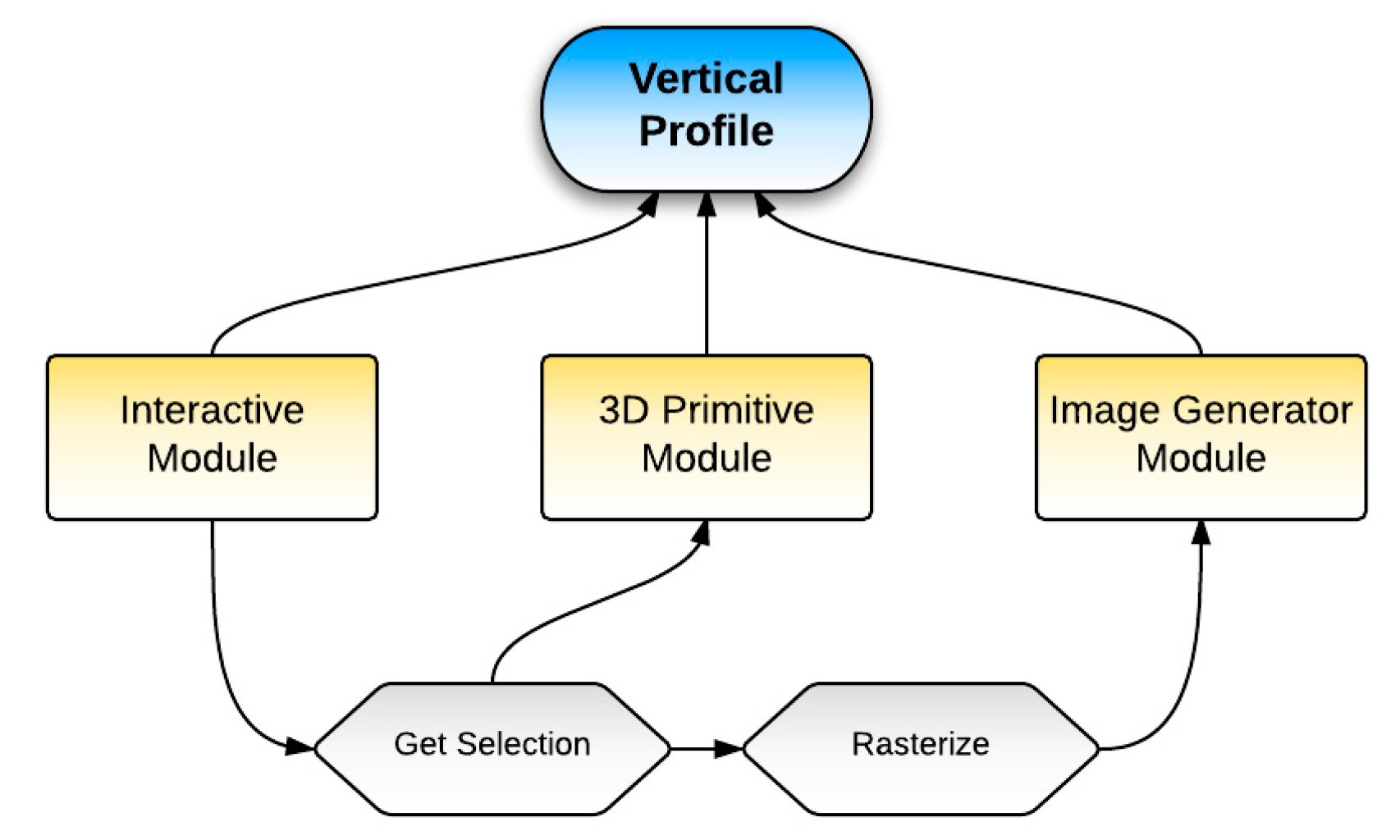
A vertical profile image provides a cross-sectional view of a cubical data. x dimension of the cross-sectional view is a user-defined path along the Earth’s surface, and y dimension is normally elevation for spatial data. Interactive vertical profile visualization has the capability to intuitively demonstrate the inner structure and information inside a 3D volume, and reveal the variation of a specific factor in a vertical direction (perpendicular to the Earth’s surface), which is very helpful in climate research [54]. Generally, this function is developed in three steps. The first is a response to user requests that involve drawing a polyline on the Earth’s surface, indicating a trajectory of interest, e.g., along the east coastline of Greenland. The second is generation of an image according to the original three-dimensional data. Each pixel in the image displays the climate variable values at coordinates (x, z), where the x-axis is the location along the trajectory, and the z-axis shows the location changes on the 29 vertical pressure levels of the raw data. The third step is displaying the image on the ground along the user-defined polyline. Three software modules are developed to handle the above tasks.
The Interactive Module (Figure 2) handles user input. The Image Generator Module acquires the data defined from the user input and converts it to a smooth image, showing the variation from ground to space as well as along the drawn polyline. The 3D Primitive Module projects the image from the Image Generator Module on a blank wall created on the surface of the virtual Earth.
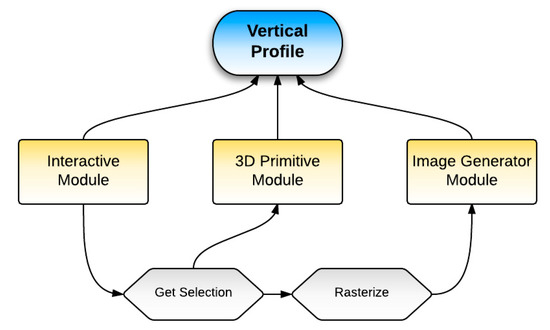
Figure 2.
The workflow for creating a vertical profile.
We built the Interactive and 3D Primitive Modules on the open source library Cesium—a very popular virtual globe platform that supports the rendering of spatial data in a 3D virtual space. The following algorithm was developed to generate the image demonstrating the change in some variables along a specific path inside the data cube.
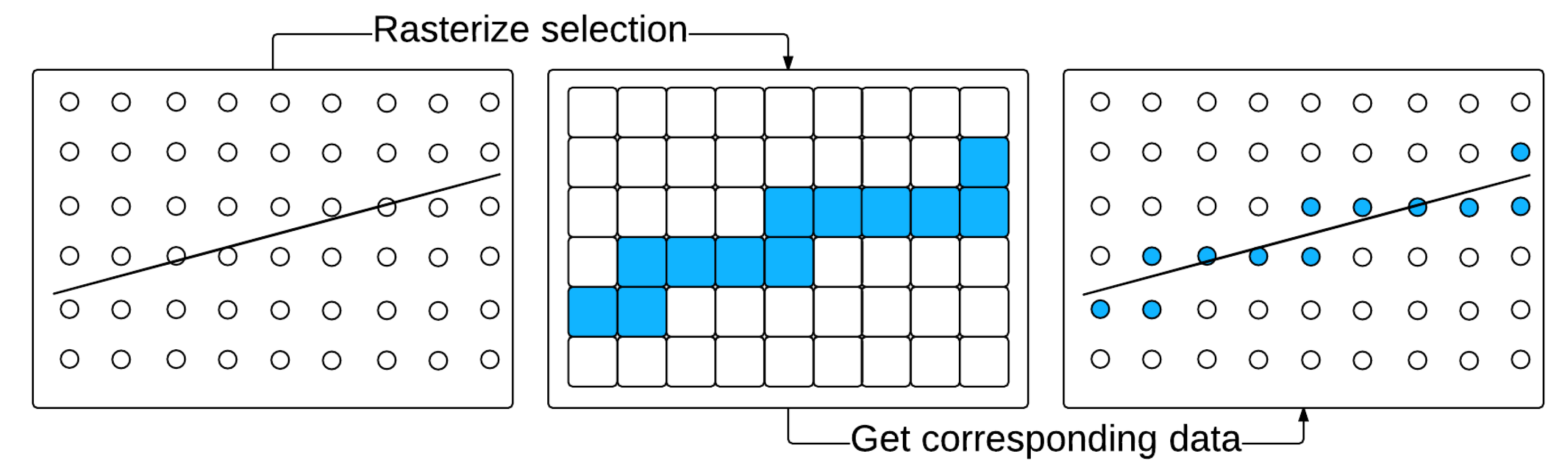
Given that 3D gridded data is being visualized, a horizontal slice of the data means that the vertical dimension is the value distribution in a given study area, identified by latitude and longitude, at a certain altitude. Note that some data might use pressure levels as the vertical dimension, but can be converted to altitude during preprocessing, if preferred. When we look at the data cube, it would look like columns of data points neatly standing on the Earth’s surface. When a path of interest is drawn on the Earth’s surface, we first need to determine all the nearby columns as the gridded data is not continuous on a 2D surface. The key idea is to rasterize the polyline representing the path. Figure 3 shows an example. Taking a horizontal data slice as a reference, the user-input vector is rasterized on a grid. The highlighted data points falling on the path of interest are extracted for all horizontal data slices to generate the vertical profile image.
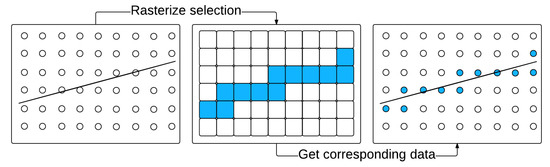
Figure 3.
Rasterization of a user-input trajectory of interest on the Earth’s Surface.
Rasterization is valid only when all the columns are evenly distributed in a grid, which means there is a specific map projection applied to the data. However, the projection of the input polyline may not always be the same as the one adopted in the original data source. For example, the polyline retrieved using the API was provided by Cesium is WGS (World Geodetic System) 84 [55], while the data used for our study is an azimuthal equidistant projection [56]. In this case, a re-projection process is required before rasterization. The projection information of a data source can usually be found in its metadata.
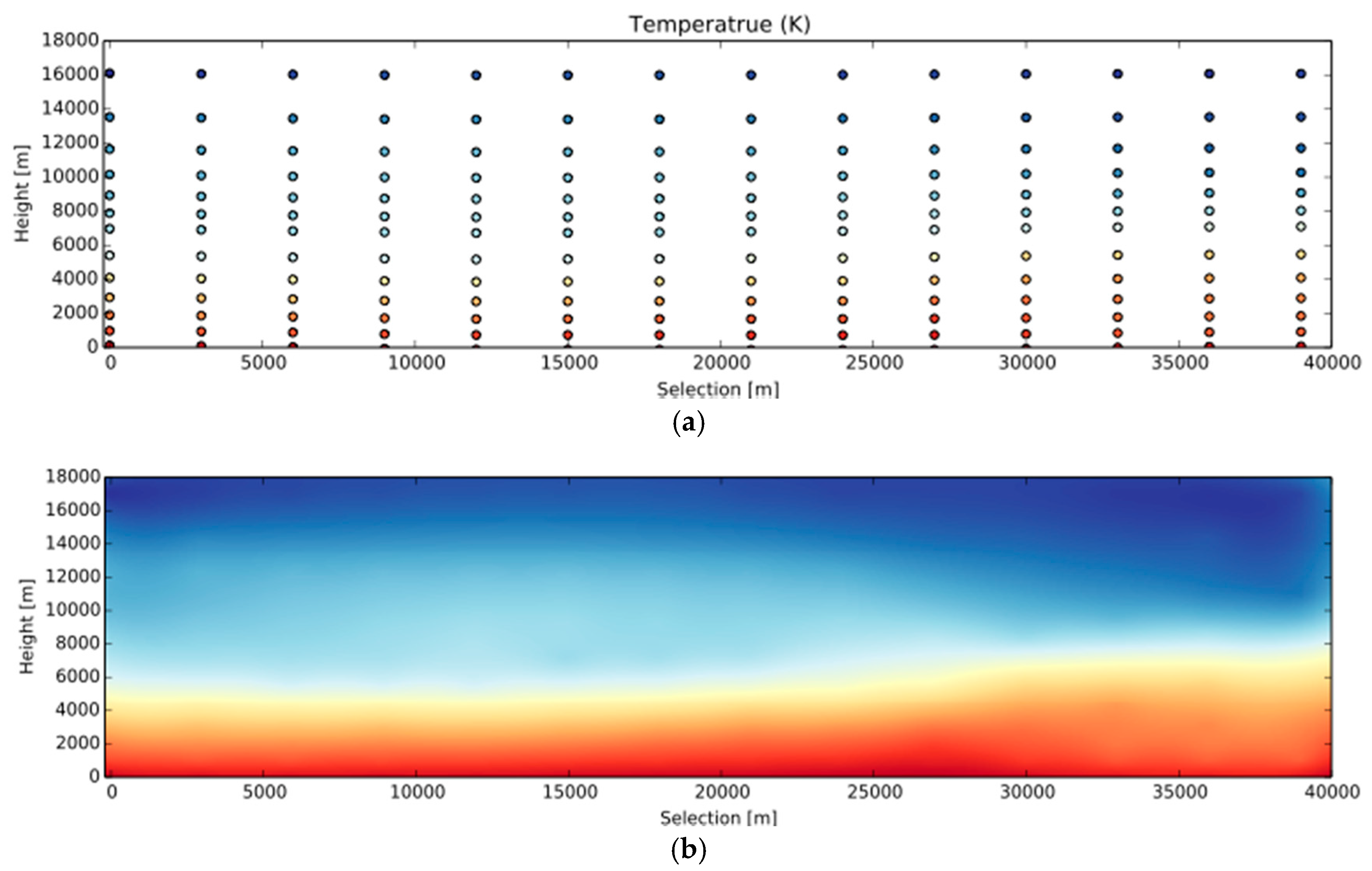
The next task is to sequentially project the selected columns on a planar coordinate system, whose axes stand for elevation and distance. In this way, a 2D grid can be built. This step unfolds the wall and lays it on a plane (if a user draws a complex path rather than a straight line). Figure 4a shows an example of the selected data points along a user chosen path. Only one image is produced and projected on 3D primitives, rather than multiple images that correspond to all the facets of the folded wall. In this new planar coordinate system, the distance between every two neighboring columns should be the same as the one in the 3D space. The great circle distance between the locations where the columns stand determines this. A final image (Figure 4b) is then generated by interpolating all the data points falling in the image region to generate the raw image matrix. Finally, this matrix is converted to a RGB image with proper color mapping.
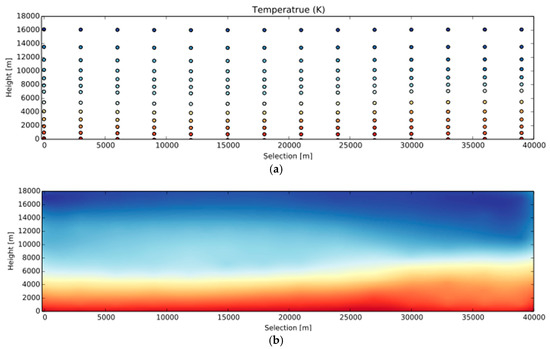
Figure 4.
An example of generating a vertical profile image through interpolation: (a) An illustration of selected data points (clustered as columns) along a path on the Earth’s surface; (b) Color-coded image after 2D interpolation (temperature increases from blue to red).
4. Graphic User Interface
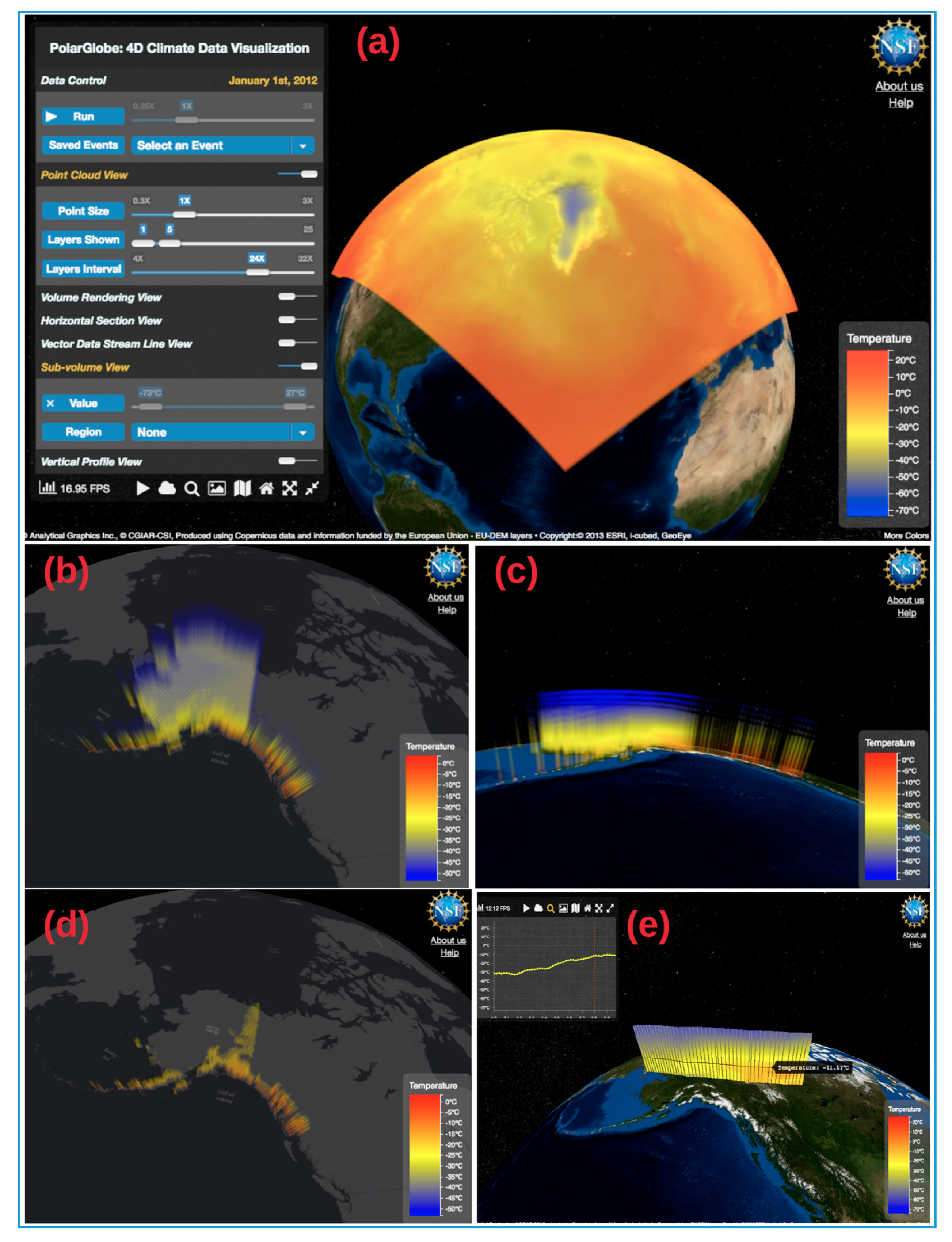
Figure 5 demonstrates the PolarGlobe GUI. The climate data used in the visualization is the air temperature output from the Polar version of the WRF Model. This data covers 20 degree latitude and north, and contains 29 vertical layers differed by pressure levels. The spatial resolution is 30 km. By applying a predefined color map, this panoramic view of data clearly shows the change in temperature with a cold spot on top of the Greenland ice sheet.
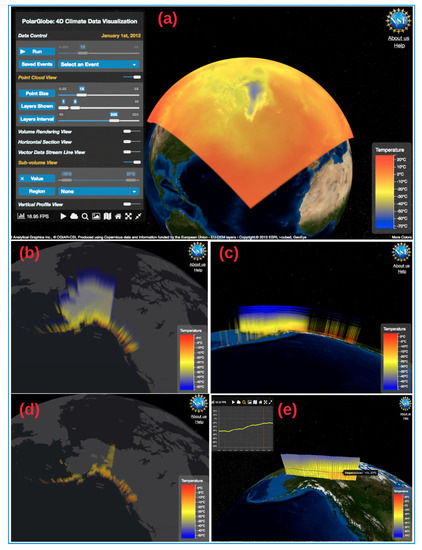
Figure 5.
Graphic User Interface of PolarGlobe (http://cici.lab.asu.edu/polarglobe2): (a) a screenshot of temperature visualization in the whole study area; (b) a close look at the distribution of air temperature in Alaska, US on 1 January 2012; (c) a view of temperature of Alaska from the side; (d) the value filtering effect (Air temperature higher than −20 degree Celsius for data presented is shown here); (e) the vertical profile view and statistics.
A spatial filter can be applied to make further exploration of the air temperature data at an area of interest, such as Alaska, US. Once “Alaska” is selected from the dropdown menu of the spatial region, the original data cube (temperature data at all pressure layers) is cut by the geographical boundary of Alaska. Figure 5b,c demonstrates the temperature data in the winter (1 January 2012), from different angles. It can be seen that it is much warmer along the coast of the Gulf of Alaska and inland (near the south) than in other parts. This observation can be verified by conducting a value filtering in the PolarGlobe system (see results in Figure 5d).
When an inner structure of the data volume needs to be examined, our vertical profile visualization will serve this purpose. Figure 5e shows the temperature change along 65 degree North near Alaska and northwest Canada. It can be observed that the near surface temperature in Canada along the trajectory of interest is higher than that in Alaska, and the value keeps increasing when moving toward the east.
5. Experiments and Results
This section provides quantitative analysis of the performance improved by the proposed methods for accomplishing real-time and interactive visualization of the voluminous dataset. The experiments were conducted on a Dell workstation with 8 cores at 3.4 GHz and 8 gigabytes memory size.
5.1. Performance on Data Loading and Rendering
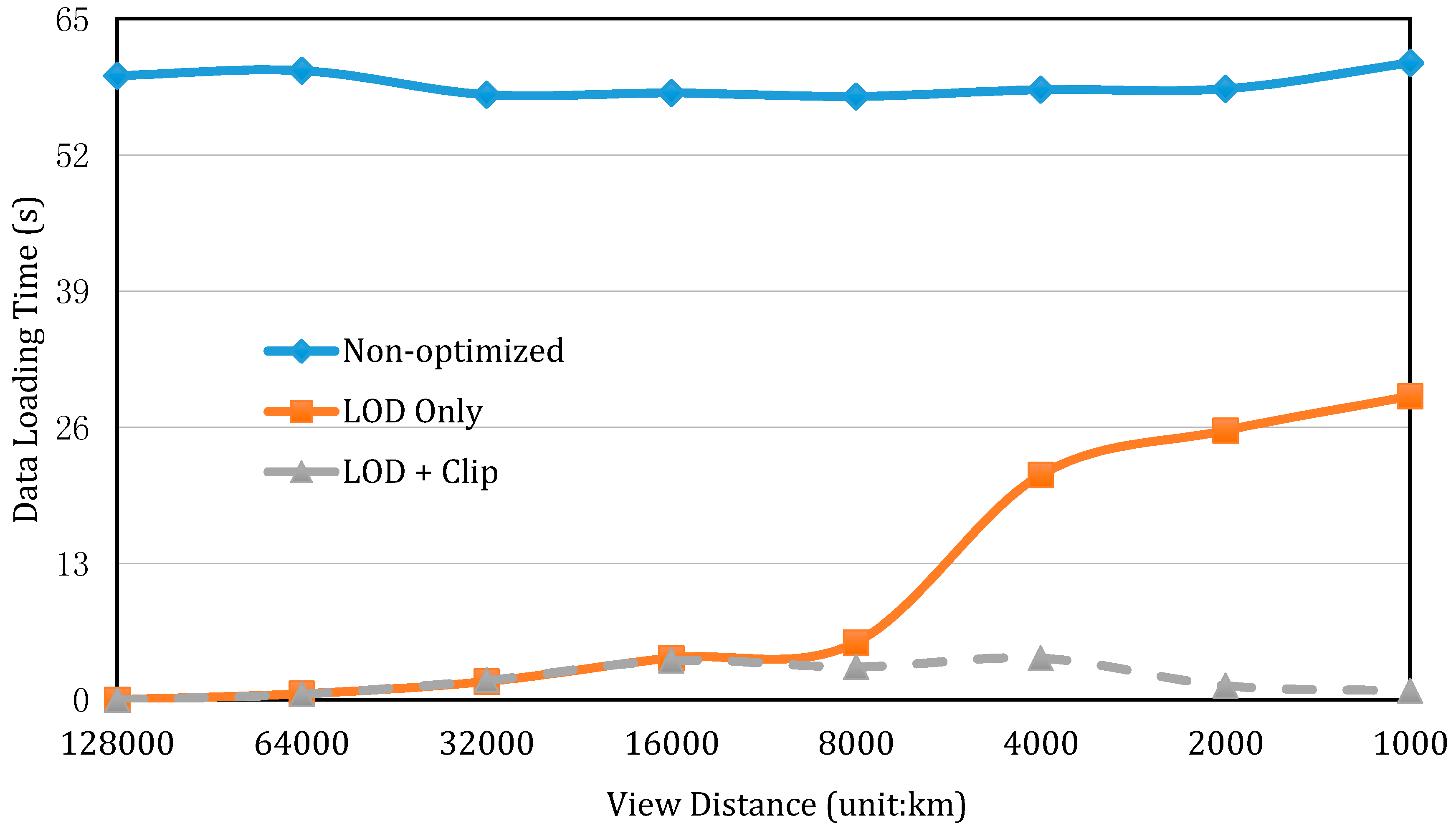
To accelerate data loading speed, we introduced the enhanced octree-based LOD and viewport clip to filter out the invisible part of the data volume to reduce data size to be loaded. This experiment provides a comparison in terms of data loading time, using: (1) the non-optimized approach, in which the entire dataset will be loading for visualization; (2) the approach that adopts only the LOD; and (3) the one with both the LOD and viewport clip, applied to reveal the advantages of the optimization strategy. In the experiment, we assume a user is viewing the Earth from space and his eye sight falls on the location of 75° W, 60° N on the Earth’s surface. As he looks closer or further, the angle remains the same and only the view distance changes. The loading efficiency under the three scenarios is compared and results are shown in Figure 6.
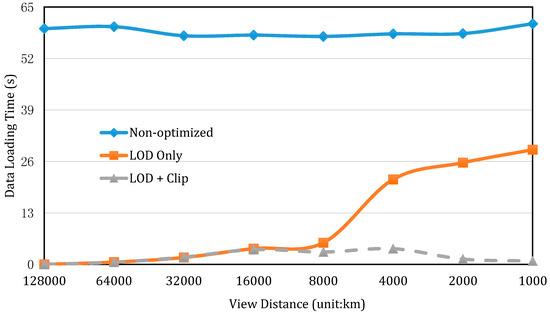
Figure 6.
Comparison of data loading time before and after applying optimization strategies as the view distance becomes shorter. (Error bars are smaller than the plot markers).
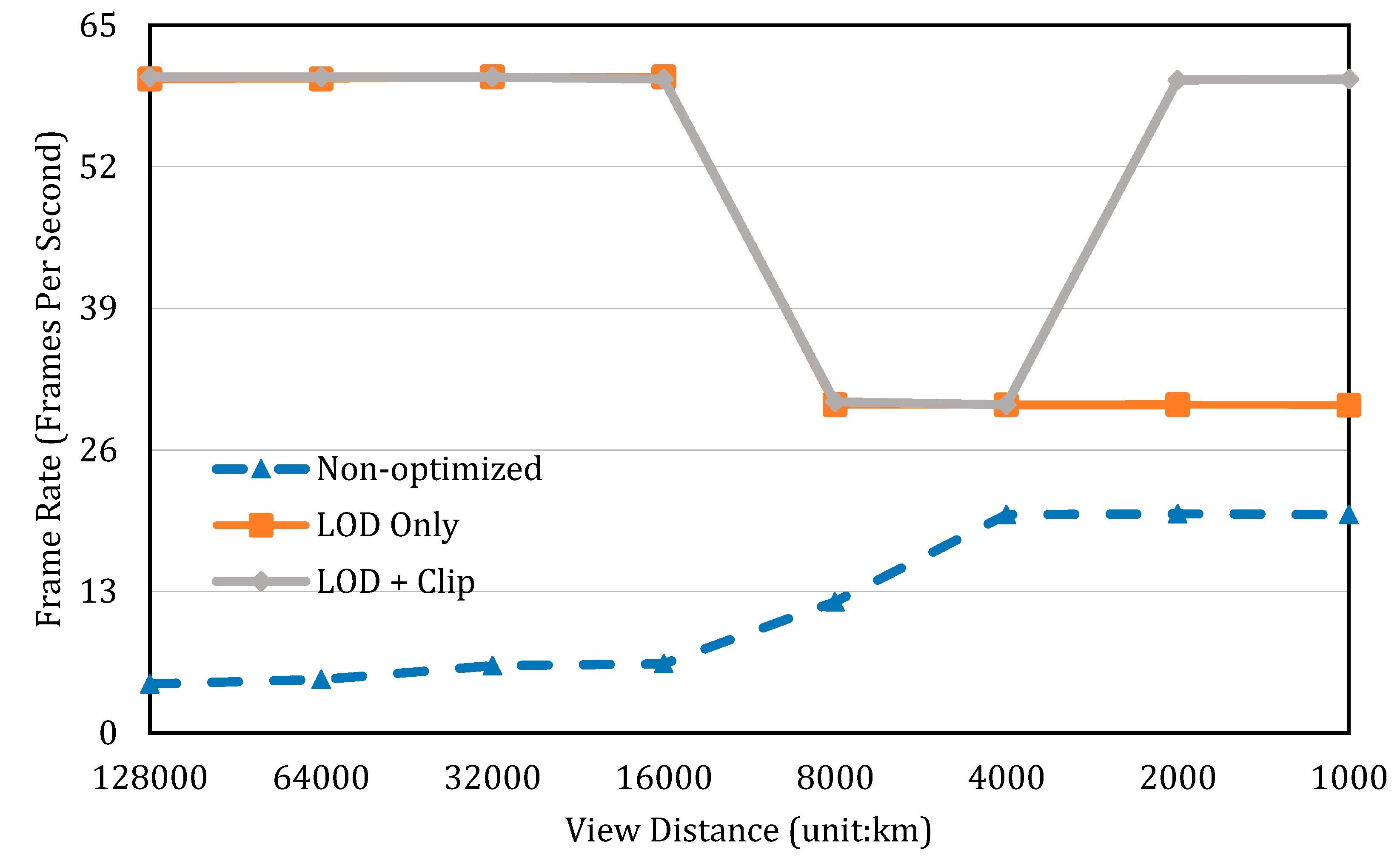
It can be observed from Figure 6 that data loading with no optimization takes much more time than in the other two situations, no matter how far away a user views the data volume. When the view distance is below 8 million meters, the loading time with LOD-adopted is comparable to the LOD + Clip. Beyond that view distance, the LOD with data clipping presents a conspicuous advantage over the LOD alone. As expected when data volume is observed in shorter distances, a greater amount of points are filtered out because of their invisibility (the smaller the data volume being loaded, the less computation burden on the graphic processor). Therefore, a higher rendering performance (in terms of frame rate) can be achieved. We also compare the rendering performances by their frame rates when refreshing the data volume. Similar results are presented in Figure 7. In Figure 7, an interesting bell-shaped curve is shown for our proposed LOD + Clip method. At the distances of 6000 km and 4000 km, the frame rate drops to about half of that at other distances. This is due to the reason that these distances are close enough to load the data at a higher level of detail, but not close enough to clip the data volume, since most of the data volume remains in the viewport. This fact can be cross validated with the results in Figure 6 (at the given two distances); there is, in fact, an increase in the data loading time. The data-loading curve starts to drop when the view distances move below 4000 km for the LOD + clip method (dashed line in Figure 6).
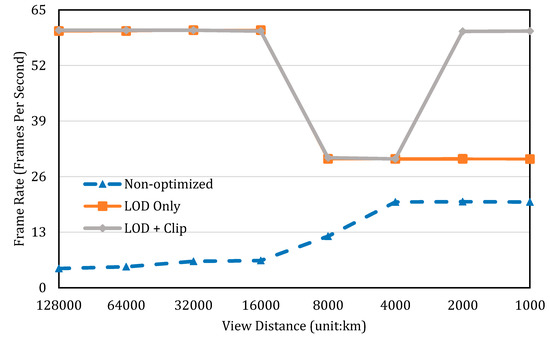
Figure 7.
Comparison of data rendering performance, before and after applying optimization strategies.
5.2. Experiment on Accuracy vs. Efficiency in Spatial Filtering and Generalization
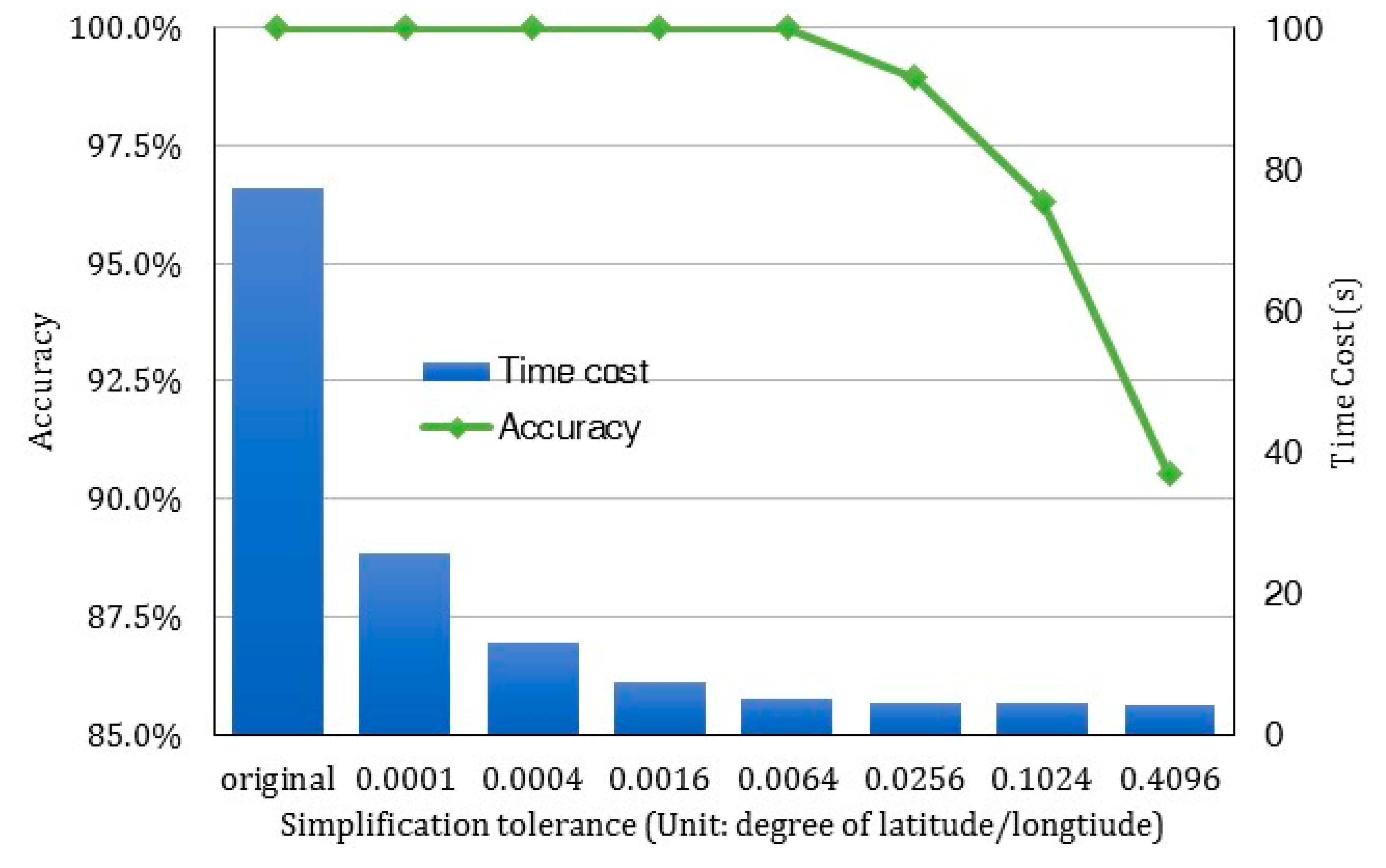
As mentioned, we introduced a simplification process for determining spatial boundaries. This clips the original data volume to support the spatial filtering operation. Knowing that an increasing level of simplification introduces a larger error in the boundary data, and thus affects the accuracy of the results, we implemented the filtered grid points. Here the level of simplification was determined by a distance tolerance, used to determine which neighboring vertices should be kept or deleted. The resulting accuracy was measured by the ratio of correctly filtered grid points, using the simplified boundary versus the results obtained by using the original boundary.
We used the boundary of Wisconsin, US as the test data (125,612 vertices in total). Figure 8 illustrates the results. The results reveal a rapid decline of time cost when distance tolerance begins to increase in the simplification process. Here, the unit of this distance tolerance is a degree of latitude/longitude. Accuracy, on the other hand, remains at 100% until the tolerance value is set higher than 0.0064. Hence, the threshold 0.0064 is an ideal parameter setting for spatial boundary simplification that maximizes both filtering efficiency and data accuracy.
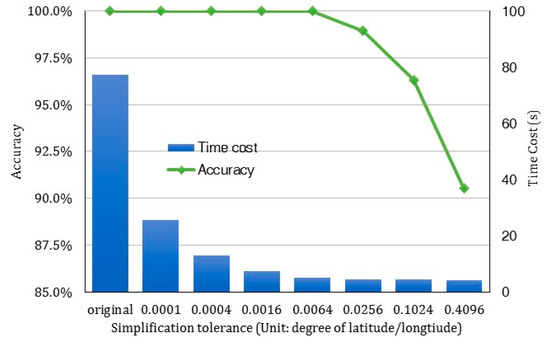
Figure 8.
A comparison between time cost and data accuracy in spatial filtering after applying simplification to the spatial boundary.
5.3. Impact of Interpolation on the Efficiency of Vertical Profile Generation and Visualization
Although interpolation is only a small part of implementing vertical profile visualization, it has the greatest impact on efficiency in generating a profile. This step is needed, since our original test data has a relatively coarse resolution—30 km, and the data points are not evenly distributed within space (see illustration in Figure 4). The time cost of the interpolation is affected by three factors: (1) the number of input points, namely, how many data values will be selected as the reference for interpolation; and (2) the number of output points. This is a measure of the resolution of the interpolated image by the total number of pixels, and (3) which interpolation method is used. We designed two experiments to reveal the impact of these three factors on the interpolation performance.
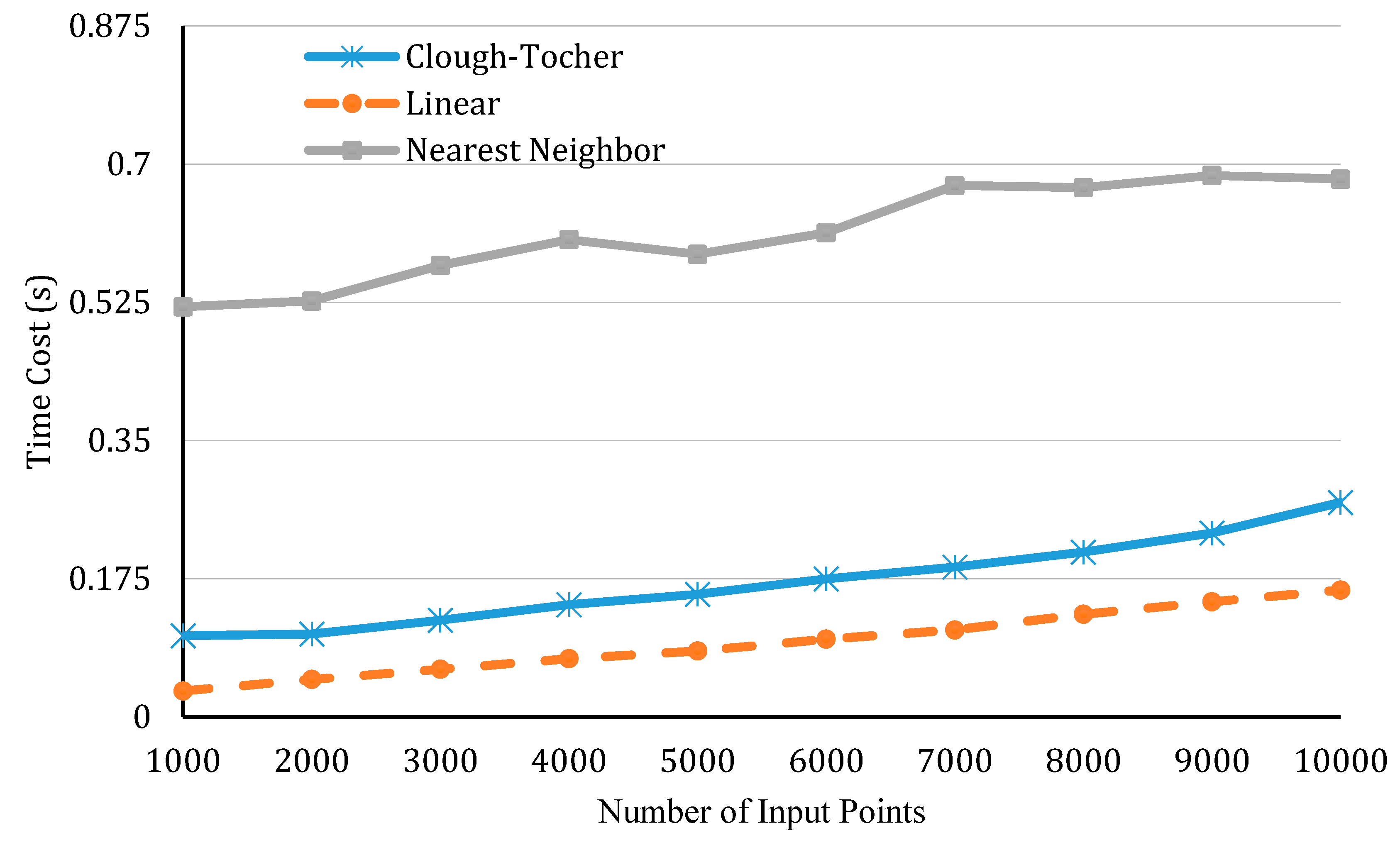
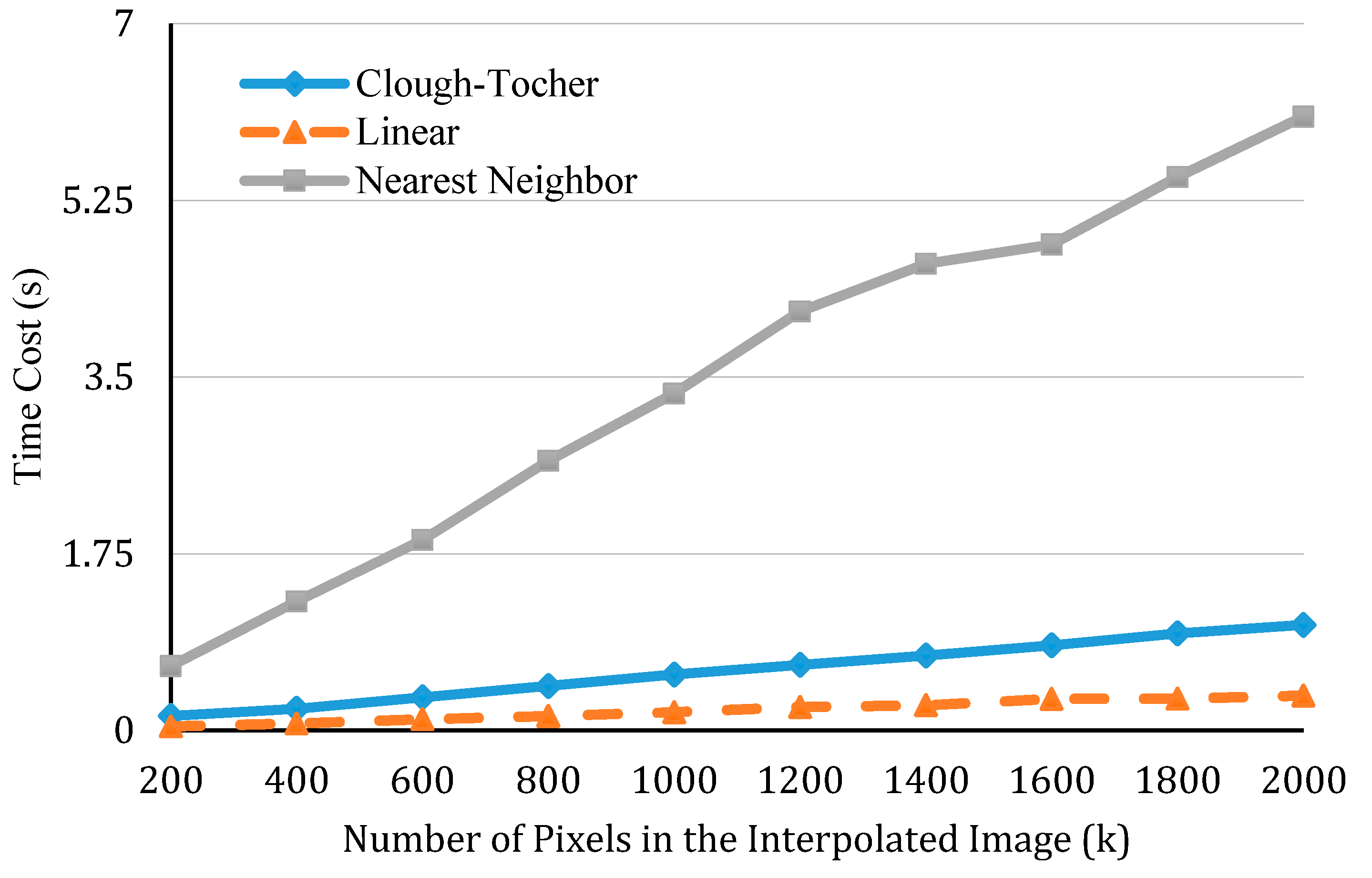
In the first one, we controlled the number of output points (the total pixel numbers of the output image) at 160,000 and compared the performance of different types of interpolation methods by altering the number of input points. Here, the comparison is applied to three types of interpolation which all meet the demand in our case. They are nearest neighbor interpolation [57], linear interpolation [58], and cubic precision Clough-Tocher interpolation [59]. In the second experiment, we controlled the number of input points at 5000 and changed the number of output points. The results of the two experiments are presented in Figure 9 and Figure 10, respectively.
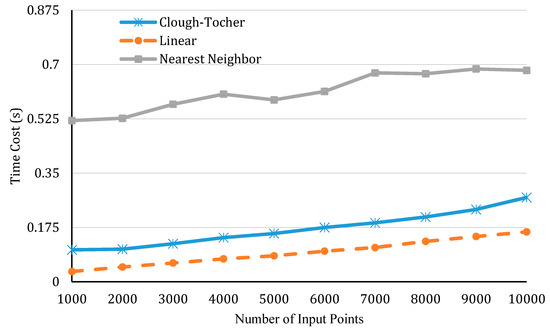
Figure 9.
A comparison of efficiency by different interpolation methods, as the number of input points increases.
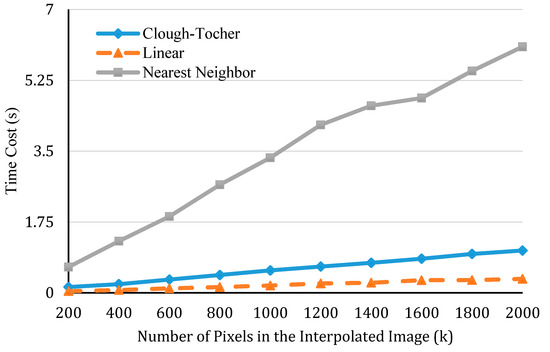
Figure 10.
Efficiency of different interpolation methods, as the required resolution of the interpolated image increases.
Both figures show that, when either the number of input points or output points increases, an increase in interpolation time can be observed. In addition, it is obvious that linear interpolation achieves the highest efficiency, while the nearest neighbor performs the worst. This is because the nearest neighbor interpolation requires the construction of a KD-tree during the processing, which costs more time. However, the speed is not the only indicator used to evaluate an interpolation method. It is more important to figure out how well an interpolation method emulates our data. Therefore, a third experiment was conducted to test the precision of interpolation.
We choose 10,353 points as the data in this experiment. These 10,353 points consist of 357 columns. In other words, 357 points in the original data grid were selected along a user drawn path on the Earth’s surface. This number is related to the density of the raw data points. On each column, there exists 29 data points (since the raw data’s z dimension is 29, representing 29 pressure levels). To evaluate the accuracy in the interpolation, part of all the data points were selected and served as the input for interpolation (we call it train data). The rest is used as test/ground truth data.
For the simulated output points, there are two values associated with them: si (the interpolated values); and the real values (ri). The accuracy is calculated using the Normalized Euclidean Distance () between the two vectors, composed respectively by the interpolated and real values:
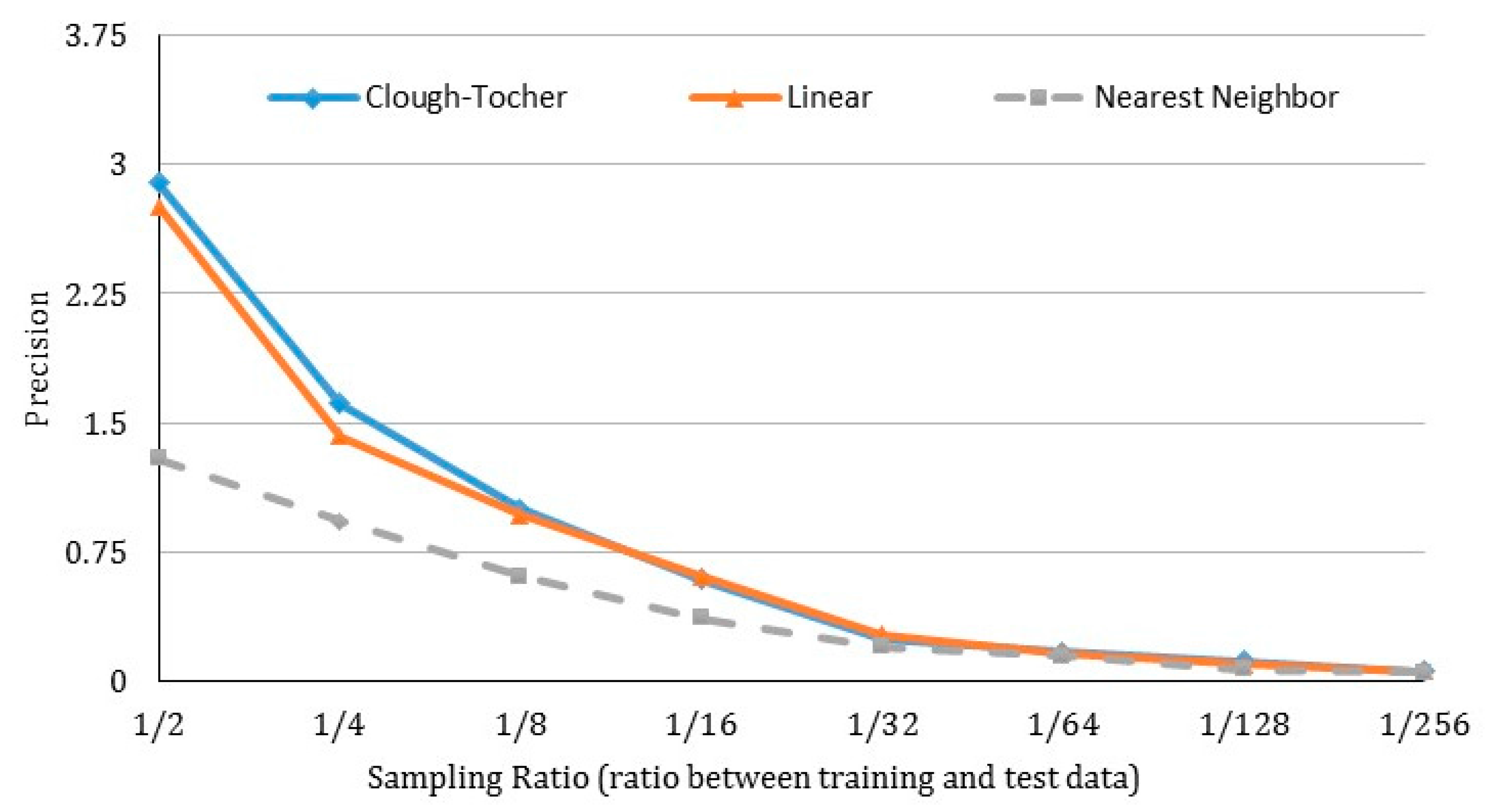
where n denotes the number of the points in the test data. When a higher is observed, a lower accuracy value will be obtained. Figure 11 demonstrates the accuracy of each interpolation approach by changing the sampling ratio between train and test data.
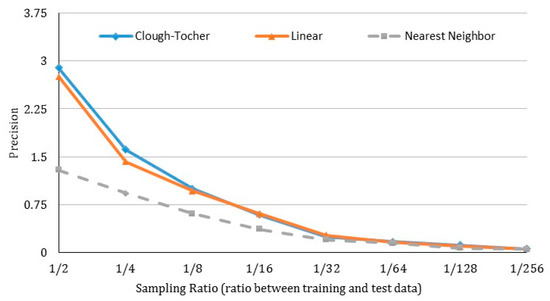
Figure 11.
A comparison of accuracy across different interpolation methods, as the number of training data used for interpolation decreases.
As shown, the accuracy of interpolation rapidly declines as fewer training data are selected, as reflected by a decreasing sampling ratio. This is especially true for linear and Clough-Tocher interpolations. On the other hand, these two methods still perform better than the nearest neighbor interpolation at each sampling rate. Clough-Tocher interpolation performs a bit better than linear interpolation when the sampling ratio is controlled above 1/8. When the ratio is below 1/8, we observe very similar resultant accuracy values. Synthesizing results from all three experiments, linear interpolation is the best fit in our visualization system, with real-time requirement due to its fast speed and high accuracy.
6. Conclusions
This paper introduces PolarGlobe, a Web-based virtual globe system to allow Web-scale access of big climate simulation data. Different from previous work, our proposed platform does not require installation of plugins. This substantially reduces the learning curve of the software tool. Technically, the major contributions of this work include: (1) a server-client architecture powered up by a new differential-storage-enhanced octree model to support efficient spatial indexing, transmission, and rendering of big climate data; (2) a combined value and spatial filter to enable perception-based visualization and interactive data exploration; and (3) vertical profile visualization to allow examination of variations in climate variables on a cross-section inside the data cube. Although primarily tested on climate simulation data, visualization techniques can be widely applied to other Earth science domains, such as oceanography, hydrology, and geology. We believe this platform will provide strong support to scientists for testing models and validating hypotheses, as well as for the general public to understand different components of the Earth system and its interactions.
In the future, we will enhance the PolarGlobe system in the following directions: first, methods will be developed to effectively present multivariate geoscientific data for an integrated analysis; second, strategies for visualizing vector data on the globe will also be exploited; and third, we will extend the current visualization capability with advanced data mining or spatial analysis capability, to equip PolarGlobe as not only a system for visualization but also for knowledge discovery.
Acknowledgments
This project is supported by the National Science Foundation (PLR-1349259; BCS-1455349; and PLR-1504432).
Author Contributions
Sizhe Wang and Wenwen Li originated the idea of the paper. Sizhe Wang developed the algorithm and the PolarGlobe system, with assistance from Feng Wang. Sizhe Wang, Wenwen Li wrote the paper. Feng Wang assists with some graphics and references. All authors discussed the implementation details of the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dasgupta, S.; Mody, A.; Roy, S.; Wheeler, D. Environmental regulation and development: A cross-country empirical analysis. Oxf. Dev. Stud. 2001, 29, 173–187. [Google Scholar] [CrossRef]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef] [PubMed]
- Tacoli, C. Crisis or adaptation? Migration and climate change in a context of high mobility. Environ. Urban. 2009, 21, 513–525. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Zhou, Y.; Shi, Y.; Zhu, X. Investigation of a coupling model of coordination between urbanization and the environment. J. Environ. Manag. 2012, 98, 127–133. [Google Scholar] [CrossRef] [PubMed]
- Emanuel, K. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Goudie, A.S. Dust storms: Recent developments. J. Environ. Manag. 2009, 90, 89–94. [Google Scholar] [CrossRef] [PubMed]
- Meehl, G.A.; Zwiers, F.; Evans, J.; Knutson, T. Trends in extreme weather and climate events: Issues related to modeling extremes in projections of future climate change. Bull. Am. Meteorol. Soc. 2000, 81, 427–436. [Google Scholar] [CrossRef]
- Mitrovica, J.X.; Tamisiea, M.E.; Davis, J.L.; Milne, G.A. Recent mass balance of polar ice sheets inferred from patterns of global sea-level change. Nature 2001, 409, 1026–1029. [Google Scholar] [CrossRef] [PubMed]
- Cook, A.J.; Fox, A.J.; Vaughan, D.G.; Ferrigno, J.G. Retreating glacier fronts on the Antarctic Peninsula over the past half-century. Science 2005, 308, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, S.R. Visualizing Climate Change: A Guide to Visual Communication of Climate Change and Developing Local Solutions; Routledge: Florence, KY, USA, 2012; p. 511. [Google Scholar]
- Giorgi, F.; Mearns, L.O. Approaches to the simulation of regional climate change: A review. Rev. Geophys. 1991, 29, 191–216. [Google Scholar] [CrossRef]
- Chervenak, A.; Deelman, E.; Kesselman, C.; Allcock, B.; Foster, I.; Nefedova, V.; Lee, J.; Sim, A.; Shoshani, A.; Drach, B. High-performance remote access to climate simulation data: A challenge problem for data grid technologies. Parallel Comput. 2003, 29, 1335–1356. [Google Scholar] [CrossRef]
- Overpeck, J.T.; Meehl, G.A.; Bony, S.; Easterling, D.R. Climate data challenges in the 21st century. Science 2011, 331, 700–702. [Google Scholar] [CrossRef] [PubMed]
- Gordin, D.N.; Polman, J.L.; Pea, R.D. The Climate Visualizer: Sense-making through scientific visualization. J. Sci. Educ. Technol. 1994, 3, 203–226. [Google Scholar] [CrossRef]
- Van Wijk, J.J. The value of visualization. In Proceedings of the IEEE Visualization VIS 05, Minneapolis, MN, USA, 23–28 October 2005; pp. 79–86. [Google Scholar]
- Galton, F. Meteographics, or, Methods of Mapping the Weather, Macmillan, London; British Library: London, UK, 1863. [Google Scholar]
- Nocke, T.; Heyder, U.; Petri, S.; Vohland, K.; Wrobel, M.; Lucht, W. Visualization of Biosphere Changes in the Context of Climate Change. In Proceedings of the Conference on Information Technology and Climate Change, Berlin, Germany, 25–26 September 2008. [Google Scholar]
- Santos, E.; Poco, J.; Wei, Y.; Liu, S.; Cook, B.; Williams, D.N.; Silva, C.T. UV-CDAT: Analyzing Climate Datasets from a User’s Perspective. Comput. Sci. Eng. 2013, 15, 94–103. [Google Scholar] [CrossRef]
- Williams, D. The ultra-scale visualization climate data analysis tools (UV-CDAT): Data analysis and visualization for geoscience data. IEEE Comp. 2013, 46, 68–76. [Google Scholar] [CrossRef]
- Li, W.; Wu, S.; Song, M.; Zhou, X. A scalable cyberinfrastructure solution to support big data management and multivariate visualization of time-series sensor observation data. Earth Sci. Inform. 2016, 9, 449–464. [Google Scholar] [CrossRef]
- Gore, A. The Digital Earth: Understanding our planet in the 21st century. Aust. Surv. 1998, 43, 89–91. [Google Scholar] [CrossRef]
- Sheppard, S.R.; Cizek, P. The ethics of Google Earth: Crossing thresholds from spatial data to landscape visualisation. J. Environ. Manag. 2009, 90, 2102–2117. [Google Scholar] [CrossRef] [PubMed]
- Boschetti, L.; Roy, D.P.; Justice, C.O. Using NASA’s World Wind virtual globe for interactive internet visualization of the global MODIS burned area product. Int. J. Remote Sens. 2008, 29, 3067–3072. [Google Scholar] [CrossRef]
- Boulos, M.N. Web GIS in practice III: Creating a simple interactive map of England’s strategic Health Authorities using Google Maps API, Google Earth KML, and MSN Virtual Earth Map Control. Int. J. Health Geogr. 2005, 4, 22. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Shen, S.; Leptoukh, G.G.; Wang, P.; Di, L.; Lu, M. Development of a Web-based visualization platform for climate research using Google Earth. Comput. Geosci. 2012, 47, 160–168. [Google Scholar] [CrossRef]
- Varun, C.; Vatsavai, R.; Bhaduri, B. iGlobe: An interactive visualization and analysis framework for geospatial data. In Proceedings of the 2nd International Conference on Computing for Geospatial Research & Applications, Washington, DC, USA, 23–25 May 2011; p. 21. [Google Scholar]
- Helbig, C.; Bauer, H.S.; Rink, K.; Wulfmeyer, V.; Frank, M.; Kolditz, O. Concept and workflow for 3D visualization of atmospheric data in a virtual reality environment for analytical approaches. Environ. Earth Sci. 2014, 72, 3767–3780. [Google Scholar] [CrossRef]
- Berberich, M.; Amburn, P.; Dyer, J.; Moorhead, R.; Brill, M. HurricaneVis: Real Time Volume Visualization of Hurricane Data. In Proceedings of the Eurographics/IEEE Symposium on Visualization, Berlin, Germany, 10–12 June 2009. [Google Scholar]
- Wang, F.; Li, W.; Wang, S. Polar Cyclone Identification from 4D Climate Data in a Knowledge-Driven Visualization System. Climate 2016, 4, 43. [Google Scholar] [CrossRef]
- Li, Z.; Yang, C.; Sun, M.; Li, J.; Xu, C.; Huang, Q.; Liu, K. A high performance web-based system for analyzing and visualizing spatiotemporal data for climate studies. In Proceedings of the International Symposium on Web and Wireless Geographical Information Systems, Banff, AB, Canada, 4–5 April 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 190–198. [Google Scholar]
- Alder, J.R.; Hostetler, S.W. Web based visualization of large climate data sets. Environ. Model. Softw. 2015, 68, 175–180. [Google Scholar] [CrossRef]
- Liu, Z.; Ostrenga, D.; Teng, W.; Kempler, S. Developing online visualization and analysis services for NASA satellite-derived global precipitation products during the Big Geospatial Data era. In Big Data: Techniques and Technologies in Geoinformatics; CRC Press: Boca Raton, FL, USA, 2014; pp. 91–116. [Google Scholar]
- Van Meersbergen, M.; Drost, N.; Blower, J.; Griffiths, G.; Hut, R.; van de Giesen, N. Remote web-based 3D visualization of hydrological forecasting datasets. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 12–17 April 2015; Volume 17, p. 4865. [Google Scholar]
- Hunter, J.; Brooking, C.; Reading, L.; Vink, S. A Web-based system enabling the integration, analysis, and 3D sub-surface visualization of groundwater monitoring data and geological models. Int. J. Digit. Earth 2016, 9, 197–214. [Google Scholar] [CrossRef]
- Moroni, D.F.; Armstrong, E.; Tsontos, V.; Hausman, J.; Jiang, Y. Managing and servicing physical oceanographic data at a NASA Distributed Active Archive Center. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–6. [Google Scholar]
- AGI. Cesium-WebGL Virtual Globe and Map Engine. Available online: https://cesiumjs.org/ (accessed on 17 January 2015).
- Brovelli, M.A.; Hogan, P.; Prestifilippo, G.; Zamboni, G. NASA Webworldwind: Multidimensional Virtual Globe for Geo Big Data Visualization. In Proceedings of the ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2016, Prague, Czech Republic, 12–19 July 2016; pp. 563–566. [Google Scholar]
- Voumard, Y.; Sacramento, P.; Marchetti, P.G.; Hogan, P. WebWorldWind, Achievements and Future of the ESA-NASA Partnership (No. e2134v1). Available online: https://peerj.com/preprints/2134.pdf (accessed on 18 April 2017).
- Li, W.; Wang, S. PolarGlobe: A web-wide virtual globe system for visualizing multidimensional, time-varying, big climate data. Int. J. Geogr. Inf. Sci. 2017, 31, 1562–1582. [Google Scholar] [CrossRef]
- Cox, M.; Ellsworth, D. Managing Big Data for Scientific Visualization; ACM Siggraph: Los Angeles, CA, USA, 1997; Volume 97, pp. 146–162. [Google Scholar]
- Demchenko, Y.; Grosso, P.; De Laat, C.; Membrey, P. Addressing big data issues in scientific data infrastructure. In Proceedings of the IEEE 2013 International Conference on Collaboration Technologies and Systems (CTS), San Diego, CA, USA, 20–24 May 2013; pp. 48–55. [Google Scholar]
- Baccarelli, E.; Cordeschi, N.; Mei, A.; Panella, M.; Shojafar, M.; Stefa, J. Energy-efficient dynamic traffic offloading and reconfiguration of networked data centers for big data stream mobile computing: Review, challenges, and a case study. IEEE Netw. 2016, 30, 54–61. [Google Scholar] [CrossRef]
- Cordeschi, N.; Shojafar, M.; Amendola, D.; Baccarelli, E. Energy-efficient adaptive networked datacenters for the QoS support of real-time applications. J. Supercomput. 2015, 71, 448–478. [Google Scholar] [CrossRef]
- Wong, P.C.; Shen, H.W.; Leung, R.; Hagos, S.; Lee, T.Y.; Tong, X.; Lu, K. Visual analytics of large-scale climate model data. In Proceedings of the 2014 IEEE 4th Symposium on Large Data Analysis and Visualization (LDAV), Paris, France, 9–10 November 2014; pp. 85–92. [Google Scholar]
- Li, J.; Wu, H.; Yang, C.; Wong, D.W.; Xie, J. Visualizing dynamic geosciences phenomena using an octree-based view-dependent LOD strategy within virtual globes. Comput. Geosci. 2011, 37, 1295–1302. [Google Scholar] [CrossRef]
- Liang, J.; Gong, J.; Li, W.; Ibrahim, A.N. Visualizing 3D atmospheric data with spherical volume texture on virtual globes. Comput. Geosci. 2014, 68, 81–91. [Google Scholar] [CrossRef]
- Kruger, J.; Westermann, R. Acceleration techniques for GPU-based volume rendering. In Proceedings of the 14th IEEE Visualization 2003 (VIS’03), Seattle, WA, USA, 13–24 October 2003; p. 38. [Google Scholar]
- Wang, F.; Wang, G.; Pan, D.; Liu, Y.; Yang, Y.; Wang, H. A parallel algorithm for viewshed analysis in three-dimensional Digital Earth. Comput. Geosci. 2015, 75, 57–65. [Google Scholar]
- Drebin, R.A.; Carpenter, L.; Hanrahan, P. Volume rendering. Comput. Graph. 1988, 22, 65–74. [Google Scholar] [CrossRef]
- National Center for Atmospheric Research Staff. The Climate Data Guide: Arctic System Reanalysis (ASR). Available online: https://climatedataguide.ucar.edu/climate-data/arctic-system-reanalysis-asr (accessed on 22 June 2017).
- Luebke, D.P. Level of Detail for 3D Graphics; Morgan Kaufmann: San Francisco, CA, USA, 2003. [Google Scholar]
- Weiskopf, D.; Engel, K.; Ertl, T. Interactive clipping techniques for texture-based volume visualization and volume shading. IEEE Trans. Vis. Comput. Graph. 2003, 9, 298–312. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartogr. Int. J. Geogr. Inf. Geovis. 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Menon, S.; Hansen, J.; Nazarenko, L.; Luo, Y. Climate effects of black carbon aerosols in China and India. Science 2002, 297, 2250–2253. [Google Scholar] [CrossRef] [PubMed]
- Malys, S. The WGS84 Reference Frame. National Imagery and Mapping Agency. 1996. Available online: http://earth-info.nga.mil/GandG/publications/tr8350.2/wgs84fin.pdf (accessed on 10 March 2017).
- Hinks, A.R. A retro-azimuthal equidistant projection of the whole sphere. Geogr. J. 1929, 73, 245–247. [Google Scholar] [CrossRef]
- Parker, J.A.; Kenyon, R.V.; Troxel, D.E. Comparison of interpolating methods for image resampling. IEEE Trans. Med. Imaging 1983, 2, 31–39. [Google Scholar] [CrossRef] [PubMed]
- De Boor, C.; De Boor, C.; Mathématicien, E.U.; De Boor, C.; De Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 1978; Volume 27, p. 325. [Google Scholar]
- Mann, S. Cubic precision Clough-Tocher interpolation. Comput. Aided Geom. Des. 1999, 16, 85–88. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).