Fuzzy Ontology Embeddings and Visual Query Building for Ontology Exploration

Abstract

Ontologies play a central role in structuring knowledge across domains, supporting tasks such as reasoning, data integration, and semantic search. However, their large size and complexity—particularly in fields such as biomedicine, computational biology, law, and engineering—make them difficult for non-experts to navigate. Formal query languages such as SPARQL offer expressive access but require users to understand the ontology’s structure and syntax. In contrast, visual exploration tools and basic keyword-based search interfaces are easier to use but often lack flexibility and expressiveness. We introduce FuzzyVis, a proof-of-concept system that enables intuitive and expressive exploration of complex ontologies. FuzzyVis integrates two key components: a fuzzy logic-based querying model built on fuzzy ontology embeddings, and an interactive visual interface for building and interpreting queries. Users can construct new composite concepts by selecting and combining existing ontology concepts using logical operators such as conjunction, disjunction, and negation. These composite concepts are matched against the ontology using fuzzy membership-based embeddings, which capture degrees of membership and support approximate, concept-level similarity search. The visual interface supports browsing, query composition, and partial search without requiring formal syntax. By combining fuzzy semantics with embedding-based reasoning, FuzzyVis enables flexible interpretation, efficient computation, and exploratory learning. A usage scenario demonstrates how FuzzyVis supports subtle information needs and helps users uncover relevant concepts in large, complex ontologies.

1. Introduction

Ontologies are formal representations of knowledge that describe the concepts in a knowledge domain, their relationships, and associated instances. They provide a structured framework for representing and reasoning about knowledge, supporting areas such as knowledge representation, artificial intelligence (AI), and data management. In knowledge representation and AI, ontologies help standardize terminology and organize domain knowledge in large datasets, enabling automated reasoning tasks such as inference, problem-solving, and theorem proving [1,2,3]. They often serve as advanced thesauri for query expansion, improving search effectiveness and interoperability [4,5]. In data management, ontologies are central to data integration by supporting the unification of heterogeneous data sources [6] and enhancing concept recognition. A key approach is ontology-based data access, which uses ontologies to enable reasoning over large datasets—typically stored in databases—to answer complex queries [7].

Ontologies are widely used to represent structured knowledge across various domains. In biology, the Gene Ontology (GO) [8] and the Sequence Ontology (SO) [9] provide standardized annotations for genes and sequences. In medicine, the Human Phenotype Ontology (HPO) [10], the Disease Ontology (DO) [11], and MeSH (Medical Subject Headings) [12] support standardized indexing and search of biomedical literature and clinical data. In the legal domain, ontologies such as LKIF-Core [13] and LOTED2 [14] support legal reasoning and document management. When no ontology exists for a given domain, one can often be developed to capture its core concepts and relationships.

A persistent challenge in working with ontologies is their size and complexity. Many widely used ontologies—such as GO and HPO—contain hundreds of thousands of concepts, making them difficult to navigate, search, and understand, particularly for non-expert users. Using such ontologies effectively requires exploratory learning, a process through which users build mental models by identifying key concepts, understanding their relationships, and uncovering structural patterns [15]. This process often involves locating landmarks (central or well-known concepts), following routes (chains of related concepts), and exploring neighborhoods (clusters of semantically related concepts).

Exploratory learning over ontologies often involves two core activities: searching for relevant concepts and querying to express complex information needs. Search is typically based on keyword matching against concept labels or textual descriptions in the ontology. While simple to use, such methods frequently fail due to vocabulary mismatch, ambiguity, or variation in phrasing. On the other end of the spectrum, formal query languages such as SPARQL [16], OWL-QL [17], SeRQL [18], and SPARQL-DL [19] offer expressive power but require users to understand both the ontology’s structure and the syntax of the query language. These limitations make them difficult to use, especially for non-experts, and the results often require further interpretation. As a result, users exploring large ontologies are left with few practical options when their information needs are vague, evolving, or difficult to articulate precisely.

To address this gap, we propose a querying approach that strikes a balance between expressiveness and simplicity. Instead of writing formal queries, users define new concepts by composing existing primitive concepts in the ontology using set operators—conjunction, disjunction, and negation. These user-defined composite concepts are treated as fuzzy queries and are compared against the ontology to retrieve the most semantically similar primitive concepts. This supports intuitive interaction, flexible query construction, and approximate matching—even when the target composite concept is not explicitly defined in the ontology or when the query is underspecified or partially conflicting. Our approach enables users, particularly non-experts, to express their intent using simple, interpretable building blocks while still benefiting from the structure and semantics of the ontology. We now illustrate this with an example.

Example 1.

To illustrate our querying approach, consider a physician, whom we refer to as the user, exploring HPO to investigate a patient’s symptoms: difficulty speaking and swallowing, with no indication of immune dysfunction. The user suspects a neuromuscular issue but is unsure of the precise terminology.

Through browsing and personal knowledge, the user finds three relevant primitive concepts: Slurred speech (HP_0001350), Dysphagia (difficulty or discomfort in swallowing, HP_0002015), and Abnormality of the immune system (HP_0002715). Using our interface, they define a composite query concept $Q$:

Q ≡ Slurred speech ⊓ Dysphagia ⊓ ¬Abnormality of the immune system.

This concept captures the co-occurrence of speech and swallowing difficulties while explicitly excluding immune-related causes. Such a combination is not explicitly defined in the ontology and would typically yield no results using standard (non-fuzzy) query tools.

Using our fuzzy querying approach, the system interprets this as a soft concept and returns the most similar known phenotypes. These may include Pseudobulbar paralysis (HP_0007024), referring to a neurological condition, which exhibits some of the patient’s symptoms, or Abnormal esophagus physiology (HP_0025270), referring to structural abnormalities of the patient’s esophagus, which could lead to food entering the airway. Both are relevant concepts to the user’s intent and could be difficult to find through keyword search alone.

This scenario is provided solely to illustrate ontology exploration and similarity-based concept retrieval and does not make claims for diagnostic or clinical usage.

To implement our querying approach, we represent ontologies as fuzzy ontologies with fuzzy interpretations, where each concept is treated as a fuzzy set assigning a membership degree to each element in the interpretation domain. Given an ontology, we use existing fuzzy reasoners to construct such interpretations that approximately satisfy the ontology’s axioms. Based on these interpretations, we introduce a novel method for generating ontology embeddings, where each concept is represented as a vector of membership degrees over a fixed, ordered set of domain elements. This allows us to precompute embeddings for all primitive concepts offline. At query time, when a user defines a composite concept using conjunction, disjunction, or negation over known primitives, its embedding is computed by applying the corresponding fuzzy operations element-wise to the membership vectors. This compositional capability enables flexible query construction and is not supported by existing ontology embedding methods. The resulting embeddings also support efficient similarity computations (e.g., cosine similarity) between user-defined composite concepts and existing primitive concepts in the ontology, enabling approximate matching even when no exact concept exists.

We implement this querying approach in FuzzyVis, a visual system for ontology exploration. In addition to standard features such as keyword search and typical ontology views, FuzzyVis provides a complex interactive visualization with features such as fisheye distortion and annotation for navigating large ontologies. Users can build visual queries by collecting relevant primitive concepts and combining them using logical operations such as conjunction, disjunction, and negation. The system computes the embedding of the resulting composite concept and returns the most similar primitive concepts as suggestions. Beyond querying, FuzzyVis supports interactive exploration by linking search, query results, and navigation. Concepts returned in results can be located in the primary visualization, and collected concepts can be reused across queries. By combining fuzzy ontology embeddings, query answering, and an intuitive visual interface, FuzzyVis enables non-experts to query and explore large ontologies effectively. It supports exploratory learning through flexible query construction, approximate matching, and structural similarity, addressing key limitations of existing ontology querying tools.

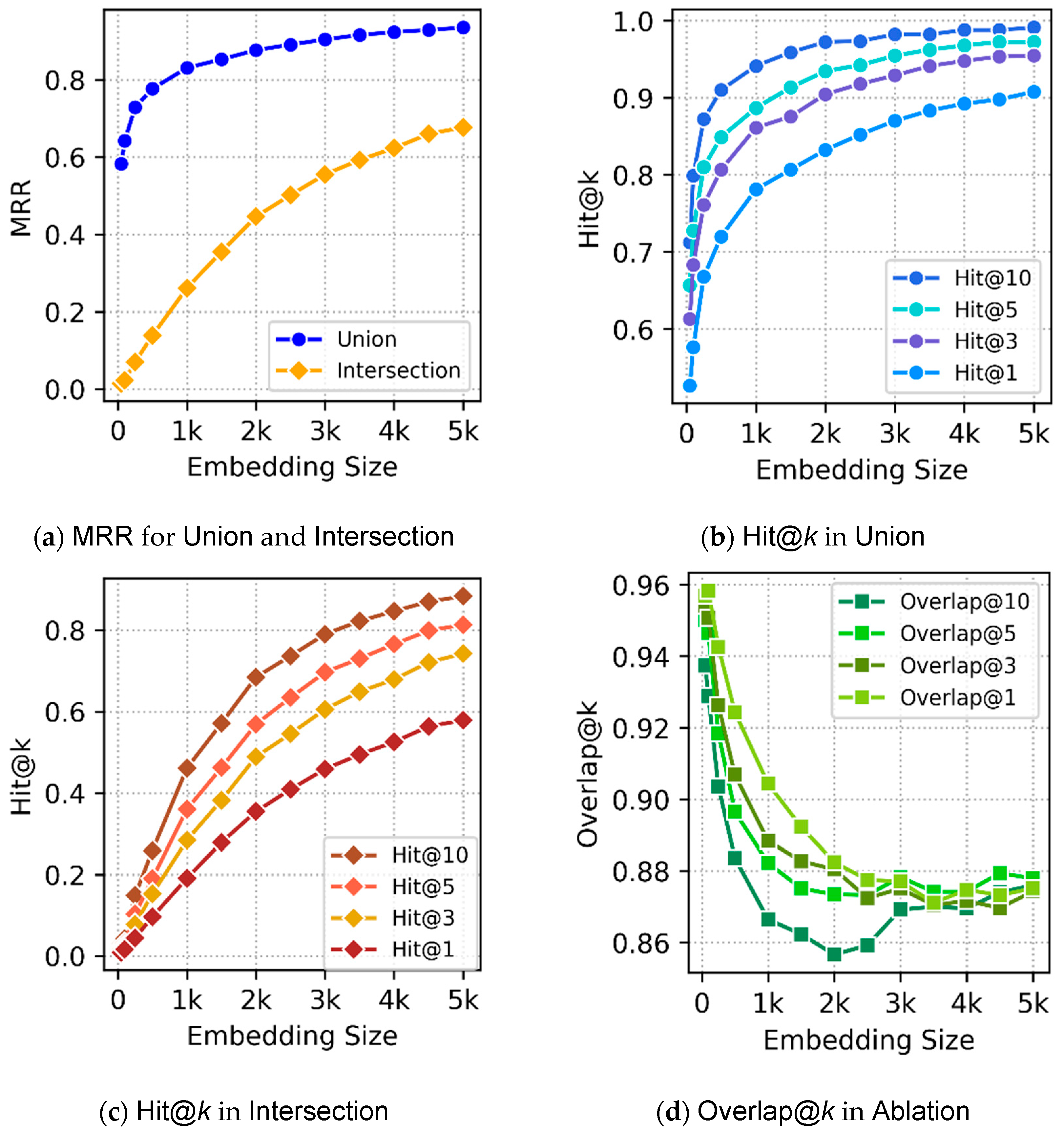
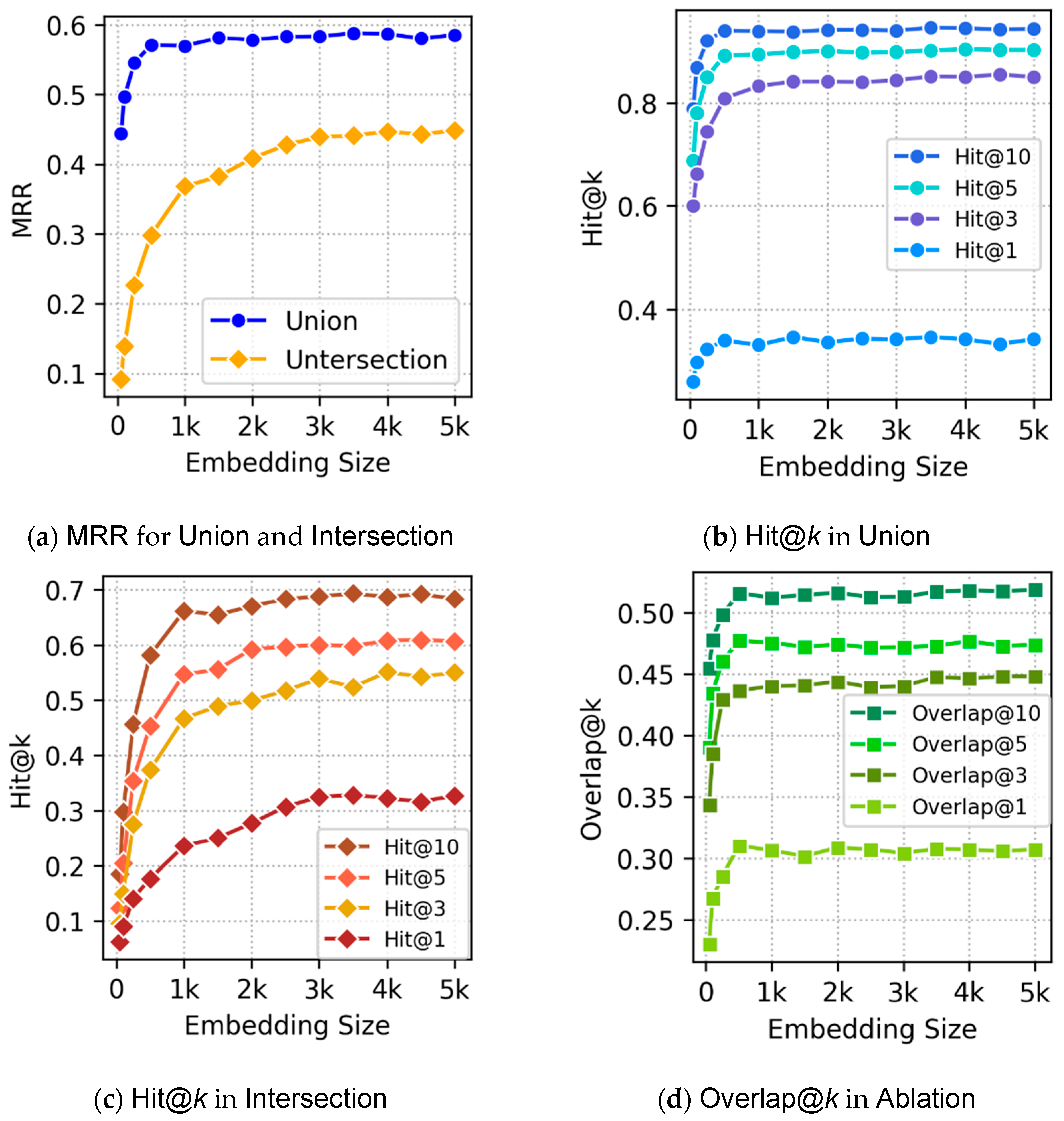
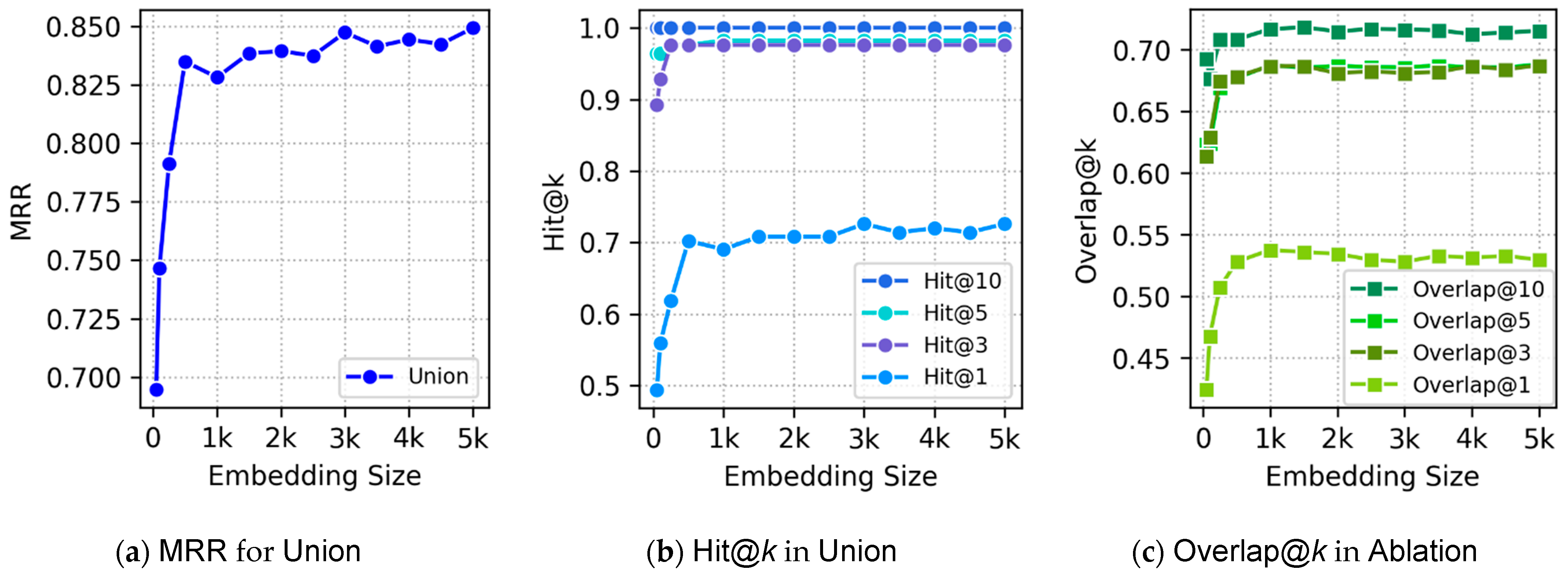
The paper is organized as follows. Section 2 reviews related work. Section 3 introduces the necessary preliminaries and background concepts. Section 4 presents our fuzzy ontology embeddings and describes our querying approach based on these embeddings. Section 5 discusses experimental evaluation of our embeddings. Section 6 details the FuzzyVis system, its implementation, and practical use cases. Section 7 concludes the paper and outlines future directions.

2. Related Work

This section reviews related work on ontology embedding methods (Section 2.1) and existing tools for ontology visualization and exploration (Section 2.2).

2.1. Ontology Embeddings

To support scalable computation over ontologies, numerous methods embed ontology elements into continuous spaces that preserve semantic relationships and enable downstream tasks such as classification, clustering, reasoning, and search [20]. Ontology embedding refers to the process of mapping elements of an ontology to structured mathematical representations—typically vectors, regions, or lattices—that reflect their semantics. Formally, an embedding function $f$ maps each ontology element $e \in \mathcal{O}$ (e.g., a concept, relationship, or individual) to a vector $f\left(e\right)=v_e \in {\mathbb{R}}^d$ in a $d$-dimensional space. Below, we review the main families of embedding methods, organized by their modeling approach:

• Translation-based embeddings. These methods model relations as translation operations in vector space. Given a triple $\left(h, r, t\right)$—where $h$ and $t$ are individuals (head and tail), and $r$ is a relation—the goal is to learn embeddings such that $v_h+v_r\approx v_t$. This approach was introduced by TransE [21], which assumes relational meaning can be captured by a fixed vector offset. Extensions such as TransH [22] and TransR [23] introduce projection mechanisms to better handle complex relations, embedding entities and relations in different spaces. While scalable and widely used for knowledge graph completion, these models are limited to triple-based structures and struggle with more complex ontology constructs such as concept hierarchies and logical combinations.
• Path-based and lexical methods. These methods extract sequential patterns from ontologies or knowledge graphs and apply language modeling techniques to learn embeddings. The key idea is that concepts or entities that frequently co-occur along paths in the graph are likely to be semantically related. RDF2Vec [24] performs walks over RDF graphs to generate sequences, which are embedded using word2vec. OWL2Vec [25] extends this to OWL ontologies by incorporating logical axioms, syntactic features, and lexical information across multiple ontology projections (e.g., logical, lexical, assertional). These methods are interpretable and scalable, especially for lightweight ontologies with rich textual annotations. However, they often lack alignment with formal semantics and cannot guarantee logical consistency.
• Geometric and neurosymbolic embeddings. These methods represent ontology elements as geometric objects (e.g., vectors, balls, boxes, or cones) in continuous space and use geometric operations to simulate logical reasoning [26]. The intuition is that logical constructs such as subsumption, conjunction, and disjunction can be modeled using spatial relationships (e.g., containment or intersection). For example, EL Embeddings [27] represent concepts as Euclidean balls, where subsumption corresponds to containment. BoxEL [28] uses axis-aligned boxes to capture more complex logical structures. Hyperbolic models embed taxonomies as convex cones to preserve hierarchical structure [29]. RotatE [30], though originally designed for knowledge graphs, uses complex rotations to capture properties like symmetry and inversion. These models offer strong logical expressiveness but are often computationally intensive and less suited for dynamic or user-defined query concepts.

In addition to vector-based methods, some models use algebraic structures such as lattices or order embeddings to capture subsumption hierarchies and logical entailment [31]. While expressive and theoretically grounded, these approaches are typically less practical.

The existing ontology embedding methods we reviewed above are designed for static ontologies with fixed concept sets and offer limited or no support for composing concepts using logical operations. For example, geometric models such as BoxEL [28] and Ganea et al. [29] cone-based model can approximate conjunction using the intersection of regions. However, they do not support negation and offer limited or no support for disjunction. Since these methods require retraining to incorporate new concepts, they are not suited for dynamic, query-time composition. This makes them incompatible with our approach, where users define new composite concepts at runtime and embeddings must be computed on the fly without retraining. Our embedding method addresses this limitation by enabling on-the-fly construction of concept embeddings through fuzzy operations, supporting efficient and flexible concept-level search over large-scale ontologies.

Fuzzy ontology embedding methods are related to ours, in particular, methods that employ fuzzification of crisp ontologies. The work of Akremi et al. [32] fuzzifies ontologies by converting them into Fuzzy OWL2 representations. They then use the fuzzy-annotated structure and lexical features to build embedding vectors. However, these embeddings are not intended for concept-level construction and instead for similarity evaluation. FRKGE [33] models entities and relations in a vector space to compute a distance measure to represent membership degrees. These membership degrees are used to optimize the embedding of triples. The resulting embedding captures both the structure of the ontology in addition to fuzzy instance membership. Beyond embedding fuzzy ontologies, these methods are focused on ontology alignment, not on on-the-fly concept construction. In contrast, our framework does not aim at ontology alignment but at interactive ontology exploration and querying. Instead of training corpus-based embeddings over a fuzzy or fuzzified ontology, we construct fuzzy embeddings directly from one or more fuzzy interpretations generated by a model-construction reasoner such as FALCON [34]. These embeddings explicitly encode graded membership and allow dynamic composition of composite concepts via fuzzy logical operators at query time, thereby enabling visual and semantic exploration of ontological knowledge without retraining.

2.2. Ontology Visualization and Exploration Tools

Ontology visualization tools are designed to help users explore, understand, and query complex ontologies. These tools typically fall into three categories:

• Indented tree views display concept hierarchies in a collapsible format, making them intuitive for browsing taxonomies. Tools such as Kaon [35] support ontology editing and provide treemap-based navigation. WebProtégé [36], a widely used collaborative editor, also adopts a tree-based layout for concept exploration. OBO-Edit [37], designed for biomedical ontologies, uses a similar structure. While effective for viewing hierarchical relationships, these tools are less suitable for exploring complex inter-concept connections or non-hierarchical structures.
• Graph-based visualizations, also known as node-link diagrams, represent ontology elements as nodes and their relationships as edges. This approach is better suited for capturing both hierarchical and non-hierarchical semantics. Tools such as ProtégéVOWL [38] and NavigOWL [39], and OntoGraf extend Protégé with interactive graph views. TGVizTab [40] and OWLPropViz [41] allow users to dynamically expand and collapse nodes. WebVOWL [42] brings this functionality to the browser, providing interactive, user-friendly visualizations based on the VOWL specification. While graph-based tools reveal richer relational context, they often struggle with visual clutter as ontology size increases.
• To improve scalability and clarity, several tools combine tree and graph layouts or adopt alternative visual metaphors. Jambalaya [43], a Protégé plugin, integrates hierarchical and relational views with enhanced layout control. PRONTOVISE [15] supports multiple visual modes, including bar charts, to compare concept properties. CODEX [44] focuses on ontology evolution and uses pie charts and word clouds to illustrate changes across versions. OntoTrix [45] replaces node-link diagrams with adjacency matrices to reduce clutter in dense graphs. Among graph visualization tools, Graffinity [46] introduces a hybrid approach that combines matrix and node-link views to support the visualization of large graphs.

In summary, tree-based tools are well-suited for browsing hierarchies, while graph-based and hybrid methods offer broader relational context. Although recent tools address scalability to some extent, visualizing and querying large ontologies in an interactive, user-friendly manner remains a challenge [47].

Most existing tools are primarily designed for navigating fixed hierarchies or inspecting predefined relations. They offer limited support for composing flexible, user-defined queries that involve multiple semantic conditions, such as conjunction, exclusion, or approximate similarity. When query functionality is available, it often relies on rigid form-based inputs or formal query languages that are difficult for non-expert users. Furthermore, many tools are built for lightweight ontologies with simple taxonomies and do not scale effectively to large, expressive ontologies with rich relational semantics. These limitations motivate the development of new tools that support intuitive and interactive construction of complex queries and enable semantic search across expressive, real-world ontologies.

3. Technical Background

This section provides the necessary background and preliminaries. We first review the basics of ontologies in Section 3.1, followed by an overview of fuzzy ontologies in Section 3.2.

3.1. Ontologies: Syntax and Semantics

In this work, we adopt the formalism of Description Logics (DLs) [48] to describe the syntax and semantics of ontologies, which is necessary for presenting our ontology embeddings. DLs are a family of logic-based languages that provide a formal, interpretable syntax and well-defined semantics for representing ontologies. They are widely used and form the foundation of popular ontology languages such as OWL [49], which is based on DLs and supports multiple concrete syntaxes, including RDF-based serializations [50]. Although our approach is not limited to DLs, we use DL notation to review fuzzy ontologies and their interpretations in order to clearly define our embeddings.

Formally, the syntax of a DL ontology $\mathcal{O}=\left(\Sigma , \mathcal{K}\right)$ consists of a signature $\Sigma =\left(\mathcal{C},\mathcal{R},\mathcal{N}\right)$, which defines the vocabulary of concept names, role (relationship) names, and individual names, and a knowledge base $\mathcal{K}=\left(\mathcal{T},\mathcal{A}\right)$ containing two types of axioms. The TBox ($\mathcal{T}$) specifies relationships between concepts, including subsumption axioms (e.g., $C⊑D$), equivalence axioms ($C\equiv D$), and disjointness axioms ($C\sqcap D⊑\perp$). The ABox ($\mathcal{A}$) contains assertions about individuals, such as $a : C$, indicating that individual $a$ is an instance of concept $C$, or $R\left(a, b\right)$, stating that individuals $a$ and $b$ are related via the role $R$. The semantics of an ontology is defined by an interpretation $\mathcal{I}=\left({\Delta }^{\mathcal{I}},{\cdot }^{\mathcal{I}}\right)$, where ${\Delta }^{\mathcal{I}}$ is a non-empty domain and ${\cdot }^{\mathcal{I}}$ is an interpretation function. This function maps each concept $C$ to a subset $C^{\mathcal{I}}\subseteq {\Delta }^{\mathcal{I}}$, each role $R$ to a binary relation $R^{\mathcal{I}}\subseteq {\Delta }^{\mathcal{I}}\times {\Delta }^{\mathcal{I}}$, and each individual $a$ to an element $a^{\mathcal{I}}\in {\Delta }^{\mathcal{I}}$.

Composite concepts are constructed using logical constructors such as conjunction ($C\sqcap D$), disjunction ($C\bigsqcup D$), and negation ($\neg C$), which correspond to standard set operations in the domain. Specifically, the interpretation of a conjunction is given by ${\left(C\sqcap D\right)}^{\mathcal{I}}=C^{\mathcal{I}}\cap D^{\mathcal{I}}$, the interpretation of a disjunction is ${\left(C\bigsqcup D\right)}^{\mathcal{I}}=C^{\mathcal{I}}\cup D^{\mathcal{I}}$, and the interpretation of a negation is ${\left(\neg C\right)}^{\mathcal{I}}={\Delta }^{\mathcal{I}}\setminus C^{\mathcal{I}}$.

An ontology is said to be consistent if all of its axioms can be satisfied simultaneously in some interpretation. Consistency is a basic requirement for reasoning and querying, as inconsistencies can make the ontology logically meaningless or prevent useful inference. A concept is satisfiable if it has at least one instance in some interpretation; otherwise, it is considered logically contradictory. These notions provide the foundation for standard reasoning tasks such as subsumption checking, which determines whether $C⊑D$ holds in all interpretations (i.e., whether every instance of $C$ is also an instance of $D$), and instance checking, which verifies whether an individual $a$ necessarily belongs to a concept $C$ across all models of the ontology. While such reasoning tasks support classification and consistency checking, they are typically handled internally by DL reasoners.

In our setting, we are more concerned with querying ontologies to retrieve individuals or concepts that match a user’s information needs. Common query types include conjunctive queries (CQs), unions of conjunctive queries (UCQs), and recursive extensions that support reachability-like conditions. DL query languages such as SPARQL-DL [19], nRQL [51], and EQL-Lite [52] combine logical reasoning with structured query syntax. However, these languages require familiarity with formal syntax and detailed knowledge of the ontology’s structure, and their evaluation is often computationally expensive. This limits their suitability for users seeking intuitive, flexible, and interactive exploration.

3.2. Fuzzy Ontologies

Fuzzy ontologies extend classical ontologies by incorporating fuzzy logic, a many-valued logic in which truth values range continuously in $[0, 1]$. This allows representing vague or uncertain knowledge, such as partial class membership or approximate relations. In contrast to crisp ontologies, where an individual either belongs to a concept or not, fuzzy ontologies allow graded membership [53,54]. For example, a patient may belong to the concept Diabetic with a degree of 0.8, reflecting partial evidence or uncertain data.

A fuzzy ontology $\mathcal{O}=\left(\Sigma , \mathcal{K}\right)$ has the same syntactic structure as a classical one, with a signature $\Sigma =\left(\mathcal{C},\mathcal{R},\mathcal{N}\right)$ and a knowledge base $\mathcal{K}=\left(\mathcal{T},\mathcal{A}\right)$. However, its semantics differ and are defined by fuzzy interpretations. A fuzzy interpretation $\mathcal{I}=\left({\Delta }^{\mathcal{I}},{\cdot }^{\mathcal{I}}\right)$ assigns the following:

• Each individual $a \in \mathcal{N}$ to an element $a^{\mathcal{I}} \in {\Delta }^{\mathcal{I}}$;
• Each concept $C \in \mathcal{C}$ to a membership function $C^{\mathcal{I}} :{ \Delta }^{\mathcal{I}}\to \left[0, 1\right]$;
• Each role $R\in \mathcal{R}$ to a fuzzy binary relation $R^{\mathcal{I}} :{ \Delta }^{\mathcal{I}}\times {\Delta }^{\mathcal{I}}\to \left[0, 1\right]$.

Here, $C^{\mathcal{I}}\left(x\right)$ expresses the degree to which an individual $x$ belongs to concept $C$, and $R^{\mathcal{I}}\left(x, y\right)$ expresses the degree to which $x$ and $y$ are related to $R$. Composite concepts are interpreted using fuzzy logical operators such as $t$-norm $\theta$, a $t$-conorm $\kappa$, and a negation function $\eta$:

$${\left(C\sqcap D\right)}^{\mathcal{I}}\left(x\right)=\theta ({\mu }_C\left(x\right), {\mu }_D\left(x\right)),$$

$${\left(C\bigsqcup D\right)}^{\mathcal{I}}\left(x\right)=\kappa \left({\mu }_C\left(x\right), {\mu }_D\left(x\right)\right),$$

$${\left(\neg C\right)}^{\mathcal{I}}\left(x\right)=\eta \left({\mu }_C\left(x\right)\right).$$

Typical choices include Gödel, Łukasiewicz, and product operators [55,56].

In general fuzzy DLs, axioms may be annotated with degrees, e.g., $⟨a : C\ge \alpha ⟩$, but different systems vary in which axiom types permit degrees [57,58]. In this work, we follow the common practice where only ABox assertions may carry degrees, while TBox axioms are treated as crisp. Support for graded TBox axioms, especially general concept inclusions, depends strongly on the underlying logic and is often restricted to acyclic settings [59,60].

A fuzzy interpretation $\mathcal{I}$ satisfies an ontology $\mathcal{O}$ if it satisfies all axioms in $\mathcal{K}$ to the required degree (typically to degree $1$ for crisp axioms). In this case, $\mathcal{I}$ is called a model of $\mathcal{O}$. Unlike full fuzzy DL reasoning—which involves computing degrees of satisfiability or entailment—our framework does not perform reasoning. Instead, we use a single fuzzy interpretation (either produced by a fuzzy DL reasoner such as FALCON or constructed synthetically for hierarchical ontologies) only as a semantic model from which to derive membership-based concept embeddings. Thus, the standard pointwise t-norm semantics for concept constructors suffice for our purposes.

Throughout the paper, we use ontologies such as HPO in their standard, crisp syntax (i.e., without explicit fuzzy axioms) and evaluate them under fuzzy interpretations solely to define semantic embeddings for concept-level similarity search.

Reasoning in Fuzzy Ontologies

Reasoning tasks in fuzzy DLs extend classical reasoning by operating over degrees of satisfaction rather than binary truth. Because axioms may hold only to a certain degree, reasoning involves determining the degree to which statements such as satisfiability, subsumption, or instance membership hold. Thus, fuzzy reasoning generalizes classical entailment by computing graded conclusions that reflect partial truth.

In general, the decidability and complexity of fuzzy DL reasoning depend strongly on the choice of operators and the expressivity of the logic, and can range from highly complex to undecidable [56,61,62]. However, for fuzzy extensions of $\mathcal{A}\mathcal{L}\mathcal{C}$ with an acyclic TBox and using either Gödel or Łukasiewicz t-norms, reasoning remains decidable under well-known restrictions [63,64].

Regarding complexity, crisp $\mathcal{A}\mathcal{L}\mathcal{C}$ with an acyclic TBox is PSPACE-complete [65]. Introducing fuzziness increases the complexity: reasoning becomes EXPTIME-complete for Gödel semantics [63] and in NEXPTIME for Łukasiewicz semantics [64]. For the product t-norm, existing reasoning algorithms are correct only for unfoldable (acyclic with additional structural restrictions) TBoxes, and no matching complexity bound is currently known [59,66].

Fuzzy DL reasoners extend classical inference procedures to handle graded membership and partial truth. They differ mainly in how they construct or approximate fuzzy interpretations. Optimization-based reasoners (e.g., FALCON [34], Hohenecker and Lukasiewicz [67]’s work) build fuzzy interpretations by solving one or more optimization problems that maximize the global satisfaction degree of ontology axioms. This is typically performed by maximizing or minimizing suitable objective functions. Constraint-based reasoners (e.g., fuzzyDL [68], GURDL [69]) translate fuzzy axioms into systems of linear or nonlinear constraints and find feasible or optimal models through constraint solving. Reduction-based reasoners (e.g., DeLorean [70], Bobillo et al. [71]’s work) approximate fuzzy inference by reducing it to one or more crisp reasoning tasks—typically using $\alpha$-cuts or thresholding to discretize truth degrees. All three families ultimately aim to identify interpretations (explicitly or implicitly) that satisfy ontology axioms to the highest possible degree.

Our framework follows the optimization-based approach, in which fuzzy reasoners such as FALCON construct fuzzy interpretations internally as part of their reasoning process. Although their primary purpose is logical inference, these systems often provide access to the fuzzy interpretations they compute (including induced membership functions). We use these internally constructed interpretations as semantic models of the ontology and, rather than performing direct fuzzy inference, use them as the basis for generating semantic embeddings of concepts. Further details are provided in Section 4.

4. Ontology Querying Using Fuzzy Ontology Embeddings

We now formalize our embedding framework and describe how fuzzy interpretations enable semantically grounded concept similarity search over large ontologies.

4.1. Embeddings from Fuzzy Interpretations

Let $\mathcal{O}$ be an ontology with concept set $\mathcal{C}$, and let $\mathcal{I}=\left({\Delta }^{\mathcal{I}}, {\cdot }^{\mathcal{I}}\right)$ be a fuzzy interpretation of $\mathcal{O}$, where ${\Delta }^{\mathcal{I}}=\left\{x_1, \dots , x_d\right\}$ is a fixed finite domain, and each concept $C \in \mathcal{C}$ is interpreted as a membership function ${\mu }_C^{\mathcal{I}} : {\Delta }^{\mathcal{I}}\to \left[0, 1\right]$.

Definition 1

 (Embedding of Primitive Concepts). For each primitive concept  $C \in \mathcal{C}$, its embedding under  $\mathcal{I}$ is the vector:

$$v_C=\left[{\mu }_C^{\mathcal{I}}\left(x_1\right), {\mu }_C^{\mathcal{I}}\left(x_2\right), \dots , {\mu }_C^{\mathcal{I}}\left(x_d\right)\right]\in {\left[0, 1\right]}^d.$$

Each dimension corresponds to a domain element $x_i$, and the embedding places $C$ within a semantic space determined by the fuzzy interpretation. Intuitively, a root concept receives high membership degrees across the entire domain, whereas leaf concepts exhibit concentrated support on a smaller region of the space.

Composite concepts are constructed using DL operators $\sqcap$, $\bigsqcup$, and $\neg$. Their embeddings are computed compositionally using fuzzy logical operators applied element-wise to primitive embeddings.

Let $\theta$, $\kappa$, and $\eta$ denote a $t$-norm, $t$-conorm, and fuzzy negation, and let $\overline{\theta }$, $\overline{\kappa }$, and $\overline{\eta }$ denote their pointwise extensions to vectors in ${\left[0, 1\right]}^d$.

Definition 2

 (Embedding of Composite Concepts). Let  $Q$ be a concept expression built using the grammar

$$Q::=C \left|\left(Q\sqcap Q\right)\right|\left(Q\bigsqcup Q\right)|\left(\neg Q\right),$$

where $C$ is a primitive concept. The embedding $v_Q \in {\left[0, 1\right]}^d$ is defined recursively:

$$v_{Q_1\sqcap Q_2}=\overline{\theta }\left(v_{Q_1}, v_{Q_2}\right),$$

$$v_{Q_1\bigsqcup Q_2}=\overline{\kappa }\left(v_{Q_1}, v_{Q_2}\right),$$

$$v_{\neg Q}=\overline{\eta }\left(v_Q\right).$$

This recursive definition provides a logically grounded embedding for any DL-style concept expression without requiring reasoning at query time.

4.2. Querying via Similarity Search

A user query $Q$ is any composite concept expression built from primitive concepts. Its embedding $v_Q$ is computed on demand using Algorithm 1, which implements the recursive Definition 2.

To retrieve relevant ontology concepts, we compare $v_Q$ to all primitive embeddings $\{v_C : C \in \mathcal{C}\}$ using cosine similarity and return the top-$k$ most similar concepts. This supports exploratory and approximate search based on semantic proximity rather than strict logical entailment.

Importantly, this retrieval process operates at the concept level, not at the instance level. The composite expression $Q$ is treated as a semantic construct whose embedding describes a region in the ontology’s conceptual space. We retrieve the most similar concepts, not individuals, and therefore do not perform instance checking, instance ranking, or fuzzy ABox reasoning. This separates our notion of querying from standard DL query answering, aligning it instead with semantic similarity search over concepts.

Once the fuzzy interpretation $\mathcal{I}$ is fixed, all primitive embeddings can be precomputed and stored in a vector index. Query processing then consists of ($1$) computing $v_Q$ and ($2$) performing nearest-neighbor search.

Our querying approach and fuzzy ontology embeddings provide several advantages for semantically grounded and scalable ontology exploration. First, the embeddings are derived from a fuzzy interpretation $\mathcal{I}$ that reflects the ontology’s axioms, ensuring that the resulting vectors capture the intended semantics even for ontologies with expressive axioms. Second, the method is fully compositional: primitive concept embeddings are precomputed once, while composite embeddings are generated on demand using efficient vectorized fuzzy operations, enabling real-time querying without retraining or re-embedding. Third, the embedding dimensionality $\left|{\Delta }^{\mathcal{I}}\right|$ is tunable via parameters of the fuzzy reasoner (e.g., the sample size in FALCON), allowing users to adjust the balance between representational richness and computational cost. Finally, because all embeddings are vectors, similarity search scales efficiently using optimized vector databases (such as FAISS [72], Qdrant, or Chroma [73]), enabling fast, semantics-aware retrieval suitable for interactive exploration.

$\mathbf{Algorithm} \mathbf{1} \mathit{Embed}(\mathrm{Q}$)
	Input: Concept expression Q
	Output: Embedding of Q
1:	$\mathbf{if} Q$ is a primitive concept C then		▷ Primitive embedding (Definition 1)
2:		$\mathbf{return} \left[{\mu }_C^{\mathcal{I}}\left(x_1\right), \dots , {\mu }_C^{\mathcal{I}}\left(x_d\right)\right]$
3:	$\mathbf{else} \mathbf{if} Q=\left(Q_1\sqcap Q_2\right)$ then		▷ Conjunction (Definition 2)
4:		$\mathbf{return} \overline{\theta }\left(Embed\left(Q_1\right),Embed\left(Q_2\right)\right)$
5:	$\mathbf{else} \mathbf{if} Q=\left(Q_1\bigsqcup Q_2\right)$ then		▷ Disjunction (Definition 2)
6:		$\mathbf{return} \overline{\kappa }\left(Embed\left(Q_1\right),Embed\left(Q_2\right)\right)$
7:	$\mathbf{else} \mathbf{if} Q=\left(\neg Q_1\right)$ then		▷ Negation (Definition 2)
8:		$\mathbf{return} \overline{\eta }\left(Embed\left(Q_1\right)\right)$

4.3. Role of Fuzzy Ontology Reasoners

In our framework, fuzzy DL reasoners are used only to obtain a fuzzy interpretation $\mathcal{I}$ of the given ontology. This interpretation provides the membership functions ${\mu }_C^{\mathcal{I}}$ for all primitive concepts $C \in \mathcal{C}$, which are then used to construct the semantic embeddings introduced in Section 4.1. No reasoning or inference task (e.g., satisfiability, consistency checking, instance retrieval) is performed during querying. Once $\mathcal{I}$ is available, all embeddings are computed independently of the reasoner.

Fuzzy DL reasoners differ in how they construct $\mathcal{I}$ and what guarantees they provide. Optimization-based reasoners, such as FALCON [34], internally generate candidate interpretations via sampling and adjust them through an optimization process to maximize global satisfaction of the ontology’s axioms under the chosen $t$-norm. Although these systems are primarily designed for reasoning, they often expose their internally constructed interpretations, including the induced membership functions. This makes them suitable as a source of $\mathcal{I}$ for embedding generation. Reasoners such as fuzzyDL [68] and DeLorean [70] also support fuzzy reasoning, but they do not provide user control over the size of ${\Delta }^{\mathcal{I}}$, which limits their flexibility for downstream embedding applications.

For embeddings, the key requirement is that the returned interpretation $\mathcal{I}$ must approximately satisfy the ontology’s axioms and provide semantically meaningful membership degrees. The embedding quality, therefore, depends on the quality of the interpretation: if $\mathcal{I}$ captures the intended structure of the ontology, then the embeddings inherit this structure. This perspective allows us to treat reasoners as interpretation generators rather than inference engines.

We chose to use FALCON in our experimental setting for two reasons. First, FALCON can create interpretations using different $t$-norms—Product, Gödel, and Łukasiewicz—allowing us to evaluate which fuzzy operator works best. Second, FALCON allows us to adjust the size of universes in interpretations, letting us control the size of embeddings. As a fuzzy reasoner, FALCON constructs interpretations $\mathcal{I}$ that partially satisfy ontology axioms. Specifically, FALCON uses the semantic constraints of the ontology’s $\mathcal{A}\mathcal{L}\mathcal{C}$ axioms to encode a differentiable loss function, and minimizing this loss yields a fuzzy interpretation in which each axiom is satisfied to a degree determined by the chosen $t$-norm. In this way, semantic consistency is approximated by the overall satisfaction degree–the more FALCON minimizes loss, the greater the satisfaction. Our approach does not rely on FALCON specifically: any fuzzy reasoner capable of providing access to a suitable fuzzy interpretation may be used.

4.4. α-Embeddings for Hierarchical Ontologies

Many real-world ontologies, especially in biomedicine, exhibit a hierarchical structure: concepts are organized along taxonomic “is-a” relationships, and the subsumption relation naturally induces a partial order. For such ontologies, the hierarchical organization strongly encodes semantic proximity—concepts that are close in the hierarchy should receive similar embeddings, whereas distant concepts should be semantically separated. To exploit this structure in a principled yet efficient way, we introduce $\alpha$-interpretations: synthetic fuzzy interpretations that capture hierarchical similarity through a controlled decay parameter. Before defining them formally, we first formalize what it means for an ontology to be hierarchical.

Definition 3

 (Hierarchical Ontology). Let  $\mathcal{O}=\left(\Sigma , \mathcal{K}\right)$ be an ontology with concept set $\mathcal{O}$, and let $⊑$ denote the subsumption relation on $\mathcal{C}$ induced by the TBox $\mathcal{T}$. We say that $\mathcal{O}$ is hierarchical if $⊑$ defines a partial order, meaning it is reflexive ($C⊑C$ for all $C \in \mathcal{C}$), antisymmetric (if $C⊑D$ and  $D⊑C$, then $C=D$), and transitive (if $C⊑D$ and  $D⊑E$, then $C⊑E$). If each concept has at most one direct parent (i.e., at most one $D$ such that $C⊑D$ and no intermediate concept lies between them), then the hierarchy forms a tree. If concepts may have multiple direct parents, the hierarchy forms a polyhierarchy or a DAG taxonomy.

This definition captures both strict taxonomic trees (e.g., IDO [74]) and more general DAG-shaped ontologies with multiple inheritance (e.g., HPO), while ensuring the absence of cycles and the validity of subsumption as a partial order.

We now define a synthetic fuzzy interpretation tailored for hierarchical ontologies. This interpretation explicitly encodes semantic proximity along the hierarchy through a decay parameter $\alpha \in \left[0, 1\right]$.

Definition 4

 (α-Interpretation). Let  $\mathcal{O}$ be hierarchical and let ${\Delta }^{\mathcal{I}}=\left\{x_1, \dots , x_d\right\}$ be a chosen finite domain. An$\alpha$-interpretation of $\mathcal{O}$ is a fuzzy interpretation ${\mathcal{I}}_{\alpha }=\left({\Delta }^{\mathcal{I}}, {\cdot }^{{\mathcal{I}}_{\alpha }}\right)$ constructed as follows. For each domain element  $x_i$:

• Select a leaf concept $L\in \mathcal{C}$.
• Set to ${\mu }_C^{\mathcal{I}}\left(x_i\right)=1$.
• For every other leaf concept  $L^{\prime }$, set  ${\mu }_{L^{\prime }}^{{\mathcal{I}}_{\alpha }}\left(x_i\right)={\alpha }^{d\left(L,L^{\prime }\right)}$, where  $d\left(L,L^{\prime }\right)$is the minimum number of edges from  $L$ and  $L^{\prime }$, over all shared ancestors, of the larger of their distances to that ancestor.
• For any internal concept  $C$ with children  $C_1, \dots , C_k$, define the following:

  $${\mu }_C^{{\mathcal{I}}_{\alpha }}\left(x_i\right)=\kappa \left({\mu }_{C_1}^{{\mathcal{I}}_{\alpha }}\left(x_i\right), \dots , {\mu }_{C_k}^{{\mathcal{I}}_{\alpha }}\left(x_i\right)\right),$$

  where $\kappa$ is a fuzzy union aggregation (e.g., probablistic sum).

This definition applies directly to tree-shaped hierarchies. For polyhierarchies (multiple inheritance), the same rules apply, with aggregation over all parents via $\kappa$. Algorithm 2 outlines the high-level procedure for constructing an $\alpha$-interpretation over a hierarchical ontology.

$\mathbf{Algorithm} \mathbf{2} \mathit{AlphaInterpretation}(\mathcal{O},\alpha , d$)
1:	$\mathrm{Initialize} {\Delta }^{\mathcal{I}}=x_1, \dots , x_d$
2:	$\mathbf{for} i = 1$$\mathrm{to} d$ do
3:		$\mathbf{Choose} \mathbf{a} \mathbf{leaf} L$ uniformly at random
4:		${\mu }_L\left(x_i\right)\leftarrow 1$
5:		for all other leaves $L^{\prime }$ do
6:			${\mu }_{L^{\prime }}\left(x_i\right)\leftarrow {\alpha }^{d\left(L,L^{\prime }\right)}$
7:		for all internal node $C$ in bottom-up order do
8:			${\mu }_C\left(x_i\right)=\kappa \left({\mu }_{C_1}\left(x_i\right), \dots , {\mu }_{C_k}\left(x_i\right)\right)$
9:	$\mathrm{return} {\mathcal{I}}_{\alpha }=\left({\Delta }^{\mathcal{I}}, {\cdot }^{\mathcal{I}}\right)$

By construction, an $\alpha$-interpretation ${\mathcal{I}}_{\alpha }$ satisfies all subsumption axioms of a hierarchical ontology. Indeed, whenever $C⊑D$, the membership degree of any domain element $x_i$ to the parent concept $D$ is obtained via a fuzzy union of the membership degrees of its children, ensuring ${\mu }_C^{{\mathcal{I}}_{\alpha }}\left(x_i\right)\le {\mu }_D^{{\mathcal{I}}_{\alpha }}\left(x_i\right)$ for all $x_i \in {\Delta }^{\mathcal{I}}$. Thus, ${\mathcal{I}}_{\alpha }$ is an exact model of any ontology whose only axioms are taxonomic subsumptions. For ontologies containing additional axioms (e.g., disjointness, existential restrictions, value constraints), an $\alpha$-interpretation may satisfy those axioms only to a degree, depending on the hierarchy structure and the chosen decay and aggregation functions. Nevertheless, for hierarchical ontologies—the primary focus of our use cases—${\mathcal{I}}_{\alpha }$ provides a coherent and semantically grounded interpretation that preserves the intended taxonomic semantics.

We chose to adopt a decaying membership function for $\alpha$-embeddings, specifically ${\alpha }^{d\left(L,L^{\prime }\right)}$, for its ease of computation, its non-reliance on any ontology-specific concept properties (e.g., descriptions), and its membership decaying exponentially as distance increases, which emphasizes local neighborhoods without doing so for distant concepts. In the literature, exponential decay functions are regularly used for graphing and taxonomy [75,76,77].

Once an $\alpha$-interpretation ${\mathcal{I}}_{\alpha }$ is fixed, embeddings for primitive and composite concepts follow directly from the general definition in Section 4.1.

Definition 5

 ($\mathsf{\alpha }$-Interpretation). For any concept  $C \in \mathcal{C}$, the  $\alpha$-embedding of  $C$ is

$$v_C^{\alpha }=\left[{\mu }_C^{{\mathcal{I}}_{\alpha }}\left(x_1\right), \dots , {\mu }_C^{{\mathcal{I}}_{\alpha }}\left(x_d\right)\right]\in {\left[0, 1\right]}^d.$$

Composite concept embeddings are computed via the recursive rules in Definition 2, using the same fuzzy operators as those used to construct the $\alpha$-interpretation.

Using the same fuzzy operators ($\theta$, $\kappa$, $\eta$) at the interpretation and embedding stages preserves semantic consistency and aligns embedding computations with the underlying fuzzy semantics for best performance.

5. Experimental Evaluation

Our experiments pursue two objectives. First, to test the usefulness of our embeddings for querying and searching ontologies. Second, to see the impact of the main parameters in our solution on the result of our approach.

5.1. Experimental Setup

We begin by outlining the experimental setup. Our solutions are implemented in Python. We use a version of FALCON’s implementation [78] to generate fuzzy ontology embeddings for ontology concepts. For α-embeddings, we directly computed them. The embeddings of primitive concepts are stored in a vector database using ChromaDB [73], which supports efficient similarity-based retrieval over dense vectors. At query time, this database is used to perform top-k search, returning the most semantically similar primitive concepts to given composite concept embeddings. All experiments were run on a workstation with 32 GB RAM and an 8-core CPU. Our implementation, along with the code to reproduce all results, is accessible on GitHub (https://github.com/Zhur-Zhur/FLOQE).

Ontologies. For experiments evaluating FALCON-embeddings, we use two real-world ontologies, the Infectious Disease Ontology (IDO) and the Plant Ontology (PO). For the $\alpha$-embedding we use three: IDO, PO, and the Human Phenotype Ontology (HPO). PO and HPO are polyhierarchy (concepts may have more than one direct parent), and IDO is a hierarchy. The differing sizes of the ontologies are shown in

Table 1. Statistics of the ontologies used in our experiments.

Ontology	# of Concepts	# of Axioms	Source
IDO	$362$	$3607$	[74]
PO	$1687$	$~\mathrm{25,000}$	[79]
HPO	$\mathrm{19,034}$	$~\mathrm{180,000}$	[10]

. FALCON could not be applied to HPO due to its size and the inability to produce a sufficiently consistent interpretation for our needs.

Baseline. We implement our fuzzy embedding and query mechanism on top of embeddings generated by a FALCON model. $\alpha$-embeddings are computed directly. For the baseline embedding, we use random membership values rather than the memberships from FALCON, which we denote by Baseline. Other common ontology embeddings, such as TransE or OWL2Vec, are not applicable in our setting, where fast runtime computation of composite concepts is necessary, as we also discussed in Section 2.1.

Parameters. For the ontologies used to evaluate FALCON- and $\alpha$-embeddings, we consider a number of parameters. The first embedding size is the number of individuals used to obtain membership values from a universe; we denote this by Emb-size. The second parameter is the fuzzy operator used: Product, Łukasiewicz, and Gödel. The third parameter is the choice of vector similarity function: Cosine, Euclidean-distance, or Dot-product. The final parameter is $\alpha$ for $\alpha$-embeddings. The default parameters for FALCON-embeddings are Emb-size = $500$, Łukasiewicz, and Cosine. Whereas, for $\alpha$-embeddings the default parameters are $\alpha =0.1$, Emb-size = $500$, Łukasiewicz, Cosine.

Evaluation Scenarios. To evaluate the quality of our embeddings and the effectiveness of similarity-based retrieval, we design five evaluation scenarios that reflect semantic relationships expected in ontology structures. Each scenario defines a pattern where the similarity between a composite concept (constructed using fuzzy operations) and an existing primitive concept should be high. These scenarios test whether the embeddings preserve logical structure and behave meaningfully under similarity search.

We consider the following five evaluation scenarios:

• Union. In hierarchical ontologies, a parent concept typically generalizes its children. We define a composite concept as the union (fuzzy disjunction) of a parent’s children and expect this composite concept to be highly similar to the parent.
• Ablation. Given a parent concept $A$ with children $\{B_1, \dots , B_k\}$, we define two concepts: (i) the union of all children except $B_i$, and (ii) the intersection of $A$ with the negation of $B_i$. These two composite concepts should yield similar top-$k$ sets under similarity search, reflecting logical consistency when a child is ablated.
• Intersection. In ontologies that are not strictly hierarchies, a concept can have multiple parents. For such concepts $C$ with direct disjoint parents $A$ and $B$, we compute the intersection (fuzzy conjunction) of $A$ and $B$ and expect within the top-$k$ results to see $C$, testing whether intersectional semantics are preserved.
• Subsumption. In a fuzzy interpretation, if $A⊑B$, then membership values for ${\mu }_B\left(x\right)$ should be greater than or equal to ${\mu }_A\left(x\right)$ across all individuals $x \in { \Delta }^{\mathcal{I}}$. We compute the percentage of individuals where this condition is violated, reflecting structural subsumption misalignment.
• Random-walk. To evaluate how similarity behaves over hierarchical distance, we construct a tree view of the ontology using subsumption relationships. For a randomly selected concept, we traverse the tree upward or downward to other concepts at increasing distances (measured by the number of edges). We then compute the similarity between the original concept and each concept at distance $p$. In meaningful embeddings, similarity is expected to decrease as the distance increases.

Evaluation Measures. For each scenario, we randomly select a set of valid concept tuples that satisfy the scenario conditions (e.g., a parent and its children for the union test). For each tuple, we define the composite concept using fuzzy operations over the relevant primitive embeddings and compute its similarity to all primitive concepts.

We evaluate the retrieved results using standard metrics:

• Mean Reciprocal Rank (MRR): The average inverse rank of the expected concept in the similarity ranking. The top-$k$ concepts were retrieved for each query; if a concept is not in the retrieved set, its score is $0$.
• Hit@k: Whether the expected concept appears in the top-$k$ most similar results.
• Overlap@k: For the child ablation test, where two top-k lists are compared, we measure the fraction of overlap between the two retrieved sets.
• Subsumption violation rate: The proportion of a concept’s embedding where the value of a child’s embedding exceeds that of its parent.
• Similarity vs. distance curve: For the random walk test, we record the average similarity between the origin and each traversed concept as a function of tree distance.

To account for randomness, we run FALCON three times for each ontology and repeat each evaluation with three independently generated testing sets. For $\alpha$-embeddings, we construct them three times as well and repeat the evaluations three times with independently generated testing sets. All reported metrics are averaged over these runs.

5.2. Experimental Results and Analysis

We now report the results and our analysis. We will discuss the takeaways at the end of this section.

5.2.1. Impact of Embedding Size

Figure 1, Figure 2 and Figure 3 show the effect of embedding size on the quality of concept similarity search. Overall, increasing the Emb-size improves performance across all scenarios—Union, Intersection, and Ablation—as measured by MRR, Hit@k, and Overlap@k. However, for FALCON-embeddings, the improvement becomes marginal beyond an Emb-size of approximately $500$, suggesting a plateau in performance. This behavior likely reflects the fact that, beyond a certain point, the individuals used to construct the concept embeddings are sufficient to capture the semantic distinctions between most concepts in the ontology.

For $\alpha$-embeddings the point at which they plateau is affected by two factors: the number of leaf nodes and $\alpha$. Leaves that have no individual with full membership—i.e.,$\forall x \in { \Delta }^{\mathcal{I}}, {\mu }_L^{\mathcal{I}}\left(x\right)\ne 1$—have embeddings that are constructed by their distance to leaves that do have full memberships; when these distances are not unique, duplicate embeddings will occur. Furthermore, in the crisp case ($\alpha =0$), such leaves will instead have matching empty set embeddings. Consequently, as the number of leaves in the ontology increases, the Emb-size must be larger to achieve sufficient coverage and prevent this. For HPO, the value of Emb-size when performance plateaus is around $3000$. The trends for the IDO and PO $\alpha$-embeddings are highly similar, except that they plateau in performance with Emb-size of $250$ and $1000,$ respectfully.

The number of duplicate embeddings is why for HPO Ablation scores appeared to get worse (Figure 1d). As the embedding size increased, the $\alpha$-embedding no longer had as many duplicate embeddings, hurting the score, until the point it plateaued when its embedding size was large enough.

An important observation is that Hit@10 for Union converges to $1$ for (Figure 1b, Figure 2b and Figure 3b), indicating that our method reliably retrieves the relevant concept among hundreds of candidates ($362$ in IDO, $1687$ in PO, and $\mathrm{19,034}$ in HPO). The same is observed for Hit@10 for Intersection with $\alpha$-embeddings.

We also evaluated the subsumption violation rate as we varied the embedding size and observed that it remained stable and very low. The average violation rate was 0.037 for PO and 0.061 for IDO across all tested Emb-size values, indicating that the subsumption test is largely satisfied by our FALCON-embeddings. α-embeddings have subsumption violation rates of 0.0 by construction.

5.2.2. Impact of Fuzzy Operator

Table 2. Comparison of fuzzy operators for PO (k = 10).

Scenario	Metric		F-Emb.			$\mathit{\alpha }$-Emb.
		Product	Łukasiewicz	Gödel	Product	Łukasiewicz	Gödel
Union	MRR	0.316	0.571	0.038	0.897	0.899	0.797
	Hit@k	0.607	0.940	0.114	0.980	0.989	0.977
Intersection	MRR	0.376	0.298	0.018	0.596	0.570	0.588
	Hit@k	0.693	0.581	0.037	0.892	0.802	0.900
Ablation	Overlap@k	0.356	0.516	0.163	0.842	0.867	0.864
Subsumption	Violation	0.054	0.037	0.377	0.0	0.0	0.0

and

Table 3. Comparison of fuzzy operators for IDO (k = 10).

Scenario	Metric		F-Emb.			$\mathit{\alpha }$-Emb.
		Product	Łukasiewicz	Gödel	Product	Łukasiewicz	Gödel
Union	MRR	0.674	0.835	0.263	0.967	0.958	0.958
	Hit@k	0.988	1.0	0.702	1.0	0.994	0.994
Ablation	Overlap@k	0.630	0.708	0.248	0.966	0.966	0.977
Subsumption	Violation	0.093	0.061	0.329	0.0	0.0	0.0

report the effect of different fuzzy operators (Product, Łukasiewicz, and Gödel) on the quality of similarity-based search. For FALCON-embeddings, the performance of fuzzy operators was that Łukasiewicz performed best, and Product outperformed it for intersection tests. The performance of Gödel was very bad. FALCON struggled to generate interpretations for Gödel operators, and its performance was significantly worse. Because Gödel t-norms are flat and non-smooth, FALCON’s gradient-based training obtains almost no signal for most terms, making optimization unstable and slow.

For $\alpha$-embeddings membership is calculated directly, and the performance between fuzzy operators is very similar. Product outperforms the others slightly. This is because membership values in $\alpha$-embeddings are computed directly using the chosen $t$-norm. Furthermore, in the crisp case of $\alpha =0$ all three $t$-norms would have the same behavior. Thus, the selection of a fuzzy operator for α-embeddings matters less and is up to user preference.

Overall, the impact of the fuzzy operator choice can vary significantly. For optimization-based methods, such as FALCON strict, smooth $t$-norms (Product, Łukasiewicz) will perform best. Whether Product or Łukasiewicz outperforms the other depends on the ontology’s structure. Though all operators follow the same general semantics for fuzzy conjunction, disjunction, and negation, the capability of a reasoner to optimize for them is critical to their performance. Consequently, gradient-based training obtains almost no signal from Gödel, making optimization unstable and slow. For $\alpha$-embeddings the choice of t-norm tends to fine-tune the results rather than drastically change them. However, in the non-crisp case, Product operators slightly outperform the others for larger ontologies with intersections.

5.2.3. Impact of Similarity Function

Table 4. Comparison of similarity functions for PO (k = 10).

Scenario	Metric	Cosine	E-Dist	Dot
Union	MRR	0.571	0.462	0.011
	Hit@k	0.940	0.641	0.033
Inter.	MRR	0.298	0.214	0.001
	Hit@k	0.581	0.426	0.006
Ablation	Overlap@k	0.516	0.371	0.917

shows the impact of the similarity function on the quality of concept retrieval for PO’s FALCON-embeddings. Overall, Cosine similarity yields the best performance across most scenarios, particularly for Union and Ablation, and performs competitively in Intersection. In contrast, Euclidean-distance similarity performs relatively poorly in Union and Ablation tests but shows strong results in the Intersection scenario, where the composite concept embeddings are sparse and concentrated near zero. This is expected, as Euclidean-distance can be more sensitive to small differences in sparse vectors, while Cosine similarity is better suited for cases where vectors have many non-zero components, such as in unions.

The Dot-product similarity function is not a useful similarity measure for our embeddings. The root concept and other concepts high up in ontology will have embedding vectors that are dense with values larger than concepts lower in the ontology. Dot-product similarity, when computed for any concept and the remainder of the ontology, will likely exhibit the highest degree of similarity to the root and its children because of this. As a result, the top-$k$ lists produced by Dot-product are largely all the same. This lack of discrimination makes Dot-product ineffective for distinguishing between concepts.

Similar trends are observed for IDO’s FALCON-embeddings and all three ontologies’ $\alpha$-embeddings.

5.2.4. Impact of $\alpha$ in $\alpha$-Embeddings

Figure 4 shows how varying $\alpha$ affects the performance of Union, Intersection, and Ablation evaluations. Overall, for each ontology and evaluation, there is a minimal $\alpha$ that has the best performance. Any increase of $\alpha$ beyond this point worsens results. For Union, the MRR score forms a downward curve, with larger ontologies being narrower. As parent concepts are constructed using the fuzzy union aggregation, the similarity between the composite concept and the parent should always be a perfect match. As discussed in Impact of Embedding Size (Section 5.2.1), the reason for the initially lower performance is duplicate embeddings, a factor that has more impact on larger ontologies when the Emb-size is small. The drop in MRR with higher $\alpha$ values is because concept embeddings start to resemble identity vectors and are no longer distinguishable. The trend for Intersection is similar to Union, and the cause is the same. Ablation shows a consistent decrease in performance as $\alpha$ increases. This is caused by the increase in similarity among siblings. As $\alpha$ increases, the negated sibling limits the maximum value of the intersection, increasingly creating a composite embedding that resembles the empty set. Inversely, the union of many highly related siblings starts to resemble an identity vector.

There are also other factors that result in the initially lower performance. For hierarchical and polyhierarchical ontologies, such as IDO, PO, and HPO, non-fuzzy $\alpha$-embeddings ($\alpha =0$) should have near-perfect performance for Union, Intersection, Ablation, and Subsumption. This is by construction, as the $\alpha$-embeddings are made using the fuzzy union aggregation, which guarantees all four. However, depending on the ontology’s structure, Union and Intersection may not perform perfectly. Union tests will perform worse if there are concepts that only have a single child, as both the child and the parent will have the same embedding. Intersection tests worsen when multiple concepts $C$ with the same direct disjoint parents $A$ and $B$—intersection siblings. Additionally, other complex structures may produce complications or result in duplicate embeddings. IDO, PO, and HPO have a few such structures. However, among the easily detectable structures, seen in

Table 5. Statistics of structures in ontologies that can reduce α-embedding performance.

Ontology	# of Single Child	# of Inter. Matches
IDO	24	—
PO	131	26
HPO	1177	76

, they comprise very small portions of the ontologies.

A useful observation is that some degree of $\alpha$ can mitigate the need for larger Emb-size. Even small values $\alpha =0.1$ will outperform the crisp case and substantially improve performance.

We did not evaluate for $\alpha =1$ as all concepts would have the same identity vector embeddings. The trends for Product, Łukasiewicz, and Gödel $t$-norms are largely the same, and thus only figures for the Łukasiewicz $t$-norm are shown for these experiments. A consistent relationship is observed between MRR and Hit@k (as seen in Figure 2 and Figure 3), thus only MRR is shown.

5.2.5. Random Walk and Concept Similarity

As shown in Figure 5 and Figure 6, in both PO and IDO, moving away from a concept in the ontology hierarchy results in a consistent decline in similarity, indicating that both our FALCON-embeddings and $\alpha$-embeddings reflect the structural semantics of the ontology. The decline is steeper at smaller distances and gradually plateaus as the distance increases. This is because once the traversal moves far enough from the original concept, the resulting concepts become sufficiently unrelated that their similarity to the original concept approaches a low baseline. Further increasing the distance does not significantly alter this similarity, as the concepts are already semantically distant.

For $\alpha$-embeddings Figure 6 shows that with very low $\alpha$ values, concepts only have a little similarity with those a few steps away. This matches the intuition that for $\alpha =0,$ concepts only have similarity to their subtree and ancestors—the majority of ontology concepts would be neither. Furthermore, having any amount of α greatly improves the distinguishability of concepts by removing the occurrence of duplicate empty set embeddings. For high α values, all concepts grow to be highly similar. Thus, $\alpha$ serves two purposes that smooth out similarity over distance: the removal of empty set embeddings and the increase in similarity among sibling concepts.

5.2.6. Comparison with Baseline

Table 6. Comparison of embeddings and baseline (k = 10).

Scenario	Metric	Basline		F-emb.		$\mathit{\alpha }$-emb.
		IDO	PO	IDO	PO	IDO	PO
Union	MRR	0.015	0.003	0.835	0.571	0.958	0.899
	Hit@k	0.020	0.00	1.0	0.940	0.994	0.989
Intersection	MRR	—	0.004	—	0.298	—	0.570
	Hit@k	—	0.003	—	0.581	—	0.802
Ablation	Overlap@k	0.68	0.028	0.708	0.516	0.966	0.867
Subsumption	Violation	0.358	0.455	0.061	0.037	0.0	0.0

compares our FALCON-embeddings and $\alpha$-embeddings with the Baseline embedding, which is constructed using random membership values. As shown, Baseline consistently underperforms across all metrics and scenarios. While the baseline provides each concept with unique identifiers, it lacks semantic alignment with the ontology. In contrast, both of our embeddings capture richer concept relationships and yield more meaningful similarities, particularly for user-defined queries involving multiple or complex constraints. $\alpha$-embeddings perform the best because they are constructed to satisfy subsumption axioms, which our evaluation tests for. At the same time, our FALCON-embeddings are derived from fuzzy interpretations trained to satisfy the full set of ontology axioms, including subsumption relationships and the overall hierarchical structure.

5.2.7. Runtime Performance Analysis

Fixing the Emb-size to 10,000 and using Baseline embeddings, the primary factor affecting query evaluation time is k, the number of similar concepts retrieved. We exclude FALCON’s training time or $\alpha$-embedding construction time from this analysis, as it is an offline cost, and report only the runtime of query answering. Figure 7 shows the runtime as k varies. As shown, our approach scales with k while consistently providing near-instant responses (under 10 ms) for all tested values of k and both ontologies.

5.3. Discussion and Takeaways

Our experiments demonstrate that fuzzy ontology embeddings provide a robust and interpretable framework for ontology-driven concept retrieval. Across all evaluation scenarios and metrics, our approach outperforms the baseline that uses random embeddings. This confirms that embeddings trained to satisfy ontology axioms—especially subsumption, intersection, and disjointness—capture meaningful semantic information that supports accurate similarity search. In particular, the union, ablation, and intersection tests show that our embeddings preserve logical structure and semantic composition, even for composite concepts not explicitly present in the ontology. α-embeddings similarly showed strong performance at satisfying ontology axioms when adjusted to match an ontology.

We also observe that the choice of hyperparameters (e.g., embedding size, fuzzy operators, similarity functions) impacts performance, but often with diminishing returns. An embedding size of around 500 for the FALCON-embedding was sufficient to saturate performance, and while different fuzzy operators yield slightly different results, they generally preserve the same semantics. Cosine similarity proves to be the most effective distance measure overall, especially for union-based queries, whereas Dot-product fails to distinguish between embeddings in most cases. Raising α for α-embeddings increases similarity among nearby concepts. Moreover, low values of α can significantly improve the performance for small embedding sizes. Finally, runtime analysis confirms that our method supports fast query evaluation, returning top-k results in under 10 ms for both ontologies. These findings suggest that our method is practical, scalable, and well-suited for flexible and semantic-aware ontology search.

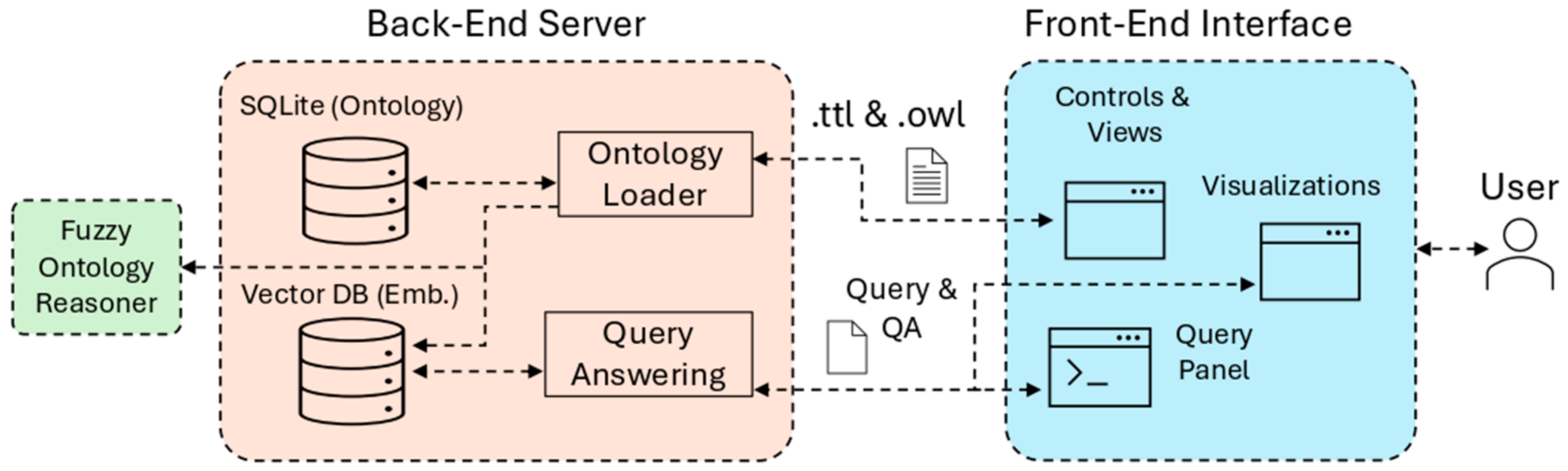
6. The FuzzyVis System

In this section, we present our prototype system, FuzzyVis. Section 6.1 describes its architecture and important implementation details. Section 6.2 further discusses the back-end server functionality. Section 6.3 does the same for the front-end interface. Lastly, Section 6.4 explores the prior Example 1 in greater depth as a usage scenario that shows how FuzzyVis supports ontology exploration and search through visual query building and approximate reasoning. FuzzyVis is a research prototype and is not approved for clinical diagnostic use.

6.1. FuzzyVis Architecture and Implementation

FuzzyVis is a web-based system designed for ontology exploration. Figure 8 shows its overall architecture. The front-end is built using HTML5, CSS, and JavaScript, with D3.js (version 7) for interactive visualizations. The back-end is implemented in Python (version 3.12) and communicates with the front-end via a FLASK API.

The system workflow begins with the user uploading ontology data in standard formats such as .owl or .ttl. The back-end then processes and stores the ontology, making it available for the front-end. Once loaded in the front-end, users can explore the ontology through interactive views and visualizations. This exploration is supported by panels and controls that allow users to manipulate views, adjust parameters, and construct queries. As users interact with the system, FuzzyVis’s front-end dynamically retrieves relevant ontology data from the back-end.

While the front-end handles user interaction and visualization, all computations—including query evaluation and similarity search—are performed on the back-end. Embeddings for primitive concepts are stored in a Chroma vector database, as described in Section 4. This enables fast query resolution, especially for ontologies with thousands of concepts and/or large embeddings.

The remainder of this section describes the back-end (Section 6.2) and front-end (Section 6.3) in more detail, following the architecture shown in Figure 8.

6.2. Back-End Server

The back-end consists of four main components: the ontology loader, ontology database (SQLite), vector (embedding) database, and the query answering component. The ontology loader handles uploaded ontologies—pre-uploaded or submitted via the front-end. It parses ontology files and stores their contents in an ontology database using the OwlReady2 python library [80]. During this process, additional metadata and statistics—such as subtree sizes and number of children—are computed and stored. The vector database stores the embeddings for each primitive concept which are generated using either an external fuzzy ontology reasoner or our $\alpha$-embeddings as we explained in Section 4.4. Just like for ontologies, users can submit embedding vectors or use pre-uploaded ones. The vector database is separate from the ontology database to perform quick similarity calculation and top-k retrieval. Our implementation uses Chroma for its vector database. The query answering component computes embeddings via the recursive rules in Definition 2 for user-defined composite concepts using the embeddings of primitive concepts from the vector database. The vector database uses these composite concept embeddings to retrieve similar primitive concepts. A FLASK server API handles communication between the back- and front-end.

6.3. Front-End Interface

The front-end is composed of several regions consisting of panels and controls that support interactive ontology exploration. Figure 9 shows an overview of the front-end interface as seen by the user. The primary visualization takes up the central region of the interface and is the user’s primary means of navigating the ontology (Figure 9A). Users can change between different visualizations—treemaps, nested lists, and network graphs—in this central region. The second region (Figure 9B), the top header, provides quick access for concept search, switching between loaded ontologies, and loading ontologies. Users can manipulate the behavior and control the presentation using the visualization controls in the leftmost region (Figure 9C). The first of the rightmost regions (Figure 9D) is the concept panels, where users can store concepts for future use and look at concept details. The second rightmost region (Figure 9E) is the query building panels, where users define queries and examine their results. FuzzyVis’s front-end is compatible with all major web browsers.

Below, we describe the main components of the front-end interface in more detail.

6.3.1. Primary Visualizations

FuzzyVis’s central region contains the primary visualization (Figure 9A). Here, users see a representation of the ontology to aid them in exploration and understanding. Each component of FuzzyVis serves to modify, control, and navigate the primary visualization, with the back-end providing any information needed by the primary visualization. The primary visualization can take the form of any suitable representation of the ontology. Visualization should meet the following criteria:

• Concept Distinguishability. Each concept in the visualization must be distinct and individually identifiable, at a reasonable scale. The density of concepts must be low enough that users can distinguish them. As well, concepts must have some clear identifier—often this is a label.
• Consistent. The visualization should represent concepts and relationships in a consistent and identifiable manner.
• Dynamic and Interactive. The visualization should react to users’ actions. Static representations may be sufficient for small and simple datasets, but ontologies are often neither small nor simple. Dynamic visualizations adapt to users’ needs and can change to show the ontology information that they are interested in, especially when presenting the entire ontology is impractical.
• Property-revealing. The visualization should present secondary information and metadata of concepts. Features such as concept descriptions, depth, subtree size, and metadata contain information necessary to understand the content of ontologies. Users may be unfamiliar with concept labels and require secondary information to understand an ontology.
• Space-efficient. The visualization should utilize the available space fully. Some ontologies have a large amount of content and visualizations that make poor use of space, are either sparse or dense to the point of uselessness.
• Structure-revealing. The visualization must showcase the primary semantic structure of the ontology. In most cases, this is the concept subsumption hierarchy. One of the primary purposes of ontologies is to express how concepts relate to one another. This information is critical to users’ understanding of ontologies.

Classical visualizations such as nested lists, icicle charts, network graphs, and treemaps only partially meet these requirements. In fact, no single static visualization can satisfy every requirement. Network graphs become unreadable with large numbers of concepts, nested lists waste space, and treemaps struggle to convey secondary information. Our approach addresses these limitations by combining the primary visualization with secondary panels for additional details and utilizing dynamic interactive visualizations. To illustrate how FuzzyVis meets these requirements, we describe the nested-treemap version of the primary visualization.

Nested-treemaps represent concepts as rectangles, place sibling concepts adjacent to each other, and nest child concepts inside their parents’ area to indicate hierarchy. They are well-suited for ontology visualization because they clearly distinguish concepts, are consistent, space-efficient, and structure-revealing. Extending nested-treemaps to be dynamic and interactive allows for the display of secondary properties and addresses the problem of excessive concept density. 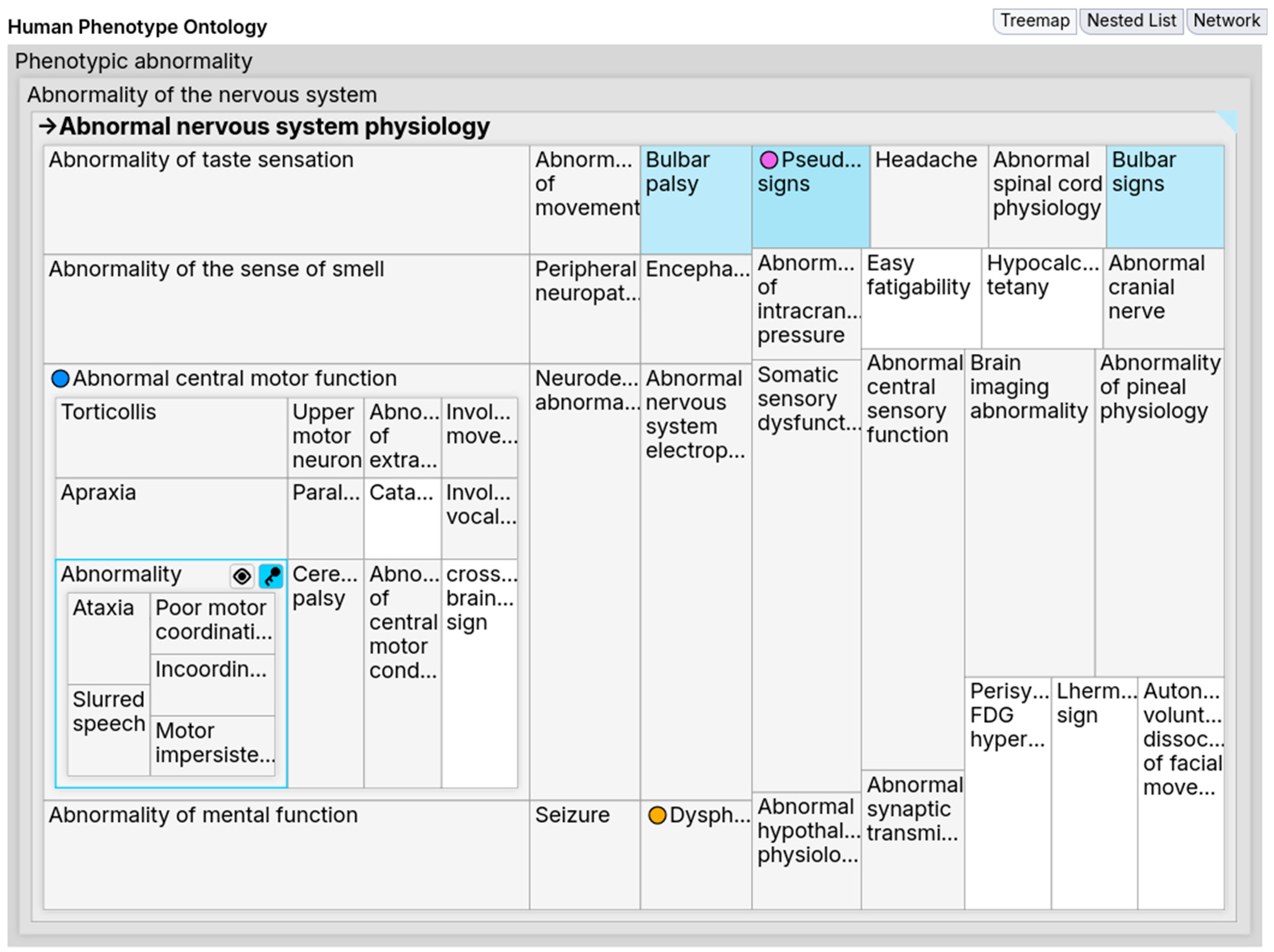Figure 10 shows FuzzyVis’s nested-treemap (hereafter, the treemap), which displays concepts within an adjustable distance of a selected concept. As users navigate, the treemap updates to show related concepts and integrates with other FuzzyVis front-end components to support exploration.

Selecting a concept in the treemap refocuses the visualization onto it, allowing users to drill down into its subtree or navigate upward to parent concepts. Users can also drag concepts to other components and pin them for later reference. Pinning creates visual marks that aid in orientation by acting as signposts. These marks help identify when a concept appears in multiple subtrees. For example, in HPO, the Cardiac valve calcification concept is a child of both Cardiovascular calcification and Abnormal heart morphology; when pinned, it becomes more noticeable in both locations, indicating structural overlap. Without such aids, users would need to manually read labels to detect these cases. Once users have collected concepts of interest, they can create queries using the Query Building Panels to guide further exploration.

Users may want to focus on a concept while retaining its context within the ontology. Simply increasing depth causes two issues. One, deeper child concepts receive minimal space, forcing users to mouse over for tooltips to identify them. Two, densely populated subtrees create visual clutter that overwhelms users. Selecting the concept alone does not solve this, as it refocuses the visualization and removes the surrounding context.

To address this, we implemented a toggle for a focus mode that enables on-the-fly visual distortions. During focus mode, when users mouse over a concept, FuzzyVis applies a discrete Cartesian distortion (often referred to as a fisheye distortion or lens), enlarging its area while preserving relative position. Within the expanded area, the subtree extends, showing the focused concept’s children; users can drill down further by mousing over these until no more space is available. If users want to explore multiple subtrees simultaneously, they can lock a concept as a locus, and the distortion will maintain multiple focal points. Moreover, locked loci can be transformed into a different visualization. For example, a concept cell can be converted to a node network graph or a panel showing class details. In essence, this technique directly addresses the problem of maintaining context while refocusing.

Figure 10 shows an example of focus mode in use. With depth set to two and Abnormal nervous system physiology selected, no concepts other than its children would be visible. Yet, with focus mode turned on, hovering over Abnormal central motor function fills the subtree with child concepts. Afterwards, when the user mouses over the child Abnormality of coordination, the subtree is further extended to show this concept’s children (e.g., Slurred speech). This can continue until a leaf node is reached or space runs out, but the user decided this depth was sufficient and locked Abnormality of coordination as a locus. Focus mode thus offers a dynamic and space-efficient way to explore deeper while maintaining orientation. Furthermore, dynamic distortions can be applied to other kinds of visualizations, such as network graphs and charts.

Users adjust the primary visualization through the Visualization Controls. For nested-treemaps, users can adjust depth, the label content (e.g., depth numbers), tiling methods, concept visibility, and highlighting. Such controls are essential, as different ontologies are best viewed with different settings. For instance, in HPO, Abnormality of the musculoskeletal system dominates the space when scaling is proportional to subtree size, making the smaller Abnormality of the voice nearly invisible. Equal scaling makes both visible, reducing the chance of missing concepts. Furthermore, users can toggle such options to see how the visualization changes—turning equal scaling on and off shows users which concepts take up the majority of an ontology while quickly returning to a view suitable for navigation. These adjustments enable richer exploration without restricting users to suboptimal visualizations.

FuzzyVis’s primary visualization, in conjunction with other front-end panels, provides a spatial overview of ontology structure and semantics. By supporting dynamic, interactive navigation, it helps users quickly form mental models and identify key regions of interest—an essential capability for working with complex knowledge domains where manual inspection would be slow and overwhelming. Ultimately, the primary visualization serves as the main interface through which users interact with and explore ontologies.

6.3.2. Header Bar, Visualization Controls, and Concept Panels

FuzzyVis’s header bar (Figure 9B) contains three components: a search bar for concept lookup, tabs for switching between ontology instances, and access to the ontology selection panel. These allow users to load ontologies, switch among them, and perform quick keyword searches. The search bar allows users to quickly navigate to or verify the existence of familiar concepts. For example, in a biomedical ontology, searching for Heart confirms whether it is present and suggests related results (e.g., Heart block) for discovery. The header tabs let users switch between multiple loaded ontologies. This aids users in comparing different regions in large ontologies, embeddings, and fuzzy operators, or exploring related ontologies. The last component is the ontology selection panel, where users can load preprocessed ontologies or upload their own and configure fuzzy logic operators.

The left region of FuzzyVis contains controls and panels for adjusting the primary visualization (Figure 9C). This region has three components: the highlight panel for applying color-based rules, the visualization control panel for adjusting the primary visualization’s behavior, and a help panel explaining system interaction. The highlight panel allows users to annotate the primary visualization by creating rules that assign colors to concepts. When a concept satisfies multiple rules, colors are blended. For example, a rule may color concepts blue if their labels contain bulbar, making concepts such as Bulbar Palsy and Pseudobulbar signs stand out. Highlighting helps users quickly identify concepts of interest to form landmark and neighborhood knowledge. Isolated colored concepts may indicate uniqueness, while clusters can suggest similarity. Highlighting thus provides essential visual cues for navigation and can be extended to support ontology-specific rules when needed. The visualization control panel configures the behavior of the primary visualization, with available options varying by visualization type. These controls let users tailor the visualization to their needs, as static parameters are often insufficient. For example, a user on a small monitor may require a more horizontal treemap layout to read labels without hovering. The final panel—help and keybindings—provides usage guidance and can be hidden if not needed. While a full interactive tutorial would be ideal, it is beyond the scope of this prototype.

The first section of the right region of FuzzyVis contains the concept panels (Figure 9D), which serve two purposes: organizing the collection of concepts for later use and displaying concept details. As users explore ontologies, they may find concepts worth revisiting or using in queries. These concepts can be scattered across the ontology, making them inconvenient to access without a collection. Details are also needed to confirm relevance. For example, in HPO, a user studying skull-related conditions may collect both Abnormal cranial nerve physiology and Abnormality of the head, despite their distance in the hierarchy. Storing them in the collection allows quick navigation between them. At the same time, the concept details provide users with details such as labels, IRIs, parents/child relations, and definitions. Overall, the concept panels allow for quick navigation and query formulation.

6.3.3. Query Building Panels

The second section of the right region contains the query building panels (Figure 9E), which allow users to create, resolve, and analyze queries. Navigating an ontology hierarchically only reveals part of its structure and semantics, and inspecting concepts one at a time can be inefficient. Query building enables nonlinear exploration, helping users verify inferences or discover related concepts. We discuss this in-depth in our usage scenario (Section 6.4).

Queries are created in the query builder control (Figure 11a) from concepts, other queries, and standard logical operators (AND, OR, NOT), corresponding to intersection, union, and negation. Once finalized, the front-end sends the query to the back-end resolver, which converts it to a composite concept. This composite concept’s embedding is compared with primitive concept embeddings, returning the top-k most similar concepts. Queries may contain any concepts, including logically inconsistent combinations, which, while ineffective when resolved with traditional embeddings, can still yield meaningful results with our fuzzy ontology embeddings.

Results are displayed in the query results panel (Figure 11b), showing similarity scores for each primitive concept. Users can expand results for details or drag them into new queries or other components. The similarity stain option in the visualization control panel colors the primary visualization according to these similarity values. This results panel offers users a quick view of how the query’s composite concept relates to the overall ontology.

6.4. Usage Scenario

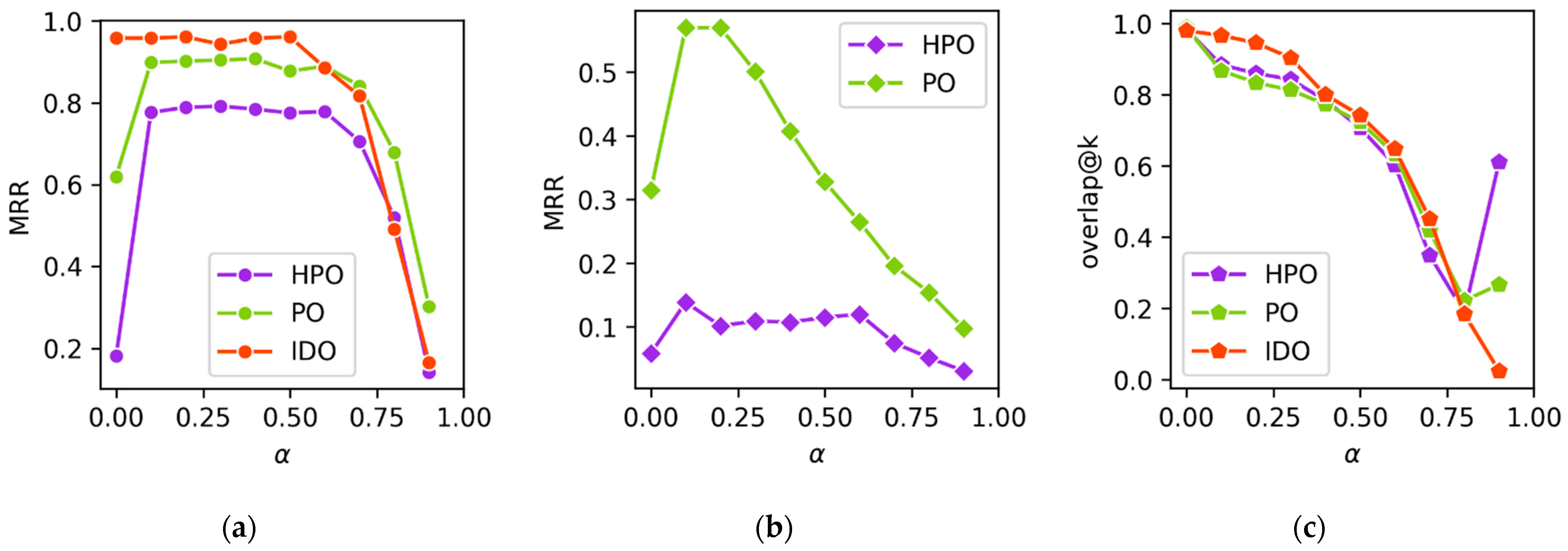
The following scenario illustrates how FuzzyVis supports ontology exploration and the practical applications of fuzzy logic queries. FuzzyVis is not intended or approved for use as a clinical diagnostic tool, and this scenario is intended to illustrate the potential of using fuzzy ontology embeddings for visual query building and exploration. We use the HPO for this scenario. We assume the user knows basic medical terms but is unfamiliar with HPO. The embedding used is an $\alpha$-embedding (as described in Section 4.4) with $\alpha =0.25$, and embedding Emb-size = 10,000. At $\alpha =0.25$ the embeddings express sibling similarity while not hurting concept distinguishability overmuch. The value for Emb-size was chosen as it was when HPO started to no longer see minor performance improvements. For fuzzy operators, we use the product t-norm for conjunction, its t-conorm for disjunction, and the standard negator for negation, as these performed best during evaluation of $\alpha$-embeddings (Section 5.2.2).

A physician, henceforth the user, has a patient who has difficulty speaking and swallowing, with no history of immune disorders and no signs of infection. To help this patient, the user has two goals. One, they want to identify possible conditions that could explain the symptoms. Two, they wish to learn about any secondary ailments that the patient may experience now or in the future. The user knows that HPO contains information about abnormal conditions, but its size and complexity necessitate the use of an exploratory tool. Thus, the user launches FuzzyVis to explore HPO and help their patient.

After FuzzyVis loads HPO, its front-end—displaying a nested-treemap as the primary visualization—presents the ontology to the user. The user starts their exploration by adjusting the settings in the visualization control panel. First, the user sets cell scaling to be equal, as the relative size of concepts is irrelevant to their goals. Second, the user sets the tiling so that labels are clearly visible. Lastly, they set visible depth to a low value—HPO has many terms, and seeing too many layers is overwhelming. Afterwards, the user creates highlight rules to stain concepts containing voice, speech, or swallowing for quick identification. With the user’s initial setup complete, they can now quickly identify concepts of interest. Users of FuzzyVis can, with little effort, set up the primary visualization in ways that streamline their future searches.

Seeing the Phenotypic abnormality concept, the user selects it and begins their search. During their search, the user encounters concepts related to their patient’s condition. These concepts are pinned (for easier identification) and added to the concept collection for use in queries. To explore more specific concepts, the user activates focus mode to drill into Phenotypic abnormality’s children. They see Abnormality of the voice, and although it does not contain what they are looking for, it is collected for query use regardless. Additionally, the user spots Abnormality of the immune system and adds it to the collection, to be negated in future queries.

Wanting to quickly find something, the user inputs speech into the search bar. Among the results is the concept Slurred speech, which matches the patient’s symptoms. Selecting it takes the user deeper into the ontology, where they then pin it. Unsure of where they are, the user toggles on the depth numbers and sees that Slurred speech is eight layers deep and has no children. Then, the user increases the depth to view the full ancestry and spots that Slurred speech is within the Abnormality of the nervous system subtree. The user selects this broader concept, reduces depth for clarity, and continues exploring.

Already the user has started to identify landmark concepts related to their problem, has learned the routes between them, and is now aware of the neighborhood in the ontology that contains concepts of interest. By quickly identifying this information, the user efficiently narrows the search space. FuzzyVis’s support for rapid, seamless navigation allows users to quickly see concept contents at a glance and freely navigate large ontologies.

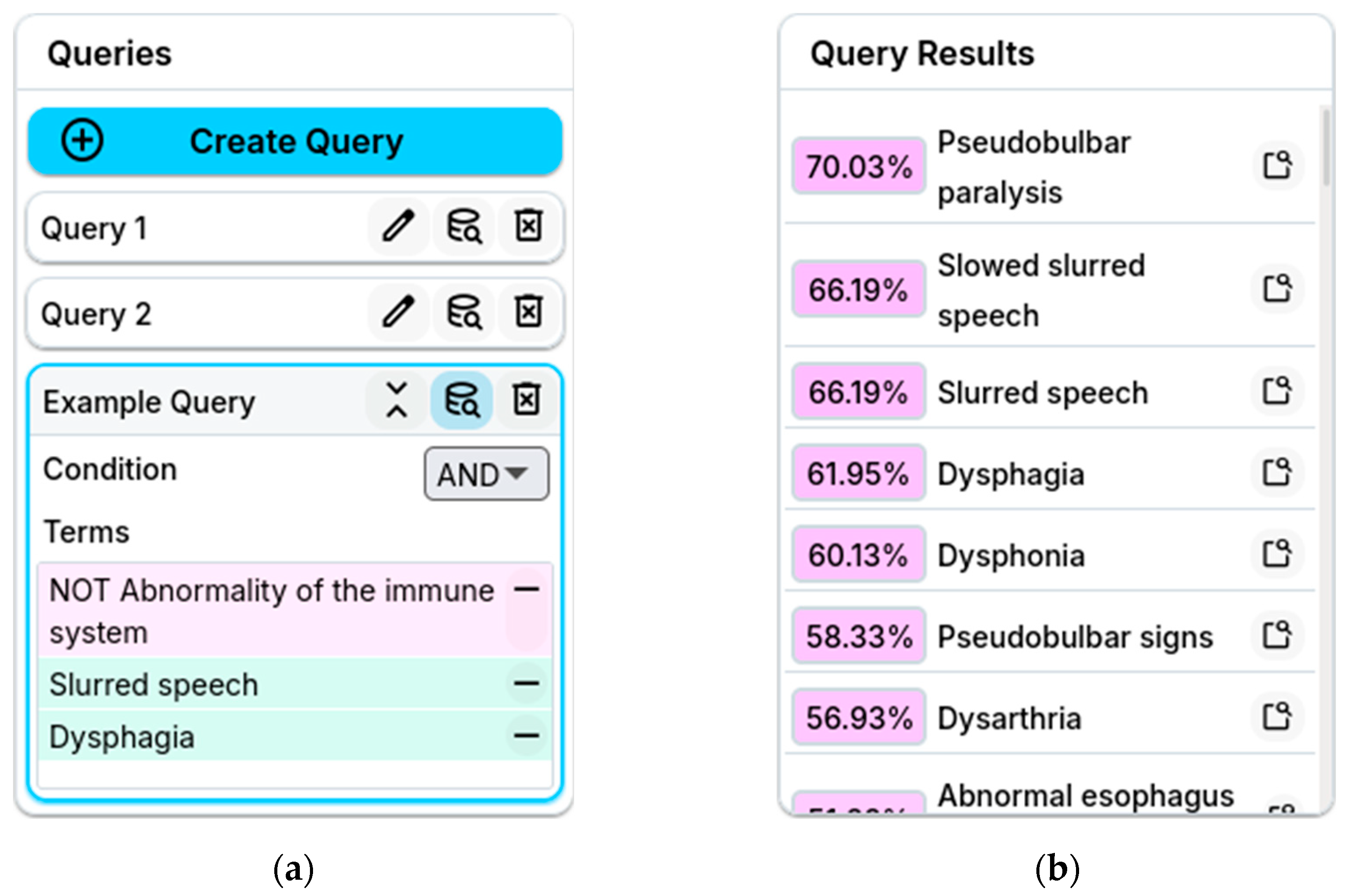
The user’s exploration continues until, within Abnormality of the nervous system‘s child concept Abnormal nervous system physiology, they encounter Dysphagia. The focus mode alternative views and concept details panel show the user that Dysphagia is the medical term for difficulty swallowing. Combined with the earlier discovery of Slurred speech, the user feels ready to construct queries. The user formulates their query as the presence of Slurred speech and Dysphagia while excluding Abnormality of the immune system. They do this by dragging concepts from the collection to the query building panel to form the composite concept $Q$₁:

Q₁ ≡ Slurred speech ⊓ Dysphagia ⊓ ¬Abnormality of the immune system.

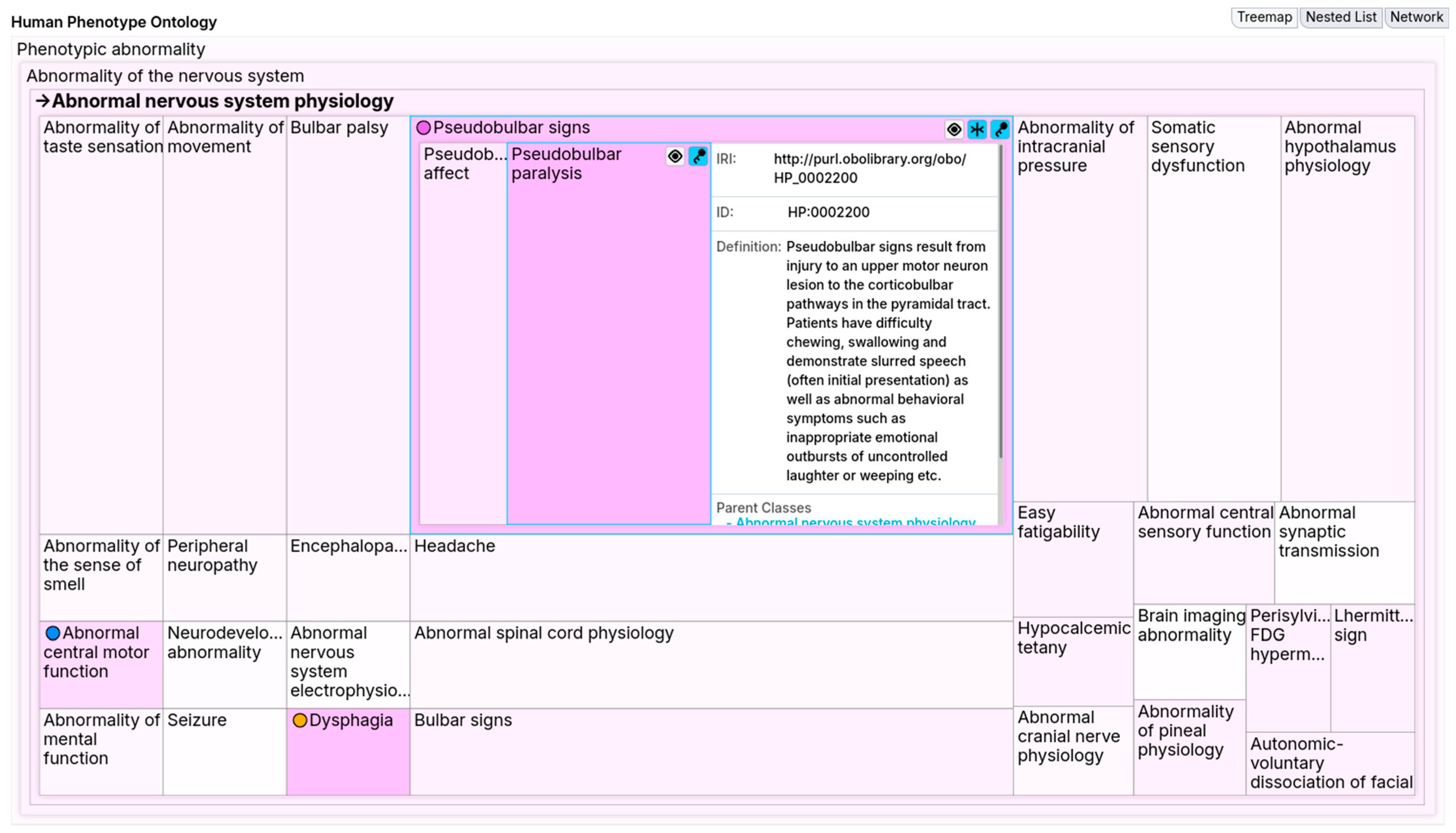
The user submits their query, FuzzyVis’s back-end instantly resolves it, and the front-end updates to show the results. Among these results are concepts such as Pseudobulbar paralysis, Pseudobulbar signs, and Abnormal esophagus physiology. Wanting to locate these concepts, the user enables the similarity stain and spots the highlighted Pseudobulbar signs. Using the focus mode, the user locks and splits Pseudobulbar signs to expand it and see its details. Notably, this reveals Pseudobulbar paralysis within Pseudobulbar signs. Figure 12 shows the combined effect of this similarity stain and focus mode, highlighting the pseudobulbar concepts. These pseudobulbar concepts point to neurological causes that explain the patient’s symptoms. On the other hand, Abnormal esophagus physiology offers an alternative explanation for the symptoms.

These results have now narrowed down potential causes that the user can investigate to diagnose their patient. Such concepts would have been difficult to find with keyword search, as the user’s vocabulary does not match the ontology’s precisely. Moreover, the user would have been unable to find these concepts with SPARQL queries for this same reason. With FuzzyVis, users build queries visually by dragging and dropping concepts and other queries, without needing to type exact labels. Furthermore, nesting queries helps users separate the components of their queries into understandable segments and construct complex concepts. By supporting fuzzy queries, FuzzyVis enables users to find relevant concepts even when their requests are imprecise.

An example of an imprecise query is the user’s search for secondary ailments. The user creates this query by updating their original one to exclude Abnormality of the voice. In a non-fuzzy system, excluding Abnormality of the voice while searching for conditions related to speech and swallowing might seem counterintuitive or overly restrictive. However, because the $\alpha$-embedding captures fuzzy membership across the ontology, the query can still yield useful insights. The new query narrows the focus to concepts returned by the original that are unrelated to Abnormality of the voice. The updated query $Q$₂ is:

Q₂ ≡ Slurred speech ⊓ Dysphagia ⊓ ¬(Abnormality of the immune system ⊔ Abnormality of the voice).

Submitting $Q$₂ returns concepts related to digestive issues, which is expected since Dysphagia belongs to the Abnormal esophagus physiology subtree under Abnormality of the digestive system. This suggests the patient’s condition may affect the digestive system. The fuzzy ontology embeddings preserve such relationships even in complex composite concepts. Armed with this knowledge, the user can further question their patient to narrow down their condition. The user asks about irritability and emotional outbursts to check for Pseudobulbar signs, and inspects the throat to check for Abnormal esophagus physiology.

This scenario demonstrates how FuzzyVis’s features and fuzzy ontology embeddings enable effective ontology exploration. Without prior knowledge of HPO’s structure or query languages like SPARQL, the user was able to find relevant concepts and understand their relationships. The interface’s interactive visualizations allow the user to build queries visually, while fuzzy logic supports the creation of useful queries even without expert knowledge. Together, these capabilities present a flexible and user-friendly approach to exploring ontological information.

7. Conclusions and Future Work

This paper presented FuzzyVis, a prototype system for visual query building over ontologies using fuzzy logic and membership-based embeddings. FuzzyVis enables users to define complex, potentially vague concepts through familiar set operations—intersection, union, and negation—and interprets these as fuzzy sets embedded in a continuous vector space. This representation supports efficient, similarity-based query evaluation. Through an interactive visual interface, FuzzyVis integrates search, navigation, query construction, and result presentation, making query formulation more accessible and intuitive, particularly for non-expert users. By combining symbolic and sub-symbolic techniques, the system supports approximate reasoning and flexible concept retrieval, in contrast to traditional methods that rely solely on formal syntax and strict logic.

As a prototype, FuzzyVis offers several avenues for future development. First, improving performance and scalability for very large ontologies remains essential, requiring optimization of both front-end visualizations and back-end embedding computations. Second, expanding functionality—such as adding collapsible tree views or new panels for organizing and comparing query results—could better support diverse user needs. Third, investigating alternative embedding techniques, especially those optimized for specific ontology types or designed for greater interpretability, may yield improved results. Finally, extending FuzzyVis to handle more expressive ontologies with richer axioms beyond hierarchical subsumption would require enhancements to both the query builder and embedding mechanism, enabling support for a broader range of logical constructs and relationships.

In parallel, systematic user studies—focusing on usability and effectiveness—can be performed to evaluate fuzzy set embeddings. Comparisons to similar tools—non-expert ontology exploration—can also be performed. Moreover, beyond ontology exploration, the underlying approach could also be adapted for related tasks such as document retrieval and triage, where interactive, fuzzy, concept-based querying may help users navigate large document corpora more effectively.