Pruning Policy for Image Classification Problems Based on Deep Learning
Abstract
1. Introduction
- We propose the following methodology to evaluate the impact of the pruning policy on a given classification problem (dataset): consider the impact of the pruning method regardless of the pruning distribution used, consider impact of the pruning distribution regardless of the pruning method used, and select the best pruning policy from a set of choices generated with different pruning methods and distribution types.
- From the case studies used in the application of the proposed methodology, it was possible to disprove the belief that the worst pruning distribution is the homogeneous one, given that, in several contexts, it was even better than its competitors.
- In addition, it should be noted that the pruning policy does not have the same effect on all image classification problems. For example, when using CIFAR10, the differences in accuracy between a good and a less good pruning policy can be less than 5%, while for the Date Fruit Dataset, the differences can be more than 10% for the same cases evaluated.
2. Preliminary Concepts
2.1. Convolutional Neural Networks
2.2. Pruning Policy
2.2.1. Criteria of the Parameters to Be Pruned
- Random: in this case, the filters to be pruned in the convolutional layers are selected randomly.
- Weight: this pruning method is based on the estimation of the importance of the layer’s filters according to their weights. In this method, the L2-norm is calculated in each filter, and the ones with the highest values are kept [30]. This is because in CNNs, the filters at each layer with higher activation maps are assumed to be more important for the performance of the network. In this case, there is no required to use random seeds because Weight is a deterministic method, i.e., it is expected to obtain the same result under the same conditions.
- SeNPIS-Faster: SeNPIS is based on class-wise importance score calculation, which includes a class-wise importance score, class-wise importance score attenuation, and overall importance score [28]. In the case of SeNPIS-Faster, the stage responsible for performing the class-wise importance score attenuation is eliminated in order to significantly reduce the computational cost of applying pruning, with a very small decrease in accuracy (less than 0.5%) compared to SeNPIS [43].
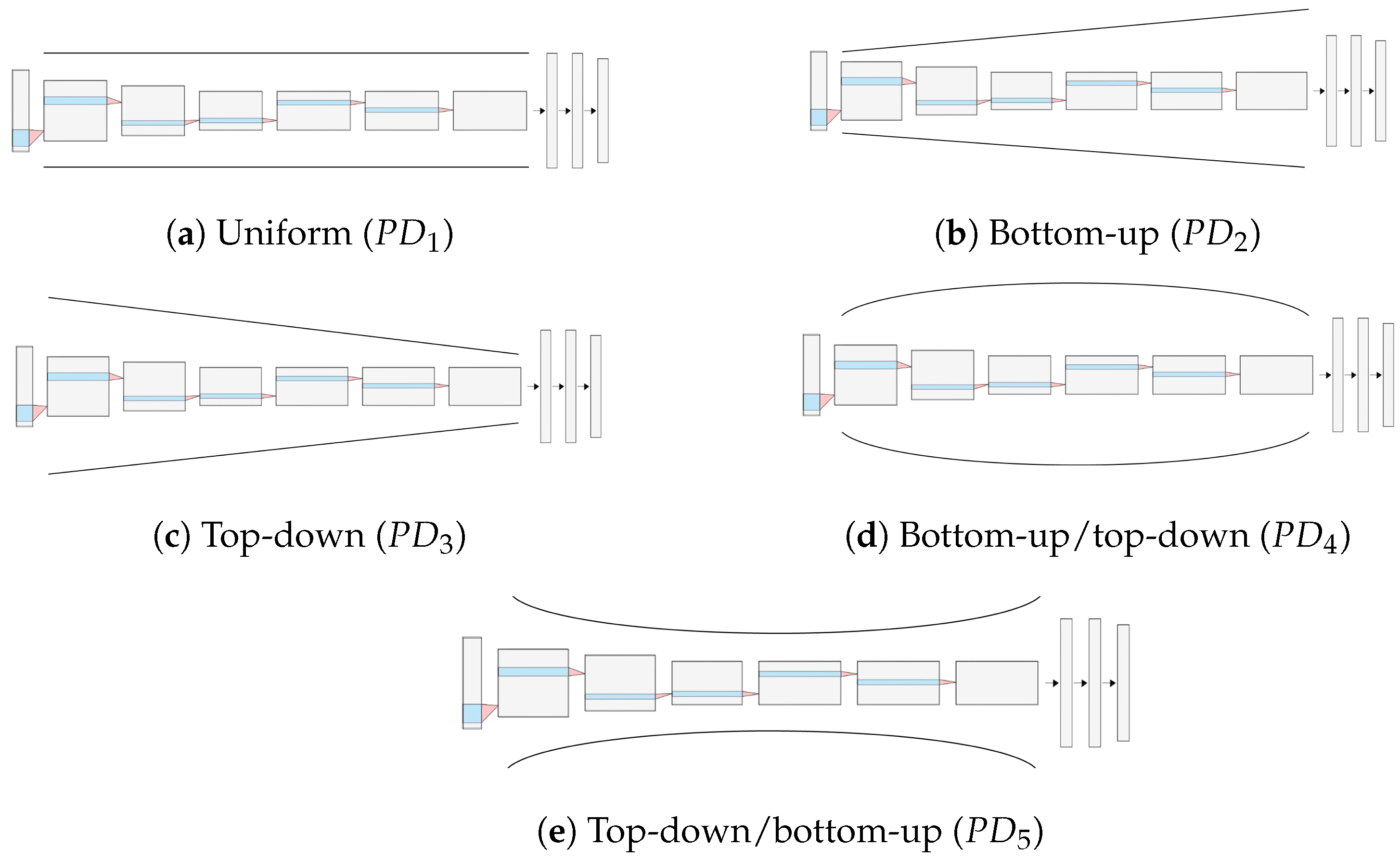
2.2.2. Pruning Distribution (PD)
2.2.3. Network Restructuring or Zeroing of the Pruned Parameters
3. Methodology
3.1. Dataset
3.2. Model Training
3.3. Pruning Hyperparameters: GPR, PD, and Pruning Method
- GPR. Three values, one low, one medium, and one high, were specifically chosen: 20%, 30%, and 50%.
- Pruning distribution. Five types of pruning distributions were selected as follows: uniform (), bottom-up (), top-down (), bottom-up/top-down (), and top-down/bottom-up ()
- Pruning method. Three methods were selected: Random, Weight, and SeNPIS-Faster.
3.4. Model Pruning and Fine-Tuning
3.5. Policy Selection
- In the first one, the impact of the pruning method vs. distribution type is evaluated for each of the GPR values. In this way, the "best pair" can be selected for a given GPR.
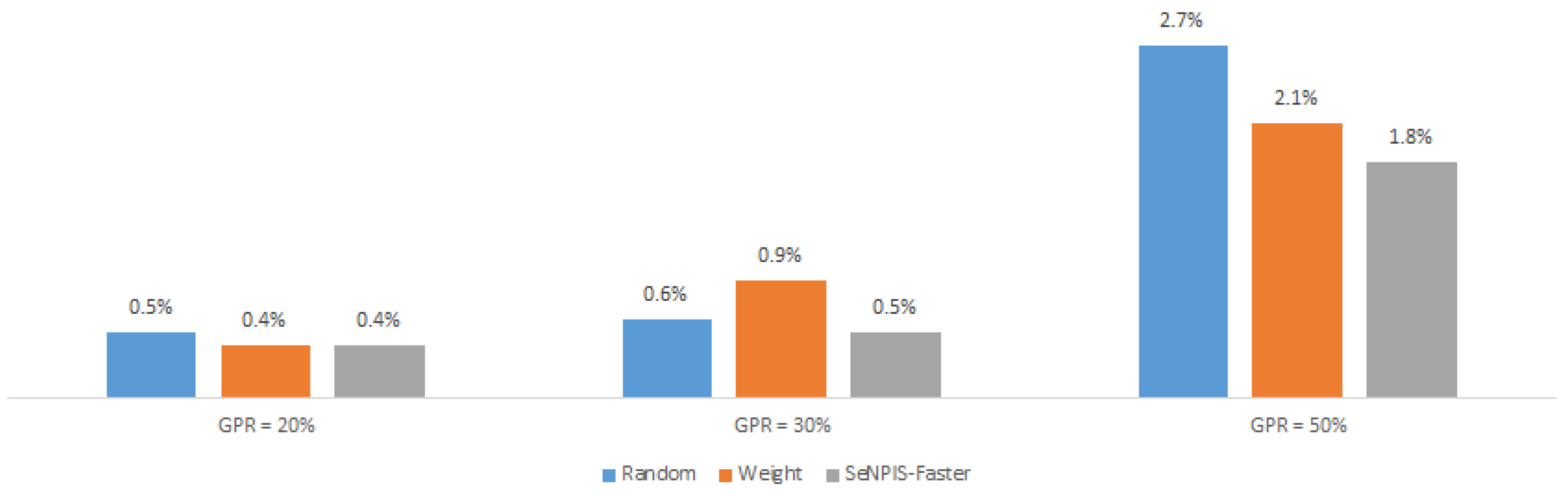
- In the second, the results are grouped by pruning method and GPR in terms of the difference between the best and worst PD. Then, the impact of the PD for each method can be assessed. A high difference value with respect to the selected metric (e.g., F1 or accuracy) means that for this pruning method with this GPR value and for this dataset, a proper PD selection is very important.
- In the third, the results are grouped by pruning distribution and GPR in terms of the difference between the best and worst pruning method. Then, the impact of the pruning method for each PD can be assessed. A high difference value with respect to the selected metric means that for this PD with this GPR value and for this dataset, a proper pruning method selection is very important.
3.6. Model Evaluation Metrics
4. Results
4.1. Case Study 1: Date Fruit Dataset
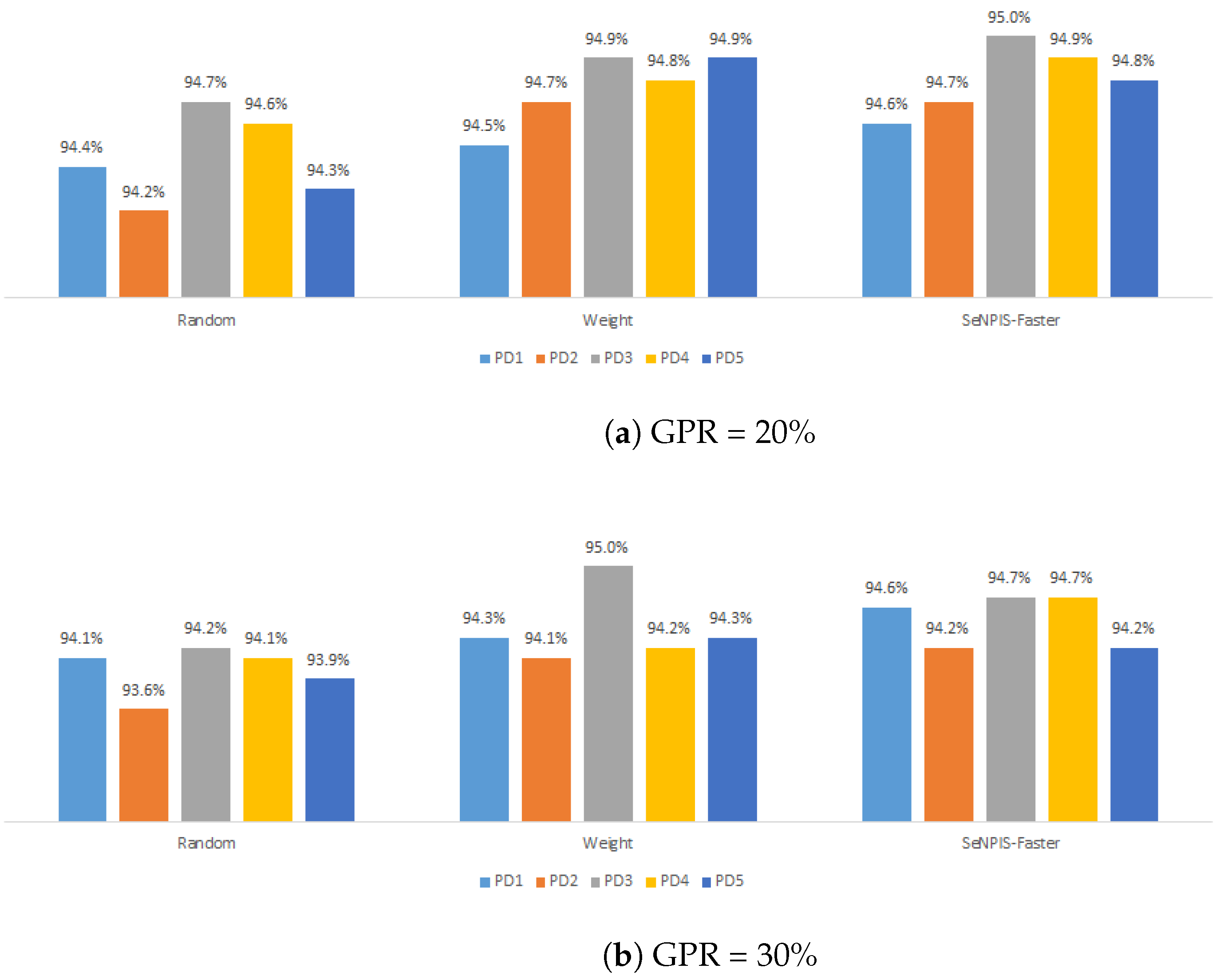
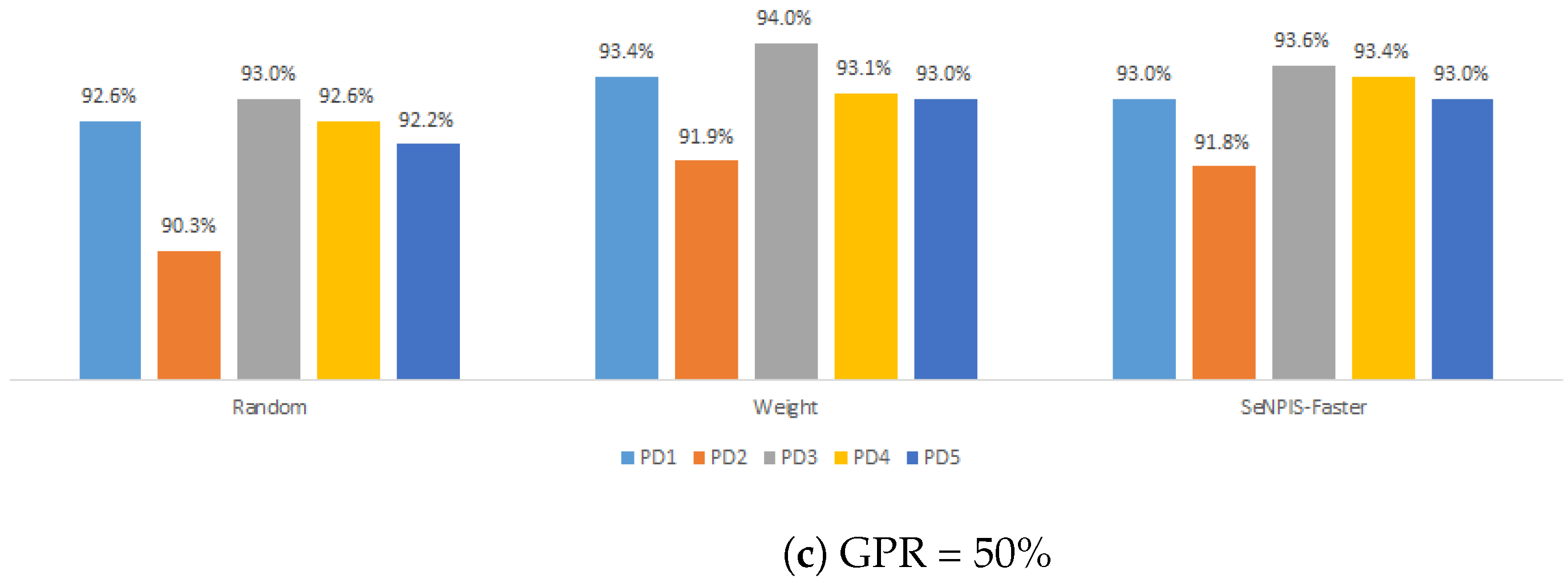
4.1.1. Selecting the Best Pair: Pruning Method vs. Pruning Distribution
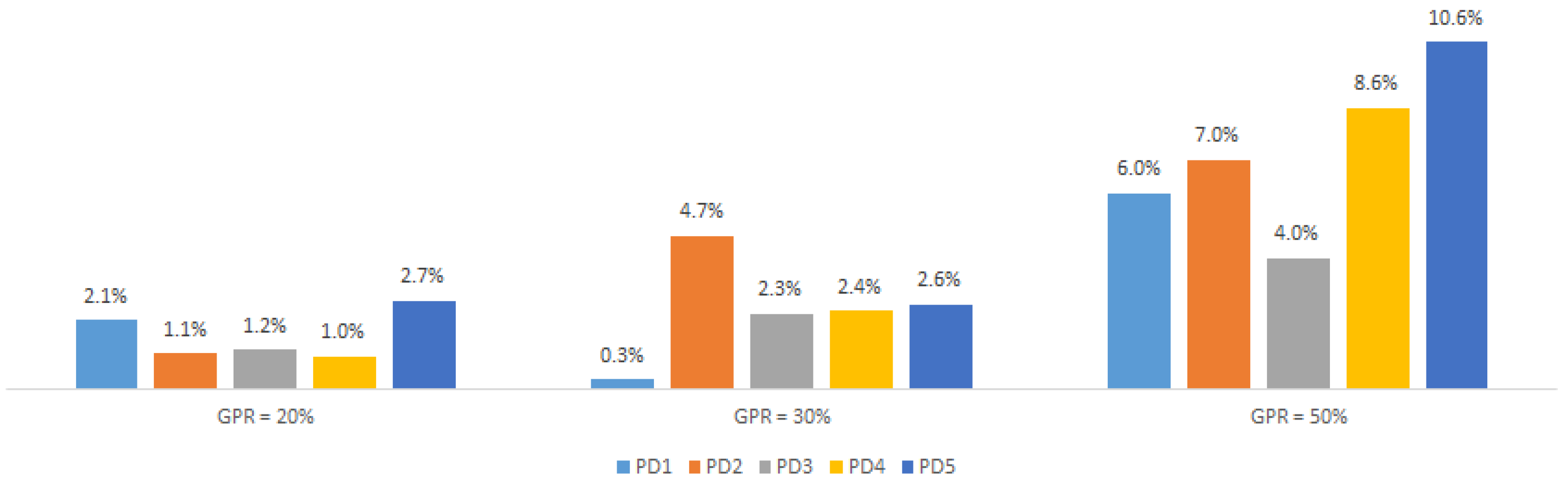
4.1.2. Impact of the Pruning Distribution
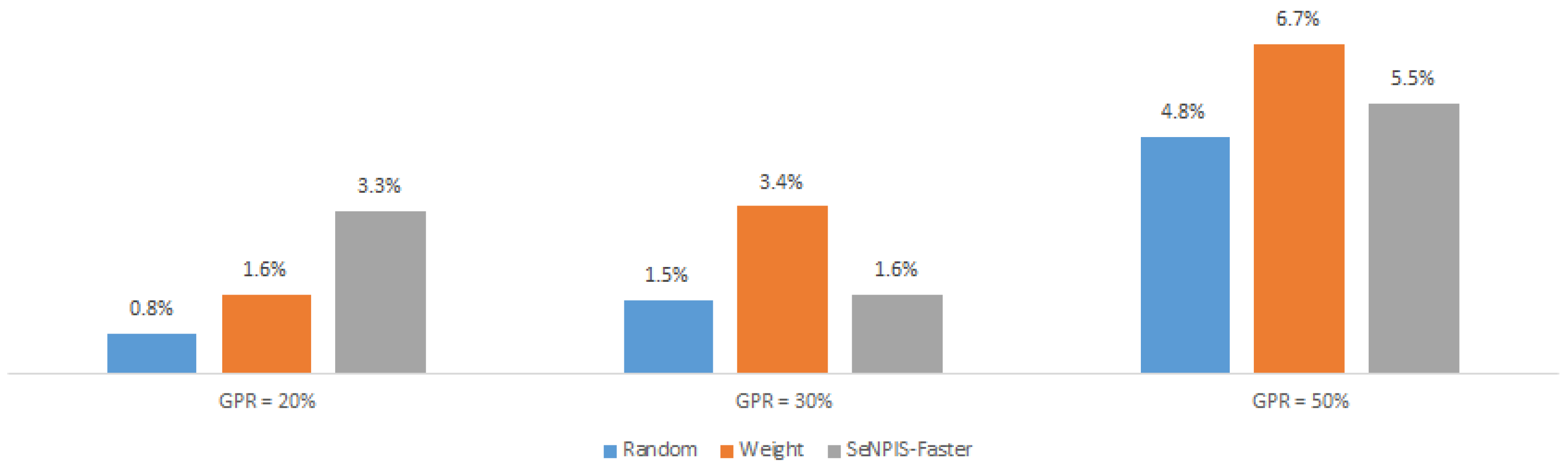
4.1.3. Impact of the Pruning Method
4.2. Case Study 2: CIFAR10
4.2.1. Selecting the Best Pair: Pruning Method vs. Pruning Distribution
4.2.2. Impact of the Pruning Distribution
4.2.3. Impact of the Pruning Method
5. Discussion
5.1. Case Study 1: Date Fruit Dataset
5.2. Case Study 2: CIFAR10
5.3. Advantages of Pruning in CNNs
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACC | Accuracy; |
| CNN | Convolutional neural network; |
| C | Channel; |
| DL | Deep learning; |
| F | Filter layer; |
| FC | Fully connected; |
| FLOPs | Floating-point operations; |
| FLOPS | FLOPs per second; |
| GPR | Global pruning rate; |
| IT | Inference time; |
| PD | Pruning distribution; |
| PR | Pruning rate. |
References
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Altaheri, H.; Alsulaiman, M.; Muhammad, G. Date Fruit Classification for Robotic Harvesting in a Natural Environment Using Deep Learning. IEEE Access 2019, 7, 117115–117133. [Google Scholar] [CrossRef]
- Du, J.; Zhang, M.; Teng, X.; Wang, Y.; Lim Law, C.; Fang, D.; Liu, K. Evaluation of vegetable sauerkraut quality during storage based on convolution neural network. Food Res. Int. 2023, 164, 112420. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhang, S.; Xue, J.; Sun, H. Lightweight target detection for the field flat jujube based on improved YOLOv5. Comput. Electron. Agric. 2022, 202, 107391. [Google Scholar] [CrossRef]
- Lin, J.; Chen, Y.; Pan, R.; Cao, T.; Cai, J.; Yu, D.; Chi, X.; Cernava, T.; Zhang, X.; Chen, X. CAMFFNet: A novel convolutional neural network model for tobacco disease image recognition. Comput. Electron. Agric. 2022, 202, 107390. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef]
- Luo, J.H.; Wu, J.; Lin, W. Thinet: A filter level pruning method for deep neural network compression. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5058–5066. [Google Scholar]
- Fountsop, A.N.; Ebongue Kedieng Fendji, J.L.; Atemkeng, M. Deep Learning Models Compression for Agricultural Plants. Appl. Sci. 2020, 10, 6866. [Google Scholar] [CrossRef]
- Alqahtani, A.; Xie, X.; Jones, M.W. Literature Review of Deep Network Compression. Informatics 2021, 8, 77. [Google Scholar] [CrossRef]
- Liang, T.; Glossner, J.; Wang, L.; Shi, S.; Zhang, X. Pruning and quantization for deep neural network acceleration: A survey. Neurocomputing 2021, 461, 370–403. [Google Scholar] [CrossRef]
- Vadera, S.; Ameen, S. Methods for Pruning Deep Neural Networks. IEEE Access 2022, 10, 63280–63300. [Google Scholar] [CrossRef]
- Reed, R. Pruning algorithms-a survey. IEEE Trans. Neural Netw. 1993, 4, 740–747. [Google Scholar] [CrossRef] [PubMed]
- Sietsma, J.; Dow, R.J. Creating artificial neural networks that generalize. Neural Netw. 1991, 4, 67–79. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Mather, P.M. Pruning artificial neural networks: An example using land cover classification of multi-sensor images. Int. J. Remote Sens. 1999, 20, 2787–2803. [Google Scholar] [CrossRef]
- Castellano, G.; Fanelli, A.; Pelillo, M. An iterative pruning algorithm for feedforward neural networks. IEEE Trans. Neural Netw. 1997, 8, 519–531. [Google Scholar] [CrossRef] [PubMed]
- Arumuga Arun, R.; Umamaheswari, S. Effective multi-crop disease detection using pruned complete concatenated deep learning model. Expert Syst. Appl. 2023, 213, 118905. [Google Scholar] [CrossRef]
- Ofori, M.; El-Gayar, O.; O’Brien, A.; Noteboom, C. A deep learning model compression and ensemble approach for weed detection. In Proceedings of the 55th Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2022; pp. 1115–1124. [Google Scholar]
- Fan, S.; Liang, X.; Huang, W.; Zhang, V.J.; Pang, Q.; He, X.; Li, L.; Zhang, C. Real-time defects detection for apple sorting using NIR cameras with pruning-based YOLOV4 network. Comput. Electron. Agric. 2022, 193, 106715. [Google Scholar] [CrossRef]
- Shen, L.; Su, J.; He, R.; Song, L.; Huang, R.; Fang, Y.; Song, Y.; Su, B. Real-time tracking and counting of grape clusters in the field based on channel pruning with YOLOv5s. Comput. Electron. Agric. 2023, 206, 107662. [Google Scholar] [CrossRef]
- Shi, R.; Li, T.; Yamaguchi, Y. An attribution-based pruning method for real-time mango detection with YOLO network. Comput. Electron. Agric. 2020, 169, 105214. [Google Scholar] [CrossRef]
- Yvinec, E.; Dapogny, A.; Cord, M.; Bailly, K. Red: Looking for redundancies for data-freestructured compression of deep neural networks. Adv. Neural Inf. Process. Syst. 2021, 34, 20863–20873. [Google Scholar]
- Liu, C.; Wu, H. Channel pruning based on mean gradient for accelerating convolutional neural networks. Signal Process. 2019, 156, 84–91. [Google Scholar] [CrossRef]
- Guan, Y.; Liu, N.; Zhao, P.; Che, Z.; Bian, K.; Wang, Y.; Tang, J. Dais: Automatic channel pruning via differentiable annealing indicator search. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9847–9858. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Qin, C.; Zhang, Y.; Fu, Y. Neural pruning via growing regularization. arXiv 2020, arXiv:2012.09243. [Google Scholar]
- Yeom, S.K.; Seegerer, P.; Lapuschkin, S.; Binder, A.; Wiedemann, S.; Müller, K.R.; Samek, W. Pruning by explaining: A novel criterion for deep neural network pruning. Pattern Recognit. 2021, 115, 107899. [Google Scholar] [CrossRef]
- Meng, J.; Yang, L.; Shin, J.; Fan, D.; Seo, J.s. Contrastive Dual Gating: Learning Sparse Features With Contrastive Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12257–12265. [Google Scholar]
- Pachón, C.G.; Ballesteros, D.M.; Renza, D. SeNPIS: Sequential Network Pruning by class-wise Importance Score. Appl. Soft Comput. 2022, 129, 109558. [Google Scholar] [CrossRef]
- Han, S. Efficient Methods and Hardware for Deep Learning. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2017. [Google Scholar]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning filters for efficient convnets. arXiv 2016, arXiv:1608.08710. [Google Scholar]
- Pachón, C.G.; Ballesteros, D.M.; Renza, D. An efficient deep learning model using network pruning for fake banknote recognition. Expert Syst. Appl. 2023, 233, 120961. [Google Scholar] [CrossRef]
- Bragagnolo, A.; Barbano, C.A. Simplify: A Python library for optimizing pruned neural networks. SoftwareX 2022, 17, 100907. [Google Scholar] [CrossRef]
- Mondal, M.; Das, B.; Roy, S.D.; Singh, P.; Lall, B.; Joshi, S.D. Adaptive CNN filter pruning using global importance metric. Comput. Vis. Image Underst. 2022, 222, 103511. [Google Scholar] [CrossRef]
- Yang, C.; Liu, H. Channel pruning based on convolutional neural network sensitivity. Neurocomputing 2022, 507, 97–106. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, C.; Yang, W.; Li, K.; Li, K. LAP: Latency-aware automated pruning with dynamic-based filter selection. Neural Netw. 2022, 152, 407–418. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, D.; Zhou, W.; Fan, K.; Zhou, Z. EACP: An effective automatic channel pruning for neural networks. Neurocomputing 2023, 526, 131–142. [Google Scholar] [CrossRef]
- Haar, L.V.; Elvira, T.; Ochoa, O. An analysis of explainability methods for convolutional neural networks. Eng. Appl. Artif. Intell. 2023, 117, 105606. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Heaton, J. Ian Goodfellow, Yoshua Bengio, and Aaron Courville: Deep learning: The MIT Press, 2016, 800 pp, ISBN: 0262035618. Genet. Prog. Evolvable Mach. 2018, 19, 305–307. [Google Scholar] [CrossRef]
- LeNail, A. Nn-svg: Publication-ready neural network architecture schematics. J. Open Source Softw. 2019, 4, 747. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, D.; Zhou, P.; Zhang, T. Model compression and acceleration for deep neural networks: The principles, progress, and challenges. IEEE Signal Process Mag. 2018, 35, 126–136. [Google Scholar] [CrossRef]
- Fu, L.; Yan, K.; Zhang, Y.; Chen, R.; Ma, Z.; Xu, F.; Zhu, T. EdgeCog: A Real-Time Bearing Fault Diagnosis System Based on Lightweight Edge Computing. IEEE Trans. Instrum. Meas 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Pachon, C.G.; Renza, D.; Ballesteros, D. Is My Pruned Model Trustworthy? PE-Score: A New CAM-Based Evaluation Metric. Big Data Cogn. Comput. 2023, 7, 111. [Google Scholar] [CrossRef]
- Altaheri, H.; Alsulaiman, M.; Muhammad, G.; Amin, S.U.; Bencherif, M.; Mekhtiche, M. Date fruit dataset for intelligent harvesting. Data Brief 2019, 26, 104514. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 13 August 2024).
- Jayasimhan, A.; Pabitha, P. ResPrune: An energy-efficient restorative filter pruning method using stochastic optimization for accelerating CNN. Pattern Recognit. 2024, 155, 110671. [Google Scholar] [CrossRef]
- Yuan, T.; Li, Z.; Liu, B.; Tang, Y.; Liu, Y. ARPruning: An automatic channel pruning based on attention map ranking. Neural Netw. 2024, 174, 106220. [Google Scholar] [CrossRef] [PubMed]
- Tmamna, J.; Ayed, E.B.; Fourati, R.; Hussain, A.; Ayed, M.B. A CNN pruning approach using constrained binary particle swarm optimization with a reduced search space for image classification. Appl. Soft Comput. 2024, 164, 111978. [Google Scholar] [CrossRef]
- Baldi, P.; Sadowski, P.J. Understanding Dropout. In Proceedings of the Advances in Neural Information Processing Systems; Burges, C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2013; Volume 26. [Google Scholar]
- Wu, H.; Gu, X. Towards dropout training for convolutional neural networks. Neural Netw. 2015, 71, 1–10. [Google Scholar] [CrossRef] [PubMed]








| Layer | Filters or Neurons | Filter Shape | Output Shape | Parameters | FLOPs |
|---|---|---|---|---|---|
| , , | , , | ||||
| 64 | (3, 3, 3) | (224, 224, 64) | 1792 | 173,408,256 | |
| 64 | (3, 3, 64) | (224, 224, 64) | 36,928 | 3,699,376,128 | |
| – | – | (112, 112, 64) | 0 | 802,816 | |
| 128 | (3, 3, 64) | (112, 112, 128) | 73,856 | 1,849,688,064 | |
| 128 | (3, 3, 128) | (112, 112, 128) | 147,584 | 3,699,376,128 | |
| – | – | (56, 56, 128) | 0 | 401,408 | |
| 256 | (3, 3, 128) | (56, 56, 256) | 295,168 | 1,849,688,064 | |
| 256 | (3, 3, 256) | (56, 56, 256) | 590,080 | 3,699,376,128 | |
| 256 | (3, 3, 256) | (56, 56, 256) | 590,080 | 3,699,376,128 | |
| – | – | (28, 28, 256) | 0 | 200,704 | |
| 512 | (3, 3, 256) | (28, 28, 512) | 1,180,160 | 1,849,688,064 | |
| 512 | (3, 3, 512) | (28, 28, 512) | 2,359,808 | 3,699,376,128 | |
| 512 | (3, 3, 512) | (28, 28, 512) | 2,359,808 | 3,699,376,128 | |
| – | – | (14, 14, 512) | 0 | 100,352 | |
| 512 | (3, 3, 512) | (14, 14, 512) | 2,359,808 | 924,844,032 | |
| 512 | (3, 3, 512) | (14, 14, 512) | 2,359,808 | 924,844,032 | |
| 512 | (3, 3, 512) | (14, 14, 512) | 2,359,808 | 924,844,032 | |
| – | – | (7, 7, 512) | 0 | 25,088 | |
| 25,088 | – | – | 0 | 0 | |
| 4096 | – | – | 102,764,544 | 205,520,896 | |
| 4096 | – | – | 16,781,312 | 33,554,432 | |
| 10 | – | – | 4,097,000 | 8,192,000 | |
| – | – | – | 134,301,514 | 30,933,948,928 |
| VGG-16 Network | |||||
|---|---|---|---|---|---|
| block1conv1 | 20 | 15 | 35 | 15 | 35 |
| block1conv2 | 20 | 15 | 35 | 15 | 35 |
| block1pool | – | – | – | – | – |
| block2conv1 | 20 | 17 | 25 | 15 | 20 |
| block2conv2 | 20 | 17 | 25 | 15 | 20 |
| block2pool | – | – | – | – | – |
| block3conv1 | 20 | 20 | 20 | 34 | 11 |
| block3conv2 | 20 | 20 | 20 | 34 | 11 |
| block3conv3 | 20 | 20 | 20 | 34 | 10 |
| block3pool | – | – | – | – | – |
| block4conv1 | 20 | 22 | 13 | 15 | 19 |
| block4conv2 | 20 | 22 | 13 | 15 | 20 |
| block4conv3 | 20 | 22 | 12 | 15 | 20 |
| block4pool | – | – | – | – | – |
| block5conv1 | 20 | 30 | 10 | 10 | 31 |
| block5conv2 | 20 | 30 | 10 | 9 | 31 |
| block5conv3 | 20 | 31 | 9 | 9 | 31 |
| block5pool | – | – | – | – | – |
| FC1 | 20 | 20 | 20 | 20 | 20 |
| FC2 | 20 | 20 | 20 | 20 | 20 |
| FLOPs (reduction %) | 36.29 | 36.29 | 36.29 | 36.29 | 36.3 |
| Parameters (red. %) | 36.11 | 43.61 | 28.09 | 28.51 | 43.29 |
| VGG-16 Network | |||||
|---|---|---|---|---|---|
| block1conv1 | 30 | 15 | 45 | 15 | 40 |
| block1conv2 | 30 | 15 | 45 | 15 | 40 |
| block1pool | – | – | – | – | – |
| block2conv1 | 30 | 20 | 35 | 30 | 20 |
| block2conv2 | 30 | 20 | 35 | 30 | 20 |
| block2pool | – | – | – | – | – |
| block3conv1 | 30 | 30 | 30 | 45 | 30 |
| block3conv2 | 30 | 30 | 30 | 45 | 30 |
| block3conv3 | 30 | 30 | 30 | 45 | 30 |
| block3pool | – | – | – | – | – |
| block4conv1 | 30 | 43 | 25 | 28 | 30 |
| block4conv2 | 30 | 43 | 25 | 28 | 30 |
| block4conv3 | 30 | 44 | 25 | 27 | 30 |
| block4pool | – | – | – | – | – |
| block5conv1 | 30 | 45 | 16 | 20 | 37 |
| block5conv2 | 30 | 45 | 16 | 19 | 37 |
| block5conv3 | 30 | 46 | 13 | 15 | 36 |
| block5pool | – | – | – | – | – |
| FC1 | 30 | 30 | 30 | 30 | 30 |
| FC2 | 30 | 30 | 30 | 30 | 30 |
| FLOPs (reduction %) | 51.33 | 51.33 | 51.34 | 51.33 | 51.33 |
| Parameters (red. %) | 51.05 | 61.24 | 40.63 | 42.36 | 54.66 |
| VGG-16 Network | |||||
|---|---|---|---|---|---|
| block1conv1 | 50 | 15 | 62 | 30 | 67 |
| block1conv2 | 50 | 35 | 62 | 30 | 67 |
| block1pool | – | – | – | – | – |
| block2conv1 | 50 | 40 | 50 | 42 | 55 |
| block2conv2 | 50 | 40 | 50 | 42 | 55 |
| block2pool | – | – | – | – | – |
| block3conv1 | 50 | 50 | 50 | 65 | 42 |
| block3conv2 | 50 | 50 | 50 | 65 | 42 |
| block3conv3 | 50 | 50 | 50 | 65 | 42 |
| block3pool | – | – | – | – | – |
| block4conv1 | 50 | 70 | 45 | 60 | 43 |
| block4conv2 | 50 | 70 | 45 | 60 | 43 |
| block4conv3 | 50 | 70 | 45 | 60 | 43 |
| block4pool | – | – | – | – | – |
| block5conv1 | 50 | 70 | 45 | 30 | 67 |
| block5conv2 | 50 | 70 | 45 | 30 | 67 |
| block5conv3 | 50 | 70 | 45 | 30 | 67 |
| block5pool | – | – | – | – | – |
| FC1 | 50 | 50 | 50 | 50 | 50 |
| FC2 | 50 | 50 | 50 | 50 | 50 |
| FLOPs (reduction %) | 74.86 | 74.86 | 74.76 | 74.85 | 74.72 |
| Parameters (red. %) | 74.99 | 84.15 | 72.65 | 66.99 | 81.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pachon, C.G.; Pinzon-Arenas, J.O.; Ballesteros, D. Pruning Policy for Image Classification Problems Based on Deep Learning. Informatics 2024, 11, 67. https://doi.org/10.3390/informatics11030067
Pachon CG, Pinzon-Arenas JO, Ballesteros D. Pruning Policy for Image Classification Problems Based on Deep Learning. Informatics. 2024; 11(3):67. https://doi.org/10.3390/informatics11030067
Chicago/Turabian StylePachon, Cesar G., Javier O. Pinzon-Arenas, and Dora Ballesteros. 2024. "Pruning Policy for Image Classification Problems Based on Deep Learning" Informatics 11, no. 3: 67. https://doi.org/10.3390/informatics11030067
APA StylePachon, C. G., Pinzon-Arenas, J. O., & Ballesteros, D. (2024). Pruning Policy for Image Classification Problems Based on Deep Learning. Informatics, 11(3), 67. https://doi.org/10.3390/informatics11030067








