3.1. Description of the Model under Development
Currently, partial verification of the counterparty’s trustworthy is usually carried out by separate specialized departments of the company based on information systems, for example, SPARK, Integrum, etc. Since these checks are time consuming and may contain errors due to the influence of the human factor, and the audit does not take into account industry-specific parameters, there is a need to automate the risk assessment process of a management decision to cooperate with a counterparty (developer company) (
Koltays et al. 2020).
The purpose of this work is to determine whether the counterparty is trustworthy or untrustworthy in order to make a management decision on cooperation with him.
At the same time, if the counterparty is trustworthy, then the possibility of cooperation is assumed with him, if the counterparty is untrustworthy, then it is not worth cooperating with him.
To achieve the goal, you must complete the following tasks:
Identify a trustworthy source of input data;
Define the input and output data of the model;
Define the requirements for the model;
Select the method of building the model;
Prepare data for modeling if necessary;
Build a model;
Check the feasibility of the model requirements;
Analyze the simulation results.
At the present time, there are many information and analytical systems that have both positive and negative aspects of the selection of counterparty companies. In this regard, the first task was to conduct an analysis of information and analytical systems to identify the best options for assessing the trustworthiness of organizations.
In order to choose a trustworthy data source, a comparative analysis of information and analytical systems for checking counterparties was carried out. These tables (table) provide a comparison of 32 systems available on the Russian market that specialize in providing information support in the field of counterparty analysis. During the selection of the optimal counterparty verification systems required to obtain trustworthy and trustworthy data, the systems were compared according to the following parameters:
User-friendly interface;
Fast request processing speed;
Daily data update;
Data upload;
Express risk assessment;
Search for company affiliations;
Availability of financial statements;
Organizational and management structure;
Availability of change monitoring.
As a result, five information systems were selected that meet all the specified requirements of the analysis: SPARK, Contour.Focus, Seldon.Basis, Kartoteka, SCREEN.
In order to determine the best one from the data of 5 information systems, the AHP proposed by T. Saaty was used (
Saaty 1990):
To find the best information and analytical system, the values of global priorities were calculated. The final rating value of each IAS (information and analytical system) for a group of criteria is calculated according to the following formula:
According to the results of this method, the following values of global priorities of information systems were obtained:
SPARK: ;
Contour.Focus: ;
Seldon.Basis: ;
Kartoteka: ;
SCREEN: .
When constructing the matrix for the correctness of calculations, the consistency of the analyzed matrices was clarified. The calculated consistency ratio of each matrix is in the range from 1.36% to 10%, which confirms the accuracy of the application of the hierarchy analysis method. Thus, using the method of AHP by T. Saaty, the best information and analytical system was identified: Spark-Interfax.
In the modeling process, a sample from the SPARK information and analytical system (IAS) (a system for Professional Analysis of markets and companies) was used as input data for the model (
SPARK 2021), which is a list of counterparties and their characteristics: The age of the company, the average number of employees, important information, net profit (loss), the period of repayment of receivables (in days), the period of repayment of accounts payable (in days), the period of turnover of fixed assets, the period of turnover of assets, the current liquidity ratio, the quick liquidity ratio, absolute liquidity ratio. SPARK is used as a tool for downloading information for this experiment, but any user can also find this information in open state sources of information absolutely free of charge.
The output data is a list of numerical states of counterparties: —the counterparty is untrustworthy; —the counterparty is trustworthy.
In this case, the model must meet the following requirements:
At the same time, the accuracy of the model is understood as the ratio of correct responses to the sum of correct and false responses.
The completeness of the model refers to the ratio of correct responses to the sum of correct responses and false omissions.
The stochastic gradient method, which can be used in machine learning, will be used as a method for constructing the model. In this case, the training will be performed on the sample first , where is objects, and is the answers of the “teacher”.
The model itself will be a linear classification model:
where
—sign of the scalar product of vector
x by vector
w.
The geometric meaning of the vector w is that it is the guiding vector of the separating hyperplane in n-dimensional space. Moreover, if the sign of the scalar product is positive, that is, the point lies on one side of the separating hyperplane, then we classify the object as a class “+1”, that is “trustworthy counterparty”. If the sign of the scalar product is negative, then we consider the object of the class “−1”, that is, “not trustworthy”.
To find an unknown vector
w, we set the problem of minimizing the functional of the proportion of incorrect answers:
This functional is discrete with respect to the weights, and therefore, in order to use the gradient method, it is necessary to reduce the problem to minimizing the smooth functional:
Enter the value
—margin of the object
:
The indent sign indicates the correctness of the classifier’s answer (positive indent corresponds to the correct answer, negative—to the wrong one), and its absolute value characterizes the degree of confidence of the classifier in its answer. Scalar product in proportion to the distance from the separating hyperplane to the object, respectively, the closer the indentation is to zero, the closer the object is to the class boundary, the lower the confidence in its belonging.
The functional according to Formula (
3) evaluates the error of the algorithm on the object using the threshold loss function
, where the function argument is indented
. To introduce a smooth functional, we evaluate this function at all points of
M:
.
After that, you can get an upper bound on the functional:
At the same time, if the upper estimate is smooth, then will be smooth. If the top score is close to zero, then the percentage of incorrect answers will also be close to zero.
The logistic loss function will be used as the upper estimate:
Thus, the objective function will be expressed in minimizing the upper bound .
3.2. Building a Model
Stochastic gradient descent is a modification of gradient descent. The essence of gradient descent is to minimize the function by taking small steps towards the fastest decrease in the function.
Gradient descent begins with initialization of the weight vector, for example, with zeros (
), and then the gradient steps are repeated in the cycle (
StochGrad 2021). We apply the method to the problem, and then the gradient step (Formula (
8)) will consist of what we subtract from the current approximation of the weight vector
the gradient vector, with some coefficient
. Repeating these steps until convergence occurs (Formula (
9)), that is, until the vector of weights begins to change only negligibly.
where
— the considered vector of weights,
—current approximation of the weight vector,
—gradient,
—gradient coefficient,
where
—accuracy.
When the gradient descends to the representation of the
j:th component of the gradient vector (Formula (
10)), there is a summation for all objects of the training sample, where the summands are summed, which, in fact, show how to change the
j:th weight in order to improve the quality on the object
as much as possible. Moreover, the whole sum shows how to change the
j:th weight in order to improve the quality of the entire training sample.
In the case of stochastic gradient descent, the gradient vector calculated over the entire sample is not calculated at one iteration, but the gradient of the functional on only one object randomly selected from the training sample (Formula (
11)).
where
l—the number of objects in the training sample.
where
-randomly selected object.
Thus, gradient descent requires summing over all the objects of the training sample at each iteration, which can be a problem if the sample is large. Stochastic gradient descent solves this problem by using only one training sample object at each of its iterations. It also allows you to train linear models on very large samples that do not fit into the computer’s memory.
For the simulation, companies whose main activity is the development of computer software, consulting services in this area and other related services were considered.
The total number of companies according to IAS SPARK (
SPARK 2021) was 34,324, of which 46.53% of the companies are “trustworthy”, 53.47%—“not trustworthy”. For the simulation, a sample with an extension was taken .csv of 3432 companies, which corresponds to the distribution of trustworthiness in the original sample (
Table 1). At the same time, trustworthiness was determined by the summary risk indicator (
Table 2): If the risk is “low”, then the company is trustworthy, if “medium” or “high”, then the company is untrustworthy. This transformation was carried out by a composite index using SPARK algorithms. According to the information from the developer company: The consolidated risk indicator is a cumulative assessment of the analytical indicators of DDI, FRI, PDI, as well as the Status of the company (the state of liquidation, bankruptcy, etc.). It represents 3 risk values: Low, medium and high. FRI: From 1 to 14—low risk, from 15 to 85-medium risk and from 86 to 99-high risk. DDI: From 1 to 40—low risk, from 41 to 70-medium risk and from 71 to 99-high risk. PDI: From 1 to 49—high risk, from 50 to 79-medium risk and from 80 to 99-low risk. We have updated the manuscript, revealing these definitions (
SPARK 2021).
The dependence between the input data was checked by calculating the correlation coefficient and evaluating it on the Cheddock scale. As a result, it was decided to exclude the “current liquidity ratio” and “quick liquidity ratio” from the input data, since there is a strong and very strong relationship between them and the “absolute liquidity ratio” (correlation coefficient values from to and greater than , respectively).
To successfully apply the machine learning method to the input data, the following transformations were performed:
the separator of the integer and fractional parts in Excel was defined as “.”;
the separation of groups of digits in Excel was removed;
the data in the text format is converted to the numeric format according to
Table 5;
abnormal values were converted: All negative values of the period of repayment of accounts payable, the period of repayment of accounts receivable, the period of turnover of fixed assets, the period of turnover of assets were determined as “−1”;
omissions in the data were removed: The omissions in the “Company size” were defined as “−1”, the remaining omissions as “0”;
the data is given for a single scale from 0 to 1.
The linear_ model.SGDClassifier() method of the sklearn Python library was used for modeling. Attribute values were accepted by default (
Sklearn 2021), except for the following:
loss–loss function, value-‘log’; random_ state;
is used to make it possible to repeat experiments, value-70;
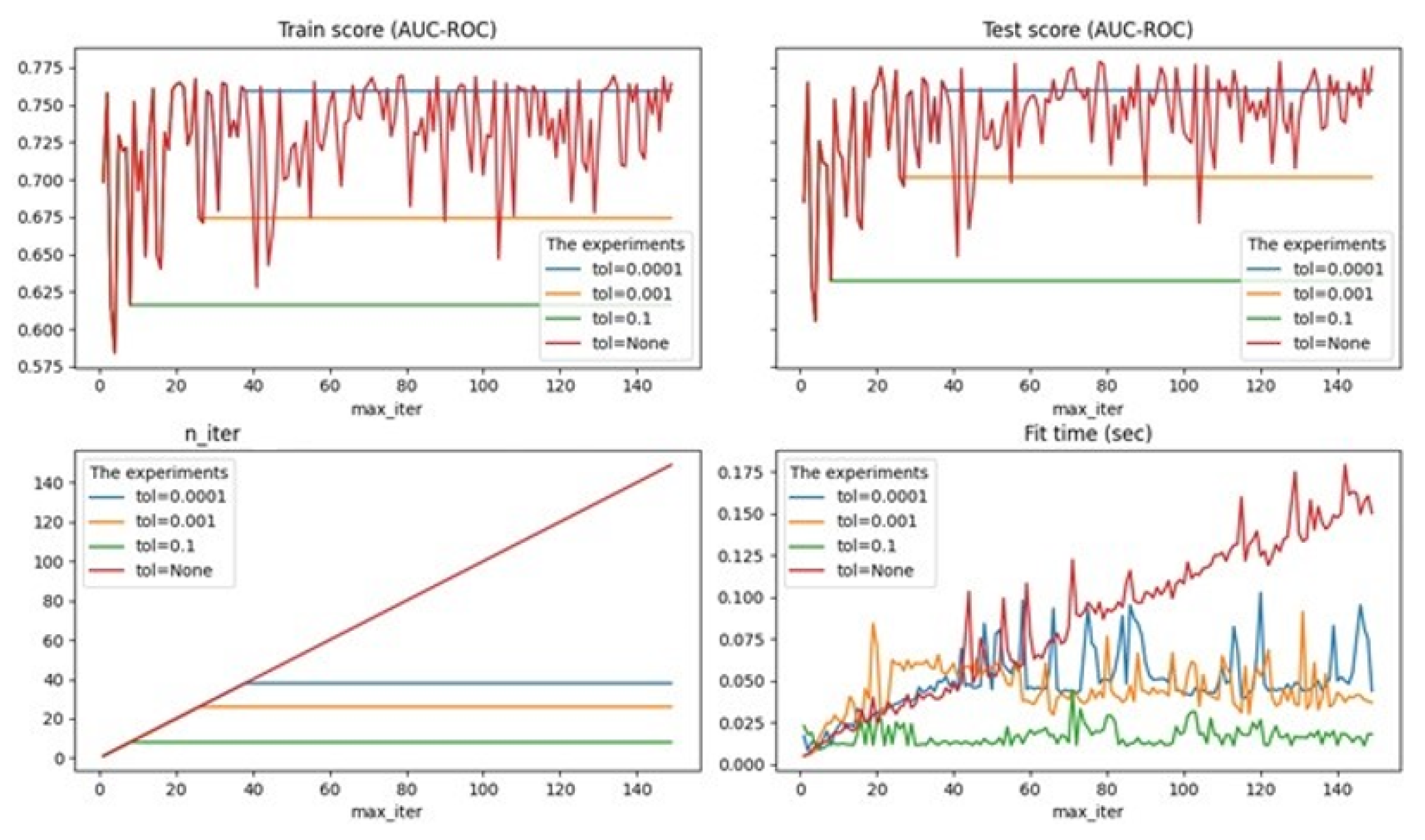
alpha is a constant that is multiplied by penalty (by default-0.0001), experiments were performed for 0.01, 0.001, 0.0001;
max_ iter—the maximum number of passes on the training data (so-called epochs), by default-1000, the optimal maximum number of passes was identified to avoid the problem of overfitting;
tol-stop criterion: Training will stop when loss > best_ loss—tol (default-0.001), experiments are performed for None, 0.01, 0.001, 0.0001.