Abstract
Seismic performance and loss assessments are required in areas of Insurance, Finance and Public Policy. Providers are Structural Engineers and Risk Management Firms. There are no current procedures to evaluate the epistemic and aleatory uncertainties for such assessments. The essential issue is whether or not there is sufficient reliability in the result to use the result as the basis for risk management decisions and actions. For a single building this may be whether or not a prescribed earthquake performance level is met, life safety or if a portfolio’s vulnerability level is acceptable, whether the. loss for a given time period is less than a stated value. A method based in part on Federal Emergency Management Agency P-695, is developed for evaluating the reliability of performance and/or loss assessments for both individual and portfolios of buildings. Consideration is given to how well the building investigation and corresponding evaluation process have been performed, the qualifications of the person(s) doing the assessment, the thoroughness of the building evaluation, the technical validity of the assessment procedure or model and what computational reliabilities are presented. The method characterizes the uncertainty of each component of the assessment procedure for each building by qualitative determined assignments. The resulting reliability measure is likely to be most useful for determining whether/or not a building has acceptable life safety performance, or if a portfolio has an acceptably low loss risk over a given period of time. In both cases, the reliability must either be sufficient to warrant action, or serve to indicate need for improved assessment.
1. Introduction to Reliability of Building Seismic Performance Evaluations
Many private owners and public institutions have taken steps to ensure that the seismic risks posed by their respective buildings are assessed and mitigated if necessary. Real estate investors and financiers often limit their investments to properties that have limited down-side risk, which may include insurance. Parts of these financial decision processes may depend on the assessed seismic risk posed by a building, and, therefore, the reliability of this assessment is of key concern. Often the questions at issue involve: whether a building meets the applicable Building Code or an owner/entities’ requirements for stability/life safety performance; or, if the building’s probable maximum loss (PML) is less than a given acceptable value. These questions are applicable to both individual buildings, and portfolios of multiple buildings that are locally or geographically dispersed.
There is inherent uncertainty in the reliability of the results of any professional evaluations, including seismic performance assessments. This general condition has been well-stated by Justice California Supreme Court Justice Roger J. Traynor:
Those who hire (professionals) are not justified in expecting infallibility, but only reasonable care and competence. They purchase the service, not insurance.(Traynor 1954)
This is a recurrent theme in California Law applied to professionals performing work for a client, and of course it applies to those performing seismic performance evaluations. We are led to believe that this observation is universal. It is in the best interests of the client to determine how reliable a report’s conclusions will be or are, and the client should not rely on the professional’s liability insurance to right the losses due to wrong decisions that may be made upon the basis of the report if it were to be incomplete or wrong. Liability insurance is an unreliable method as a risk mitigation measure. This paper addresses exactly this problem: How can the reliability of a seismic performance assessment be evaluated? The recommended procedures developed address the following issues for both single and portfolios of buildings:
- Quality measured by the acceptable reliability or level of uncertainty of the reported seismic performance assessment.
- Confidence limits for reported assessed numerical loss value: where these limits are based on the assessor’s statement of uncertainty together with the uncertainty in: the analytic methods, available information and the investigation procedures employed and the data processing procedures used.
ASTM International (ASTM) E2557 and E2026 provide standards for the assessment of seismic risk (Probable Maximum Loss, PML) statistics for individual and locally compact groups of buildings, and a current ASTM Working Group is developing similar standards for portfolios of geographically distributed buildings located within defined seismic hazard zones. These standards are widely used, primarily by the financial industry, for the evaluation of the damageability risk of buildings being considered for real estate investments or securities evaluations. Accordingly, ASTM E2026 describe varying degrees of investigation ranging from Level 0 (a screening or “desk top” investigation) to Level 3 (a highly detailed technical investigation and analytical evaluation). The user-client prescribes the level(s) of investigation to apply to building stability (BS), site stability (SS), building damageability (BD), contents damageability (C) and business interruption (B) according to the user-client’s acceptable reliability or tolerance for uncertainty. A shortcoming of these standards is that they give no means of determining the degree of reliability of the assessment, except by designation of the Level of investigation. As voluntary standards, they depend on the performer to self-certify compliance with the referenced standard, in contrast with building codes which have an independent assessment before approval for construction.
The ASTM standards states that the selection of the level of investigations performed should be acceptable to suit the purpose of the user/client. Generally, the lower the tolerance for uncertainty and the higher the seismic hazard, the higher the level of investigation should be, all other things being equal. Of course, the cost and time of performing an investigation increases with the level and therefore the choice may be limited by the user’s resources. For a given assessment based on a defined investigation level, this paper provides a method of determining a quantitative and qualitative measure of the related uncertainty and corresponding reliability, ranging from Superior to Poor. The method describes the means of expressing and combining both quantitative and qualitative information related to the components used in the assessment process. It is important to recognize that the ASTM standards do not provide an enforcement mechanism, therefore, there are essentially no controls or limitations on providers. The User hires a professional to perform a level of review as specified in the Standards, then relies on the same professional to indicate that they actually complied with the level, however there are NO consequences if the professional did something less. As a result, it is left up to the user/client to evaluate the reliability of the application of the methods and conclusions and to determine whether the provider has employed the necessary technical knowledge and care to perform the assessment. It is the responsibility of the user to apply and/or require quality assurance steps before using the results, or otherwise possibly suffer the consequences of making decisions based on non-reliable assessment results. The reliability is dependent on many factors, few of which may be mentioned or even considered within the evaluation report itself. This condition also applies to risk measures concerning portfolios of buildings. If the reliability is determined to be insufficient, then further investigation and analysis may be required before a responsible decision can be made based on reported findings.
Federal Emergency Management Agency (FEMA) P-154 and American Society of Civil Engineers (ASCE 41) are widely used tools for the evaluation of a building’s expected seismic performance, and either/or both may be employed (ASCE 2016a; FEMA P-154 2013). Often the decisions for investment and use, as well as retrofit of buildings, are made that rely on the results of these tools. For both FEMA P-154 and ASCE 41, there is a need to be able to determine the reliability of the reported evaluations in order to ensure that risk management decisions are made that are consistent with a knowledge of the degree of possible variability of the evaluation.
Performing an engineering study of an existing building can be an expensive and time-consuming process. FEMA P-154 and the ASCE 41 Tier 1 Check List Form evaluations have the advantage of being significantly less costly than a full engineering assessment of a building (such as FEMA P-58 or ASCE 41, Tier 3). A P-154 assessment is based on: the identification of certain building characteristics and risk issues, scoring these against a checklist, determining a cumulative score and comparing this value to a prescribed acceptable score for life safety performance, such as 2.0 or more as a score. P-154 allows the assessor to rate the degree of each of the key damageability issues on the Level 1 Form and permits the assessor to make some adjustments by means of a Level 2 Form. The adjustments are based on a more detailed description of the characteristics that affect the building’s expected performance. This is most useful to justify that a building is acceptable even though its initial Level 1 tabulated score is less than 2.0 or other values depending on the level of seismic hazard of the site, with higher values for less risky sites. Alternatively, the Level 2 Form can serve to provide detailed information that can lower or raise the score from that of the Level 1 Form, providing some additional reliability of the result. When ASCE 41 or P-154 procedures are used to support a Building Permit application they are closely reviewed for reliability; otherwise, the results are self-certified by the performer unless the user conducts a review.
An ASCE 41 assessment can be performed at different Tiers ranging from Tier 1, which is a low-intensity evaluation using Checklists, to Tier 3, which requires significant engineering investigation and analysis. The results of the Tiers are evaluated based on three possible outcomes for a given performance issue: Compliant, Not Compliant and Not Applicable. If any issue is found to be Not Compliant, then the Tier is considered to fail, that is, the building does not comply with the ASCE 41 requirements. Tier 1, the lowest assessment level, was designed to have a small probability that the result would call a Bad building Good (a Type I error consistent with common decision theory practice) and a higher probability that it would call a Good building Bad (Type II error). In effect, the ASCE 41 Tiers 1 through 3 provide a triage system, where if a building fails one Tier, then the next one can be performed, which is more intensive and may change the previous conclusion. The assessment tends to stop when the assessor is convinced that either no more information is likely to change the conclusion, or the resources for this purpose are exhausted. It is well established in the literature that the policy decision to minimize Type I errors, without considering the consequences of Type II errors is ill-advised. This is because the probability of a Type II error goes up as the probability of a Type I error goes down, (Benjamin and Cornell 1970)—obviously the only effective way to avoid Type I errors is to do nothing. Therefore, we are led to the conclusion that when ASCE 41 Tier 1 assessments are to be used for making decisions regarding a building’s acquisition, occupied use period and/or a retrofit investment, it is necessary to determine the reliability of the ASCE 41 Tier 1 Performance Level assignment. If the reliability is too low (uncertainty too high) for the decision-making process, then it is necessary either to abandon the project or to invest in a higher-level assessment. In recognition that acceptable reliability is key to the decision process, in this paper a method to regularize the evaluation of reliability is developed rather than the alternative of asking other expert(s) for their opinion. The method proposed provides documented support for conclusions concerning the assessment’s reliability. For seismic safety purposes, it is obvious that calling a Bad building Good can have significant consequences. Whether a P-154 or an ASCE 41 evaluation has been or will be performed, there is the fundamental issue of what the reliability of the evaluation is and whether a responsible decision can be made based this evaluation. We will discuss the reliability process in terms of ASCE, FEMA and ASTM procedures. However, the issues involved in these evaluations are essentially the same, since these procedures result in a binary decision whether a building’s seismic performance is either acceptable or not acceptable for the performance objective of life safety or damage limitation. In addition, the evaluation of the reliability of results from proprietary PML and Portfolio Risk (often called Catastrophe Models, or CAT, discussed in Section 3.1) procedures will be treated.
Before proceeding to the Assessment Reliability procedure, it is helpful to understand the current general process of solving Engineering and Economic problems. These problems, including those of reliability, risk and decision making, are solved within the by models. This model contains the set of physical and probabilistic models (assigned parameter values), which are employed as mathematical idealizations of reality to render a solution. The selected model may contain inherently uncertain quantities or components and may be made up of sub-models that are also imperfect representations of reality, giving rise to additional uncertainties. Since the selection of a specific tractable model is necessary to solve the problem, an important part of formulating the complete model involves the representation of the related uncertainties such that some measure of the reliability of a predicted outcome is available. Any selected method of this representation of the uncertainty characteristics must be stated within as part of the selected model description. In the context of modeling, there can be many sources of uncertainty, as either aleatory or epistemic. The word aleatory is derived from Latin meaning rolling of dice. Thus, an aleatoric uncertainty is one that is presumed to be an intrinsic randomness of a phenomenon. The word epistemic from Greek meaning knowledge. Thus, an epistemic uncertainty is one that is presumed as being caused by lack of knowledge (concerning actual behavior or a lack of sufficient data for an adequate empirical representation). The reason that it is useful to have this distinction of the uncertainty sources within the context of an engineering analysis model is that the epistemic part in the model can be addressed by introducing auxiliary non-physical variables. These variables capture information obtained through the gathering of more data or use of more advanced scientific principles and/or more detailed analyses. An uttermost important point is that these auxiliary variables define statistical dependencies (correlations), between the components of the model, in a clear and transparent way, (Der Kiureghian and Ditlevsen 2009). For example, if the random errors in prediction of a damage ratio were to be assumed (by the modeler) to have a Normal Probability Distribution (perhaps for tractability or ease of presentation) where the true error distribution is actually best represented by a Beta Distribution; this would be a source of epistemic error. When the corresponding mean and variance parameters of an assumed Probability Distribution function are evaluated by sample estimates that are based on a smaller sample of observations than the number required to obtain an acceptable range of confidence limits for the true parameter values, this would be classed as aleatory error. Epistemic uncertainty can be reduced by acquiring knowledge and information concerning the behavior of the system, and aleatoric uncertainty can be reduced by an increase in observations, tests, or simulations required for sample estimation of model parameters. In practice, systems under analysis cannot be characterized exactly—the knowledge of the underlying phenomena is incomplete. This leads to uncertainty in both the values of the model parameters and on the hypothesis supporting the model structure. This defines the scope of the uncertainty analysis which we shall investigate herein.
The problem at hand is how to characterize the uncertainties caused by epistemic decisions (modeling assumptions, prediction equations and excluded considerations) that formed the analytical basis of seismic loss assessments. These assessed uncertainties will be evaluated by the Qualitative—Quantitative Matrix system that will be discussed in Section 2.2. We choose to call this the epistemic portion of the uncertainty or Reliability Level. For both Single Building and Portfolio assessments, the aleatory error can be a function of the level of investigation. For Portfolio assessments, it is assumed that the aleatoric (sample size) error in assigned parameter values and resulting portfolio loss statistics will be controlled by the corresponding sufficiently large number of Monte Carlo simulations employed in the CAT model as discussed in Section 4.
Further, as a derivative question, if the level of uncertainty of the assessed result is not acceptable, what steps can be taken to make the level acceptable (e.g., further investment in higher levels of investigation, particularly for high value buildings)? The uncertainty contribution of each component of the assessment process can serve to guide this resource allocation decision.
The reliability of an assessment depends on the validity of the assumptions and idealizations of the components employed in the assessment. Specifically, the quality of information concerning the components of the assessment and the validity of assumptions used in the prediction model can significantly impact the performance and/or loss conclusion; however, in current practice these impacts are not normally considered as part of the uncertainty assessment. These unconsidered or un-mentioned sources of uncertainty must be identified and included in the total representation of the reliability of the results. An example, using Qualitative Terminology concerns the level of information used to represent an individual building’s damageability characteristics. This information can be obtained by means of a building visit by an experienced evaluator (Good), a review of the construction documents by an experienced Structural Engineer (Good) or simply a Desktop assessment based in inferred characteristics of the building from photographs (Poor). In summary, there are alternatives (such as the ASTM E2026 levels of investigation) in the data collection, parameter specification and damageability analysis methods that can have a significant effect on the assigned performance level or loss assessment. The purpose here is to provide a method by which a user can evaluate the reliability of the results by assigning and combining the uncertainties corresponding to the components or steps involved in a given assessment process.
The proposed method in this paper allows for representation of uncertainty for each of the individual issues or components in a performance evaluation and/or loss assessment process, along with their combination of these uncertainties for the total uncertainty of reported results of the process. The development of the reliability of the damageability quality assessment process for a single building or portfolios of buildings are discussed in the following sections:
- Section 2 addresses the quality of the individual building damageability assessment. The quality of the algorithm that determines the damage ratio loss for the building or portfolio of buildings in a single assumed earthquake event is discussed. This will be required of a single building if that is all that is being assessed, or for each of the buildings in the all under consideration, or each of the buildings in a portfolio. It forms the basis on which all evaluations are completed.
- Section 3 discusses the concept of Portfolio Loss and its respective components of the assessment process. It provides the method of evaluating and combining the measures of uncertainty of each component of the process. It establishes the practical need for Monte Carlo Simulation for the evaluation of the risk of aggregated loss due all possible Earthquake Events in the defined seismic region.
- Section 4 addresses the uncertainty issues in determining the computed loss statistics from the Monte Carlo simulations of aggregated portfolio loss. The concept of “Bootstrap” sampling is introduced for the non-parametric statistical analysis of the Monte Carlo simulations: this provides the means of describing and evaluating the uncertainty in the estimated Portfolio Loss Statistics. These statistics are evaluated from the results of Monte Carlo simulations that aggregate the loss estimates of the portfolio for all possible earthquakes that can occur (the Event Set) and the representation of the statistical variability of how each of the individual buildings respond to these events.
- Section 5 addresses the evaluation of the uncertainty of reported portfolio loss assessment values to reflect both the aleatoric uncertainty of the computation process and the epistemic quality of the assessment process as a whole. Epistemic means in this context: Of or pertaining to knowledge or the conditions for acquiring it, (Halpern 2017). Finding reliability for these possible individual issues allows characterization of the reliability of the total process. This will provide not only the representation of the reliability of the findings, but also suggestions of ways that the quality of the results can be efficiently improved by the altering of some aspects of how the process is undertaken. Furthermore, the descriptive identification of individual issues and related sources of uncertainty can be employed before the assessment is performed, in order to specify investigative and procedural requirements to better ensure that the assessment results will provide have acceptable reliability to make decisions.
2. Assessing an Individual Building
2.1. Key Issues Impacting Reliability of an Individual Building Assessment
The evaluation of the representation of uncertainty for a loss assessment for an individual building requires a careful identification and consideration of all of the issues and elements, herein termed as components, that can contribute to this uncertainty. For the evaluation of the uncertainty measure for each component in the assessment process, we are interested not only in the technical descriptive characteristics of the component but also the temporal currency and reliability of the observations as represented by the skill, expertise and experience of the person(s) involved in implementation and/or evaluation of the component. Both the technical characteristics and the quality of the assigned values impact the reliability of the results. It is proposed that the most efficient method of characterizing the reliability of the results of an assessment report is by the evaluation of the uncertainty of the individual components of the building assessment, and then combining these uncertainties to quantify the total uncertainty and corresponding reliability of the resulting assessment. The problem of combining qualitative terms that express degree of uncertainty will be addressed in Section 2.3. The following Issues are considered to be important for evaluation of individual building performance assessment:
- (1)
- Seismic Exposure: The characterization of the severity of the seismic hazards at the building site, including intensity and related risk of damaging ground motions, surface faulting, liquefaction-induced settlement and landsliding.
- (2)
- Design Basis: What were the seismic design criteria under which the building was designed, and/or retrofitted or otherwise altered since construction? This includes the seismic requirements as well as the standard of practice used.
- (3)
- Quality of Evaluation Information and related Assessor: Were the design and/or modification retrofit documents available for review? Did the qualifications of the assessor meet ASTM 2026 guidelines for Senior Assessor? Was the building visited by the assessor?
- (4)
- Configuration and Load Path: What are the vertical and horizontal irregularities of the structure? Does the lateral load-resisting system accommodate any irregularities? Is there an effective load path? Does the detailing of the lateral load resisting system provide adequate ductility to accommodate expected demands? What is the potential collapse mechanism? Is this mechanism capable of sustaining the ASCE 7 Design Level Earthquake (2/3 MCER) or ASCE 41 BSE-2E displacements without collapse? (ASCE 2016a, 2016b; FEMA P-2012 2018).
- (5)
- Compatibility: Are the deformational characteristics of the building’s structural and nonstructural elements compatible with the expected seismic drifts? Is there any unintended interference from other stiff elements that could cause failure of critical support elements?
- (6)
- Condition: Are the structural elements in good condition or deteriorated? Are any deteriorated elements important to the seismic resistance and stability? Is there any damage due to past earthquakes, accidents or fires, and is this damage important to the seismic resistance?
- (7)
- Building Location: The specificity of how the location of the building is determined, such as by address, city, county or ZIP code, can greatly impact the reliability of how the earthquake site and seismic ground motions are determined and whether these hazards are representative of the site. Having an accurate location for each building is critical not only to determine the individual building’s location with respect to the hazards that are posed, but also to assure that the building is not systematically mislocated.
If the assessment includes a loss estimate, such as damage ratio or expected dollar loss, then also assess:
- (8)
- Building Damage Determination: How were the damageability values determined for given intensities of site ground motion? What model is used, and what is its basis? Does the model report a damageability probability distribution function for the results or a single value? If the results are expressed as a probable loss, is it specifically defined as an ASTM E2026 scenario loss (SEL, SUL) or a probable loss PL, see Note 1 at the end of the paper for these terms definitions.
- (9)
- Building Replacement Construction Cost: The replacement construction cost is the basis for almost all building damageability loss assessment procedures. The damageability loss is evaluated for a given event by multiplying the corresponding computed damage ratio times the building replacement construction cost. The Market value of a building is not a reliable indicator of building replacement construction cost. (Where other issues, such as contents damage, lost rents and revenues are considered, all contributions should be expressed in dollars.)
2.2. Evaluating Reliability for Individual Building Assessments
The Quality Rating System method proposed here is analogous to that used in FEMA P-695 (FEMA P-695 2009, Section 3.4, also known as ATC-63). The individual component uncertainties are represented by their assigned Coefficients of Variation (β factors). For a building performance prediction Equation (such as for the P-695 collapse fragility, or for here, as the damage ratio) that can be represented as a product of multiple components, the uncertainty contribution due to an individual component can be represented by a random multiplier on the estimated system value. Therefore,
- The total uncertainty is the result of a chain of multiplication of the uncertainty of individual components that make up the decision process. These are considered to be independent, random variables are represent subjectively determined values reflecting the uncertainty introduced by the modeling decisions. Each of the these can be considered as successive Bayesian updates (Fenton and Neil 2019) to the prior calculated value from the risk model of added information considered.
- Each uncertainty multiplier is assumed to have a lognormal distribution with mean one and standard deviation βi. This is consistent with prior practice in FEMA P-695 as the basis of the current Edition of ASCE 7, and Thiel and Zsutty (2018). For instance, βi = 0.1 indicates a roughly ±10% change (e0.1) of the estimated component value or βi = 0.2 indicates roughly ±22%, etc. This provides an intuitive understanding why the total β for the process can be represented as the Root Mean Square (RMS) of component βi values, see Section 2.3. An alternative Simple Average approach of a simple linear model is presented in the section for those who are not comfortable with the RMS approach. As will be show shown in Section 2.3, the comparisons of their results are close except that the RMS is more conservative than the alternate Simple Average approach.
These component βi factors can be estimated without the need of knowing the mean or median values of the respective underlying components. The final combined index must include uncertainty measures for all the components that impact the reliability of the assessment value or score. This value or score is used for the binary conclusions: The building either meets the criteria of the specific requirements used procedure or does not, or the assessed loss value is too high to proceed with an action. The method of aggregation of the uncertainty indices for all of the components of the building assessment will be discussed in Section 5. This assessment may in terms of: a PML value1, an evaluation score from a P-154 assessment, an Earthquake Performance Level (I to VII) in terms of compliance to California Existing Building Code (CEBC) requirements or a deficiency list of demand/capacity ratios for individual elements of the structure from ASCE 41 Tier 3 analysis.
The reliability evaluation process used in this paper is an extension of a procedure used in FEMA P-695 for Quantification of Building Seismic Performance Factors, (Deierlein et al. 2008). Specifically, the problem involved the prediction of building collapse displacement or fragility due to earthquakes, using the results of non-linear time history analyses of selected examples of prototype building structural systems. The key questions addressed were how to assign quality measures of the factors, used in the calculation of collapse displacement, and how these quality of knowledge measures can be combined to relate to the certainty (reliability) of the results of the collapse displacement estimation process? For a given factor (or component) used in the collapse estimation process, a measure of uncertainty (a β value: 0 < β < 1) was assigned corresponding to three qualitative levels of Quality of Description of the factor (High, Medium and Low) and three levels of its assessed Quality of Implementation Characteristics (High, Medium and Low). FEMAP-695 Section 3.4 presents a simple matrix, shown in Table 1, that provides a single quantitative evaluation of β based on the paired qualitative assessments of: Quality of Implementation (High, Medium, Low) corresponding to a specific description Quality of Component Description Measure (High, Medium, Low). The lower the β value, the greater the certainty (reliability) of the result; conversely, the higher the β value, the lower the certainty (unreliability). The means of assigning the required quality measures shall become clear below that presents 3 × 3 matrices for how the pairs of quality for each of the nine components are assigned. An analytically determined numerical value of β can be can be expressed as a qualitative linguistic term by use of Table 2 following the numerical upper and lower bounds for each term in the assignment of the linguistic quantitative term. The β values of Table 1 are the same as used in P-695 with the exception that P-695 did not make an assignment of a (Low, Low) value, which we call Bad and assign a β = 1.0.

Table 1.
Assessment matrix for the implementation application of a quality measure for a considered issue or component. Each of the assignments of High, Medium and Low is described by text specific to the component under discussion. A value of 0.10 is taken as the very reliable (little uncertainty), and 1 is not reliable (complete uncertainty). This Table is the same for all Quality Measures.

Table 2.
Reliability qualitative terminology and their associated uncertainty quantitative values. When a β value has been determined quantitively, we propose to use the numeric bounds for assignment of a qualitative linguistic term for the value.
A most important advantage of being able to assign a quantitative uncertainty factor βi for each component i used in an evaluation process (analogous to the FEMA collapse displacement as described above), or for our objective of building loss assessment, is that these quantitative βi values (0 ≤ βi ≤ 1) can be combined in a statistically valid procedure to provide the total uncertainty of the result of the evaluation. This was accomplished as discussed above by assuming that the uncertainties are multiplicative in their impacts, and lognormally distributed with mean one. The multiplicative process of lognormal standard deviations of the individual components to be combined as the standard deviations as the Square Root of the Squares; and it does not need knowledge of the mean. It is essential to note that the combinatory process would be quite subjective if the levels of uncertainties were to be left in Qualitative terms.
For the proposed method of evaluating the uncertainty of an assessed damageability or a related Performance Level, the approach described above for the assignment of qualitative uncertainty expressions by the matrices of Table 3 here and similar tables elsewhere, and the corresponding quantitative βi factors by Table 1 and Table 2 is necessary because building damageability assessments are based on varying degrees of professional knowledge and related judgements. The expression of the likelihood for building response and the corresponding degree of uncertainty is based, primarily, on the experience and qualifications of the assessor and on access to information available concerning the specific characteristics of the building and related seismic risks. For a particular building, detailed engineering analyses and on-site materials testing and investigation (such as ASTM E2026 Level 3 investigations) are usually not feasible. Furthermore, actual seismic performance data for current building types is not sufficient to provide accurate empirical prediction. As a consequence, it is necessary to utilize expert judgmental qualitative values as a major basis for loss assessments. At best, these judgmental values are based on experience and information obtained from building construction documents and/or a building visit when possible. Table 2 gives a simple qualitative ranking based on qualitative terms Superior, Good, Fair, Poor and Bad and their corresponding (judgmentally assigned) qualitative uncertainty measures (β values). The number (five) of the qualitative terms of Table 2 has the benefit of being odd such that there is a subjective middle or neutral representation for judgement heuristics. Table 1 gives how the β values can be assigned where two descriptors Quality Measure and Implementation Characteristics, refer to the matrices of Table 3, rather than one judgmental choice made concerning a particular issue, component or step involved in the assessment process where Table 2 applies.

Table 3.
Each of the nine components listed in this Section require assessment using Table 1 for the assessed quality of the component βi, where i is the component issue under discussion. The following matrices describe Table 41. These considerations are intended to assess both the principal and secondary influences that impact the resulting damageability and stability of the building. It is prudent to check the resulting determination as discussed in Section 4 and possibly reconsider the assignments for individual items based on these observations. References are made to ASCE 41 ground motions BSE-1E and BSE-2E, which are, respectively, the probabilistic ground motions with 20% and 5% probability of exceedance in 50 years. See Table 1 and Table 2 for the assignment of the βi value.
For a particular building assessment, the β values of the Table 1 should be considered as starting values that may be modestly adjusted if the resulting uncertainty evaluation is clearly between the matrix values for a specific use. For example, the assignment of an interim value of 0.275 if the judgement is that an assessment is better than Fair and less than Good, or 0.25 if it is closer to Good than to Fair. In addition, note that when a particular evaluation from Table 2 is not sufficiently reliable for the user/client’s purpose, additional analyses and/or investigation expenditures can serve to reduce the initially high β value such that an acceptable total reliability can be achieved. In many cases it may not be clear that definitive choices can be made in the Table 1 assignments. If we designate the probability of the Quality Measure as Pj for the three Measures j = H, M and L and as probability Qk for the Implementation Characteristics, and βjk be the corresponding β value in Table 1 for row j and column k, then the appropriate combined βi value is determined as:
This simple average approach is used to determine the assigned value since we are in essence interpolating between the β values of the component matrix. For example, if the Quality Measure was assigned as Medium with probability 100% and the Implementation Characteristic High with probability 75%, and to Medium with probability 25%, then the β value would be 0.237; if the same probabilities were assigned to both, then the β value would be 0.153. We recommend that when there is complete uncertainty in the characteristics of a Measure or its Implementation, that Poor or Bad is assigned depending on whether there is insufficient or no information on which to evaluate the characteristics.
It is also important to recognize that Table 1 essentially provides a quantitative way to define the qualitative terms of performance: Superior, Good, Fair, Poor and Bad. For many cases decision makers may prefer to express their judgements to their peers in qualitative terms. Similarly, users, particularly for non-technical audiences, may feel more comfortable or effective in using these qualitative terms for the justification of an economic decision rather than quantitative values, which would require more explanation and possibly confusion. Our goal is to use these same terms to describe the reliability/uncertainty of the assessment results. Table 2 provides guidance on how to assign quantitative β values according to the pairs of qualitative expressions for component Quality Measure and Implementation Characteristics as obtained from the Table 3 component matrix evaluations. The β values, since they are measures of uncertainty, serve to indicate that the higher their value—the lower the reliability. For the specific objective of evaluating the reliability of a building assessment, the following procedure, as developed in the next Sections, will be used:
- For each component i (i = 1 to 9), under assessment, Table 3 provides descriptive matrices for corresponding qualitative terms either as a pair of component Quality Measure and Implementation Characteristics description, or a single descriptor used for of the component evaluation, βi by direct application of the Table 1 values to the individual matrix locations.
- In some cases, there is the quality measure that combines the quality of implementation within its description, then the assignment is direct and the quality assignment is directly given, then use Table 2 to directly assign the βi.
- The resulting N = 9 quantitative βi values are combined by the RMS Equation (2) discussed in Section 2.3 to give β as the quantitative measure of this aspect of the assessment.
- Entering this β value into Table 2. provides the corresponding qualitative description.
An important advantage of the quantitative βi values for each component is that the total uncertainty β of the assessed damageability and related Performance Level assignment may be evaluated in a mathematically consistent procedure (RMS), as discussed in Section 2.3. Rationally, it would not be possible express the Total Uncertainty as a combined effect of a set of different qualitative terms, except by assigning the most prevalent value which is not very compelling.
In a single-property loss assessment, an ASTM Level 1 or higher investigation is deemed an engineered study, while Level 0 is considered a desktop study and has no required technical professional input. In practice, it is common that the Portfolio study reports are vague in stating how the individual building’s seismic characteristics were determined, and what the qualifications of the qualifications of the assessor were. The miss-characterization or miss-representation of primary characteristics such as construction type, year built, lateral load resisting system, condition, occupancy, etc., can result in substantial biases in estimated seismic risks. In practice, it is becoming more common that stakeholders engage seismically experienced professionals for the review of these critical inputs before the actual analyses are implemented by the damageability models. The related investigative tasks for specified properties may include:
- Review/verify that the construction type assigned to the building is appropriate.
- Review/verify that the occupancy type assigned to the building is appropriate.
- Review/verify that the year built and year upgraded (if any) assigned is appropriate and the extent of any modification(s) or upgrades is properly considered.
- Review/verify that secondary modifiers that are building specific are provided by suitably qualified and experienced engineers and properly represented in the CAT model.
- Review/verify that the site seismic hazards have been properly considered, that is confirm that the building is not at a site that is subject to site failure (faulting, liquefaction or landsliding) within the supporting portion of the site.
It is assumed that these technical assessments are completed by an individual(s) that have seismic civil and structural engineer knowledge but are not qualified at the level required by ASTM E2026 to do such studies at Level 1 or higher. The bulleted items level of effort does not qualify as an ASTM Level 1 of Investigation as defined in the ASTM Standards, which typically requires site visits and design drawing reviews as well as the assessor be qualified to ASTM E2026 specified experience and capabilities. To accommodate this important and growing practice in portfolio risk studies, we consider an intermediate Level of Investigation between ASTM Level 0 and Level 1, which can distinguish with more fine detail than the ASTM levels at the low end, by assessing a quality level for the assessment results to help users distinguish the results that can be relied upon from those that cannot. For this purpose, the authors add an ASTM Level 0.5 of Investigation with a corresponding definition that the bulleted items above are followed. This allows some flexibility in the limited ASTM definitions, and the capabilities of the persons assigning the seismic characteristics are given, (Lee et al. 2021). We propose the definition of this be referred to this level of investigation as a Simi-Engineered Assessment in which the property damageabilities are characterized based on general, not specific, information about the building types, characteristics and site conditions. The purpose of this new defined Level is to reduce the uncertainty in damageability of individual assets by limiting the potential for basic errors in essential inputs, such as misinformation on building year-built, number of stories, occupancy, existing damage to the structural system and its condition, lateral force resistance system type and quality, modifications to the structural system or mischaracterization of construction types. Under the present requirements of ASTM Level 0, the potential for errors and mischaracterizations may be so large that its use may result in unacceptable levels of uncertainty in seismic performance characteristics. Alternatively, the cost of implementation of a Level 1 examination of the plans for the building and observation of its construction characteristics may not be feasible. The proposed Level 0.5 provides a compromise that makes serious errors much less likely.
Table 3 presents a set of proposed evaluation criteria in the form of descriptive matrices for assignment of each of the nine components impacting the assessment of the reliability of the building’s damageability evaluation and/or the resulting assigned Performance Level. These matrices provide qualitative descriptions to characterize the conditions of how the component issue is described and its evaluation is implemented and allow the corresponding quantitative βi uncertainty value to be found from Table 1 and the corresponding Qualitative expression from Table 2. It is emphasized that these descriptions are intended to guide the assignment of the βi values and that there may be additional characteristics of the process that are important in a particular application. Therefore, it is advised that the value assigned be adjusted, either by revising the Table entries or by adjusting the resulting values by the method of Equation (1), to reflect the value that best describes the professional opinion and experience of the assessor for the circumstance and conditions. As an example, for a FEMA P-154 assessment, if initially a Level 1 assessment for a particular building was used and the outcome was determined to be inadequate, then the performance of a Level 2 investigation can either change or confirm its acceptability rating. The increased Quality due to the use of Level 2 can be used to justify subsequent decisions concerning the building.
2.3. Determination of Reliability/Uncertainty Values for Individual Building Assessments
The determination of the reliability for a specific building’s quality evaluation requires a mathematically defensible (statistically valid) method of combining the individual component uncertainties are combined to reach an aggregated value, or measure of uncertainty, for the specific assessment process. As discussed in the beginning of Section 2.2 with the use of the model format of FEMA P-695, it is assumed the damage assessment process can be represented as a multiplicative function of the assigned component values [e.g., (ground motion intensity) times (building damageability characteristics) times …] such that the logarithm of the assessed value is in the form of a sum of the logarithms of the components. For the purpose of mathematical tractability and consistent with the level of accuracy in the Qualitative-Quantitative relations in Table 1 and Table 2, it will be assumed that the Probability Distribution of the random error in the assigned value for each measure is Log-Normal with a unit mean value and that the assigned βj is the standard deviation as discussed above, as well as the coefficient of variation since the mean is one. These assumptions allow the determination of the combined uncertainty as a square root of the mean sum of the squares. While we have proposed nine critical components that affect the reliability of an ASCE 41, P-154, ASTM PML evaluation or other applications may consider more or fewer issues. Therefore, we will consider M issues in the assessment calculations to make the method appropriate for general application.
The evaluation of the combined uncertainty in an assessed value is based on the Probability Rule for the Variance of a Sum of independent random variables being equal to the sum of the individual variances (2). Given the M values of for the each of the independent jth issues, and using the assumption that the is the standard deviation of the random error in the value of issue j element, the combined uncertainty is the root mean sum of the squares (RMS) of the values as:
In the left expression it is assumed that all of the uncertainty components have equal importance. The expression on the right assumes that the individual issues have differing weights of importance, with being the assumed weighting factor for the jth uncertainty source. For the particular objective of this uncertainty procedure that relates qualitative and quantitative descriptions, the division by M in the left- and right-radical is to ensure that the β value remains between 0 and 1 such that Table 2 can be used for the qualitative description of this mathematical (quantitative) result. This also achieves the desired result that if all of the values are the same that the assigned β is the same as the individual value. The left-side relationship of Equation (2), called RMS here, is interpreted as introducing no bias into the computation since all components are treated equally, and the right-side, called Weighted Average (WA), as introducing a weighting corresponding to the subjective belief in the component’s relative importance to the reliability of the result. Each weighting is an assumption; it is suggested that the right-side Equation be used only if there is a significant difference in the assessed importance of some elements compared to others. This may occur where some of the damageability or loss contributions are less important when compared to others for a particular building.
Equation (2) is the primary mathematical tool used to aggregate uncertainty values ( or similar items) used throughout this paper, although Equation (3) as given below provides a simpler alternative, but not as well based on statistical methods. It is important to note for some evaluations that not all of the components will be important, and those deemed unimportant may be excluded from the computation. Therefore, not all assessments will have nine components of interest. It may also be true that there are other elements that bear on the reliability of the assessment that must be added. We advise that the basis for such additions and/or subtractions be documented in the report.
The purpose of this proposed reliability of assessment method is to provide the user with a qualitative description of the reliability of a given result: specifically, a quantitative β value is evaluated and then entered into Table 2 to provide the equivalent qualitative term describing the assessment. In this way we do not have to consider the nuance of meaning of a change, such as 0.01, in the β value, but instead use a qualitative term to represent the reliability. The basic presumption is that the user of an assessed value is better justified (and more comfortable) to make decisions if Good or Superior apply, and reject decision making if the reliability is Poor or Bad. The method also serves to identify the specific components and implementations where investment in more information may improve the rating.
Alternative Mean: It could be argued that use of the average (rather than the RMS) of the contributors to be an appropriate way to assess the net reliability of the resulting evaluation, since it does not require assuming that the β values are surrogates for the standard deviation of the logarithms of the individual component in the analysis, and the aggregation approach does not require independence of the component assigned values. There is a rich literature on the subject of linear models to predict outcomes of complex systems. An improper linear model is one in which the weights are chosen by some non-optimal method to yield a defensible conclusion. The weights may be chosen to be equal, on the basis of intuition of an expert, or at random. Research has found that improper models may have great utility, but it is hard to substantiate in many cases. The linear model cannot replace the expert in deciding such things as what to look for, but it also precisely this knowledge of what to look for in the reaching of the decision that is the special expertise people have. In summary, proper linear models work for that very simple reason. People are good at picking out the right predictor variables and at weighting them in such a way that they have a conditionally monotone relationship with the criterion. People are bad at integrating information from diverse and incomplete sources. Proper linear models are good at such integration when the predictions have a conditional monotone relation to the criterion, (Dawes 1979). This basic topic is the subject of several volumes of review papers on heuristics and biases that have substantiated this finding in many applications in psychology, medicine and other applications, (Gilovich et al. 2002). The authors believe that a proper linear model proposed herein is well applied to the problems of seismic assessment reliability determination. The justification would be that this form represents the average or expected error.
We assume two types of simple averages: one is that the weights of the elements are equal, and the other is that an experienced expert in seismic assessment selects them to reflect the relative importance of the individual elements in influencing the decision. In some cases where numerical values are being aggregated, this could be set equal to the replacement cost of the building. This will be called the Simple Average (SA) combination approach, either by a simple average of equally weighted values (left) or weighted values (right). Equation (3) is the primary alternative means to aggregate used throughout this paper but is generally not preferred to Equation (2).
Table 4 provides the β values for the RMS and the Simple Average alternatives for different assumptions of the β values. The Table shows the impact of completing a portion of the issues with a common β value by a better or poorer assessment procedure than the balance, where the β values are a given level for all but one or two values which are different, termed 1× and 2× in the Table. While the resulting values are comparable for some combinations, the Simple Average yields systematically higher reliability factors (that is lower β) for all 1× and 2× values. The range of the ratio of the RMS β values to their simple average range from 1.000 to 1.673 for the 1× comparisons, with the 2× values being in a tighter range of 1.000 to 1.458. We find the RMS approach is consistently the most conservative, and can be better justified on a mathematically basis, if the multiplicative model of components is accepted. The RMS aggregation procedure will be used for the further developments dealing with single building and portfolio assessments. We also note that the Simple Average has standing as a proper linear model that has been substantiated in many binary decision-making processes. Its use is acceptable to the authors, if not preferred.

Table 4.
Impact on the Building β of having all but indicated βi values fixed at the same value, with one (1×) or two (2×) βi values set at the variable β value. Two aggregation approaches are used: RMS of the βi Equation (2), and simple average. Appropriate linguistic ratings can be assigned using Table 2.
As seen in Table 4, changes in having either one or two higher or lower than the principal β values can alter the model’s reliability index significantly. The clear implication of this table is that accepting less than Fair component reliability as the basis for the component assessment, makes it very unlikely that the assessment will acquire a Fair rating or better. In contrast, when Superior or Good is the base assessment, one can allow one or two components at a lesser rating and still acquire a Good or Fair rating. This behavior may be considered in the formulation of a strategy when it is intended to increase the building assessment’s reliability with the most efficient use of available resources. In addition, the behavior exhibited in the Table provides a direct way to see what would be needed to improve the reliability of the assessment conclusion where there is a concern that the reliability is too low upon which to base a decision. Often the most important link in the assessment procedure concerns whether or not the assessor has access to the structural design drawings, has visited the building to examine its condition and/or has the qualifications to do the assessment. For example, if the assessment does not have any of these afore mentioned attributes, then the rating of Component 3, Basis for Evaluation is likely to be Poor or Bad. The raising the Component 3′s rating can dramatically change the β value from 0.5 or lower to 0.2 or lower. If the base value of assessment is Good, then the reliability could go from Fair to Good or better by this single action. If, in addition, a second attribute is improved, then Table 4 makes it clear that the impact can be significant. It is important to note that if there is concern about reliability of the assessment and the results will be an essential factor in making fiduciary decisions, it is appropriate to set the criteria for the performer/provider of the assessment to meet the client’s goals before the assessment is commissioned. The purpose is to minimize the possibility of results that are not sufficiently reliable to use for related decision purposes.
2.4. Aggregation of Building Damageability Uncertainties for a Portfolio
In the evaluation of Portfolio uncertainties in Section 5, it is necessary that a representation be determined for the overall damageability uncertainty for the group of buildings considered. This is represented by a weighted aggregation of the uncertainty values for each of the individual buildings as determined from Section 2.3. Since it is most common that portfolios consist of buildings having different levels of investigation, it is important that the corresponding βi differences be reflected in the reliability estimate for the portfolio loss assessment. We will use the building replacement value to provide the weighting for each building. This aggregate for the building evaluation for the portfolio is similar to the weighted version of Equate 1:
where A is the aggregated damageability uncertainty for the Portfolio, is the damageability uncertainty for the ith building in the portfolio of N buildings and ci is the replacement cost of the building. The same caution applies to these equations as was discussed in Section 2.3. The same caution applies to use of these equations as was discussed in Section 2.3. There is no reason to suppose that a simple average be used here because the value of the βi is easily defended since these are independent structures and thereby the βi are independent.
Not surprisingly, when all of the buildings have the same implemented damageability assessment procedure, that is, the A value for the group is identical to the common β value for each. For an existing portfolio analysis, the values are fixed, and the uncertainty index A is fixed. However, for a portfolio that has yet to be assessed, or for one that is in part to be reassessed, there is an opportunity to make choices that specify the level of investigation for those individual buildings that can significantly impact the A value. This pre-assessment specification applies as well to the indexes B and C to be developed, respectively, in Section 3 and Section 4. It should be noted that the Proposed Investigation Level 0.5, as discussed in Section 2.2, may be particularly useful for those specific buildings that pose a significant element of the loss risk and when a Level 1 assessment is not feasible because of time limits or lack of resources.
2.5. Example Application for Decisions Concerning a Single Building’s Acceptability
A pivotal issue in real estate management of a building may be whether a seismic assessment’s findings are of adequate quality to make a decision of the future use, modification, lease or purchase of a building. We presume that an evaluation prepared has determined whether or not the building is acceptable is based on the client’s purpose for having the assessment completed. Here, the focus is on the quality of the building evaluation and the issue is to decide whether the building is acceptable for occupancy or not based on its seismic evaluation and conformance to an established standard. In the State of California, the usual measure of the assessed seismic performance for a building, new or existing, is the degree to which the building meets the seismic performance requirements of the California Building Code. In California the standard for a state-owned building, including the University of California (UC) and California State University (CSU) Systems, is the degree to which the building meets the seismic performance requirements of the California Existing Building Code. For new buildings this code requirement is an adaptation of ASCE 7, and for existing buildings it is CEBC Section 317 and the following Sections of the 2019 Edition of the California Existing Building Code (CEBC). The issue for decision making is that conformance with Building Code objectives is a binary process: the building either meets or does not meet the criteria. A satisfactory way to express the seriousness of a particular level of non-code acceptability decision is to use a rating scale to express the degree of risk. A satisfactory way of describing the seriousness of a particular assigned level of non-code acceptability is to use a rating scale to express the degree of risk. For this purpose, the California State University System and the University of California have assigned a category method for Earthquake Performance Rating Levels based on CEBC evaluations, see Table 5.

Table 5.
CSU Ratings of Earthquake Performance Levels for Existing Buildings from the current edition of the CSU Seismic Policy based on level of CEBC Structural compliance, Part 10 of the CBC, (CSU 2020). The University of California also uses these definitions, as do most California State Agencies. For levels III through V, the assessing engineer can increase of decrease the rating if it is supported by the independent peer reviewer. These follow the requirements of the CEBC, where the ASCE 41 BSE-1E an BSE-2E are defined differently that they are in ASCE 41 by not allowing the capping of values by those for a new building, BSE-1 and BSE-2.
Generally, a Level IV rated building can be used without limitations, and a newly leased or purchased building must meet the same requirement, (CSU 2020). In the long term, the CSU and UC policies are to have all of their buildings meet or exceed this Level of seismic performance requirements. However, the objective of achieving a Level IV rating for deficient buildings can be very demanding. In order to provide incentives, the CSU has chosen to accelerate the seismic retrofit work by enforcing the following CEBC requirements:
- For existing buildings, any time that a building has proposed work requiring a building permit under the CEBC, that if the work is of the type and/or extent that exceeds stated triggers that require a seismic evaluation, see Table 6, then the building must be seismically evaluated and if indicated, actions must be taken, within the proposed work, to make the building consistent with CEBC requirements.
 Table 6. Reproduction of Sections 317.3.1 of the 2019 CEBC setting the conditions under which a seismic evaluation is required for a building.
Table 6. Reproduction of Sections 317.3.1 of the 2019 CEBC setting the conditions under which a seismic evaluation is required for a building.
It should be noted that the stated triggers for a required CEBC assessment do not necessarily require assessment whenever a modification of the building is proposed that requires a permit. The work must be in excess of the stated trigger limits. In addition, since 1992, in order to achieve due diligence for the life safety performance of all of its facilities, the CSU has performed regular assessments, at all campuses, to determine those buildings in its inventory which pose a significant seismic risk. When such an assessment determines that the vulnerability is too high to accept, then CSU decides on whether the building warrants retrofit as soon as resources become available (listed as Priority I) or be retrofitted whenever any permitted work (no trigger limits) is proposed (listed as Priority 2). These decisions depend on the Ratings of seismic performance indicated in Table 5. In addition, the CSU has determined that a building identified as posing an unacceptably high life safety risk will either require administrative action to seismically retrofit the building in a short-specified term or cease use of the building.
The above description of the CSU Performance Requirements in terms of Rating values, provides an example of where the proposed Uncertainty and Quality evaluation methodology can be applied. The resulting uncertainty evaluations can be used as guides for risk management decisions governing retrofit of existing buildings, along with the decisions concerning lease or purchase of additional buildings. When a building has been assessed to determine its seismic performance by use of FEMA P-154 or ASCE 41, or other means, an assessment of the uncertainty A corresponding Quality of the conclusions of should be made by the proposed method. Table 7 provides an example of how these uncertainty measures could be used to guide decisions. For the case of a Poor or Bad Quality evaluation, it is recommended that no decision be made based upon the evaluation, unless the risk is managed by requiring earthquake insurance, with an appropriate deductible. With the prevalent insurance rates, it may be more cost-effective to refuse the investment opportunity rather than incur the cost of a more reliable damageability assessment.

Table 7.
Proposed decision matrix for how to act upon the assessed confidence in the reliability of assigned seismic performance level of the building. These requirements are for the CBC occupancy Seismic Category I, II and III. See text for the descriptions of the Lists. The option always exists to delay determination of how to proceed by commissioning a more complete seismic assessment.
3. Uncertainty for Portfolio Assessment Procedures
3.1. How Do the Problems of Assessing Portfolios of Buildings Differ from a Single Building?
Most portfolio seismic analyses focus on the determination of dollar loss, or the ratio of loss to replacement cost, caused by earthquake occurrences. The portfolio of buildings is located at sites that are not subject to the same degree of seismic hazard from any one of the earthquakes that could impact some of the portfolio’s members. This loss, and its probability of being exceeded, play an important role in many financial decisions. For a Portfolio Loss assessment due to the risk of all possible damaging events in the hazard zone, the evaluation of the loss for each of the individual buildings is essential; however, these are not sufficient since for the aggregation of the loss there are other factors that impact the reliability of the estimate. These include: correlation of damage for a given event, consideration of all of the multiple possible seismic events and the statistical response of each building to these events, and the dispersion of building damageabilities and values. Of these factors, only the loss reliability value for the individual buildings was included in the Section 2 issues. In addition, concerning representation of individual building uncertainties, it is usual that the resources and effort available per building is considerably less than those for a single property assessment, except perhaps for a few very high value properties at a high seismic-risk location. Furthermore, it is important to recognize that the ASTM E2557 (ASTM E2557-16a 2016) procedures used for the Scenario Loss Assessments (SEL, SUL) for single buildings or multiple buildings at a single site cannot be aggregated for an equivalent Portfolio Loss at multiple sites because of the different earthquake ground motion at the sites due to the same earthquake event, and there are multiple possible events for the seismic zone. The scenario measures SEL and SUL for a Portfolio due to a specified event can be misleading (unless possibly for the special case where the high value properties are concentrated near to the source of the selected scenario event) because of the multiple sources and dispersed locations of high value properties.
Typically, Portfolio Loss Assessment reports will indicate the aggregated losses likely to buildings where the individual losses include repair cost and possibly building contents loss and lost rents and revenues. Reported loss assessment values are usually given with the probability of losses being exceeded over a specified time period, commonly one year. Probable Loss (PL) is defined by ASTM E2026-16a was described in Footnote 1 above. PL values are expressed in terms of the damage ratio and are generally limited to earthquake loss associated with the earthquake ground-shaking hazard but may include losses from other earthquake hazards as prescribed by a User. PL values are given either as a value with specified return periods, or as values that have specified probabilities of exceedance in a given time period. This definition serves the same purpose for geographically distributed portfolios.
For the case where the Portfolio building sites are geographically distributed, any given event can cause intensities of ground motion and corresponding levels of damage that are different for each building site. The Portfolio Probable Loss must consider the effects of all possible damaging events in the hazard region together with the likelihood of the event occurring. The event representation problem typically is addressed by the formation of Event Sets that represent all of the possible earthquakes that can impact one or more of the buildings in the portfolio. The Event Set includes all damaging magnitudes, location on features (seismic source: faults, areas) and corresponding recurrence rates for each of the features in the seismic zone.
The general concept of ASTM’s Probable Loss (PL) as adapted and applied to portfolios offers the only means of expressing total risk to a portfolio due to all possible damaging events from all seismic sources that can impact any one of the portfolio buildings. Additionally, the PL process provides for the representation of the uncertainty of each building’s damageability response to the site ground motions.
A major difference between portfolio versus single building assessment is that the portfolio structures are distributed over large areas, possibly national in scope, and it is crucial to characterize the correlations of ground motion for all building sites. This problem is addressed in portfolio analysis by selecting Event Sets that represent all of the possible earthquakes in aggregate that can impact one or more of the buildings in the portfolio with proper correlation. The Portfolio Probable Loss statistics are derived for all possible statistics of the building losses in each of the event set earthquake ground motions, which reflect the weighted probability of the event, the site ground motion in this event and the statistics of the loss due to this ground motion to the building, aggregated over all buildings in a portfolio and all members of the event set. A purely analytical derivation is not practical because of the complexity of the integrals of loss functions in each event times probability density functions for all buildings and locations, sometime thousands. In addition, complicating this analysis is that the site ground motions due to each event are often complicated probabilistic computations with many trees of conditional random variable distribution functions. The formal mathematics can be described, but their complexity does not allow closed form solutions.
As a result, Monte Carlo simulations are usually the only practical computational approach to the determination of the probability distribution of Portfolio Loss for a one-year time period. These simulations are performed within what is termed as a Catastrophe (CAT) Model. A very large sample size of simulations is made to provide sufficient precision (by the Law of Large Numbers) for determination of the Probability Distribution Function and corresponding Loss Statistics.
CAT modeling is the term used for a computer-based analysis procedure to determine the financial threat of a group of properties (the portfolio) due to all of the seismic events that can occur during a stated time period and impact on one or more of the properties. The determination of the statistical loss distributions for the portfolio involves the modeling of two types of uncertainties (epistemic and aleatory). In the modeling process, it is difficult to determine whether a particular uncertainty should be put in the aleatory or the epistemic category. It is up to the model’s builder to make this distinction. The choice depends in part on scientific knowledge, but much more so, on the practical need for limiting the sophistication of the model in order to make the model feasible for use. In most cases, the calculations in these models are performed by the Monte Carlo method that may require millions of simulations to achieve numerically stability of the results; as a consequence, economy of computation is imperative, (Zio 2013). The parameters that are included in a particular CAT model that include uncertainty can be characterized as aleatory because they are treated as random variables based on a limited amount of data and/or expert judgement. Other parameters that are selected as single values can be categorized as either epistemic or aleatory. The computational results can characterize those uncertainties included in the simulations (sample estimation error) for the given model, but these do not address the epistemic uncertainties introduced by the assumed probability distribution types and related parameters and methods as employed in the model. Therefore, the simulation results cannot fully reflect the epistemic uncertainty of the result. This is because, ordinarily, the providers do not address the basis on which the analytic portions of the model were selected and the degree of accuracy (and possible bias) introduced in the results. As an example, when a specific event ground motion intensity is to be evaluated at a building site, attenuation model is used to determine the numerical value of this site intensity? There is often more than one acceptable model that can each produce different results for the same assumptions of the event. It could be argued that the use of a fault tree (with weighted likelihood for say three models) resolves this “single choice” difficulty; however, in fact, the use of multiple weighted ground motion model results does not fully resolve the uncertainty problem because the weights (measures of credibility) for each branch need to be judgmentally assumed. In addition, there is a lack of more fundamental (epistemic) knowledge such as the compressive and shear strength of the rock rupturing, location and size of rupture, the direction and speed of the induced rupture, the geology of the travel path, etc.
It is helpful to mention here that a typical Portfolio Loss Assessment process (CAT) involves a very large sample set of the simulated Portfolio Loss Values. The mathematical justification for the use of this data set to infer probability statements concerning Portfolio Loss is provided by the notion of the Indifference Principal, in which each calculated outcome can be considered to be equally likely to occur, (Halpern 2017). The principal of indifference is that all elementary outcomes of the simulations are equally likely, the core assumption that underlays probability theory. Thereby, the probability distribution for the loss in designated period can be directly determined by order statistics evaluation of the simulations. No a priori probability distribution function needs to be assumed, but the empirical distribution function from the simulations serves this purpose.
The process of Portfolio Loss Assessment proceeds as follows: given the structural description, replacement cost and site location of the buildings within the defined seismic hazard zone having location and activity description of the seismic sources, determine and evaluate the following components or steps:
- Ground shaking source including segments activated, magnitudes, event-to-site distances to each building in the portfolio (termed the Event Set). Attenuation relations to each building site, site soil types and surface intensity effects. Each element of the Event Set requires a temporal evaluation of its likelihood of occurrence.
- Site-specific hazards (e.g., liquefaction, landslides, fault rupture).
- Structural damage prediction relation (usually in terms of damage ratio) in terms of site ground motion intensity and building damageability characteristics, include damage due to any site-specific hazards.
- Losses (building repair and restoration, contents, business interruption, demand surge, i.e., increase of costs immediately after the event when demand for services and materials exceed supply). Loss is a function of damage ratio, plus any additions due to site-specific hazards. Cost of building replacement should be based current construction cost estimate.
- Aggregation of individual property losses and probabilities into portfolio probable loss statistics, accounting for uncertainty in individual building losses and aggregation of uncertainties for portfolio loss.
- Estimates for Portfolio Loss statistics.
At its core, the problem of determining portfolio loss assessment reliability involves: the representation of the reliability in hazard assessment (source seismicity, site ground motion and other hazards), the representation of the reliability of the damageability characteristics of each building in the portfolio, including the consequences of any existing site hazards (liquefaction-, landsliding- or settlement-induced), and other secondary consequences (fire or demand surge losses). For the reliability/uncertainty related to the damageability characteristics of EACH individual building, the approach will be as developed in Section 2 for each building and then these uncertainties will be aggregated (weighted by respective replacement values, see Equation (6)) for the uncertainty of portfolio damageability. The results will be included as a part of the complete portfolio uncertainty and corresponding qualitative reliability of Section 4.
3.2. Assessing Uncertainty/Reliability for Portfolio Loss Assessments
This section addresses how to determine the reliability of a portfolio assessment. Herein, for clarity we use γ in place of β to represent the uncertainty parameter for the components and results of the Portfolio Loss Assessment. We assume that the CAT model provider will report the statistical characteristics of the assessment approach such that these can be verified to be valid within the laws of probability and statistics. Typically, a computation of portfolio probable loss statistics (such as loss value having a given probability of exceedance in a given time period) is performed using sequential Monte Carlo simulations of: event seismicity, site ground motion intensity, building damageability, associated building costs and losses and aggregated portfolio losses. Each of these steps require an assignment of a probability density function and related parameters from which the Monte Carlo simulations are selected. The simulated aggregate loss results provide a large size sample that allows the determination of the empirical probability density function of the annual portfolio loss. The entire procedure is termed as the CAT Model. The number of assigned parameters is usually kept to a minimum so that the computations are achievable. As a consequence, there are many assumptions and parameter value assignments in the simulation process whose uncertainties are not considered (normally not reported) as part of the uncertainty of the final calculated loss statistics. These unconsidered or unmentioned (epistemic) sources of uncertainty in the CAT Model must be identified and included in the total measure of the uncertainty of the results. For example, the complex Earth’s crustal deformation models, seismicity models, earthquake rupture models and ground motion prediction models may be greatly simplified by a CAT Model developer for the purpose of practical implementation. The building site ground motion intensity measure due to a given event could be represented as Peak Ground Acceleration or Response Spectrum Values (Good), or worse, such as the Modified Mercalli Intensity ratings for the region of the site (Poor). Similarly, the effects of the site soil column characteristics on the surface ground motion intensity may be derived from a site-specific soil assessment (Superior) or from large scale geologic hazard maps (Poor). Another example concerns the level of information used to represent the individual building’s damageability parameters. This information can be from: a building visit by an experienced evaluator (Good), the assessment of the construction drawings by an experienced Engineer (Better), or simply a review of Desktop photos and real estate documents by an experienced structural engineer (Fair) or by one with no technical experience (y). Furthermore, the observed building deficiencies (including primary and secondary influences) the CAT Model: (Good) if entered or (Poor) if not entered. The building damageability parameter evaluations for a given building within the portfolio can be performed at any level of reliability as discussed above. These levels may vary for different buildings within the portfolio and the corresponding individual uncertainties must be included in the aggregated uncertainty weighted by the building replacement value of the portfolio loss statistics. In summary, there are various alternatives in the data collection, parameter specification, data input and analysis methods used in a given CAT Model: the specific choices of these alternatives and representation of their related quality, method of implementation and measure of uncertainty can have a significant effect on the reliability of the corresponding CAT loss statistics. The purpose here is to provide a method by which a user can evaluate the reliability of the CAT results by assigning and combining the uncertainties corresponding to the options and alternatives used in a given CAT Model.
3.3. Evaluation of Characteristics and Components in Portfolio Loss Assessment
There are three principal sources of uncertainty for portfolio loss assessments: first, the way in which the damageability of the individual buildings making up the portfolio is determined (uncertainty of damage assessed in Section 2); second, how the CAT model determines the loss for the individual buildings and then aggregates this loss for total portfolio loss; and third, what the combinatory statistics of the simulations process is numerically. The computational statistics of the damageability analysis will be addressed in Section 4. In this section, we address the uncertainty of loss aggregation in Portfolio Loss Assessment process. For most portfolios, the site seismic hazard along with the individual building damageability characteristics and related reliability level of knowledge are different for each property in each possible damaging event. Computationally, Portfolio Assessment uses the concept of Event Sets to characterize the overall seismic hazard (see Section 3.1). Furthermore, building damage values due to a given Event are correlated, and this must be recognized in the summation or aggregation of building losses due to all possible events. Therefore, the representation of the Event Set is a key element in any portfolio assessment to ensure that the aggregated damage loss for the set of buildings is properly determined. The key components and sources of uncertainty in the evaluation of portfolio damage loss statistics that are related to the determination of loss of individual buildings and portfolio loss aggregation are:
- (1)
- Event Set (ES)—Event Sets represent the earthquake events by location, magnitude range, recurrence rates and other characteristic of the event such as nucleation, rupture initiation, that are used to characterize the events included in the related event intensity computations along with their site attenuation distances. Concerning magnitude range, generally, a magnitude 5.0 earthquake is capable of damaging an existing Unreinforced Masonry Bearing Wall building in the near field, and a magnitude 5.75 is capable, in the near field, of damaging a newly constructed building designed to current building standards. It is often useful (for computational efficiency) to characterize the seismic hazard by identifying those particular sets of events that cannot impact portions of the portfolios, and thereby allow the uncoupling of the risks for these different areas. This uncoupling of certain portions influences how the CAT model is developed and has implications for computational efficiency of the CAT model but does not have any significant effect on the reliability of the loss results. It is also essential that recurrence rate information is available for each seismic source. Where a main fault can produce events on different segments or combinations of these segments, each with magnitude range and rates of occurrence, then the resulting events and corresponding return period shall be included in the event set. The reoccurrence rate for each event in the event set is necessary, such that each simulated event losses and resulted aggregated portfolio loss can be associated with this reoccurrence rate. From each source, there must be a sufficiently large number of simulated events that the sample magnitude-frequency distribution (MFD) Empirical Distribution Function that can yield useful loss return periods over a wide range of values, allowing determination of the loss estimate associated with the longest mean return period of interest (practically represented by Order Statistics of the simulated values tail). This is termed the Empirical MFD rather than the implied definitive MFD because it is based on a finite number of simulations and may not adequately represent the true MFD.
- (2)
- Loss Aggregation (LA)—Description of how the loss Probability Distribution Function (PDF) or the Cumulative Probability Distribution Function (CPDF) reported is determined for the portfolio. This is the process by which each individual building loss due to a given event is aggregated for the whole portfolio of buildings, and the result is then aggregated for all events in the event set. This needs to be performed in a statistically valid manner to provide the Portfolio Loss Statistics having a given return period. While there is the option of assuming the CPDF (such as Log-Normal or Beta distribution) and evaluating the related parameters in terms of the sample estimates based on the simulated loss data, this mathematical representation is subject to epistemic error. For the case where Monte Carlo Simulation can produce the required very large sample size, it is preferable to use the non-parametric ranked order statistics as described above. A typical process for the successive simulation is as follows:
- (A)
- From the Event Set randomly select an Event with known characteristics and determine (by selected ground motion models site soil effects) the PDF of ground motion intensity at each impacted building site in the portfolio to this event.
- (B)
- For each building, determine the Damage Ratio PDF (refer to Matrix 7 in Table 3) due to the item A ground motion randomly selected Item A.
- (C)
- For each building, determine loss PDF of simulated damage ratio for the site for each portfolio building.
- (D)
- Aggregate all building losses for portfolio loss due to selected event from the PDF for the event (Item A), PDF of the site response (Item B) and loss PDF (Item C). This yields one simulation loss for the Portfolio in the event assessed. This loss will have a Return Period associated with the selected Event.
- (E)
- Repeat the above sequence with a sufficiently large number of simulations necessary to define (with acceptable sampling error) the PDF of the random Portfolio Loss due to all possible independent events and corresponding independent responses buildings. For a given return period the Portfolio Loss Statistics are determined from this PDF.
- (3)
- Demand Surge Consideration (DS)—Repair costs are based on the building replacement cost times predicted damage ratio. The reliability of the replacement cost is addressed for each building in Item 8 of Table 3 for individual buildings. Demand Surge reflects the influence of repair cost inflation due to post-earthquake demand for construction materials and labor costs of repair while the market is distorted. There is a surge in pricing for building services and materials as demand for limited supply is significantly increased in the post-event emergency period. See Olsen and Porter (2011), for a recent review of how demand surge is estimated. When cost escalation in the time period after the earthquake is not important, then issue 3 can be ignored.
Discussion: Demand surge is an issue for individuals and institutions that sustain losses in large-scale natural disasters, particularly for property insurers and governments that finance reconstruction. Estimates of demand surge following large-scale natural disasters have quantified a general increase of costs ranging from 10 to 40% following Hurricane Katrina to 50% after Cyclone Larry. For specific materials and labor items, news reports have documented price increases of 30% for oriented strand board following Hurricane Katrina to a 2000% increase for securing a tarpaulin to a damaged roof after the 1999 Sydney hailstorm. The higher repair costs at each property result in a greater loss for an insurer that indemnifies many properties in an affected area. For a single insurer, this additional loss caused by demand surge may mean the difference between survival and ruin. For example, 20th Century Insurance, based in the Los Angeles area, was nearly bankrupted by claims following the 1994 Northridge Earthquake, a disaster that produced a reported 20% demand surge. (Olsen and Porter 2011). Often this item is estimated by multiplying the calculated cost by a factor representing the expected increase of costs where demand far exceeds the supply of both skilled manpower and materials.
For the above components, the corresponding uncertainty measures are to be determined similarly to the procedure for single building procedure by the descriptive quality Matrices in Table 8 and the use of Table 1 or Table 2 for the quantitative and qualitative expressions. All of these uncertainties in portfolio loss evaluation steps as well as the related uncertainties in the individual building loss estimates for the building damageability evaluations are ones that need the attention of the user to make sure that the reliability of the CAT Model Portfolio Loss Statistics is consistent with the requirements for the user’s decision-making process. At a minimum, Items 1 and 2 should be considered.

Table 8.
Definitions of Quality Measure and Implementation characteristics for the components of the portfolio evaluation. For purposes of clarity, we characterize the portfolio component uncertainty by γ rather than the β used for single building assessments.
Table 8 gives matrices for assignment of the qualities of Assessment and Implementation of each of the three components impacting the uncertainty and corresponding qualitative reliability of the Portfolio CAT Model loss statistics. This matrix procedure follows the approach used for individual building uncertainty evaluations of Section 2.3. These matrices are intended to provide qualitative representations of how the element issue was addressed to yield the corresponding quantitative uncertainty ri. The manner of combining these ri values for the total Portfolio Uncertainty and Quality will be discussed in the next sub-sections where the resulting γi values will be combined (RMS) to represent the total measure of uncertainty of the resulting CAT Model loss statistics.
3.4. Determination of Reliability of Assessments Procedures for a Portfolio of Buildings
Having the qualitative measures for Quality Description and Implementation for each component, the corresponding uncertainty values , for j = 1 to 3 components can be determined from Table 1, where is the Tabulated β from Table 1. We now have a basis for evaluation of the uncertainty factor for the loss aggregation in Portfolio Loss Assessment process. By use of procedures similar to those employed for individual buildings, the uncertainty of the portfolio is taken as the RMS of the uncertainties of the three components using Equations (1) or (2). The value resulting B is the uncertainty contribution of the Portfolio Model evaluation. Since there is only one portfolio model, there are not separate values determined for each building. The contributions of the individual building’s assessment reliability will be discussed in Section 5. The division is to ensure that B remains between zero and one. In order to define the Quality of the Portfolio Assessment, the quantitative value can be transformed to its equivalent qualitative term by the use of Table 2. For statistical reasons the RMS evaluation is preferred over the Simple Average, since its basis is comparable to evaluation used in an RMS process, not just an assumption of equal contribution by addition. B is determined as:
At this point, we have achieved the basic objective of describing the Quality of the building assessment results either as a numerical B or as qualitative descriptor ranging from Superior to Bad. The user now has this qualitive basis for the justification of decisions. Furthermore, if reliability needs improvement, the uncertainty contribution of each component is identified, and resources can be allocated to improve related information or adjustments in any particular component.
4. Uncertainty of Sample Estimates from Loss Simulations
4.1. Considerations of the Uncertainty Issues of Portfolio Loss Statistics
The determination and form of the assumed probability functions and related operations required for the analytic evaluation of portfolio loss statistics have such mathematical complexity that a closed form mathematical expression is virtually impossible to determine for any measure. In addition, it is difficult and, in cases not possible, to evaluate confidence limits for the results—other than by judgmentally assigned epistemic uncertainty values. The epistemic issues have been discussed in Section 3. However, these computational results are subject to sampling (aleatory) error. This section addresses this last major source of uncertainty that can affect the quality of the Portfolio Loss Statistics. It is well established that the number of simulations in a Monte Carlo process has a large influence on the reliability of the estimated statistics—where this reliability is represented by the degree to which the sample estimates are representative of the true value being evaluated by the process.
The Monte Carlo simulation process provides a large sample size data set of N portfolio loss values which when ranked from largest-to-smallest, including all zero values, is sufficient to determine the non-parametric Complementary Cumulative Probability Distribution Function (CCPDF) for the portfolio loss. The CCPDF allows direct determination of the likelihood of any portfolio loss value being exceeded in a year, PL, as well as in a specified time period of T years for any loss being exceeded or being in any defined loss range. This process provides probability values from 0 to 1.0 with high precision, but not necessarily accuracy. The reliability analysis of this paper is intended to determine the degree of reliability of the estimate, that is, its accuracy or measure of uncertainty. The number of simulations must be sufficient to converge to the true value within specified limits of accuracy, however, even then, the uncertainty bounds for losses will not be reduced to zero. The client/user must be provided with a sufficient representation of this uncertainty in order to make responsible decisions.
It is usual practice that each simulated value L is the Portfolio Loss that can occur during a one-year period of exposure to all possible earthquakes that can occur. The ranked (largest to smallest) order statistics of the simulated values provides a sample representation of the CCPDF. This provides an estimate of the probability of exceedance for any specific simulated value. However, while we can clearly state a numerically precise value for this estimate, we need to pay attention to the following advice of Wasserman and many other authors related to such estimates: the main point to keep in mind is that an estimate of fn without some sense of the confidence set is usually not useful. (Wasserman 2006, p. 57) (N.B., fn is the probability density function estimate for loss.)
While the reliability/uncertainty of the sample estimate of a probability of exceedance or any other portfolio loss statistics can be improved by increased number of simulations, the accuracy is also dependent on the method of drawing samples from the simulated data set; this sampling procedure will be addressed in the next Section. Typically, the number of simulations, N, depending on the characteristics of the portfolio, is very large. The following section addresses the issue of expressing the uncertainty of the loss statistics that are estimated from the simulated data (e.g., coefficient of variation, CV). It is important to recognize that it is common that financial decisions are based on the high, but rare reported PL value (such as for 500-year return period), and therefore it is most important to be able to assess the reliability of estimates of these upper tail portions of the loss. Special attention is needed because fewer simulated values occur in the upper tails (since there is a lower probability of being selected in the simulation process).
We discuss two issues on this subject to characterize the uncertainty of the CAT computational results as presented in a Portfolio PML report:
- The quality of the definition of the calculated loss parameters from the CAT model.
- How the uncertainty in the Portfolio loss distribution function has been represented, such as, is a confidence value given for the reliability of the specific loss results, including CV, and probability of exceedance and any other numerical statistic of the process.
These issues are addressed in the next sections.
4.2. A Reliability Computational Approach Using Bootstrap Sampling
With the advent of fast, high capacity, computational systems, new techniques of data sampling are now feasible. Wasserman reports on the extensive statistical literature concerning how to interpret Monte Carlo simulations and extract reliable information from them, (Wasserman 2006). Obviously, the number of simulations has a great impact on the reported loss statistics. The basic issue when making a financial or policy decision based on a loss estimate is to have a measure of the reliability of the reported loss value for a specified likelihood of being exceeded (e.g., 50th and 90th Percentiles, or 225- and 500-year return period). In classic Parametric Statistics the width of Confidence Bands for an estimated parameter is, essentially, inversely proportional to the square root of sample size N. However, for the Non-Parametric Statistics (e.g., order statistics) of simulated data, the confidence bands vary with the number of data values greater than the Statistic that is being estimated. It is observed that the accuracy of the CCPDF for seismic loss estimates decreases with increasing loss values. Thiel and Zsutty show this in the case for 17 sites in California, Nevada, Oregon, Utah, Washington and Guam for the same marginal seismic performing building types, (Thiel and Zsutty 2018), and for individual buildings having a wide range of damageabilities, from very low to very high, at 14 US sites, including Alaska, (Thiel 2001). The model portfolio assessed below also exhibits this behavior. For the user/client, in practice, it is common that the financial decisions based on portfolio loss assessment are usually focused on the PL tail risk, for example, a 250- or 500-year return period for exceedance, equivalent to a respective annual probability of exceedance of 0.4% or 0.2%. These low probability, high damage loss levels, are characterized as the tail risk portion of the loss curve and also may be characterized in practice as the right tail risk. It is reasonable for the uncertainty of the evaluations of these very low probability of exceedance loss values to have higher uncertainties because, in their high value range, there are radically fewer simulation results than for the values nearer to the central losses. Therefore, we assert that to use a full range of complementary cumulative probability distribution function uncertainty values to represent the uncertainty of all loss values would be advantageous. The following discussion proposes an approach to how the uncertainty for a given loss value can be determined based on how Monte Carlo damage assessment results are statistically examined by sampling procedures.
Given that we have the results of a Monte Carlo simulation of N loss values from the assessment of the earthquake loss of a given portfolio, we propose a rather direct way to determine the reliability statistics of the loss values of interest. The simulation results are given as a group of losses {Li, i = 1, N} that could occur in a one-year exposure due to the hazard of the Event Set. This group must include all the simulations that resulted in zero values. The group represents all the realizations of the probabilistic process of assessing the aggregated loss value for the portfolio. By the process of ordering the values of Li, from largest to smallest, we can directly estimate the probability that any selected value Lj will be equaled or exceeded by determining the ratio of the ranked sequence number Nj of the element Lj to the number N of total simulations (this is called an Order Statistics method of determining an empirical CCPDF. In terms of Non-Parametric Statistics, the Probability of (L ) is estimated by the ratio Nj/N. From the full set of N loss values, we could also determine: the estimate of the Portfolio Expected Loss as the sample expected value, the median loss, along with the loss variance. Further, with the CCPDF we can estimate the likelihood of exceeding any loss level. However, the basic problem is that we need confidence intervals for these and other specified loss statistics based on sample estimate values. In order to fulfill this requirement, we will employ what is termed in statistics a Bootstrap resampling procedure to develop the confidence intervals for loss values of interest from the Monte Carlo array of Portfolio Loss simulations.
Classical Parametric Statistical Methods assume that sample data are drawn from a known Probability Distribution Function and use the full sample of size N to estimate the parameter values of the assumed Probability Distribution. Applicable parametric tests are then employed to compare the sample estimates to the true parameter values. For example, for an assumed Normal Distribution, the confidence limits of the true mean value involve use of the Student’s t-distribution (with N − 1 degrees-of- freedom) about the sample average value. However, for the case of Portfolio Loss we have no a priori notion of what the true Probability Distribution function is for this loss, and as a consequence we have chosen to use non-parametric statistical methods. Non-parametric statistical uncertainty assessment depends on the observation that the sample set of values represents all of the reliable information available, and there is no need to assume a parametric probability distribution function for the data. This observation is particularly applicable for the case of Monte Carlo simulations where the sample size can be of the order of 104 or more. Specifically, we will use Bootstrapping: a method that uses M resamples with replacement of each individual randomly selected data value, from the original data in order to form M sets of independent possible occurrences based on the same data. Bootstrapping can be used to assign measures of accuracy (mean, variance, confidence interval, prediction error, or any other statistic) to sample estimates from the M resampled sets, (Efron and Tibshirani 1993; Wasserman 2006; Davison and Hinkley 2009; Halpern 2017). The resulting set of M sample estimates can be assumed to be from an independent, identically distributed population of N simulated data values. The basic steps of the Bootstrap procedure are as follows:
- (1)
- Construct an empirical probability distribution function, , from the sample placing a probability of 1/n at each point x1, x2, …, xN. When this is ordered from smallest to largest, it is the empirical distribution function (EDF) of x, which is the nonparametric maximum likelihood estimate (MLE) of the population distribution function F(x).
- (2)
- Determine the k loss values for which probability confidence limits are desired, and determine what number of resamples, M, should be completed.
- (3)
- Select a random sample of size N equal to the number of simulations with replacement from the original set of values. This is the resample set .
- (4)
- Calculate the statistics for each from this resample, yielding , where i is the sequence number of the kth resample.
- (5)
- Repeat Steps 2 and 3 M times. The confidence values for each loss of interest is represented by the set .
- (6)
- Construct a probability distribution for from the M ’s by placing a probability of 1/M at each point, , , … . This distribution is the Bootstrap estimate of the sampling distribution of , . From this the standard deviation and the mean determined the CV can be calculated, as can any percentile statistic of the process. The implementation of this step is discussed below. (adapted from Mooney et al. 1993).
Note that even though each resample has size N equal to that of the complete data set, the randomized selection of each value, with replacement, results in a different set of the N values in probability. It is possible that some initial values will have multiple realizations in a resample and some values will not appear at all. Since it is unusual that in Portfolio loss analysis many simulations, often 100,000 simulations made of the order of 100 or fewer resample may be sufficient. If for one or more of the loss values of interest, the number selected is not sufficient to acquire an acceptable confidence limit, then additional resamples can be implemented with limited effort. As will be seen, the CV converges quicky with 30 resamples for the 500K Model Portfolio simulations. As Efron and Tibshirani state: bootstrapping is used not to learn about general properties of statistical procedure, as in most statistical procedures, but rather to assess the properties for the data at hand. Nonparametric bootstrap inferences are asymptotically efficient. That is, for large samples they give accurate answers no matter what the population, (Efron and Tibshirani 1993). These results are technically considered to be more accurate aggregate statistics of the simulated process than the raw set of original values would provide by the original simulations, (Davison and Hinkley 2009).
A simple and reliable way to make this conversion to continuous values is to use the Microsoft Excel functions Percentile.Inc(array,k) or Percentile.Exc(array, k) to determine the array value at a specified percentile of interest (k). This is an implementation of the percentile methods discussed by Davison and Hinkley (2009). These functions use interpolation methods to obtain values not limited to the specific values for each element in the sorted array. We expect this method to work well for the Bootstrap samples for Portfolio Loss because the functional form of the empirical distribution functions is quite regular, approximating an exponential decay function. One can use the Percentile.Exc function to determine the percentile exclusive of the first and last values in the array or use the Percentile.Inc function to determine the percentile inclusive of the first and last values in the array. We prefer the Inc version, although they tend to yield the same results for 10 or more sets, but they do not for a smaller number of values.
4.3. Example Results for a Model Portfolio of Buildings
We analyze an example of assessed loss results for a model portfolio that was the subject of a recent paper by Lee et al. (2021). The portfolio is composed of 99 buildings in two regions within California as shown by the map of their locations along with their relative values, see Figure 1. The total replacement value of the portfolio is about $2.3 billion, with about $1.7 billion in Southern California and $0.6 billion in Northern California. Among the 100 buildings, 77 are low-rises (1–3 stories), 17 are mid-rises (4–7 stories) and 5 are high-rises (8 stories and above). The portfolio was modeled using HAZUS damage method (HAZUS 2013). All low- and mid-rises are modeled as Concrete Shear Walls (HAZUS Model Building Type: C2L and C2M, respectively) and all high-rises are modeled as Steel Moment Frame (HAZUS MBT: S1H). The seismic Design Code used varies according to the age of a building, with pre-1975 modeled as Moderate Code (MC) and post-1975 modeled as High Code (HC). Occupancy Type is uniformly COM4—Professional/Technical Services (Office). For damage uncertainty, a random ASTM 2024-16a Level of Investigation 0, 1 and 2 is assigned for each building. Lee et al. (2021) performed a Monte Carlo simulation of 500,000 losses for a one-year period of exposure to the related events sets. These simulated annual losses include the possibility of several earthquakes occurring within the same year time window, and also include zero values when no damaging events occur. Figure 2 gives a graphic indication of the loss values in a year and the probabilities of their exceedance. Note the large number of zero loss simulations, as expected. It is often useful to plot the complementary cumulative distribution function to verify that it is regular. The model portfolio data of Table 9 are plotted in Figure 2, which indicates that the base data are regular in that they are monotonically decreasing in a smooth, uninterrupted manner. Portfolio loss curves are typically of this shape.
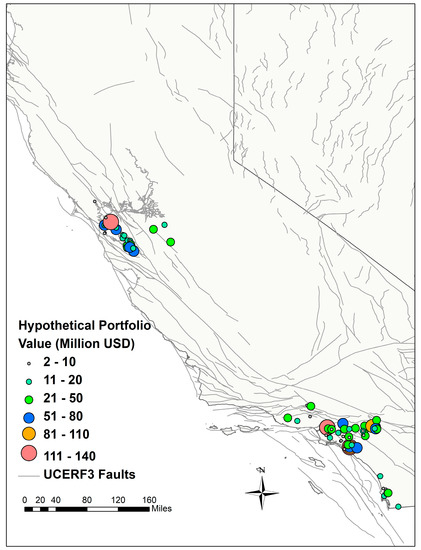
Figure 1.
Reproduction of the model 99 building portfolio assess by Lee indicating the location and value of the buildings by the color and size of the filled circle. (Lee et al. 2021).
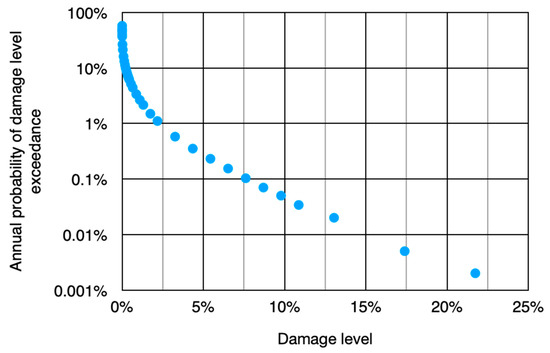
Figure 2.
The empirical complimentary probability loss distribution function for the model 99 building portfolio of the Example, (Lee et al. 2021).

Table 9.
Probability that the loss to the model portfolio (P Excd.) exceed the stated values for the Lee et al. 2021 Model Portfolio. The loss simulations were reported to the dollar. No deductibles were considered in the loss calculations.
From the table of 500 K simulations, we formed M = 30 Bootstrap random selections of N = 500 K simulations, each individual value selection with replacement, that is, each entry was determined as a random selection from the original simulated loss table. Thus, the 30 sets constitute a selection of 15 M samples from the original 500 K loss simulations. The Bootstrap sampling method is used to examine the reliability of the mean, standard deviation and other statistics (such as high tail values) of a random set of resampled simulations; here the procedure is to refine their values by computing the specified statistics for each of the 30 independent resamples and comparing them, (DiCiccio and Efron 1996; Davison and Hinkley 2009; Wasserman 2006). The probability values were determined using the Excel Percentile.Inc function for the resample results as discussed above.
Table 10 assesses the differences from the median of the upper and lower bounds and other statistics of the Bootstrap results for the N = 500 K total simulations. The Lee and Bootstrap values are close for the averages. Note that the values for the average match well those of the original data set from (Lee et al. 2021), as expected for such a large sample. However, the variability increases drastically as the damage values increase. It is clear that the estimation process using 30,500 K resamples worked quite well. Lest this be viewed as a major task, the run time on an IMAC Excel spreadsheet was less than 10 min to produce these results. Using the values of Table 10 we can determine a lower and upper bound 80% confidence limits for the annual risk of a $100 M loss as (0.343%, 0.362%). For comparison we have calculated the corresponding 90% confidence limits as [0.305%, 0.421%]. We shall call these the confidence limit (CL) bounds for a specified probability of exceedance limits. The upper limit represents the highest risk and is thereby more likely to be weighted in financial risk management decisions. However, it is prudent to consider the whole range to remain objective.

Table 10.
Bootstrap for 500K30 simulation of the Model Portfolio loss values to determine the probability ranges for individual loss values. The 10% and 90% headers indicate the probability of the damage exceeding raw loss value. CV is the coefficient of variation (Standard Deviation/Average). The Lee (Lee et al. 2021) values are the probabilities associated with the original simulation data set. The remaining values were determined from the statistics of the resampled sets using the Percentile.Inc. function.
As will be seen in Section 5.2, the CV plays an important role in the description of the degree of reliability of the portfolio estimates of loss statistics. We will consider two approaches to presenting the loss and the probability of the loss being exceeded; one focusing on the dollar amount, and the other on the probability that the loss is exceeded. In practice it is common that portfolio loss reports focus on the probability that a given dollar loss is exceeded, or on the loss for a given probability of exceedance. Many insurers are interested in the likelihood of losses exceeding a fixed dollar value. Table 11 reviews the calculated CVs for different dollar losses to the Model Portfolio. These values clearly indicate that if large loss values are of interest, then the number of simulations M in the bootstrap sample has a significant influence on the uncertainty of the results. It may be convenient to specific the criteria for acceptability uncertainty are set in terms of the probability that critical loss values of interest. Table 12 shows first the damage values expressed as PL for the 500K30 analysis, and the CV results for the four simulation strategies of Table 11 over a wider range of probability values. As a caution, strictly speaking the very high CV values can be lowered by performing more bootstrap resamples. However, a high number of resamples will not change the probability loss value above 10% by much, and the basic degree of uncertainty as obtained from Table 2 will still be qualitatively evaluated as Good or better, (see bias estimation for Monte Carlo simulation in Davison and Hinkley 2009). It is notable that the CV values are similar over the full range of lower loss percentages for the different simulation numbers, but their CV values become significantly larger as the loss value increases. This makes sense if you note that the number of non-zero expected number of occurrences for 5% exceedance probability is 25,000 for the 500K30 case, of which 43% are zero, or about 14,250 losses greater than zero, while for 0.0056% exceedance probability the number is 28 non-zero values, on which the CV for the loss value depends. Clearly, the confidence in drawing firm conclusions is significantly different for these two values as seen in the comparative CV values. The annual expected loss to the portfolio (AEL), shown at the bottom of Table 12, is the calculated value of a “lower bound fair value” for the insurance cost. In many cases the loss will be determined using a deductible, in which case the loss would be lower but the analysis will be similar.

Table 11.
Comparisons of the CV of the dollar losses for the Model Portfolio for different Bootstrap approaches depending on the original loss Monte Carlo simulation sizes of N = 20 K, 100 K, 200 K and 500 K. 500K30 means 30 resamples of 500 K each.

Table 12.
Comparisons of the loss values with the CV for the percentage loss for exceeding the loss value for the Model Portfolio for different Bootstrap approaches depending on the original loss Monte Carlo simulation total. 500K30 means 500 K. The portfolio value is $2.3 Billion. The column Occurrence indicates the probability of the loss value is exceeded as determined from the 500K30 simulations results. The annual expected loss, AEL, of the 500K30 simulations is 0.122% and the CV of this loss for the different simulation numbers are as indicated; The CV are so low because there are so many loss simulations below this loss value.
4.4. Assigning an Uncertainty Parameter for Computation of Statistics from Simulated Data
There are two primary issues that have been discussed above that can affect the Quality and related uncertainty of reported Portfolio Loss Statistics:
- First, whether or not the CAT Model loss assessment procedure has been described sufficiently in order to verify that the methods are valid and the input is representative of the portfolio and location. Were the reported results described in an appropriate statistical terminology related to loss and risk occurrence? In order to detect possible sources of uncertainty, there should be a reasonably descriptive presentation of the CAT Model procedures by the performer so as to allow the user/client to assess the validity of the essential steps of the model and their implementation.
- Second, whether or not the computational uncertainties in the reported results are presented and, if so, how were these uncertainties determined and does the procedure have statistical validity? If the provider gives confidence bands it is assumed that they will provide at a minimum, loss value confidence estimates for specified loss statistics specified by the client or confidence bands for all the loss values reported. Few CAT models are known to report confidence ranges or even provide qualitative discussions of confidence for loss values. In the opinion of the authors this is an important addition to the reporting of loss values in Portfolio studies and will serve to provide a considerable enhancement of knowledge to the users/client for purposes of decision making. See Section 4.4.
Table 13 presents the matrix process proposed to be used to determine the uncertainty factor for these two issues. From each matrix, the resulting pair of Quality assignments (for Description and Implementation) are to be used in Table 1 and Table 2 to evaluate the Portfolio Computations uncertainty value C. The resulting quantitative value can be expressed as a qualitative term from Table 2.

Table 13.
Definitions of Measure Characteristics and Implementation Characteristics for the components of the Loss Simulations evaluation. These are assumed to be given as a probability of the damage level confidence bound for median probability for a given dollar loss. Not all loss values will have the same confidence span. The resulting uncertainty values determined from Table 1 will be labeled C. Note that the actual computed CV is not considered in this evaluation, it is considered in Section 4.
We have considered the problem of how to assign a qualitative reliability term for a particular loss value that has a CV value of 0.50. The authors would characterize this value for a loss as Bad. Using this assignment as the basis for measurement, we can express the qualitative uncertainty of a given CV(L) value by using one half of the limits the Table 2 entries as appropriate interpretations of CV reliability terms assignments. Table 14, is used to characterize these as uncertainty, S. Using these definitions, only 1 of the 500K30 loss values (20%) in Table 12 would qualify as rated Bad, and all the loss values below12.5% for the 20K30 to 500K30 bootstraps would qualify as Fair or better; all of the AELs rate Superior. Since these uncertainties are variable based on the loss value under consideration, we have not included them in the quality assessment considered in this Section but will use it in Section 5.2 for rating a numerical loss reliability.

Table 14.
Assignment matrix for the uncertainty assessment of a specific CV value, termed S. These assignments will be used in Section 5.2. These were determined as one-half the Table 2 limit values for the qualitative level.
5. Portfolio Reliability Evaluation
5.1. Statement of the Uncertainty Issues Considered
This section addresses the combination of the uncertainties involved the results of Portfolio Loss Assessment. The prior Section 2, Section 3 and Section 4 have addressed the assignment of the uncertainties in terms as quantitative measures of the reliability or quality of each of the essential phases of a portfolio loss evaluations. These measures are:
- The combined uncertainty of the individual building damageability assessments A as determined in Section 2.4.
- The uncertainty of the algorithm (CAT Model) that determines the aggregated loss for the portfolio of buildings in earthquake events, as represented by B in Section 3.4.
- The uncertainty of the Monte Carlo computational process employed to simulate the aggregated portfolio loss (here, in terms of loss due to a one-year period of exposure to the event set hazard), and how the statistical sampling uncertainties of the reported loss results, as represented by C in Section 4.4.
We note that A and B have to do with the theoretical (epistemic and aleatory) uncertainties introduced by the method of analysis, and C relates to the (aleatory) uncertainties of evaluating the specific reported results from the simulated data set. In this Section we combine these measures into a value that applies to the results of the Portfolio Loss assessment. We designate the quantitative uncertainty of the Portfolio by the symbol R. As before, the quantitative values of uncertainty are used in order to provide a logical method of combination by the use of the RMS method employed in Equation (2):
In the left Equation it is assumed that all of the uncertainty measures have equal importance. The Equation on the right allows the assignment of differing weights of importance, for the jth uncertainty measure. The authors prefer the RMS option because in our opinion the three contributors to the uncertainty of the portfolio are of equal importance. However, there may situations, perhaps depending on the special characteristics of the portfolio, or the particular situation of the user-client, where the WA option might be useful. It is important to note that when only one building is being assessed, that the B is not applicable and the Equation (6) is reduced to only including A and C, and reduction of the divisor to 2. If the analysis has only one site, but possible several buildings, then R depends on only A, and R = A.
R represents the uncertainty/reliability of the assessment and includes the representation of the epistemic error in the CAT Model and associated simulation process, and the aleatory error in the sample estimates of the portfolio loss statistics. The quantitative value of R can be expressed as an equivalent qualitative term by use of Table 2—if desired for effective communication.
It is interesting to evaluate the impact of different levels of quality for the three measures (A, B and C) on the overall reliability of the portfolio using the RMS procedure. The results can useful for indicating where more information is required to achieve an acceptable reliability or for setting requirements for a proposed assessment. The RMS rating for one Superior, one Good and one Fair is 0.24, which falls in the range given in Table 2 for Good. Table 15 allows the evaluation of many of the possible options assuming that the values of the elements are consistent with Table 2 central values. It is clear that the likelihood of getting an acceptable rating (Fair) is not possible if one of the valuations is Bad. However, as long as none of the ratings are below Fair, it is still possibly to acquire a Fair rating. If the client is careful in the setting of the criteria for the completion of the assessment report, then it should be relatively easy to achieve a Good or better rating for A. Furthermore, it should not be difficult for any competent technical provider performed to acquire a Good or better rating for B. The governing likely issue will be the justification for the incremental cost of getting a Good or better rating for A, which may require locating and reviewing the drawings and having a qualified person visit the building. This could be accomplished by managing the level of investigation prudently; for example, doing the higher level of investigations for selected buildings, particularly for those of high value or very high loss risk, and the toleration of a lower level for those buildings of low relative value—the objective being to achieve financial feasibility. The introduction of the proposed ASTM level of Investigation LI0.5 = 0.5, in Section 4.2, for Portfolio Assessments, should facilitate the focusing of added effort on those assets making the largest contribution to the uncertainty of the high, tail-end loss values.

Table 15.
Impact on the having various A, B and C values from the qualitative value set, with one (1×) or two (2×) values set at a different variable value.
It is necessary in the author’s view for the client who proposes to utilize the results of a seismic assessment to determine whether the methods used are expected to yield results that are sufficiently reliable to warrant action. The uncertainty index provides a direct manner to make a decision on its reliability. Table 16 provides an example of how this uncertainty measures could be used to guide decisions. For the case of a Poor or Bad Quality evaluation, it is recommended that no decision be made based upon the evaluation, unless that decision is made to reassess risk. If action is necessary, then complete a higher level of evaluation to be its basis. This should include pre-investigation considerations of the requirements for the assessment to be accomplished, and a pre-qualification of the performed to verify that they are capable of meeting the reliability requirements for the actions under consideration. Note that Table 15 suggests by exclusion of the orange highlights the combinations of A, B and C assessment values likely to yield Superior, Good or Fair R index values for any assessment based its characteristics. The matrix Table 3, Table 8 and Table 13 should aid the client is setting the minimum standards for procurement of seismic assessments that are acceptable. Clearly it would be useful for clients to set the criteria for its seismic assessment at a level sufficient to be actionable before the assessments are accomplished.

Table 16.
Proposed decision matrix for how to act upon the assessed confidence in the reliability of assigned seismic performance level of the building R.
When a building or portfolio has been assessed to determine its seismic performance and uncertainty R assessment, then R provides a basis for deciding whether or not actions are warranted based on the assessment’s conclusions. Table 16 provides example guidance of how the uncertainty measure could be used to guide decisions. For the case of a Poor or Bad R rating, the authors recommended that no decision be made based upon the evaluation, except possible to complete a more reliable assessment on which to make a decision. A Fair rating is in the author’s opinion marginally reliable depending on the decision to be made/A Good or Superior rating should be adequate in most circumstances.
The Thiel-Zsutty Revised (TZR) model damage estimation for single buildings, (Thiel and Zsutty 2017a, 2017b), expresses the reliability of the damage estimation process through assignment of an α multiplier factor applied to the computed standard deviation of the Beta Distribution model. The α factor can range from 0.25 to 1.5, depending on the respective quality of the estimation process. The R value, as presented in TZR Section 8 and adapted for single building damageability, can be employed to evaluate this α factor. By the tacit assumption that: α = 0.4 for an R rating of Superior, 0.75 for R of Good, 1.0 for R of Fair, 1.25 for R of Poor and, 1.5 for R of Bad, then a relation can be made by the logarithmic fit of α = 0.486 ln(R) + 1.530, for the assigned numerical value of R that is representative of the quality of methods used; this curve fit has a squared correlation of r2 = 0.993, rated as quite good. This allows the use of detailed process leading to the single building R rating to be employed for the standard deviation modification of the TZR model.
5.2. Influence of Portfolio Assessment Reliability on a Portfolio Loss Estimate
For those cases where the numerical loss values are reported in the assessment, we are now in a position to rate of the reliability of these values based on the corresponding values of the R of the portfolio assessment. However, while the value of C gives credit (better Quality) if the CV is reported for a loss value, there is, as yet, no representation of the effect of the corresponding (large or small) value of the CV. The influence of the CV cannot be included directly in the C value because the CV is different for each specific loss statistic: we need to know what loss statistic is, such as, mean, or 500-year return period, in order to know the corresponding CV. As noted in Section 4.4.2 for the Model Portfolio Example in Table 11 and Table 12, the value of the CV increases significantly for the high tail loss levels having low probabilities of exceedance: these CV values range from less than 1% to over 66%, depending on how many Monte Carlo simulations are completed and how far out the tail loss is considered. The total uncertainty of a specific loss statistic can be determined by combining the uncertainty of the portfolio, R, with the uncertainty of the computations as represented by the CV value of the respective loss statistic as noted in Table 14. As noted in Section 5.1, if the reliability index R is rated as Poor or Bad, then this formula should not be used; the quality of such an assessment is not judged sufficient to recommend use of the assessment’s results Table 17 presents recommendations of the reliability index for a given loss computation based on the quality index of the Portfolio assessment procedure R from Equation (6) and the CV value for the loss S from Table 14.

Table 17.
A qualitative rating assignment based on the aggregate reliability of CAT portfolio risk estimates based on the reliability of the CAT model computations and the Reliability value R and the S assessment for the individual numerical value for the loss being evaluation. Note that for each loss values considered, a separate Reliability Value applies. Consistent with the recommendations of Section 5.1, R values of Poor and Bad are not considered.
It is recognized that the individual client’s needs and conditions may cause different values to be assigned for these thresholds. Referring to the values of Table 12 for the Model portfolio, the AEL, that is the expected or average annual portfolio loss, has CV values less than 5% for all the simulations completed. As a result, even if the assessment quality R is rated as Fair, the reliability of the damage estimate will be Good. For a loss of 15% or lower, the 500K30 values are all in the Superior, which will yield a Good evaluation overall for an R value of Fair evaluation, while only for losses less than about 6% will the 20K30 values be Good. The message is that having enough simulations completed can have an important influence on the reliability of the values computed and subsequently used in the financial decision. The advantage of obtaining an increase in simulations is that it does not require an increase in the analysts’ time, but only computer time. If small adjustments are made to some building investigations using the approach of Section 2.2 to identifying the buildings that contribute the most to the tail-loss contribution values, then it may be easy to achieve a CV less the 5%, (Lee et al. 2021).
6. Conclusions
The essential purpose of this paper is to understand and evaluate the uncertainty in reported results of Seismic Loss assessment. It is important to recognize that there is inherent uncertainty in the results of all professional seismic performance assessments; this condition was well stated by Justice Roger J. Traynor in 1954: those who hire (professionals) are not justified in expecting infallibility, but only reasonable care and competence. They purchase the service, not insurance. Another applicable warning is where the consultant is providing probability estimates of loss values important to financial decisions: the main point to keep in mind is that an estimate of fn without some sense of the confidence set is usually not useful. (Wasserman 2006, p. 57). Confidence limits that determine the loss ranges that have specific upper and/or lower limits of probability are specifically addressed in this paper in Section 4 in a way not previously discussed in seismic loss presentations. The authors wish to emphasize that statistical sampling error and possible bias, herein characterized as uncertainty, is a feature of any statistical technique or of its results. The expected value of the results differs from the true underlying quantitative parameter being estimated. As a general conclusion, when a client considers the use of a seismic loss assessment result as a basis for a decision and they do not want to be a victim of a decision gone wrong, then there should be a careful consideration and specification of the scope of services for their seismic loss studies. This consideration is needed in order to provide an acceptable reliability/uncertainty of the results. Furthermore, in order to detect possible sources of epistemic uncertainty, there should be a reasonably descriptive presentation of the CAT Model procedures by the provider to allow review by the user/client or design consultant who will be using the results. Further when results are reported, there should be an evaluation of the reliability of the results, e.g., quality and or confidence limits. This follows the legal definition of being prudent, a term that means to obtain reliable data, use good judgment, be wise, sensible and reasonably cautious.
Presently ASTM 2026 provides definitions of level of investigation of 0, 1, 2 and 3 are to be useful in Portfolio Seismic Loss Assessment, it is proposed that an intermediate Level 0.5 to be added, as discussed in Section 4.2 and by Lee (Lee et al. 2021). This intermediate level allows less intense, but financially feasible investigations of the seismic performance characteristics of the buildings that make up the portfolio. It specifies the necessary qualifications of the investigator, and thereby provides a better chance of yielding acceptable reliable conclusions.
This paper has provided an approach to the evaluation of the uncertainties in the process of performing an assessment, and the expression of the confidence that a decision maker should have in making decisions relying on the results of the assessment. The specific performance or loss assessments, along their measures of uncertainty are summarized as follows:
- (1)
- For a Single Building:
- Quality measures of the results of a specific seismic evaluation (Superior to Bad) that recognizes all of the sources of uncertainty of the assessment procedure and its execution by the consultant/provider. These include the decisions made in the approach selected for the engineering evaluation and the execution of the assessment. These measures provide an effective tool to describe the degree of uncertainty of damage ratio values for individual buildings, which may be ASTM E2026 Scenario Loss, Probable Loss of other statistics of the loss values.
- Quantitative confidence limits for the loss values where these limits represent uncertainties due to both those of the computations, and the influence of the quality measures for the assessment performed. The recommended coefficient of variation (CV) and corresponding confidence limits (CL) for numerical results includes both the epistemic damage prediction model uncertainty and the epistolic aleatory sample estimation uncertainty.
- Quality of earthquake performance rating levels when used for non-numerical evaluations, including safe or not-safe for use, and assigned CEBC related performance ratings assignment I to VII.
- (2)
- For a or portfolio of buildings located in one or more independent seismic hazard regions:
- Quality measures (Superior to Bad) of assessed loss statistics including SML, SEL, SUL and for ASTM 2026 Scenario values, and for portfolio Probable Loss values, PL. The Quality measures include all of the sources of uncertainty of the assessment procedure and its execution by the providing consultant, including decisions made in the approach, the use/or not of engineering evaluation and the execution of the assessment. The quality of the description of the task required for the evaluation of the necessary components, and the quality of the investigator performing the task are both represented in the component quality assignment matrices. Quality must be assigned for input of investigation results into the CAT model. Secondary modifiers are also necessary input.
- Introduction of the Bootstrap sampling method for estimation of Portfolio Loss Statistics for a set of Monte Carlo simulations of the aggregated loss, together with a method for evaluation of appropriate CV for the estimated values.
- Introduction of total reliability assessments for portfolio loss estimate to represent both the aleatory Bootstrap sampling error of estimates based the Monte Carlo simulations and with the epistemic uncertainty of the assumptions of the CAT Model application. This leads to different characterizations of the reliability of different loss statistics results from those usually prepared from Monte Carlo simulations. For example, extreme “tail losses”, which are the losses above a particular probability level of occurrence, have higher uncertainty central loss values that is often the most informative maximum loss value to consider.
Setting Criteria for Seismic Assessments Before they are Performed and Completed: Clearly it would be useful for a client to set the criteria for its seismic assessment at a level sufficient to be actionable before the assessment is performed. The Matrix Table 3, Table 8 and Table 14 serve to aid the client is setting the minimum standards for performance of a seismic assessments and Table 15 and Table 16 measures indicate whether or not particular procedures are likely to meet the client’s needs.
Concerning Portfolio Loss Assessment: For the case where Quality and/or Confidence Limits of an assessment have been found to be not acceptable for prudent decisions. The procedures of this paper allow the identification of components where changes can decrease uncertainty. The probability distribution function and statistics for the entire portfolio loss assessment can be examined and modified to reflect not only the computational uncertainty, but also the modeling uncertainty and how an improved assessment can be performed. It is immediately obvious that increasing the number of properties, when possible, in the portfolio can be more influential to achieve a stated reliability goal, than would be an improvement in way in which the seismic losses of the individual properties are determined. However, for the most common case of given specific portfolio, it is likely that the only way to improve an assessment’s reliability is to improve the total reliability of the assessment procedures for selected buildings-principally, those of high value and proximity to major event sources. Again, the specification of the intermediate Level 0.5 of investigation as discussed in Section 4.2, can be very effective in decreasing uncertainty; the cost consequences of a qualified investigator may be quite acceptable in return for the resulting increase in reliability for decisions involving large investments.
Where Can the Reliability Assessments be Useful? At any time that the analysis is intended to inform a decision, either a priori to set the criteria such that the reliability of the results will meet the user’s needs, or a posteriori to determine if reported assessments are considering to be of adequate reliability to warrant their use. There are a wide variety of decision-making applications, not all of which require a numerical evaluation of the likely risk of damage likely, for example:
- Whenever a technical assessment has been accomplished of a building’s seismic performance. This includes decisions concerning:
- -
- When a building may be used, leased or purchased and there is a prudent or required necessity that the occupants, contents and/or functions performed in the building warrant protection and the assessed result is intended to inform this decision.
- -
- When insurance is in question as to whether or not it is necessary and if the premiums are acceptable.
- -
- Whether a building provides adequate seismic performance, e.g., PML report, in order to be considered as a surety for a loan, mortgage or other financial instrument.
- Whenever a technical assessment has been accomplished for the seismic loss risk for a portfolio of buildings seismic performance, and/or whether the buildings are essentially the same seismic hazard, or at a number of sites, subject to differing seismic hazards. The decisions include:
- -
- Whether insurance policies provide appropriate risk coverage consistent with client’s needs.
- -
- Whether the Real Estate Portfolio’s seismic loss risk is acceptable to investors or financers, and the degree of risk posed by the portfolio to asset protection including the in-place insurance, particularly to evaluate whether the risk of loss to the tranche is commensurate to the premium. In the world of investing and insurance, a tranche is used to describe a security that can be split up into smaller pieces with varying risk and return and subsequently sold to investors.
- Whenever a technical assessment has been accomplished to support regulatory or policy decisions, public or private, where these policy decisions:
- -
- Limit or allow use of a specific buildings that are subject to seismic hazards after the event. Examples include assessment of emergency services buildings for continuity of service after the event. Note that this may become more prevalent, as the State of California is encouraging local building departments to require post-event serviceability for retrofits and new building design.
The uncertainty evaluation method as developed in this paper can be applied for many other technical risk management procedures where complex models are developed to provide critical results for decisions, and the third-party decision makers need a measure to determine the reliability of these results. The method is particularly applicable where the evaluation requires the processing of both quantitative (numerical) and qualitative (expert opinion) measures of uncertainty.
Cost control is usually a paramount consideration in the investment decision-making process. When the stakes are high, investors may be willing to pay more to have seismic loss assessment accomplished well and will most likely focus on high-end effort for the high relative value buildings. Common acceptable standards for reliability would be at a minimum of the Good level, and for those properties expected to be large contributors to the loss, probably a Superior reliability is advisable. This paper provides a basis for prescribing the requirements of the assessment, before the work is accomplished, such that the results will have a desired quality.
Quality issues are possibly more important for insurance applications than for equity investment. For insurance, there are often some tranches of the risk for very low probability of occurrence losses. It is the values at these right tail limits of the risk curve that can have the greatest influence on the likelihood of payments being required. However, at these tail limits, there is the highest potential for uncertainty (high CV). Therefore, setting the premium for providing such insurance depends on understanding the degree to which these computed tail losses can be relied upon. This includes the possible upper and lower bounds of the estimated risk that has the most influence on the actual total loss risk. As seen in Table 12 for the model portfolio, the CV can be quite large and the probability of occurrence very low at the tail of the distribution. These influences are so large, and have such profound implications for the risk levels, that it would be prudent for the insurer to set the quality limits required for the high-risk tranche before the loss investigations are performed This action is necessary to reduce the likelihood of a financial mistake to an acceptably low level. The message is clear.
Lastly: This paper, with its proposed method (parallel to that of FEMA P-695) of describing and evaluating uncertainty, can serve as an organized model for future improvements in seismic loss assessments. Furthermore, the method can be applied to many other professional processes where the reliability of results is required. We expect that actual applications in seismic loss assessment will result in improvements when users find that there are better ways of specifying some of the Measure and Implementation descriptions of the quality matrices. These future applications may also show the need for other components to supplement or replace the matrix elements in this procedure, as suggested in Section 2.2.
Author Contributions
This paper had contributions by each of the authors in all aspects of the paper conceptualization and development. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This paper is the sole intellectual work of the authors; they were supported in part by their firms, where applicable, with no other external support. The authors appreciate the useful reviews of their colleagues: Gary S. Varum, S.E. of Telesis Engineers, Eugene Trahern, S.E., of Cascade Crest Engineering, William Graf, PE of ImageCat and comments from members of ASTM Working Group Subcommittee WK55885–Seismic Risk Assessment of Real Estate Portfolios, who are developing a standard for Seismic Portfolio Damageability Assessment, of which the authors are members. The authors appreciate the improvements of the paper based on the comments of the peer reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
Note
| 1 | ASTM E2026 defines Scenario Loss as: Scenario Loss (SL) is the earthquake damage loss expectation to building systems and site improvements and where User-prescribed, building contents and/or related business interruption loss, associated with specified earthquake events on specific fault(s) affecting the building. SL values are expressed in terms of the damage ratio defined as damage repair-cost/building replacement cost in present day dollars. The SL is generally limited to earthquake loss associated with the earthquake ground-shaking hazard, but may include losses from other earthquake hazards, as prescribed by a User. Scenario Expected Loss (SEL) is the expected value of the scenario loss for the specified ground motion of the earthquake scenario selected. Scenario Upper Loss (SUL) is the scenario loss that has a 10% percent probability of exceedance due to the specified ground motion of the scenario considered. ASTM defines Probable Loss (PL) as: earthquake loss to the building systems that has a specified probability of being exceeded in a given time period, or an earthquake loss that has a specified return period for exceedance. A PL value is meant to reflect, in a statistically consistent computational manner, all of the epistemic uncertainties that can impact damage estimates, including: when and where earthquakes occur and with what magnitude, recurrence rate, attenuations of ground motions at the site, local site effects and performance of the building systems in these ground motions. (ASTM E2026-16a 2007). |
References
- ASCE. 2016a. Seismic Rehabilitation of Existing Buildings, American Society of Civil Engineers. ASCE/SEI Standard 41-17. Reston: American Society of Civil Engineers. [Google Scholar]
- ASCE. 2016b. Minimum Design Loads for Buildings and Other Structures. ASCE/SEI Standard 7-16. Reston: American Society of Civil Engineers. [Google Scholar]
- ASTM E2026-16a. 2007. Standard Guide for Seismic Risk Assessment of Buildings. Conshohocken: ASTM International. [Google Scholar]
- ASTM E2557-16a. 2016. Standard Practice for Probable Maximum Loss (PML) Evaluations for Earthquake Due-Diligence Assessments. Conshohocken: ASTM International. [Google Scholar]
- Benjamin, Jack R., and C. Allin Cornell. 1970. Probability, Statistics, and Decision for Civil Engineers. New York: McGraw Hill. [Google Scholar]
- California Building Standards Code (CBC). 2019. California Code Regulations, Title 24, California Building Standards Commission, Sacramento, California, 2019 edition. This Includes Both the Requirements for New Buildings (Part 2) and Existing Buildings (Part 10). The CBC Is Available for Purchase from Numerous Publishers or Is Viewable at No Cost through Many Libraries. Available online: https://www.dgs.ca.gov/BSC/Codes (accessed on 1 July 2021).
- CSU. 2020. CSU Seismic Requirements. Long Beach: California State University, Office of the Chancellor. [Google Scholar]
- Davison, Anote 1ony Christopher, and David Victor Hinkley. 2009. Bootstrap Methods and Their Application, 11th ed. Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge: Cambridge University Press. [Google Scholar]
- Dawes, Robyn M. 1979. The Robust Beauty of improper liner models in decision making. American Psycologist 34: 571–82. [Google Scholar] [CrossRef]
- Deierlein, Gregory G., Abbie B. Liel, Curt B. Haselton, and Charles A. Kircher. 2008. ATC 63 Methodology for Evaluating Seismic Collapse Safety of Archetype Building. Paper presented at Proceedings, ASCE Structures Congress 2008, Vancouver, BC, Canada, April 24–26. [Google Scholar]
- Der Kiureghian, Armen, and Ove Ditlevsen. 2009. Aleatory or epistemic? Does it matter? Structural Safety 31: 105–12. [Google Scholar] [CrossRef]
- DiCiccio, Thomas J., and Bradley Efron. 1996. Bootstrap Confidence Intervals. Statistical Science 11: 189. [Google Scholar] [CrossRef]
- Efron, Bradley, and Robert J. Tibshirani. 1993. An Introduction to the Bootstrap. New York: Chapman and Hall/CRC. [Google Scholar]
- FEMA P-154. 2013. Rapid Visual Screening of Building for Potential Seismic Hazards: A Handbook, 3rd ed. Washington, DC: Federal Emergency Management Agency. [Google Scholar]
- FEMA P-2012. 2018. Assessing Seismic Performance of Buildings with Configuration Irregularities: Calibrating Current Standards and Practices. Washington, DC: Federal Emergency Management Agency. [Google Scholar]
- FEMA P-695. 2009. Quantification of Building Seismic Performance Factors. Washington, DC: Federal Emergency Management Agency. [Google Scholar]
- Fenton, Norman, and Martin Neil. 2019. Risk Assessment and Decision Analysis with Bayesian Networks, 2nd ed. New York: Chapman and Hall/CRC. [Google Scholar]
- Gilovich, Thomas, Dale Griffin, and Daniel Kahneman. 2002. Heuristics and Biases, The Psychology of Intuitive Judgement. Cambridge: Cambridge University Press. [Google Scholar]
- Halpern, Joseph Y. 2017. Reasoning about Uncertainty, 2nd ed. Cambridge: MIP Press. [Google Scholar]
- HAZUS. 2013. Advanced Engineering Building Module (AEBM)—Technical and User’s Manual, MH 2.1, Developed by Department of Homeland Security. Washington, DC: Federal Emergency Management Agency Mitigation Division. [Google Scholar]
- Lee, Yajie, Charles C. Thiel Jr., and William P. Graf. 2021. Mark Ellis Seismic Risk Assessments for Real Estate Portfolios: Impact of Engineering Investigation on Quality of Seismic Risk Studies, Manuscript under review; request pdf copy of manuscript or published text from: yjl@imagecatinc.co. Earthquake Spectra. Submitted. [Google Scholar]
- Mooney, Christopher Z., Christopher F. Mooney, Christopher L. Mooney, Robert D. Duval, and Robert Duvall. 1993. Bootstrapping A Nonparametric Approach to Statistical Inference. Series/Number 07-095. Thousand Oaks: Sage Publications. [Google Scholar]
- Olsen, Anna H., and Keith A. Porter. 2011. What We Know about Demand Surge: Brief Summary. Natural Hazards Review 12: 62–71. [Google Scholar] [CrossRef]
- Thiel, Charles C., Jr. 2001. Earthquake Damageability Criteria for Due Diligence Investigations. Journal of the Structural Design of Tall Buildings 10: 1–31. [Google Scholar] [CrossRef]
- Thiel, Charles C., Jr., and Theodore C. Zsutty. 2017a. The Thiel–Zsutty earthquake damage model, reformulated and extended. The Structural Design of Tall and Special Buildings 26: 1348. [Google Scholar] [CrossRef]
- Thiel, Charles C., Jr., and Theodore C. Zsutty. 2017b. The revised Thiel–Zsutty earthquake damage model—Reformulated and extended—Part 2. The Structural Design of Tall and Special Buildings 26: 1394. [Google Scholar] [CrossRef]
- Thiel and Zsutty. 2018. Evaluating the Safe Interim Use of Seismically Deficient Building. The Structural Design of Tall and Special Buildings. [Google Scholar] [CrossRef] [Green Version]
- Traynor, Roger J. 1954. Opinion by Justice Roger J. Traynor. Gagne v. Bertran 43: 481–89. [Google Scholar]
- Wasserman, Larry. 2006. All Nonparametric Statistics. New York: Springer. [Google Scholar]
- Zio, Enrico. 2013. The Monte Carlo Simulation Method for System Reliability and Risk Analysis. New York: Springer. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).