1. Introduction
Predictive modelling techniques have been widely used in auto insurance pricing (
Xie and Lawniczak 2018;
Xie 2019;
Ayuso et al. 2019;
Parodi 2012;
Yunos et al. 2016;
Yan et al. 2009) and other fields of study such as bankruptcy prevention and prediction (
Kliestik et al. 2018;
Kovacova et al. 2019). In auto insurance, the main reason for the prevalence of predictive modelling is their superior power in accurately pricing insurance contracts and the statistical soundness of the approaches used, mostly when auto insurance rates are regulated (
Verbelen et al. 2018). If insurance rates are not regulated, then the merit of predictive modelling is still apparent as its use in pricing helps to avoid the adverse selection of insurance policies (
Dionne et al. 1999). Recently, the use of machine learning techniques such as artificial neural networks (ANN) has been an emerging approach for insurance pricing. They can often achieve a high level of model prediction accuracy (
Fialova and Folvarcna 2020;
Gao and Wüthrich 2018;
lseri and Karlık 2009;
Sun et al. 2017;
Wuthrich 2019;
Yeo et al. 2001). When ANNs are used for pricing, the high prediction accuracy of loss costs is mainly due to its capability to model the non-linear relationships between the independent variables and the response variable. For instance, in
Yunos et al. (
2016), the backpropagation neural network (BPNN) model was used as a tool to model both claim frequency and claim severity. This study illustrates the capability of BPNN in explaining the non-linear relationships of loss data. Furthermore, the predictive modelling techniques of machine learning have been successfully used for detecting insurance claim fraud (
Bhowmik 2011). Due to models’ natural complexity, ANN and other sophisticated models have not been heavily used by insurance companies and regulators. From the rate regulation perspective, the major downside of using ANN is its low explainability due to the iterative nature of the neural network algorithms and the non-closed form, non-linear relationships between input variables and the output response. Thus, insurance companies often have difficulty explaining the model output, so the justification of methodologies’ appropriateness becomes challenging. It is often difficult to derive the risk relativities for risk factors when using ANNs due to non-linearity among the risk factors and the complex nature of ANNs. It is also hard to obtain consistent estimates of risk factors’ impact on the model response, which different network architectures may cause. Therefore, an ANN model is often treated as a black box, particularly for the multiple hidden-layer models. It provides minimal explanatory insights into the input variables’ relative influence on the output variable in the model prediction process (
Olden and Jackson 2002).
Explainable artificial intelligence (AI) or explainable machine learning is now a new focus and an essential aspect when using machine learning techniques or algorithms for real-world applications (
Adadi and Berrada 2018;
Dosilovic et al. 2018;
Samek et al. 2017;
Wuthrich 2019). This concept has also played an essential role in auto insurance rate regulation. The interest in explainable AI has dramatically increased since 2016, and various review papers have been recently published. In
Arrieta et al. (
2020), the existing literature and contributions already made in the field of explainable AI have been surveyed. A series of challenges faced by explainable AI, including the model explainability, was also addressed. In
Beaudouin et al. (
2020), context-specific explainable AI was discussed using a multidisciplinary approach. However, the concept of explainability could be dated back to the 1970s when applied expert systems and rule-based models became popular (
Adadi and Berrada 2018). Explainable data analytics, a sub-field of explainable AI, has recently attracted considerable attention in the machine learning community. For instance, the 2019 IEEE Symposium on Explainable Data Analytics (EDA) in Computational Intelligence is the first conference focusing on explainable data analytics. EDA aims to study suitable analytical tools, which can be used to produce information from data that facilitates decision-making or gives meaningful explanations on the impact of the input variables on the outputs in modelling. The analytical techniques in EDA include, but are not limited to, statistical measures, feature extraction, dimension reduction, and sparse methods (
Lu et al. 2005;
Maitra and Yan 2008;
Ribeiro et al. 2006). In business intelligence for risk management, the explainability of models becomes a critical aspect as it leads to a better understanding of how the decisions are being made. The better the understanding of the models used, the more confidence and the better control of the risk, in particular for auto insurance rate-making (
Hsiao et al. 1990;
Kim and Canny 2018;
Farbmacher et al. 2019). This is why explainable machine learning is attracting dramatic attention when machine learning techniques are used for real-world applications. The main effort to research explainable AI is to better understand the algorithms used, mathematically, statistically, or computationally, as they can be extremely complicated. This may call for methods that are able to balance the model complexity and the desired explainability of the model used.
From both insurance pricing and rate regulation perspectives, it is essential to investigate the impact of risk factors on claim frequency or claim severity (
Gilenko and Mironova 2017). When a complicated mathematical model is used for pricing or capturing the loss pattern, it is critical to study the impact or conduct a sensitivity analysis of risk factors in the model (
Asmussen and Rubinstein 1999). In rate regulation, the requirement of model explainability may imply the need to estimate or evaluate the importance of risk factors (
Frees 1998). Different machine learning techniques and applications require different types of explainability. Algorithms used by governments are subject to higher explainability requirements (
Beaudouin et al. 2020). In the machine learning community, many techniques used for capturing variable importance have been investigated. Interpretable models, including linear regression, logistic regression, generalized linear models (GLM), generalized additive models (GAM), and decision tree, have been well studied and used for evaluating variable importance due to the fact that model coefficients can be easily used for the study of the effect size of the variables. Although these models are more interpretable, they are limited in capturing more complicated non-linear relationships, which usually lack functionality. The second type of approach to study the interpretability of data is the model-agnostic method, and it has been successfully used in actuarial science (
Henckaerts et al. 2020). Partial dependence plot (PDP) (
Friedman 2001), permutation feature importance (
Fisher et al. 2019), and shapely values (
Sundararajan and Najmi 2019) are examples of the model-agnostic methods. The most significant benefit of using the agnostic approach is the flexibility of using machine learning methods, including the black box models, which are crucial for more complex real-world problems. A PDP plot shows the marginal effect of the variable on the predicted outcome of selected machine learning models, while permutation feature importance measures the increase of model error after permuting the feature variables. The model-agnostic methods provide friendly and convenient graphical tools for machine learning approaches.
In this work, we aim at improving the explainability of input factors in ANN for rate regulation purposes. We try to better understand the impact of various risk factors on statistical data reporting, which is of high-level statistical plan data (
Furst et al. 2019). The statistical plan information is a crucial source for insurance regulation, and it summarizes the loss information at the industry level. However, the statistical plan data’s direct use without further processing by the mathematical model is quite limited due to its descriptive nature. Furthermore, it is difficult to know what contributes more or less to the insurance loss if only focusing on the descriptive measures in the statistical plan data reporting. Thus, it is difficult to see the driving force of insurance loss and decide the benchmark measures associated with risk factors by looking at these statistical data reports. Therefore, the benchmarks used for rate regulation are obtained by applying rate-making methodologies to these statistical plan data, typically through statistical modelling, such as GLMs, GAMs or ANNs. Unlike insurance pricing, which mainly targets the study of risk factors that significantly impact the calculation of insurance prices, we focus on major risk factors for insurance rate regulation purposes. In the current research, ANNs and their importance measures of predictors have not yet been investigated in the field of insurance rate-makings from the regulation perspective. This objective makes our contribution to the current research novel and unique. In this work, to better understand the constructed ANN models and their model outputs, we study the importance of major risk factors affecting the claim frequency and the claim severity. We consider accident year (AY), reporting year (RY), territory, coverage, and the Size-of-Loss (in terms of log-scale of the upper limit of Size-of-Loss intervals) as major risk factors. Here, the Size-of-Loss is the loss bracket, rather than the insurance loss amount caused by drivers. The level associated with this factor can be predefined based on the historical pattern of the loss data, mainly on range of loss amounts. Considering both the accident year and reporting year as risk factors, data from different accident years or other reporting years may significantly affect the analysis results. The risk affecting insurance pricing could be due to the information associated with different accident years or other reporting years. From year to year, the general level of claims may fluctuate heavily (
Dugas et al. 2003). The data variability may also be due to the case reserve update for different accident years or various data reporting years. For territory, coverage, and Size-of-Loss, they are common risk factors that appear in rate regulation and are commonly used for auto insurance pricing (
McClenahan 2014).
This work emphasizes measuring and interpreting the importance of risk factors using ANN. We aim to estimate and evaluate the importance of risk factors, although the modelling techniques may deal with the problem at each risk factor’s level. The significance of this work is to propose a novel approach for analyzing major risk factors, in terms of their impact to claim counts, claim amounts, and average loss per claim, for rate regulation purposes. To the best of our knowledge, this study is the first attempt to model claim counts and claim amounts using neural network models and Size-of-Loss data in the actuarial domain. This paper is organized as follows. In
Section 3, the methods, including artificial neural networks and variable importance measures, are discussed. In
Section 4, the obtained results using industry size of loss data are presented and analysed. Finally, we conclude our findings and provide further remarks in
Section 6.
2. Data
In this work, we use datasets from the Insurance Bureau of Canada (IBC), which is a Canadian organization responsible for insurance data collections and their statistical data reporting in the area of property and casualty insurance (
Xie and Chua-Chow 2020). During the data collection process, insurance companies report the loss information, including the number of claims, number of exposures, loss amounts, as well as other key information such as territories of loss, coverages, driving records associated with loss, and accident years. These statistical data are reported regularly (i.e., weekly, biweekly, or monthly). At the end of each half-year, the total claim amounts and claim counts reported by all insurance companies are aggregated by territories, coverages, accident years, etc. The statistical data reporting is then used for insurance rate regulation to ensure the premiums charged by insurance companies are fair and exact. The dataset used in this work consists of summarized claim counts, claim amount, and average loss cost by different sizes of loss, which are represented by a set of non-overlapping intervals. These summary of loss information are aggregated by major coverages, i.e., Bodily Injuries (BI) and Accident Benefits (AB). The data were also summarized by different accident years, by different report years and by different territories, i.e., Urban (U) and Rural (R).
To carry out the study, we organize data by coverages (AB and BI) and by territories (U and R). We consider the data from different reporting years and accident years as repeated observations. There are two reporting years, 2013 and 2014, respectively. There is a set of rolling most recent five years of data corresponding to five accident years for each reporting year. Therefore, for this study, we have in total ten years of observation. In addition, since we have both Accident Benefits and Bodily Injuries as the coverage type and Urban and Rural as the territory, we consider the following four different combinations, Accident Benefits and Urban (ABU), Accident Benefits and Rural (ABR), Bodily Injuries and Urban (BIU), and Bodily Injuries and Rural (BIR). These data are then formed into a data matrix with a dimension, where 40 is the total number of observations, and 24 is the number of total intervals of the Size-of-Loss.
3. Methods
In this work, we focus on improving the explainability of neural network models. We first identify the suitable model by balancing the model errors and network architecture complexities. This process is like the cross-validation procedure in the usual predictive modelling. Due to the non-linearity of neural networks, the model error does not need to decrease when increasing the network architecture. The model selection is made by searching for a suitable scale of network architecture that achieves the minimum model error within a set of small-scale neural networks and cross-validated by the root mean square error (RMSE). In this section, we mainly discuss how artificial neural networks work as a regression modelling problem. To give a more understandable explanation, we focus on the discussion of low scale neural networks. We then discuss how to measure the importance of the variables in ANN models.
3.1. Artificial Neural Networks
Let us first discuss the case of an Artificial Neural Network (ANN) with one hidden layer. That is, the network includes the input layer, one hidden layer, and the output layer. Suppose in the ANN model that there are
D inputs
,
, …,
, and
hidden units
,
, …,
in the hidden layer. A unit
within the hidden layer is defined as
where
is the activation that is composed of the linear combination of input variables
, their weights
, and the bias
. The superscript (1) in the weights indicates that components correspond to the first hidden layer. This allows us to extend the model for multiple layers, instead of just one. The function
is called the activation function, which is usually non-linear and differentiable. In most cases, the activation function is chosen to be sigmoidal (
Bishop 2006). If the function
is an identity, the hidden unit becomes a linear combination of input variables. Within this case, if we further assume that the weight values at the hidden value is a set of values resulting in a maximum variance of
, then
is exactly the
jth principal component of the inputs variable
,
,…,
. Given the hidden unit
in the hidden layer, the resulting output unit activation
in the output layer (which becomes the second hidden layer for the multiple hidden layer case) is defined as
where
represents the weights and
is the bias term. The superscript (2) in the weights implies that the components correspond to the output layer or the second hidden layer if the model has multiple hidden layers. The units
,
, …,
in the output layer or the second hidden layer using the same activation function
become
Let us now consider a more general case with multiple hidden layers. Assume that the total number of hidden layers is
L, and there are
hidden units
,
, …,
in the
lth hidden layer; we can write the
hidden layer units as follows:
for
, and
. If we further assume that the total number of observations is
N, the final output of the ANN for the
kth input vector of
X becomes
3.2. Measuring and Evaluating Importance of Risk Factors in ANN
For Equation (
5), by realizing that
is a function of
, we can think of a new form of
y in terms of
as follows
To further investigate the importance of the risk factors, we first consider the Taylor series expansion of
y at the first order, which is given as follows
Here,
is referred to the sensitivity coefficient of
and may be used to represent the effect of risk factor
when holding other variables constant. Since we do not have the explicit functional form of
in ANN, deriving the sensitivity coefficient is impossible. A possible solution is the Lek’s profile method (
Gevrey et al. 2003). The Lek’s profile approach evaluates the effect of each input variable to the output variable by holding the remaining explanatory variables constant.
In 1991, a method based on the weight values of ANN was proposed by Garson; hence, it is referred to as Garson Algorithm (
Garson 1991). This algorithm can be illustrated using an ANN with three layers, namely the input layer, the hidden layer and the output layer. Suppose that
is the connection weight values between input variable
i and the neuron
j at the hidden layer.
is the connection weight value between the
jth neuron at the hidden layer and the final regression output. The importance of risk factor
i based on the Garson algorithm for the non-linear regression using ANN is defined as
It is a doubly normalized, weighted average. This weighted average is the average of connection weights between the hidden layer and the output layer, which is
, using the connections weight values between the input layer and hidden layer, normalized by the total weight values, which is
. Their total sum further normalizes the obtained weighted average to get the final importance measure of risk factors. This is to force the variable importance measure to be between 0 and 1. However, the definition in (
8) is sensible within a given ANN model. It may not be ideal for comparison among ANN models due to the different variable importance measures for different models. In this work, we propose an approach by further re-scaling the
to facilitate the comparisons among different models, which is given as follows.
so that
. This implies that the Garson algorithm can only capture the magnitude, but not the sign of variable importance. In addition, the Garson algorithm is applicable for single hidden-layer networks only. This may be considered a drawback, but the main benefit of using the Garson algorithm is the better explainability for a simple network (i.e., single layer network). For the multiple hidden layers network, we must consider another similar measure, called the Olden function (
Olden et al. 2004), which is given as follows
The function calculates variable importance as the product of the raw input-hidden and hidden-output connection weights between each input and output neuron and sums the product across all hidden neurons. This measure is then re-scaled to ensure the results obtained from different ANN models are comparable. This re-scaling is given as follows.
so that
. This re-scaling reflects both the magnitude and the sign of variable importance by the Olden function. Since the weight values can be positive or negative, and the sum of the product across all hidden neurons may be cancelled out, the effect of input factors can be reduced.
To avoid the effects of the network’s initial weight values on estimating variable importance, we apply a re-sampling approach. By running the ANN model fitting repeatedly (e.g., 100 times in this work), we obtain a set of weight values to estimate the mean variable importance measure and its sampling error, respectively, for each risk factor. This repeated Monte Carlo experiment is applied to each ANN architecture that we consider. Still, we are particularly interested in the results corresponding to the best ANN architecture among all the models we considered, obtained from the evaluation of goodness-of-fit on different ANN models.
For a practitioner, the Garson or Olden approaches’ choice seems to make a significant difference in terms of the variable importance. Our study shows that the Garson function achieves a consistent result for claim counts and claim amounts. The single-layer network with multiple units performs almost the same as the multiple layer models, as their model standard errors are close. Therefore, in regulatory review, when a single-layer network architecture can capture the data, the Garson function should be considered. The main benefit of using the Garson function is its evaluation of the variable importance of input factors using the factor’s effect size, which is more comparable to the factor’s effect size in GLM or GAM.
The average loss per claim count involves both claim frequency and severity; a more complicated network architecture may be required. Therefore, the Olden function becomes a better choice to quantify the variable importance. It is suitable for the situation when multiple layer networks are needed. In terms of the accuracy measure of variable importance using the Garson algorithm or the Olden function, since they are directly linked to network architecture, they are not comparable.
4. Results
We use Size-of-Loss distributions, by different territories and different coverages, at the industry level from a regulator in Canada to illustrate the proposed method’s application. The sample data from the 2009 accident year in 2013 statistical data reporting are presented in
Table 1. This table shows Size-of-Loss distributions for different combinations of coverage (AB or BI) and territory (Urban or Rural) for both claim counts and claim amounts. The claim counts are the reported counts, and the claim amounts (in thousand) are the ultimate losses. The claim counts and claim amounts are further used to derive the average loss per claim count, which is computed by dividing the loss by the count associated with each Size-of-Loss interval. Therefore, we have three different response variables: claim counts, claim amounts, and the average loss per claim count. All observations from those three response variables are transformed using the logarithmic function to improve the fitted model’s variance stability. (Note that, in rate regulation, we deal with aggregate loss, in which we do not have zero loss problems, unlike the case for individual loss.) For input variables, there is accident year (AY), reporting year (RY), log-scale of the upper limit of Size-of-Loss interval (i.e., log.UpperLimit), territory, and coverage. All input and output variables’ observations are normalized before fitting to the ANN models with the logistic activation function.
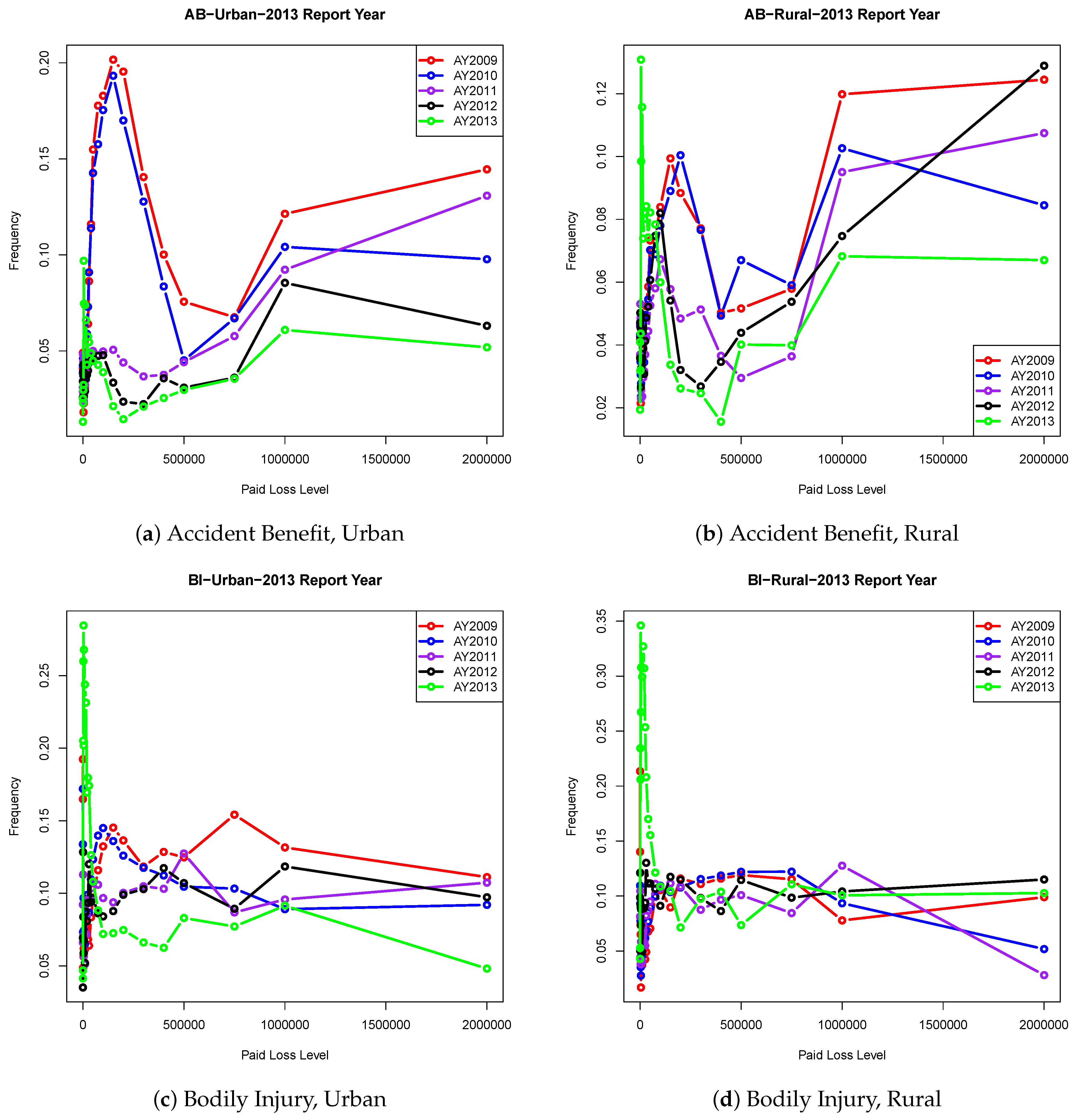
To know more about the Size-of-Loss data distributional behaviour, we present the frequency distribution in
Figure 1. The distributions in all types appear to be heavy-tailed, with AB frequency distributions being very extreme. Also, the frequency distributions for AB type seem to have more modes than the data distribution for BI. Within the same coverages, the distributions behave similarly for both Urban and Rural. To see which ANN is more suitable for our data, we first study the network architectures. We consider various combinations of the number of hidden layers and the number of the hidden unit. We consider the cases with one and two hidden layers only. The further increase in the neural network complexity is not recommended due to the constraint of the model stability requirement.
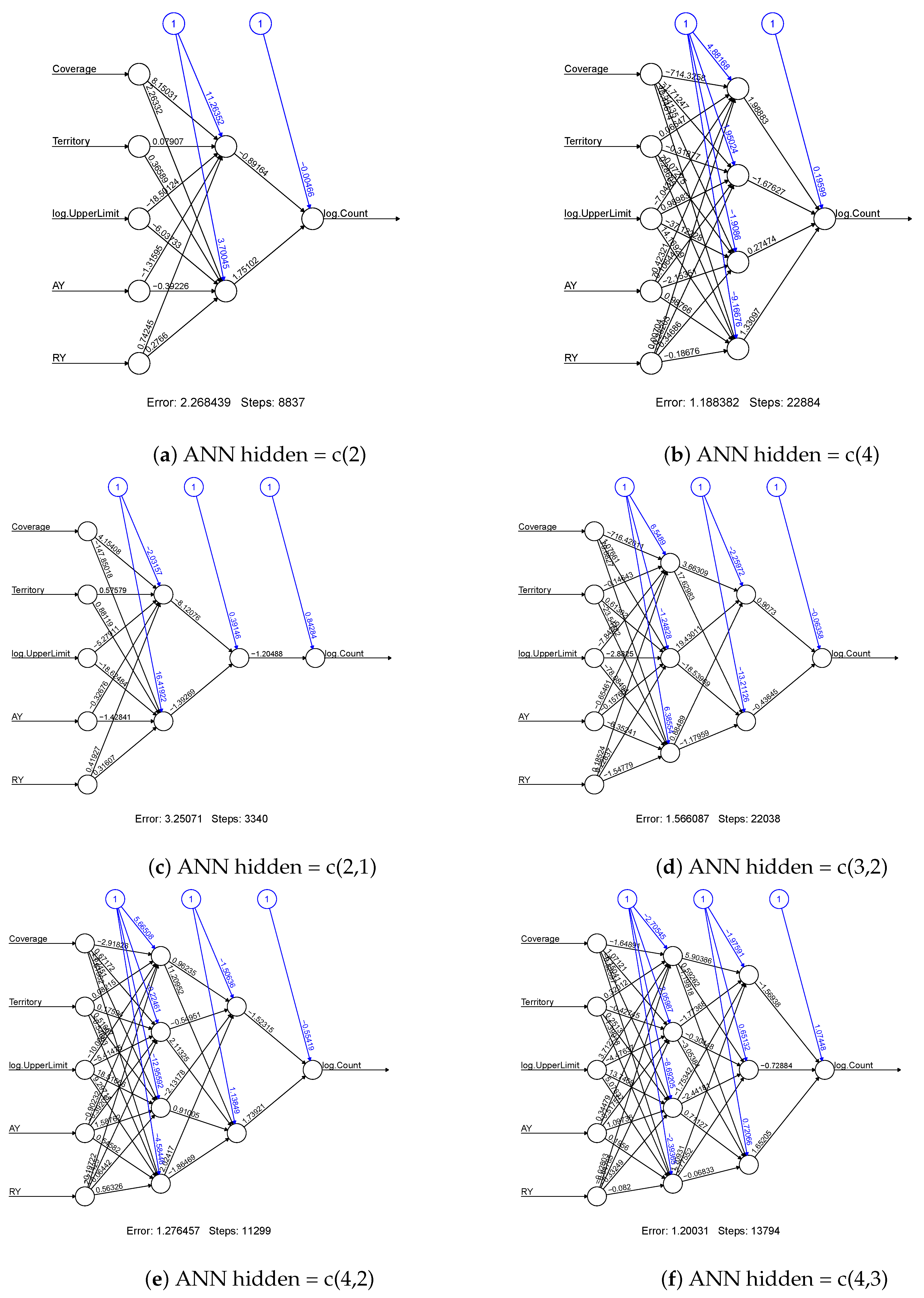
Figure 2 displays the network architectures that use the claim counts as the output variable, while
Figure 3 presents the ones associated with claim amounts. For each connection within the network, the obtained weight values are displayed. These weight values are used to evaluate the variable importance, which will be discussed later. The blue colour connections are referred to as the weight values of the networks’ bias term, and they are similar to the intercept term in a linear regression model.
As we can see from the (a) of
Figure 2 and
Figure 3, the variables of coverage and log. UpperLimit have considerably higher weight values than other input variables. This simplest ANN model gives us some degree of model explainability in terms of the input variables’ contribution through the weight values. However, this simplest model leads to a higher sum of squared errors, which may not be acceptable in terms of model fitting accuracy. When the model complexity is increased, it becomes difficult to observe the variable importance by looking at the weight values. This is why we consider how to improve the model explainability in this work. On the other hand, as shown by the sum of squared errors for the models, the model has four hidden units in the first hidden layer, and three hidden units in the second layer (denoted by ANN-c(4,3)) outperform others. However, ANN-c(4,3) has the highest model complexity that leads to the poorest explainability. According to our experiments, model fitting results are easily affected by initial values, so model stability is low for a high complexity model. However, the model with a lower network complexity, i.e., the network with a single hidden layer and four units within the layer (denoted by ANN-c(4)) seems to be a better choice from both the sum of squared error and network stability perspectives. After identifying the suitable models for modelling claim counts and claim amounts, we then measure the variable importance using the fitted model’s weight values. In this focus, we use the Garson algorithm and Olden function to compute variable importance measures for the selected model (i.e., ANN-c(4)).
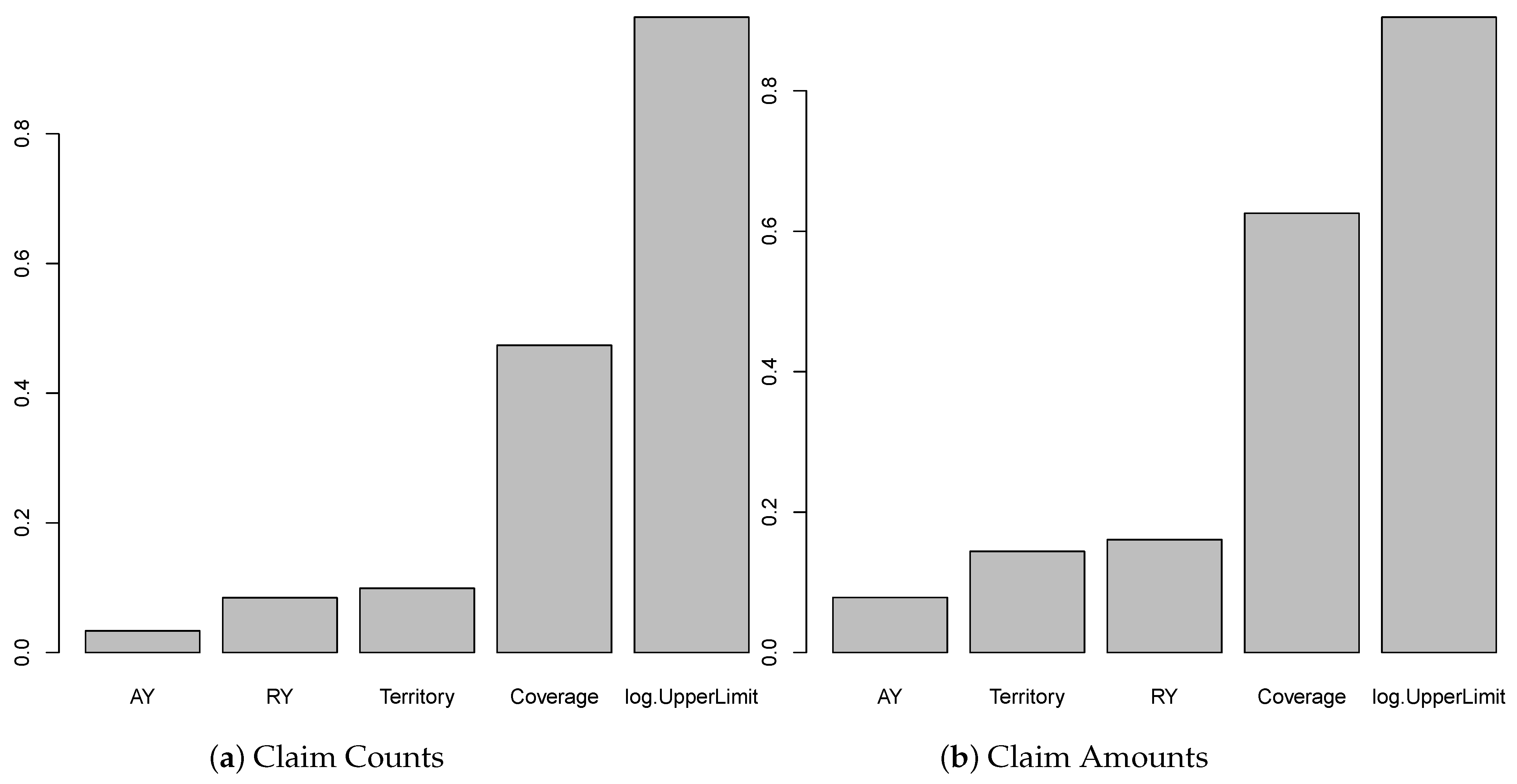
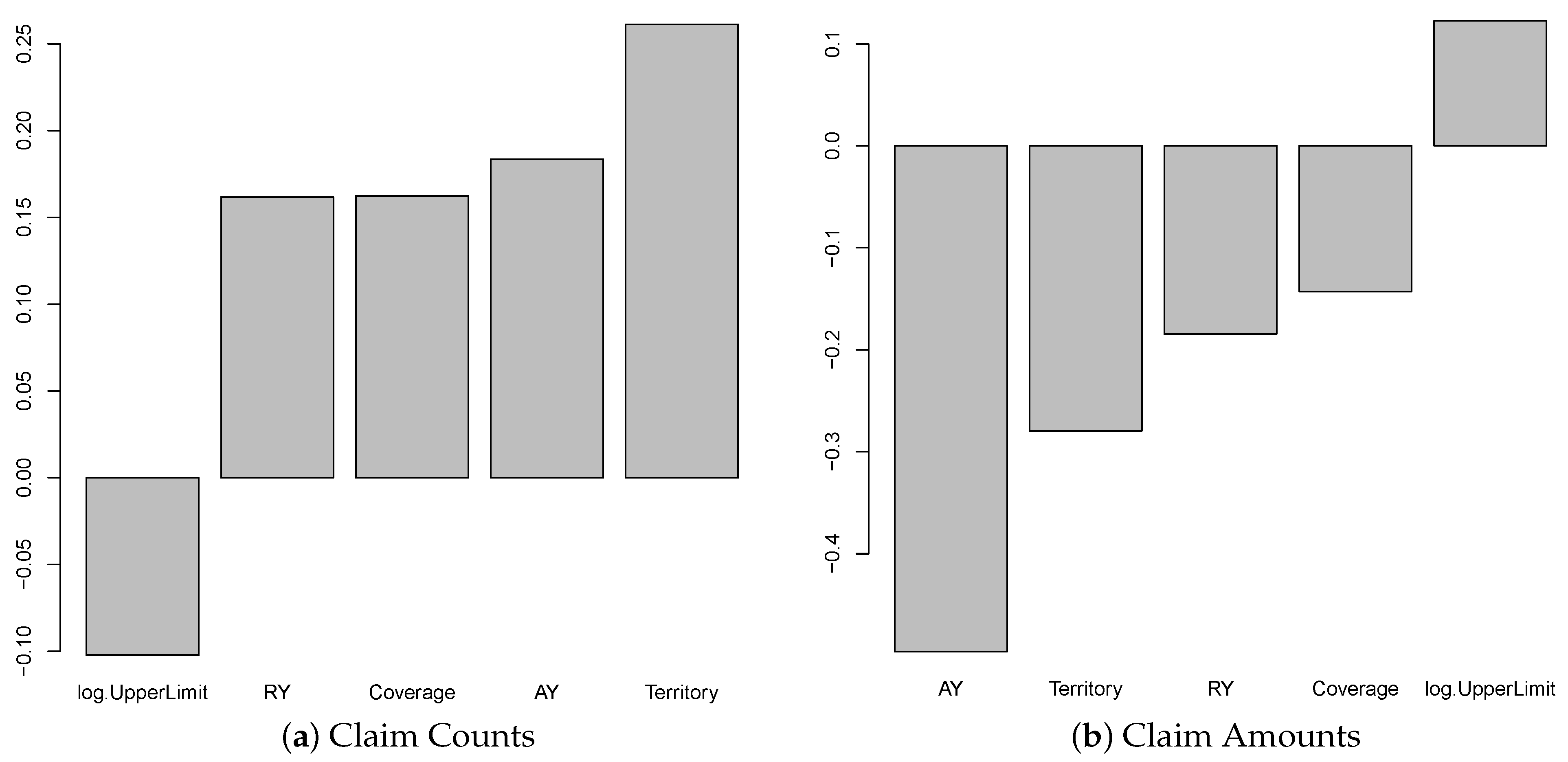
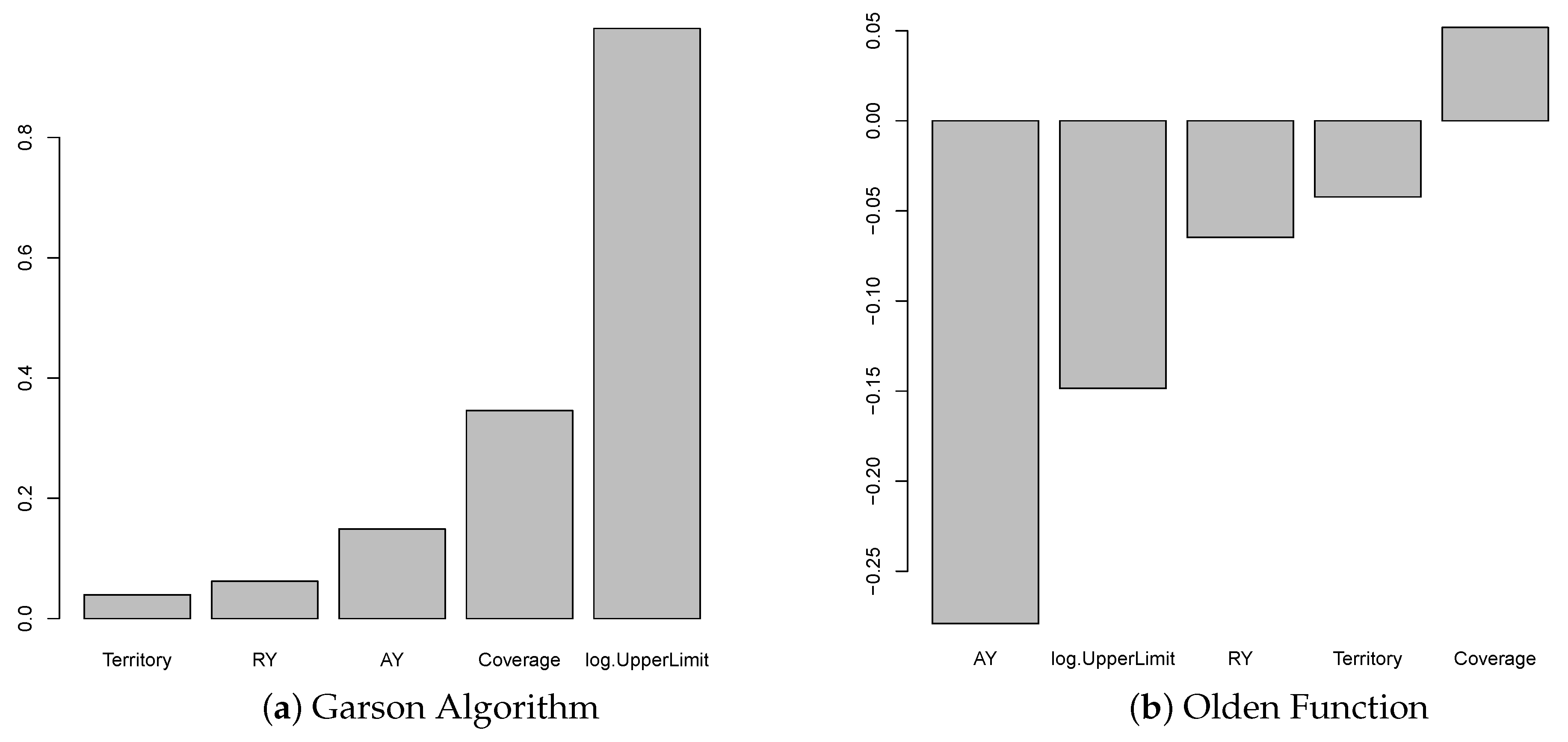
Figure 4 shows the results by the Garson algorithm, while
Figure 5 presents the ones by Olden function. These results are obtained by running the ANN-c(4) model fitting for the given data independently, repeatedly, for 100 times, and the average measures of variable importance are computed for each risk factor. This re-sampling approach aims to minimize both the bias of the estimate and the uncertainty caused by different network architectures and the networks’ initial values.
Figure 4 shows that the results using the Garson algorithm for claim counts and claim amounts as the response variable are reported. From
Figure 4, we observe that Size-of-Loss and coverage are more important than others in contributing to the explanation of the variation of the response variable. This may suggest that, for the model we consider, i.e., ANN-c(4), these two risk factors are essential to both claim counts and claim amounts. The result has coincided with the case of using the average loss per claim count, which will be discussed later. Due to the Garson algorithm, only the magnitude of the weight values is considered, but not the sign of the weight values. We are unable to see if the risk factors contribute to the response variable positively or negatively through the weight values of ANN. However, the obtained results for the models we consider are consistent among all response variables, which essentially suggest that coverage and Size-of-Loss are the driving forces for differentiating the patterns of claim counts and claim amounts. To compare the results using different methods,
Figure 5 shows the variable importance measures produced by Olden function, which takes both the sign and the magnitude of weight values into consideration. Interestingly, we observe that Size-of-Loss has a negative effect on the claim counts, while the effect on claim amounts becomes positive. This makes sense because we expect that with the increase of Size-of-Loss, the claims counts are decreased. The positive impact on the claim amount may be due to the significant increasing losses. Another important observation is that territory is the most critical variable that leads to the positive effect on claim counts, while AY is the most dominant variable that leads to the negative impact on claim amounts. Since we label the data from urban as one and the data from rural as zero, the positive effect on claim counts implies that urban areas cause significantly more claim counts than the rural area. For the claim amounts model, AY is the most dominant variable and has a negative effect on claim amounts. This may indicate that the decrease of projected loss amounts for more recent accident year. Since the impact from RY on claim amount is also negative, part of the reduction in the projected claim amount may be due to adjustment of case reserve in the new reporting year.
When the claim counts and claim amounts are used to calculate the average loss per claim count, and it is then used as the response variable for the ANN models, the variable importance results behave differently from either claim counts or claim amounts models when the Olden function is used, but the most important variable remains the same. However, this result is consistent with the claim counts and claim amounts models if the Garson algorithm is used. This can be seen from
Figure 6, which displays the Garson algorithm and Olden function results, respectively. Moreover, in
Figure 6, the Garson algorithm shows that AY is the third most crucial variable, whereas, in the Olden function, AY has the most considerable magnitude of any variable by far. Similarly, the Garson algorithm shows that log.UpperLimit is important, but the Olden function shows a distant second in terms of importance. We should note that the Garson function only works for a single layer network, and the variable importance measure is based on the weight value of this first layer network. However, the Oden function uses the weight values from all hidden layers of the network. Because of this difference in measuring variable importance, we do not expect similar results from these two methods. This is why we observe the different results. Since the Oden function is applied to the multiple layers network and the model performs better than a single layer network, we believe that the results are considered more credible than the results of the Garson function.
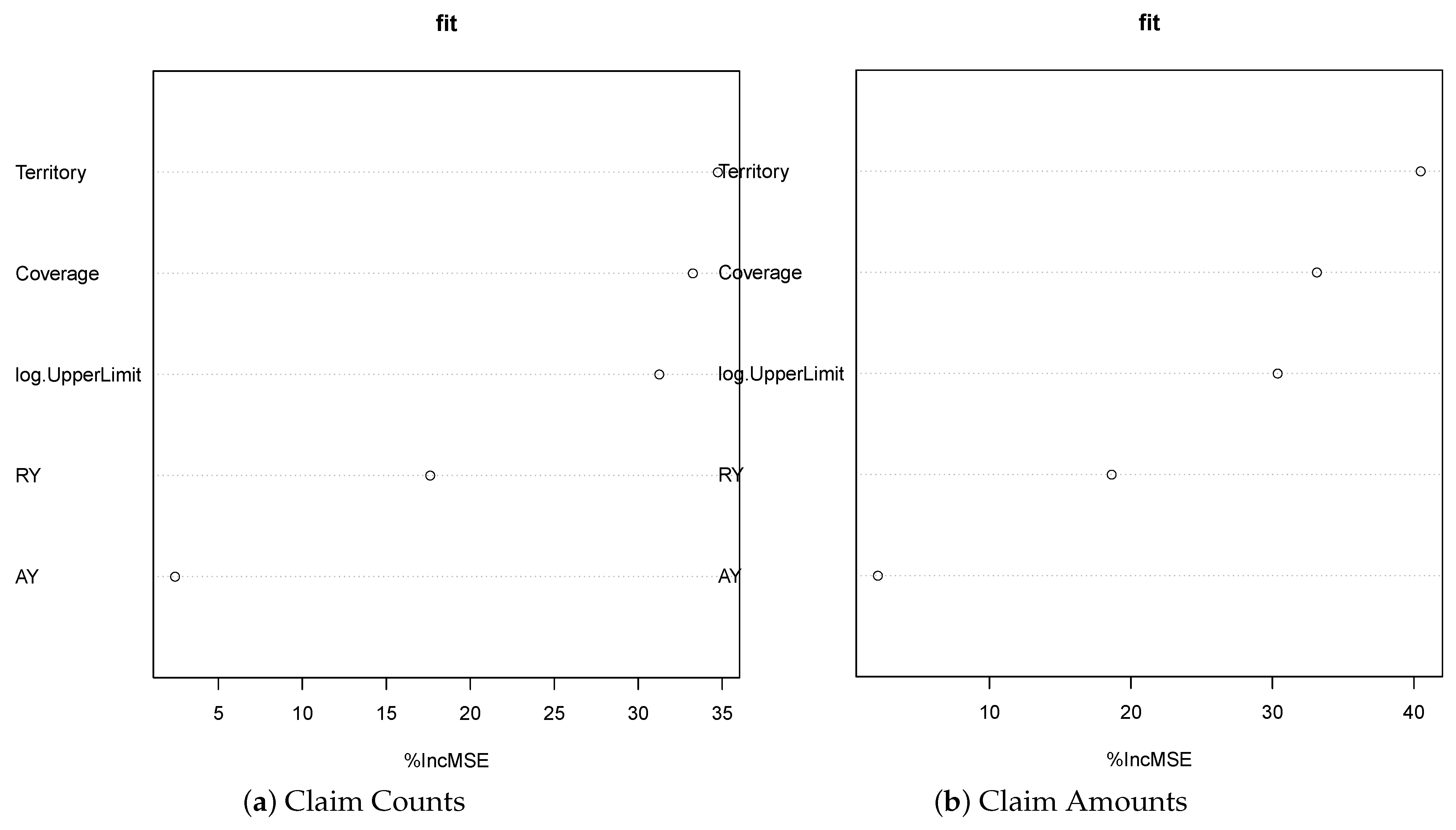
In this work, we compare the Garson function results to the feature importance measures obtained using the random forest model to train a model, which is displayed in
Figure 7. We observe that these two approaches behave similarly in identifying the importance of the input variables. Still, the results corresponding to the Garson function are more distinguished. The Garson function suggests that log.UpperLimit variable is the most influential, while the Territory variable is the most important feature by the feature importance method. Since Garson’s variable importance measures are more distinguishable, we conclude that the Garson function results are more appealing than the feature importance measures. We also present the partial dependence plots for both AY and log.UpperLimit as an example, which is displayed in
Figure 8. These partial dependence plots were obtained using the random forest method to train a model for making predictions of claim amounts. We observe that the predicted values of claim amounts are quite sensitive to these two variables. Within our approaches, the variable importance for log.UpperLimit is picked up well by the Garson method, while the importance of the AY variable was achieved by using the Olden function for the multiple-layer ANN model.
To better understand how the variable importance measures are affected by different ANN models, we estimate the sample means of variable importance and sampling errors. The results are displayed in
Table 2,
Table 3 and
Table 4, and they were calculated using the normalized Olden function. Different models lead to different estimates of the variable importance. The experimental results shown in all these tables may suggest the difficulty of interpreting the results when different models are considered. Therefore, it is critical to identify a most reliable model and make inferences by conditioning on the assumption that the selected model is the true model. With this in mind, we compare the variable importance measures for major risk factors under the best ANN architecture, and these results are presented in
Table 5. Overall, the variable importance measures all appear to be large and not very different, except for the case of the claim count as the input, in which the importance measure of AY is smaller than other variables.
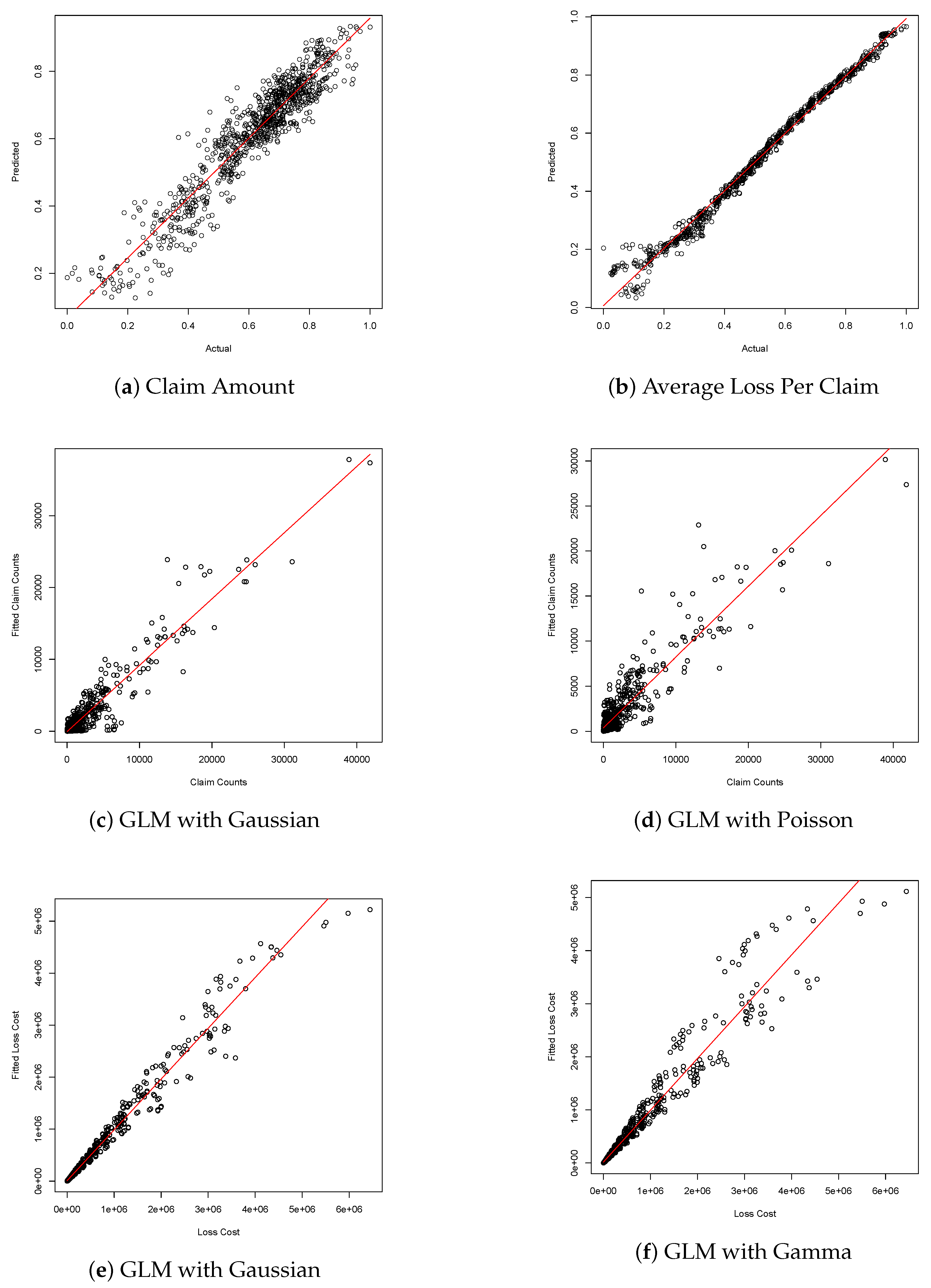
Finally, to see the performance of the model that we chose, we display the plots of predicted values versus actual output values in
Figure 9, for both cases of the claim amount and average loss per claim as response variables. From the result, we can see that the ANN-c(4) with the average loss per claim count outperforms the ANN-c(4) with the claim amount. This result was also compared to GLM results, where the selected one are reported in
Figure 9, and we found that ANN-c(4) outperforms the GLM.
5. Discussion
In the context of interpretable machine learning, interpretable models have been widely used. In actuarial science, linear models (LM), GLM, and GAM are popular modelling tools in auto insurance pricing to obtain risk relativities (
Ohlsson and Johansson 2010;
Xie and Lawniczak 2018). A linear model is a suitable choice when variables appear to be linearly related to the model response variable; it does not work well for the situation where interaction among variables or non-linear relationships are found. GLM overcomes the limitation of multiple linear regression models, where the normality and constant variance are often assumed. By extending the error probability distribution from a normal distribution to an exponential family (
Dobson and Barnett 2008), GLM enables a line of choices for the error distribution. It also allows one to specify the functionality between the variance of the response variable and the mean response so that the model can capture the extra dispersion caused by the data. However, in the context of measuring the importance of risk factors, GLM has certain limitations. In auto insurance rate-making, many independent variables or risk factors are categorical types. The independent variables within the GLM are designed as dummy variables based on the levels of categorical variables. Measuring the importance of the variable within GLM can be done easily for each factor level but not for the whole factor itself. The model captures the contribution of different combinations of the levels among the factors considered. Unlike ANN, the input variables are the factors with various levels, and the weight values are obtained for each input variable. It is possible to derive the variable importance for a numeric variable in GLM by calculating the
t-test statistics for the coefficients or obtaining the
p-value of the statistical test. When the GLM contains categorical variables, an F-test may be used to address the significance of the contribution of the variables, but it is difficult to measure the importance using the F-statistics. This is because the F test is quite sensitive to the violation of normality, which is often the case when dealing with loss distribution. Therefore, it requires further consideration of some suitable approaches to derive the importance measures of each underlying categorical variable when using GLM for pricing, but this is out of the scope of this paper. The use of ANN enables us to measure the variable importance directly, no matter the type of the input variables. It does not require the error distribution assumption or running statistical tests, which may be sensitive to the assumption on the sampling distribution. These are considered another advantage for ANN when comparing with other predictive modelling techniques. Furthermore, our empirical study shows that ANN outperforms the GLM when modelling the size of loss data. The mean square errors of the model residuals are much smaller than the GLM approach. The residuals of ANN model are much more homogeneous than the ones from GLM models. Evaluating ANN with the study of variable importance measure leads to a better understanding of risk factors’ effects to make more informed decisions in rate-making or rate regulation. When this is the case, insurance regulators are more comfortable in judging the appropriateness of risk relativity in rate fillings conducted by insurance companies.
According to the recent survey of Kagglers in terms of choice for machine learning tools, R has been a preferred tool for Business Analyst, Data Analyst, Data Miner, Predictive Modeller, and Statistician, who are often involved in insurance rate making. Due to this work’s nature, we adopt R and its package, called "neuralnet", to implement our study results. The main reason for making this choice is that it has been widely used for machine learning applications. It is an excellent tool for graphical representation of the model with the weights on each connection in neural network models, particularly for a small number of input variables, like in our case. This package uses backpropagation for parameter calibration and allows flexible settings through custom-choice of error and activation function.
6. Conclusions and Future Work
A single metric such as prediction accuracy is an incomplete description of most real-world tasks in predictive modelling. The need for model interpretability is due to incompleteness in a given problem formulation. It is not enough to get higher prediction accuracy; it is also necessary to know how the model accurately predicts. There is no explicit mathematical definition of model interpretability or data explainability. A non-mathematical description is of how much a model user can understand the cause of the decisions in the decision marking or how consistently a learned model can predict an accurate result. Our work belongs to the first type. It aims at providing some guidance on what advanced rate-making methodologies are suitable for facilitating the rate-filing review process. From the insurance regulator’s point of view, it is critical to know the insights of methods used for rate-making and the potential impact of risk factors and the mathematical model used to conduct the analysis. This makes the justification of any decision made more accessible and transparent to management responsible for a higher level of impact from regulatory policies, particularly the determination of reform and significant change of maximum coverage levels of insurance losses. On the other hand, the insurance loss data explainability improvement can help stakeholders better understand the nature of data patterns and the relationship between risk factors and the loss level metrics, such as loss counts, loss amounts, and loss costs. Therefore, decision-makers can make better policies or regulations that fit real-world situations, and communication between the insurance companies and regulatory authorities will become smoother and more effective.
In this work, the modelling problems of how claim counts, claim amounts, and average loss per claim are related to major risk factors in auto insurance rate regulation were considered. The major risk factors include accident year, reporting year, territory, coverage, and Size-of-Loss. Artificial neural network models were applied within the problem, and variable importance measures were introduced to improve the model explainability. The obtained results from different approaches of using weight values of ANN to measure the variable importance were compared, and the most dominant risk factors were identified. Through the study, we found that the variable importance measures by the Garson algorithm or Olden function can help identify the critical variables that contribute to explaining the variation of the response variable in ANN models. The obtained results were not necessarily consistent, since the variable importance measures make use of the different sources of information from the fitted model. However, our study shows that both Size-of-Loss and coverage are two crucial factors for claim counts, claim amounts, and average loss per claim. This finding is based on the selected low-complexity ANN model, in which the Garson algorithm is applicable.
Due to the complexity and lack of model explainability, neural network models have not yet been used in auto insurance rate regulation. This work illustrates the applicability of using a small-scale network architecture for modelling the claim frequency or claim severity by balancing the model complexity and its explainability. This work demonstrates the usefulness of proposed insurance rate regulation methods, particularly from the rate-filing perspectives. Although this study focuses on analyzing major risks only, the proposed method can be applied to more general insurance pricing problems. Therefore, insurance companies may use ANN models to predict future claim losses or future claim counts by pricing groups or individuals. That is to say, this work can be extended to the case when we have many observed zeroes in the response variable. However, in this case, the logarithm transformation on the loss cost to improve model variance homogeneity is not applicable. Another key aspect of using neural networks is the choice of network architecture. This is similar to other predictive modelling approaches, which aim for the optimal model via some cross-validation to evaluate the model error and select the suitable model based on the minimum cross-validated model error. Improving model explainability was our focus. Therefore, it is not recommended to apply a large-scale network architecture unless the model is interpretable. Our approach searches ofr the optimal network architecture within a designed search space, and this idea can be generalized to risk-factor study using individual claim loss. From this study, we have seen that the Size-of-Loss is a significant risk factor. In the future, further investigation of this factor may be needed to better understand the uncertainty behind the data observation and the relationship between Size-of-Loss and other statistical measures of loss, such as loss frequency. Our future work will focus on estimating Size-of-Loss probability distribution using multivariate statistical approaches such as functional principal component analysis and finite mixture models.