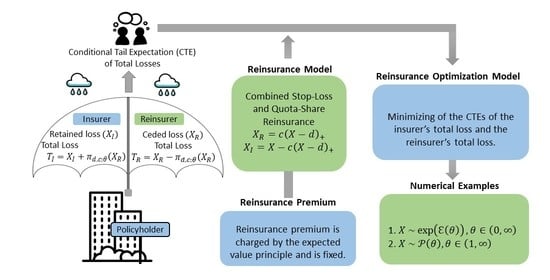
1. Introduction
Under a reinsurance contract, a loss faced by an insurer is partially ceded to a reinsurer. As a consequence, the insurer is liable for the remaining loss, called the retained loss, and a fixed reinsurance premium, which has to be paid to the reinsurer. Meanwhile, the liability of the reinsurer is the ceded loss subtracted by the reinsurance premium. However, as noted by
Cai and Tan (
2007), there is a classic trade-off between the retained loss and the ceded loss. When the loss ceded to the reinsurer is too large, the reinsurance premium charged will also be too high. On the other hand, reducing the reinsurance premium will make the insurer retain a potentially large loss. Accordingly, the insurer needs a reinsurance with optimal design.
Optimizing the reinsurance design from the perspective of the insurer has been carried out by many researchers using various approaches. For instance,
Gajek and Zagrodny (
2000) considered an optimization criterion of minimizing the variance of the loss retained by the insurer. Meanwhile,
Kaluszka (
2004) obtained optimal reinsurance arrangements through a mean-variance approach. More recently,
Cai and Tan (
2007) derived optimal retentions for a stop-loss reinsurance as the solutions to the minimization of value-at-risk (VaR) and conditional tail expectation (CTE) of the insurer’s total loss. As demonstrated by
Cai et al. (
2008) under these two risk measures, the optimal reinsurance can be in the form of stop-loss, quota-share, or their combination. The optimization on the former two reinsurance contacts was investigated further by
Tan et al. (
2009) who also employed the VaR- and CTE-based criteria. Several extensions of the stop-loss reinsurance, such as limited stop-loss and truncated stop-loss, were derived as the solutions to the optimization problem of
Chi and Tan (
2011) under the VaR and conditional VaR (CVaR) risk measures. In particular, optimal parameters for the limited stop-loss reinsurance were found by
Zhou et al. (
2015). Meanwhile,
Zhou et al. (
2011) and
Putri et al. (
2021) investigated the optimality of the combination of quota-share and stop-loss reinsurance. The other studies on the reinsurance optimization from the insurer’s viewpoint under the above risk measures may be found in
Lu et al. (
2014),
Lu et al. (
2016),
Du et al. (
2019), and
Hu et al. (
2021). In contrast, optimizing the reinsurance treaty from the perspective of a reinsurer was undertaken by
Tan et al. (
2020). Specifically, they minimized the VaR and the CTE of the reinsurer’s total loss.
An optimal form of reinsurance from the insurer’s perspective, however, may not meet the reinsurer’s goal, and vice versa. In order to derive the optimal reinsurance accepted by both the insurer and the reinsurer, another approach is required to optimize an objective function constructed from their joint perspective. For instance, a criterion of maximizing the joint survival probability and the joint profitable probability from the perspective of both the insurer and the reinsurer was proposed by
Cai et al. (
2013). Based on the results in
Cai et al. (
2013),
Fang and Qu (
2014) derived optimal retentions for a combination of quota-share and stop-loss reinsurance by maximizing the joint survival probability. In addition to employing the joint survival probability, other criteria were also taken into consideration by
Zhang et al. (
2018) to determine an optimal retention level of a quota-share reinsurance. Such optimization criteria include minimizing the total variance, the total VaR, and the total tail-VaR (TVaR) of the insurer’s loss and the reinsurer’s loss.
To ensure that reducing the loss from one party can not be carried out without increasing the loss from another party, a convex combination of the risk measures of the losses for both parties was recently utilized by several authors instead of just summing them. For instance,
Cai et al. (
2016) suggested an optimization criterion of minimizing a convex combination of VaRs of the insurer’s total loss and the reinsurer’s total loss. In particular,
Liu and Fang (
2018) implemented this approach on their study to obtain optimal parameters for the quota-share and stop-loss reinsurance designs. More recently, the above optimization criterion was also adopted by
Jiang et al. (
2017),
Fang et al. (
2019), and
Chen and Hu (
2020) by using the same VaR risk measure. They found that the combined stop-loss and quota-share reinsurance is one of the optimal solutions to their optimization problems.
In this paper, we aim to explore the combined stop-loss and quota-share reinsurance. We study, in
Section 2, the survival function of the loss ceded to the reinsurer and that of the loss retained by the insurer in the presence of this reinsurance contract. In
Section 3, we then optimize the combined stop-loss and quota-share reinsurance from the joint perspective of the insurer and the reinsurer by developing a new optimization criterion similar to
Jiang et al. (
2017),
Fang et al. (
2019), and
Chen and Hu (
2020). Instead of using the probability-based risk measure of VaR, an alternative risk measure of CTE is employed to overcome its weaknesses by taking into account the magnitude of the losses beyond the VaR (
Syuhada et al. 2021). Specifically, we derive explicit expressions of optimal retentions for the reinsurance we design by minimizing a convex combination of CTEs of the insurer’s total loss and the reinsurer’s total loss. An estimation for the resulting optimal retentions is also presented in
Section 4 with numerical examples when the initial loss faced by the insurer is assumed to follow an exponential or Pareto distribution.
Section 5 concludes our study.
2. Combined Stop-Loss and Quota-Share Reinsurance
Let
X be loss or risk transferred from an insured to an insurer. This loss may be an aggregate of individual losses that form an insurance portfolio. In this paper, the loss
X is assumed to be a non-negative random variable with survival function
determined by a parameter
, where
denotes a parameter space. We also assume that
is continuous and strictly decreasing on the interval
with a possible jump at
. Consequently, the inverse function
exists on the interval
. In addition, the expectation of
X,
, is assumed to be finite. Its value may be computed from the survival function
through integration, i.e.,
For illustration purposes throughout this paper, we follow a suggestion of
Burnecki et al. (
2021) assuming an exponentially distributed loss
with survival function
where
, which is equal to the reciprocal of its mean. As a comparison, we may also assume
X to follow a Pareto distribution,
, with a heavier tail. Its survival function is defined as follows:
Its parameter, , denoting the tail index belongs to . This consideration is to make sure that its mean, , exists.
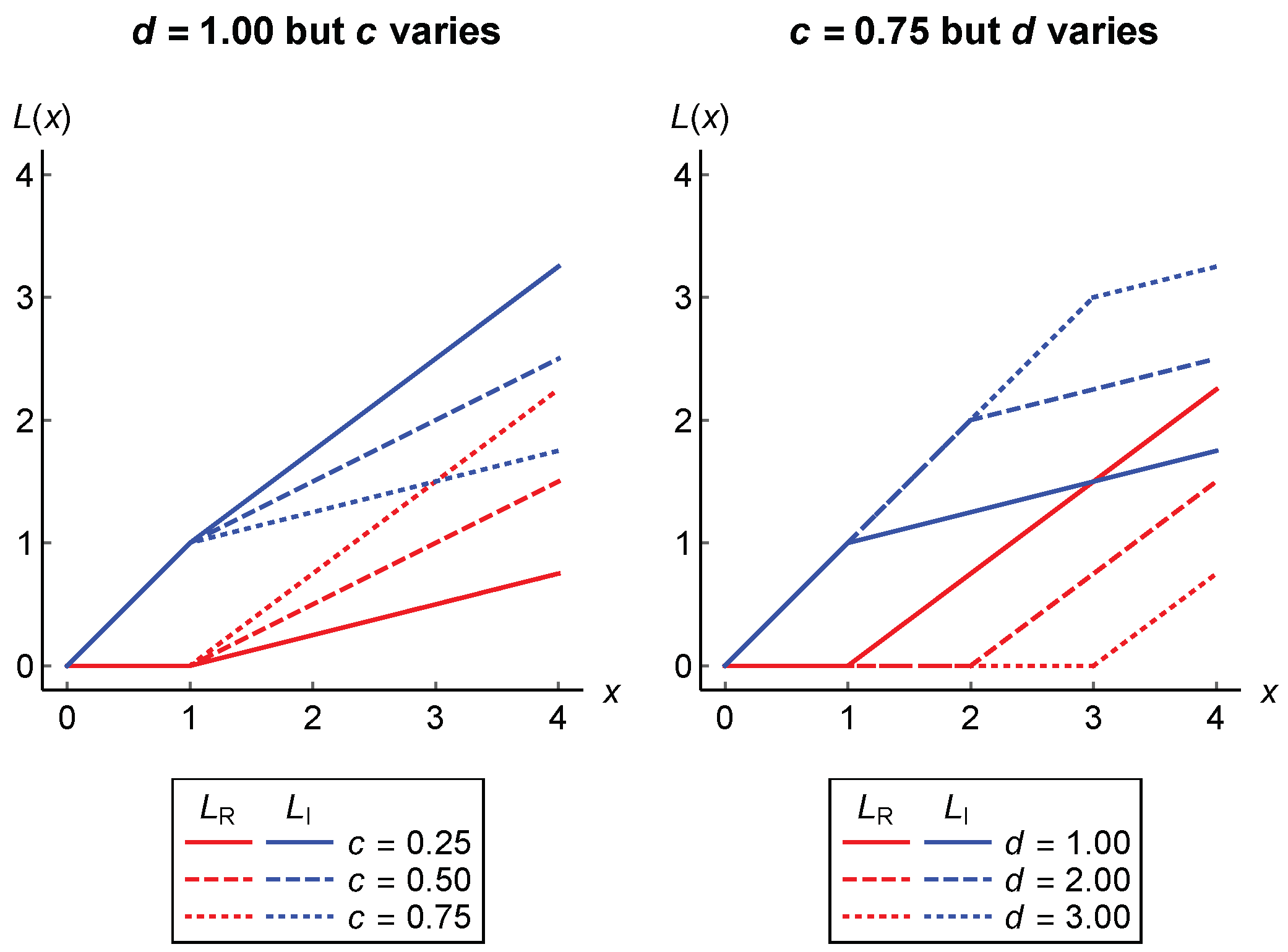
Under a reinsurance designed in a fixed time period, the insurer decides to reduce the loss X by ceding the part of X, say for a function satisfying , for all , to a reinsurer. Meanwhile, the remaining loss of size , where with , for all , is retained by the insurer. In other words, in the presence of reinsurance contract, the initial loss X is split into two parts such that . We then use the notations and to denote those parts. We call them ceded loss and retained loss, respectively, whilst the functions and are usually known as ceded loss function and retained loss function, respectively.
When a quota-share reinsurance is designed, the insurer cedes a level
c of the initial loss
X, i.e.,
, to the reinsurer. This means that both the insurer and the reinsurer are involved in facing the loss with unlimited liability (
Gray and Pitts 2012). However, the insurer may need to be protected from the potential large loss by retaining the loss up to a limit
d only. An excess of size
is covered by the reinsurer, where
. This goal may be achieved by designing a stop-loss reinsurance. See
Tan et al. (
2009) and
Liu and Fang (
2018) for a more detailed study on those reinsurance contracts.
In this paper, we consider combining the above two reinsurance contracts by firstly setting a retention limit
d and, then, affixing a retention level
c such that the loss ceded to the reinsurer is given by
The above ceded loss may also be expressed in the form of
, where
is an indicator function of a set
A. Consequently, the insurer is liable for the retained loss of size
where
means
. We call this design a combined stop-loss and quota-share reinsurance. Under this combination, it is obvious that both the ceded loss function
and the retained loss function
are increasing with respect to
x on
. See
Figure 1 to investigate their curves.
We see that the pure stop-loss reinsurance is a special case of the above contract for . Meanwhile, if the retention limit d is set to be zero, we then have the pure quota-share reinsurance. However, when the value of c is equal to zero, there is no reinsurance and, as a result, the insurer is liable for all the losses. We, in this paper, assume in order to ensure that the insurer truly shares a portion of loss to the reinsurer, instead of retaining all the losses. The notation for a pair of d and c is considered to remind us that d is the first retention affixed in designing the combined stop-loss and quota-share reinsurance.
Since the ceded loss
and the retained loss
are the functions of
X, their distribution may be determined based on the distribution of
X. By employing a simple technique, from Equation (
3), the survival function of the ceded loss
may be derived as follows:
Meanwhile, according to Equation (
4), the survival function of
is given by
It is obvious that the survival function
is always discontinuous at
whilst the discontinuity of
at
occurs when the survival function of the initial loss
X is discontinuous at this point. In
Figure 2, we present their curves for the cases of exponential and Pareto random losses with equal mean, i.e., 1. Their comparison to the curves of the survival functions under the pure stop-loss and pure quota-share reinsurance is also illustrated in this figure.
3. Reinsurance Optimization under CTE Risk Measure
As stated before, in the presence of the (combined stop-loss and quota-share) reinsurance contract, the insurer cedes the part of the loss to the reinsurer. As a consequence, the reinsurance premium of size
has to be paid by the insurer to the reinsurer. The insurer is thus liable for the total loss
defined as the sum of the retained loss
and the reinsurance premium
, i.e.,
whilst the total loss
of the reinsurer is given by
In this paper, the reinsurance premium charged by the reinsurer is assumed to be determined by the expected value principle, that is
, where
is a fixed safety loading factor. Note that the expected value of the ceded loss
may be represented by
, where
therefore the above reinsurance premium may be expressed as below:
3.1. CTE of Total Losses
When a reinsurance is agreed between the insurer and the reinsurer, the insurer’s objective is actually to manage its risk. In addition to making a profit, the reinsurer also aims to control its own risk ceded from the insurer. A so-called value-at-risk (VaR), widely used in quantitative risk management, may be taken into consideration to measure the potential magnitude of such risks. Basically, VaR is a single value denoting the maximum loss that is likely to occur at a specified
level of significance. For the initial loss
X, the VaR is formally defined by
for all
, which means that the VaR is the
-quantile of the distribution of
X. As stated in
Section 2, the survival function
is assumed to be continuous and strictly decreasing on the interval
. This assumption implies that the inverse function of
exists on this interval and, as a result, we obtain
for all
. Meanwhile, the trivial case, that is
, occurs for each
belonging to
. It is easy to verify that
is strictly decreasing with respect to
on
, which means that, for all
, we have
In fact, the VaR depends only on the probability of the occurrence of the losses and provides no information about the magnitude of the losses that exceed it and may have severe impact (
Syuhada et al. 2021). Alternatively, conditional tail expectation (CTE) may be required to correct for these weaknesses. At the
level of significance, the CTE of the loss
X is defined as the conditional expectation of
X, given all its values exceeding the corresponding VaR, that is
This indicates that the CTE is more appropriate than the VaR since it takes into account the magnitude of losses beyond the VaR. Furthermore, the more important advantage of the CTE over the VaR is that the CTE is coherent under suitable conditions whilst the VaR is not since it fails to satisfy the axiom of subadditivity. Note that the CTE and the VaR are related as below:
Since is strictly decreasing with respect to on , also does.
We assume that the reinsurer and the insurer use the CTE to measure their own losses, instead of considering the VaR. Hence, our concern is now to implement the CTE to the reinsurer’s total loss and the insurer’s total loss. By
and
we denote the CTEs of the total losses
and
at possibly different levels of significance
and
, respectively. From Equations (
7)–(
9), we employ the translational invariance property to derive preliminary expressions of such CTEs as follows:
and
We have noted, in
Section 2, that the survival function
always has a jump, from the point
to the point
, whilst the jump of the survival function
possibly occurs from
to
. These facts imply that the VaR of the ceded loss
is equal to zero at the significance level of
and
for all
.
To avoid the above trivial cases, the significance levels used by the reinsurer and the insurer are assumed to be
and the retention limit is then assumed to satisfy
. We completely consider the pair of retentions
belonging to a set
. By combining Equations (
3), (
4), (
11)–(
13), and by employing the axioms of coherence of risk measures, we derive under the above assumptions the explicit expressions of both
and
summarized in the following proposition.
Proposition 1. For given levels of significance , we haveand Proof. It is known that
, for
. Hence, when
, it is obvious that
and the event
occurs if and only if the event
occurs. By using the axioms of coherence, we therefore obtain
According to Equation (
12), the result given in Equation (
14) is then derived by subtracting the above result by the reinsurance premium.
At the significance level of
, its VaR may be expressed as below:
When
, the event
occurs if and only if the event
occurs. We then employ the axioms of coherence to compute the CTE of
as follows:
Meanwhile, for
, the event
occurs if and only if the event
or
occurs. Consequently,
By combining the above results, we may express
Based on Equation (
13), the CTE of
given in Equation (
15) is derived when
is added by the reinsurance premium. □
For the initial loss
with survival function given in Equation (
1), it is easy to obtain
,
, and
. Accordingly, both the CTEs of the reinsurer’s total loss and the insurer’s total loss are given by
On the other hand, if
with survival function provided in Equation (
2), we have
,
, and
. As a result, the reinsurer’s total loss and the insurer’s total loss have the following CTEs:
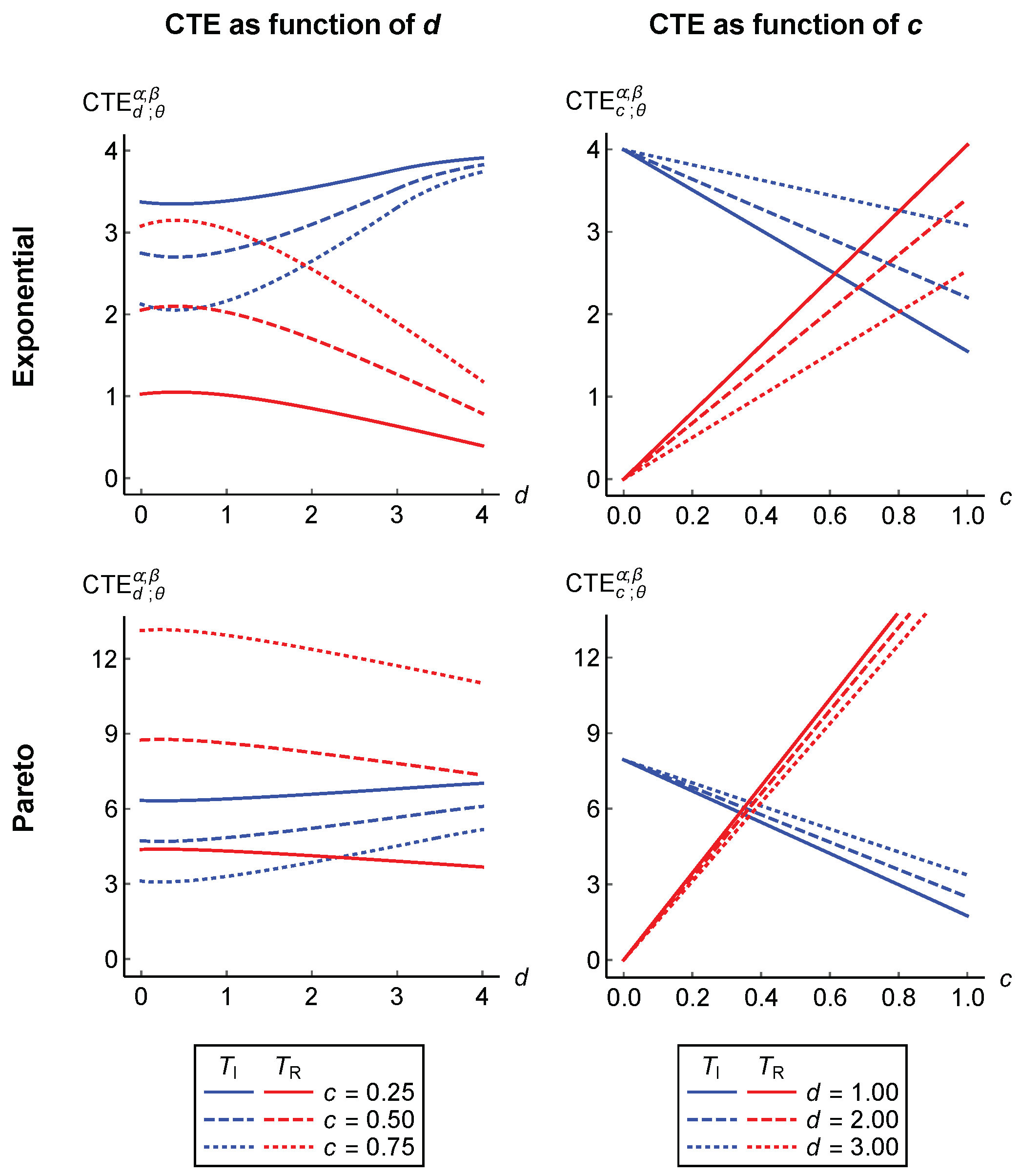
The influence of the retention limit
d and the retention level
c on the values of the above CTEs is depicted in
Figure 3. It may be observed that as the value of
d increases, the value of
initially decreases and, then, increases after attaining its minimum. Meanwhile, the increase of
initially occurs and is then followed by the decrease after reaching a peak. Furthermore, as the value of
c increases, the value of
decreases linearly whilst the value of
increases linearly. This illustration indicates that
is shown to be inversely proportional to
, which means that the CTE of the total loss for one party decreases as the CTE of the total loss for another party increases. This relationship may noticeably be observed from the other visualizations provided in
Figure 4 and
Figure 5.
3.2. Optimization from Joint Perspective of Insurer and Reinsurer
We have assumed that the CTE is utilized by both the insurer and the reinsurer to measure their own total losses. From the perspective of the insurer, the insurer desires to buy the combined stop-loss and quota-share reinsurance whose parameters denoting retentions are solutions to the optimization problem
Meanwhile, from the reinsurer’s viewpoint, the reinsurer prefers to offer the combined stop-loss and quota-share reinsurance whose retentions are solutions to the optimization problem
However, the optimal retentions of the combined stop-loss and quota-share reinsurance for one party are different from those for another party and is not optimal from its perspective. We, therefore, do not consider finding the minimizers of the CTEs of the insurer’s total loss and the reinsurer’s total loss by solving Problems (
16) and (
17) separately. Since the increase of the total loss faced by one party causes the decrease of the total loss covered by another party, we, in this paper, aim at carrying out the following optimization problem:
where
for a specified weighting factor
. Minimizing such a convex combination of
and
considered as the objective function is expected to produce optimal retentions that are acceptable to both parties. Note that when
is set to be one, we actually do the optimization from the point of view of the insurer. Meanwhile, the optimization from the reinsurer’s perspective is for
. This means that Problems (
16) and (
17) are special cases of Problem (
18).
For simplicity, we introduce the following additional notations:
By substituting the CTEs of the total losses for both the insurer and the reinsurer, given in Equations (
14) and (
15), to Equation (
19), we may formulate the objective function in terms of the above notations as follows:
The pair of optimal retentions
is summarized in the following theorems whose proofs are explained in
Appendix A. Since the value of
d depends on both
and
, and hence on both the significance levels of
and
, the theorems are provided separately under the condition (1)
or (2)
.
Theorem 1. Under the condition , the optimal retentions as the solutions to Problem (18) are derived for with the following values: - 1.
when and ;
- 2.
for any constant when and ;
- 3.
when and ;
- 4.
for any constant when and .
Theorem 2. Under the condition , the optimal retentions as the solutions to Problem (18) are derived for with the following values: - 1.
when , , and ;
- 2.
for any constant when , , and ;
- 3.
when and ;
- 4.
for any constant when and .
Theorems 1 and 2 above tell us important results of optimizing the combined stop-loss and quota-share reinsurance as follows. First, when the loading factor is chosen such that the value of is higher than the significance levels used by both the insurer and the reinsurer, the optimal retention limit may be found to be equal to the VaR of the initial loss at the probability level of . The value of this optimal retention limit is lower than both and . Meanwhile, if is too small and, as a result, is too large, then we may set the VaR of X at the level as the optimal retention limit. This is because the possible value of d is bounded above by this VaR. The optimality of the retention limit is achieved when the other criteria involving the weighting factor and the parameter of the distribution of X are satisfied.
Second, the optimal retention level is determined based on the condition whether the values of and evaluated at the retention limit are equal. If the former is lower than the latter, we obtain , which means that the objective function employed in the optimization problem attains its minimum at the unique point . Meanwhile, the equality makes the minimum value of attained at each point . This situation allows us to choose any number in as the optimal retention level .
In
Figure 6 and
Figure 7, we illustrate the surfaces of
when the initial loss
X is assumed to follow an exponential distribution
and a Pareto distribution
, respectively. Such surfaces are provided according to the results in Parts 3 and 4 of Theorem 1 and Parts 1 and 2 of Theorem 2. These illustrations are respectively denoted into four cases as follows.
Case A: where is uniquely minimized (see row 1 and column 1).
Case B: where is non-uniquely minimized (see row 1 and column 2).
Case C: where is uniquely minimized (see row 2 and column 1).
Case D: where is non-uniquely minimized (see row 2 and column 2).
When
, the pair of optimal retentions for the combined stop-loss and quota-share reinsurance are given by
Meanwhile, below we express the pair of optimal retentions when
X follows
:
4. Estimation for Optimal Retentions with Numerical Examples
We see that the optimal retentions
and
for the combined stop-loss and quota-share reinsurance, which have been derived in
Section 3, depend on an unknown parameter,
, of the loss distribution and may be viewed as functions of
. Their explicit expressions have been found when, for instance, the loss
X is assumed to follow an exponential distribution
,
, or a Pareto distribution
,
. In this section, we now consider finding the estimate for
,
. When the parameter
in the optimal retentions
and
is replaced by
, we then obtain a pair
of the estimated optimal retentions.
Suppose that
is a sample of size
n randomly drawn from
X. From this random sample, the estimate
may be found by employing the well-known maximum likelihood method. If
denote the realizations of
, respectively, such
is a solution to the optimization problem
where
is the log-likelihood function evaluated at
. Such an objective function is given by
, where
is the probability function of
X.
When the random sample is drawn from the exponential distribution
, a statistic
may be found to be an estimate for
, where
is the mean of the random sample. By substituting such
to the optimal retentions given in Equation (
20), we derive their estimate as follows:
where
represents
or
, whilst
is a constant in
. By taking their expected value, we find that
and
. This shows that when the initial loss is exponentially distributed, the pair
is an unbiased estimate for the pair
of the optimal retentions for the combined stop-loss and quota-share reinsurance.
On the other hand, if the random sample from
is taken into consideration, we derive the following statistic for estimating
:
Consequently, based on Equation (
21), the estimate for the retention limit is given by
where
, whilst
is a constant in
. It is easy to verify that
, for all
, and, hence, the statistic
has a gamma distribution
with probability function
,
. As a result,
whilst
that differs from
, for all
. If its limit is taken as
, we then obtain
This indicates that the pair is a biased estimate for the pair if the initial loss follows the Pareto distribution. However, such an estimate is expected to be close to the actual value of the optimal retention when the sample size n is large enough.
To investigate the impact of the sample size
n on the estimated parameter
as well as on the pair
of the estimated optimal retentions and the corresponding value of the objective function minimized at such
, we provide numerical examples. Specifically, we conducted numerical simulations for various values of
and
n through a Monte Carlo approach with
runs. The accuracy of those estimates is assessed by using root-mean-square error (RMSE) defined by
where
denotes an actual value of the parameter
, the optimal retention, or the minimized objective function whilst
is its estimate computed at the
jth run, for all
.
The results of the numerical simulations are provided in
Table 1 with four panels based on four cases (A, B, C, and D) stated at the end of
Section 3. Each row at each panel compares the exponential and Pareto random losses with equal mean. We find that as the sample size increases, the estimates for the parameter, the optimal retention, and the minimized objective function tend to be more accurate with small RMSE. When the actual parameter decreases indicating that the mean of the initial loss increases, the RMSE of the parameter estimate decreases. However, the accuracy of the estimates for the optimal retention and the minimized objective function appears to decrease due to the increase of their RMSE. Furthermore, the Pareto distribution produces less accurate estimates than the exponential loss. This is in line with the theoretical explanation discussed above. The accuracy is extremely poor when the actual parameter of the Pareto distribution is close to 1. This is because its tail is heavier with evidence of having extreme simulated losses.
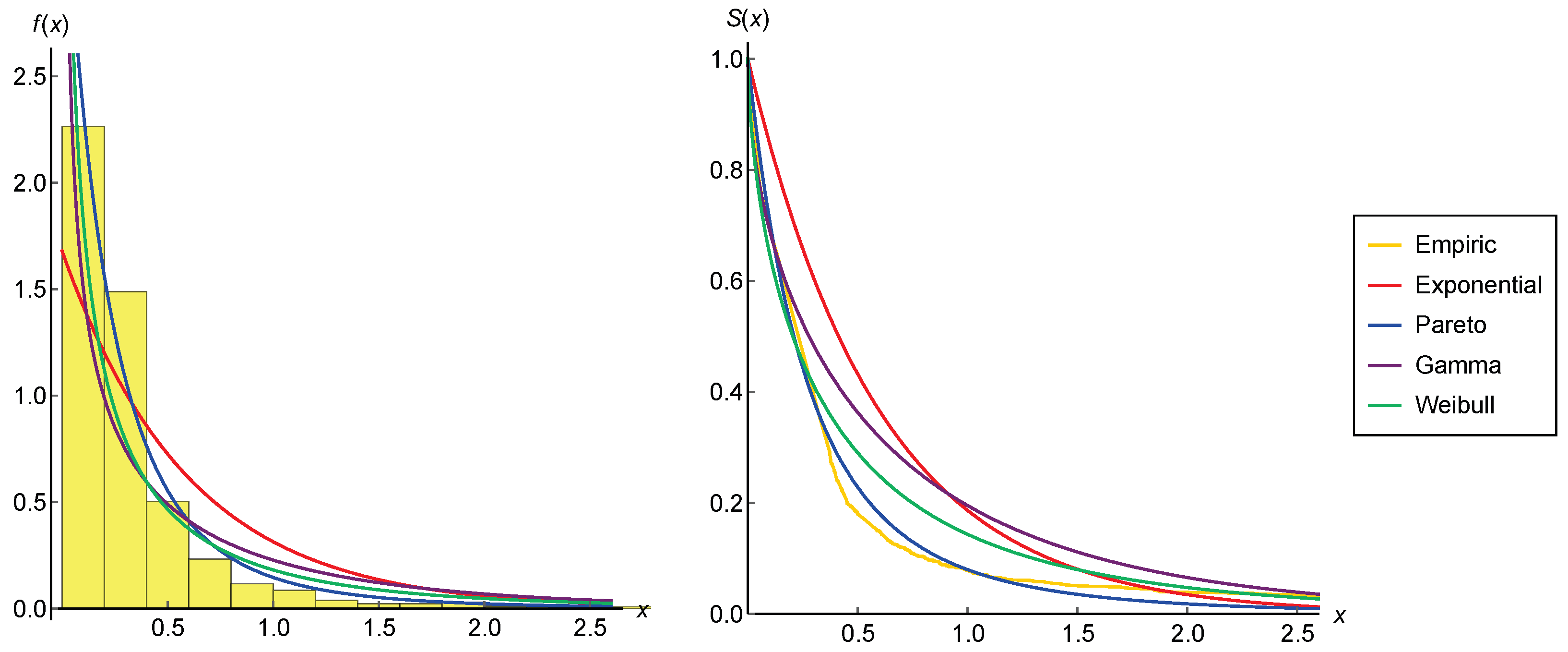
To illustrate a more complete overview of our theoretical findings, we employ a real data set consisting of total economic losses or claims (in ten thousand dollars) from
claimants. Such claims arise from automobile bodily injury insurance coverages; see
Frees (
2010). Statistics, including four (central) moments of these empirical data, are given in
Table 2. An extremely high empirical kurtosis, that is found to be equal to 794.67, leads us to employ a heavy-tailed loss model for such data. In addition to the exponential and Pareto distributions, we also consider the gamma and Weibull distributions in our modeling.
Table 2 compares the values of their maximized log-likelihood function
and Akaike information criterion (AIC) defined by
, where
k is the dimension of their parameter space. From the comparison of their goodness-of-fit, the Pareto distribution seems to fit well to the empirical data with the highest log-likelihood function and the lowest AIC value. The value of its estimated parameter (about 3.65) indicates the existence of its moments up to an order of 3. The goodness of the Pareto distribution in fitting the empirical distribution of the data may also be observed in
Figure 8.
According to the estimated Pareto distribution for the claim data, we compute the estimates for the optimal retention limit and the objective function denoting the convex combination of the CTEs when the combined stop-loss and quota-share reinsurance is agreed between an insurer and a reinsurer. The estimation is carried out when the loading factor
varies and when the weighting factor
ranges on
. The results presented in
Figure 9 show that, for a fixed
, the larger the loading factor, the higher the estimated optimal retention limit. This is because the reinsurance premium paid to the reinsurer increases. This increase is followed by the increase of the minimized convex combination of the CTEs of the total losses for both parties. However, the increase of the optimal retention limit is not affected by the weighting factor. The weight is found to give an impact on its existence only. On the other hand, the minimized objective function appears to vary as the weight used varies.
5. Conclusions
This paper discusses the combined stop-loss and quota-share reinsurance designed by firstly setting a retention limit and, then, affixing a retention level. For various values of these retentions, the survival functions of the loss retained by the insurer and the loss covered by the reinsurer are investigated. We further apply the risk measure of CTE to quantify the total loss of each party after a fixed reinsurance premium formulated by the expected value principle is included. It is found that the CTE of one party’s total loss decreases as the CTE of another party’s total loss increases, and vice versa. We, therefore, develop a convex combination of these CTEs, at possibly different significance levels, as an objective function in the optimization framework. The retentions that are optimal from both the insurer’s and the reinsurer’s perspectives are shown to have explicit expressions under several optimality criteria depending on the loading factor, the significance levels, the weight, and the parameter of the initial loss distribution. These theoretical findings are then supported by an estimation with numerical examples which shows that the larger the mean of the initial loss, the poorer the accuracy of the estimated optimal retentions. The loading and weighting factors play vital roles in determining the existence of these optimal retentions. In addition, the loading factor also affects their magnitude.
For further research, the reinsurance optimization may be studied under general model settings by taking several constraints into account as in the works of
Cai et al. (
2017) and
Chen (
2021). Furthermore, we may also use a more general risk measure, such as a distortion risk measure, to quantify the total loss covered by each party; see, e.g.,
Lo (
2017),
Jiang et al. (
2018),
Lo and Tang (
2019), and
Jiang et al. (
2021).